Li-Ion Battery-Flywheel Hybrid Storage System: Countering Battery Aging During a Grid Frequency Regulation Service
Abstract
1. Introduction
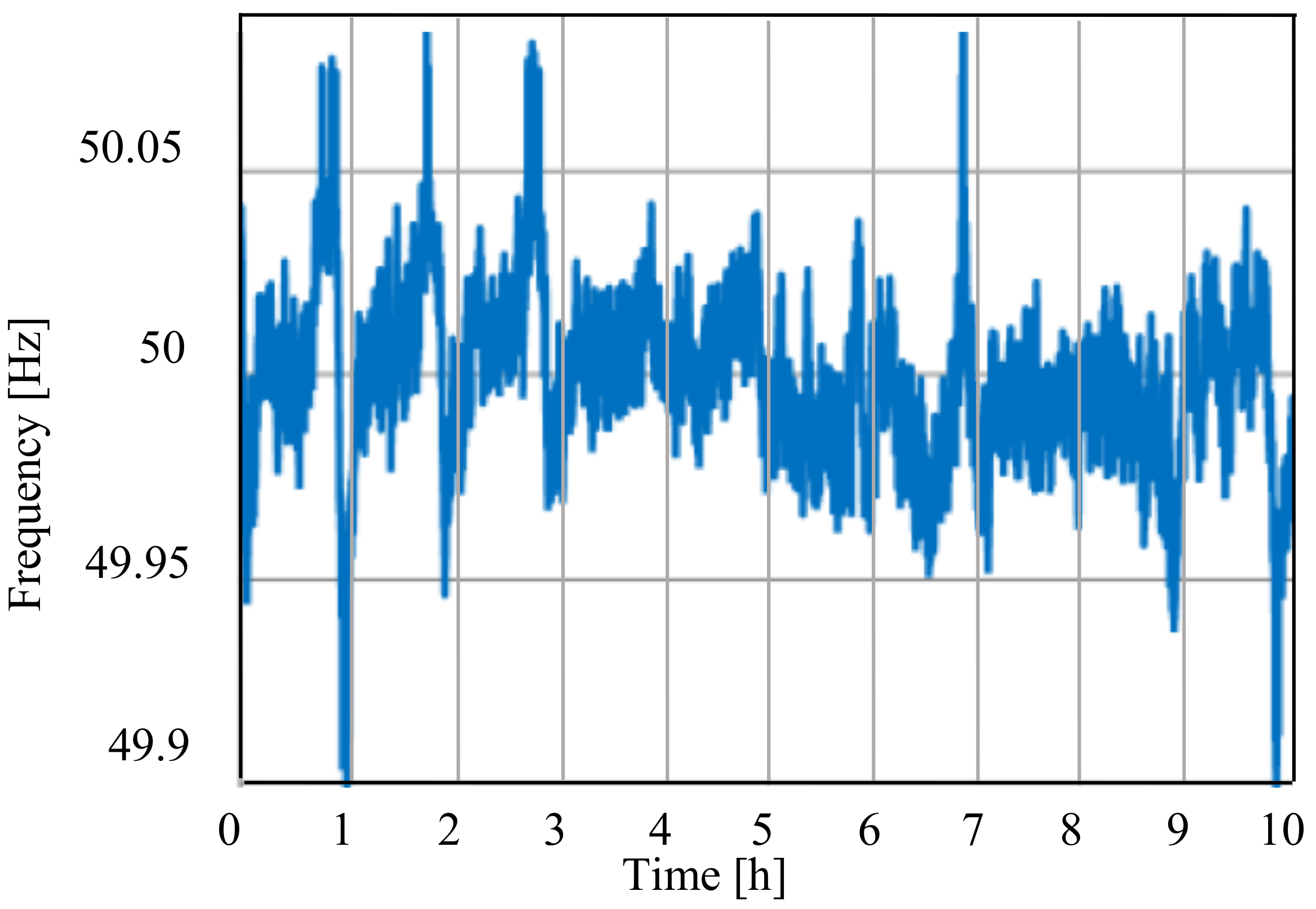
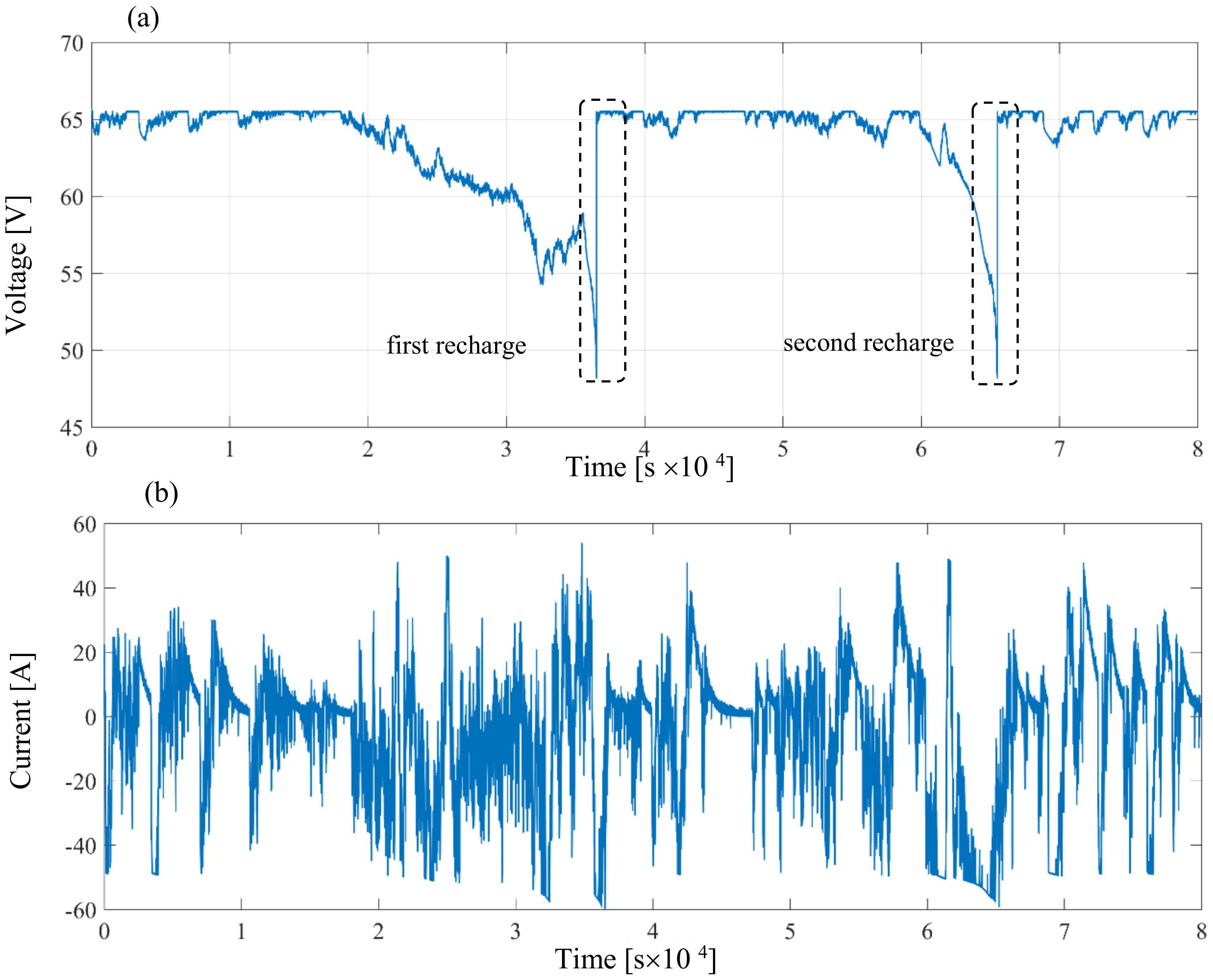
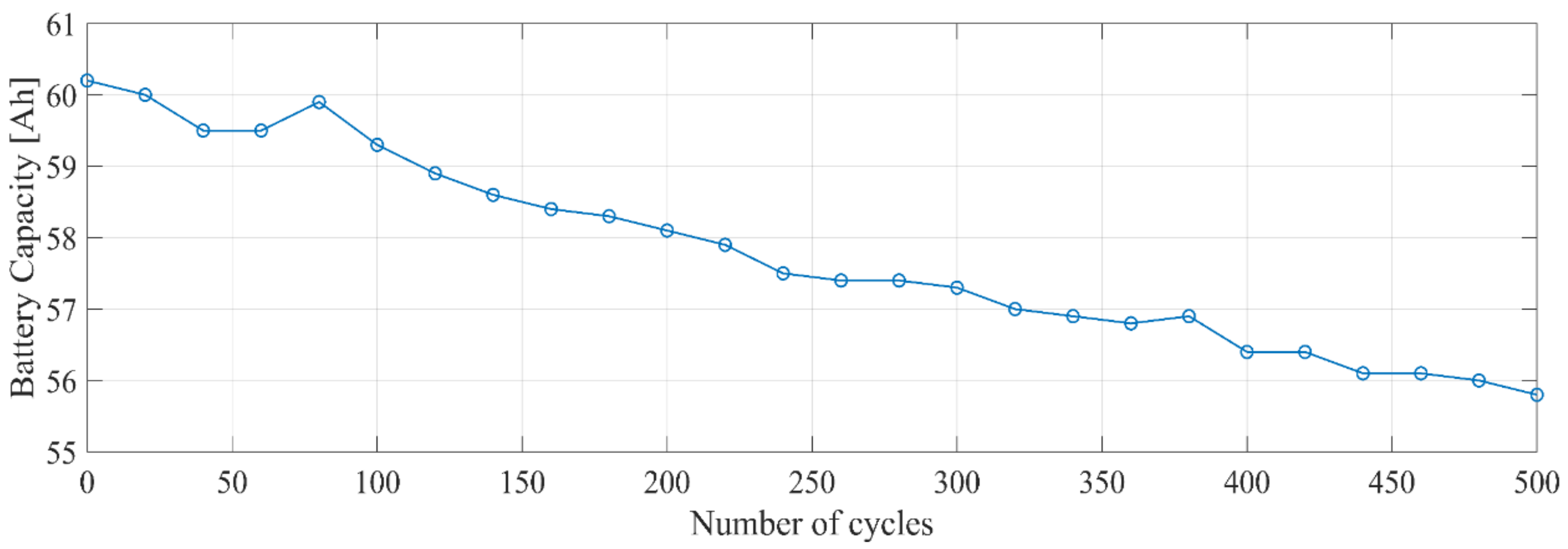
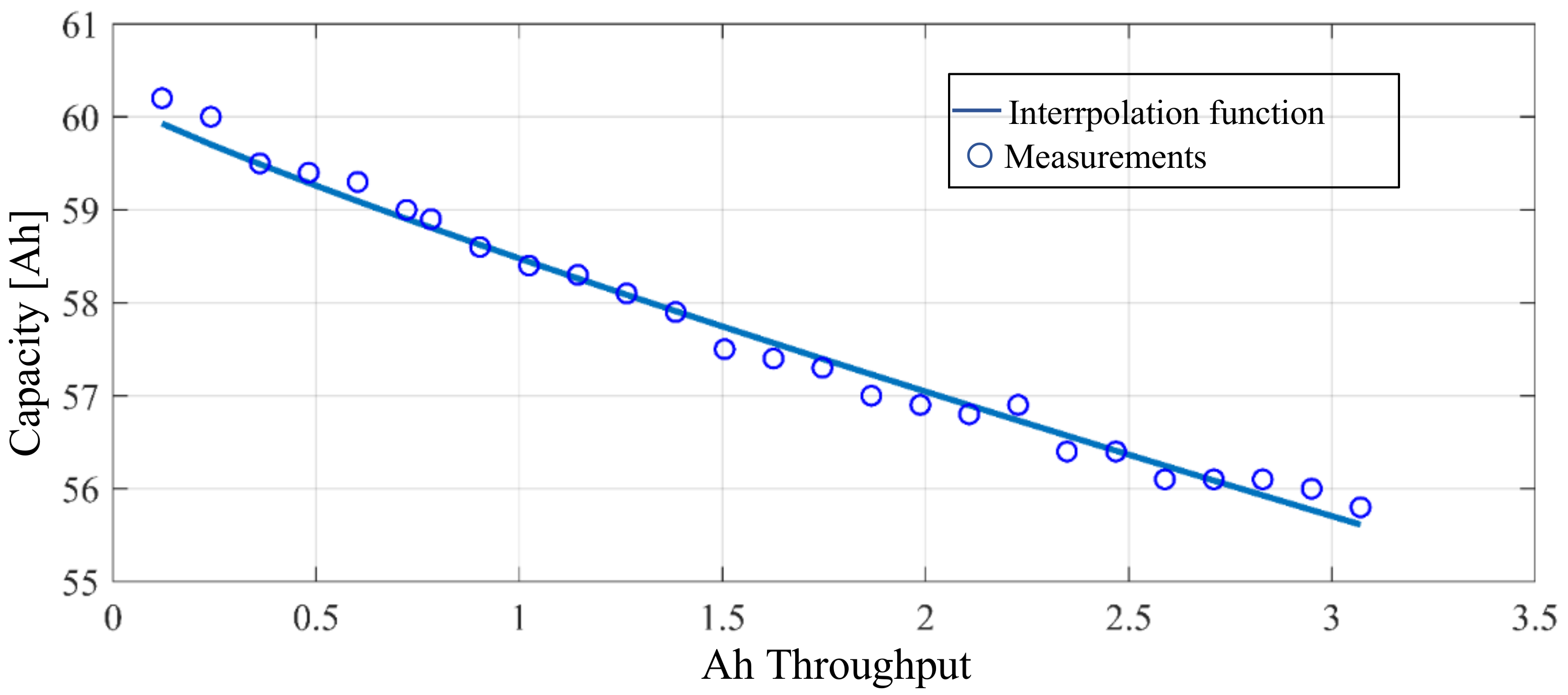
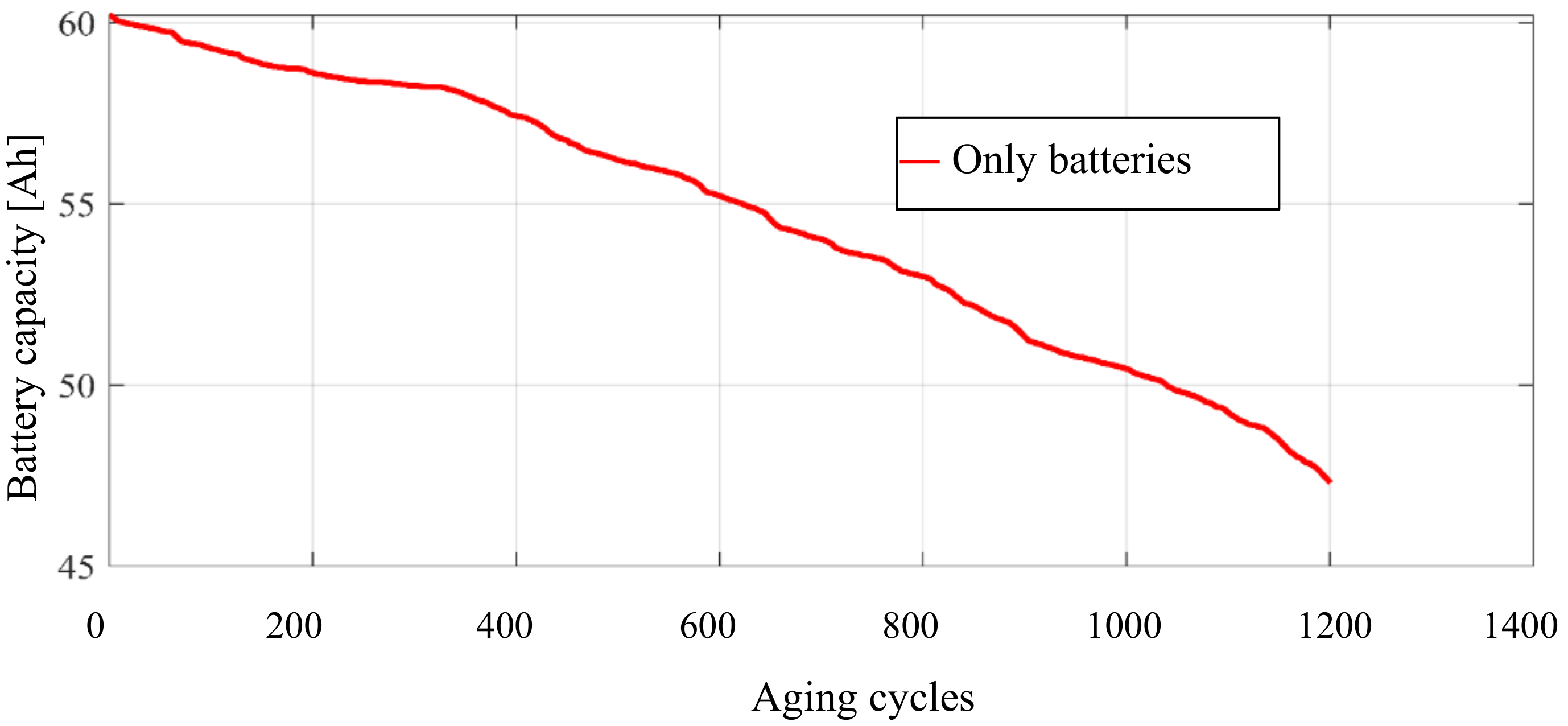
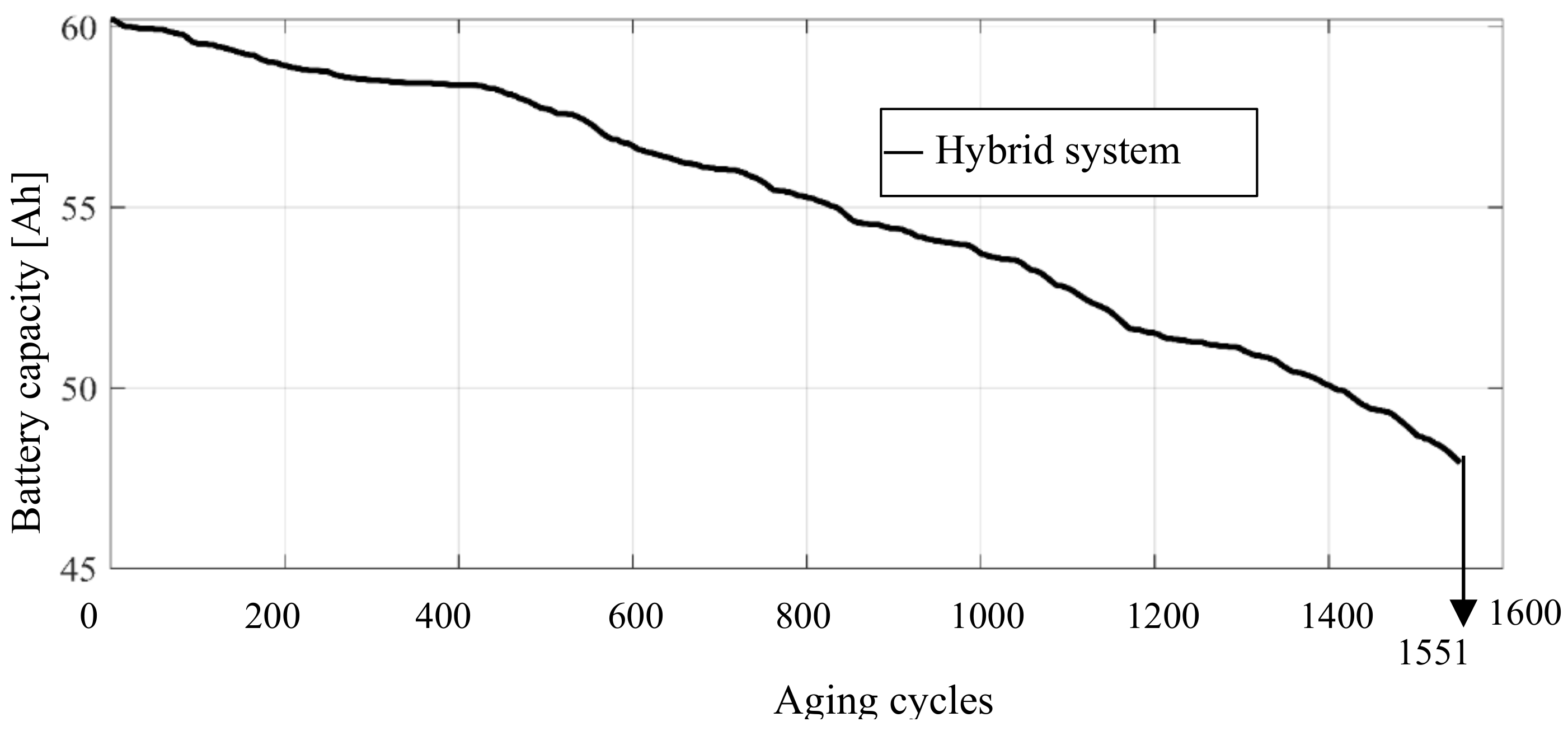
2. Battery Aging Following Frequency Regulation Cycles
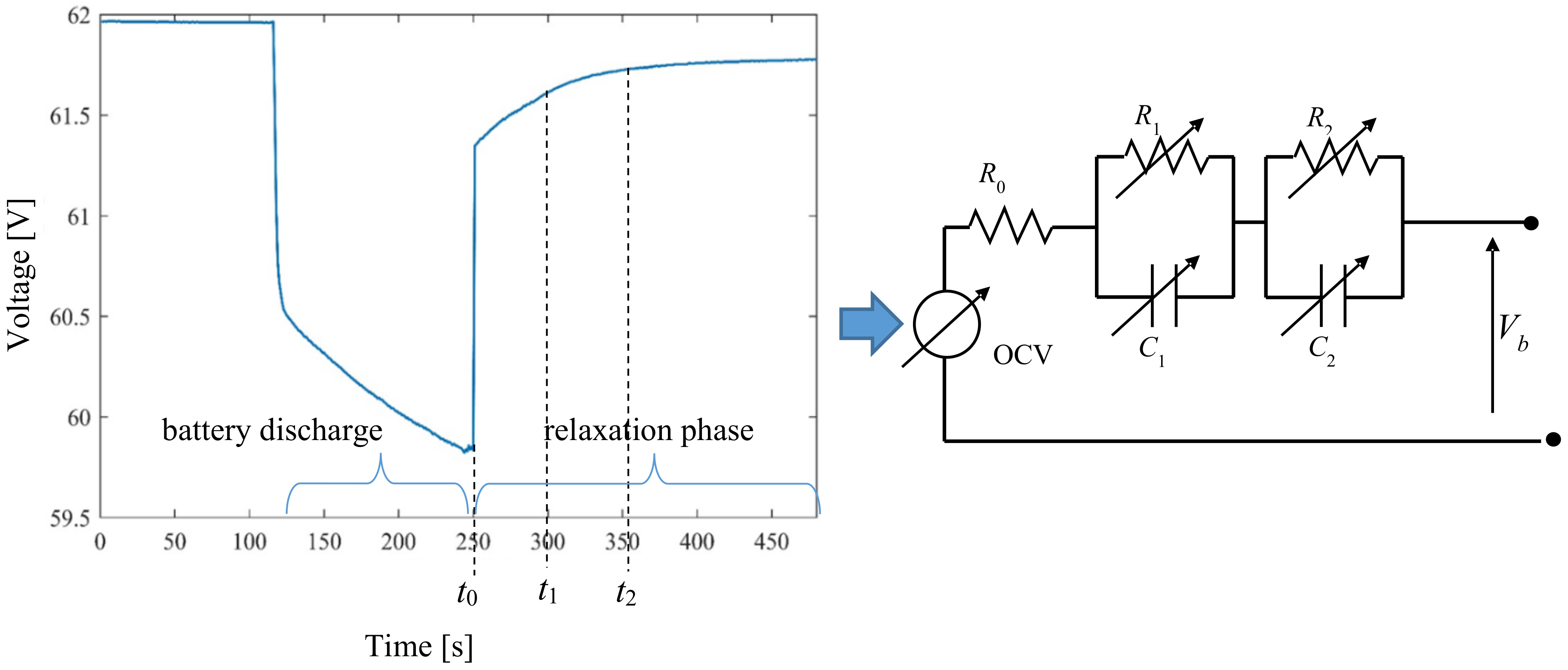
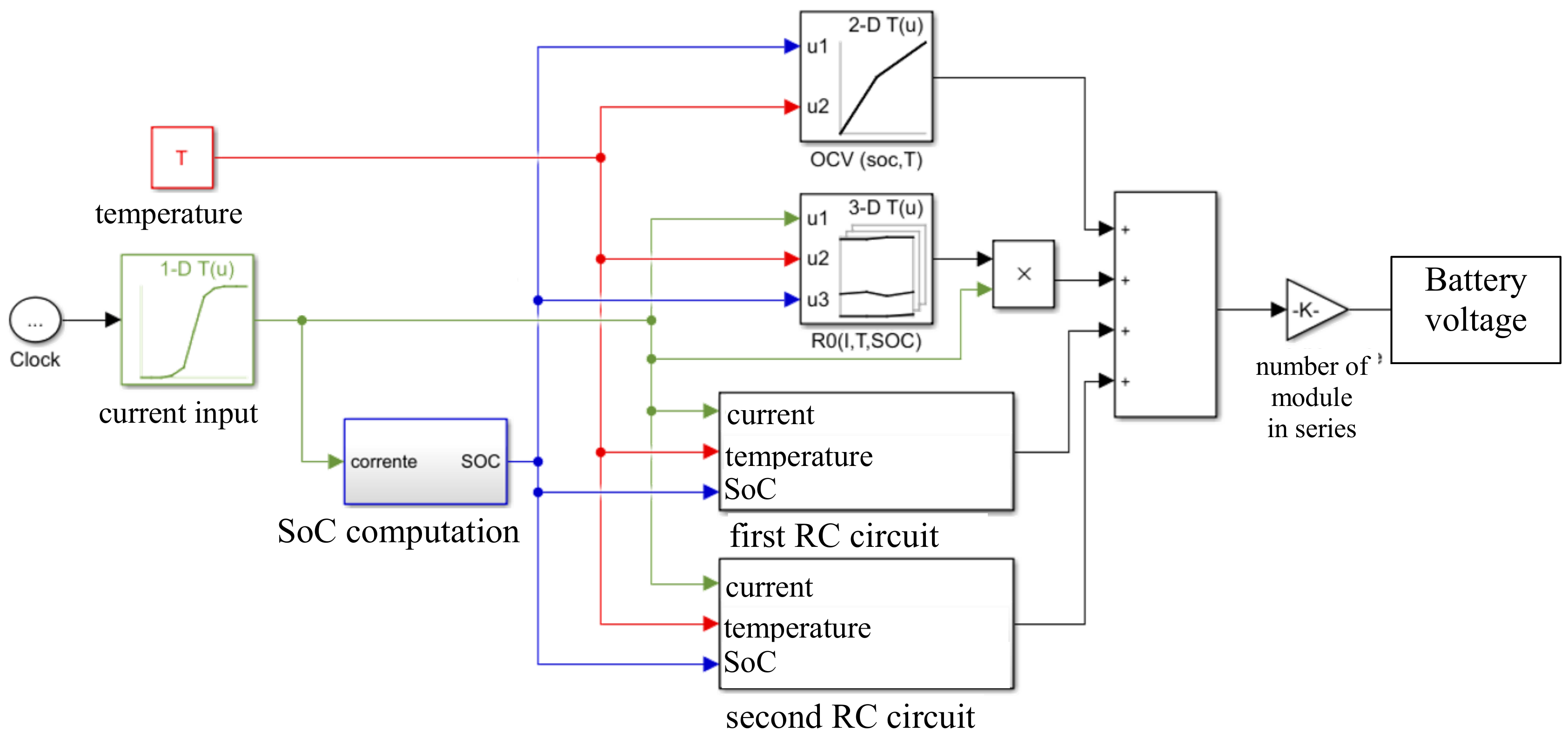
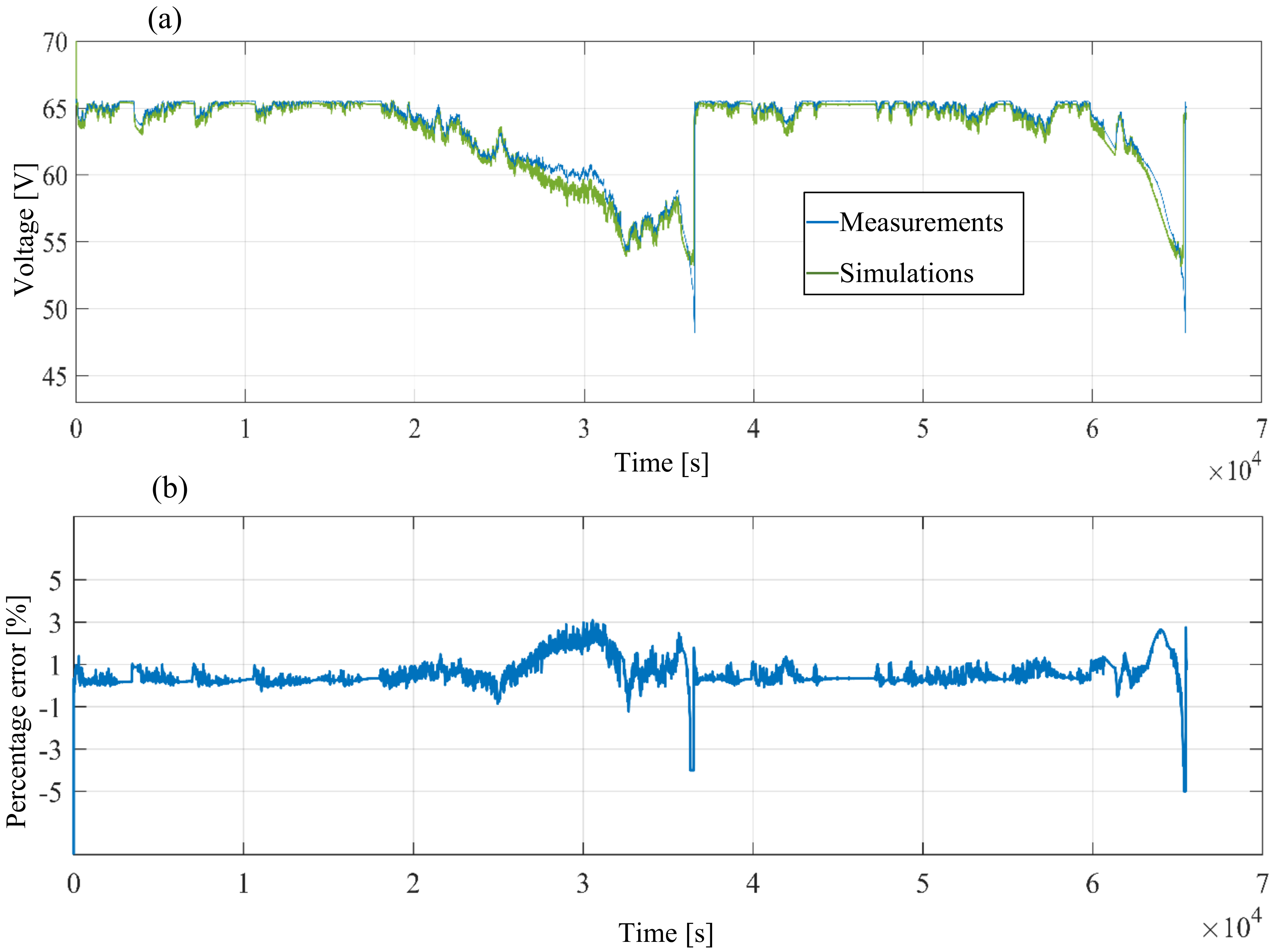
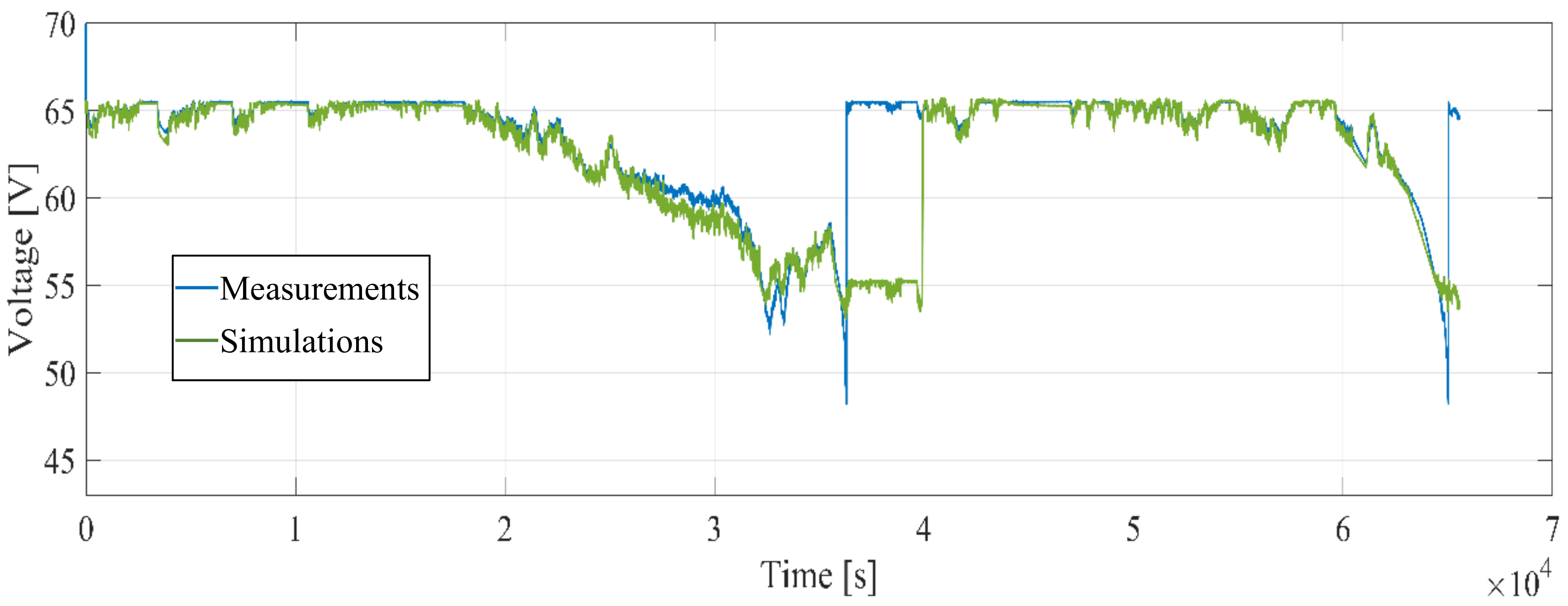
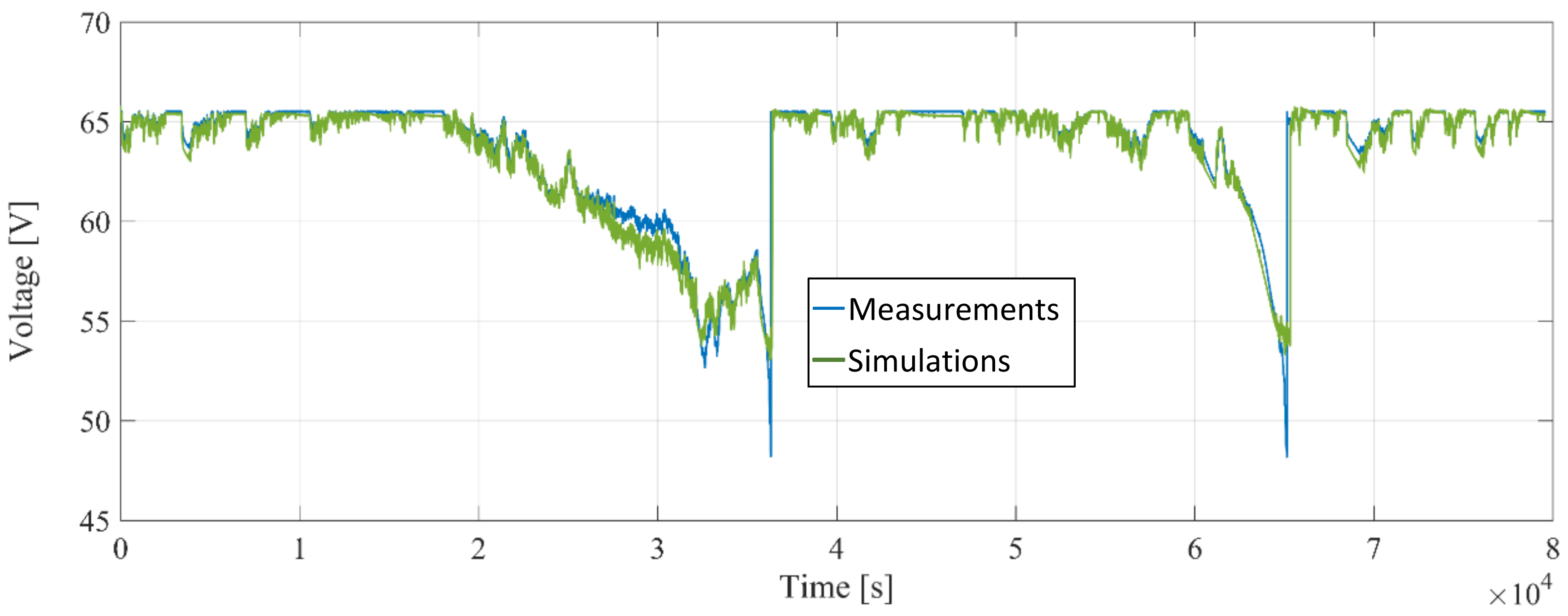
2.1. Battery Electric Model Validation
3. Flywheel Electrical Model
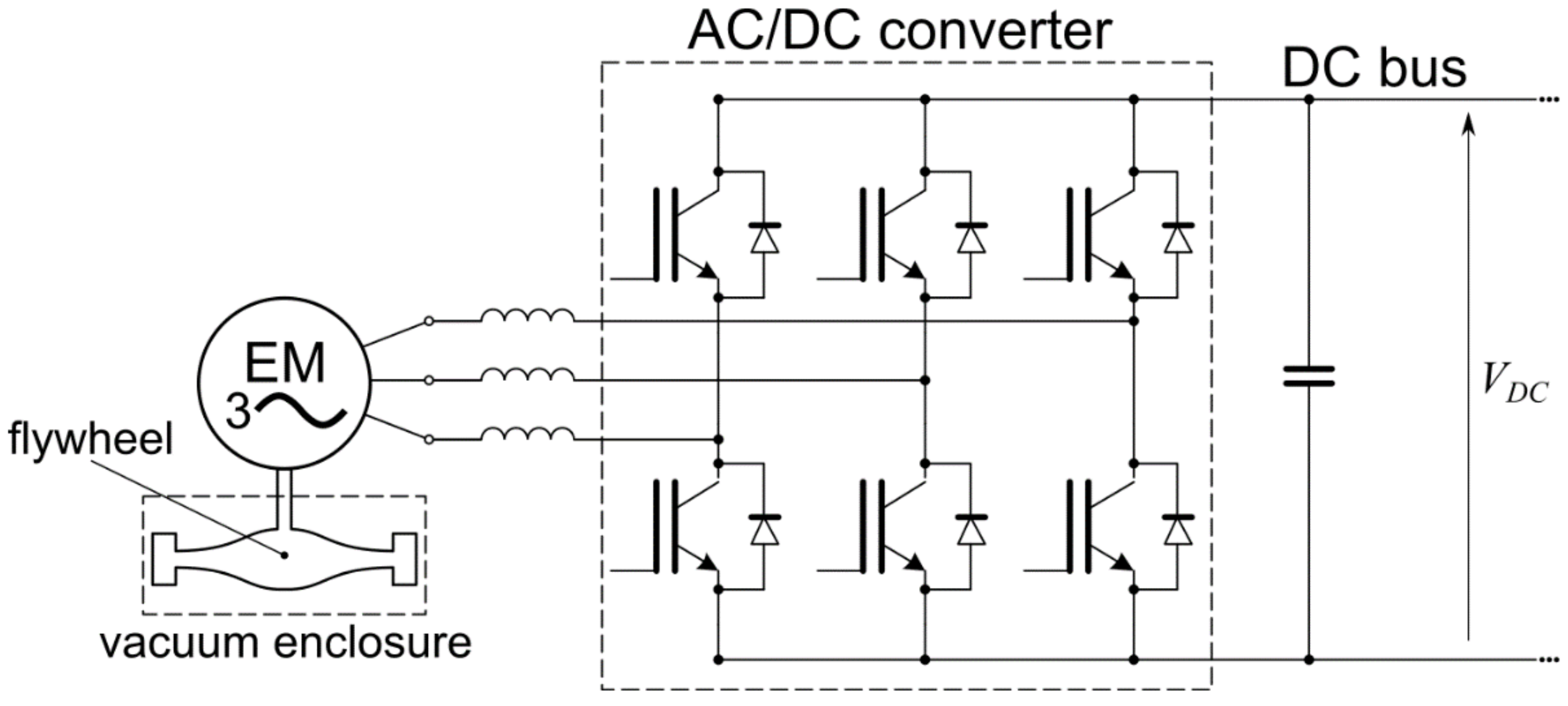
3.1. Flywheel System
3.2 Formulation of the Model Parameters
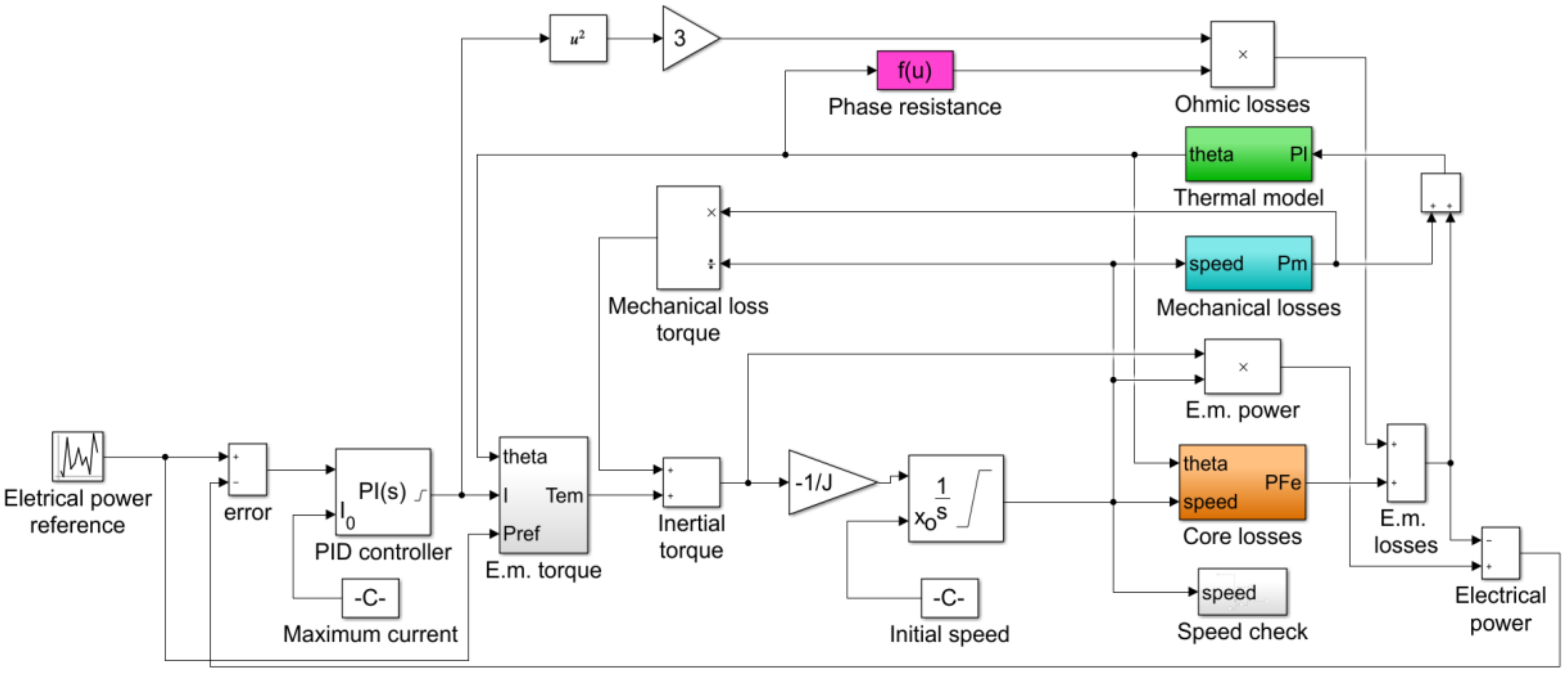
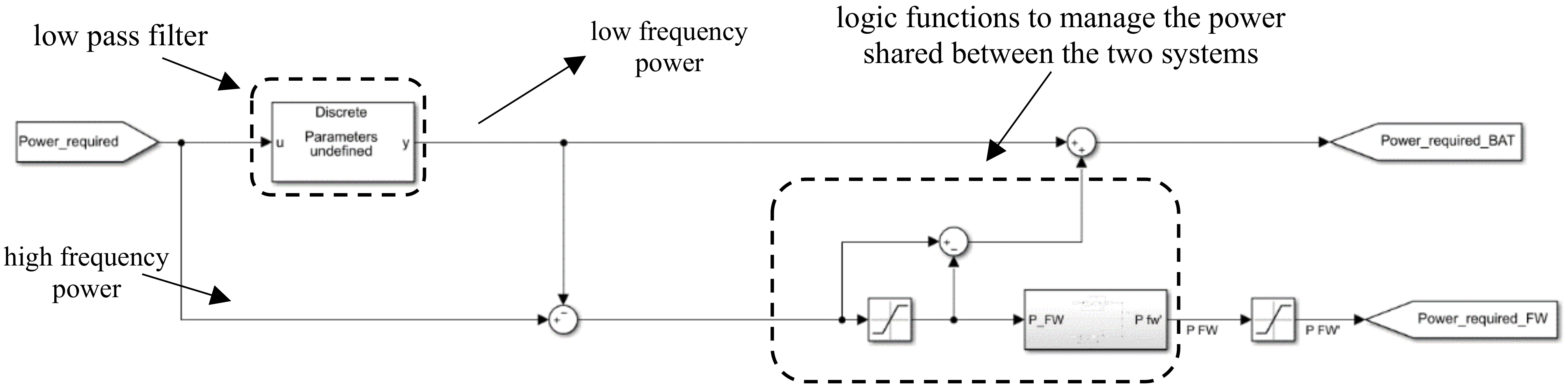
3.3. Simulation Scheme
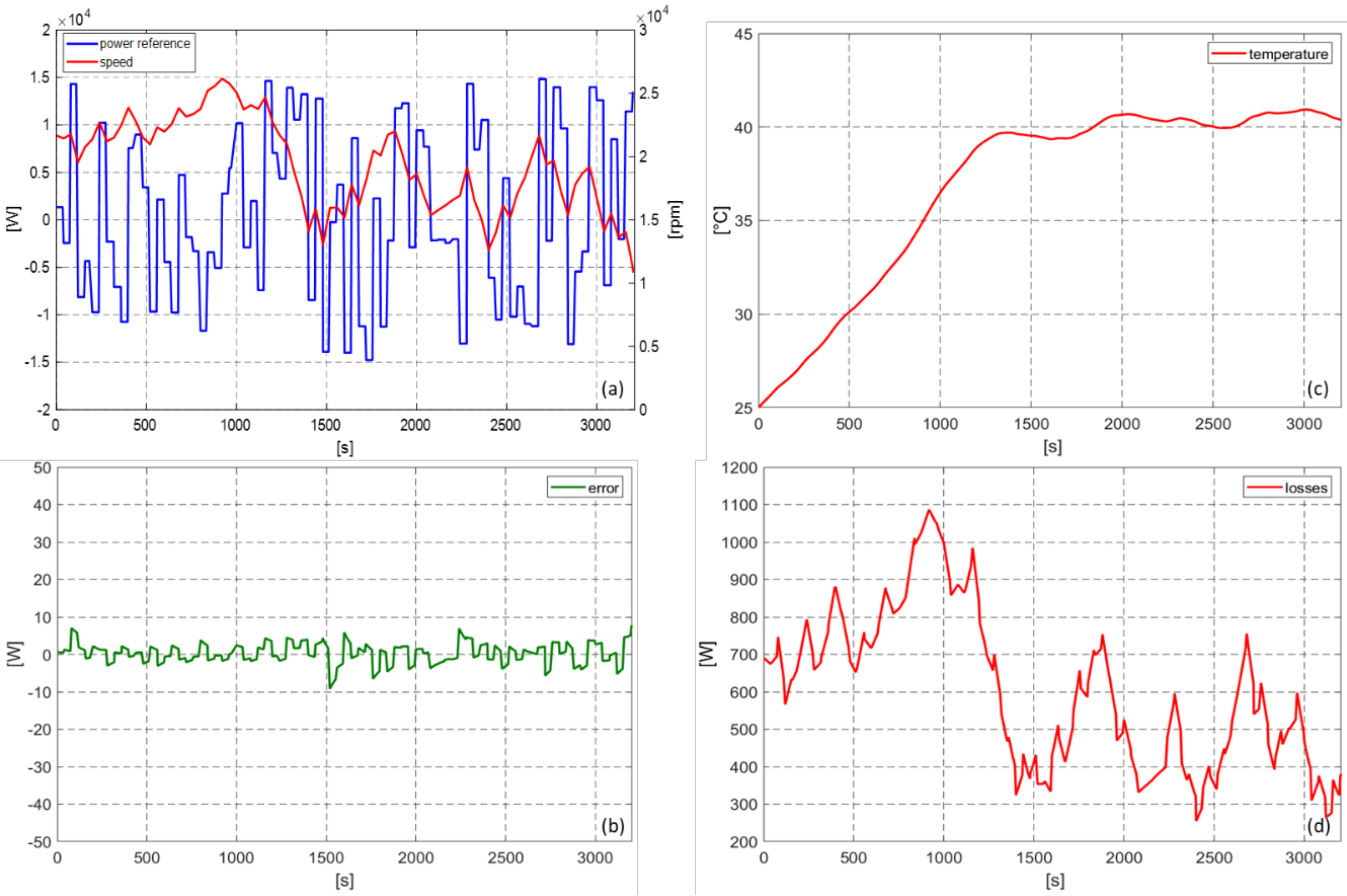
- the power error is very low, confirming the current control effectiveness for the output electrical power regulation;
- the speed suitably tracks the requested accelerating and decelerating conditions; however, the prevalent output power requirement during this test results in a temporarily switch off of the flywheel system to recharge it;
- the temperature increase is more significant during the first part of the test because of the higher losses, particularly the mechanical ones; after that, it stabilizes to values compatible with short operating cycles.
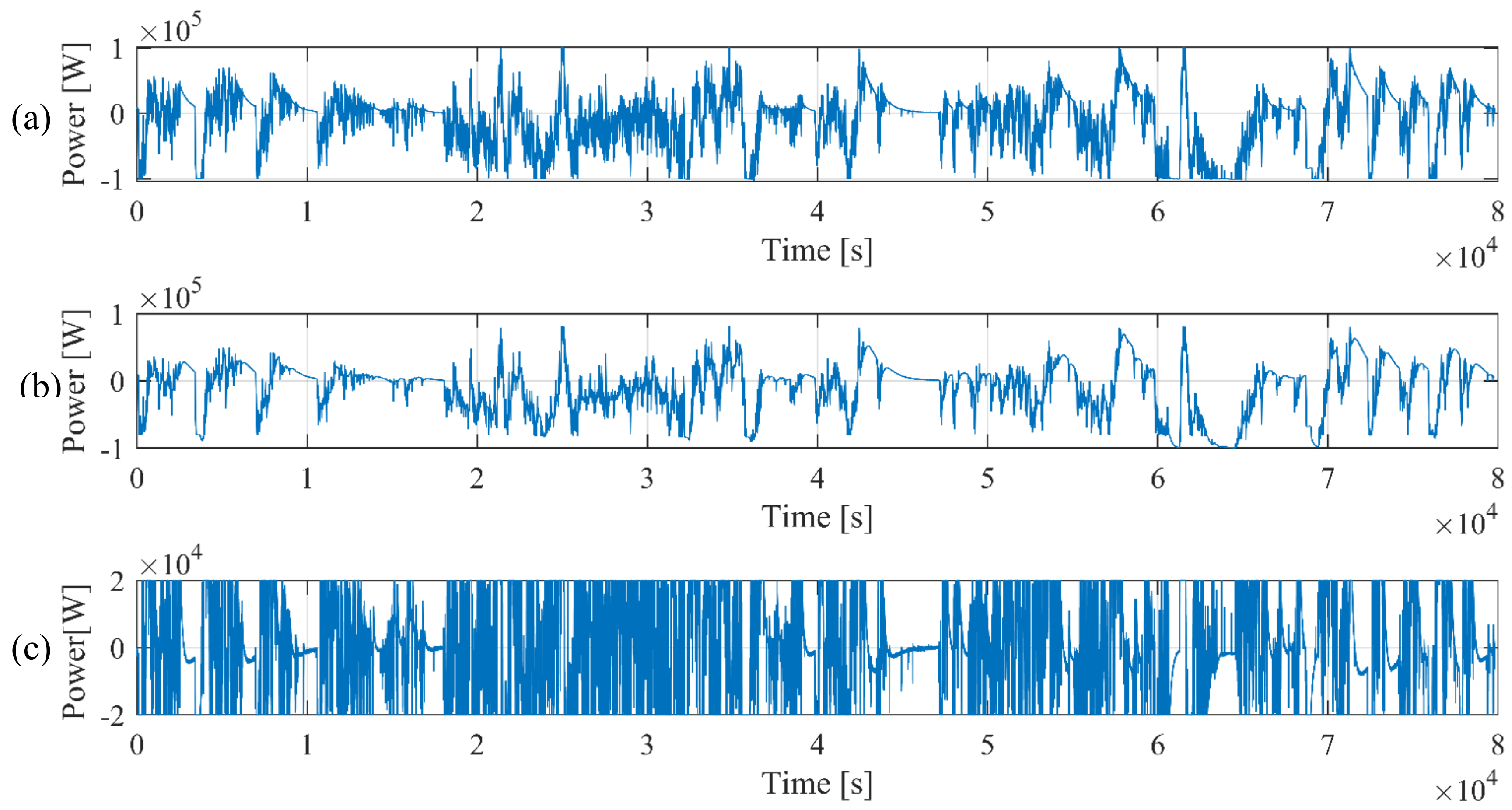
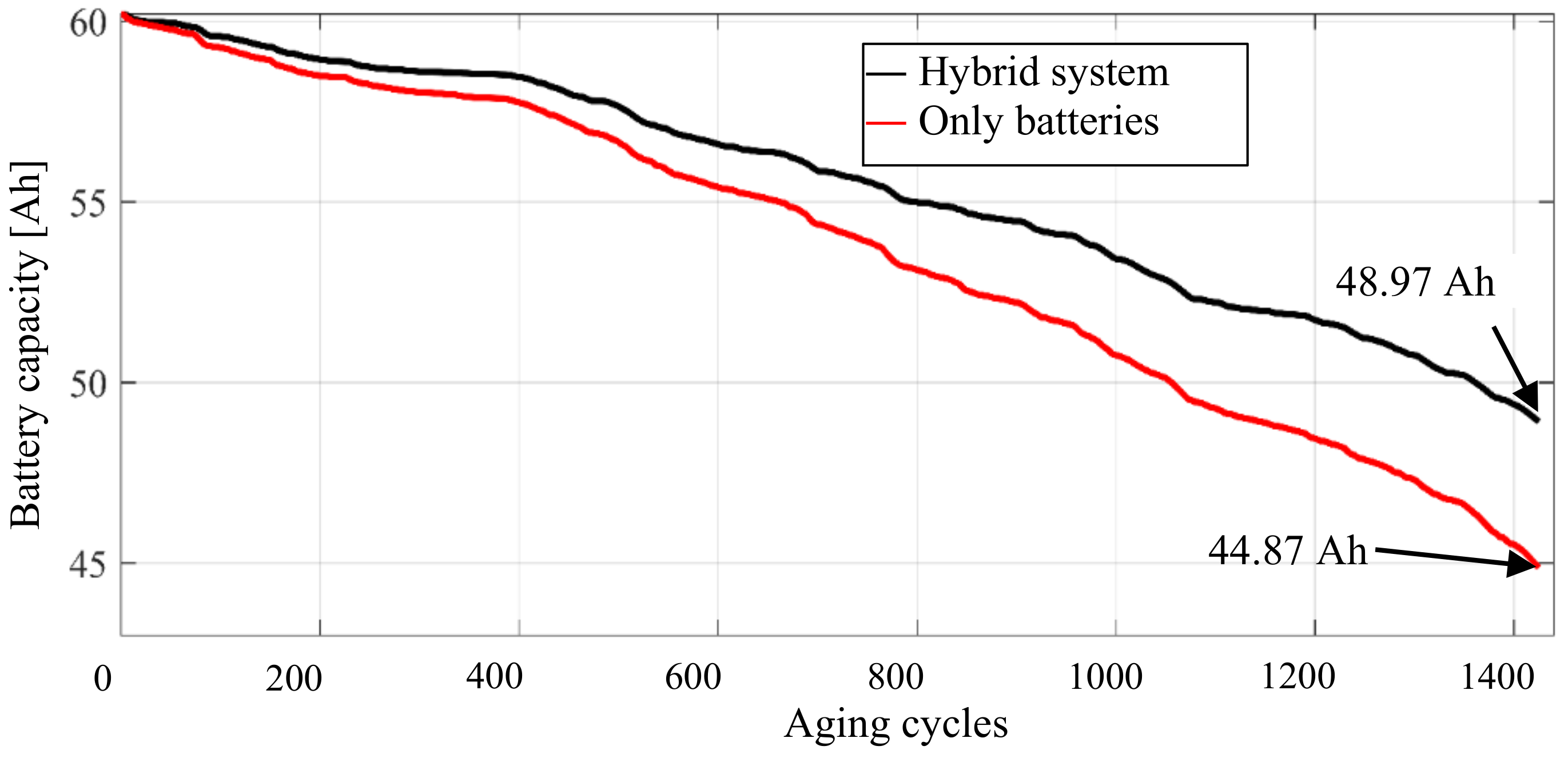
4. The Hybrid Storage System Simulation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Luo, X.; Wang, J.; Dooner, M.; Clarke, J. Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl. Energy 2015, 137, 511–536. [Google Scholar] [CrossRef]
- Zhao, H.; Wu, Q.; Hu, S.; Xu, H.; Rasmussen, C.N. Review of energy storage system for wind power integration support. Appl. Energy 2015, 137, 545–553. [Google Scholar] [CrossRef]
- Benato, R.; Bruno, G.; Palone, F.; Polito, R.M.; Rebolini, M. Large-scale electrochemical energy storage in high voltage grids: Overview of the Italian experience. Energies 2017, 10, 108. [Google Scholar] [CrossRef]
- Mehr, T.H.; Masoum, M.A.S.; Jabalameli, N. Grid-connected Lithium-ion battery energy storage system for load leveling and peak shaving. In Proceedings of the Australian Power Engineering Conference (AUPEC), Hobart, TAS, Australia, 29 September–3 October 2013. [Google Scholar]
- Enache, S.D.; Mircea, I.; Mircea, P.M. Study of the Influence of Lithium Batteries on the Power Network. In Proceedings of the International Conference on Applied and Theoretical Electricity (ICATE), Craiova, Romania, 25–27 October 2012. [Google Scholar]
- Stroe, D.-I.; Knap, V.; Swierczynski, M.; Stroe, A.-I.; Teodorescu, R. Operation of a Grid-Connected Lithium-Ion Battery Energy Storage System for Primary Frequency Regulation: A Battery Lifetime Perspective. IEEE Trans. Ind. Appl. 2016, 53, 430–438. [Google Scholar] [CrossRef]
- Dambone Sessa, S.; Palone, F.; Necci, A.; Benato, R. Sodium-nickel chloride battery experimental transient modelling for energy stationary storage. J. Energy Storage 2017, 9, 40–46. [Google Scholar] [CrossRef]
- Dambone Sessa, S.; Crugnola, G.; Todeschini, M.; Zin, S.; Benato, R. Sodium nickel chloride battery steady state regime model for stationary electrical energy storage. J. Energy Storage 2016, 6, 105–115. [Google Scholar] [CrossRef]
- Benato, R.; Dambone Sessa, S.; Guglielmi, F.; Partal, E.; Tleis, N. Ground Return Current Behavior in HVAC Insulated Cables by means of MCA. Energies 2014, 7, 8116–8131. [Google Scholar] [CrossRef]
- Benato, R.; Dambone Sessa, S.; Guglielmi, F.; de Zan, R.; Gualano, A.; Guizzo, L.; Rebolini, M. Linee elettriche in infrastrutture stradali/ferroviarie: Un utilizzo affidabile delle sinergie. L’Energia Elettrica 2014, 91, 49–62. [Google Scholar]
- Benato, R.; Dambone Sessa, S.; Guizzo, L.; Rebolini, M. The synergy of the future: High voltage insulated power cables and railway-highway infrastructures. IET Gener. Transm. Distrib. 2017, 11, 2712–2720. [Google Scholar] [CrossRef]
- Benato, R.; del Brenna, M.; di Mario, C.; Lorenzoni, A.; Zaccone, E. A New procedure to compare the social costs of EHV-HV overhead lines and underground XLPE cables. In Proceedings of the CIGRÉ 2006, Paris, France, 27 August–1 September 2006. [Google Scholar]
- Farhadi, M.; Mohammed, O. Energy storage technologies for high-power applications. IEEE Trans. Ind. Appl. 2016, 52, 1953–1961. [Google Scholar] [CrossRef]
- Benato, R.; Dambone Sessa, S.; Musio, M.; Palone, F.; Polito, R.M. Italian experience on electrical storage ageing for ancillary services chiefly primary frequency regulation. Energies 2018, 11, 2087. [Google Scholar] [CrossRef]
- Lazarewicz, M.L.; Rojas, A. Grid frequency regulation by recycling electrical energy in flywheels. In Proceedings of the IEEE Power Engineering Society General Meeting, Denver, CO, USA, 6–10 June 2004. [Google Scholar]
- Amiryar, M.E.; Pullen, K.R. A review of flywheel energy storage system technologies and their applications. Appl. Sci. 2017, 7, 286. [Google Scholar] [CrossRef]
- Schwungrad Energie. Flywheel-Battery Hybrid for Grid Stability. In Proceedings of the EERA Workshop, San Sebastian, Spain, 22 March 2017. [Google Scholar]
- Esche, R.V.D.; Tudi, R. Benefit of Hybrid Storage System with Flywheel; Technical report; Stornetic Company: Jülich, Germany, 2016. [Google Scholar]
- Prodromidis, G.N.; Coutelieris, F.A. Simulations of economical and technical feasibility of battery and flywheel hybrid energy storage systems in autonomous projects. Renew. Energy 2012, 39, 149–153. [Google Scholar] [CrossRef]
- Shao, Q.; Zhao, Y.; Du, S.; Du, Y. A novel hybrid energy storage strategy based on flywheel and lead-acid battery in wind power generation system. Int. J. Control Autom. 2015, 8, 1–12. [Google Scholar] [CrossRef]
- Benato, R.; Dambone Sessa, S.; Bevilacqua, F.; Palone, F. Measurement-based lithium-manganese oxide battery model. In Proceedings of the 2017 AEIT International Annual Conference, Cagliari, Italy, 20–22 September 2017. [Google Scholar]
- Wanga, J.; Liua, P.; Garnera, J.H.; Shermana, E.; Soukiaziana, S.; Verbruggeb, M.; Tatariab, H.; Musserc, J.; Finamorec, P. Cycle-life model for graphite-LiFePO4 cells. J Power Sources 2011, 196, 3942–3948. [Google Scholar] [CrossRef]
- Yulong, J.P.; Cavagnino, A.; Vaschetto, S.; Feng, C.; Tenconi, A. Flywheel Energy Storage Systems for Power Systems Application. In Proceedings of the 6th International Conference on Clean Electrical Power (ICCEP), Santa Margherita Ligure, Italy, 27–29 June 2017. [Google Scholar]
- Genta, G. Kinetic Energy Storage: Theory and Practice of Advanced Flywheel Systems; Butterworth & Co.: London, UK, 1985; pp. 80–87. [Google Scholar]
- Andriollo, M.; Tortella, A. Preliminary Design of an Axial Flux Machine with Careless Stator for Flywheel Applications. In Proceedings of the XIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 3–6 September 2018. [Google Scholar]
- Gieras, J.F. Design of Permanent Magnet Brushless Motors for High Speed Applications. In Proceedings of the 7th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 22–25 October 2014. [Google Scholar]
- Heins, G.; Ionel, M.; Patterson, D.; Stretz, S.; Thiele, M. Combined experimental and numerical method for loss separation in permanent-magnet brushless machines. IEEE Trans. Ind. Appl. 2016, 52, 1405–1412. [Google Scholar] [CrossRef]
| Rank Characteristics | Module Characteristics | ||
|---|---|---|---|
| Number of modules | 16 module + 1 BMS | Number of cells | 16 + 1 BMS |
| Dimensions | 1049 × 549 × 1851 mm | Dimensions | 485 × 510 × 162.5 mm |
| Weight | 1000 kg | Weight | 48 kg |
| Capacity | 60 Ah | Capacity | 60 Ah |
| Rated voltage | 947.2 V | Rated voltage | 59.2 V |
| Nominal Energy | 47.7 KWh | Nominal Energy | 2.98 kWh |
| Operating voltage range | 768–1054.7 V | Operating voltage range | 48–65.92 V |
| Rated discharge time | 1 h | Rated discharge time | 1 h |
| Operational Data | Sizes | ||
|---|---|---|---|
| Rated power | 20 kW | Active length | 120 mm (EM) |
| Speed range | 10,833 rpm÷32,500 rpm | Airgap width | 2 mm (EM) |
| Max current rms value | 223 A | Outer diameter | 400 mm (EM) 500 mm (FWR) |
| Max torque (@40 °C) | 17.62 Nm | Flywheel disc height | 91 mm |
| Max phase voltage (@40 °C) | 90 V | Rotating mass | 9 kg (EM) 73 kg (FWR) |
| Temperature range | 25 °C ÷ 130 °C | Rotational inertia | 1.17 kgm2 |
| Quantity | Value | Quantity | Value |
|---|---|---|---|
| Phase resistance | = 0.3 mΩ | Thermal time constant | = 60 min |
| Torque constant | = 0.079 Nm/A | Thermal capacitance | = 4 104 J/°K |
| PM temperature coefficient | = −0.2 %/°C | Reference speed | = 32,500 rpm |
| Mechanical loss coefficients | = 0.0272 Ws/rad = 3.63∙10−8 Ws3/rad3 | Core loss coefficients | = 0.081 Ws/rad = 1.3∙10−8 Ws2/rad2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dambone Sessa, S.; Tortella, A.; Andriollo, M.; Benato, R. Li-Ion Battery-Flywheel Hybrid Storage System: Countering Battery Aging During a Grid Frequency Regulation Service. Appl. Sci. 2018, 8, 2330. https://doi.org/10.3390/app8112330
Dambone Sessa S, Tortella A, Andriollo M, Benato R. Li-Ion Battery-Flywheel Hybrid Storage System: Countering Battery Aging During a Grid Frequency Regulation Service. Applied Sciences. 2018; 8(11):2330. https://doi.org/10.3390/app8112330
Chicago/Turabian StyleDambone Sessa, Sebastian, Andrea Tortella, Mauro Andriollo, and Roberto Benato. 2018. "Li-Ion Battery-Flywheel Hybrid Storage System: Countering Battery Aging During a Grid Frequency Regulation Service" Applied Sciences 8, no. 11: 2330. https://doi.org/10.3390/app8112330
APA StyleDambone Sessa, S., Tortella, A., Andriollo, M., & Benato, R. (2018). Li-Ion Battery-Flywheel Hybrid Storage System: Countering Battery Aging During a Grid Frequency Regulation Service. Applied Sciences, 8(11), 2330. https://doi.org/10.3390/app8112330








