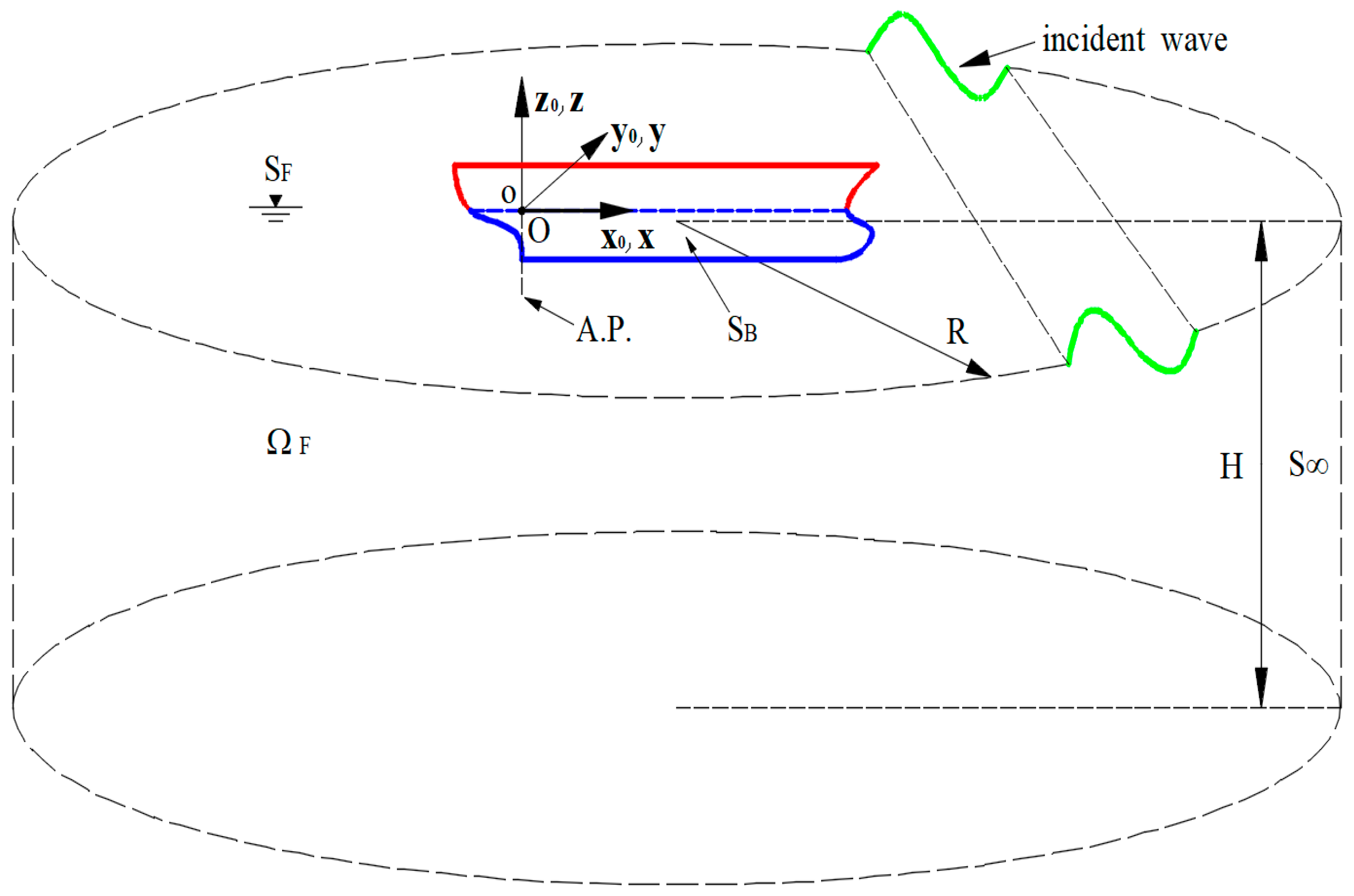
Figure 1.
Mathematical description of ship-fluid interaction.
Figure 1.
Mathematical description of ship-fluid interaction.
Figure 2.
Overview of the model setup.
Figure 2.
Overview of the model setup.
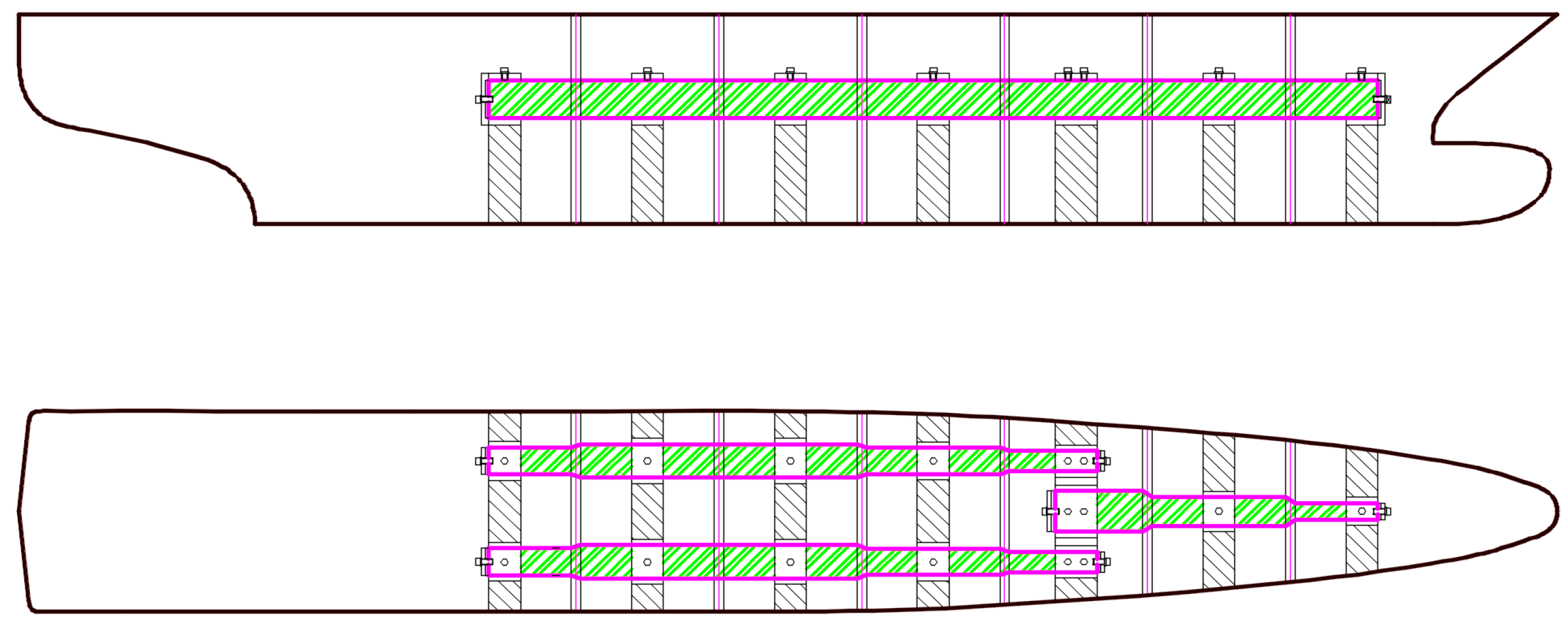
Figure 3.
General arrangement of elastic backbones.
Figure 3.
General arrangement of elastic backbones.
Figure 4.
The ship model towing tank. (a) Wave tank at work; (b) Wave generator
Figure 4.
The ship model towing tank. (a) Wave tank at work; (b) Wave generator
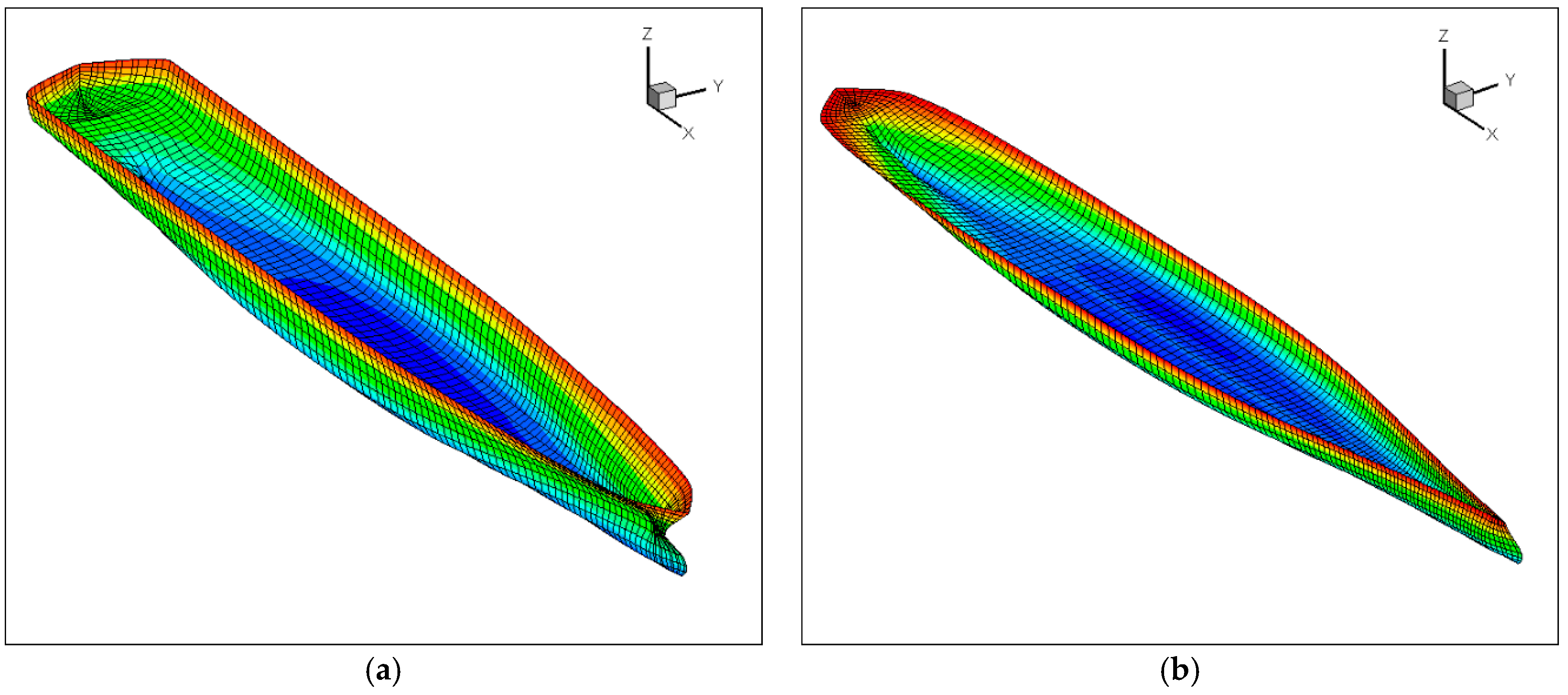
Figure 5.
Mesh information. (a) Panels of the whole hull surface; (b) Panels of the wet surface for [FR] and [FD].
Figure 5.
Mesh information. (a) Panels of the whole hull surface; (b) Panels of the wet surface for [FR] and [FD].
Figure 6.
Uneven cross sections for calculation of slamming loads.
Figure 6.
Uneven cross sections for calculation of slamming loads.
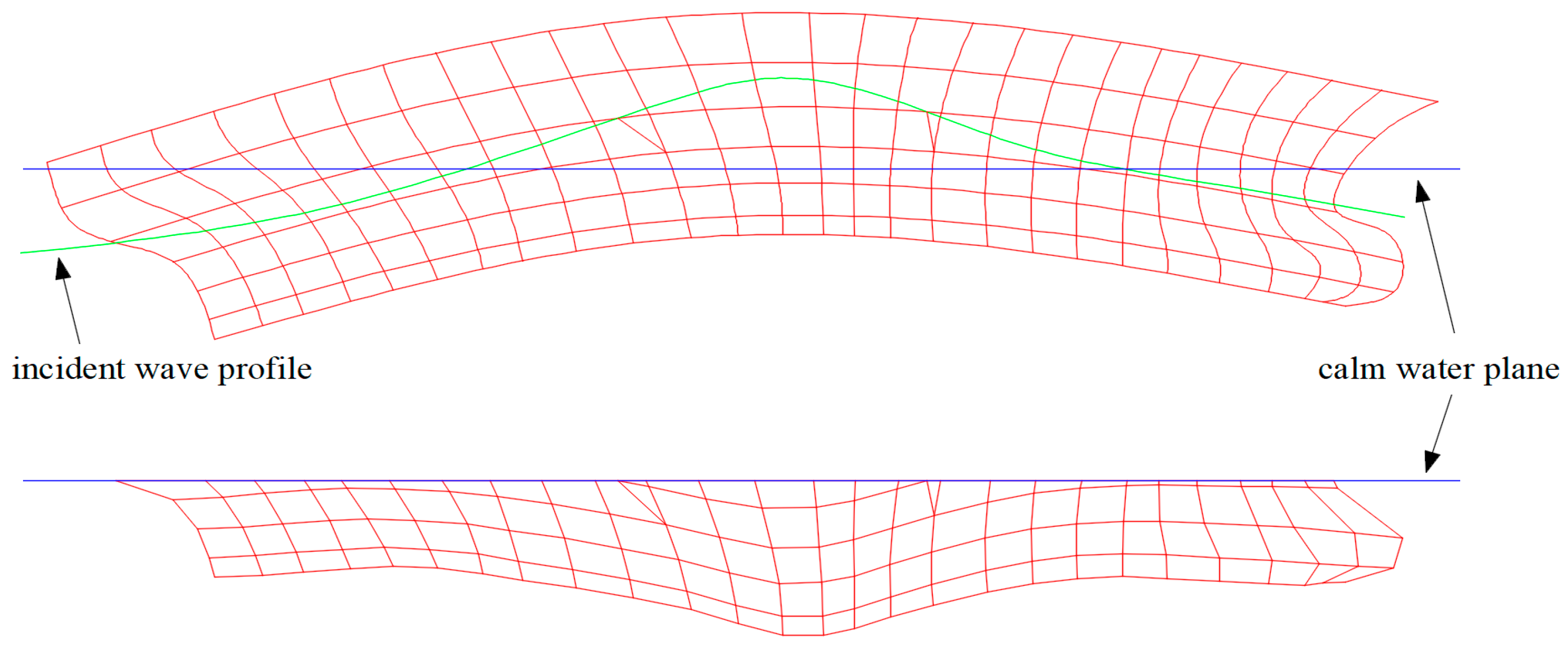
Figure 7.
Acquisition of instantaneous wetted surface during computation.
Figure 7.
Acquisition of instantaneous wetted surface during computation.
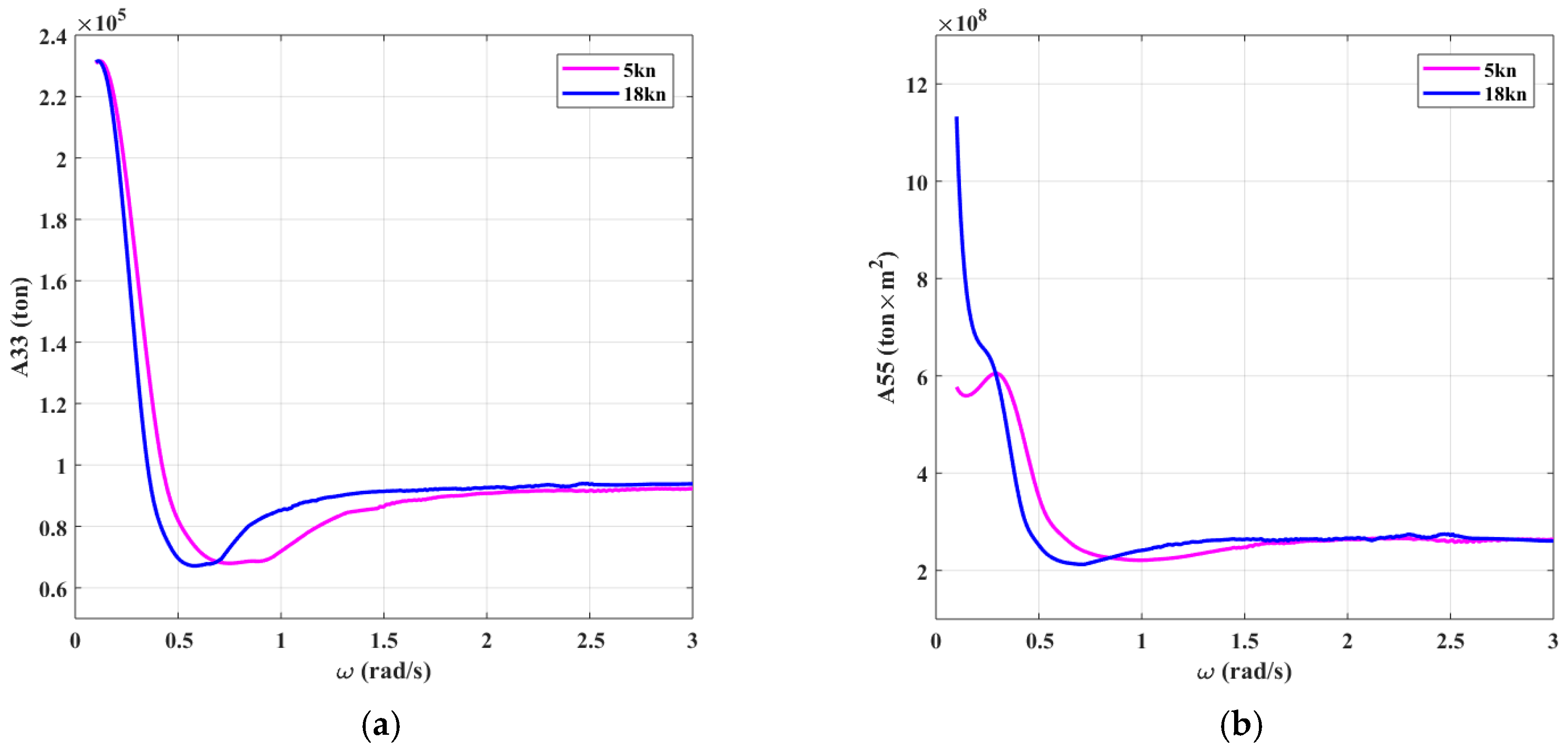
Figure 8.
Added mass coefficients. (a) A33; (b) A55
Figure 8.
Added mass coefficients. (a) A33; (b) A55
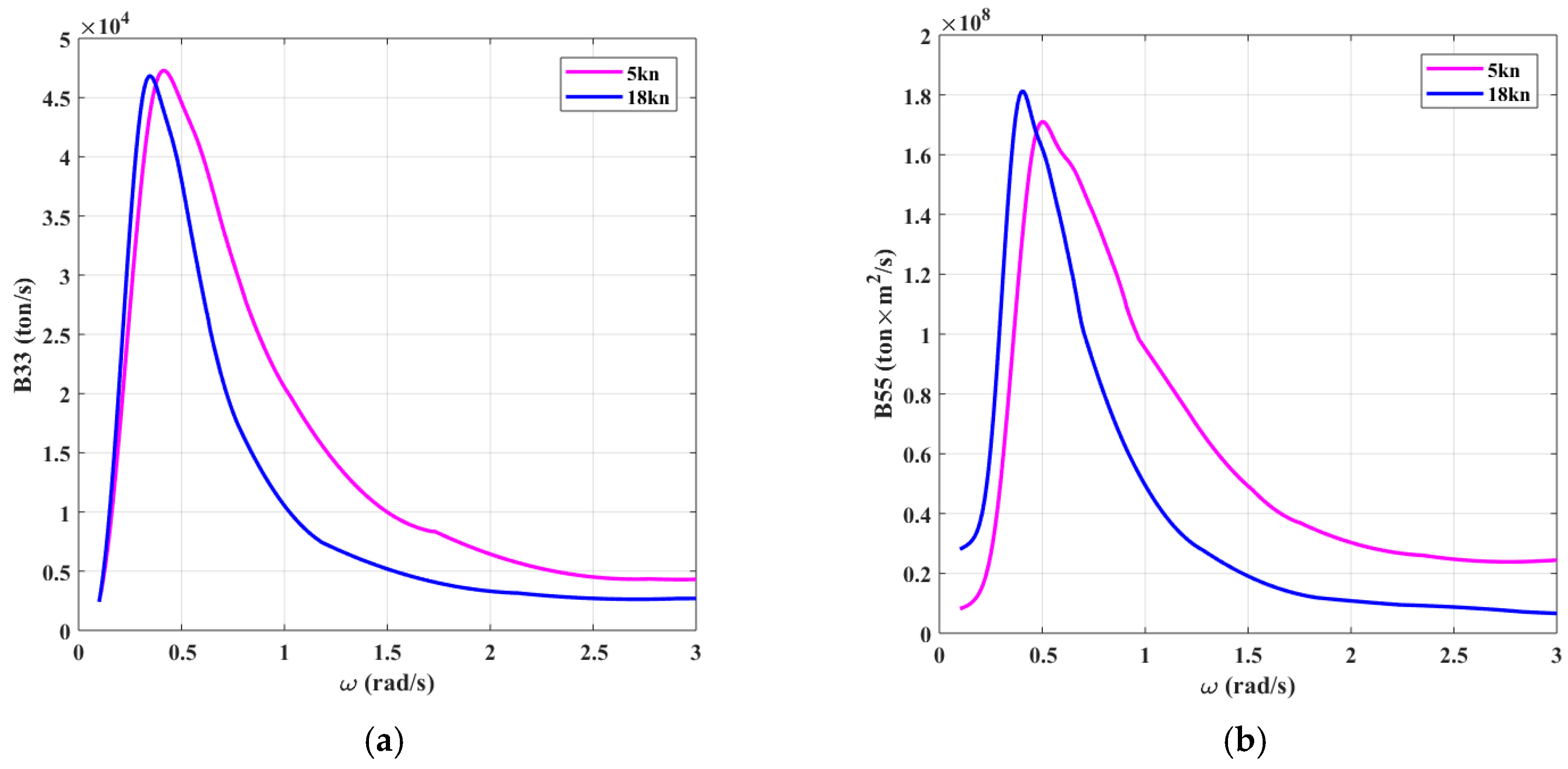
Figure 9.
Damping coefficients. (a) B33; (b) B55
Figure 9.
Damping coefficients. (a) B33; (b) B55
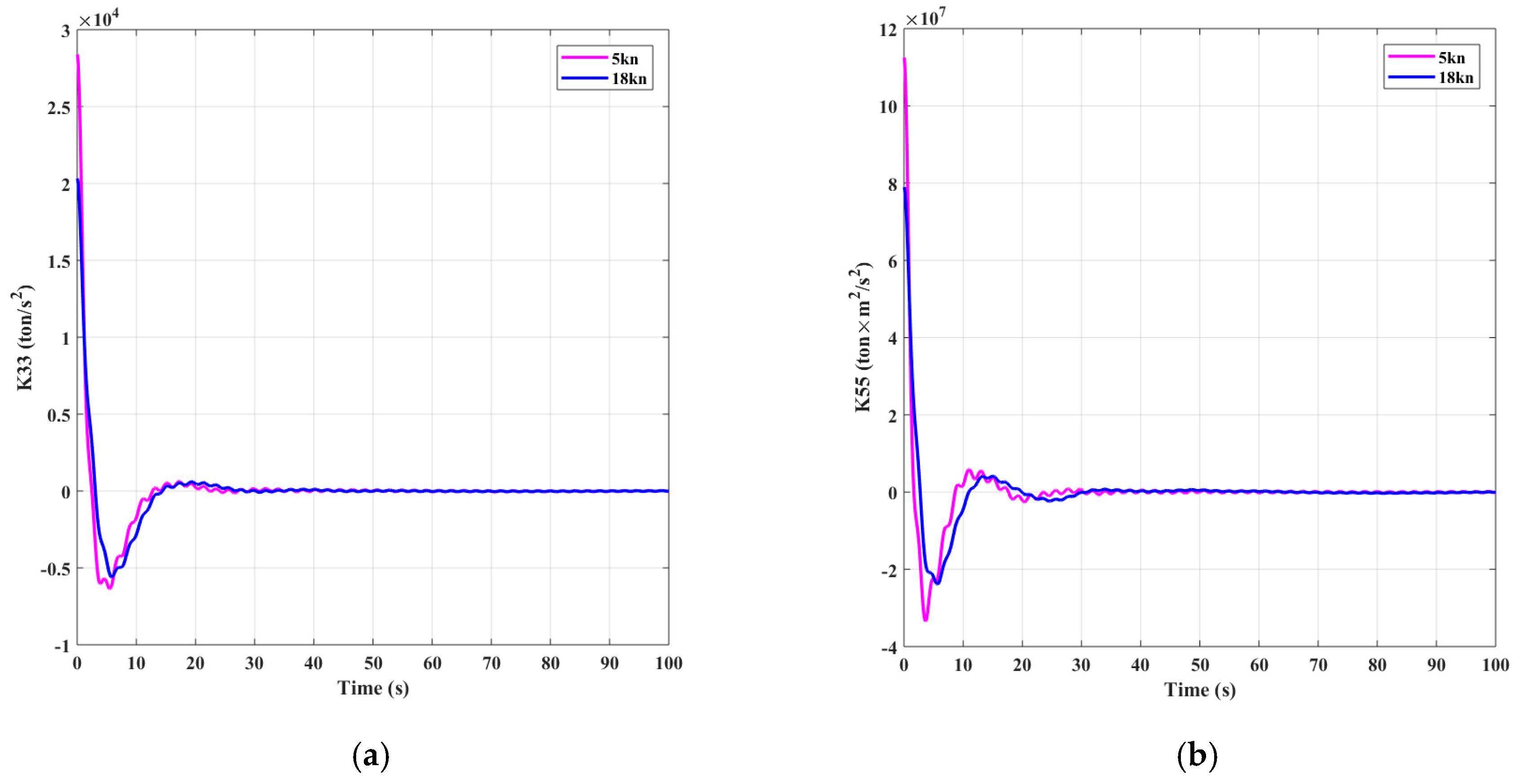
Figure 10.
Retardation functions. (a) K33; (b) K55
Figure 10.
Retardation functions. (a) K33; (b) K55
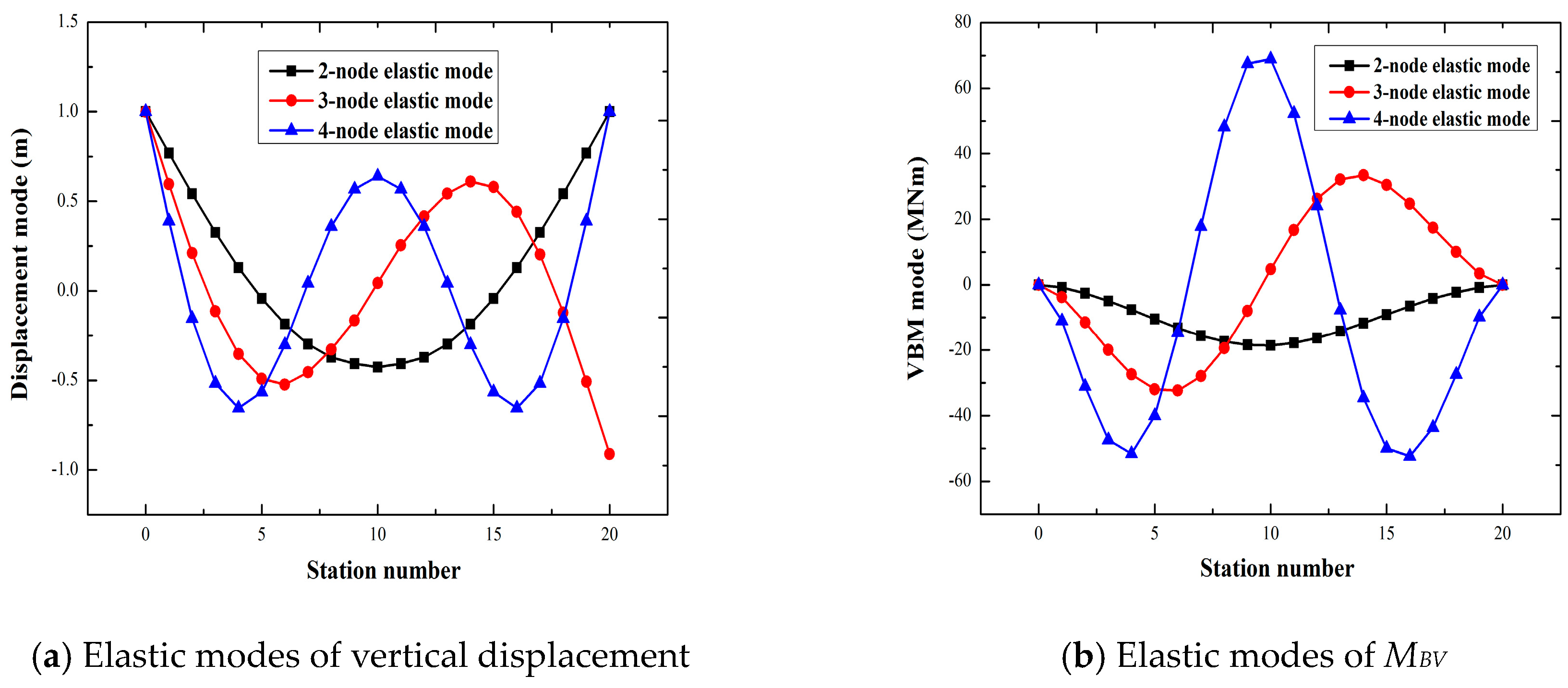
Figure 11.
First three elastic modes.
Figure 11.
First three elastic modes.
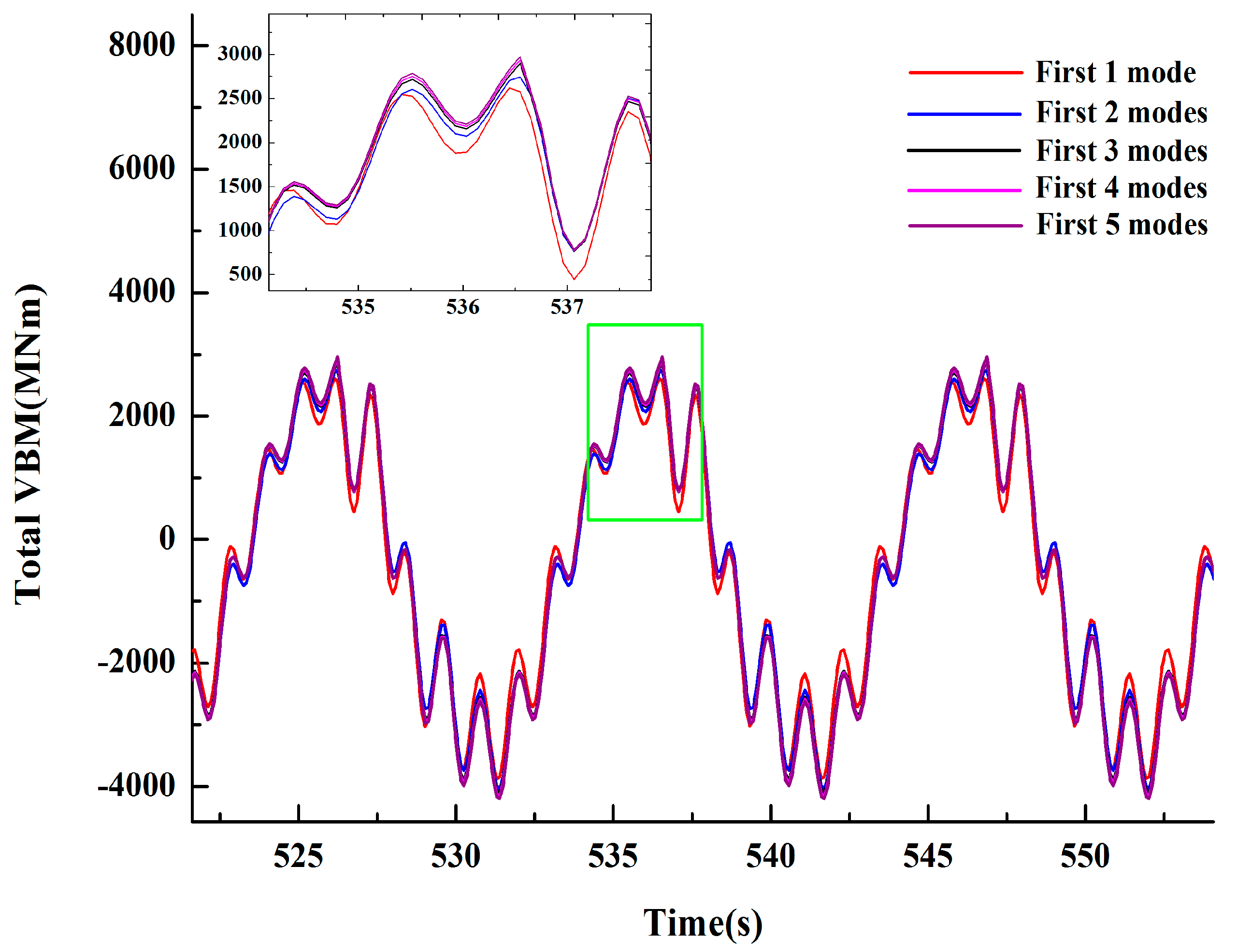
Figure 12.
Effects of orders of elastic modes on total MBVs amidships (ship velocity: 18 kn, wave height: 9 m, wave period: 13.28 s).
Figure 12.
Effects of orders of elastic modes on total MBVs amidships (ship velocity: 18 kn, wave height: 9 m, wave period: 13.28 s).
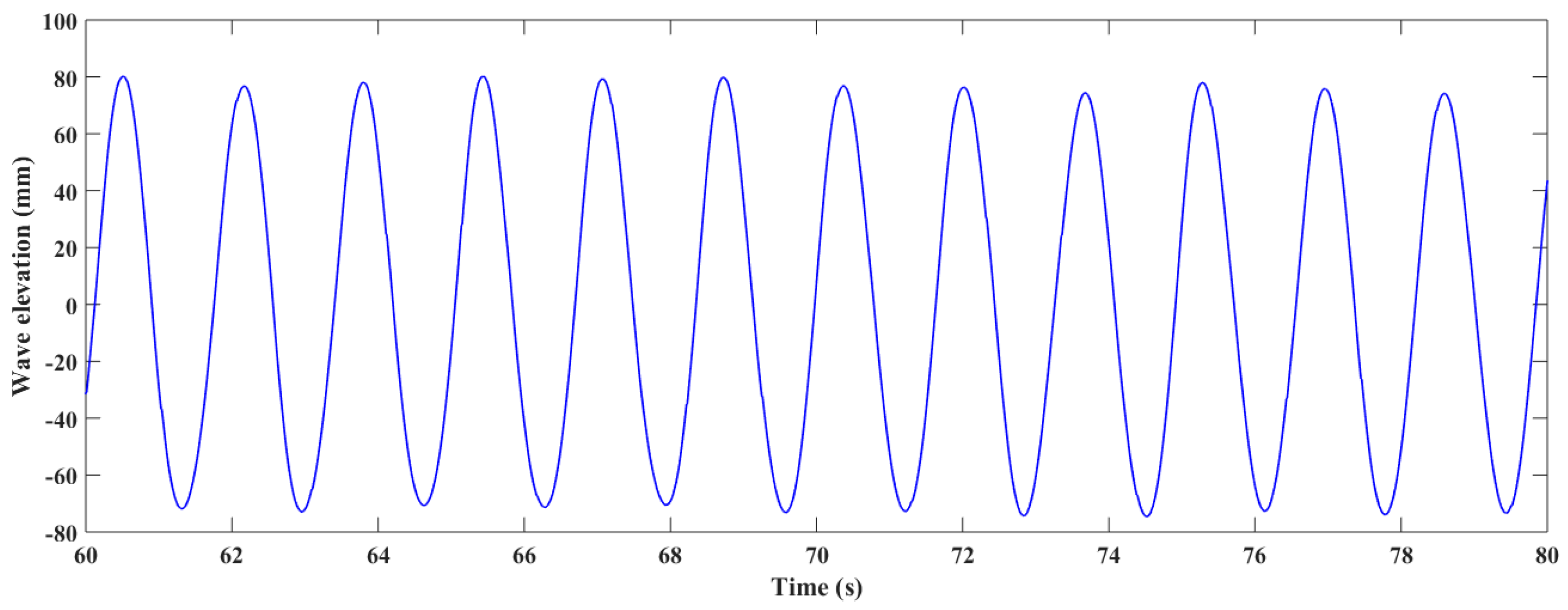
Figure 13.
Experimentally measured time series of regular wave condition 2.
Figure 13.
Experimentally measured time series of regular wave condition 2.
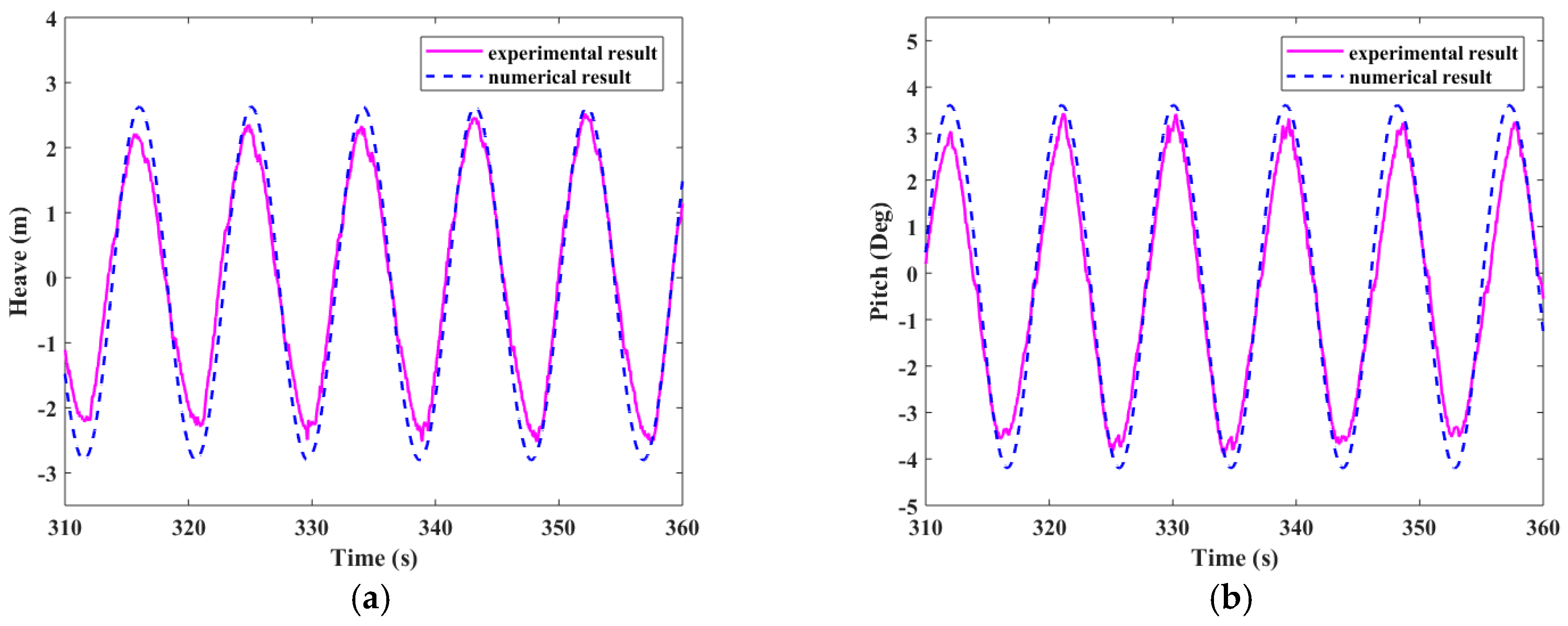
Figure 14.
Motion response in regular wave condition 1. (a) Heave (m); (b) Pitch (deg)
Figure 14.
Motion response in regular wave condition 1. (a) Heave (m); (b) Pitch (deg)
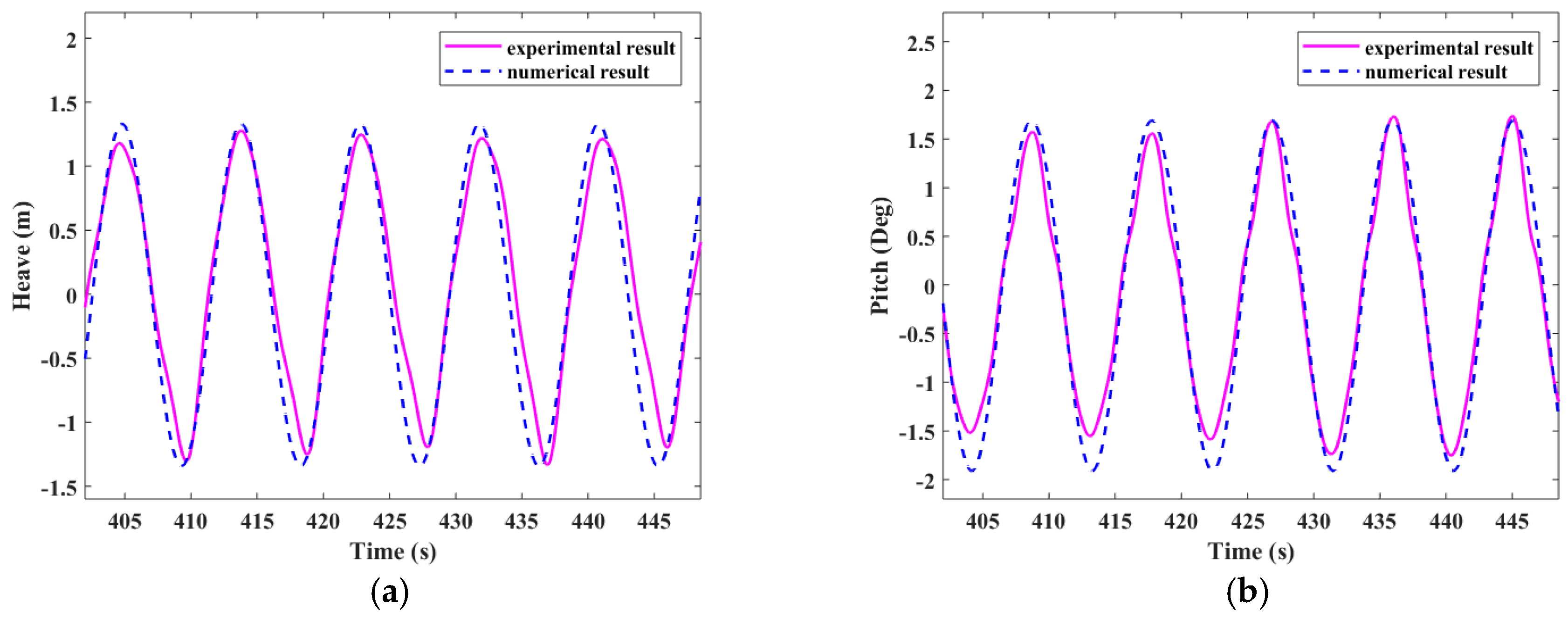
Figure 15.
Motion response in regular wave condition 2. (a) Heave (m); (b) Pitch (deg)
Figure 15.
Motion response in regular wave condition 2. (a) Heave (m); (b) Pitch (deg)
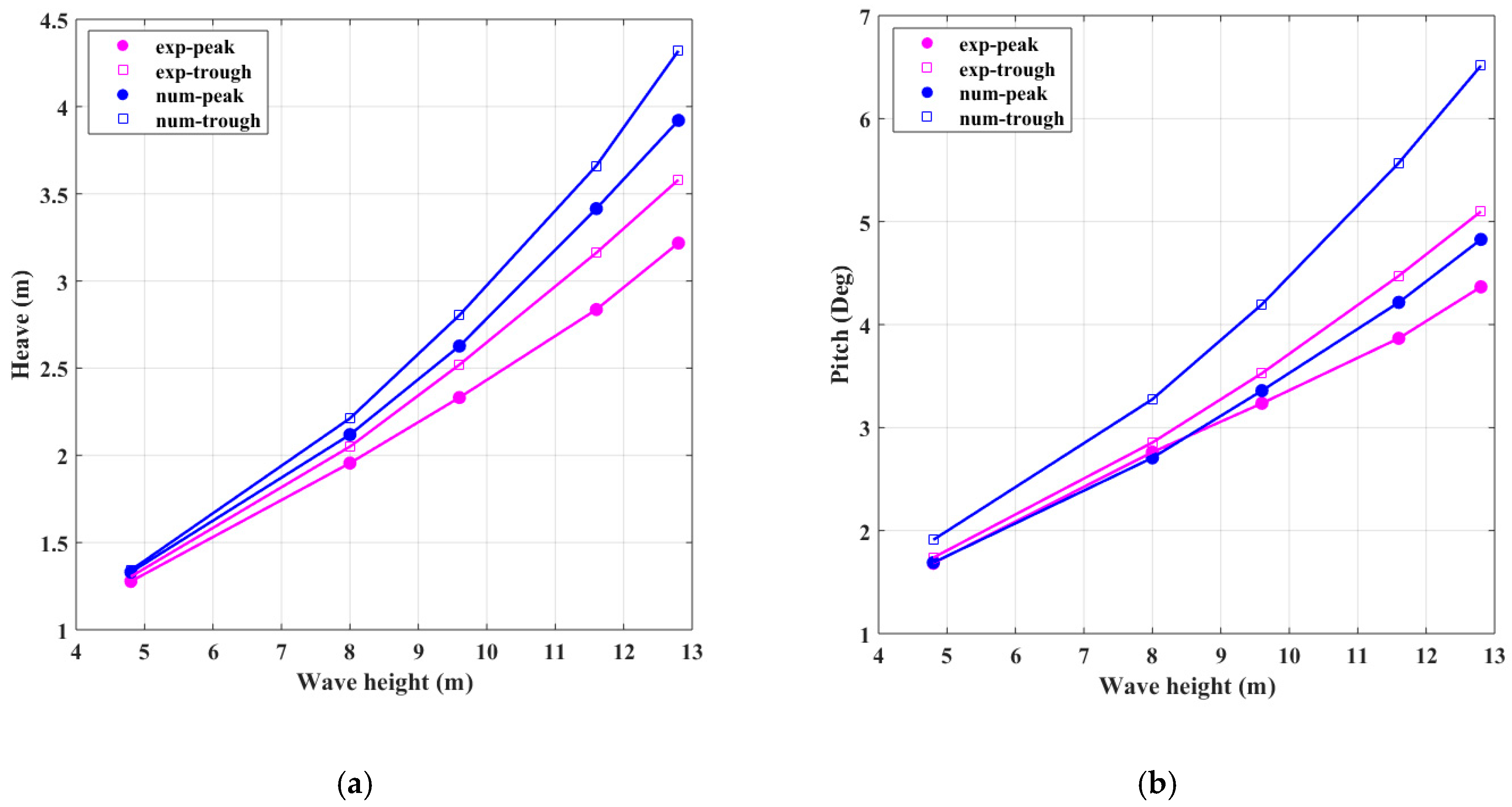
Figure 16.
Motion responses at different wave heights (V = 18 kn, λ/L = 1.0). (a) Heave responses; (b) Pitch responses.
Figure 16.
Motion responses at different wave heights (V = 18 kn, λ/L = 1.0). (a) Heave responses; (b) Pitch responses.
Figure 17.
Total MBV in regular waves. (a) Regular wave condition 1; (b) Regular wave condition 2
Figure 17.
Total MBV in regular waves. (a) Regular wave condition 1; (b) Regular wave condition 2
Figure 18.
Low frequency MBV in regular waves. (a) Regular wave condition 1; (b) Regular wave condition 2.
Figure 18.
Low frequency MBV in regular waves. (a) Regular wave condition 1; (b) Regular wave condition 2.
Figure 19.
High frequency MBV in regular waves. (a) Regular wave condition 1; (b) Regular wave condition 2.
Figure 19.
High frequency MBV in regular waves. (a) Regular wave condition 1; (b) Regular wave condition 2.
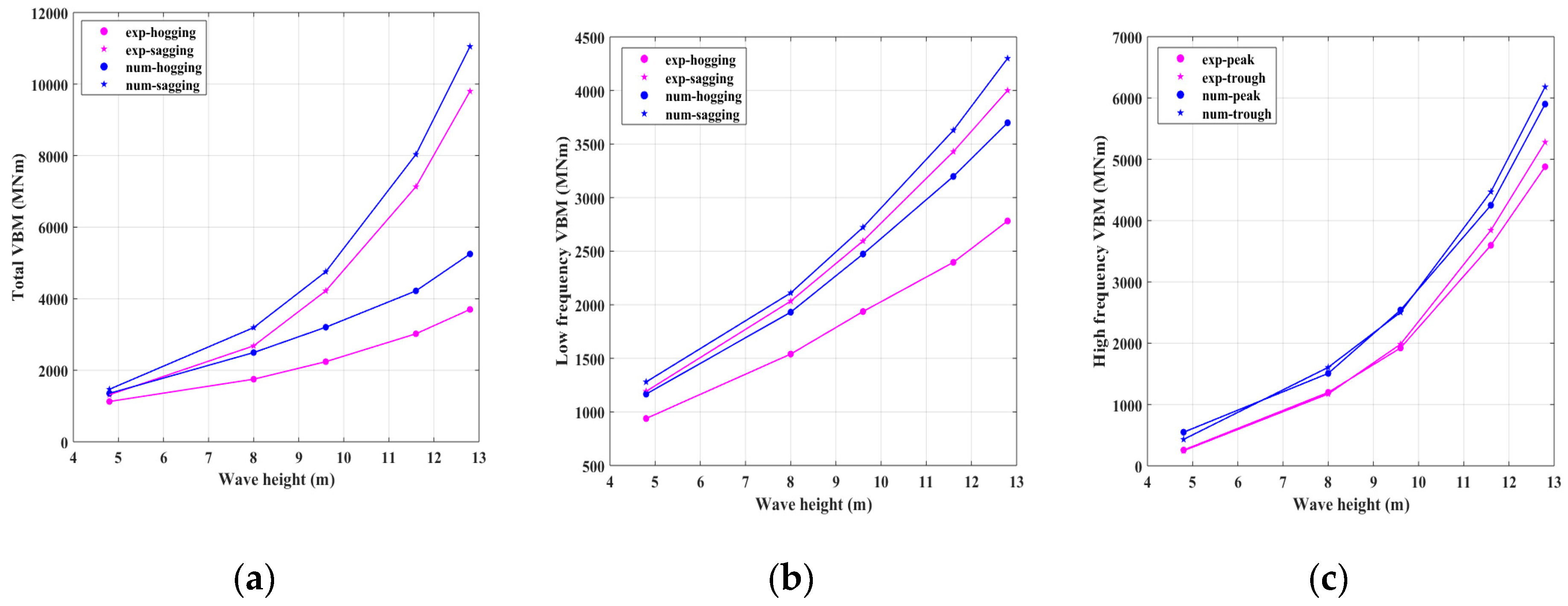
Figure 20.
MBV responses at different wave heights (V = 18 kn, λ/L = 1.0). (a) Total MBV; (b) Low frequency MB; (c) High frequency MBV.
Figure 20.
MBV responses at different wave heights (V = 18 kn, λ/L = 1.0). (a) Total MBV; (b) Low frequency MB; (c) High frequency MBV.
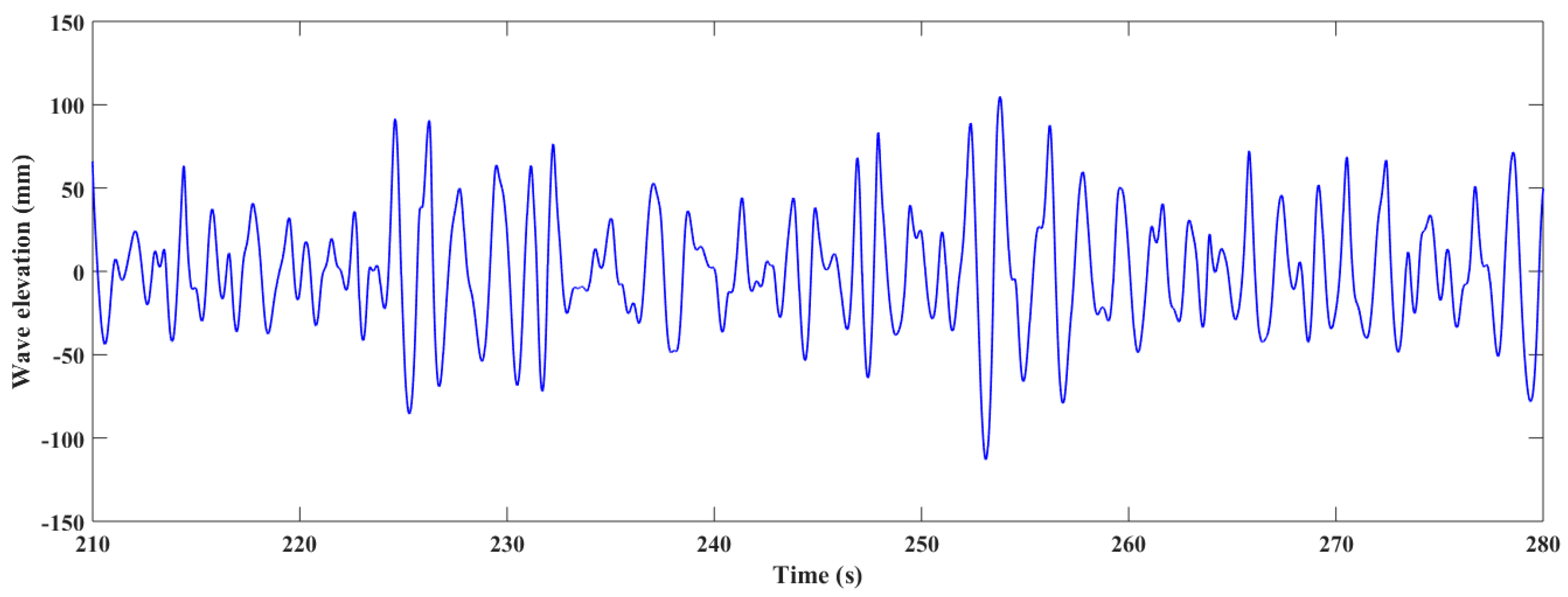
Figure 21.
Experimentally measured time series of irregular wave condition 2.
Figure 21.
Experimentally measured time series of irregular wave condition 2.
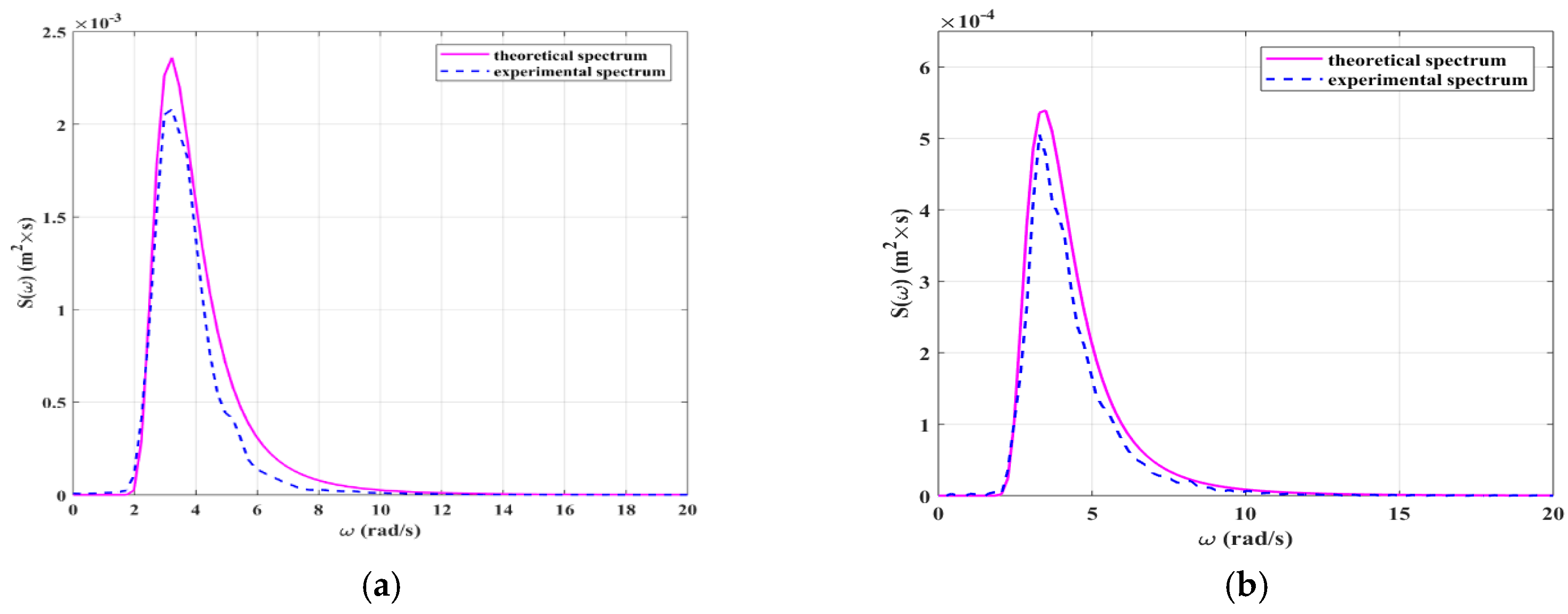
Figure 22.
Comparison of wave spectra. (a) Irregular wave condition 1; (b) Irregular wave condition 2.
Figure 22.
Comparison of wave spectra. (a) Irregular wave condition 1; (b) Irregular wave condition 2.
Figure 23.
Heave responses in irregular wave condition 1. (a) Experimental result; (b) Numerical result
Figure 23.
Heave responses in irregular wave condition 1. (a) Experimental result; (b) Numerical result
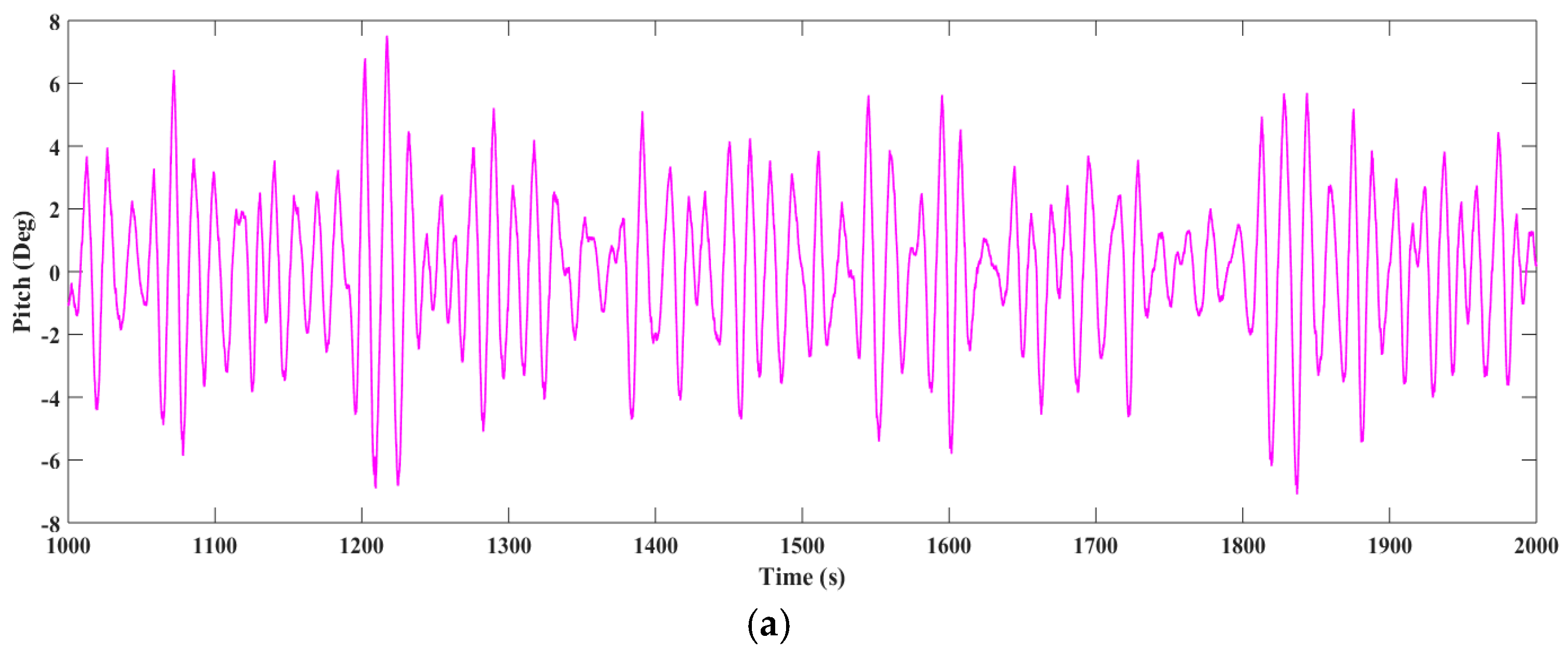
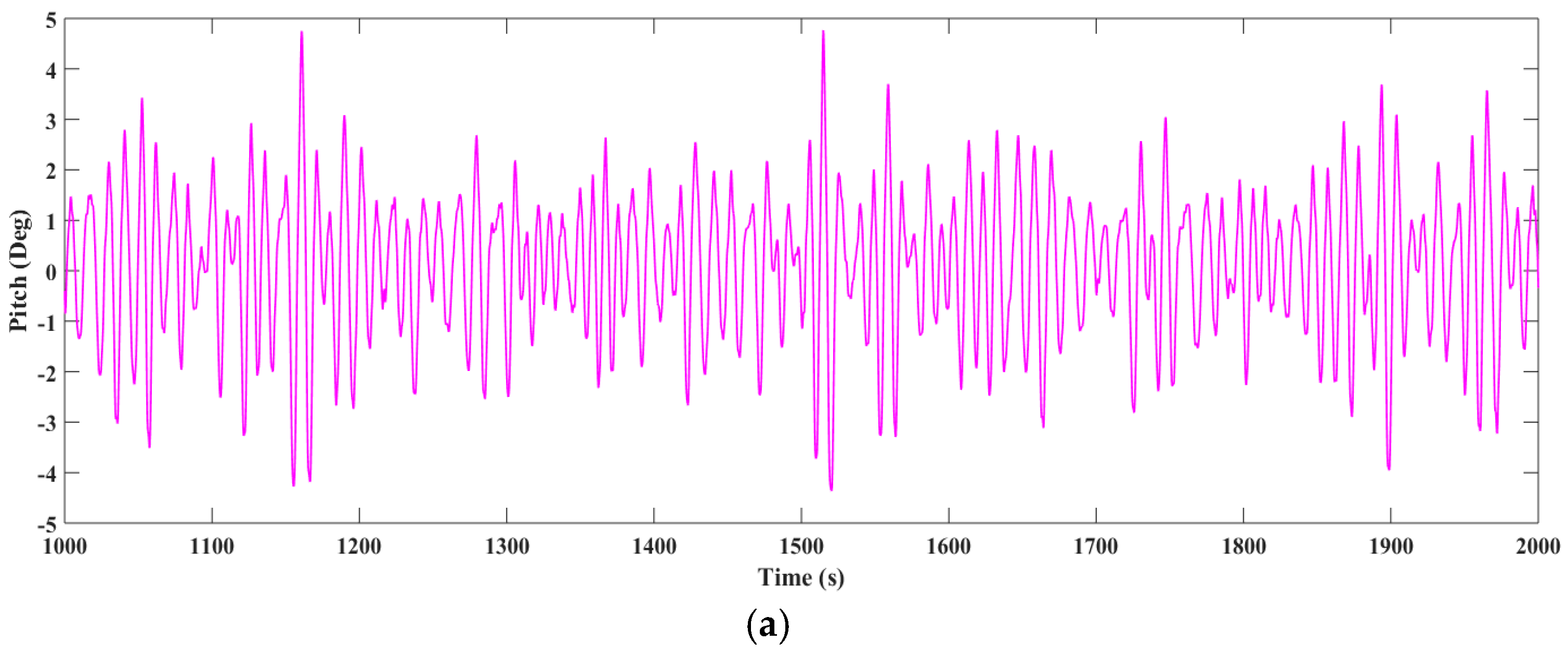
Figure 24.
Pitch responses in irregular wave condition 1. (a) Experimental result; (b) Numerical result
Figure 24.
Pitch responses in irregular wave condition 1. (a) Experimental result; (b) Numerical result
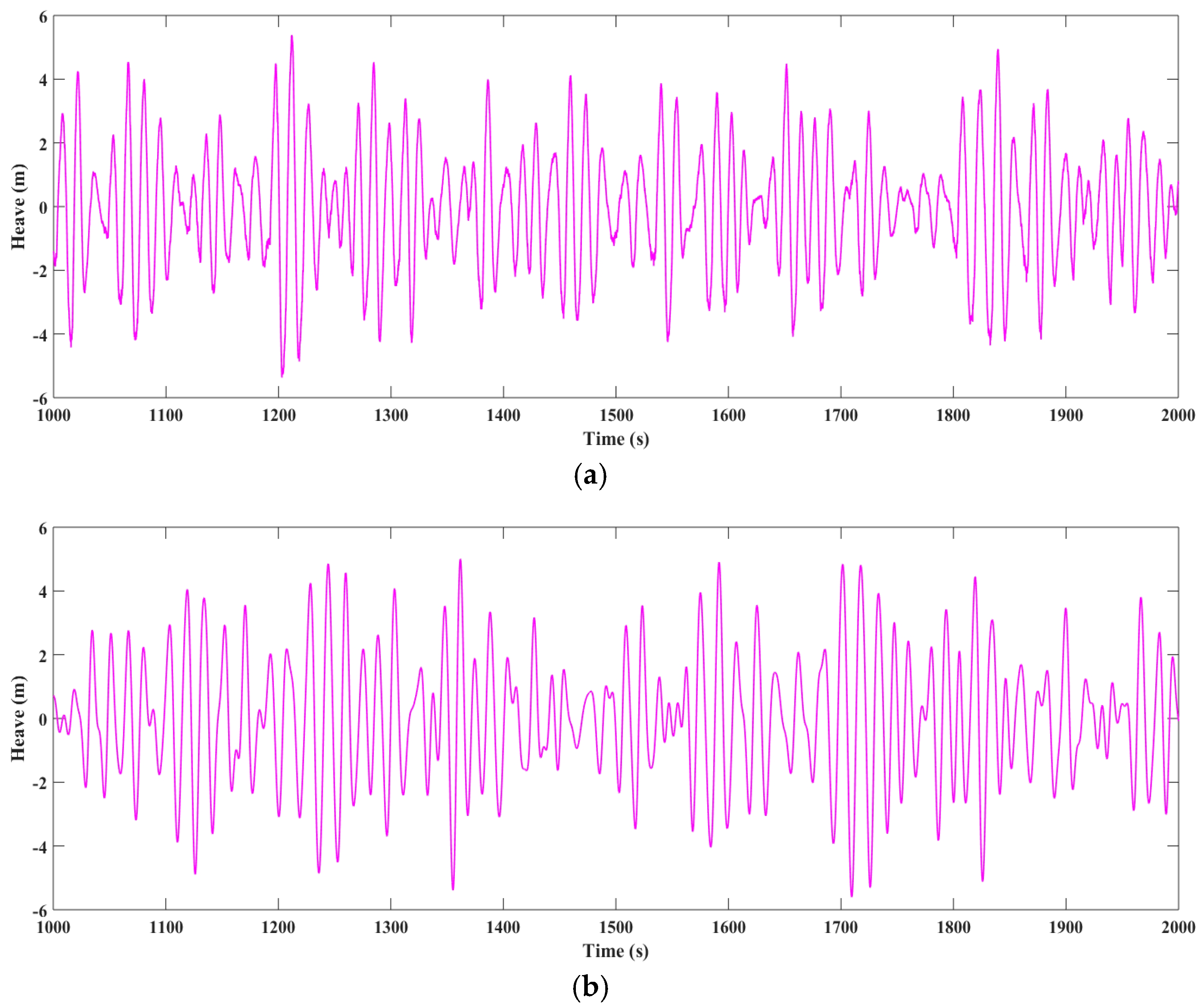
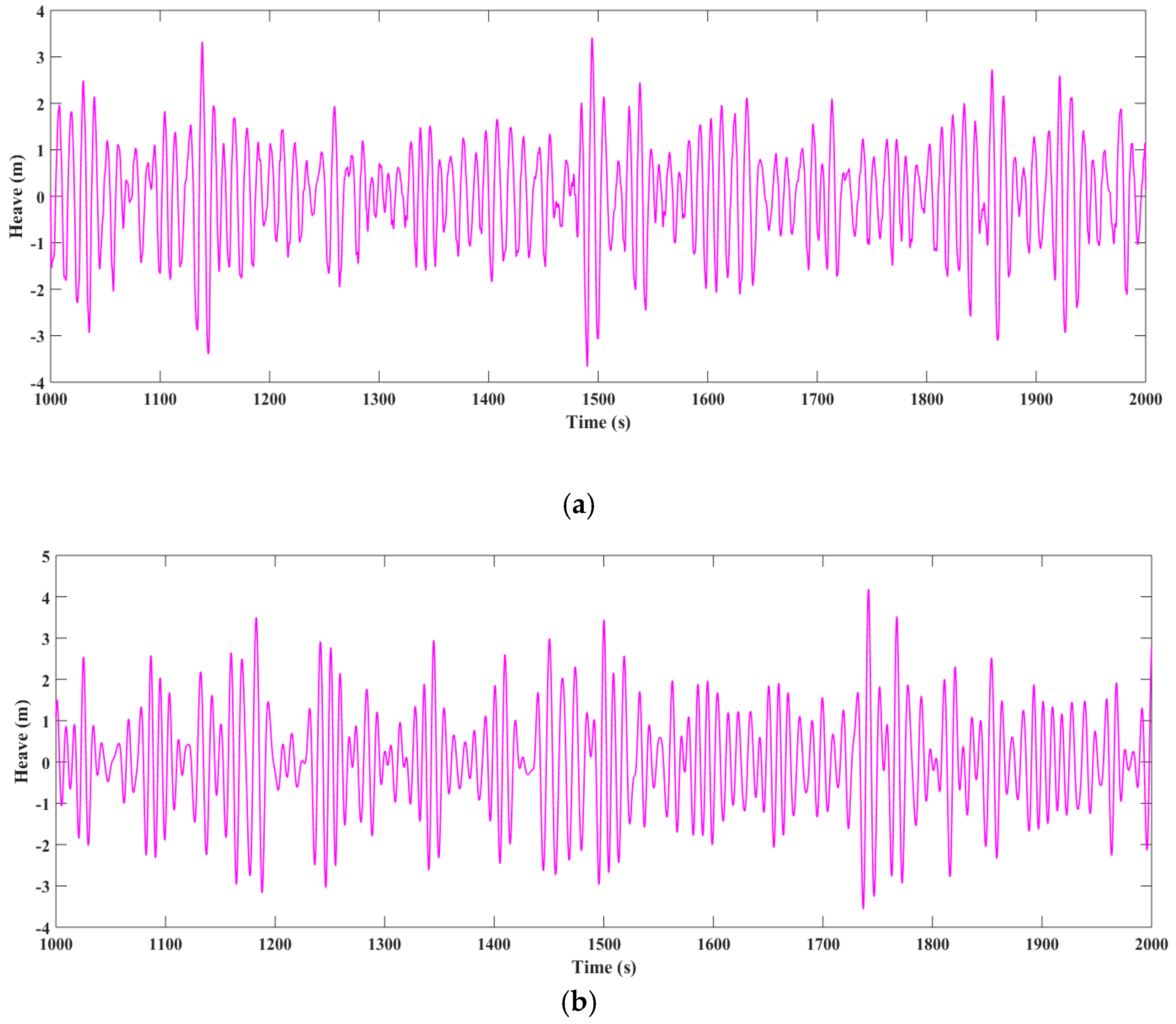
Figure 25.
Heave responses in irregular wave condition 2. (a) Experimental result; (b) Numerical result
Figure 25.
Heave responses in irregular wave condition 2. (a) Experimental result; (b) Numerical result
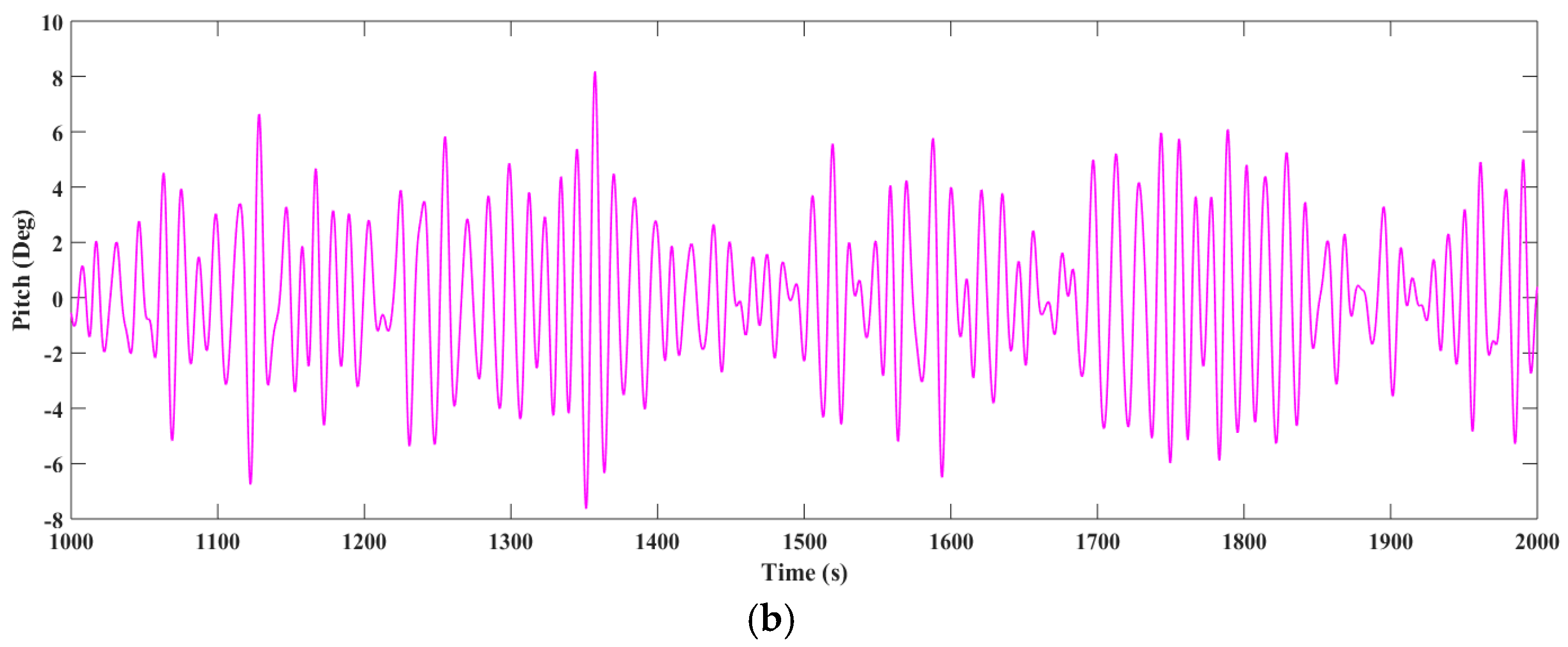
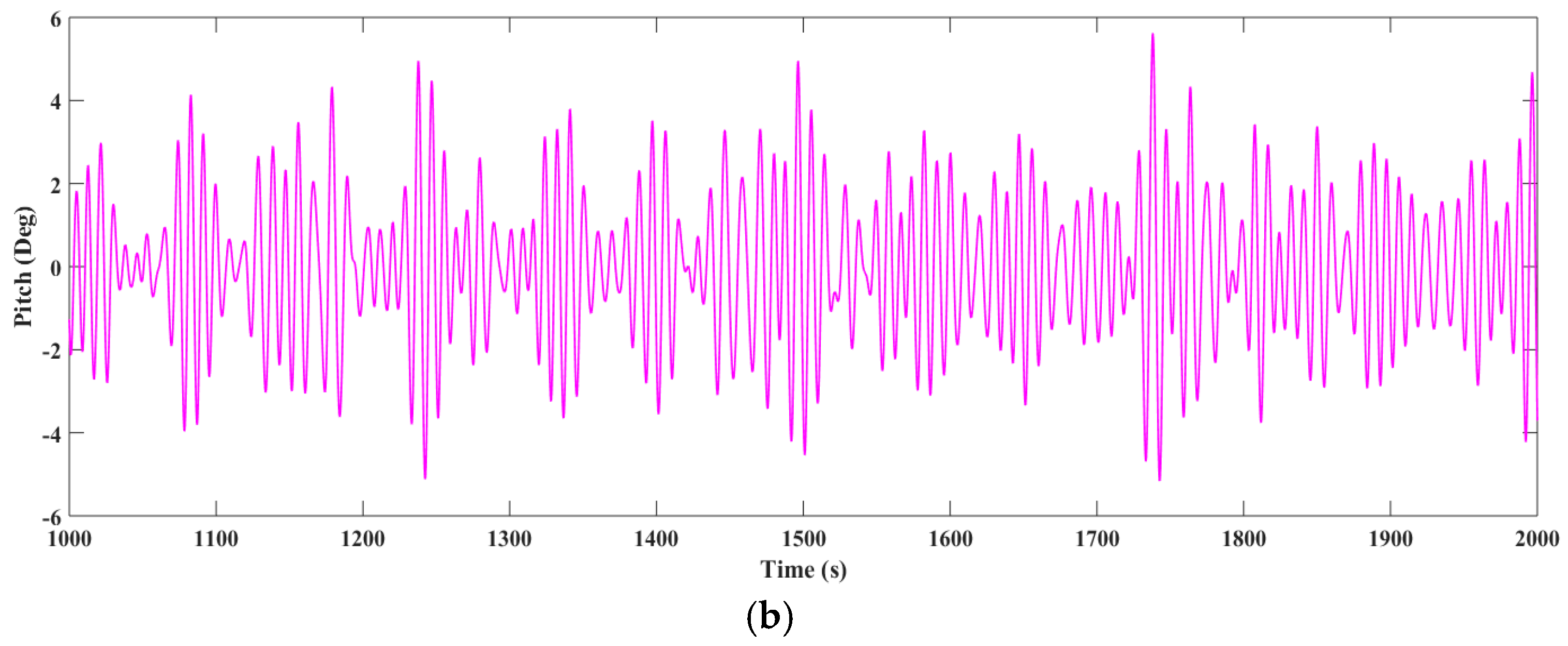
Figure 26.
Pitch responses in irregular wave condition 2. (a) Experimental result; (b) Numerical result.
Figure 26.
Pitch responses in irregular wave condition 2. (a) Experimental result; (b) Numerical result.
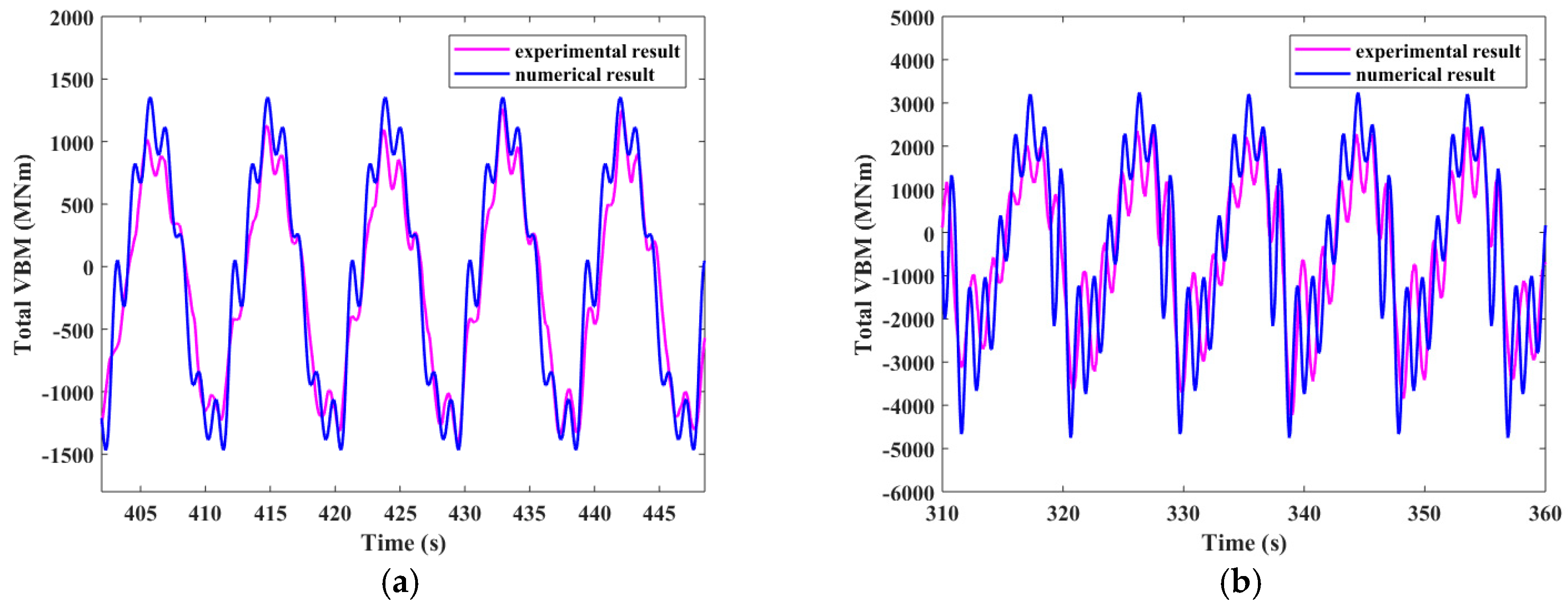
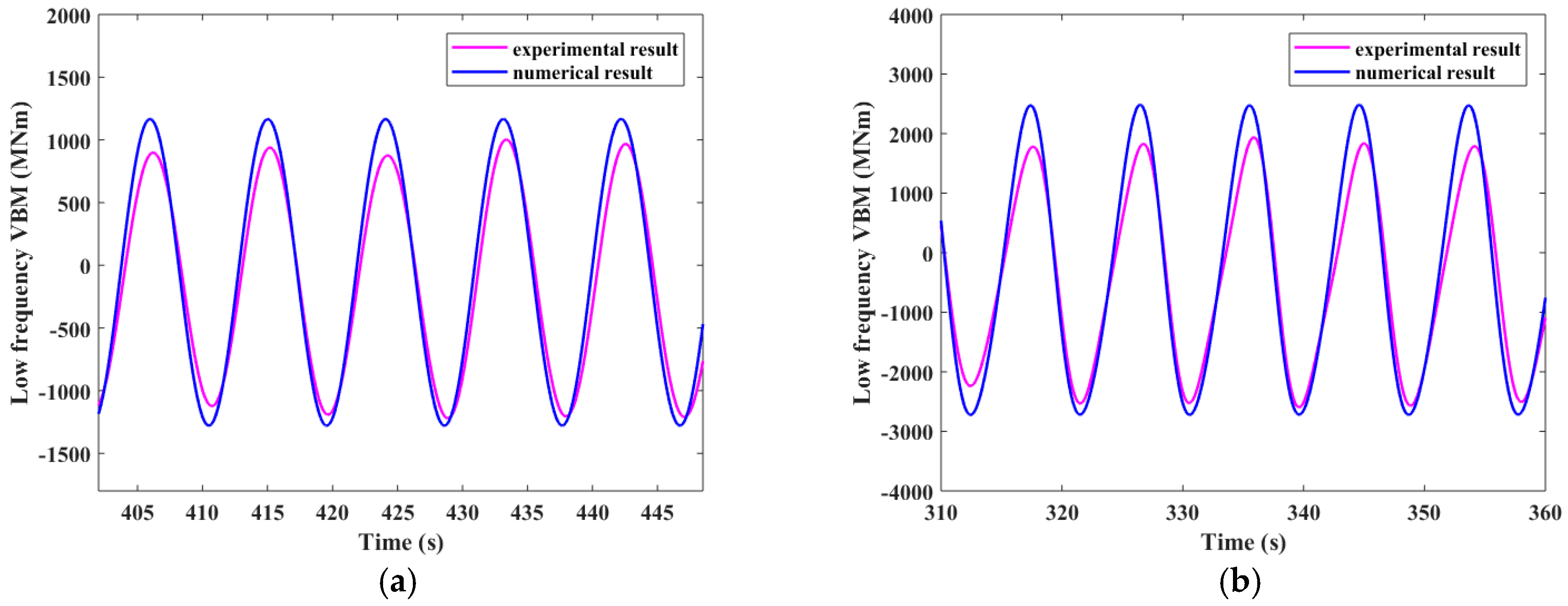
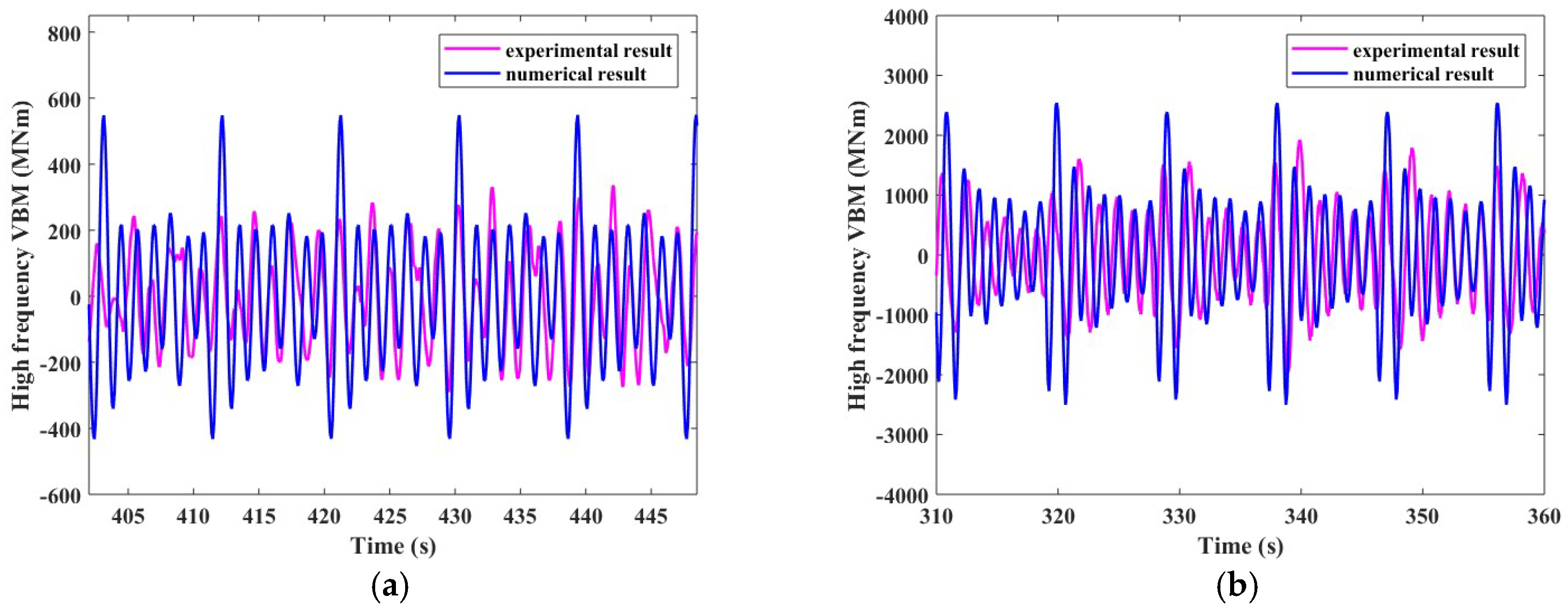
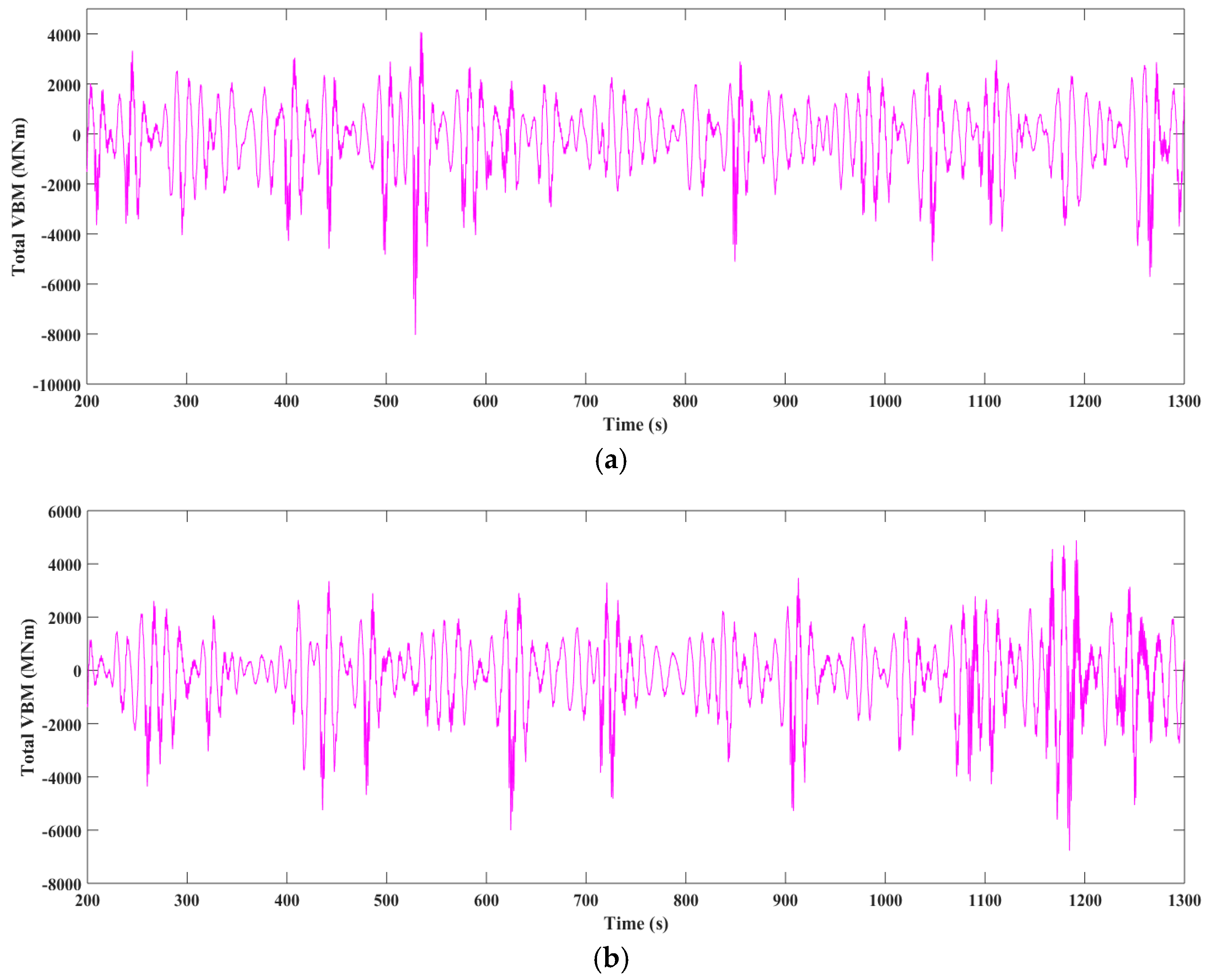
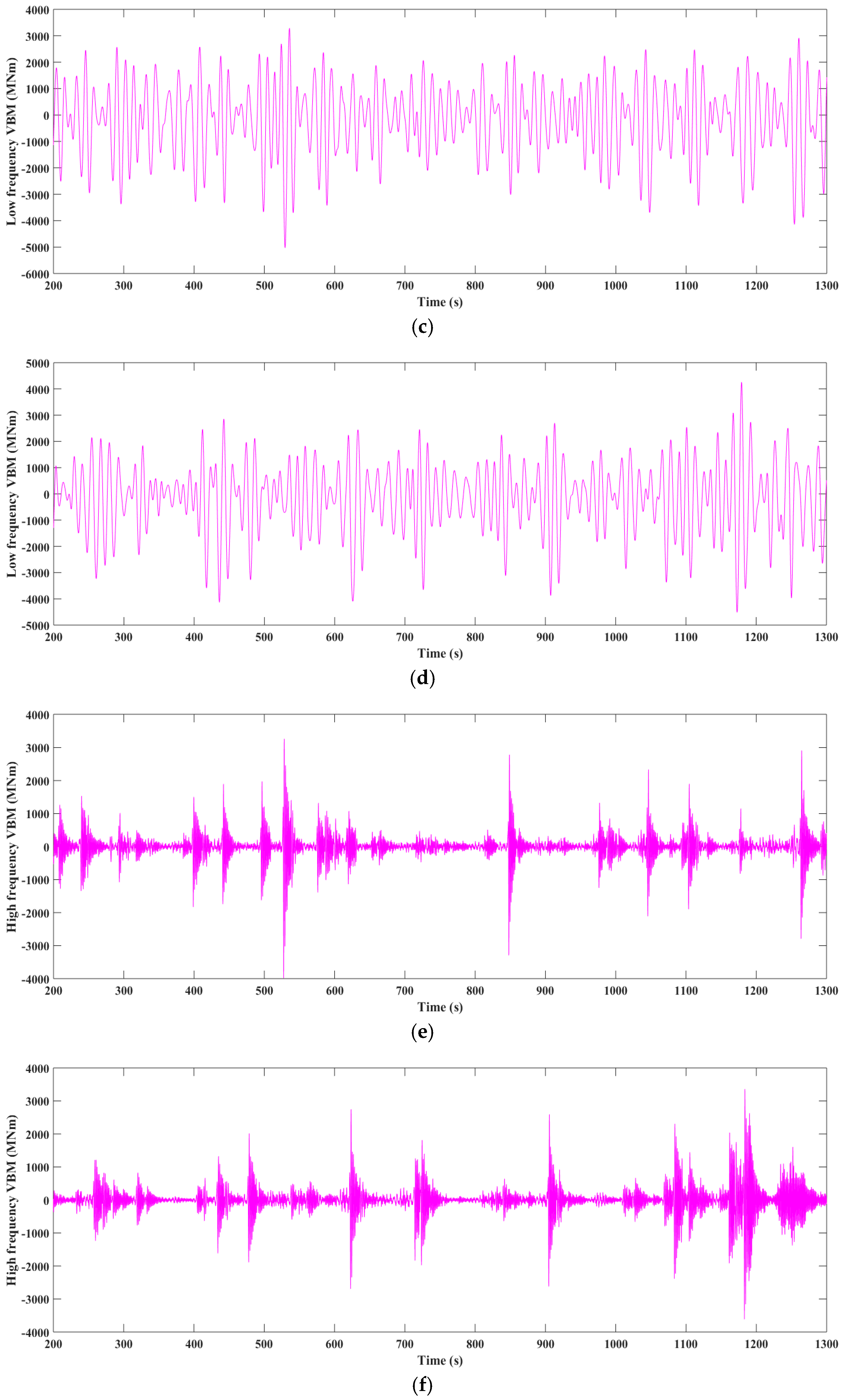
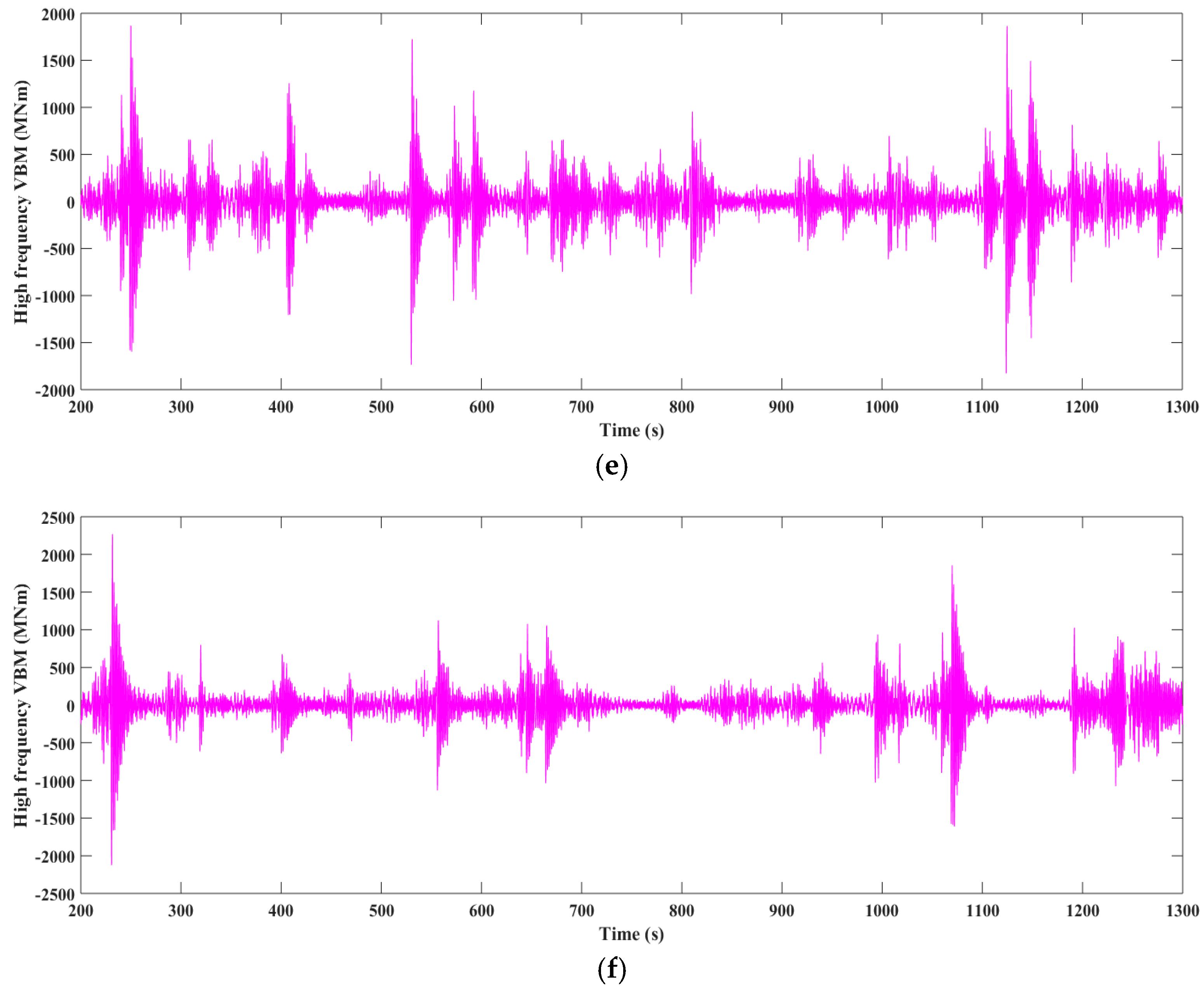
Figure 27.
Time history of MBVs amidships in irregular wave condition 1. (a) Experimental result of total MBV; (b) Numerical result of total MBV; (c) Experimental result of low frequency MBV; (d) Numerical result of low frequency MBV; (e) Experimental result of high frequency MBV; (f) Numerical result of high frequency MBV.
Figure 27.
Time history of MBVs amidships in irregular wave condition 1. (a) Experimental result of total MBV; (b) Numerical result of total MBV; (c) Experimental result of low frequency MBV; (d) Numerical result of low frequency MBV; (e) Experimental result of high frequency MBV; (f) Numerical result of high frequency MBV.
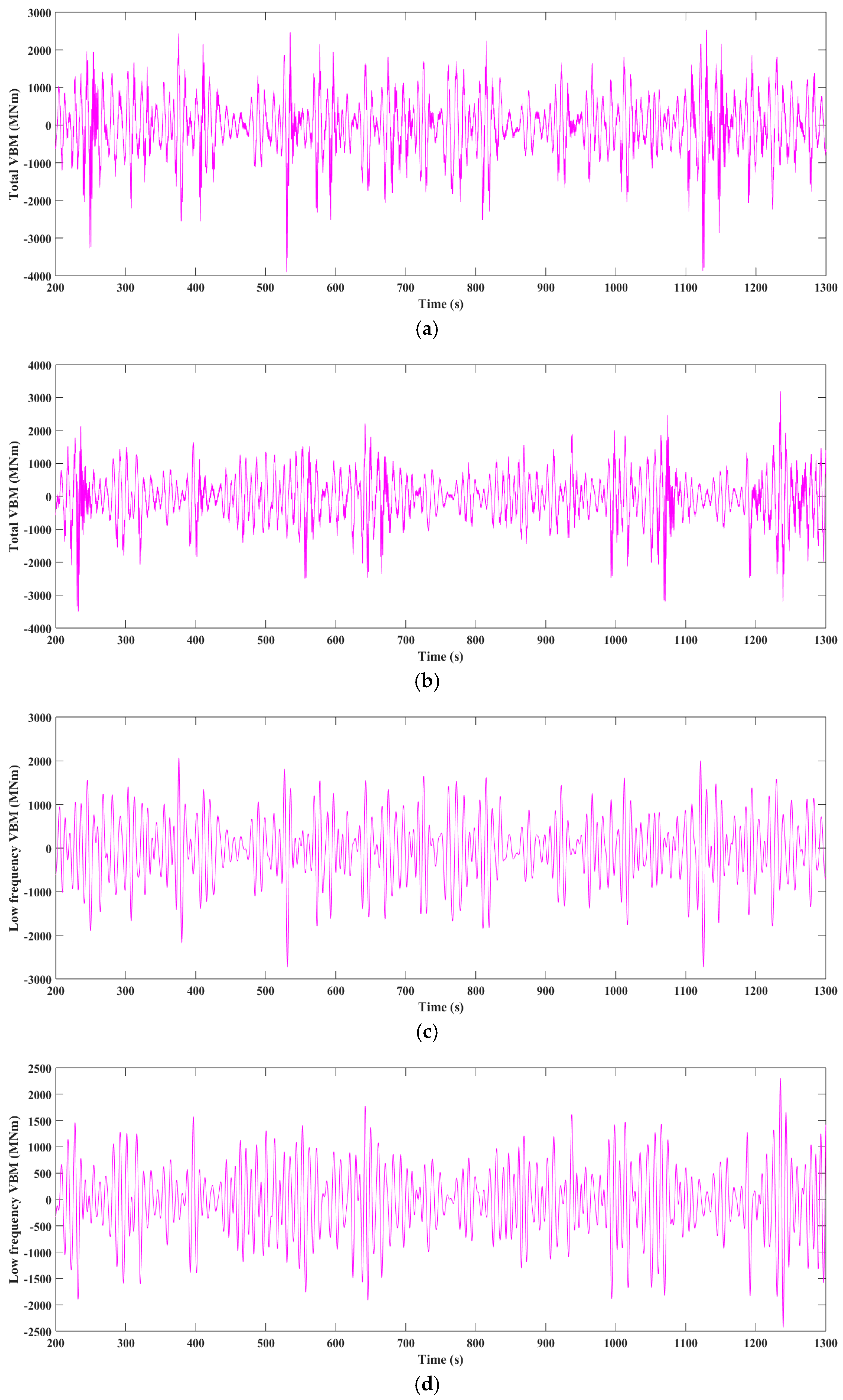
Figure 28.
Time history of MBV amidships in irregular wave condition 2. (a) Experimental result of total MBV; (b) Numerical result of total MBV; (c) Experimental result of low frequency MBV; (d) Numerical result of low frequency MBV; (e) Experimental result of high frequency MBV; (f) Numerical result of high frequency MBV.
Figure 28.
Time history of MBV amidships in irregular wave condition 2. (a) Experimental result of total MBV; (b) Numerical result of total MBV; (c) Experimental result of low frequency MBV; (d) Numerical result of low frequency MBV; (e) Experimental result of high frequency MBV; (f) Numerical result of high frequency MBV.
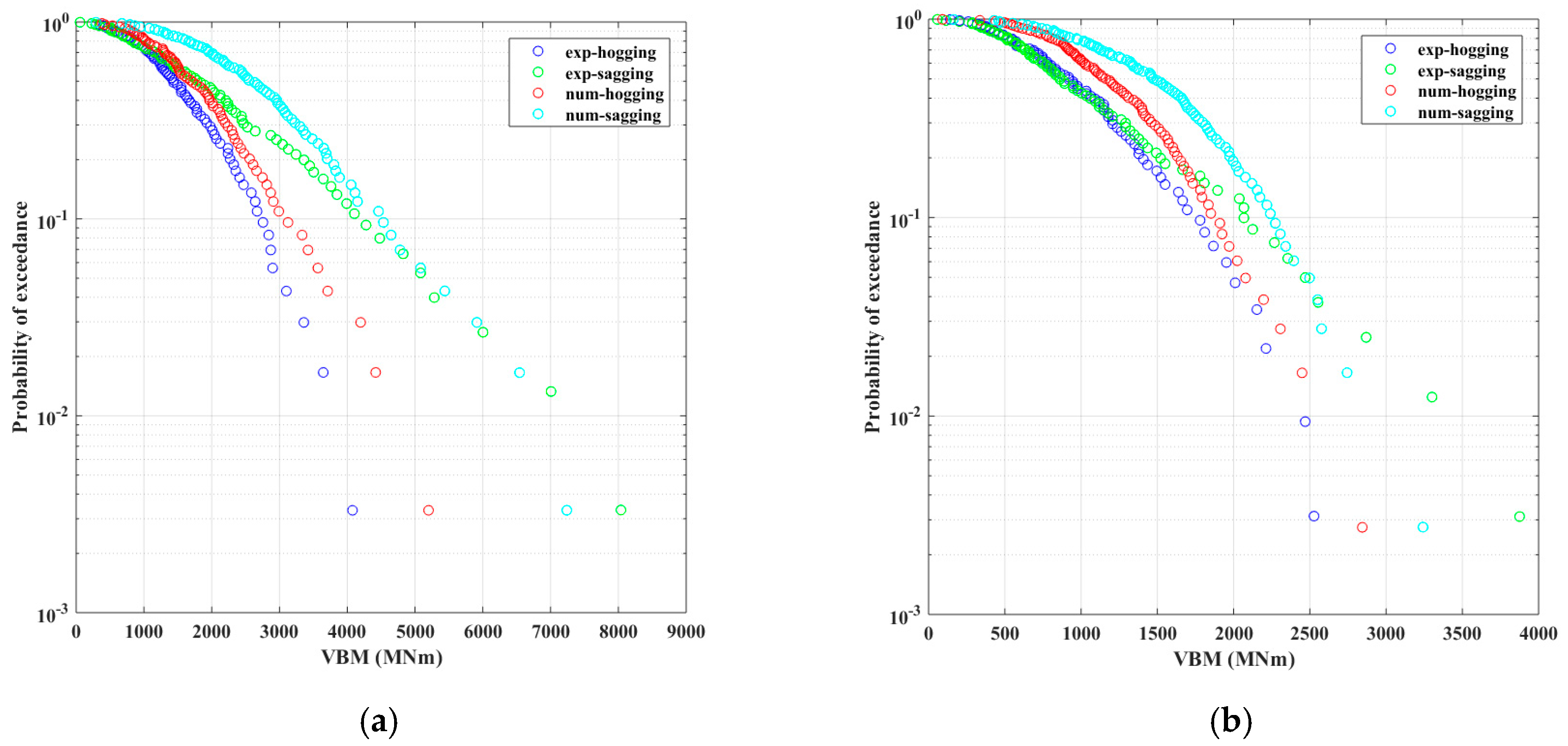
Figure 29.
Probability of exceedance of total MBV responses in irregular waves. (a) Irregular wave condition 1; (b) Irregular wave condition 2.
Figure 29.
Probability of exceedance of total MBV responses in irregular waves. (a) Irregular wave condition 1; (b) Irregular wave condition 2.
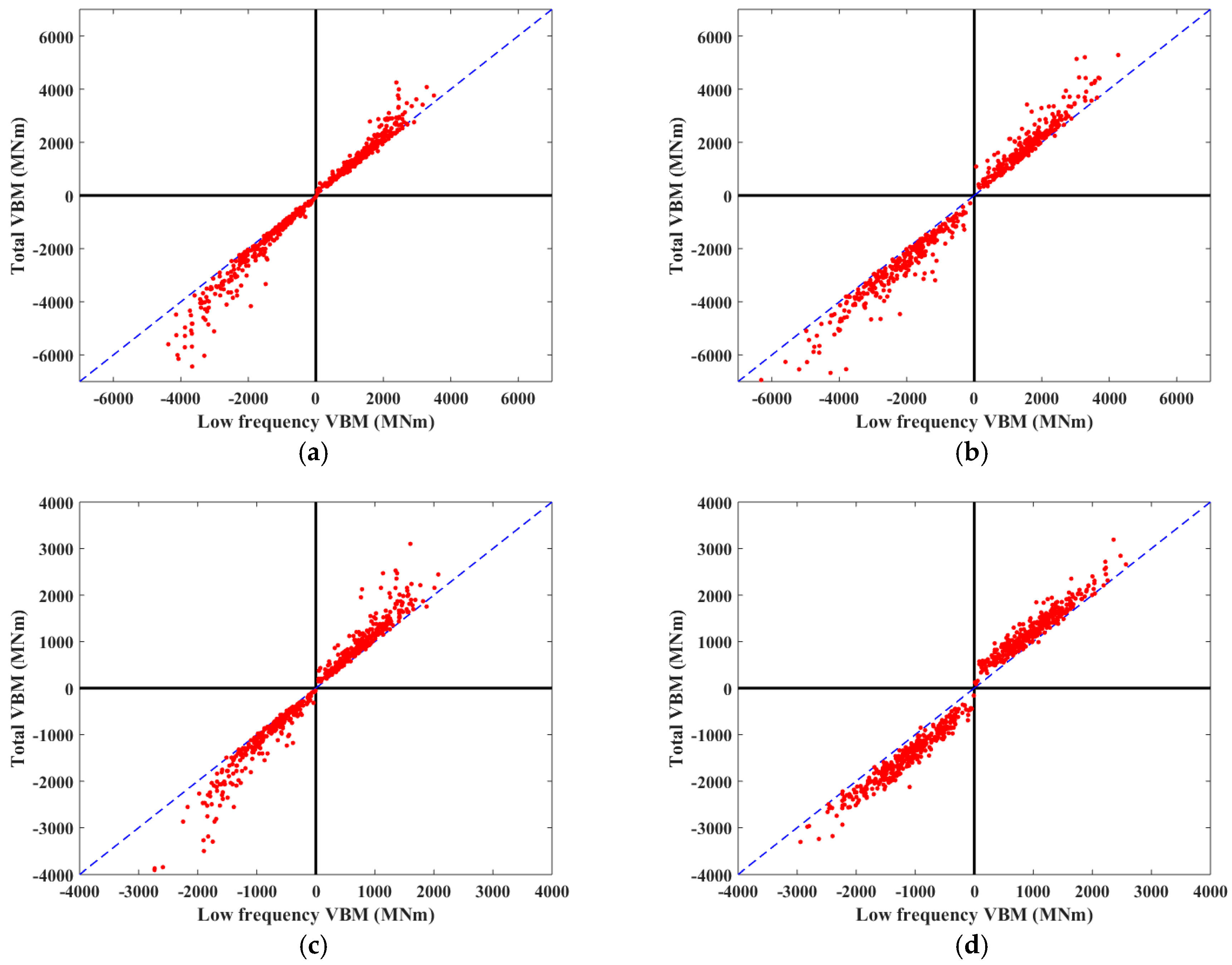
Figure 30.
Relationship between low frequency MBVs and total MBVs. (a) Experimental result for irregular condition 1; (b) Numerical result for irregular condition 1; (c) Experimental result for irregular condition 2; (d) Numerical result for irregular condition 2.
Figure 30.
Relationship between low frequency MBVs and total MBVs. (a) Experimental result for irregular condition 1; (b) Numerical result for irregular condition 1; (c) Experimental result for irregular condition 2; (d) Numerical result for irregular condition 2.
Table 1.
Main particulars of the model.
Table 1.
Main particulars of the model.
| Scale | 1:64 |
| Displacement (kg) | 195 |
| Length waterline (m) | 4.30 |
| Length overall (m) | 4.85 |
| Breadth (m) | 0.51 |
| Designed Draft (m) | 0.12 |
Table 2.
Capacities of the towing tank.
Table 2.
Capacities of the towing tank.
| Parameters | Capacity |
|---|
| Carriage speed (m/s) | 0.1~6.0 |
| Wave period (s) | 0.4~4.0 |
| Wave natural circular frequency (rad/s) | 1.57~15.70 |
| Wave length (m) | 0.25~24.99 |
| Maximum regular wave height (m) | 0.4 |
| Maximum irregular significant wave height (m) | 0.32 |
Table 3.
Experimental conditions extracted for analysis.
Table 3.
Experimental conditions extracted for analysis.
| Wave Conditions | Vessel Speed V (kn) | Wave Height H (m) | Wave Period T (s) |
| Regular wave condition 1 | 18 | 4.8 | 13.28 |
| Regular wave condition 2 | 18 | 9.6 | 13.28 |
| Wave Conditions | Vessel Speed V (kn) | Significant Wave Height H1/3 (m) | Characteristic Wave Period Tz (s) |
| Irregular wave condition 1 | 5 | 18.5 | 12.5 |
| Irregular wave condition 2 | 18 | 9.185 | 11.5 |
Table 4.
Comparison of wet natural frequencies.
Table 4.
Comparison of wet natural frequencies.
| Order of Mode | Numerical Results (Hz) | Experimental Results (Hz) | Relative Error (%) |
|---|
| First | 0.752 | 0.727 | 3.439 |
| Second | 1.531 | 1.703 | −10.100 |
| Third | 2.151 | 2.679 | −19.709 |
Table 5.
Comparison of regular wave characteristics at model scale.
Table 5.
Comparison of regular wave characteristics at model scale.
| | Condition 1 (4.8 m, 13.28 s) | Condition 2 (9.6 m, 13.28 s) |
|---|
| Experiment | Target | Error (%) | Experiment | Target | Error (%) |
|---|
| Wave height (mm) | 76.36 | 75.0 | 1.81 | 150.09 | 150.0 | 0.06 |
| Wave period (s) | 1.65 | 1.66 | −0.6 | 1.65 | 1.66 | −0.6 |
Table 6.
Comparison of irregular wave parameters at model scale.
Table 6.
Comparison of irregular wave parameters at model scale.
| | Condition 1 (H1/3 = 18.5 m, Tz = 12.5 s) | Condition 2 (H1/3 = 9.185 m, Tz = 11.5 s) |
|---|
| Experiment | Target | Error (%) | Experiment | Target | Error (%) |
|---|
| Significant wave height H1/3 (mm) | 277.504 | 289.063 | −4.0 | 139.891 | 143.516 | −2.53 |
| Characteristic wave period Tz (s) | 1.609 | 1.563 | 2.94 | 1.413 | 1.438 | −1.75 |
Table 7.
Statistical parameters of heave and pitch at CG of ship.
Table 7.
Statistical parameters of heave and pitch at CG of ship.
| Item | Condition 1 (V = 5 kn, H1/3 = 18.5 m, Tz = 12.5 s) | Condition 2 (V = 18 kn, H1/3 = 9.185 m, Tz = 11.5 s) |
|---|
| Experiment | Calculation | Error | Experiment | Calculation | Error |
|---|
| Heave | Peak significant value (m) | 3.59 | 4.03 | 12.26% | 2.15 | 2.48 | 15.35% |
| Trough significant value (m) | −3.67 | −4.04 | 10.08% | −2.22 | −2.53 | 13.96% |
| Mean value (m) | −0.06 | −0.025 | ———— | 0.0082 | −0.0037 | ———— |
| Standard deviation (m) | 2.63 | 2.90 | 10.27% | 1.56 | 1.75 | 12.18% |
| Pitch | Peak significant value (deg) | 4.75 | 5.27 | 10.95% | 2.97 | 3.47 | 16.84% |
| Trough significant value (deg) | −4.84 | −5.32 | 9.92% | −3.18 | -3.51 | 10.38% |
| Mean value (deg) | 0.025 | −0.00044 | ———— | 0.0065 | 0.00003 | ———— |
| Standard deviation (deg) | 3.42 | 3.74 | 9.36% | 2.20 | 2.49 | 13.18% |
Table 8.
Statistical parameters of total MBVs at amidship.
Table 8.
Statistical parameters of total MBVs at amidship.
| Item | Condition 1 (V = 5 kn, H1/3 = 18.5 m, Tz = 12.5 s) | Condition 2 (V = 18 kn, H1/3 = 9.185 m, Tz = 11.5 s) |
|---|
| Experiment | Calculation | Error | Experiment | Calculation | Error |
|---|
| Peak significant value (MNm) | 2519.82 | 2912.30 | 15.58% | 1604.38 | 1792.53 | 11.73% |
| Trough significant value (MNm) | −3896.74 | −4235.16 | 8.68% | −1880.67 | −2140.40 | 13.81% |
| Mean value (MNm) | −287.73 | −454.16 | ——— | -37.25 | −132.46 | ———— |
| Standard deviation (MNm) | 2247.94 | 2595.24 | 15.45% | 1216.78 | 1466.81 | 20.55% |