A Real-Time Measurement Method of Air Refractive Index Based on Special Material Etalon
Abstract
:1. Introduction
2. Theory
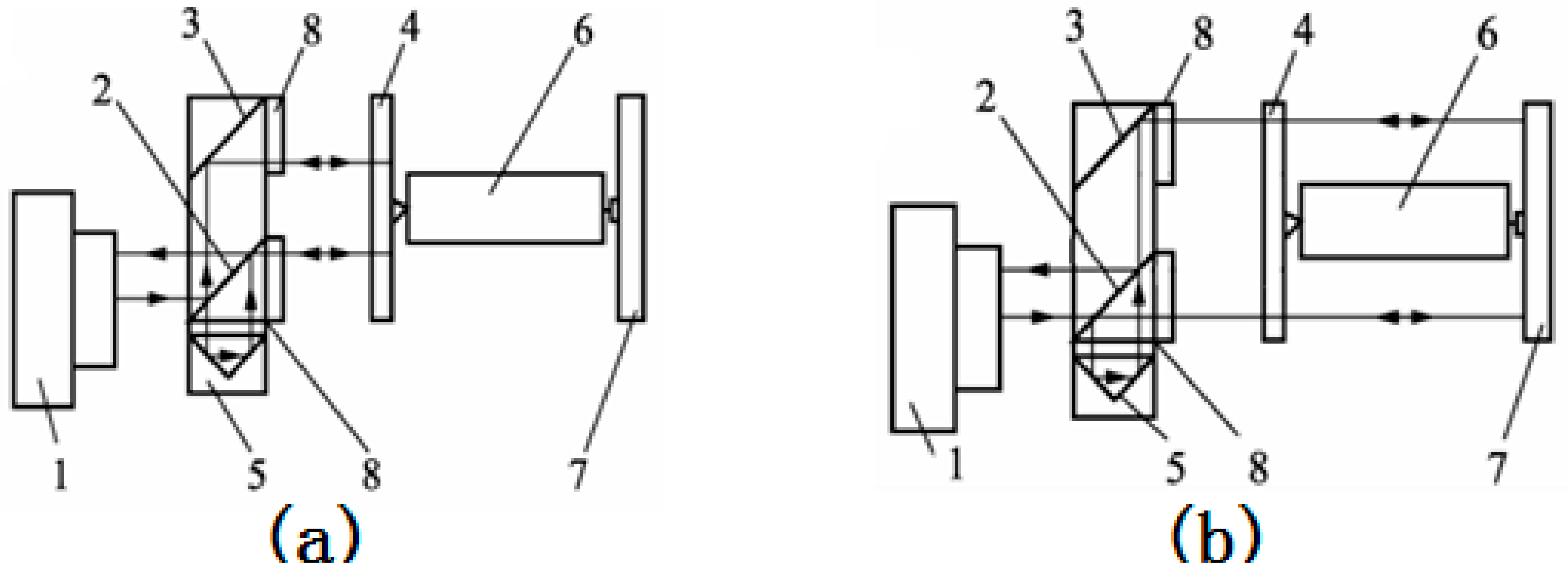
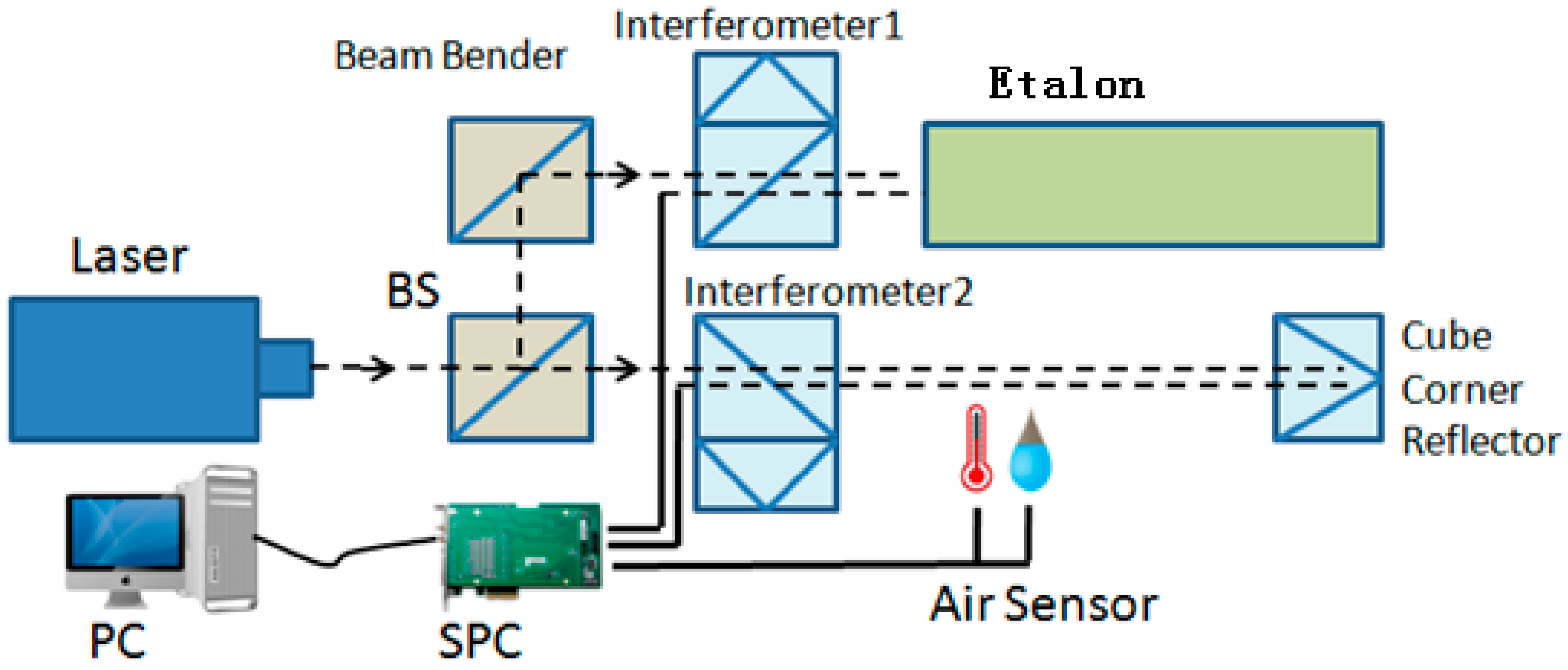
2.1. Principle of Measurement
2.2. Measurement Model
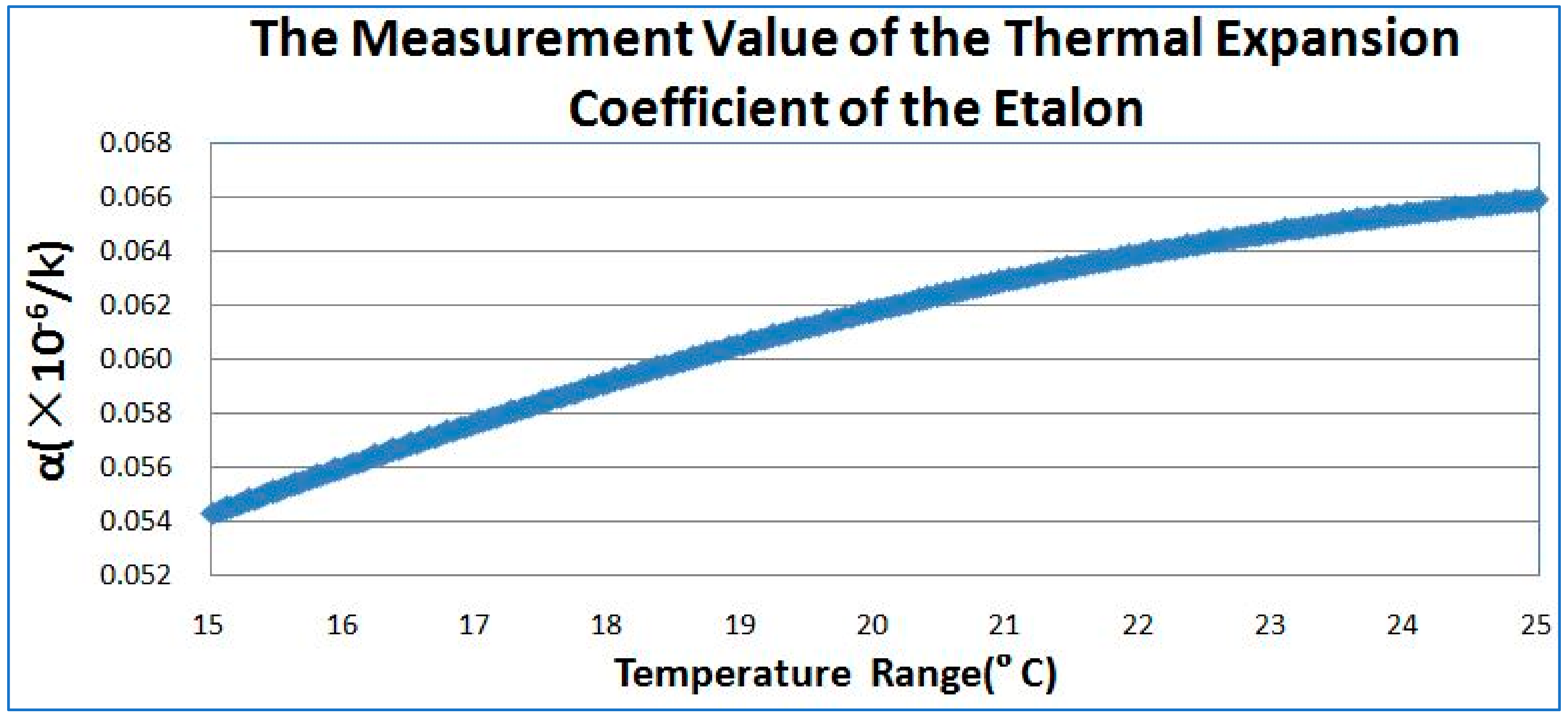
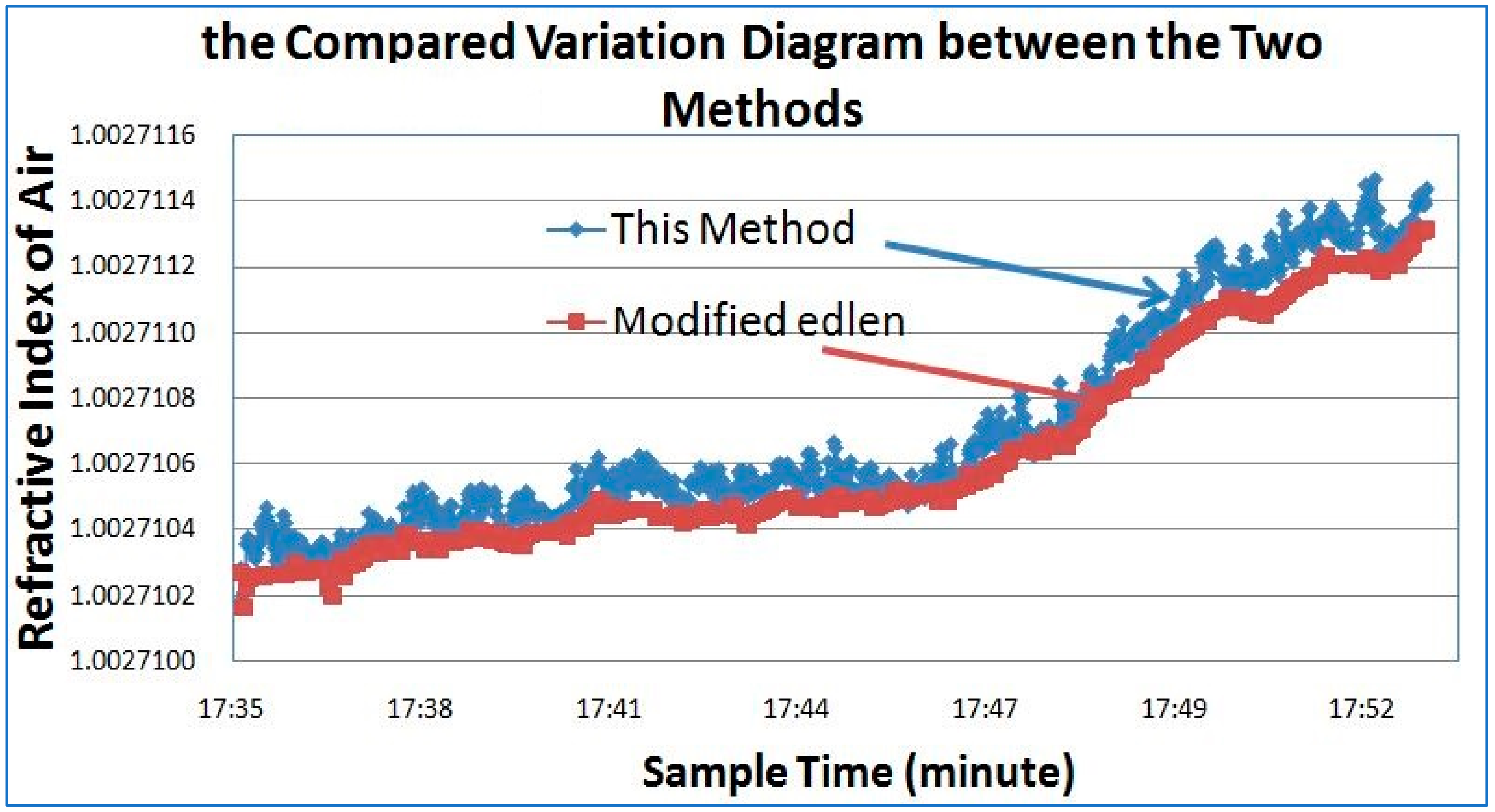
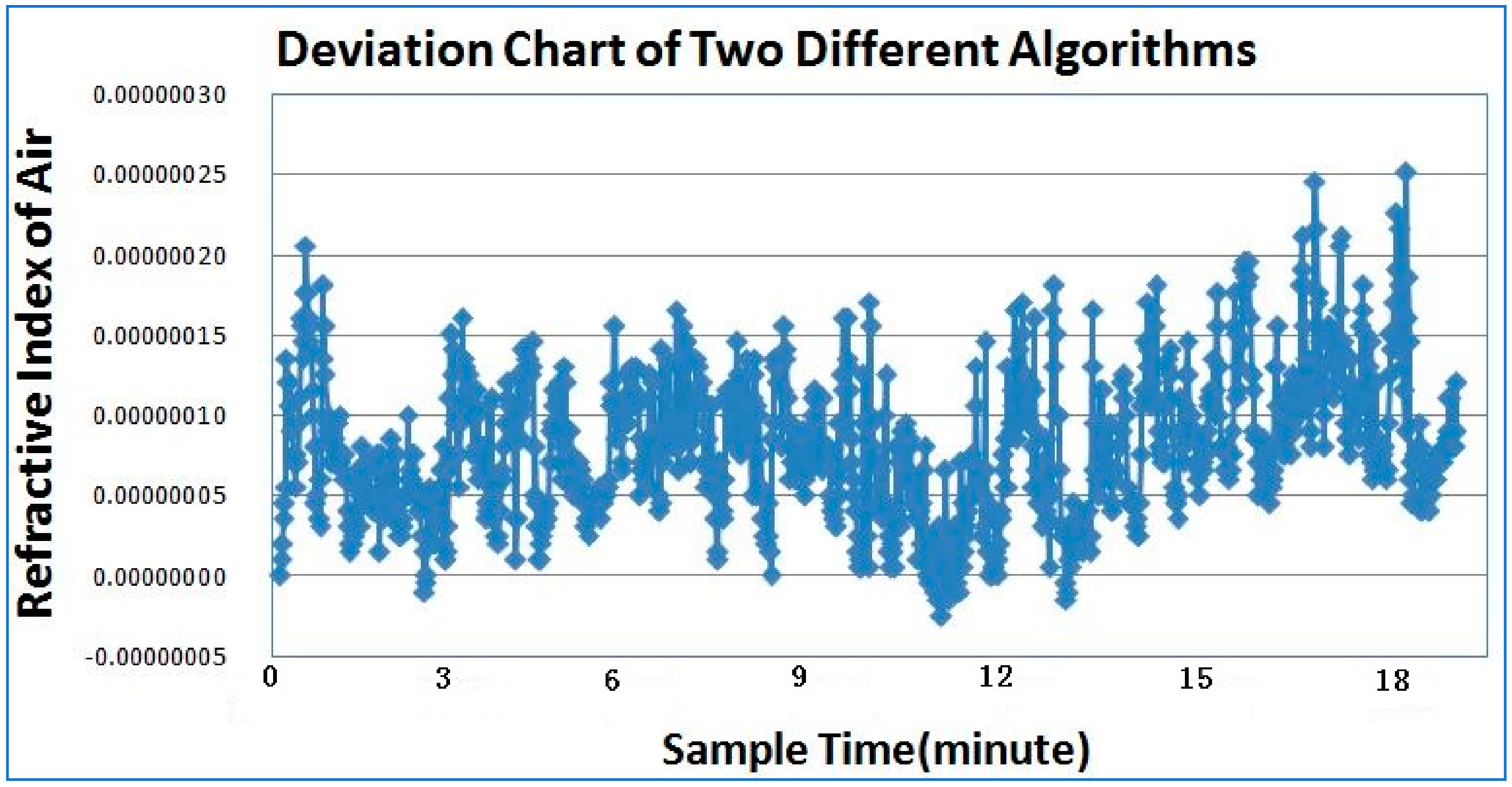
3. Experiments and Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Minoshima, K.; Arai, K.; Inaba, H. High-accuracy self-correction of refractive index of air using two-color interferometry of optical frequency combs. Opt. Express 2011, 19, 26095–26105. [Google Scholar] [CrossRef] [PubMed]
- Li, D.G.; Zhang, G.X. Measurement and compensation for refractive index of air using a pre-evacuated airtight sealed cavity. Opt. Precis. Eng. 2001, 9, 80–84. [Google Scholar]
- Li, D.G.; Zhang, G.X. Measuring refractive index of air by using a pre-evacuated airtight sealed cavity and its accuracy analysis. Opt. Tech. 2000, 26, 499–501. [Google Scholar]
- Ciddor, P.E. Refractive index of air: New equations for the visible and near infrared. Appl. Opt. 1996, 35, 1566–1573. [Google Scholar] [CrossRef] [PubMed]
- Edlén, B. The refractive index of air. Metrologia 1966, 2, 71–80. [Google Scholar] [CrossRef]
- Birch, K.P.; Downs, M.J. Correction to the Updated Edlén Equation for the Refractive Index of Air. Metrologia 2005, 31, 315–316. [Google Scholar] [CrossRef]
- Bonsch, G.; Potulski, E. Measurement of the refractive index of air and comparison with modified Edlen’s formulae. Metrologia 2003, 35, 133–139. [Google Scholar] [CrossRef]
- Giacomo, P. Equation for the Determination of the Density of Moist Air (1981). Metrologia 2005, 18, 33–40. [Google Scholar] [CrossRef]
- Beers, J.; Doiron, T. Short Communication: Verification of Revised Water Vapor Correction to the Index of Refraction of Air. Metrologia 1992, 29, 315–316. [Google Scholar] [CrossRef]
- Birch, K.P.; Reinboth, F.; Ward, R.E.; Wilkening, G. The Effect of Variations in the Refractive Index of Industrial Air upon the Uncertainty of Precision Length Measurement. Metrologia 1993, 30, 7–14. [Google Scholar] [CrossRef]
- Stone, J.A.; Zimmerman, J.H. Index of Refraction of Air. Available online: https://emtoolbox.nist.gov/Wavelength/Documentation.asp#IndexofRefractionofAir (accessed on 29 October 2018).
- Cui, J.J.; Liu, X.B.; Kang, Y.H.; Zhang, H.; Li, J.S. Calibration on Measurement System for the Refractive Index of Air Based on Edlen Formula. Acta Metrol. Sin. 2014, 35, 210–215. [Google Scholar]
- Zhang, X.D.; Su, Y.C.; Ye, X.Y. Thermal Expansion Coefficient Measurement with Precision Interferometer. Acta Metrol. Sin. 2012, 33, 1–4. [Google Scholar]
- Ren, G.Y. Precision Measurement for Feature Length of Cylinder Acoustic Resonator Cavity. Acta Metrol. Sin. 2012, 33, 212–214. [Google Scholar]
- Ren, G.Y.; Wang, W.N.; Wang, Z.J. Uncertainty Analysis for Measurement of Step Gauges Based on Coordinate Measuring Machine. Acta Metrol. Sin. 2008, 29 (Suppl. S1), 151–153. [Google Scholar]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, G.-Y.; Qu, X.-H.; Ding, S. A Real-Time Measurement Method of Air Refractive Index Based on Special Material Etalon. Appl. Sci. 2018, 8, 2325. https://doi.org/10.3390/app8112325
Ren G-Y, Qu X-H, Ding S. A Real-Time Measurement Method of Air Refractive Index Based on Special Material Etalon. Applied Sciences. 2018; 8(11):2325. https://doi.org/10.3390/app8112325
Chicago/Turabian StyleRen, Guo-Ying, Xing-Hua Qu, and Shuang Ding. 2018. "A Real-Time Measurement Method of Air Refractive Index Based on Special Material Etalon" Applied Sciences 8, no. 11: 2325. https://doi.org/10.3390/app8112325
APA StyleRen, G.-Y., Qu, X.-H., & Ding, S. (2018). A Real-Time Measurement Method of Air Refractive Index Based on Special Material Etalon. Applied Sciences, 8(11), 2325. https://doi.org/10.3390/app8112325



