LIDAR Point Cloud Registration for Sensing and Reconstruction of Unstructured Terrain
Abstract
1. Introduction
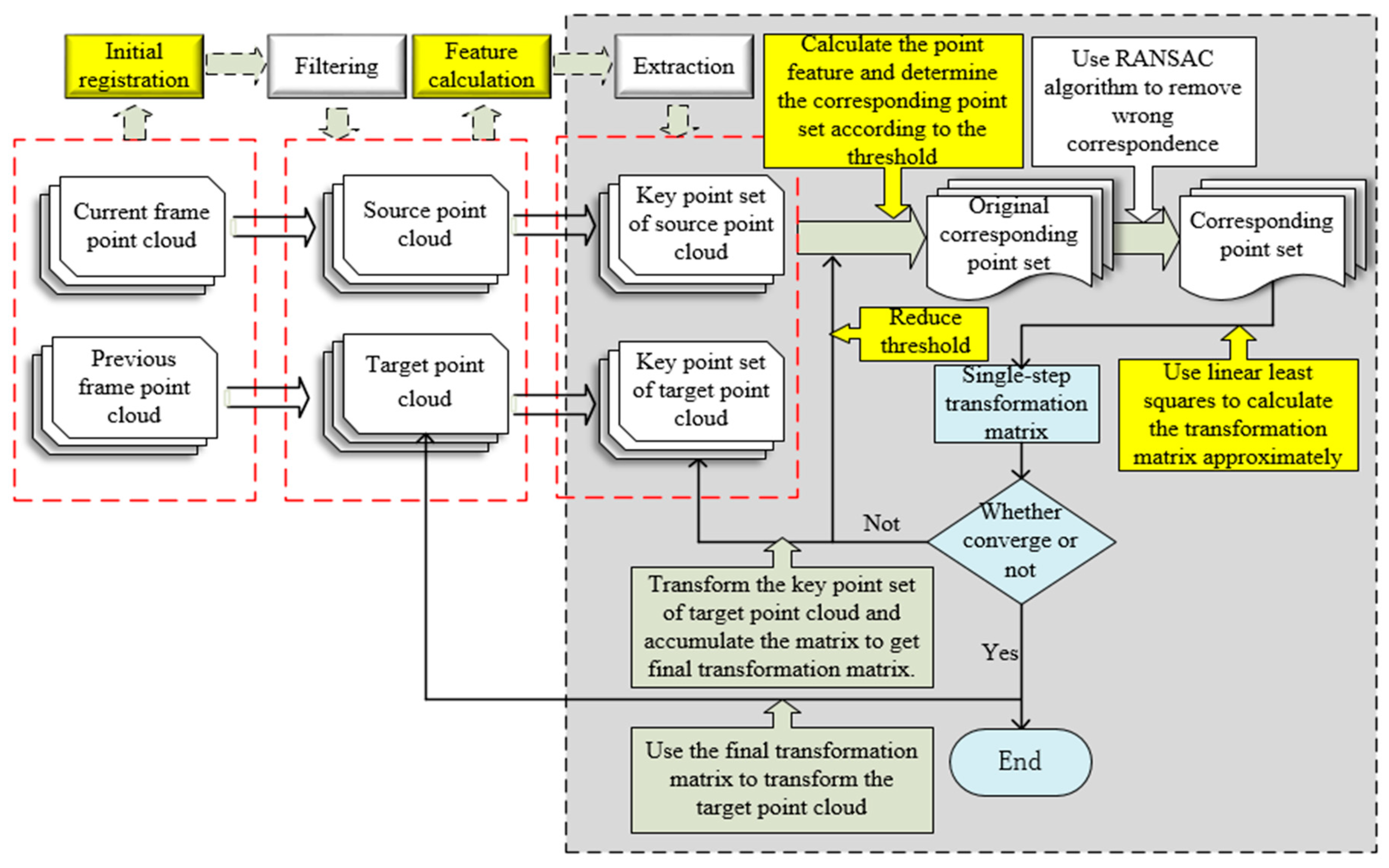
2. Initial Registration
3. Accurate Registration
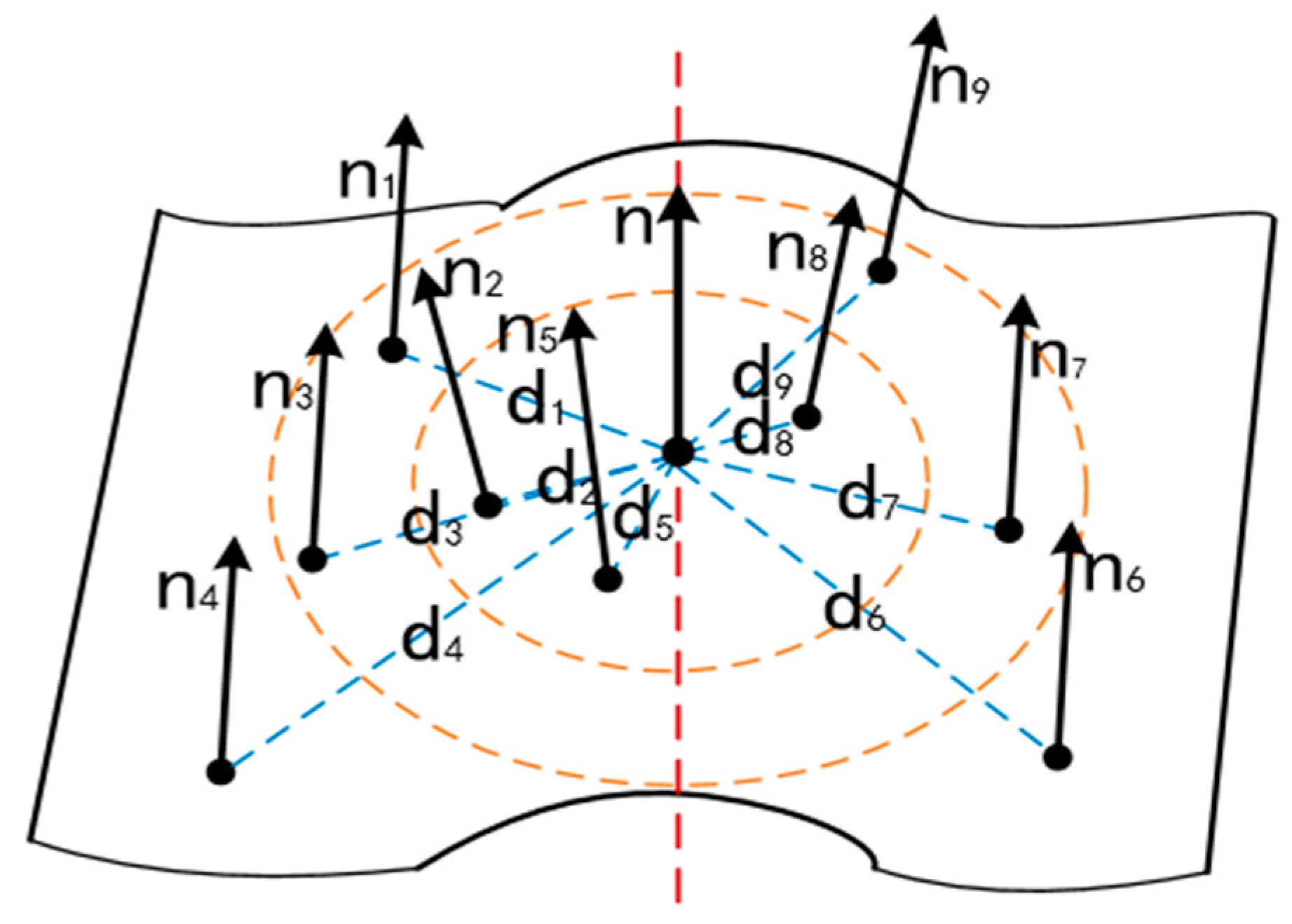
3.1. Key Points Extraction
3.2. Building Neighborhood Feature Descriptor
3.3. Transform Matrix Calculation
4. Experimental Results and Analysis
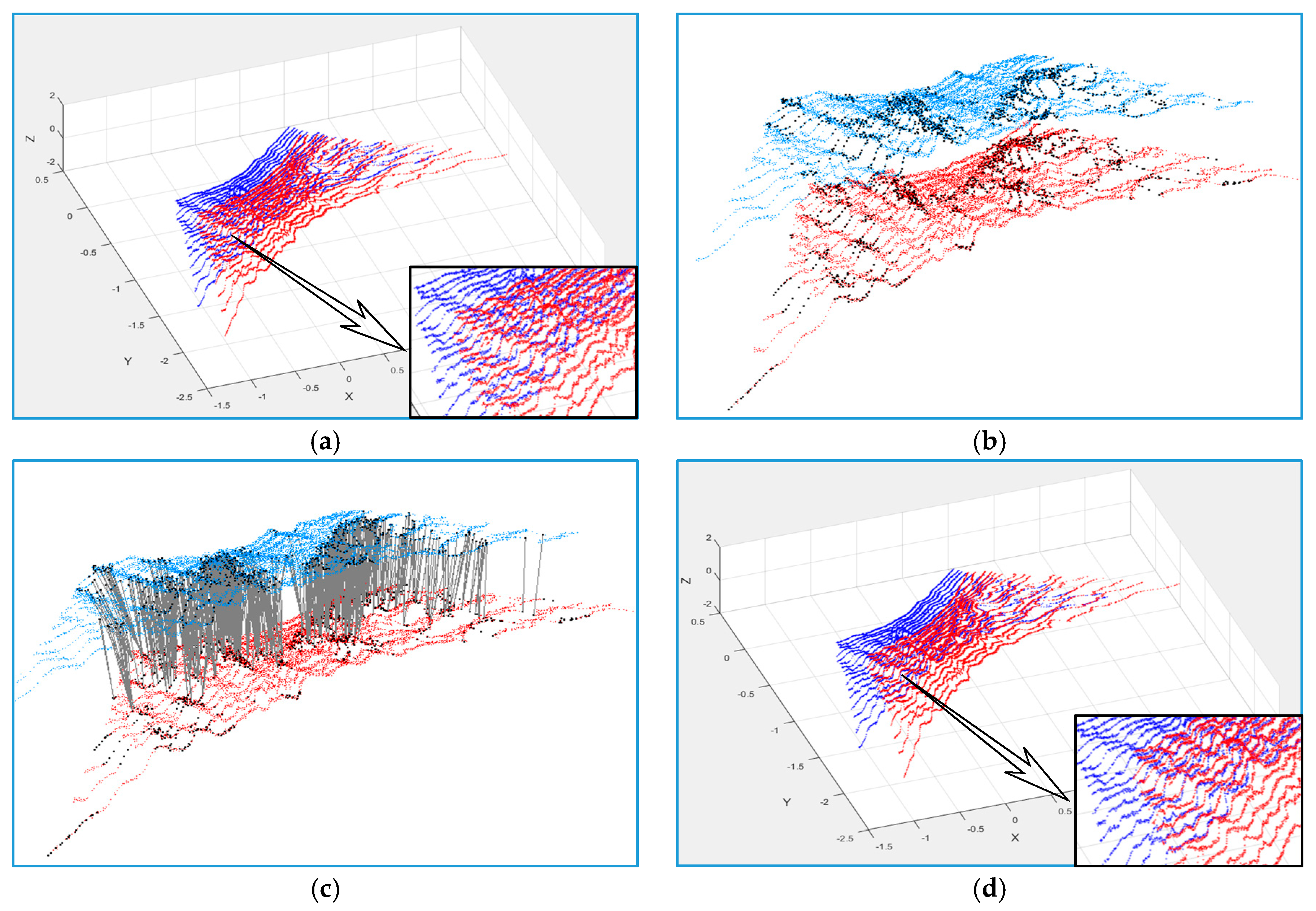
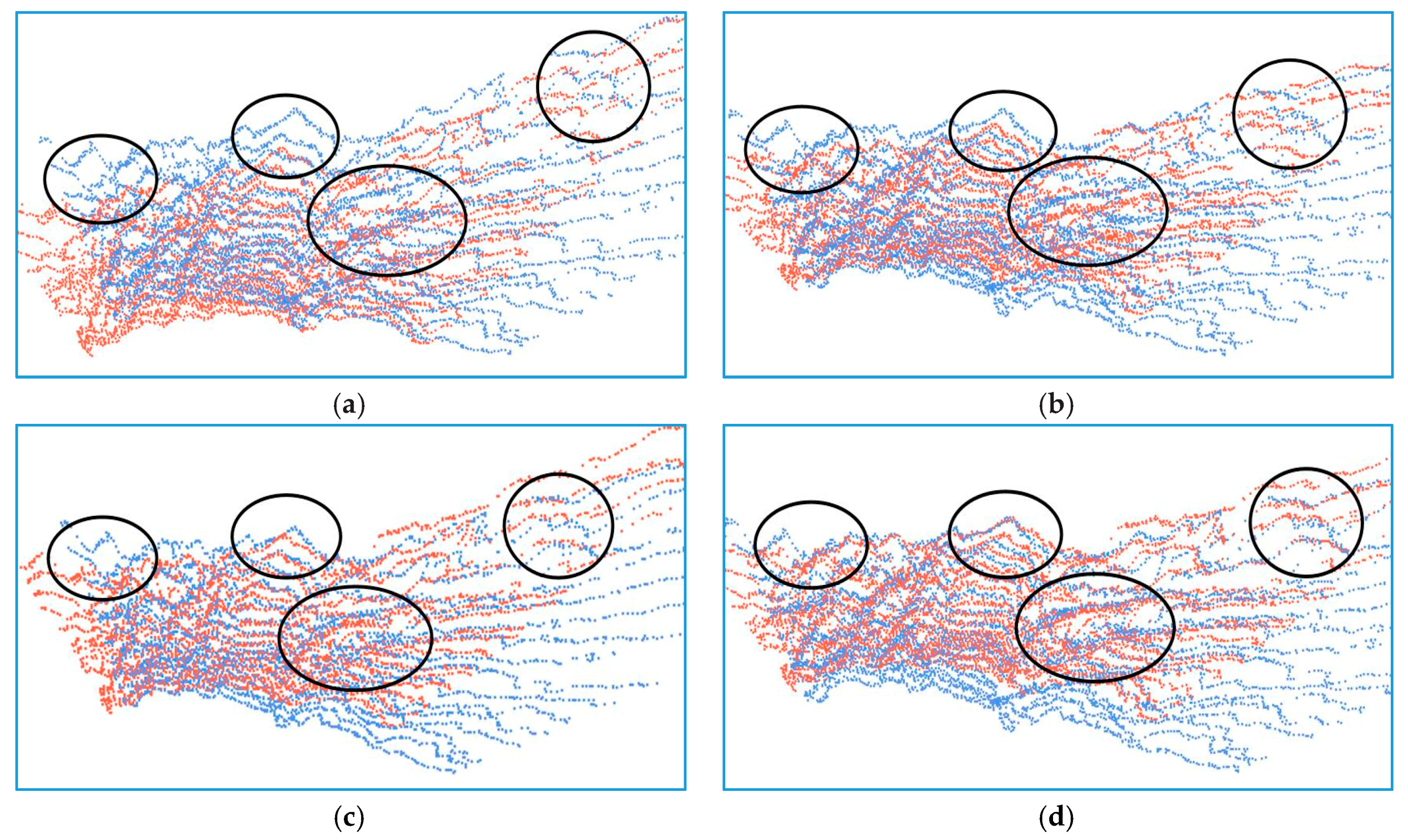
4.1. Validity Validation of our Improved ICP Algorithm
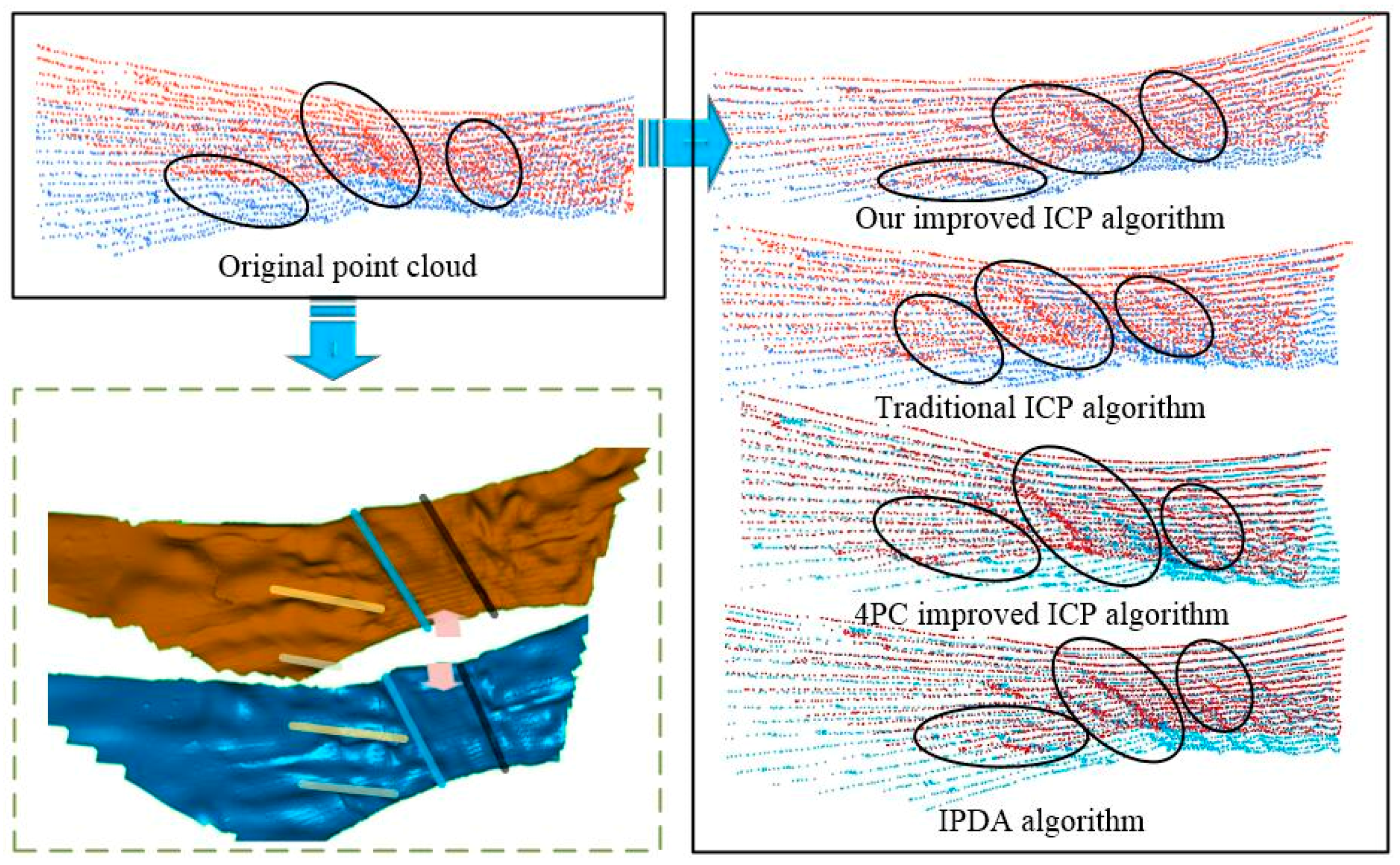
4.2. Superiority Validation of our Improved ICP Algorithm
- (1)
- Conduct initial registration and filtering for the original point cloud pair to obtain the source point cloud and the target point cloud.
- (2)
- Use our improved ICP algorithm to register target point cloud with source point cloud, and then record the data.
- (3)
- Use our key point extraction method to obtain the key point sets of the source point cloud and the target point cloud, and then use traditional ICP algorithm, 4PC improved ICP algorithm [28] and IPDA (Integrated Probabilistic Data Association) algorithm [29] separately to register the two key point sets, and finally record the data.
4.3. Necessity Validation of the Initial Registration
4.4. Fast Acquisition of Point Cloud Information for Timeliness Demand
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Oskiper, T.; Sizintsev, M.; Branzoi, V.; Samarasekera, S.; Kumar, R. Augmented Reality binoculars. IEEE Trans. Vis. Comput. Gr. 2015, 21, 611–623. [Google Scholar] [CrossRef] [PubMed]
- Lv, Z.Y.; Shi, W.Z.; Zhou, X.C.; Benediktsson, J. Semi-Automatic System for Land Cover Change Detection Using Bi-Temporal Remote Sensing Images. Remote Sens. 2017, 9, 1112. [Google Scholar] [CrossRef]
- Han, M.; Bo, Z.; Qian, K.; Fang, F. 3dlocalization and mapping of outdoor mobile robots using a Lidar. J. Huazhong Univ. Sci. Technol. 2015, 43, 315–318. [Google Scholar]
- Gézero, L.; Antunes, C. An efficient method to create digital terrain models from point clouds collected by mobile lidar systems. ISPRS Int. Arch. Photogramm. Remote Sens. Spati. Inf. Sci. 2017, 42, 289–296. [Google Scholar] [CrossRef]
- Van der Mark, W.; Groen, F.C.A.; Van Den Heuvel, J.C. Stereo based navigation in unstructured environments. In Proceedings of the IEEE Conference on Instrumentation and Measurement Technology, Budapest, Hungary, 21–23 May 2001; Volume 3, pp. 2038–2043. [Google Scholar]
- Zhang, T.; Du, Y.; Lu, F. Super-Resolution Reconstruction of Remote Sensing Images Using Multiple-Point Statistics and Isometric Mapping. Remote Sens. 2017, 9, 724. [Google Scholar] [CrossRef]
- Balsa-Barreiro, J.; Lerma, J.L. Empirical study of variation in Lidar point density over different land covers. Int. J. Remote Sens. 2014, 35, 3372–3383. [Google Scholar] [CrossRef]
- Balsa-Barreiro, J.; Avariento, J.P.; Lerma, J.L. Airborne light detection and ranging (Lidar) point density analysis. Sci. Res. Essays 2012, 7, 3010–3019. [Google Scholar] [CrossRef]
- Li, R.; Liu, J.; Zhang, L.; Hang, Y. LIDAR/MEMS IMU integrated navigation (SLAM) method for a small UAV in indoor environments. In Proceedings of the Inertial Sensors and Systems Symposium, Karlsruhe, Germany, 16–17 September 2014; pp. 1–15. [Google Scholar]
- Zhang, X.; Shi, H.; Pan, J.; Zhang, C. Integrated navigation method based on inertial navigation system and Lidar. Opt. Eng. 2016, 55, 044102. [Google Scholar] [CrossRef]
- Besl, P.; Mckay, N. A method for registration for 3D shapes. In Sensor Fusion IV: Control Paradigms and Data Structures; International Society for Optics and Photonics: San Diego, CA, USA, 1992. [Google Scholar]
- Li, W.; Song, P. A modified ICP algorithm based on dynamic adjustment factor for registration of point cloud and CAD model. Pattern Recognit. Lett. 2015, 65, 88–94. [Google Scholar] [CrossRef]
- Li, S.; Wang, J.; Liang, Z.; Su, L. Tree point clouds registration using an improved ICP algorithm based on kd-tree. In Proceedings of the Geoscience and Remote Sensing Symposium, Beijing, China, 10–15 July 2016; pp. 4545–4548. [Google Scholar]
- Liu, J.; Zhang, X.; Zhu, J. ICP three-dimensional point cloud registration based on K-D tree optimization. Eng. Surv. Map. 2016, 25, 15–18. [Google Scholar]
- Wang, K.; Li, X.; Lei, H.; Zhang, X. An ICP algorithm based on block path closest point search. In Journal of Physics Conference Series; IOP Publishing: Bristol, UK, 2017; p. 012063. [Google Scholar]
- Zheng, Z.; Li, Y.; Wang, J. LiDAR point cloud registration based on improved ICP method and SIFT feature. In Proceedings of the IEEE International Conference on Progress in Informatics and Computing, Nanjing, China, 18–20 December 2016; pp. 588–592. [Google Scholar]
- Yang, B.; Zang, Y. Automated registration of dense terrestrial laser-scanning point clouds using curves. ISPRS J. Photogramm. Remote Sens. 2014, 95, 109–121. [Google Scholar] [CrossRef]
- Ye, Q.; Yao, Y.; Gui, P.; Lin, Y. An improved ICP algorithm for Kinect point cloud registration. In Proceedings of the International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery, Changsha, China, 13–15 August 2016; pp. 2109–2114. [Google Scholar]
- Hou, D.X.; Wang, Y.H.; Zong-Chun, L.I. Constraints improved ICP algorithm based on eliminating error correspondence points. Sci. Surv. Mapp. 2015, 40, 103–107. [Google Scholar]
- Mitra, N.J.; Gelfand, N.; Pottmann, H.; Guibas, L. Registration of point cloud data from a geometric optimization perspective. In Proceedings of the 2004 Eurographics/ACM SIGGRAPH symposium on Geometry processing, Nice, France, 8–10 July 2004; pp. 22–31. [Google Scholar]
- Yao, J.; Ruggeri, M.R.; Taddei, P.; Sequeira, V. Automatic scan registration using 3D linear and planar features. 3D Res. 2010, 1, 22. [Google Scholar] [CrossRef]
- Ono, K.; Ono, R.; Hanada, Y. 3D surface registration using estimated local shape variation. In Proceedings of the IEEE Conference on Control Technology and Applications, Kohala, HI, USA, 27–30 August 2017; pp. 1362–1367. [Google Scholar]
- Zhang, X.Ð.H.; Gao, X.J. Registration of Point Clouds Based on Differential Geometry of Surfaceâ™s Feature. Appl. Mech. Mater. 2011, 101–102, 232–235. [Google Scholar]
- Zhang, X.J.; Zhong-Ke, L.I.; Wang, X.Z.; Pei-Jun, L.; Wang, Y. Research of 3D point cloud data registration algorithms based on feature points and improved ICP. Trans. Microsyst. Technol. 2012, 31, 116–248. [Google Scholar]
- Jiang, J.; Cheng, J.; Chen, X. Registration for 3-D point cloud using angular-invariant feature. Neurocomputing 2009, 72, 3839–3844. [Google Scholar] [CrossRef]
- Rusu, R.B. Semantic 3D Object Maps for Everyday Manipulation in Human Living Environments. KI Künstliche Intelligenz 2010, 24, 345–348. [Google Scholar] [CrossRef]
- Low, K.L. Linear Least-Squares Optimization for Point-To-Plane ICP Surface Registration; University of North Carolina: Chapel Hill, NC, USA, 2004. [Google Scholar]
- Liu, J.; Shang, X.; Yang, S.; Shen, Z. Research on Optimization of Point Cloud Registration ICP Algorithm. In Proceedings of the Pacific-Rim Symposium on Image and Video Technology, Sydney, Australia, 18–22 November 2017; pp. 81–90. [Google Scholar]
- Agamennoni, G.; Fontana, S.; Siegwart, R.Y.; Sorrenti, D.G. Point Clouds Registration with Probabilistic Data Association. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Daejeon, Korea, 9–14 October 2016; pp. 4092–4098. [Google Scholar]


| Equipment | Specifications |
|---|---|
| Laser scanner (vlp-16) | Measurement range: up to 100 m, Accuracy: ±3 cm (typical), Angular resolution(horizontal): 0.1–0.4°, 100 × 65 mm, 0.83 kg |
| IMU (Xsens MTi-700) | Latency: <2 ms, Gyroscopes: 450°/s, Accelerometers: 200 m/s2, 57 × 42 × 23 mm, 0.055 kg |
| Encoder (E6B2-CWZ6C) | Incremental, Resolution: 1000 P/R, Maximum speed: 6000 r/min, φ40 mm, 0.085 kg |
| Point Cloud Pair (Point Number) | Algorithm | Key Point Number | Iteration Number | Average Registration Time/ms | Registration Error/m |
|---|---|---|---|---|---|
| PCPair1 (17456,17728) | Our improved ICP | 677,561 | 8 | 632 | 0.004456 |
| Traditional ICP | 677,561 | 7 | 1226 | 0.009770 | |
| 4PC improved ICP | 677,561 | 6 | 956 | 0.008124 | |
| IPDA | 677,561 | 8 | 5120 | 0.004221 | |
| PCPair2 (17920,17856) | Our improved ICP | 580,576 | 12 | 762 | 0.003982 |
| Traditional ICP | 580,576 | 15 | 1490 | 0.004877 | |
| 4PC improved ICP | 580,576 | 13 | 1162 | 0.004543 | |
| IPDA | 580,576 | 12 | 6235 | 0.003542 |
| Point Cloud Pair | Without Initial Registration | With Initial Registration | ||||
|---|---|---|---|---|---|---|
| Iteration Number | Average Registration Time/ms | Registration Error/m | Iteration Number | Average Registration Time/ms | Registration Error/m | |
| PCPair1 | 13 | 1043 | 0.006954 | 8 | 632 | 0.004456 |
| PCPair2 | 14 | 1030 | 0.004543 | 12 | 762 | 0.003982 |
| PCPair3 | 12 | 960 | 0.004643 | 11 | 696 | 0.004572 |
| Algorithm 1 Align Point Clouds (C, L, P, D). |
| Input: Point cloud of current frame C, point cloud of previous frame L, IMU data set P, encoder data set C |
| Output: Point cloud of current frame that transformed to the global coordinate |
| ⊳Initial registration |
| for eachp1 ∈ P do |
| ifL.timestamp = p1.timestamp then ⊳Find corresponding attitude data by time stamp |
| return p1 |
| end if |
| end for |
| for eachd1 ∈ D do |
| ifL.timestamp = d1.timestamp then ⊳Find corresponding displacement data by time stamp |
| return d1 |
| end if |
| end for |
| transformCloud(L, p1, 0) ⊳Function: transform the point cloud of previous frame into its own navigation coordinate system |
| for eachp2 ∈ P do |
| ifC.timestamp = p2.timestamp then ⊳Find corresponding attitude data by time stamp |
| return p2 |
| end if |
| end for |
| for eachd2 ∈ D do |
| ifC.timestamp = d2.timestamp then ⊳Find corresponding displacement data by time stamp |
| return d2 |
| end if |
| end for |
| transformCloud(C, p2, d2 − d1) ⊳Function: transform the point cloud of current frame to the navigation coordinate system of previous frame |
| ⊳Accurate registration |
| pairTransform ← pairAlign(L, C) ⊳Function: accurate registration, return the matrix |
| ⊳Transform the point cloud to the global coordinate system which is the navigation coordinate system of the first input point cloud |
| transformPointCloud(C, globalTransform ∗ pairTransform) |
| ⊳Calculate the transformation from C1 to C2, C1 is the point cloud obtained by transforming C into its own navigation coordinate system, C2 is the point cloud obtained by transforming c into the navigation coordinate system of previous frame. |
| transform_ ← computeTransform(p2, d2 − d1) |
| ⊳Update global transformation |
| globalTransform ← globalTransform ∗ pairTransform ∗ transform_ |
| returnC |
| Unstructured Terrain | Actual Terrain/m | Terrain Point Cloud/m | |||
|---|---|---|---|---|---|
| Small gully terrain | 2.59 | 2.61 | 2.5222 | 2.5310 | 0.9958 |
| Deep pit terrain | 2.62 | 2.03 | 2.5923 | 1.9909 | 0.9912 |
| Big bulge terrain | 4.01 | 2.87 | 3.9622 | 2.8281 | 0.9972 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Q.; Wu, J.; Hu, H.; Xiao, C.; Chen, W. LIDAR Point Cloud Registration for Sensing and Reconstruction of Unstructured Terrain. Appl. Sci. 2018, 8, 2318. https://doi.org/10.3390/app8112318
Zhu Q, Wu J, Hu H, Xiao C, Chen W. LIDAR Point Cloud Registration for Sensing and Reconstruction of Unstructured Terrain. Applied Sciences. 2018; 8(11):2318. https://doi.org/10.3390/app8112318
Chicago/Turabian StyleZhu, Qingyuan, Jinjin Wu, Huosheng Hu, Chunsheng Xiao, and Wei Chen. 2018. "LIDAR Point Cloud Registration for Sensing and Reconstruction of Unstructured Terrain" Applied Sciences 8, no. 11: 2318. https://doi.org/10.3390/app8112318
APA StyleZhu, Q., Wu, J., Hu, H., Xiao, C., & Chen, W. (2018). LIDAR Point Cloud Registration for Sensing and Reconstruction of Unstructured Terrain. Applied Sciences, 8(11), 2318. https://doi.org/10.3390/app8112318






