1. Introduction
Acoustic noise control is essential for reducing the noise level in modern society since noise seriously affects human health [
1,
2]. Passive noise control, which is based on using reactive devices, e.g., Helmholtz resonators and quarter wavelength resonators, and using resistive materials, e.g., acoustic linings and porous membranes, is very effective for reducing high-frequency noise, but not so effective for low-frequency noise reduction. Active noise control (ANC) based on the principle of superposition is an appealing method for low-frequency noise reduction [
3,
4,
5,
6]. In practice, passive noise control and ANC methods are usually combined to provide wideband noise reduction.
In ANC systems, the filtered-x least mean-square (FxLMS) algorithm is widely used to update the weights of the control filter, but the complexity of the FxLMS algorithm increases linearly with the filter length. In certain applications, the control filter is on the order of several thousand. Therefore, the FxLMS and other time-domain algorithms, e.g., the filtered-x affine projection (FxAP) [
7,
8,
9], are too complex, which is prohibitive for real-time systems. The frequency-domain adaptive filter (FDAF) [
10,
11,
12,
13,
14,
15,
16,
17] has been successfully used in echo cancellation [
18,
19,
20,
21], acoustic feedback cancellation [
22], and beamforming [
23] due to its good convergence behavior and low complexity. In [
24,
25,
26,
27], the block LMS (BLMS) was extended to ANC applications and the corresponding frequency-domain implementation was provided. The experiment in [
27] used both the periodic and band-limited signals as the reference signals, but the delay problem was not discussed. In [
28], a more efficient implementation of BLMS was presented, where the filtering of the reference signal by the secondary path was also implemented using FFT. Meanwhile, the fast Hartley transform (FHT) was adopted to reduce the complexity. The frequency-domain implementation was extended to the multichannel case in [
26,
29]. The aforementioned algorithms are obtained by applying the FDAF originally used in echo cancellation to the ANC problem. However, the algorithm requirements for echo cancellation and ANC are quite different. Specifically, the direct use of the FDAF for ANC introduces two kinds of delays. First, there is at least one-block delay between the input of the reference signal and the output of the cancelling signal because the FDAF algorithm is implemented on a block-by-block basis. This delay can violate the causality constraint, which is a major concern for broadband ANC [
4,
30,
31]. Second, the delay between the weight adaptation and the observation of the error signal is introduced because of the effect of the secondary path. The behavior of the filtered-x algorithm is similar to that of the delayed-LMS algorithm, which reduces the upper bound of the step size and slows the convergence and reconvergence rate [
32]. In addition, the peak complexity of the FDAF algorithms presented in [
28] is quite high because the FFT operation should be completed in one sampling interval; therefore, these algorithms are impractical for real-time implementation.
Many approaches have been proposed to reduce the two kinds of delays. The modified filtered-x structure [
33,
34] was used in the frequency-domain ANC in [
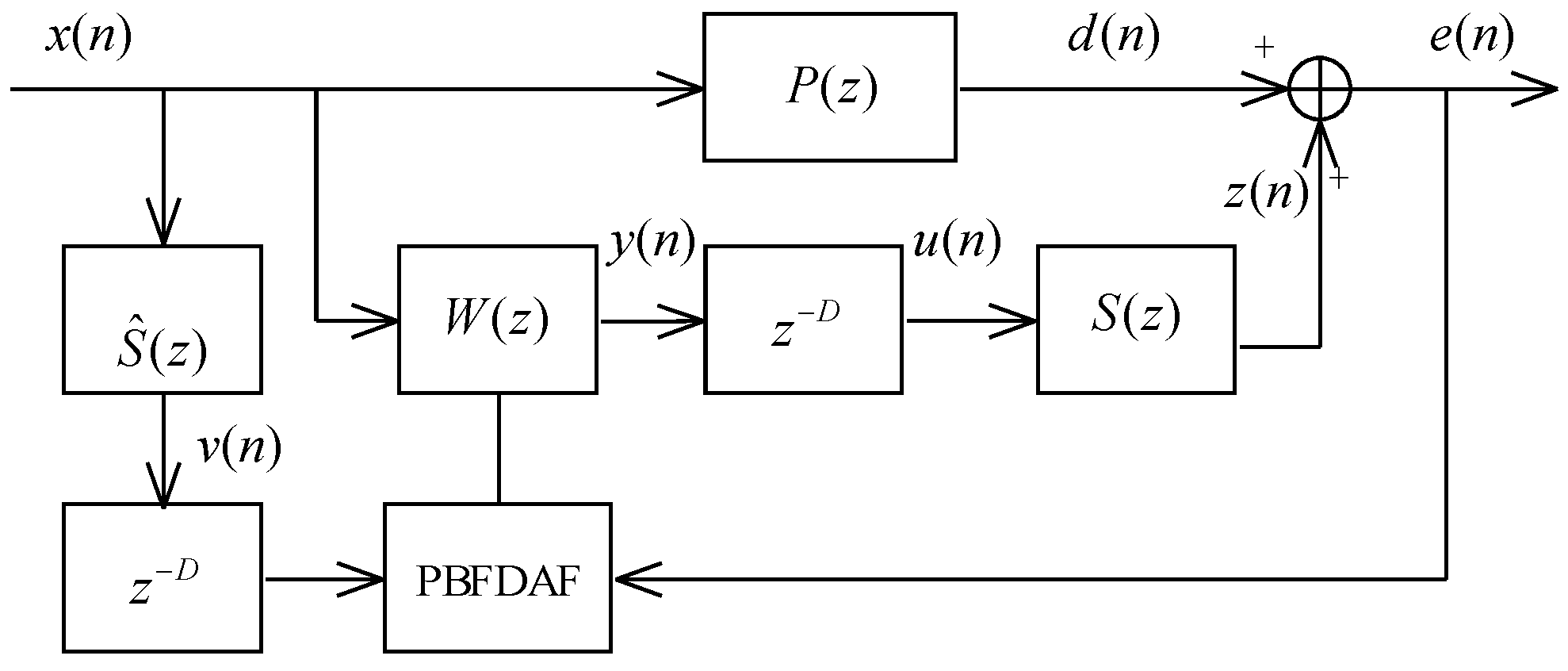
35], which makes the adaptive algorithm behave like the standard FDAF and thus removes the delay in the weight adaptation. The partitioned-block FDAF (PBFDAF) algorithm was introduced for ANC to reduce the delay in the signal path [
36,
37,
38,
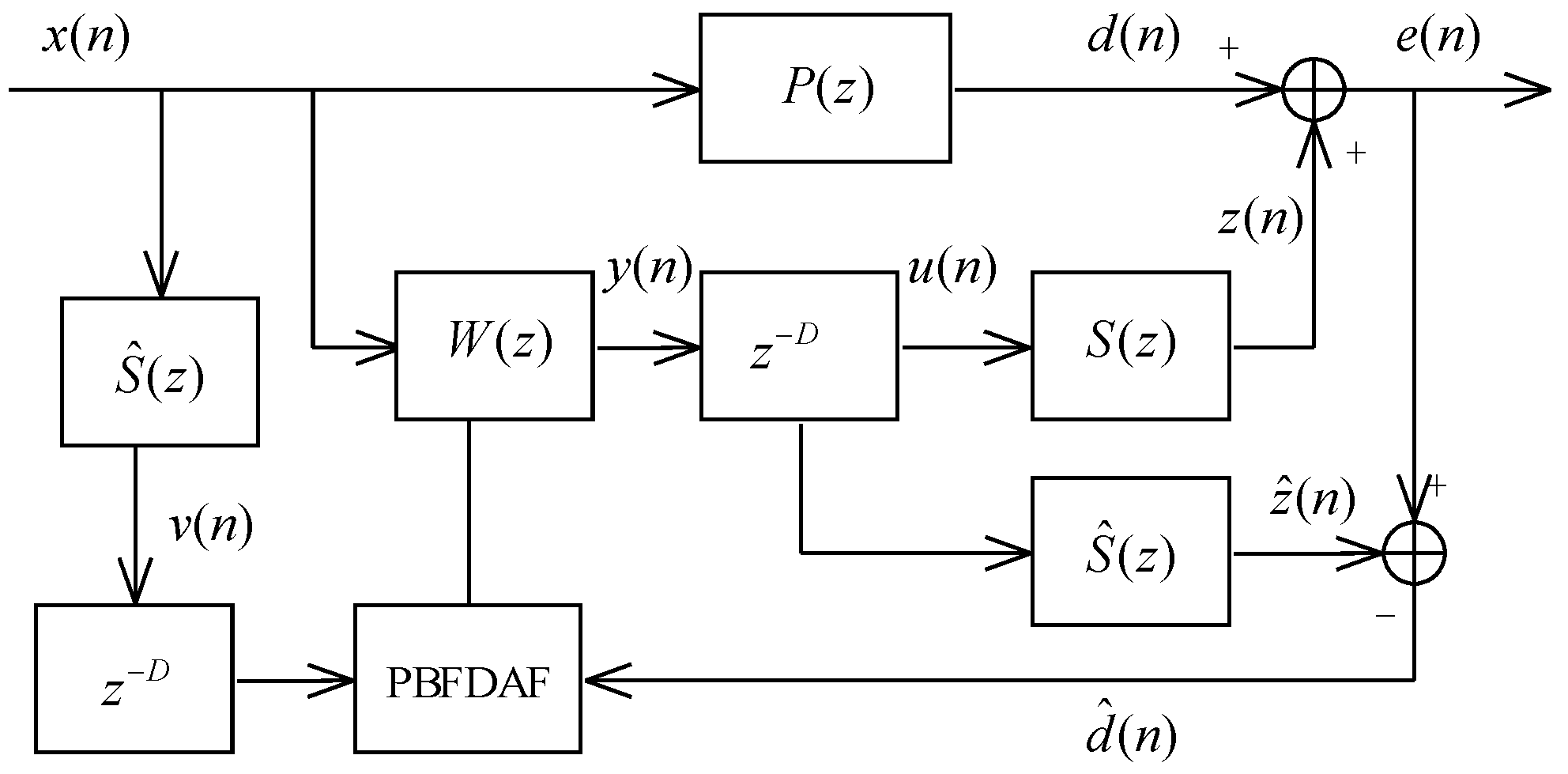
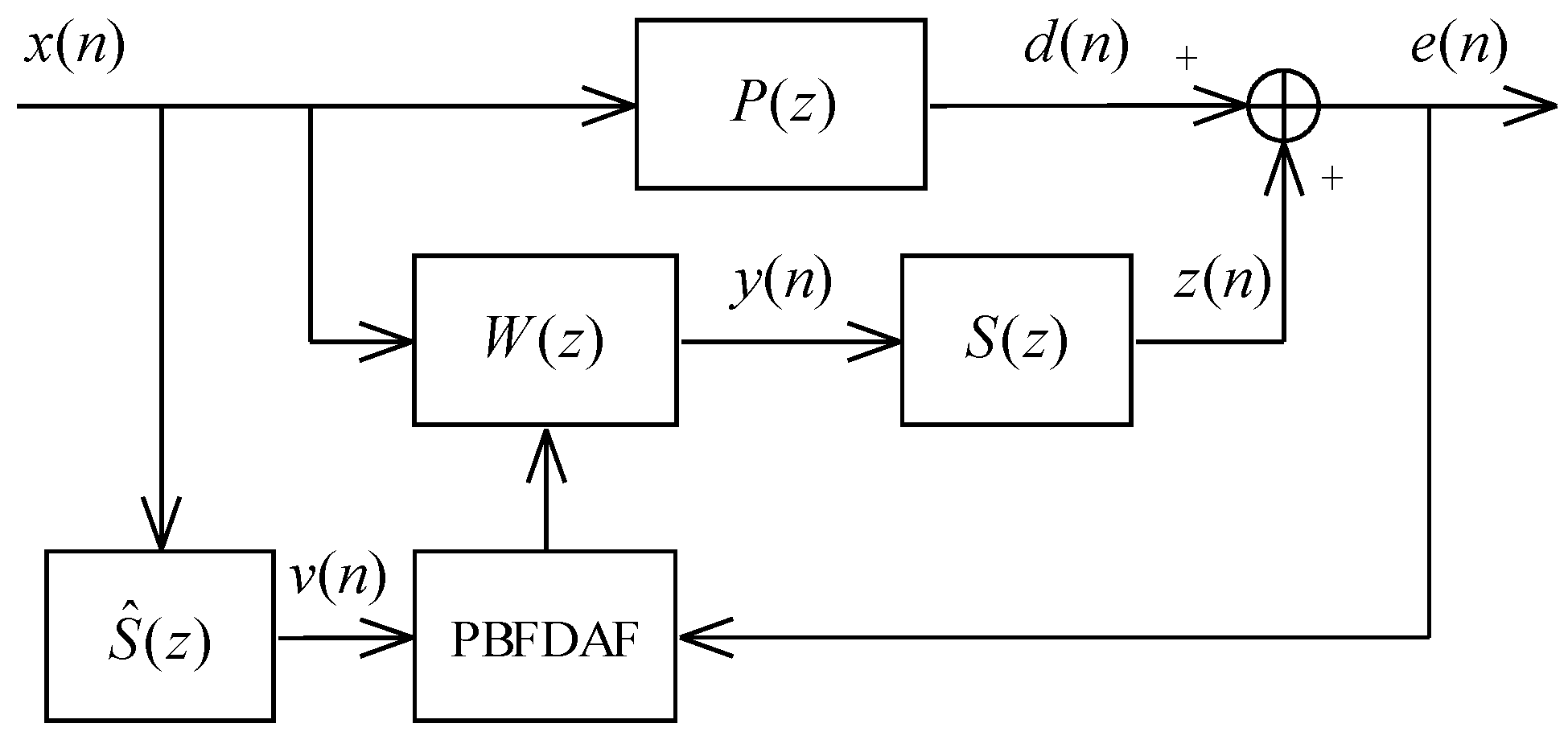
39]. This is achieved by partitioning the whole impulse response into several small sections, but this method does not completely eliminate the input-output delay. Several delayless algorithms were then proposed to totally remove the delay in the signal path. The calculation of the adaptive filter output can be implemented directly using the time-domain convolution and hence the delay in the signal path is removed [
40,
41,
42,
43]. However, the complexity of the convolution in the time domain is still high. In [
44], a delayless FDAF algorithm originally used in echo cancellation [
45] was extended to ANC, but the computational burden at certain sampling periods is rather high. Two computationally efficient FDAF algorithms for ANC were proposed in [
46,
47] using the delayless approach in [
48,
49], but the delay in the filter adaptation is not removed.
Although many efforts have been devoted to the frequency-domain FxLMS algorithms, these algorithms are not well compared and analyzed. To fill this gap, this paper presents a comprehensive review of the frequency-domain FxLMS algorithms. Only mono-channel algorithms are considered in this paper, since they can be straightforwardly extended to the multi-channel case. The conventional frequency-domain FxLMS algorithms are reviewed, and then the effects of the two kinds of delays on the overall performance are analyzed. Specifically, it was found that calculating the adaptive filter output and the weight vector update in different ways leads to different convergence performances, which is quite different from system identification problems. The update-first approach is then proposed to improve the stability. Several delayless frequency-domain algorithms for ANC are surveyed, but these algorithms did not remove the delay related to the secondary path. To address this problem, we present a new delayless frequency-domain FxLMS algorithm to completely remove the aforementioned two types of delays and overcome the shortcomings of the state-of-the-art frequency-domain FxLMS algorithms. The complexity of the frequency-domain approaches in terms of both peak and average multiplications per sample are evaluated. Simulations are carried out to evaluate the convergence performance and stability of the frequency-domain FxLMS algorithms.
2. FxLMS Algorithm
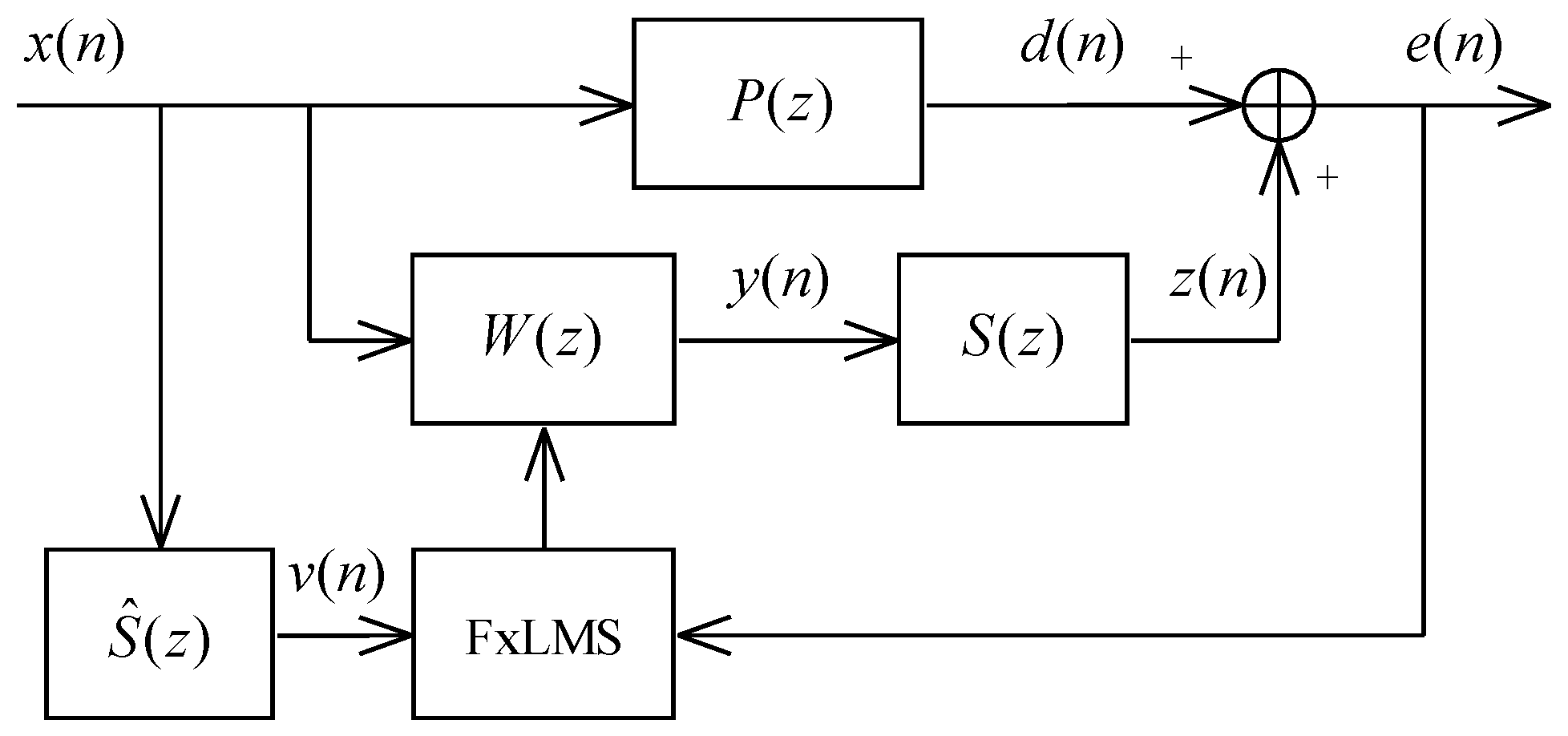
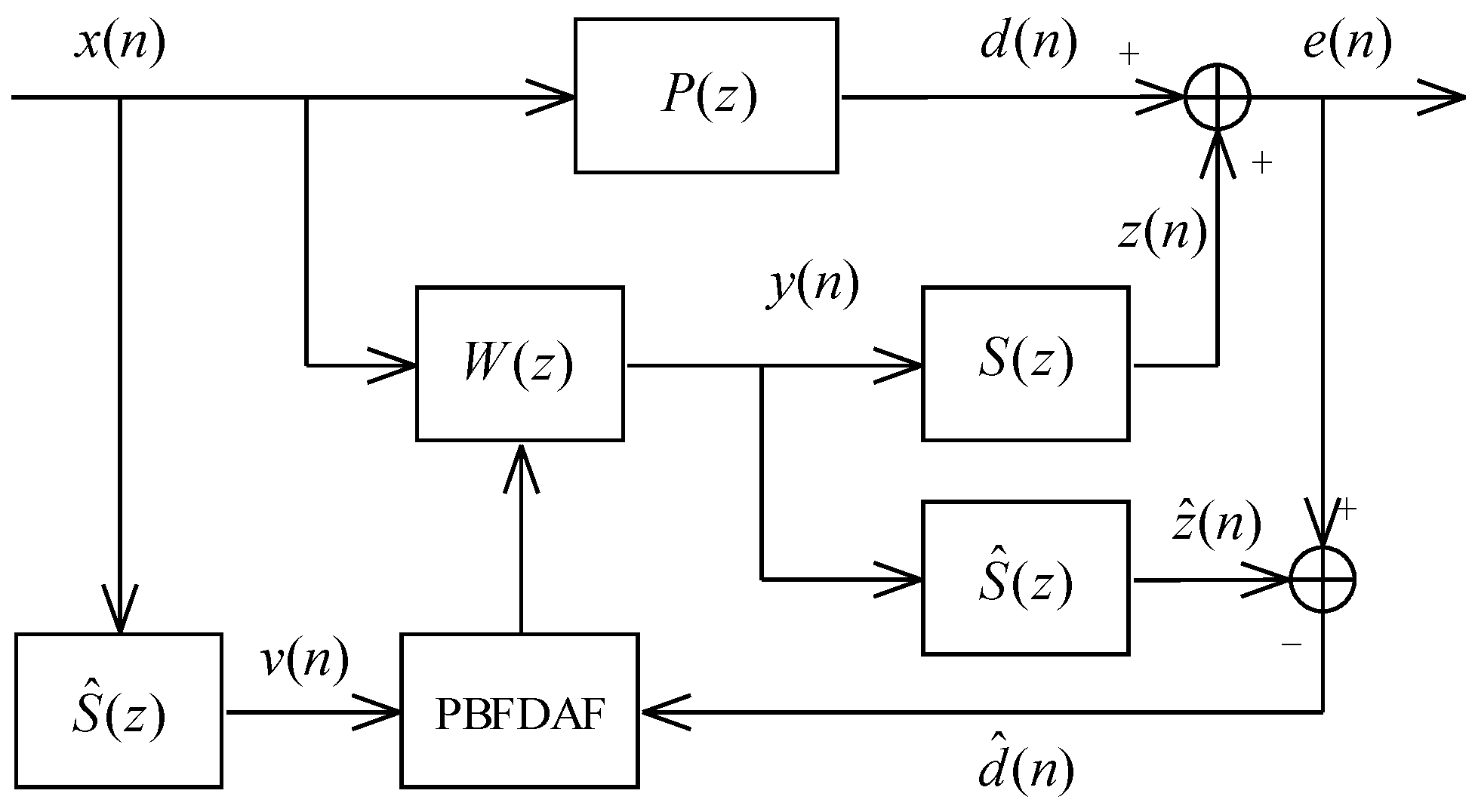
The diagram of the FxLMS algorithm is presented in
Figure 1, where
is the primary path and
is the secondary path. We define the weight vector of the control filter at the time index
n as
with a length of
. The reference signal
is picked up by a reference microphone and then filtered by the adaptive filter to generate the cancelling signal
driven by a secondary loudspeaker
where
is the reference signal vector. The cancelling signal
is then filtered by the secondary path
to obtain the control signal
at the location of the error microphone
where
, and
is the weight vector of the secondary path with a length of
. The residual error signal picked up by the error microphone is
where
is the disturbance signal at the error microphone.
The FxLMS algorithm is commonly used to update the weight vector [
3,
4]
where
is the step size, and
the filtered reference signal vector, where the filtered reference signal
is given by
where
, and
is an estimate of the actual weight vector of the secondary path. An accurate estimate of the secondary path is required for the FxLMS to work properly, which can be obtained by an offline- or online-modeling method [
4,
6].
The FxLMS algorithm requires multiplications. In certain scenarios, the length of the weight vector may reach several thousand taps. Thus, the computational complexity is a major concern for real-time systems.
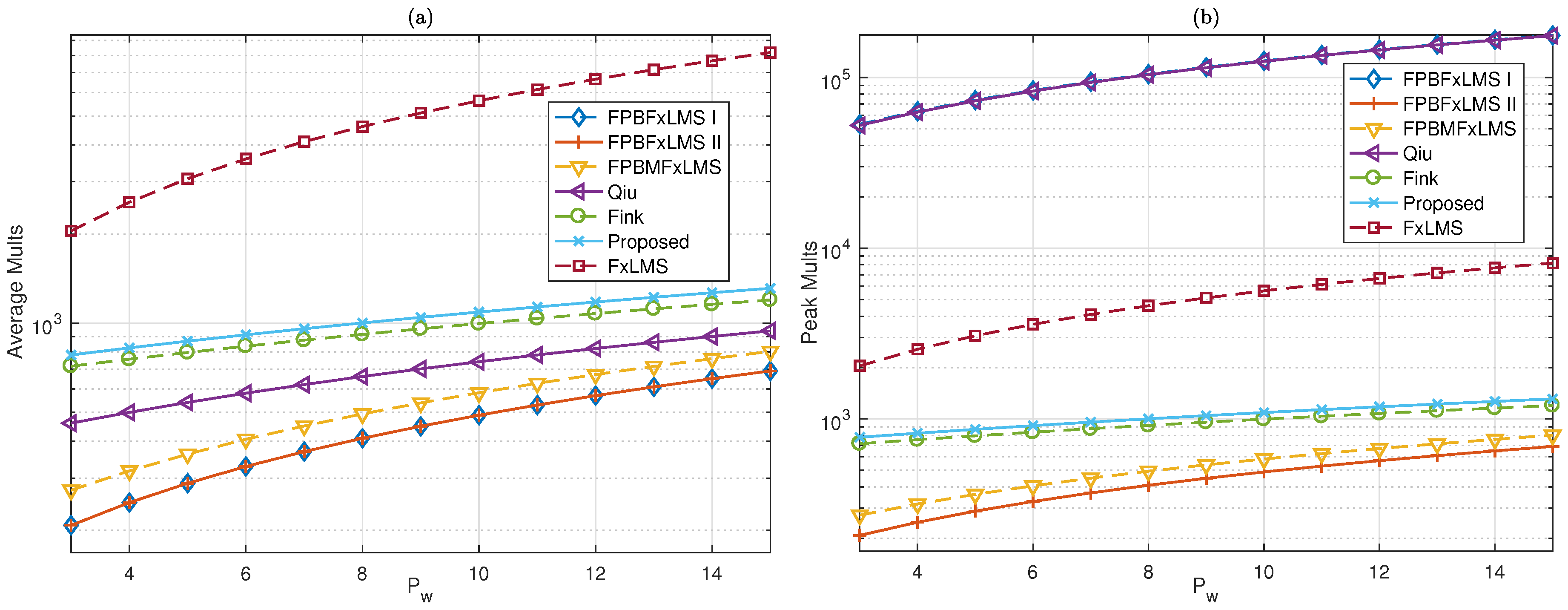
6. Evaluations
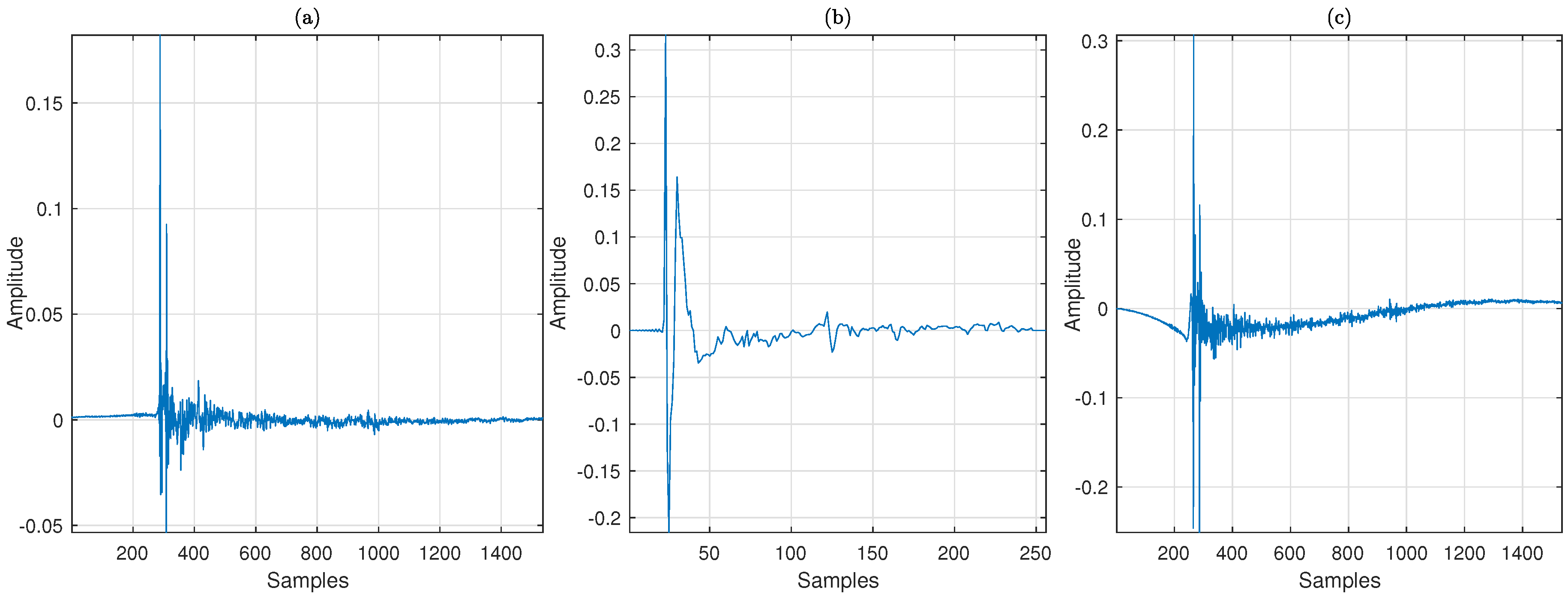
In this section, we carry out computer simulations to evaluate the convergence performance of several frequency-domain algorithms in the context of ANC. The sampling rate is
Hz. The length of the primary and secondary path are
and
, respectively. The optimal solution of the control filter is computed using the MINT method [
52] and has a length of
. Their corresponding time-domain impulse responses are plotted in
Figure 7.
Figure 7c shows that maximum delay allowed in the signal path is
to guarantee the causality condition of the system. The signal-to-noise ratio (SNR) measured at the error microphone is 30 dB. Two signals, i.e., the narrow band signal between 100–800 Hz and a multi-tone signal at 40, 340 and 700 Hz, are used as the reference. The convergence performance is evaluated by the learning curve given by
where
and
denote the powers of the disturbance signal
and the error signal
, which are computed recursively as
where
is the smoothing factor. In the following, we use
and
.
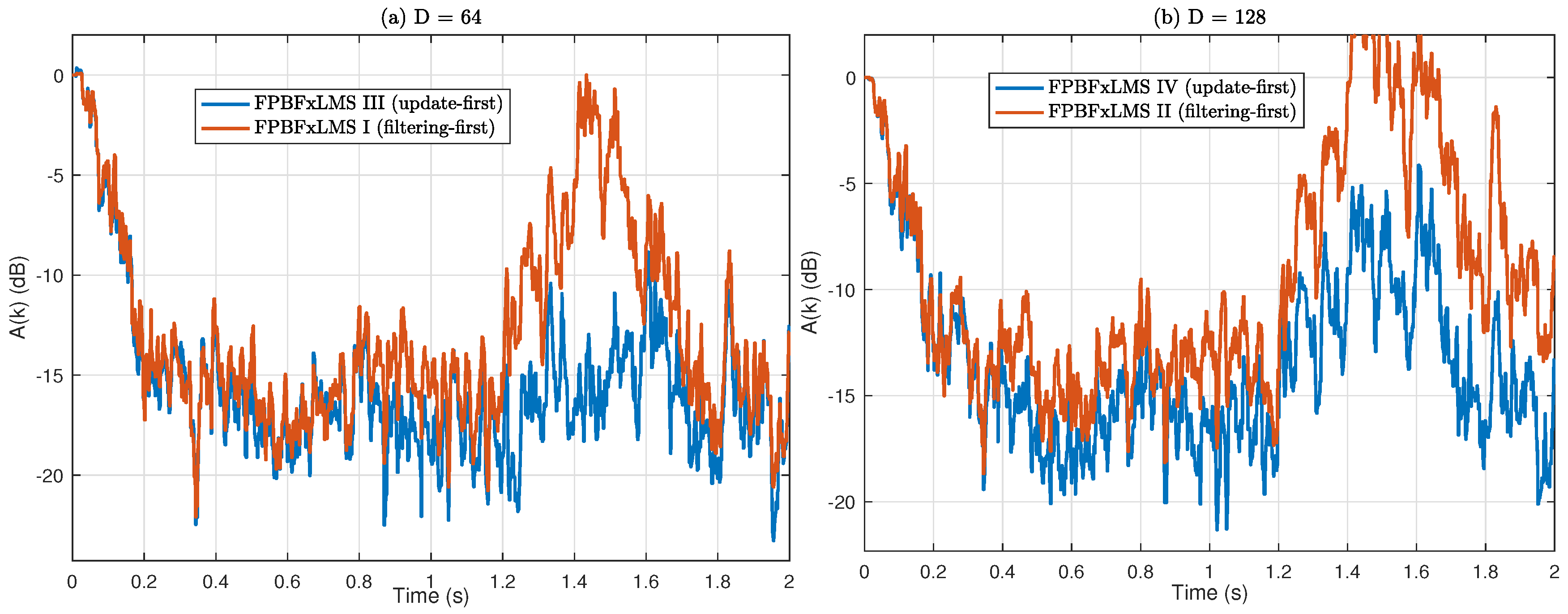
Figure 8 compares the convergence performance of the filtering-first and update-first approaches in
Table 1,
Table 2,
Table 3 and
Table 4. The narrow band noise is used as input, and the block length is
. The update-first approach is more stable than the filtering-first approach given the same step size, which agrees with the above analysis. In addition, the two methods have the same complexity, and hence the update-first approach is recommended for practical implementation.
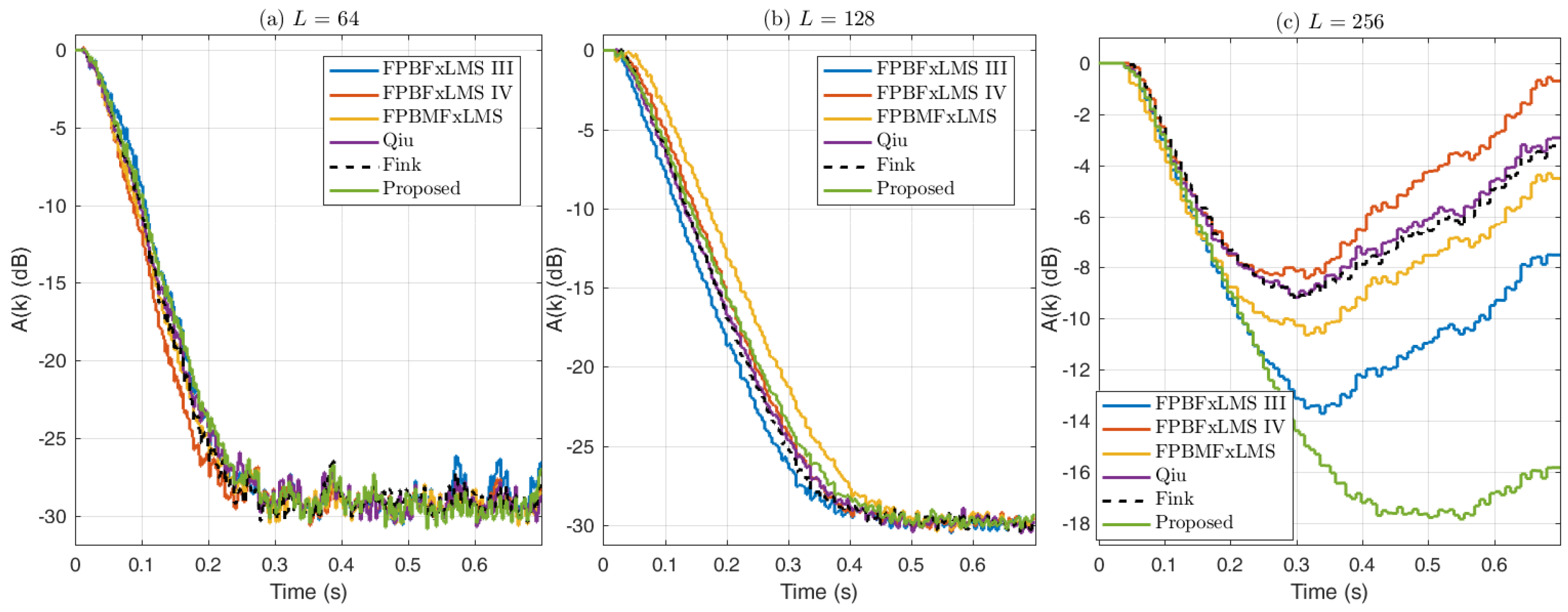
The effect of the block length on the convergence performance of several frequency-domain FxLMS algorithms is investigated in
Figure 9 and
Figure 10. In
Figure 9, we use the multi-tone signal as the reference, and the step size
. The block length is set to
. All the algorithms are convergent for
, while they diverge for
. We found that all the algorithms can converge using a smaller step size
for the block length
. For the multi-tone input, all the frequency-domain algorithms can converge if a sufficiently small step size is employed.
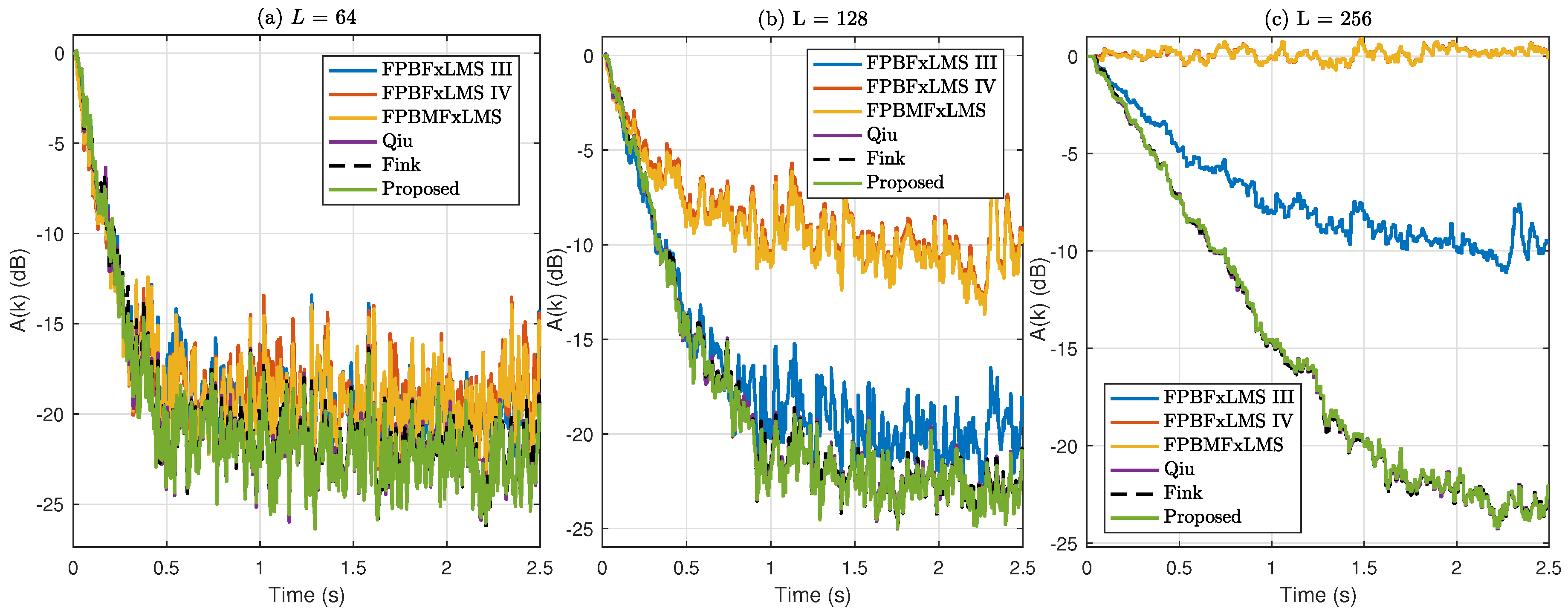
The experiment in
Figure 9 is repeated using the narrow band noise as input, and the learning curves are presented in
Figure 10. The three delayless frequency-domain algorithms are stable and have a similar convergence for narrow band noise input in all the experiments. However, their convergence rate decreases as the block length. The convergence performance of the traditional frequency-domain FxLMS algorithms is dramatically affected by the block length. For
, the causality condition is fulfilled for all the algorithm involved, and they exhibit a similar convergence. When the block length is
, the FPBFxLMS IV and the FPBMFxLMS algorithms with a delay of
do not gain any noise reduction, and the FPBFxLMS III algorithm with a delay of
only exhibits a 10-dB noise reduction. The experiment demonstrates that the delay in the signal path has a major effect on the broadband noise reduction.
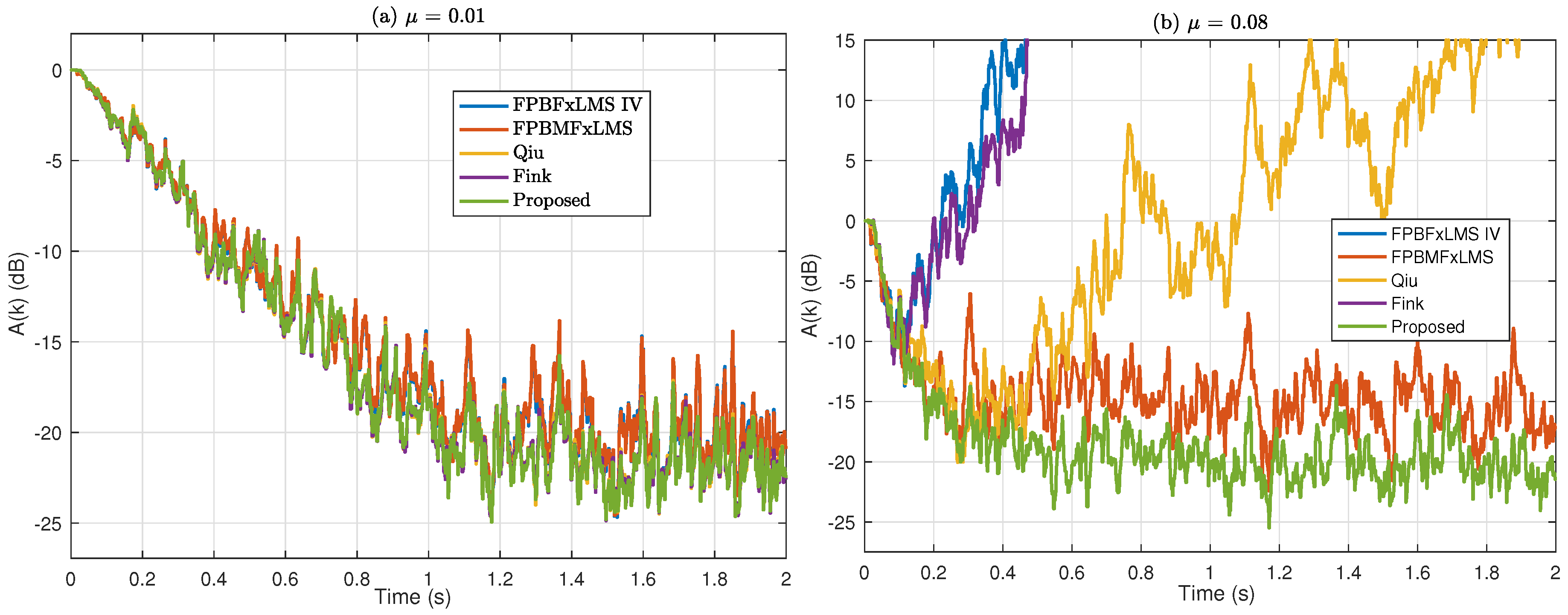
In
Figure 11, we investigate the stability of the frequency-domain algorithms with and without the modified filtered-x structure. Specifically, we compare the FPBFxLMS IV, FPBMFxLMS, and three delayless algorithms. The narrow band white noise is used as the reference. We use a small step size
for
Figure 11a and a large step size
for
Figure 11b. All the algorithms involved exhibit a similar convergence performance when the step size is small. However, when a large step size is adopted, the frequency-domain algorithms without the modified filtered-x structure diverge, but the modified filtered-x algorithms are stable because the available step size of the modified filtered-x algorithm is larger than those of the FxLMS-type algorithms. The proposed delayless algorithm outperforms all the other methods.
7. Conclusions
This paper presented a comprehensive review of the frequency-domain FxLMS algorithms in terms of convergence performance, stability, and computational burden. Practical applications include active noise control of open windows [
53], the ventilation system [
54], and automotive cabins [
55], where several thousands of coefficients are required to model the control filters. The frequency-domain algorithms used in ANC and system identification are quite different. First, broadband ANC is sensitive to algorithm latency, and a large delay may cause the system to fail. Second, direct use of an FDAF for ANC results in a delay in the weight update and the observation of the error signal, which reduces the maximum step size of the algorithm.
This paper reviewed the delayless filtering methods and the modified filtered-x structures to address the two delay problems. Specifically, the update-first approach was proposed to improve the stability of the FPBFxLMS algorithms. Several frequency-domain FxLMS algorithms have a very high peak complexity and thus are not practical for real-time systems, although these algorithms are correct in theory. A computationally efficient delayless frequency-domain algorithm was proposed that combines the hybrid fast filtering approaches and the modified filtered-x structure, which completely removes the aforementioned two types of delays. Extensive simulations were carried out to evaluate the convergence performance of the state-of-the-art frequency-domain FxLMS algorithms.
However, more work needs to be done regarding the frequency-domain FxLMS algorithms. For instance, the step size bound of the traditional frequency-domain FxLMS algorithms in
Table 1,
Table 2,
Table 3 and
Table 4 should be determined. Analyzing the statistical convergence behavior of the frequency-domain FxLMS algorithms is an interesting topic [
56,
57,
58,
59].