Microparticle Manipulation and Imaging through a Self-Calibrated Liquid Crystal on Silicon Display
Abstract
1. Introduction
2. Materials and Methods
2.1. LCoS Display Self-Calibration
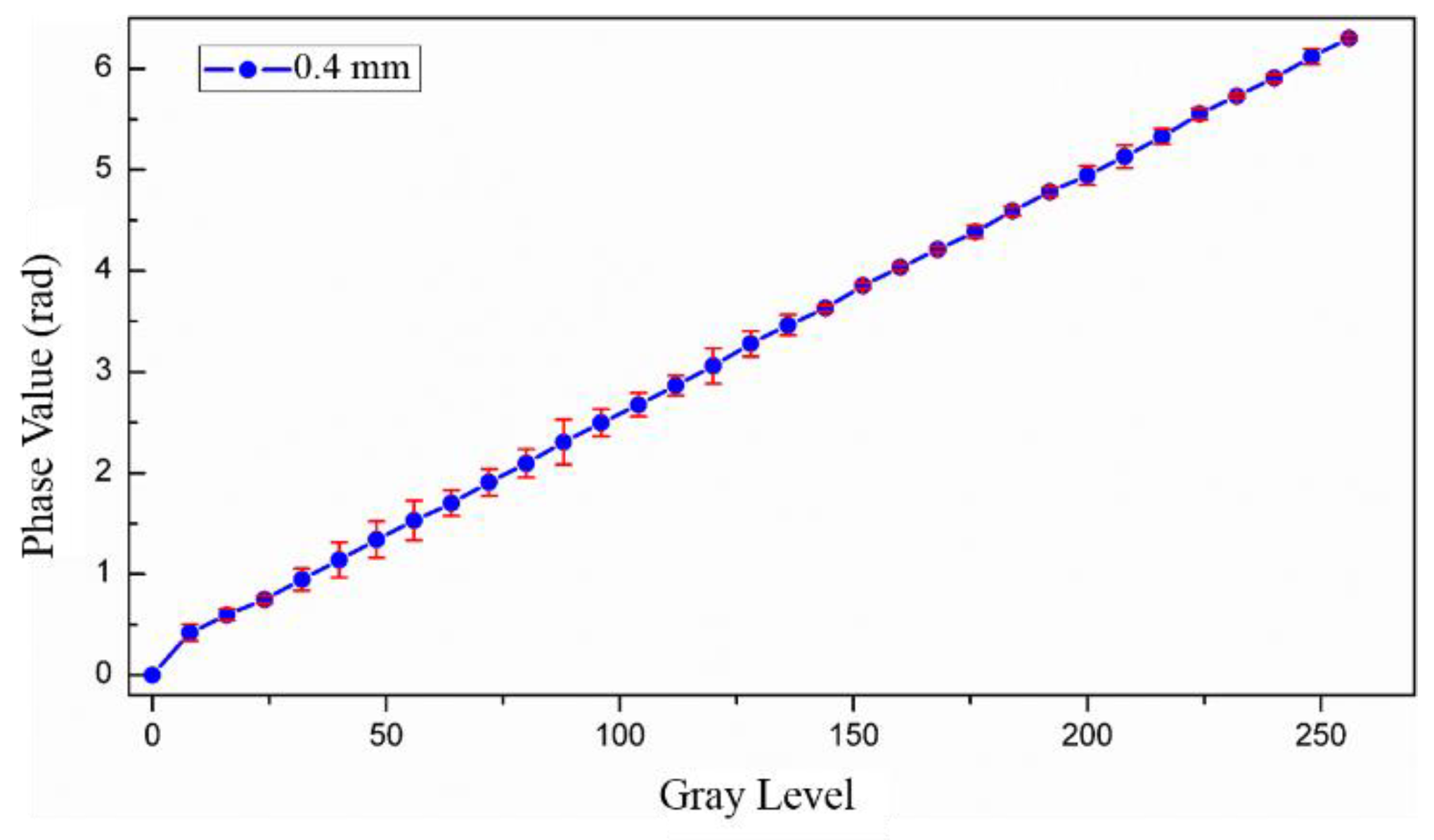
2.1.1. Phase-Voltage Calibration
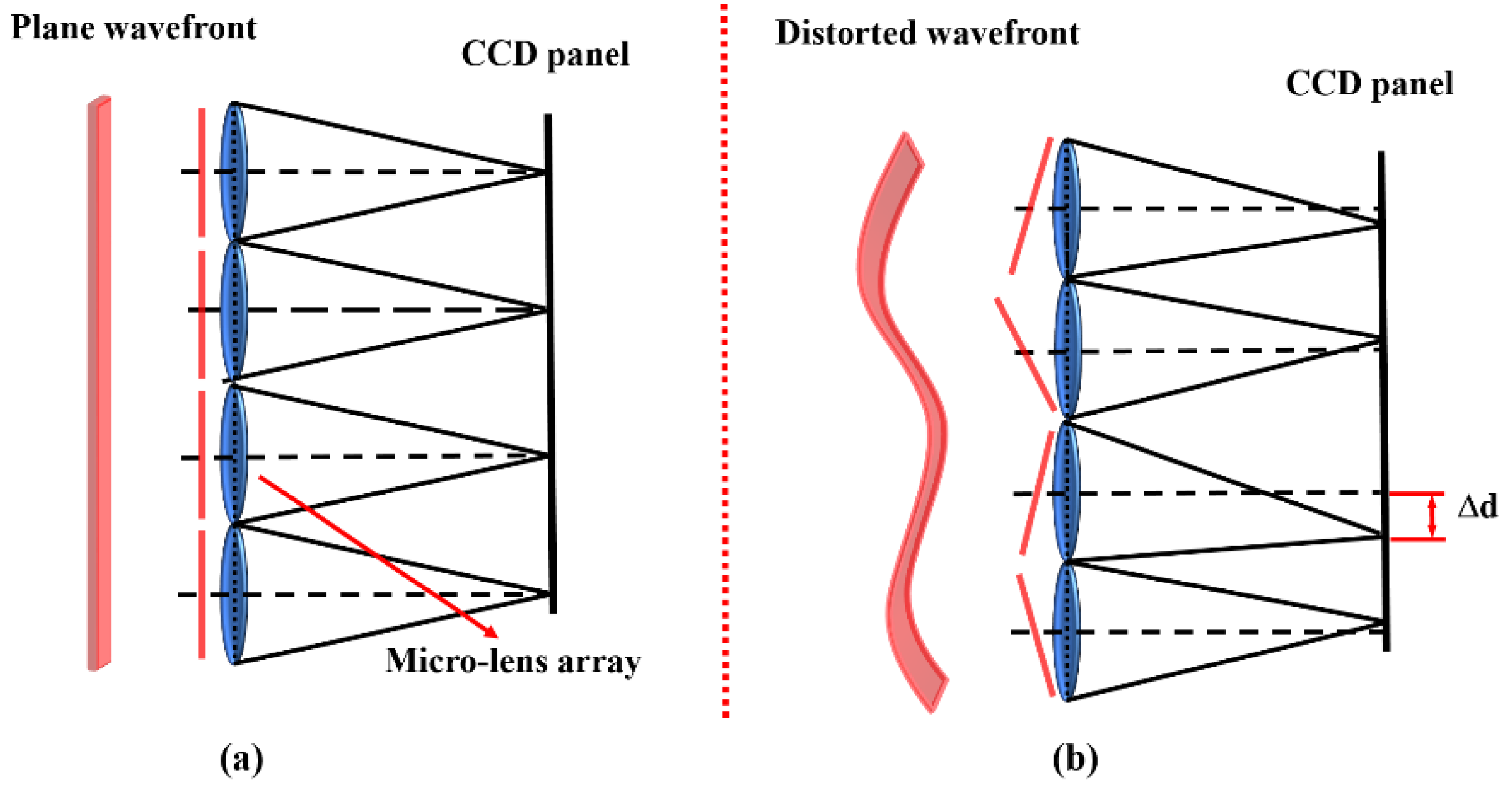
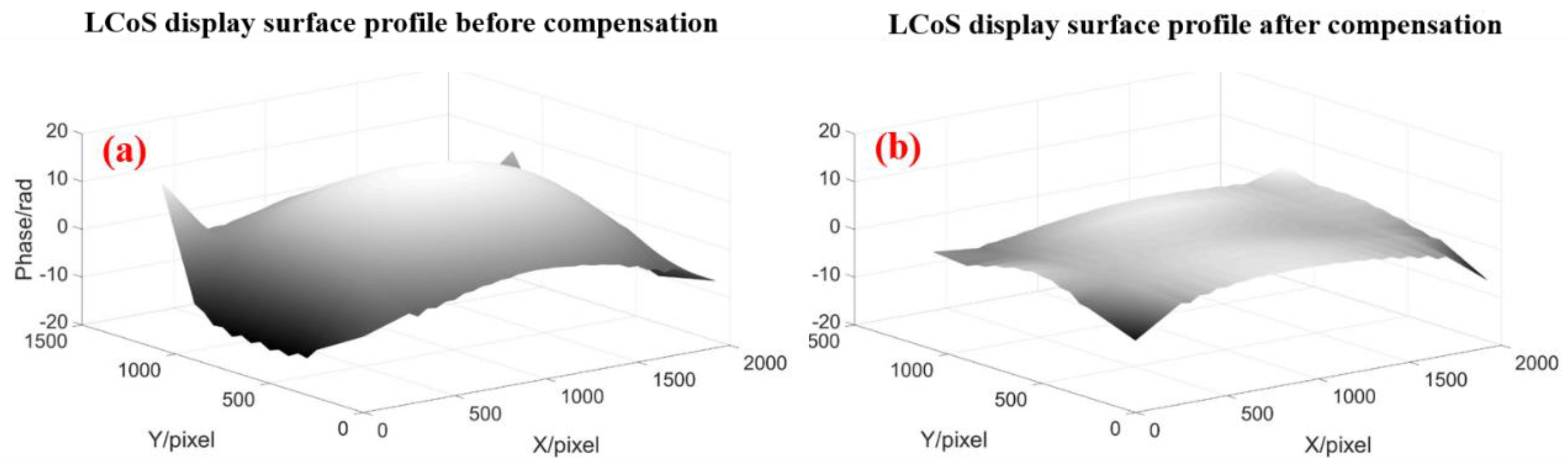
2.1.2. Surface Profile Calibration
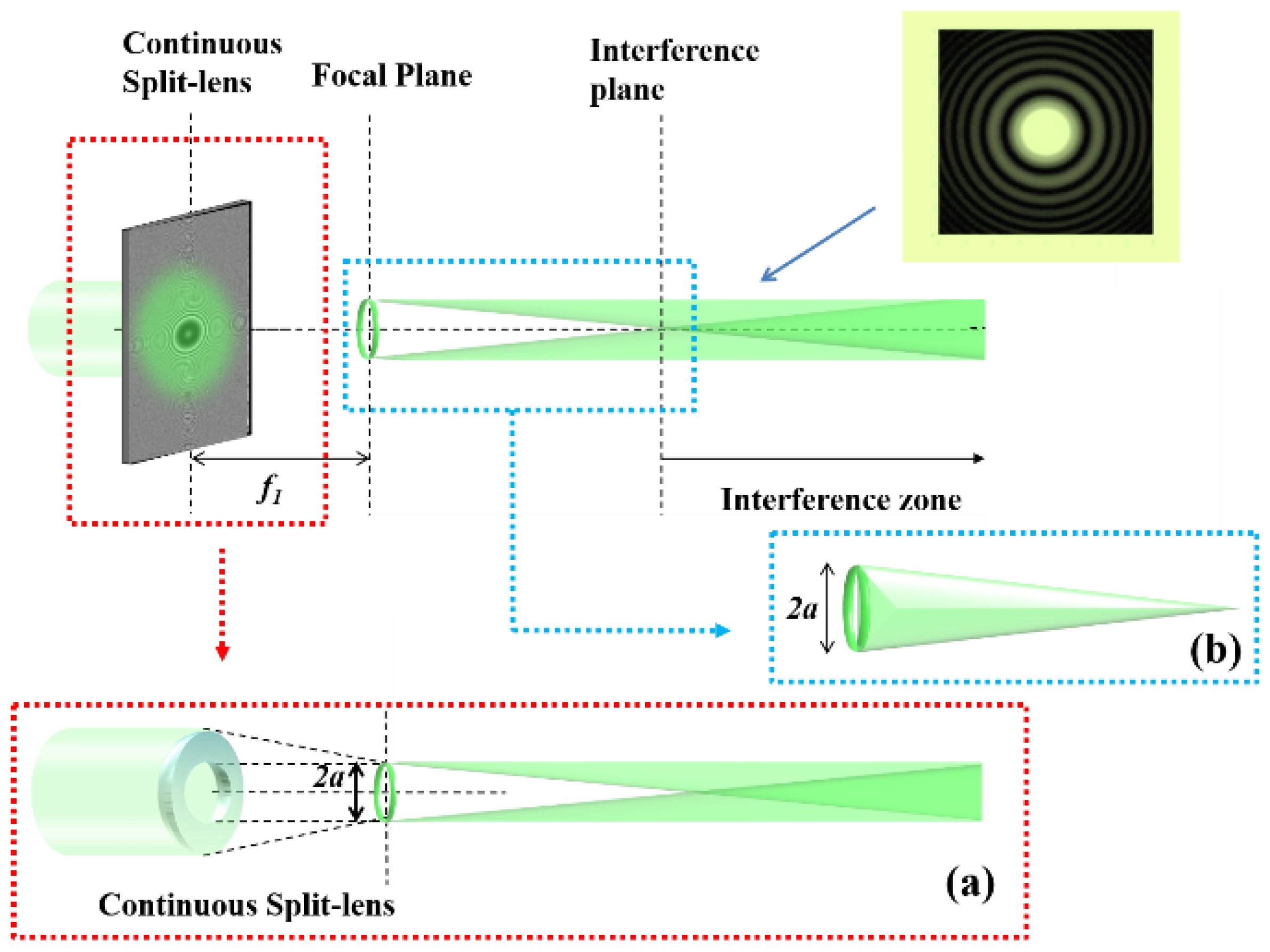
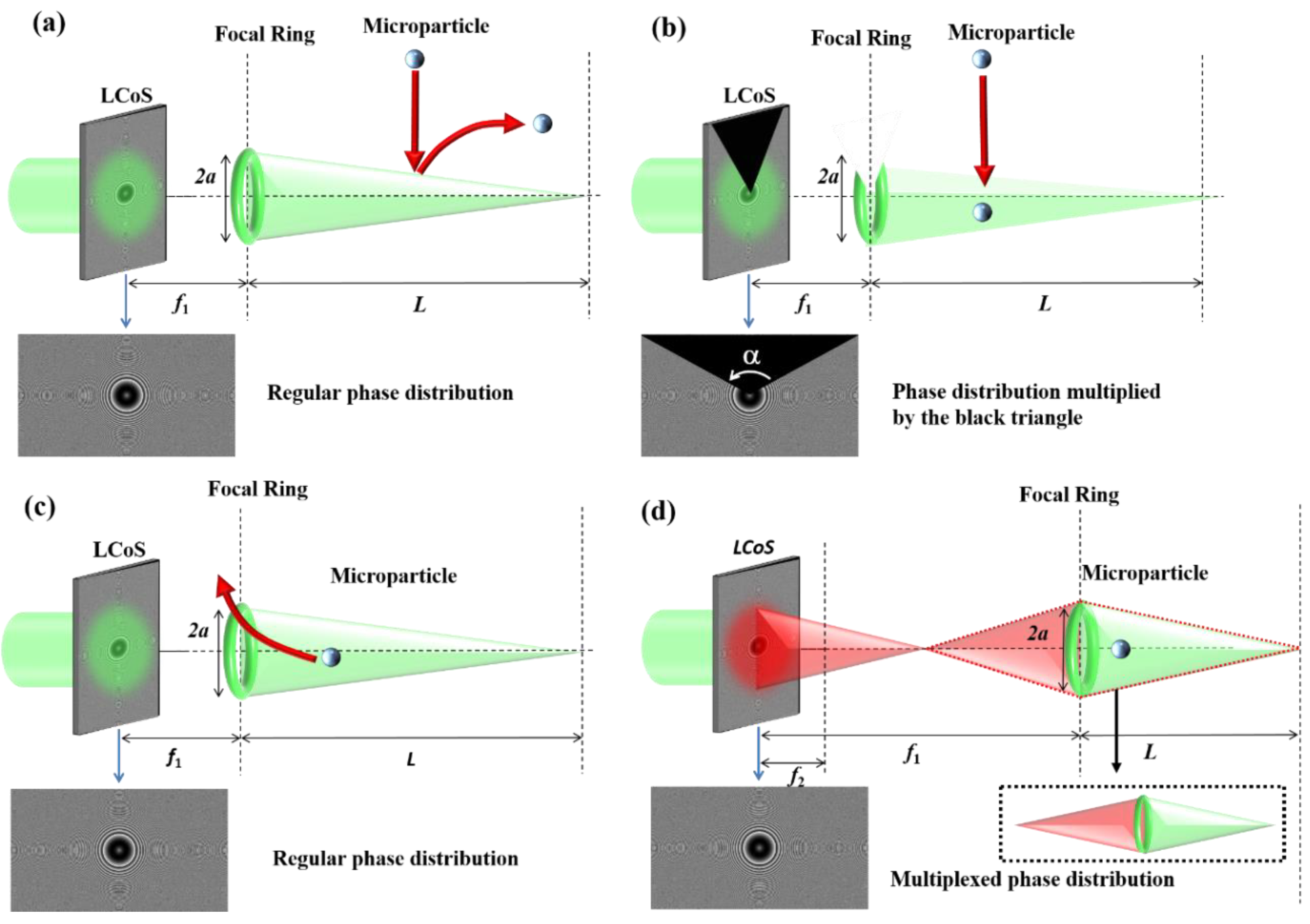
2.2. Microparticle Manipulation through Light Structures Created by a LCoS Display
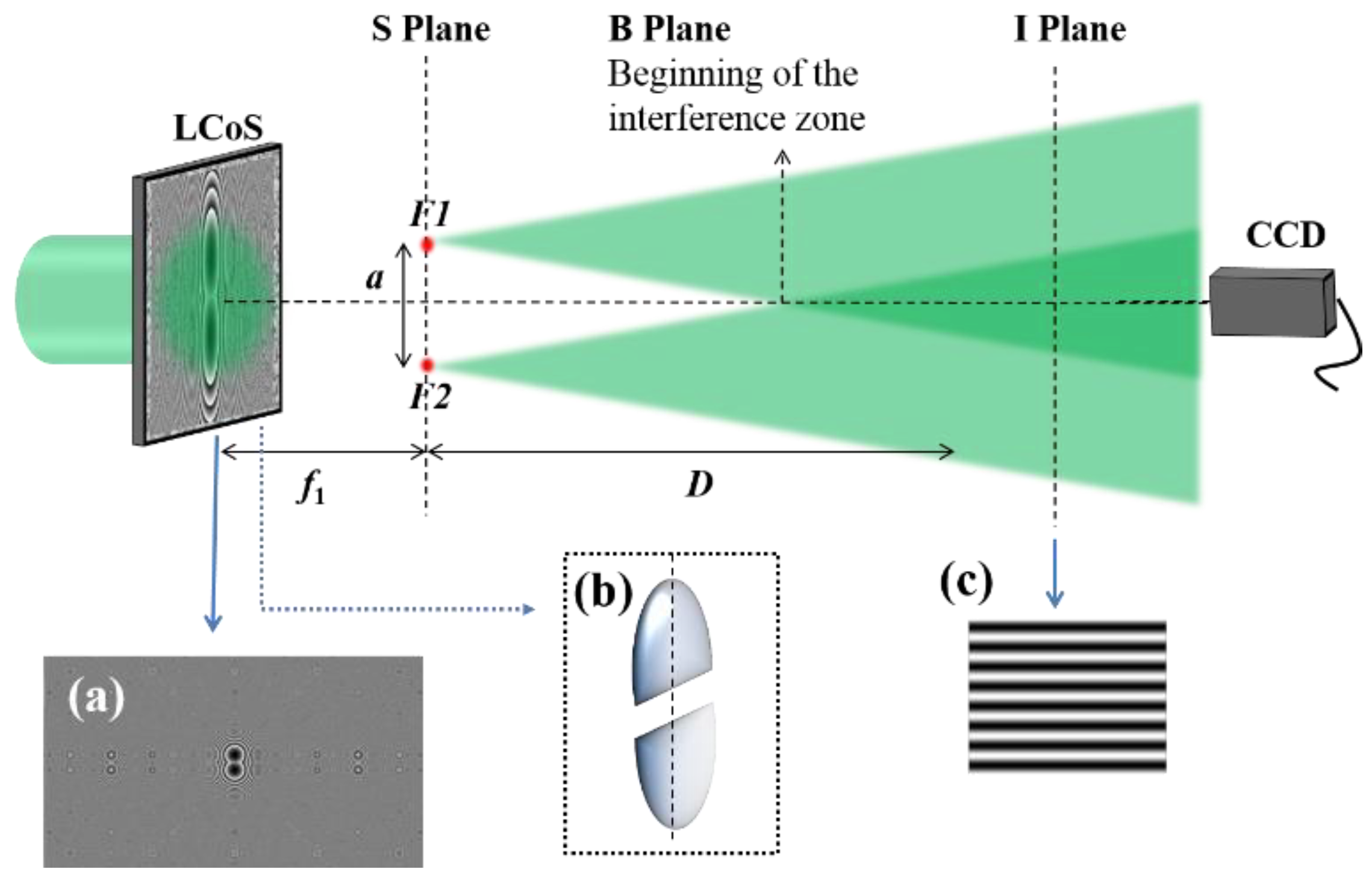
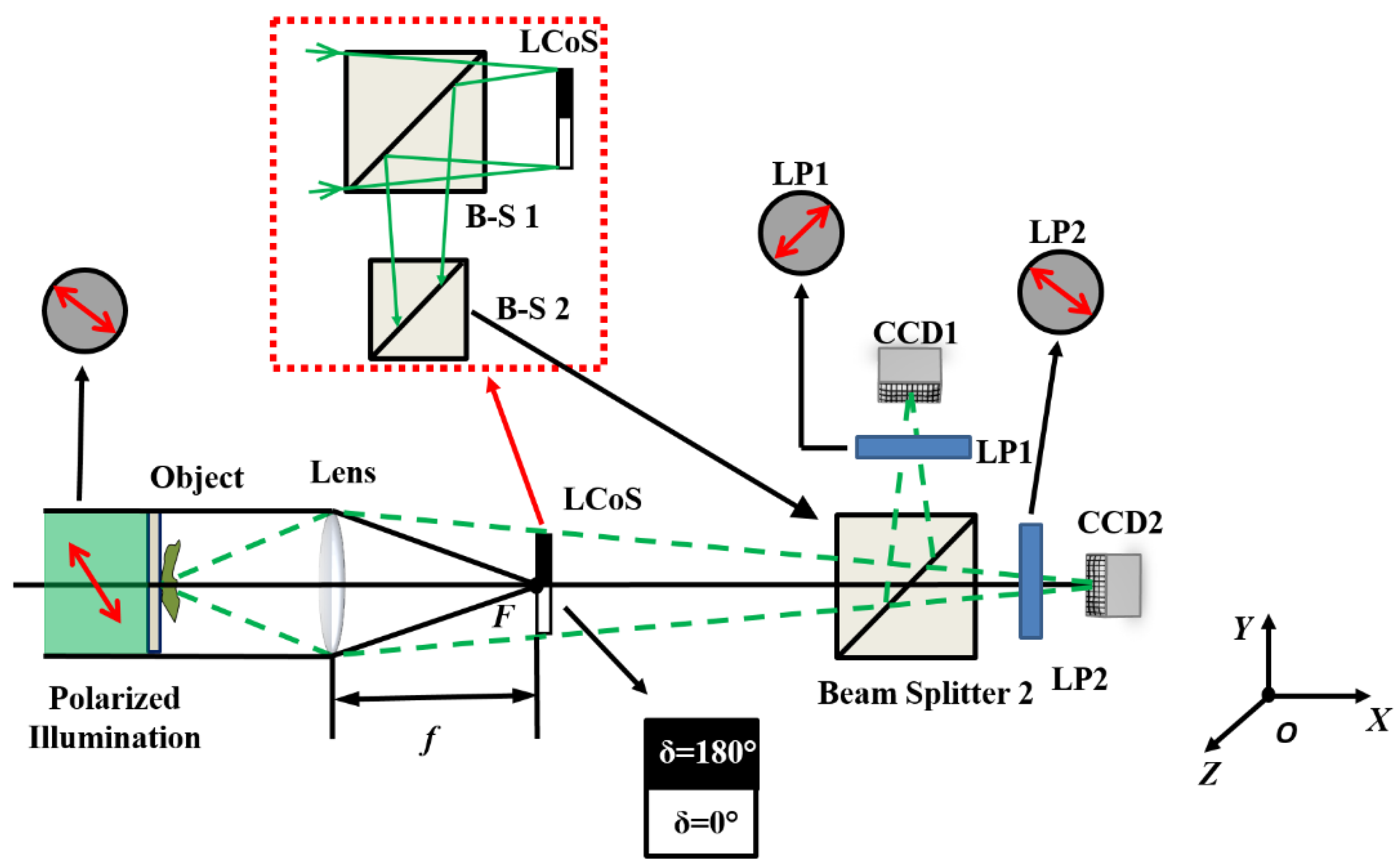
2.3. LCoS Display Based Inline Holographic System
3. Results
3.1. LCoS Display Self-Calibration
3.1.1. Phase-Voltage Calibration
3.1.2. Surface Homogeneity Calibration
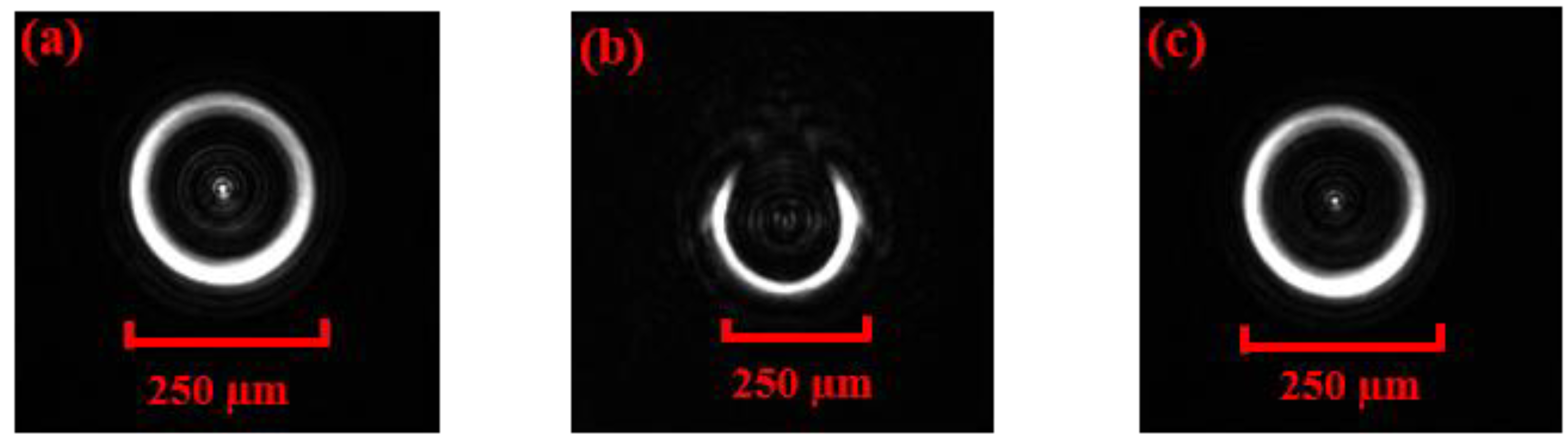
3.2. Microparticle Manipulation through the LCoS Display Generated Split-Lens Schemes
3.3. LCoS Display Based Inline Holographic System
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mu, Q.; Cao, Z.; Hu, L.; Li, D.; Xuan, L. Adaptive optics imaging system based on a high-resolution liquid crystal on silicon device. Opt. Express 2006, 14, 8013–8018. [Google Scholar] [CrossRef] [PubMed]
- Fernández, E.J.; Prieto, P.M.; Artal, P. Wave-aberration control with a liquid crystal on silicon (LCOS) spatial phase modulator. Opt. Express 2009, 17, 11013–11025. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; You, Z.; Chu, D. Fundamentals of phase-only liquid crystal on silicon (LCOS) devices. Light Sci. Appl. 2014, 3, e213. [Google Scholar] [CrossRef]
- Matsumoto, N.; Itoh, H.; Inoue, T.; Otsu, T.; Toyoda, H. Stable and flexible multiple spot pattern generation using LCOS spatial light modulator. Opt. Express 2014, 22, 24722–24733. [Google Scholar] [CrossRef] [PubMed]
- Marquez, A.; Moreno, I.; Iemmi, C.; Lizana, A.; Campos, J.; Yzuel, M.J. Mueller-Stokes characterization and optimization of a liquid crystal on silicon display showing depolarization. Opt. Express 2008, 16, 1669–1685. [Google Scholar] [CrossRef] [PubMed]
- Ni, J.; Wang, C.; Zhang, C.; Hu, Y.; Yang, L.; Lao, Z.; Xu, B.; Li, J.; Wu, D.; Chu, J. Three-dimensional chiral microstructures fabricated by structured optical vortices in isotropic material. Light Sci. Appl. 2017, 6, e17011. [Google Scholar] [CrossRef] [PubMed]
- Kowalczyk, A.P.; Makowski, M.; Ducin, I.; Sypek, M.; Kolodziejczyk, A. Collective matrix of spatial light modulators for increased resolution in holographic image projection. Opt. Express 2018, 26, 17158–17169. [Google Scholar] [CrossRef] [PubMed]
- Fuentes, J.L.M.; Moreno, I. Random technique to encode complex valued holograms with on axis reconstruction onto phase-only displays. Opt. Express 2018, 26, 5875–5893. [Google Scholar] [CrossRef] [PubMed]
- Vinas, M.; Dorronsoro, C.; Radhakrishnan, A.; Benedi-Garcia, C.; Lavilla, E.A.; Schwiegerling, J.; Marcos, S. Comparison of vision through surface modulated and spatial light modulated multifocal optics. Biomed. Opt. Express 2017, 8, 2055–2068. [Google Scholar] [CrossRef] [PubMed]
- Qaderi, K.; Leach, C.; Smalley, D.E. Paired leaky mode spatial light modulators with a 28° total deflection angle. Opt. Lett. 2017, 42, 1345–1348. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Q.; Rumley, S.; Bahadori, M.; Bergman, K. Photonic switching in high performance datacenters [Invited]. Opt. Express 2018, 26, 16022–16043. [Google Scholar] [CrossRef] [PubMed]
- Lizana, A.; Zhang, H.; Turpin, A.; Van Eeckhout, A.; Torres-Ruiz, F.A.; Vargas, A.; Ramirez, C.; Pi, F.; Campos, J. Generation of reconfigurable optical traps for microparticles spatial manipulation through dynamic split lens inspired light structures. Sci. Rep. 2018, 8, 11263. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Lizana, A.; Van Eeckhout, A.; Turpin, A.; Iemmi, C.; Márquez, A.; Moreno, I.; Torres-Ruiz, F.A.; Vargas, A.; Pi, F.; et al. Dynamic microparticle manipulation through light structures generated by a self-calibrated Liquid Crystal on Silicon display. Proc. SPIE 2018, 10677, 106772O. [Google Scholar] [CrossRef]
- Fuentes, J.L.M.; Fernández, E.J.; Prieto, P.M.; Artal, P. Interferometric method for phase calibration in liquid crystal spatial light modulators using a self-generated diffraction-grating. Opt. Express 2016, 24, 14159–14171. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Lizana, Á.; Iemmi, C.; Monroy-Ramirez, F.A.; Márquez, A.; Moreno, I.; Campos, J. LCoS display phase self-calibration method based on diffractive lens schemes. Opt. Lasers Eng. 2018, 106, 147–154. [Google Scholar] [CrossRef]
- Zhang, H.; Lizana, A.; Iemmi, C.; Monroy-Ramírez, F.A.; Marquez, A.; Moreno, I.; Campos, J. Self-addressed diffractive lens schemes for the characterization of LCoS displays. Proc. SPIE 2018, 10555, 105550I. [Google Scholar] [CrossRef]
- Lizana, A.; Vargas, A.; Turpin, A.; Ramirez, C.; Estevez, I.; Campos, J. Shaping light with split lens configurations. J. Opt. 2016, 18, 105605. [Google Scholar] [CrossRef]
- Cofré, A.; Vargas, A.; Torres-Ruiz, F.A.; Campos, J.; Lizana, A.; Sánchez-López, M.M.; Moreno, I. Dual polarization split lenses. Opt. Express 2017, 25, 23773–23783. [Google Scholar] [CrossRef] [PubMed]
- Lobato, L.; Márquez, A.; Lizana, A.; Moreno, I.; Iemmi, C.; Campos, J. Characterization of a parallel aligned liquid crystal on silicon and its application on a Shack-Hartmann sensor. Proc. SPIE 2010, 7797, 77970Q. [Google Scholar] [CrossRef]
- Schwiegerling, J.; DeHoog, E. Problems testing diffractive intraocular lenses with Shack-Hartmann sensors. Appl. Opt. 2010, 49, D62–D68. [Google Scholar] [CrossRef] [PubMed]
- López-Quesada, C.; Andilla, J.; Martín-Badosa, E. Correction of aberration in holographic optical tweezers using a Shack-Hartmann sensor. Appl. Opt. 2009, 48, 1084–1090. [Google Scholar] [CrossRef] [PubMed]
- Lizana, A.; Moreno, I.; Marquez, A.; Iemmi, C.; Fernandez, E.; Campos, J.; Yzuel, M.J. Time fluctuations of the phase modulation in a liquid crystal on silicon display: Characterization and effects in diffractive optics. Opt. Express 2008, 16, 16711–16722. [Google Scholar] [CrossRef]
- Ramírez, C.; Lizana, A.; Iemmi, C.; Campos, J. Method based on the double sideband technique for the dynamic tracking of micrometric particles. J. Opt. 2016, 18, 065603. [Google Scholar] [CrossRef]
- Ramirez, C.; Lizana, A.; Iemmi, C.; Campos, J. Inline digital holographic movie based on a double-sideband filter. Opt. Lett. 2015, 40, 4142–4145. [Google Scholar] [CrossRef] [PubMed]
- Jovanovic, O. Photophoresis—Light induced motion of particles suspended in gas. J. Quant. Spectrosc. Radiat. Transf. 2009, 110, 889–901. [Google Scholar] [CrossRef]
- Barry, J.F.; McCarron, D.J.; Norrgard, E.; Steinecker, M.H.; DeMille, D. Magneto-optical trapping of a diatomic molecule. Nature 2014, 512, 286–289. [Google Scholar] [CrossRef] [PubMed]
- Maunz, P.; Puppe, T.; Schuster, I.; Syassen, N.; Pinkse, P.W.; Rempe, G. Cavity cooling of a single atom. Nature 2004, 428, 50–52. [Google Scholar] [CrossRef] [PubMed]
- Ashkin, A.; Dziedzic, J.M.; Yamane, T. Optical trapping and manipulation of single cells using infrared laser beams. Nature 1987, 330, 769–771. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Monroy-Ramírez, A.F.; Lizana, A.; Iemmi, C.; Bennis, N.; Morawiak, P.; Piecek, W.; Campos, J. Wavefront imaging by using an inline holographic microscopy system based on a double-sideband filter. Opt. Lasers Eng. 2019, 113, 71–76. [Google Scholar] [CrossRef]
- Cheng, C.; Chern, J. Symmetry property of a generalized billet’s n-split lens. Opt. Commun. 2010, 283, 3564–3568. [Google Scholar] [CrossRef]
- Yaroslavsky, L.P.; Moreno, A.; Campos, J. Frequency responses and resolving power of numerical integration of sampled data. Opt. Express 2005, 13, 2892–2905. [Google Scholar] [CrossRef] [PubMed]
- Cheng, C.; Chern, J. Quasi bessel beam by billet’s n-split lens. Opt. Commun. 2010, 283, 4892–4898. [Google Scholar] [CrossRef]
- Cuche, E.; Marquet, P.; Depeursinge, C. Spatial filtering for zero-order and twin-image elimination in digital off-axis holography. Appl. Opt. 2000, 39, 4070–4075. [Google Scholar] [CrossRef] [PubMed]
- Hong, J.; Kim, M.K. Single-shot self-interference incoherent digital holography using off-axis configuration. Opt. Lett. 2013, 38, 5196–5199. [Google Scholar] [CrossRef] [PubMed]
- Meng, H.; Hussain, F. In-line recording and off-axis viewing technique for holographic particle velocimetry. Appl. Opt. 1995, 34, 1827–1840. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.-L.; Hill, S.C.; Coleman, M. Photophoretic trapping of absorbing particles in air and measurement of their single-particle Raman spectra. Opt. Express 2012, 20, 5325–5334. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Cannan, D.; Liu, J.; Zhang, P.; Christodoulides, D.N.; Chen, Z. Observation of trapping and transporting air-borne absorbing particles with a single optical beam. Opt. Express 2012, 20, 16212–16217. [Google Scholar] [CrossRef]
- Pedrini, G.; Osten, W.; Zhang, Y. Wave-front reconstruction from a sequence of inter- ferograms recorded at different planes. Opt. Lett. 2005, 30, 833–835. [Google Scholar] [CrossRef] [PubMed]
- Grilli, S.; Ferraro, P.; De Nicola, S.; Finizio, A.; Pierattini, G.; Meucci, R. Whole optical wavefields reconstruction by Digital Holography. Opt. Express 2001, 9, 294–302. [Google Scholar] [CrossRef] [PubMed]






© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Lizana, A.; Van Eeckhout, A.; Turpin, A.; Ramirez, C.; Iemmi, C.; Campos, J. Microparticle Manipulation and Imaging through a Self-Calibrated Liquid Crystal on Silicon Display. Appl. Sci. 2018, 8, 2310. https://doi.org/10.3390/app8112310
Zhang H, Lizana A, Van Eeckhout A, Turpin A, Ramirez C, Iemmi C, Campos J. Microparticle Manipulation and Imaging through a Self-Calibrated Liquid Crystal on Silicon Display. Applied Sciences. 2018; 8(11):2310. https://doi.org/10.3390/app8112310
Chicago/Turabian StyleZhang, Haolin, Angel Lizana, Albert Van Eeckhout, Alex Turpin, Claudio Ramirez, Claudio Iemmi, and Juan Campos. 2018. "Microparticle Manipulation and Imaging through a Self-Calibrated Liquid Crystal on Silicon Display" Applied Sciences 8, no. 11: 2310. https://doi.org/10.3390/app8112310
APA StyleZhang, H., Lizana, A., Van Eeckhout, A., Turpin, A., Ramirez, C., Iemmi, C., & Campos, J. (2018). Microparticle Manipulation and Imaging through a Self-Calibrated Liquid Crystal on Silicon Display. Applied Sciences, 8(11), 2310. https://doi.org/10.3390/app8112310




