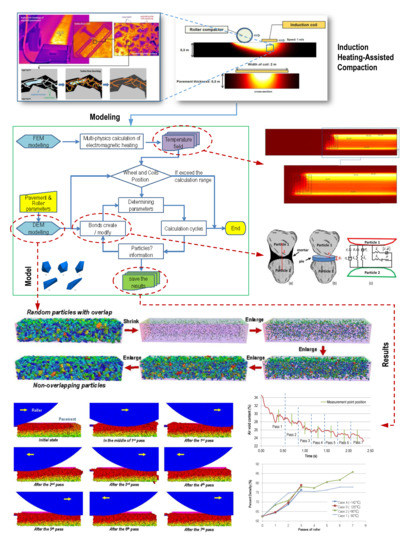
1. Introduction
1.1. Development of Low Temperature Asphalt
Asphalt concrete mix is a combination of asphalt binder and mineral particles of various sizes (i.e., filler and aggregates). The minerals and the binder act as the structural skeleton and glue of the asphalt mix, respectively. Conventional asphalt mixes are produced and compacted at temperatures higher than 150 °C because the viscosity of asphalt binder impedes its workability at ambient temperatures. However, working with mixes at such high temperatures, greenhouse gas emissions and fumes are produced. For this reason, the asphalt industry is constantly looking for solutions to lower energy demands and reduce emissions, and the utilization of technologies that can reduce the in-plant mixing and in-field compaction temperatures of asphalt pavements are under evaluation. These technologies are named low temperature asphalt (LTA) [
1,
2,
3] technologies, and the asphaltic materials developed incorporating these technologies are produced at temperatures 30 °C lower (or more) than temperatures typically used in the production of hot-mixed asphalt (HMA).
There are important environmental and health benefits associated with lower production temperatures, including lower fuel consumption and greenhouse gas emissions and reduced exposure of workers to asphalt fumes. Lower production temperatures can also potentially improve pavement performance by providing added time to mix compaction and allowing improved compaction during cold weather paving conditions. Porous Asphalt (PA) concrete is taken as case material in this research to study the construction process of low temperature porous asphalt pavement, and thus named LTPA hereinafter.
1.2. Development of Porous Asphalt
A lot of effort has been spent worldwide and in the Netherlands on developing new materials and design specifications for durable PA pavement layers [
4,
5]. PA concrete mixes are mainly used as surface courses [
6,
7], and it is well known that these mixes have been developed as a material solution to increase skid resistance as well as to reduce splash during a rainstorm. Typically, an asphalt surface layer is placed, which has high air void contents, to absorb tire-pavement noise and provide good riding smoothness to reduce vehicle vibration-related noise. Factors such as aggregate characteristics, mix design, construction variables, and environment play crucial roles in the performance of PAs.
The compaction process of PAs differs from those of the conventional dense-graded mixes, which involve both static steel wheel rollers and pneumatic-tired rollers [
8]. PAs are typically compacted only by a static steel roller with a few passes over the surface [
9,
10]. However, a serious problem in the compaction process of PAs is the aggregate segregation during laying down and the quick reduction of laying temperature when the continuity of material supply to the construction site is irregular [
11]. The aggregate segregation causes unevenness in asphalt pavement surface and texture, whereas the rapid temperature reduction mainly causes inadequate compaction. All the before-mentioned leads to poor PA performance.
1.3. Induction Heating-Assisted Asphalt Compaction
Asphalt compaction enhances interlocking of the aggregate-sized particles that increase the internal friction of the mix and this, in turn, provides a material with adequate stiffness and strength. However, inadequate compaction results in low mix density, high air void content, and a reduction of mix fatigue life [
9]. Moreover, temperature is an important factor in mix compaction. As temperature drops, the viscosity of asphalt mix is increased and hence coated aggregate mobilization reduction will result to diminished air-void content of mix and the time required to obtain the same degree of compaction increases [
9,
12].
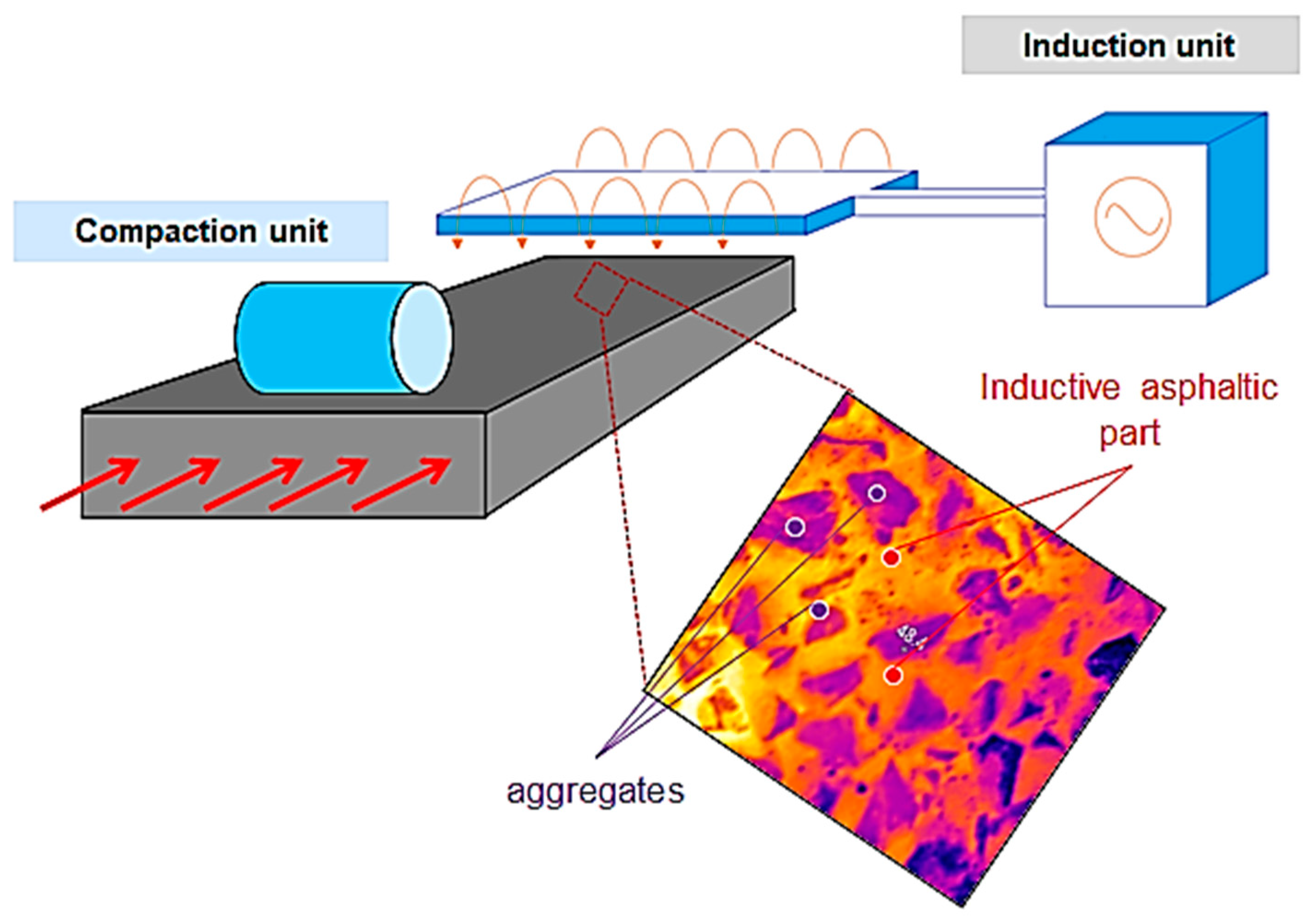
Within this framework, in order to control the temperature profile of laid asphalt mix during compaction and consequently improve the mix compactability, the implementation of induction heating (IH) technology is proposed. IH is a technique recently introduced in pavement engineering [
13,
14,
15,
16]. When an alternating electrical current is applied across an induction coil, an alternating magnetic field is developed. If the coil is placed in the vicinity of a material with inductive particles (e.g., asphalt including inductive fibers or filler-sized particles), then eddy currents are induced in the particles and heat is generated through Joule’s law. The heat generated by electromagnetic induction increases the temperature of the mix and enables viscosity reduction through local melting of the binder. In this paper, a continuous IH compaction process, which consists of a continuously moving induction coil system and a roller compactor (
Figure 1), was applied in LTPA-type mixes.
2. Objectives
The IH compaction process is complicated, and involves three coupled physics: (i) Electromagnetic induction, (ii) heat conduction, and (iii) viscoelastic mechanics. Due to the complex composition of the asphalt mix, the nonlinear mechanical behavior, and the interaction between different physics, this compaction of pavement structures can be optimized through experiments. However, the experimental studies are both expensive and time-consuming. Numerical simulations can avoid the shortcomings faced by experimental studies and provide an efficient way for this kind of research.
In the past, the finite element method (FEM) has been used to analyze the heating performance of inductive asphalt mortar under static [
15] and moving [
16] electromagnetic sources, but the compaction characteristics of asphalt mixtures have not been discussed. Considering that asphalt mix is a kind of granular material, and the FEM faces many difficulties in solving large deformation problems, some scholars have used the discrete element method (DEM) to simulate the indoor asphalt compaction process, but without electromagnetic heating [
18,
19].
The highlight of this paper is to combine these three physics together and study the on-site compaction process of asphalt mix through continuous and discontinuous mechanical computation approaches. Specifically, the COMSOL Multiphysics (V5.3, COMSOL Inc., Stockholm, Sweden, 2017) FEM and PFC3D (V5.0, Itasca Consulting Ltd., Minneapolis, MN, USA, 2017) DEM were employed in this study to simulate the IH compaction process. FEM performs well in simulating electromagnetic heating and the evolution of temperature fields, whereas DEM has the advantage in analyzing the large deformation and complex mechanical behavior of asphalt pavement caused by particle reorganization.
The analyses have been divided into three sequential steps: (i) The prediction of temperature field during IH, (ii) the adjustment of the material parameters of asphalt mortar, and (iii) the execution of the corresponding compaction analysis. The main objectives were to (i) demonstrate the impact of induction technology on the heat generation on the pavement surface by coupling and solving electromagnetic and heat transfer phenomena under a continuously moving induction coil, and (ii) simulate the compaction process using the discrete element method and predict the effect of induction technology on this process in different compaction environments.
3. Simulation of Induction Heating-Assisted Compaction in Porous Asphalt
3.1. Modeling of Asphalt Induction Heating
Multiphysics modeling of electromagnetic heating provides a quick framework of analysis that is especially suited for the study of complex composite materials such as asphalt mixes. A model for inductive pavement structures has been developed elsewhere [
16]. In this research, the governing equations of induction heating with continuously moving coils and the material parameters implemented in the current model are given as well. Herein, two single-turn coils were utilized with a 0.01 m height and 0.2 m width. The selected operational conditions for this IH analysis were 70 kHz and 4 kV at 20 °C, considering the convenient induction examination at room temperature. The temperature development was studied with the same speed as the moving speed of the roller compactor, at 1 m/s (~3.6 km/h). An inductive pavement and the air domain above the pavement surface were designed in such a way that the induction coils were located in the center. To simplify the response of the heated material, it was assumed to be a homogeneous continuum medium with isotropic properties.
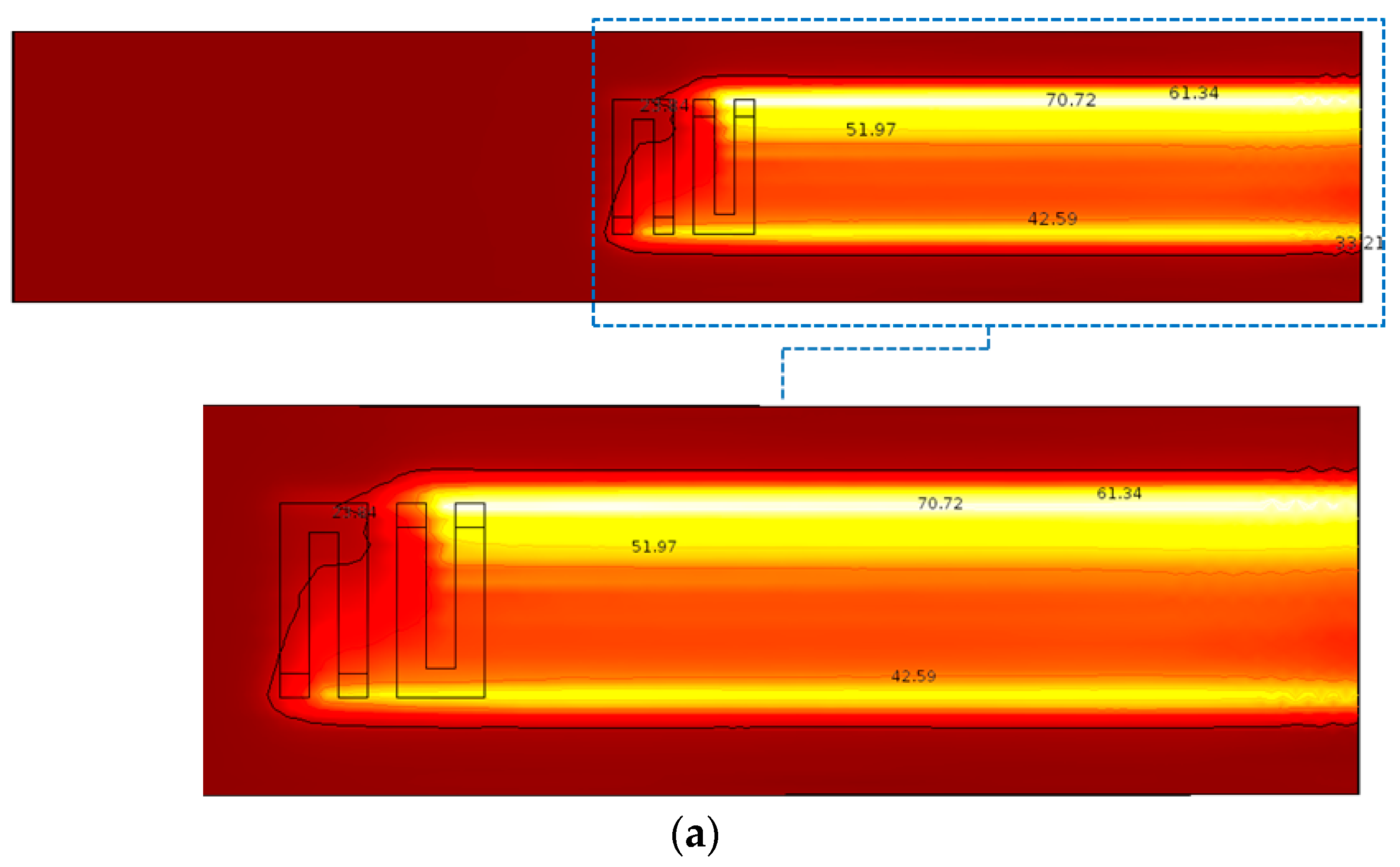
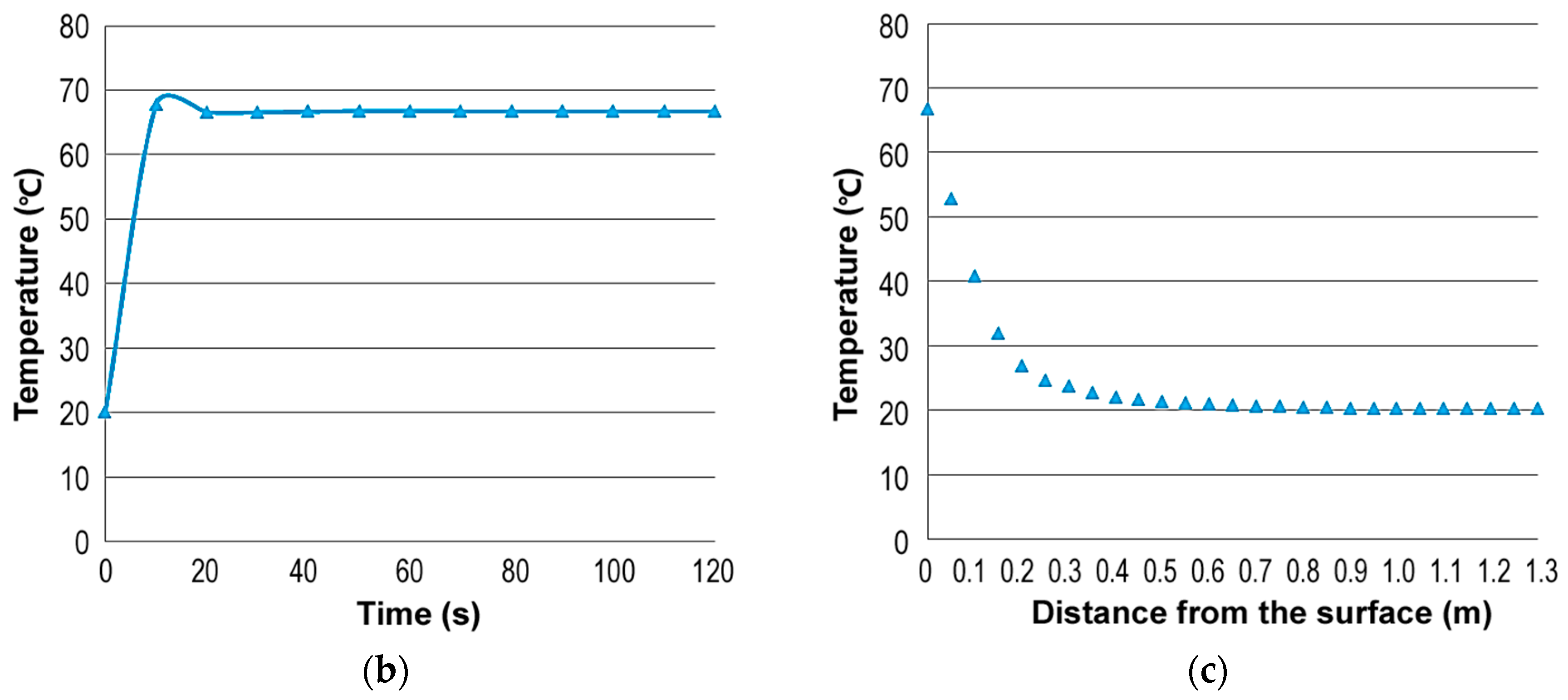
The temperature development and the heat pattern of inductive pavement layer were predicted, and the results after 120 s of induction are shown in
Figure 2. In
Figure 2a, the contour lines show the evolution of the temperature gradient at the asphalt surface, and the maximum generated temperatures appeared close to the coil’s gates where the concentration of magnetic fields was higher. However, apart from the highest reached temperature of the surface of the asphalt layer, increased IH efficiency (the temperature after 120 s of induction) resulted also within the asphalt layer (
Figure 2b). The temperature distribution from the top to the bottom of the inductive asphalt layer is illustrated in
Figure 2c. This distribution inside the layer shows the advantage of utilizing the induction technology as a heating technique to minimize temperature reduction phenomena during asphalt compaction. Thus, the viscosity of asphalt mixes could be maintained, increasing the time required for adequate compaction under low temperature conditions.
3.2. Modeling of Asphalt Mix
DEM modeling is a computational approach in which the discontinuous materials are modeled as individual elements, and it was introduced by Cundall et al. [
20,
21]. This approach allows the simulation of complex and heterogeneous materials, taking into account the contacts and the interaction of particles within the aggregate skeleton. Wang et al. studied the compaction mechanics of asphalt concrete through DEM modeling [
18]. Chen developed a viscoelastic contact model and applied DEM to simulate three commonly used compaction methods for hot-mix asphalt gyratory compaction, asphalt vibratory compaction, and kneading compaction [
19]. Even so, the simulation of roller compaction of asphalt pavement remains to be carried out.
3.2.1. Material Selection
During the years, Dutch authorities and contractors have tried to address the issues of surface pavement layers by developing PA mixes. Two characteristic examples of surface layers commonly used in the Netherlands are (i) two-layer PA with a 0/16 and 0/8 aggregate matrix in the bottom and top layer, respectively, and (ii) single-layer PA with a 0/16 aggregate matrix [
10], which was used in this study (
Table 1). In the PA with a 0/16 aggregate gradation, steel slag particles (finer fraction 2 mm) were added as low-cost inductive agents by replacing mineral aggregates of the same fraction.
3.2.2. Micromechanical Modeling of Asphalt Mix
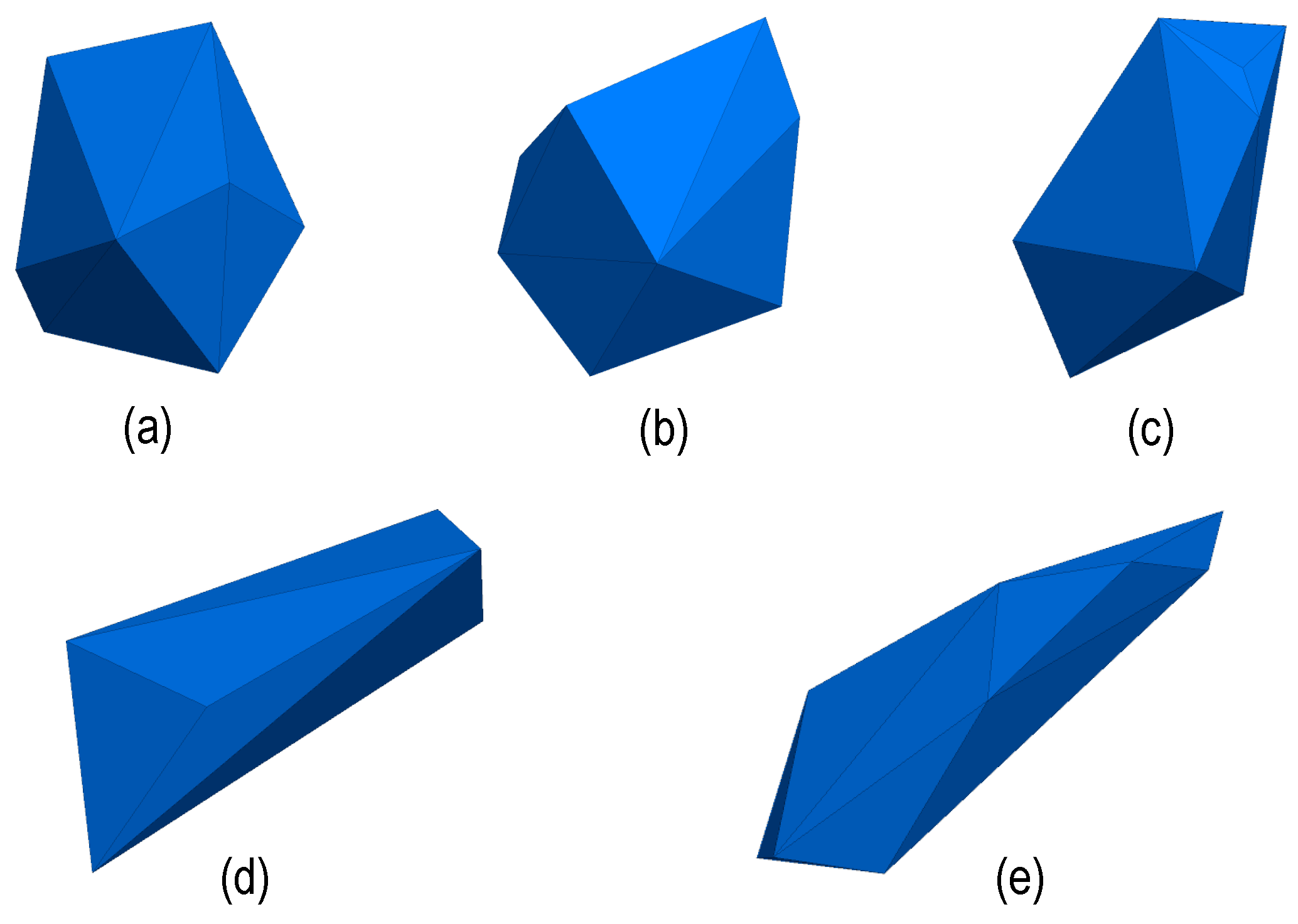
To simplify the micromechanical modeling of LTPAs, the mix was divided into three different individual constituents: (i) Coarse aggregate particles larger than 2.0 mm, (ii) asphalt mortar, and (iii) air voids. Considering that the shape of the coarse aggregates, which formed the aggregate skeleton in the mix, has a major impact on mix compaction and performance [
22,
23,
24], five different particles with complex geometries (
Figure 3) were developed to compose the PA 0/16 material. The shape of each aggregate particle was randomly chosen from these five shapes. The values of
L:
W:
H denoted the ratio of the particle’s length, width, and height, respectively, and they were used to control the flatness and elongation of particles (
Figure 3).
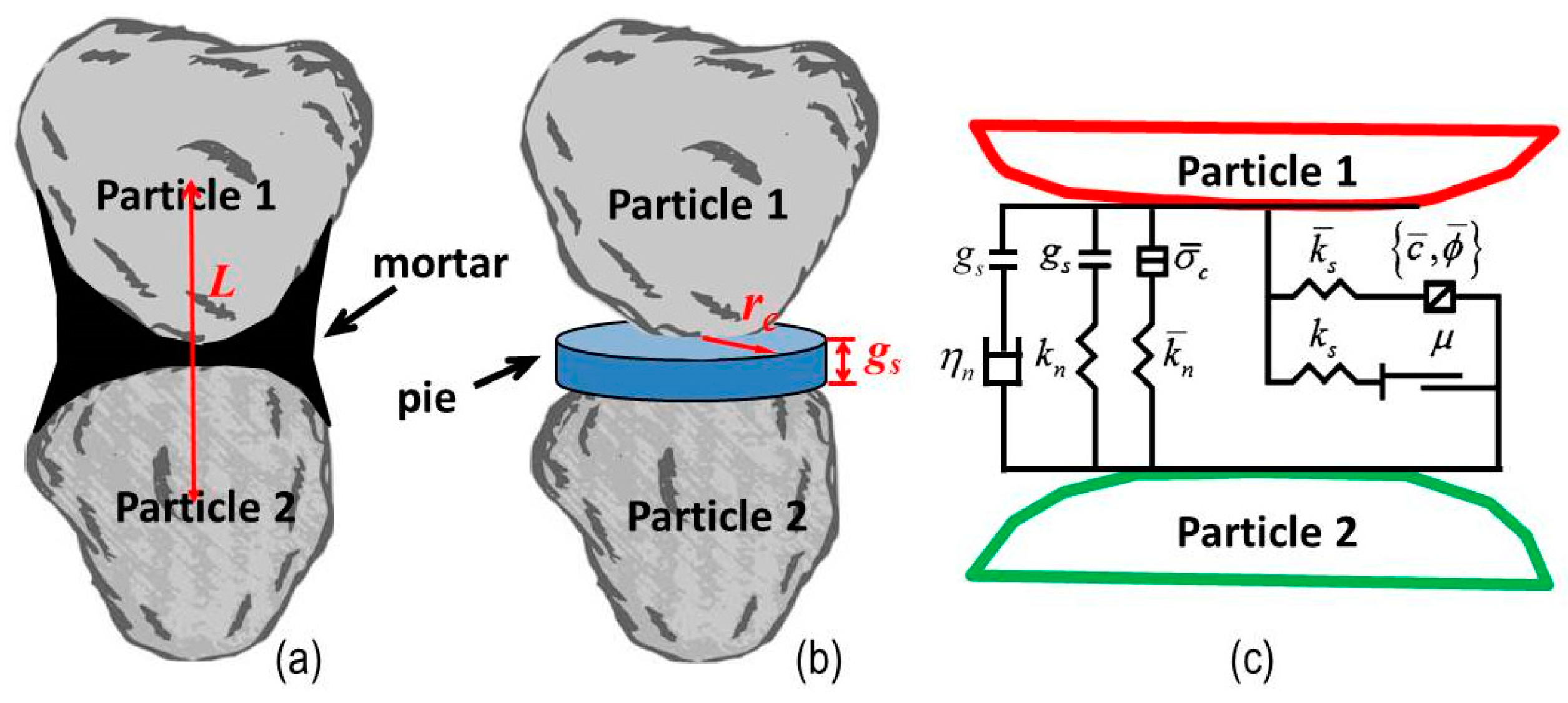
For the DEM modeling, asphalt mortar (i.e., asphalt binder, mineral filler, and fine sand), which was added as the bond between the generated coarse aggregate particles in the analyses, was considered to be a continuum and homogeneous. The bond was envisioned as a pie made by many elastic springs and viscous dashpots lying on the contact plane and centered at the contact point of two particles, as seen in
Figure 3. When the pie was bonded, it could resist the tensile force and the relative rotation moment until the tensile strength or shear strength limit of the spring was exceeded. After the break of contact bonds, only compressive forces were active.
Due to the fact that when two aggregates are covered by mortar, they are easily glued together during movement, the broken bond may be reglued again when the particles are close enough. This is the biggest different between compaction simulation and the common mechanical analysis for asphalt mix. This mechanism could be realized through continually judging and generating new bonds when necessary but keeping the state of old bonds unchanged during the cycle.
The pie-shaped bond model was determined by five key parameters related to asphalt mortar. These parameters were (i) the normal stiffness , (ii) the shear stiffness
, (iii) the tensile strength
, (iv) the shear strength
(calculated by cohesion
c and angle of internal friction
), and (v) the pie radius
. Parameters such as the gap between the particles
, the viscosity of contact
, and the friction of contact
should also be taken into account in the model development, as seen in
Figure 4. The particle contact behavior was governed by Kelvin–Voigt constitutive laws, and tension was determined through the Mohr–Coulomb failure criterion.
3.2.3. Model Parameters Determination
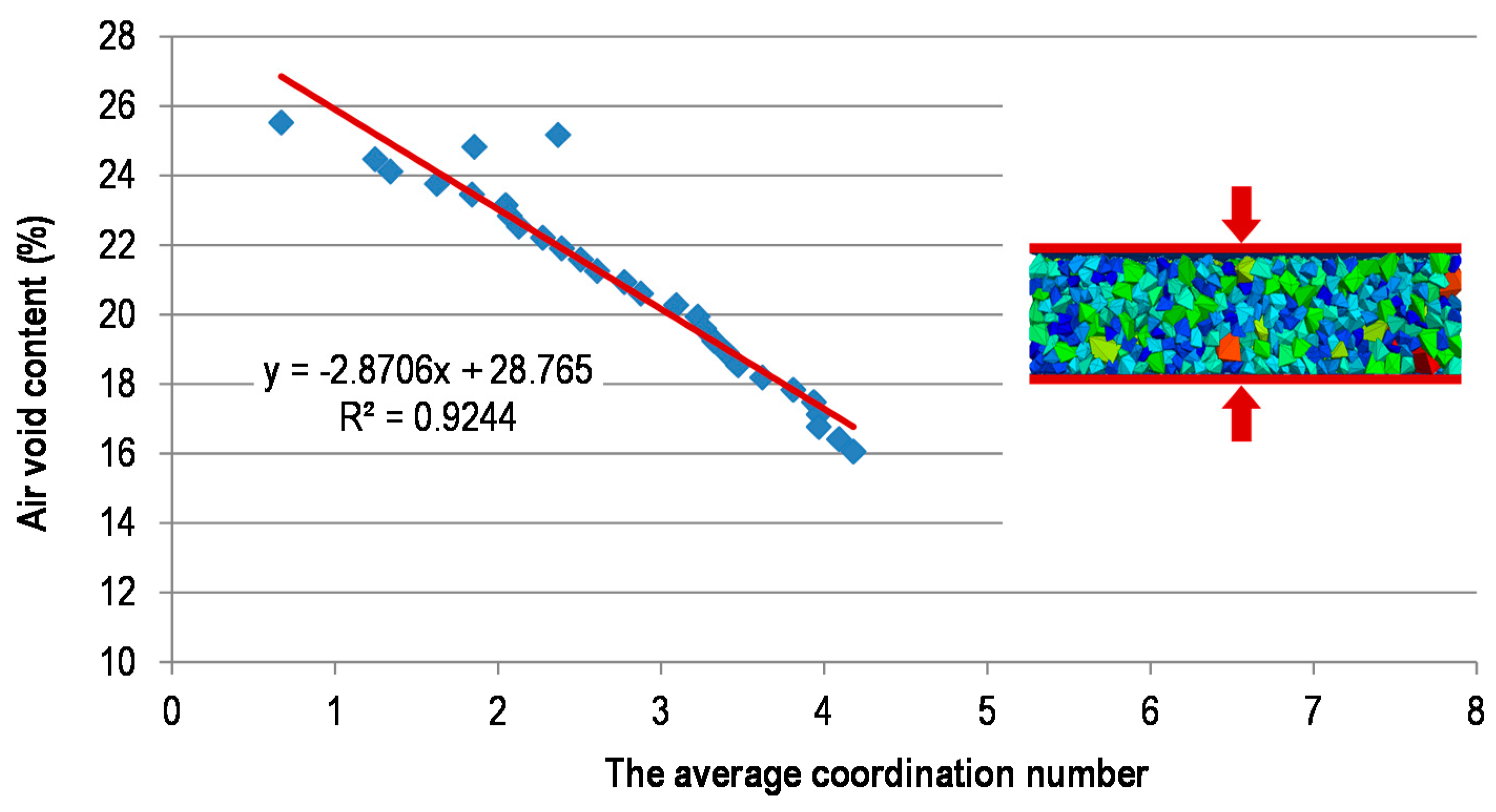
The previously mentioned five parameters had a great influence on the degree of asphalt compaction and were determined by the mix temperature. However, the compactability of the mix, which was influenced by the temperature as well, was determined by the air void content. Research [
25] has shown that the air void content is linearly related to the coordination number. The coordination number of a particle is defined as the total number of particles which are in contact with it. In this paper, the air void content of the mix was changed by compressing the same pavement DEM model, and the relationship was obtained as shown in
Figure 5:
where
n is the air void content,
is the average coordination number of aggregates, and
and
A are coefficients.
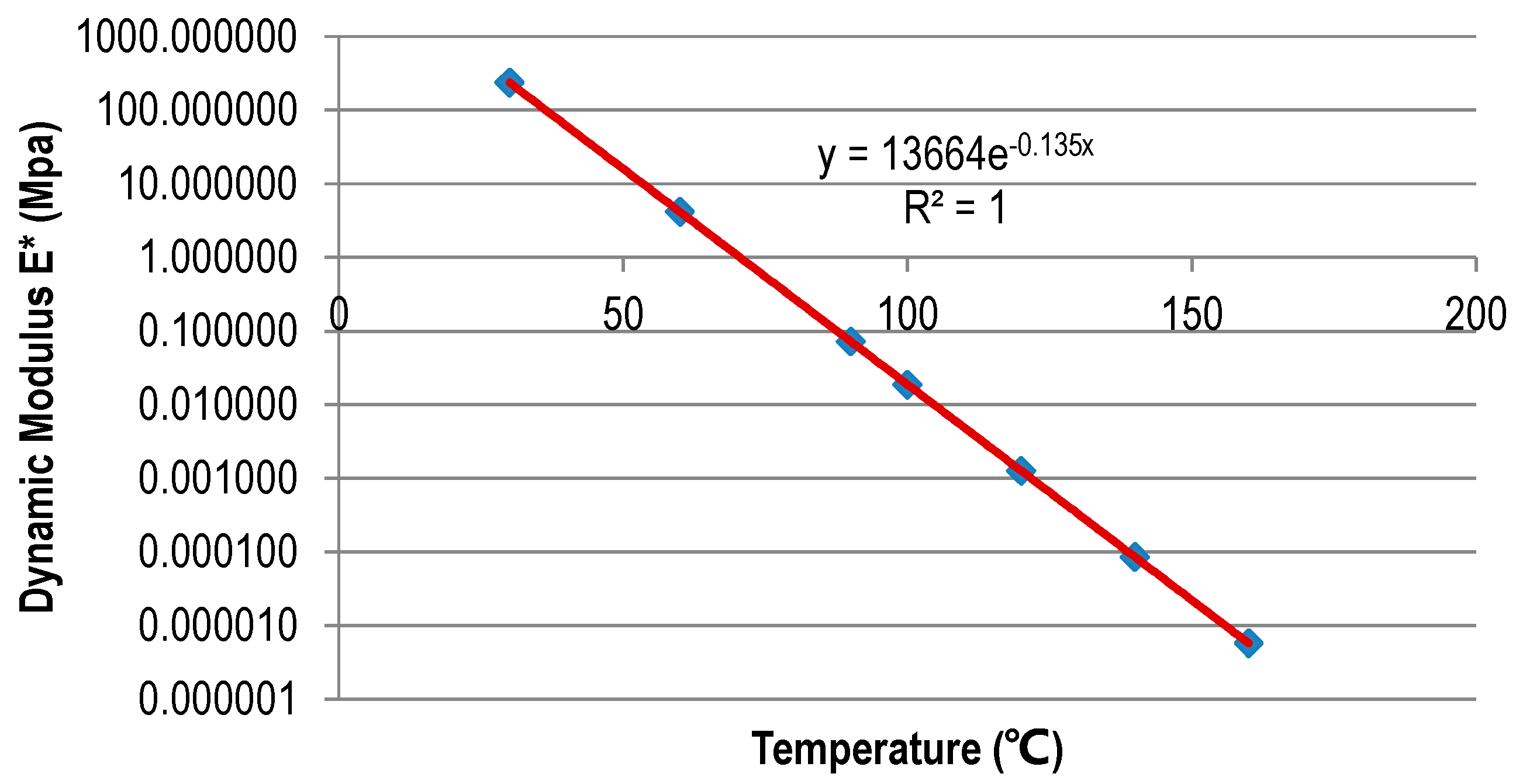
Stiffness of Asphalt Mortar
The relationship of the dynamic module of asphalt mortar under different temperatures was investigated by Fernandes et al. [
26], and it was expressed as shown in Equation (2),
where
E* is the dynamic modulus of the mortar (MPa),
T is the temperature, and
and
α are the complex parameters.
In this bond model, the stiffness of asphalt mortar was only produced by a cluster of springs. The dynamic modulus was replaced by the stiffness, and the relation is given in Equation (3),
where
K is the stiffness of the bond (MPa/m) and
L is the distance between the centroid of two particles that are bonded. This relationship shows that the value of stiffness is reduced when two particles are moving away and by keeping dynamic modulus constant.
In this research, the dynamic modulus of LTPA mortar was assumed to obey the curve shown in
Figure 6, and the stiffness in normal direction was kept the same as that in shear direction.
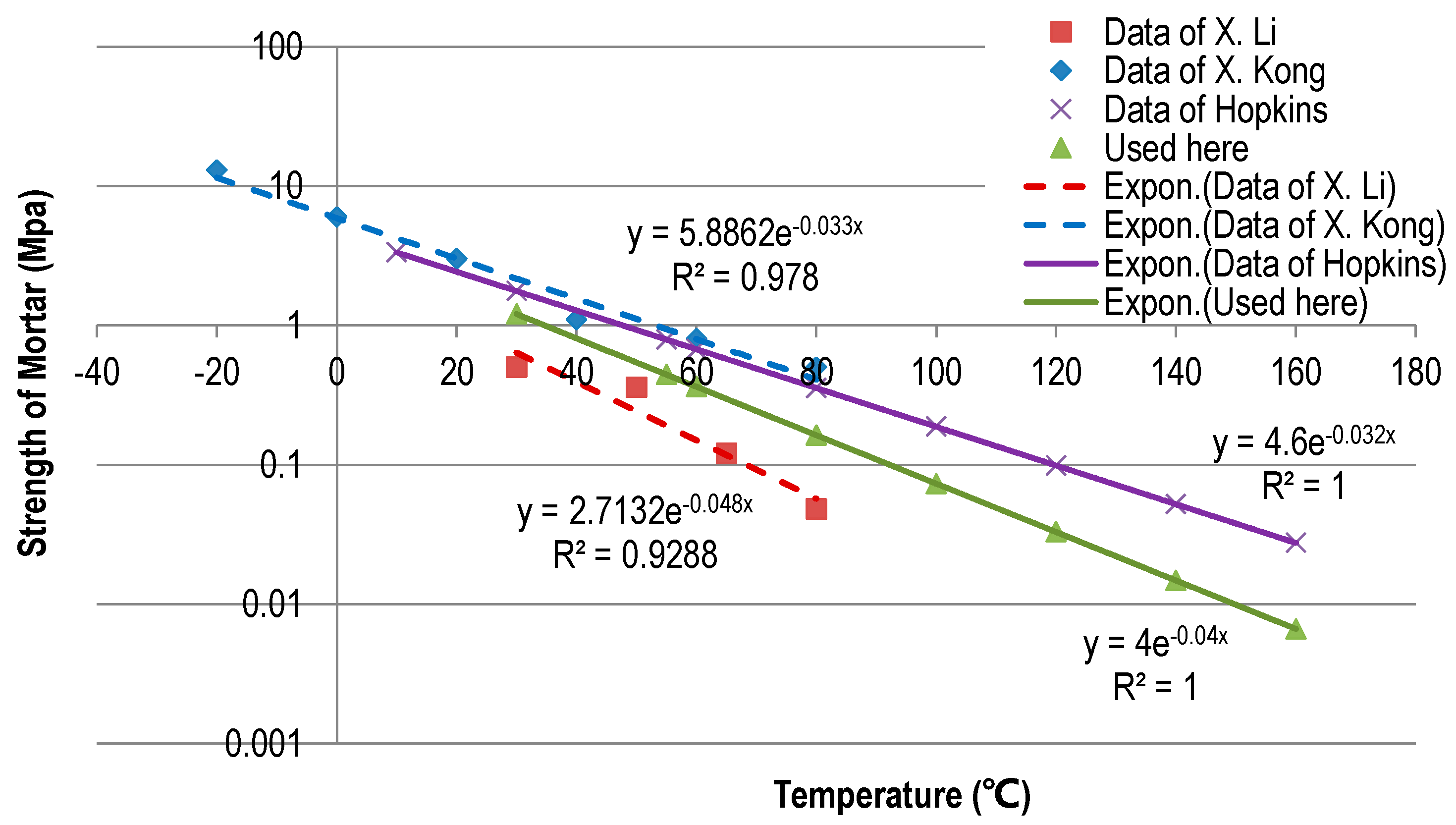
Strength of Asphalt Mortar
Since the asphalt mortar was assumed to be a viscoelastic material, a peak value of stress and permitted strain existed. When a bond exceeds any one of these limits, the bond can be treated as broken and the rheological property of mortar is easily reflected. The tensile and shear strength of asphalt mortar have been investigated and the obtained results demonstrate that the strength is exponentially related to temperature [
27,
28,
29,
30] (
Figure 7 and Equation (4)):
where
is the tensile strength and
and
β are the corresponding parameters.
The elastic energy stored in the springs of the bond could not be released, as it was obviously not consistent with the purpose of simulation. Therefore, a critical strain should be applied onto the model. Then the effective strength of mortar can be written as
where
is the effective strength and
is the critical strain. In this research,
is given by Equation (6),
Angle of Internal Friction
Since the failure mode of asphalt mortar was controlled by the Mohr–Coulomb strength criterion, the shear strength of the mortar was determined by the normal stress
, the cohesion
c, and the internal friction angle
[
31]. Herein, only the angle of internal friction is discussed, which was influenced by the temperature and the compactability of the mix [
29,
30]. This parameter referred not only to the attribution of asphalt mortar but also to the whole interaction of contacted particles. In Hopkins et al.’s research [
29], the angle of internal friction was given by Equation (7) as a function of temperature:
As shown in Tinoco et al.’s report [
30], the internal friction angle reduces with an increase in the air void content of the mix. The obtained data are listed in
Table 2. Based on these results, the angle was determined by the following function,
where
is the internal friction angle of the bond,
is the friction angle based on the temperature,
is the coefficient caused by the variation in air void content, and
is the corresponding expression of
in the form of a coordinate number, which is given by
Table 2 as well.
Bond Radius
The bond radius greatly influenced the bond damage in the asphalt mortar. An easy way to obtain this parameter was to calculate it through the total effective volume of the asphalt mortar. Moreover, it was assumed that the bond radius ratio
ζ was defined as the ratio of bond radius
rc to the minimal radius
of equivalent sphere with the same volume as the bonded particles. The total effective volume of mortar and the radius ratio
ζ could be estimated by Equations (9) and (10):
where
Vm is the total volume of mortar,
Nb is the total number of bonds at a given time, and
L is the distance of two bonded particles, as in Equation (3).
When asphalt mortar becomes denser, the bond radius obviously becomes larger. However, it is difficult to give an explicit equation between them. Here,
L is assumed to be lineally related to the air void content within a short content range. Thus, distance
L can be described using coordination numbers as
where
is the particle’s coordination number and
and
are the corresponding coefficients.
Also, by substituting Equation (11) into Equation (10), Equation (12) is formulated:
where
ε is the enlargement multiplier of bond radius ratio
ζ, and
s is the coefficient related to the coordination number.
3.3. Modeling of Pavement Compaction
Before simulating the compaction process of LTPA, a new model had to be created. Since there is not a mature approach to create such models directly with the required air void content, in order to make full use of the DEM mechanics and to keep the gradation distribution of the mix unchanged, the following procedure ensued: (i) Calculation of the total volume of particles according to the pavement model size and the required and initial air void content, (ii) calculation of the particle numbers of different sizes on the basis of the mix gradation, (iii) random generation of these particles (where the particles may have overlapped each other), (iv) shrinkage of all the particles by 50 times, for example, and (v) enlargement of the particles step by step (between each step, the overlaps were eliminated through DEM simulation). If each particle enlarged
times per step, all the particles would change back to their original size again after 10 steps, and meanwhile, the air void content of the pavement model would reach the value that was set (
Figure 8). Note that, in this process, a pie-shaped bond model would be unnecessary and an elastic contact model would be enough.
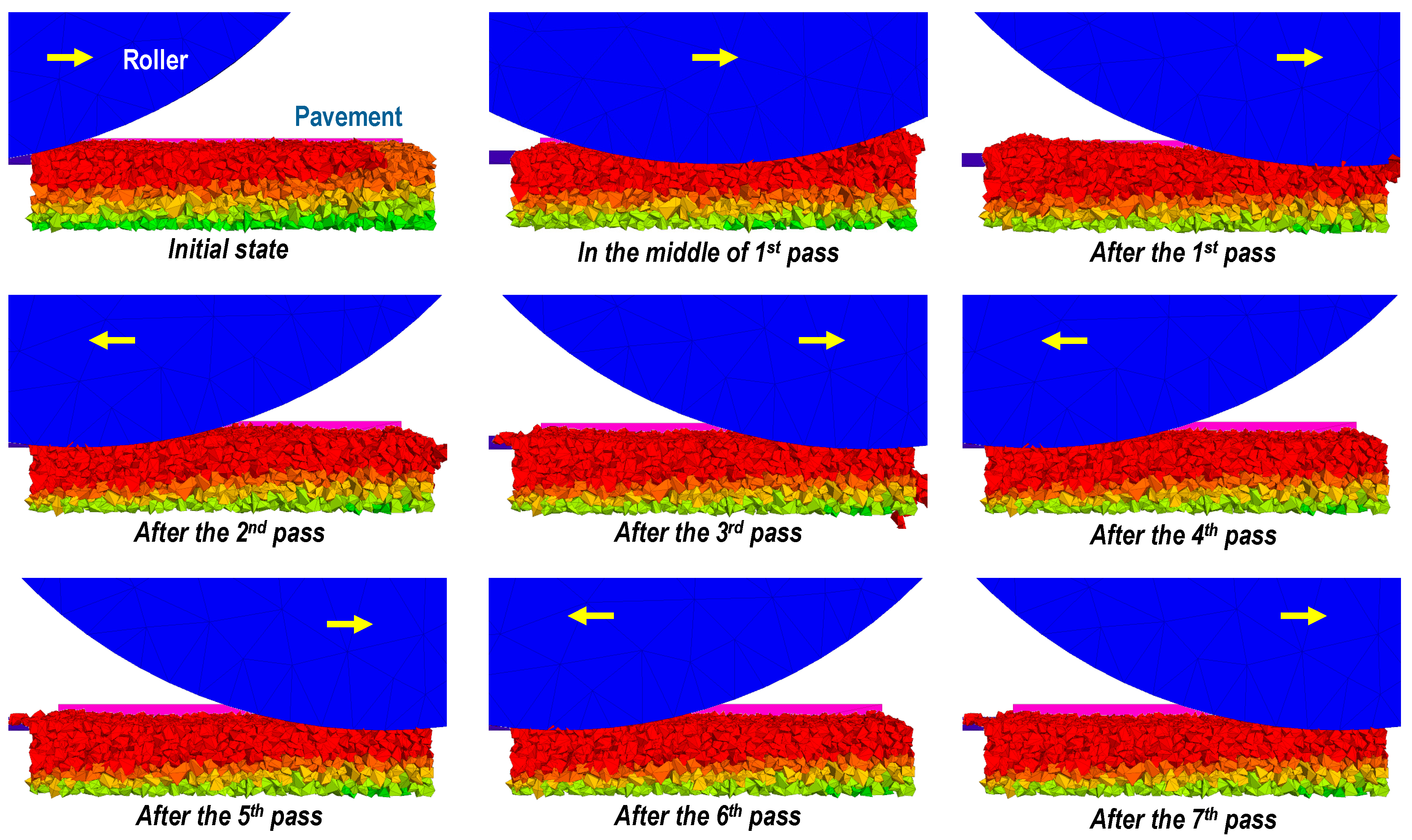
The compaction procedure was achieved by a rigid wheel (roller wheel), which was modeled by a polyhedral shell with many small facets and rolls on the pavement model with a given weight. When the roller moved close to the border of the pavement model, one pass finished. Then the roller would go back to its original location and repeat this procedure until the end, as seen in
Figure 9.
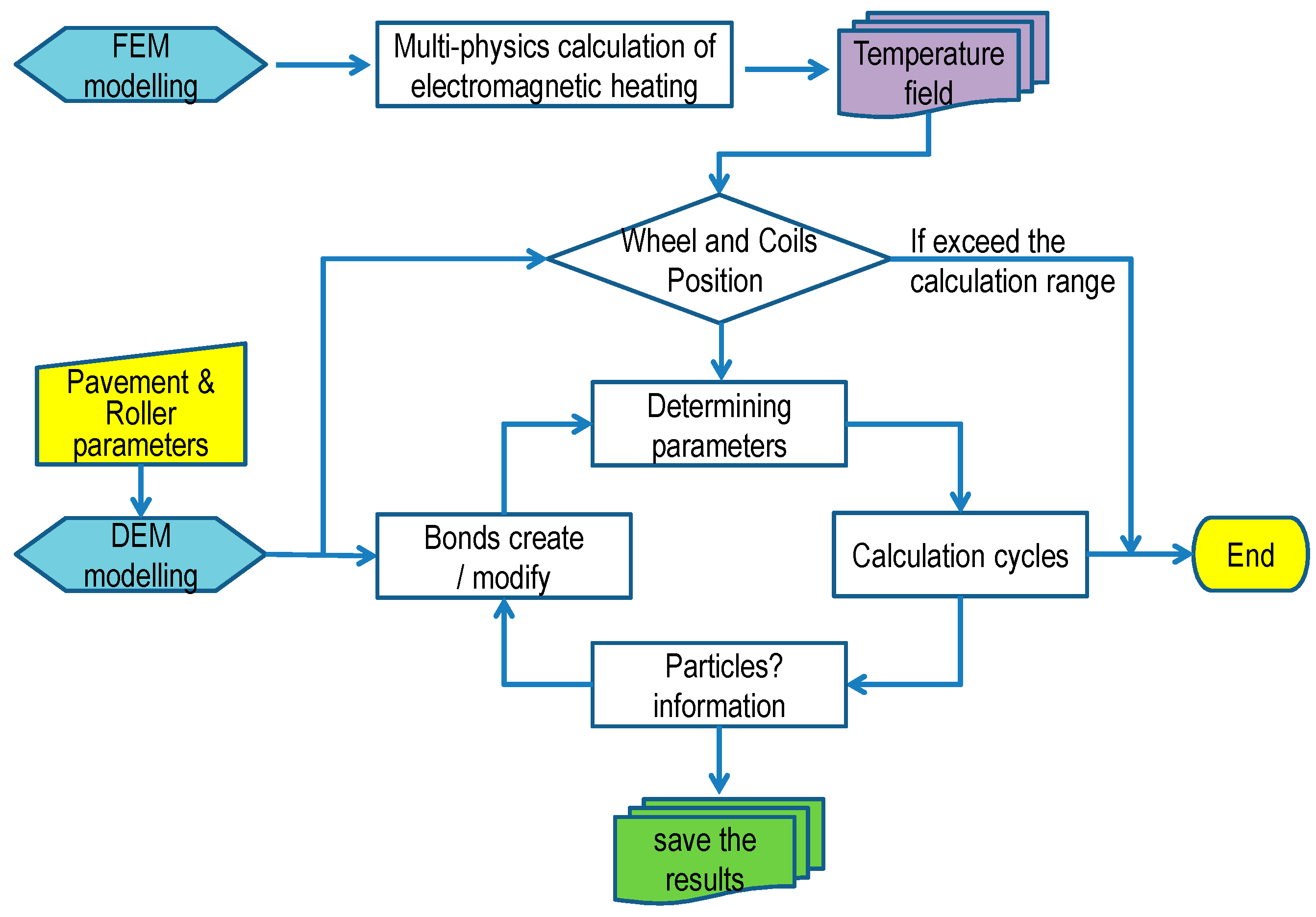
A schematic flow diagram of the coupling methodology is demonstrated in
Figure 10, which explains how the two modeling methods combined together. As can be seen from this figure, three key relations of the process were used, (i) to adjust the temperature field according to the position of the roller, (ii) to modify the bond parameters between the particles according to the temperature and mechanical state of the investigation point, and (iii) to update the open and closed states for the particles according to the force and displacement relationship between them.
4. Results and Main Findings
The asphalt pavement compaction model was created by taking into account the effect of IH and its generated temperature field, which was calculated before. It was assumed that the generated heat for asphalt pavements of an initial temperature of 20 °C was also valid for higher initial temperatures. All the parameters of the asphalt compaction process are shown in
Table 3.
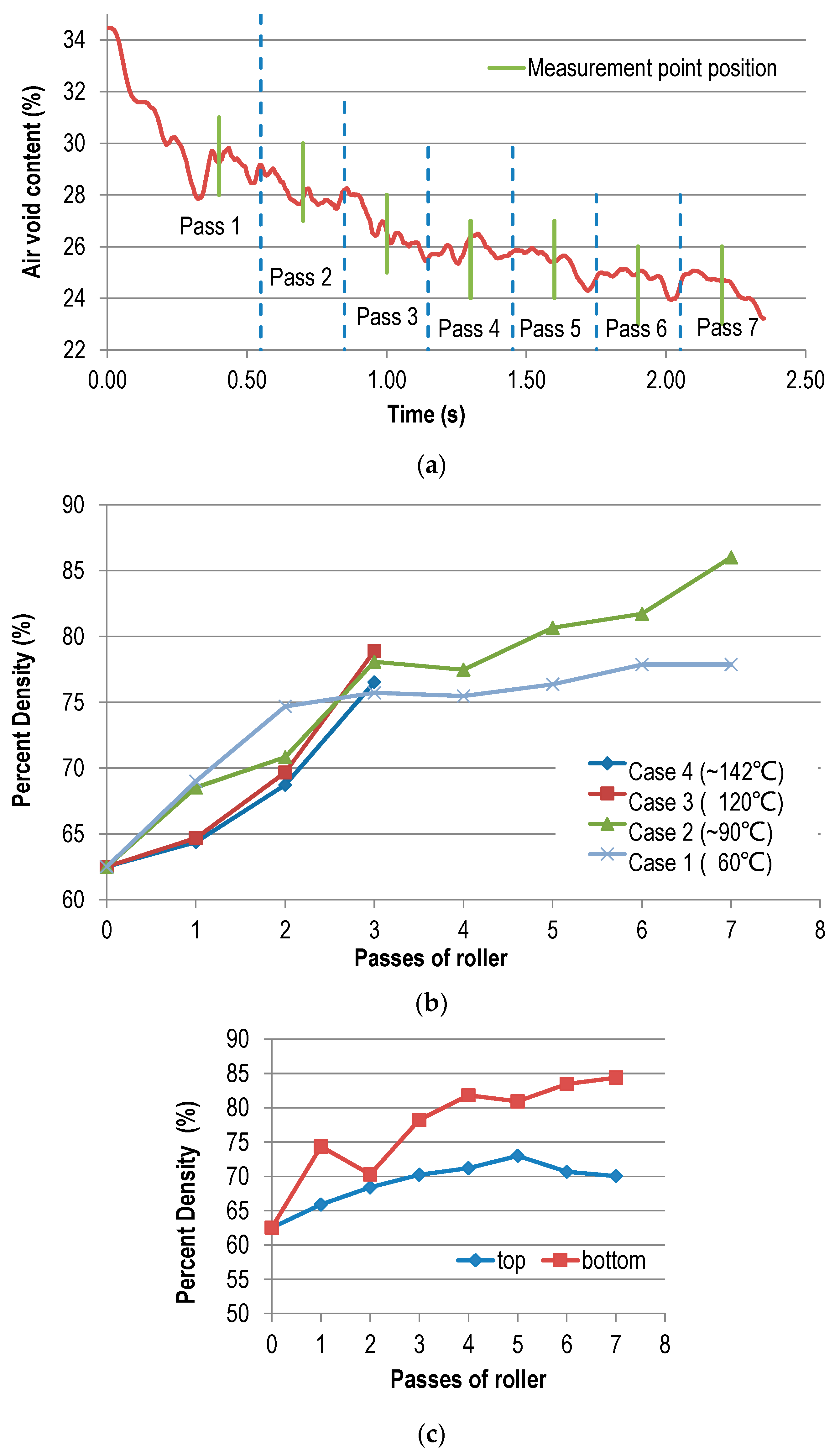
The relation of asphalt compactability or air void content to the roller passes are shown in
Figure 11. Four cases were considered.
Low temperature group:
| Case 1: Mix temperature T0 = 60 °C | without IH. |
| Case 2: Mix temperature T0 = 60 °C | with IH (surface temperature of Tf = ~90 °C). |
High temperature group:
| Case 3: Mix temperature T0 = 120 °C | without IH. |
| Case 4: Mix temperature T0 = 120 °C | with IH (surface temperature of Tf = ~142 °C). |
In
Figure 11a, it was found that during the first pass (initial compaction), the air void content fluctuated dramatically and the mix was easily flown. If taking the studied point (the midpoint of the model) as a reference, when the compactor came close to it, the mix air void content declined because of the aggregates’ pushing movement. When the roller moved to the right above the point, many bonds were broken, caused by tensile stress, and the air void content showed a slight increase. When the roller moved off this point, the air void content went down again and the mix recompacted. With passes increased, the air void content continually declined, whereas fluctuation started to be stable and the variation amplitude of porosity reduced.
Figure 11b shows that the entire compaction process could be divided into two distinct stages, the early stage (passes < 3) and the late stage (passes > 3). In the early stage, the mix density during compaction could be sorted in descending order as Case 1 > Case 2 > Case 3 > Case 4. That is to say, (i) relative to the high temperature group (Case 3 and Case 4), the low temperature group (Case 1 and Case 2) showed much higher density in the early stage, and (ii) regardless of the high temperature group or low temperature group, the density of the mix without IH was higher than that with IH in the early stage (i.e., Case 1 > Case 2, Case 3 > Case 4).
In the late stage of compaction, the mix density at higher temperatures eventually exceeded the density at low temperatures (i.e., Case 2 > Case 1). The phenomenon happened mainly due to the fact that higher temperatures do not always increase the mix density, but they can increase the mobility of particles, leading to bad mix compactability. Further, IH operated efficiently in the late compaction stage when the mix density reached a certain value, rather than at the very beginning. Also, the effect of IH on the asphalt compaction process was not obvious at higher temperatures.
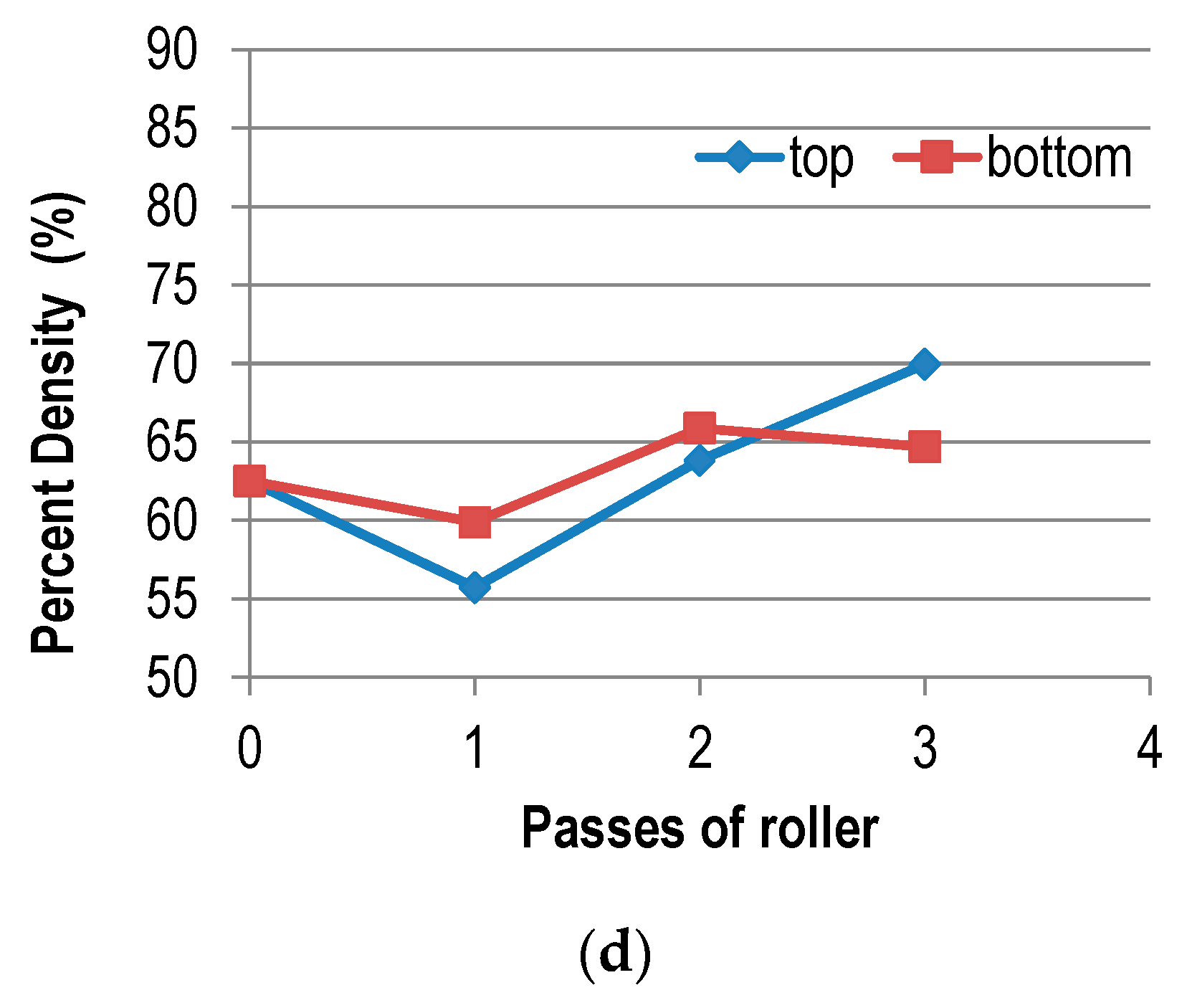
Figure 11c,d demonstrates the change of density at different depths (top and bottom) with increasing roller passes. These curves in
Figure 11c show that the density of the bottom layer changed considerably compared to that of the top layer when the mix was at low temperature. This might have been caused by two reasons. One was the boundary conditions, and the other was the change of stiffness balance due to IH. Since the bottom layer had much stronger border restrictions than the top layer, for such a granular material, the density would obviously be larger. Furthermore, the stiffness of the top mix was also reduced more than that of the bottom mix since being heated. According to the law shown in
Figure 11b, the compaction effect of the bottom layer would be higher than that of the top layer. But for high temperature cases,
Figure 11d shows that the difference in density in different layers was not distinct because the balance of stiffness changed little when the mix was at high temperature.
5. Conclusions and Recommendations
This paper introduced a computational method combining two modeling tools to simulate asphalt pavement compaction assisted by induction heating. The proposed method allowed the dynamic change of microstructural parameters of asphalt mortar in a DEM tool according to the moving temperature field predicted by an FEM tool.
Additionally, based on the analyses, the asphalt compaction process could be divided into the early and late stages. In the early stage, the density of the mix compacted, with induction technology remaining the same. In the late stage, the mix density was larger when induction heating was applied. Thus, induction heating was more suitable at lower temperatures. Furthermore, induction heating mostly influenced the balance of stiffness at different pavement depths. For high temperatures, the effect of induction was minimal. However, for lower temperatures, heating always led to a higher density at the bottom of the pavement than at the top.
Although the objective of this paper was mainly to discuss induction heating-assisted compaction technology and the developed numerical approach, it is very necessary to carry out lab-scale tests to obtain the required parameters in further research and then to verify the results of these analyses.
Author Contributions
Conceptualization, X.L. and A.(T.)S.; methodology, C.Z. and P.A.; modelling, C.Z. and P.A.; writing original draft preparation, C.Z. and P.A.; writing review and editing, X.L. and L.H.; supervision, A.(T.)S.
Funding
This research received no external funding.
Acknowledgments
The first author would like to acknowledge the financial support of Sino-Dutch Bilateral Exchange Scholarship and EP-Nuffic of the Netherlands.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- CROW. Low Temperature Asphalt for a Sustainable Pavement; CROW Publication 319; CROW: Ede, The Netherlands, 2013; ISBN 978 90 6628 613 9. (In Dutch) [Google Scholar]
- European Asphalt Pavement Association. The Use of Warm Mix Asphalt; EAPA-Position Paper; EAPA: Brussels, Belgium, 2014. [Google Scholar]
- Hanz, A.J.; Faheem, A.; Mahmoud, E.; Bahia, H.U. Measuring Effects of Warm-mix Additives: Use of Newly Developed Asphalt Binder Lubricity Test for the Dynamic Shear Rheometer. In Transportation Research Record: Journal of the Transportation Research Board; Transportation Research Board: Washington, DC, USA, 2010; Volume 2180, pp. 85–92. [Google Scholar]
- Smith, H.A. Performance Characteristics of Open-Graded Friction Courses; NCHRP Synthesis of Highway Practice, No. 180; Transportation Research Board, National Research Council: Washington, DC, USA, 1992. [Google Scholar]
- Van Der Zwan, J.T.; Goeman, T.; Gruis HJA, J.; Swart, J.H.; Oldenburger, R.H. Porous Asphalt Wearing Courses in the Netherlands: State of the Art Review. In Transportation Research Record: Journal of the Transportation Research Board; Transportation Research Board: Washington, DC, USA, 1990; pp. 95–110. [Google Scholar]
- Kandhal, P.S.; Mallick, R.B. Open Graded Friction Course: State of the Practice; Transportation Research Board, National Research Council: Washington, DC, USA, 1998. [Google Scholar]
- Hagos, E.T. The Effect of Aging on Binder Properties of Porous Asphalt Concrete. Ph.D. Thesis, TU Delft, Delft, The Netherlands, 2008. [Google Scholar]
- Austroads. The Influence of Compaction on the Performance of Dense Graded Asphalt; Austroads Project TT1353; Austroads: Sydney, Australia, 2011. [Google Scholar]
- Lu, Q.; Harvey, J.T. Laboratory Evaluation of Open-Graded Asphalt Mixes with Small Aggregates and Various Binders and Additives. In Transportation Research Record: Journal of the Transportation Research Board; Transportation Research Board: Washington, DC, USA, 2011; pp. 61–69. [Google Scholar]
- Alvarez, A.E.; Martin, A.E.; Estakhri, C.K.; Button, J.W.; Glover, C.J.; Jung, S.H. Synthesis of Current Practice on the Design, Construction, and Maintenance of Porous Friction Courses; Technical Report. No. FHWA/TX-06/0-5262-1; Texas Transportation Institute: Houston, TX, USA, 2006. [Google Scholar]
- Molenaar, A.A.A.; Meerkerk, A.J.J.; Miradi, M.; Van der Steen, T. Performance of Porous Asphalt concrete. J. Assoc. Asphalt Paving Technol. 2006, 75, 1053–1094. [Google Scholar]
- Kragh, J.; Goudert, L.; Sandberg, U. OPTHINAL: Optimization of Thin Asphalt Layers. ERA-NET Road; Final Report, Project No. VV 2009/40520; Danish Road Institute (DRI): Hedehusene, Denmark, 2011. [Google Scholar]
- García, Á.; Schlangen, E.; van de Ven, M.F.C.; Liu, Q. Electrical Conductivity of Asphalt Mortar Containing Conductive Fibers and Fillers. Constr. Build. Mater. 2009, 23, 3175–3181. [Google Scholar] [CrossRef]
- Liu, Q.; Schlangen, E.; García, Á.; van de Ven, M.F.C. Induction Heating of Electrically Conductive Porous Asphalt Concrete. Constr. Build. Mater. 2010, 24, 1207–1213. [Google Scholar] [CrossRef]
- Apostolidis, P.; Liu, X.; Scarpas, A.; Kasbergen, C.; van de Ven, M.F.C. Advanced Evaluation of Asphalt Mortar for Induction Healing Purposes. Constr. Build. Mater. 2016, 126, 9–25. [Google Scholar] [CrossRef]
- Apostolidis, P.; Liu, X.; Kasbergen, C.; Scarpas, A.; van de Ven, M.F.C. Toward the Design of an Induction Heating System for Asphalt Pavements with the Finite Element Method. In Transportation Research Record; 2633-16 TRB; National Research Council: Washington, DC, USA, 2017; pp. 136–146. [Google Scholar]
- Apostolidis, P. Induction Healing of Asphalt Mixes with Steel Slag: The Case of Motorway A31, North Holland. In Presentation to Rijkswaterstaat: Ministrie van Infrastrucuur en Waterstaat; Rijkswaterstaat: Utrecht, The Netherlands, 2017. [Google Scholar]
- Wang, L.; Zhang, B.; Wang, D.; Yue, Z. Fundamental Mechanics of Asphalt Compaction through FEM and DEM Modeling. In Analysis of Asphalt Pavement Materials and Systems: Engineering Methods; American Society of Civil Engineers: Reston, VA, USA, 2007; pp. 45–63. [Google Scholar]
- Chen, J. Discrete Element Method (DEM) Analyses for Hot-Mix Asphalt (HMA) Mixture Compaction. Ph.D. Thesis, University of Tennessee, Knoxville, TN, USA, 2011. [Google Scholar]
- Cundall, P.A. A Computer Model for Simulating Progressive, Large-scale Movements in Block Rock Systems. Proc. Symp. Int. Soc. Rock Mech. 1971, 2, 129–136. [Google Scholar]
- Cundall, P.A.; Strack, O.D. A Discrete Numerical Model for Granular Assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Dondi, G.; Simone, A.; Vignali, V.; Manganelli, G. Numerical and Experimental Study of Granular Mixes for Asphalts. Powder Technol. 2012, 232, 31–40. [Google Scholar] [CrossRef]
- Dondi, G.; Simone, A.; Vignali, V.; Manganelli, G. Discrete element modelling of influences of grain shape and angularity on performance of granular mixes for asphalts. Procedia-Soc. Behav. Sci. 2012, 399–409. [Google Scholar] [CrossRef]
- Zhou, C.; Zhang, M.; Li, Y.; Lu, J.; Chen, J. Influence of Particle Shape on Aggregate Mixture’s Performance: DEM results. Road Mater. Pavement Des. 2017. [Google Scholar] [CrossRef]
- Huang, Q.; Zhan, M.; Sheng, J.; Sheng, J.-C.; Zhang, X. Numerical Method to Generate Granular Assembly with any Desired Relative Density based on DEM. Chin. J. Geotech. Eng. 2015, 37, 537–543. [Google Scholar]
- Fernandes, M.R.S.; Forte, M.M.C.; Leite, L.F.M. Rheological Evaluation of Polymer-modified Asphalt Binders. Mater. Res. 2008, 11, 381–386. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Wang, S. Study of High Temperature Performance of Asphalt Mastic Based on Dynamic Viscoelastic Mechanics. J. Highw. Transp. Res. Dev. 2007, 2, 16–20. [Google Scholar] [CrossRef]
- Kong, X.; Liu, Y.; Zhang, Y.; Zhang, Z.; Yan, P.; Bai, Y. Influences of Temperature on Mechanical Properties of Cement Asphalt Mortars. Mater. Struct. 2014, 47, 285–292. [Google Scholar] [CrossRef]
- Hopkins, T.C.; Sun, L.; Slepak, M.E.; Slepak, M.E. Bearing Capacity Analysis and Design of Highway Base Materials Reinforced with Geofabrics; Research Report KTC-05-21/SPR-238-02-1F; Kentucky Transportation Center: Lexington, KY, USA, 2005. [Google Scholar]
- Tinoco, F.H.; Handy, R.L.; Hoover, J.M. Void Ratio and Shear Strength of Two Compacted Crushed Stones. In Proceedings of the Iowa Academy of Science; Iowa Academy of Science: Cedar Falls, IA, USA, 1966; Volume 73, pp. 219–233. [Google Scholar]
- Mohr-Coulomb Theory. Available online: https://en.wikipedia.org/wiki/Mohr%E2%80%93Coulomb_theory (accessed on 27 October 2018).
Figure 1.
Induction heating-assisted pavement compaction process [
17].
Figure 1.
Induction heating-assisted pavement compaction process [
17].
Figure 2.
Finite element method (FEM) results of induction heating on pavement: (a) thermal field distribution on the pavement surface, (b) surface temperature development of the pavement, and (c) temperature distribution in the pavement after 120 s of induction.
Figure 2.
Finite element method (FEM) results of induction heating on pavement: (a) thermal field distribution on the pavement surface, (b) surface temperature development of the pavement, and (c) temperature distribution in the pavement after 120 s of induction.
Figure 3.
Generated coarse aggregate particles: (a,b) L:W:H = 1:1:1, (c,d) L:W:H = 1:0.8:0.6, and (e) L:W:H = 1:0.5:0.25.
Figure 3.
Generated coarse aggregate particles: (a,b) L:W:H = 1:1:1, (c,d) L:W:H = 1:0.8:0.6, and (e) L:W:H = 1:0.5:0.25.
Figure 4.
Schematic of contact conditions between the coarse aggregate particles: (a) asphalt mortar, (b) pie-shaped bond, and (c) physical model of the bond.
Figure 4.
Schematic of contact conditions between the coarse aggregate particles: (a) asphalt mortar, (b) pie-shaped bond, and (c) physical model of the bond.
Figure 5.
Determination of model parameters: The relationship between air void content and the average coordination number.
Figure 5.
Determination of model parameters: The relationship between air void content and the average coordination number.
Figure 6.
Determination of model parameters: Dynamic modulus of low temperature porous asphalt (LTPA) mortar.
Figure 6.
Determination of model parameters: Dynamic modulus of low temperature porous asphalt (LTPA) mortar.
Figure 7.
Determination of model parameters: Strength curves of asphalt mortar from the literature.
Figure 7.
Determination of model parameters: Strength curves of asphalt mortar from the literature.
Figure 8.
Generation process of pavement model.
Figure 8.
Generation process of pavement model.
Figure 9.
Simulation of pavement compaction process (due to space limitations, only part of the wheel is retained in the picture).
Figure 9.
Simulation of pavement compaction process (due to space limitations, only part of the wheel is retained in the picture).
Figure 10.
Schematic flow diagram of the overall coupling methodology.
Figure 10.
Schematic flow diagram of the overall coupling methodology.
Figure 11.
Simulation results: (a) The air void content changed as passes increased at 60 °C with induction heating; and (b) a comparison of compaction effects for different cases and percent densities at different depths for (c) Case 2 (~90 °C) and (d) Case 4 (~142 °C).
Figure 11.
Simulation results: (a) The air void content changed as passes increased at 60 °C with induction heating; and (b) a comparison of compaction effects for different cases and percent densities at different depths for (c) Case 2 (~90 °C) and (d) Case 4 (~142 °C).
Table 1.
Aggregate gradation of porous asphalt (PA) 0/16 mix based on the Dutch standard (RAW 2005).
Table 1.
Aggregate gradation of porous asphalt (PA) 0/16 mix based on the Dutch standard (RAW 2005).
| Sieving Size (mm) | 22.4–16.0 | 16.0–11.2 | 11.2–8.0 | 8.0–5.6 | 5.6–2.0 | 2.0–0.063 | <0.063 |
|---|
| Cum. ret. (%) | 4 | 25 | 57 | 80 | 85 | 95.5 | 100 |
| % ret. by weight | 4 | 21 | 32 | 23 | 5 | 10.5 | 4.5 |
Table 2.
Internal friction angle as a function of air void content and the used coefficient .
Table 2.
Internal friction angle as a function of air void content and the used coefficient .
| AirVoidContent(%) | 22 | 21.5 | 21 | 20.5 | 20 | 19 | 18 | 17 |
| Angle of internal friction φ (°) | 47.5 | 51.0 | 52.0 | 52.5 | 52.7 | 53.0 | 53.4 | 53.5 |
| Coord. Number | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| γnc | 0.000 | 0.543 | 0.826 | 0.913 | 0.946 | 0.961 | 0.967 | 0.978 | 0.989 | 0.996 | 1.000 |
Table 3.
Parameters used in the discrete element method (DEM) analysis.
Table 3.
Parameters used in the discrete element method (DEM) analysis.
| Parameters | Values |
|---|
| Pavement model | |
| model size | 50 cm (length) 50 cm (width) 8 cm (thickness) |
| particles size | 2–22.4 mm (PA 0/16) |
| Roller Parameters | |
| wheel size | 100 cm (diameter) 200 cm (width) |
| wheel weight | 5 tons (one wheel) |
| Mortar parameters | |
| air void content estimated | |
| dynamic modulus (MPa) | E* = |
| critical strain | = |
| effective strength (MPa) | = |
| initial bond radius ratio | = 0.06 |
| enlargement multiplier of bond radius | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).