Featured Application
In this work the anomalous mechanical behavior of uranyl carbonate mineral rutherfordine is unveiled by performing high-quality theoretical solid-state calculations. This study provides a theoretical framework which may be utilized to study the mechanical behavior of all types of solid materials. In the context of Radioactive Nuclear Waste Disposal, this framework provides in a very detailed, safe, and cheap way, of obtaining these properties which may be applied to the study of the main components of the spent nuclear fuel.
Abstract
The mechanical behavior of the uranyl carbonate mineral, rutherfordine, UO2CO3, was studied by means of theoretical solid-state methods based in Density Functional Theory using plane waves and pseudopotentials. The results of the computations reported in this work show that this mineral exhibits the important negative Poisson ratio (NPR) phenomenon. In order to show that this feature is not an artifact associated to the theoretical treatment employed, additional calculations were carried out using very large calculation parameters. These calculations improved the mechanical description of this mineral and confirmed its auxeticity, i.e., it shows NPR values. Rutherfordine is a highly anisotropic material showing a maximum value of the NPR of the order of −0.3 ± 0.1 for applied stresses directed along the X axis, the transverse direction being the Y axis perpendicular to the structural sheets in rutherfordine structure. The underlying reason for this observation is that under the effect of applied positive pressures, the interlayer space between the sheets of rutherfordine vary in the opposite way to the expected behavior; that is, it decreases instead of increasing.
1. Introduction
Since the uranyl carbonate mineral, rutherfordine, was shown to be a highly anisotropic material [1], and there is a strong symmetry independent correlation between the value of the elastic anisotropy index [2] and the values of the maximum and minimum Poisson’s ratios [3,4], the mechanical properties of this material were reinvestigated with special emphasis in the study of the associated Poisson ratios. The theoretical solid-state methods used here are based on Density Functional theory using plane waves and pseudopotentials [5]. These methods have already been employed successfully to study the structural, spectroscopic, mechanical, and thermodynamic properties of a rich set of secondary phases of spent nuclear fuel (SNF) [1,6,7,8,9,10,11,12,13,14,15].
Several published works in which the theoretical methodology has been used in the research of auxetic materials, i.e., exhibiting negative Poisson ratios (NPR) [16,17,18], are given in References [19,20,21,22,23,24,25,26,27,28,29,30,31,32]. For example, we may recall the papers by Keskar and Chelikowsky [19] and Grima et al. [20] on crystalline SiO2, Grima et al. [21] on zeolitic compounds, Yao et al. [22] on crystalline cellulose, Tan et al. [23,24] on zeolitic imidazolate frameworks (ZIFs), and Du et al. [25] on black phosphorus. The description of solid-state crystalline compounds using computational modeling techniques appears to be sufficiently advanced nowadays to predict their mechanical properties in good agreement with experimental values. A complete review of the literature concerning the NPR phenomenon has been reported in Reference [33]. Very recent studies performed in our laboratory in which the theoretical methods have been successfully employed in order to study the anomalous mechanical behavior of several important solid materials are those of the cyclic oxocarbon acids [33], uranyl squarate monohydrate [34] and oxalic acid [35].
In the context of radioactive waste management, the large expansion in volume and mechanical stress resulting from the corrosion of spent nuclear fuel (SNF) during storage [36,37,38,39,40] is one of the main hazards that must be avoided in the disposal of high level radioactive nuclear waste (HLRNW) [41]. The large increase in volume of SNF may result in the increase of the pressure suffered by the components of the barrier system used in a deep geological disposal of HLRNW and can lead to certain problems in the containment of the waste. The existence of potential problems related to the containment and isolation of HLRNW should be reduced to a minimum in order to avoid as much as possible the possibility of liberation of radionuclides to the environment.
In a previous study [1], a very small positive value of the averaged Poisson ratio for rutherfordine was obtained, much lower than those found for other secondary phases of SNF, which were studied in other recent works [7,9,11,14,15]. For this reason and the large mechanical anisotropy found for rutherfordine mineral [1], the corresponding rutherfordine Poisson ratios as a function of the direction of the applied stress for all the possible transverse directions, were determined in this study. As a result, negative Poisson ratios in some directions were found. In order to confirm this result, additional extensive computations aimed to obtain very high-quality theoretical results were performed. Furthermore, the reason for the negative Poisson ratio found in rutherfordine was encountered by performing theoretical solid-state calculations of rutherfordine structure under increasing pressures.
In this paper, a theoretical framework has been developed, which may be utilized to study the mechanical behavior of SNF components in a very detailed, safe, and cheap way, and may be applied to the waste main components, such as non-stoichiometric uranium oxides. By modifying several characteristics of the fuel components (as its composition), its mechanical behavior may be changed and significantly improved. This methodology may also be used in order to study the mechanical properties of the modified fuel components in order to confirm that these changes will be effective in improving its mechanical behavior.
2. Methods
As in a previous work [1], the specialized version of Perdew–Burke–Ernzerhof functional for solid materials [42] was used to study the mechanical properties of the uranyl carbonate mineral, rutherfordine. This functional is implemented in the CASTEP (Cambridge Serial Total Energy Package) program [43], a module of the Materials Studio package [44] (Dassault Systèmes BIOVIA, version 8.0, San Diego, 2017) which was employed in all the calculations. The pseudopotentials employed for the carbon and oxygen ions in the unit cell of rutherfordine were standard norm-conserving pseudopotentials [45] provided by the CASTEP program, and the norm-conserving relativistic pseudopotential employed for uranium ion was developed in our laboratory in previous works [6,7].
The atomic positions and unit cell parameters of rutherfordine were optimized by using the Broyden–Fletcher–Goldfarb–Shanno method [5,46] with a convergence threshold on atomic forces of 0.01 eV/Å. This method was also used in order to optimize the structure of the material considered under the effect of different applied pressures. The calculation parameters used in this work, that is, the kinetic energy cut-off and k-point mesh [47], 1050 eV and 9 × 4 × 10 (50 k points), respectively, were much larger than the ones used in a previous work [1], 1000 eV and 5 × 3 × 6 (18 k points), in order to confirm the previous results and to obtain a high quality description of the mechanical behavior of rutherfordine mineral. The elastic constants required to calculate the mechanical properties of the considered material and to study the mechanical stability of its crystal structure were obtained from stress-strain relationships using the finite deformation method [1,48].
From a theoretical point of view, the theoretical solid-state calculations reported in this paper have been carried out with the best available methods applicable to the study of crystalline materials and with very demanding high-quality calculation parameters. The present computations could be improved by using more advanced energy-density functionals as hybrid or meta-functionals, but their efficient implementation in the current solid-state codes is still under development. A restriction, which could be removed from the calculations, is the core-valence approximation. This could be made by including explicitly the inner uranium electrons in the calculations, thus avoiding the use of pseudopotentials. However, the realization of all-electron calculations is very complicated and expensive, especially for systems containing rare earth elements. The norm-conserving relativistic pseudopotential developed in our laboratory [6,7] has permitted to perform very precise studies of the structural, spectroscopic, mechanical, and thermodynamic properties of uranium containing materials [6,7,8,9,10,11,12,13,14,15], and the results were in very good agreement with the experimental data in all the cases in which they were available for comparison.
3. Results
3.1. Mechanical Stability
Materials with orthorhombic unit cells have 9 non-degenerate elastic constants in the symmetric stiffness, C, matrix [49,50]. The computed values of these constants for rutherfordine mineral are given in Table 1 together with the results obtained in a previous work [1]. In this table, the standard Voigt notation for the indices of the elements of the stiffness matrix (Cij) is used [49]. For orthorhombic systems, a set of necessary and sufficient conditions for mechanical stability are known [50,51]. These conditions were adequately satisfied by the computed stiffness tensor. As it can be seen in Table 1, the computed values of the elements of the stiffness matrix are in good agreement with those of the previous work [1].

Table 1.
Computed elastic constants, Cij, for rutherfordine mineral.
3.2. Mechanical Properties
The mechanical properties of polycrystalline rutherfordine were determined according to the Voigt [52], Reuss [53], and Hill [54] schemes. As in the previous article [1], the Reuss approach was chosen as the best one because it provided the best approximation to the bulk modulus computed from the equation of state. The results obtained for the bulk, shear, and Young moduli and the Poisson ratio (B, G, E, and ν, respectively) are given in Table 2. Also, the ductility [55], hardness [56], and universal anisotropy [2] indices were determined. Rutherfordine is a brittle material because the ductility index, D, is smaller than 1.75 [55,57,58]. The computed Vickers hardness, H, was 4.1, corresponding to a hard material [7,56]. Finally, the computed universal anisotropy index, AU = 13.28, is even higher than that found in our previous calculations. This large anisotropy is the consequence of the large difference between the values of the elastic constants along the different directions and derives directly from the differences in bonding strength between the atoms belonging to the unit cell of rutherfordine in the different directions [1].

Table 2.
Computed mechanical properties of rutherfordine. The values of the bulk, shear, and Young moduli (B, G, and E) are given in in GPa.
3.3. Negative Poisson Ratio
For a stress directed along a certain direction applied to a solid material, the Poisson ratio [16,17,18] is defined as the negative value of the ratio of the resulting differential transverse and longitudinal strains, ν = − δϵtrans / δϵlong. In this relationship, the strain, i, is the variation of the solid size, ΔLi, along direction i divided by the original size, Li, ϵi = ΔLi / Li. A positive sign is expected for the Poisson ratio because when a positive pressure is applied along a certain direction to the solid, a contraction along the longitudinal direction and an extension along all the transverse directions is usually found. However, negative values of the Poisson ratio are theoretically possible and some materials exhibit anomalous NPRs [16,17,18] for certain longitudinal and transverse directions. These solids laterally expand when they are stretched or laterally shrink when compressed. These materials are known as auxetic [59].
The visualization of the variation of the mechanical properties with the strain orientation is generally quite complicated. The ElAM code was developed by Marmier et al. [4] in order to reduce this difficulty to a large extent. 3D representations of the most important elastic properties of rutherfordine were obtained employing this code and are displayed in Figure 1. For the case of the shear modulus and Poisson ratios, depending on two directions (the longitudinal and transverse directions [4]), Figure 1C,D give the representation of the surface of maximum G and ν, respectively; that is, the surface formed with the maximum values of these properties for the given direction of the longitudinal strain and all possible transverse directions. These maximum surfaces are usually very similar for compounds with related structures [14,15] and are very useful to identify shearing effects in the phase transformations between related materials [14,60]. While the surfaces of the minimum Poisson ratio are very different even for related materials, their analysis is also very useful, since it may reveal the existence of negative values of the Poisson ratio. The surface of the minimum Poison ratio of rutherfordine obtained from the computed elasticity matrix is displayed in Figure 2, and shows that rutherfordine is an NPR material, the value of the lowest Poisson ratio being νmin = −0.29. The direction of the minimum Poisson ratio is ULmin = (1.0, 0.0, 0.0), and the corresponding transverse direction is UTmin = (0.0, 1.0, 0.0). The same effect was observed when the elasticity data obtained in the previous work [1] was analyzed and the corresponding value of the lowest Poisson ratio was νmin = −0.27.

Figure 1.
Elastic properties of rutherfordine as a function of the orientation of the applied strain: (A) Compressibility; (B) Young modulus; (C) maximum shear modulus; (D) maximum Poisson ratio.
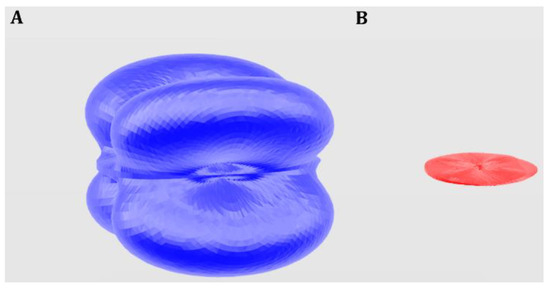
Figure 2.
Computed surfaces of the maximum (A) and minimum (B) Poisson ratio of rutherfordine.
4. Discussion: Crystal Structure Deformation as a Function of the Applied Pressure
The structure of this material under the effect of different pressures applied along the direction of the minimum Poisson ratio was optimized to analyze the structural variations produced by the application of pressure. The lattice parameters and volumes obtained for 11 different applied pressures along this direction are reported in Table 3.

Table 3.
Computed lattice parameters and volumes of the rutherfordine unit cell at different applied pressures directed along ULmin.
The material is compressed along ULmin for positive pressures and, as a consequence, the unit cell volume decreases (as the length along the ULmin direction, which in this case coincides with the [100] crystallographic direction). However, although the c lattice parameter increases, the length along the transverse direction (b axis) decreases instead of increasing. That is, the material shrinks laterally when compressed, thus exhibiting negative Poisson ratios. Table 4 reports the values of selected interatomic distances between the atoms in the structure of rutherfordine. The meaning of these distances may easily be understood from Figure 3.

Table 4.
Selected interatomic distances (in Å) in the rutherfordine crystal structure at different applied pressures directed along ULmin. The last row in the table (Δ) gives the variation of the bond distances at P = 7.0 GPa with respect to those at P = 0.0 GPa.
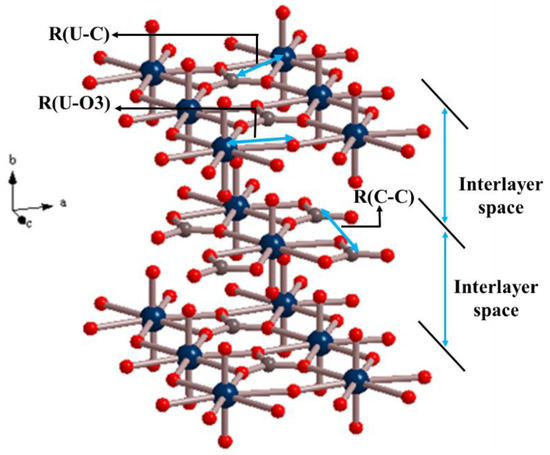
Figure 3.
View of the microscopic crystal structure of rutherfordine showing the meaning of the U-O3, U-C, C-C, and interlayer R(IL) distances given in Table 4. Color code: U-Blue; C-Grey; O-red.
As it can be readily observed in Table 4, the main variations of the distances resulting from the application of increasing pressures directed along ULmin are the decrease of the U-O3 and C-C bond distances, responsible for the decrease of the a lattice parameter caused by the application of pressure, and the expected increase of the C-C bond distance yielding to the increase of the c lattice parameter. However, the distance between the rutherfordine layers (or, equivalently, the b lattice parameter or the distance along the transverse direction), which are held together only by van der Waals forces, decreases. This last variation is opposite to the expected behavior. This is the reason of the negative Poisson ratio (NPR phenomenon) in rutherfordine.
5. Conclusions
The mechanical behavior of the uranyl carbonate mineral, rutherfordine, UO2CO3, was studied in detail using theoretical solid-state methods based in Density Functional Theory using plane waves and pseudopotentials. The results have shown that rutherfordine mineral exhibits the negative Poisson ratio phenomenon. The theoretical calculations were performed with very large calculation parameters, the results being of very high quality. The values of a large series of relevant mechanical properties, including the bulk, shear, and Young moduli, the Poisson ratio, and ductility, hardness, and anisotropy indices, were reported. These calculations provided a mechanical description of this mineral in very good agreement with that obtained in our previous work [1] and confirmed the auxeticity of this material. Rutherfordine is a highly anisotropic material showing a minimum value of the negative Poisson ratio of the order of −0.3 ± 0.1 for applied stresses directed along the X axis, the transverse direction being the Y axis perpendicular to the structural sheets in rutherfordine structure.
The negative Poisson ratio phenomenon in rutherfordine is the consequence of the anomalous variation of the interlayer distance between the sheets in rutherfordine under the effect of the applied pressures. The interlayer space varies in the opposite way to the expected behavior; that is, it decreases instead of increasing. A similar mechanism leading to NPR values was recently found in the cyclic oxocarbon [33] and oxalic [35] acids, which are also characterized by crystal structures involving structural elements as sheets or chains, which are not bonded directly, but held together by means of weak van der Waals interactions. Therefore, it is likely that other materials having this type of crystal structure also exhibit the NPR phenomenon. These materials should be further analyzed due to the importance of mechanical behavior in real systems, such as in the context of nuclear waste repositories, where increments in volume may result in an unacceptable build-up of pressures high enough to change the properties of the engineered barrier system or influence groundwater inflow.
Funding
This research received no external funding.
Acknowledgments
Supercomputer time by the CTI-CSIC center is greatly acknowledged. This work has been carried out in the context of a CSIC–CIEMAT collaboration agreement: Caracterización experimental y teórica de fases secundarias y óxidos de uranio formados en condiciones de almacenamiento de combustible nuclear. I also want to thank Dr. Ana Maria Fernández for reading the document and many helpful comments.
Conflicts of Interest
The author declares no conflict of interest.
References
- Colmenero, F.; Bonales, L.J.; Cobos, J.; Timón, V. Thermodynamic and Mechanical Properties of Rutherfordine Mineral Based on Density Functional Theory. J. Phys. Chem. C 2017, 121, 5994–6001. [Google Scholar] [CrossRef]
- Ranganathan, S.I.; Ostoja-Starzewski, M. Universal Elastic Anisotropy Index. Phys. Rev. Lett. 2008, 101, 055504. [Google Scholar] [CrossRef] [PubMed]
- Lethbridge, Z.A.D.; Walton, R.I.; Marmier, A.S.H.; Smith, C.W.; Evans, K.E. Elastic Anisotropy and Extreme Poisson’s Ratios in Single Crystals. Acta Mater. 2010, 58, 6444–6451. [Google Scholar] [CrossRef]
- Marmier, A.S.H.; Lethbridge, Z.A.D.; Walton, R.I.; Smith, C.W.; Parker, S.C.; Evans, K.E. ElAM: A Computer Program for the Analysis and Representation of Anisotropic Elastic Properties. Comput. Phys. Commun. 2010, 181, 2102–2115. [Google Scholar] [CrossRef]
- Payne, M.C.; Teter, M.P.; Ailan, D.C.; Arias, A.; Joannopoulos, J.D. Iterative Minimization Techniques for Ab Initio Total-Energy Calculations: Molecular Dynamics and Conjugate Gradients. Rev. Mod. Phys. 1992, 64, 1045–1097. [Google Scholar] [CrossRef]
- Bonales, L.J.; Colmenero, F.; Cobos, J.; Timón, V. Spectroscopic Raman Characterization of Rutherfordine: A Combined DFT and Experimental Study. Phys. Chem. Chem. Phys. 2016, 18, 16575–16584. [Google Scholar] [CrossRef] [PubMed]
- Colmenero, F. Characterization of Secondary Phases of Spent Nuclear Fuel under Final Geological Disposal Conditions: Experimental and Theoretical Studies. Ph.D. Thesis, Universidad Autónoma de Madrid, Madrid, Spain, 17 September 2017; 443p. [Google Scholar] [CrossRef]
- Colmenero, F.; Bonales, L.J.; Cobos, J.; Timón, V. Study of the Thermal Stability of Studtite by In Situ Raman Spectroscopy and DFT Calculations. Spectrochim. Acta A 2017, 174, 245–253. [Google Scholar] [CrossRef] [PubMed]
- Colmenero, F.; Bonales, L.J.; Cobos, J.; Timón, V. Structural, Mechanical and Vibrational Study of Uranyl Silicate Mineral Soddyite by DFT Calculations. J. Solid State Chem. 2017, 253, 249–257. [Google Scholar] [CrossRef]
- Colmenero, F.; Bonales, L.J.; Cobos, J.; Timón, V. Density Functional Theory Study of the Thermodynamic and Raman Vibrational Properties of γ-UO3 Polymorph. J. Phys. Chem. C 2017, 121, 14507–14516. [Google Scholar] [CrossRef]
- Colmenero, F.; Bonales, L.J.; Timón, V.; Cobos, J. Structural, mechanical, and Raman spectroscopic characterization of layered uranyl silicate mineral uranophane-α by DFT Methods. Clay Miner. 2018, 1–32. [Google Scholar] [CrossRef]
- Colmenero, F.; Fernández, A.M.; Cobos, J.; Timón, V. Thermodynamic Properties of Uranyl Containing Materials Based on Density Functional Theory. J. Phys. Chem. C 2018, 122, 5254–5267. [Google Scholar] [CrossRef]
- Colmenero, F.; Fernández, A.M.; Cobos, J.; Timón, V. Temperature Dependent Free Energies of Reaction of Uranyl Containing Materials Based on Density Functional Theory. J. Phys. Chem. C 2018, 122, 5268–5279. [Google Scholar] [CrossRef]
- Colmenero, F.; Cobos, J.; Timón, V. Periodic DFT Study of the Structure, Raman Spectrum and Mechanical Properties of Schoepite Mineral. Inorg. Chem. 2018, 57, 4470–4481. [Google Scholar] [CrossRef] [PubMed]
- Colmenero, F.; Fernández, A.M.; Cobos, J.; Timón, V. Becquerelite mineral phase: Crystal structure and thermodynamic and mechanic stability by using periodic DFT. RSC Adv. 2018, 8, 24599–24616. [Google Scholar] [CrossRef]
- Lakes, R.S. Negative-Poisson’s-Ratio Materials: Auxetic Solids. Annu. Rev. Mater. Res. 2017, 47, 63–81. [Google Scholar] [CrossRef]
- Greaves, G.N.; Greer, A.L.; Lakes, R.S.; Rouxel, T. Poisson’s Ratio and Modern Materials. Nat. Mater. 2011, 10, 823–837. [Google Scholar] [CrossRef] [PubMed]
- Lakes, R.S. Foam Structures with a Negative Poisson’s Ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef] [PubMed]
- Keskar, N.R.; Chelikowsky, J.R. Negative Poisson’s Ratios in Crystalline SiO2 from First-Principles Calculations. Nature 1992, 358, 222–224. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R.; Alderson, A.; Evans, K.E. An Alternative Explanation for the Negative Poisson’s Ratios in α-Cristobalite. Mater. Sci. Eng. A 2006, 423, 219–224. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R.; Zammit, V.; Williams, J.J.; Evans, K.E.; Alderson, A.; Walton, R.I. Natrolite: A Zeolite with Negative Poisson’s Ratios. J. Appl. Phys. 2007, 101, 086102. [Google Scholar] [CrossRef]
- Yao, Y.T.; Alderson, K.L.; Alderson, A. Modeling of Negative Poisson’s Ratio (Auxetic) Crystalline Cellulose Iβ. Cellulose 2016, 23, 3429–3448. [Google Scholar] [CrossRef]
- Tan, J.-C.; Civalleri, B.; Erba, A.; Albanese, E. Quantum Mechanical Predictions to Elucidate the Anisotropic Elastic Properties of Zeolitic Imidazolate Frameworks: ZIF-4 vs. ZIF-zni. CrystEngComm 2015, 17, 375–382. [Google Scholar] [CrossRef]
- Ryder, M.R.; Tan, J.-C. Explaining the Mechanical Mechanisms of Zeolitic Metal–Organic Frameworks: Revealing Auxeticity and Anomalous Elasticity. Dalton Trans. 2016, 45, 4154–4161. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Maassen, J.; Wu, W.; Luo, Z.; Xu, X.; Ye, P.D. Auxetic Black Phosphorus: A 2D Material with Negative Poisson’s Ratio. Nano Lett. 2016, 16, 6701–6708. [Google Scholar] [CrossRef] [PubMed]
- Dagdelen, J.; Montoya, J.; De Jong, M.; Persson, K. Computational Prediction of New Auxetic Materials. Nat. Commun. 2017, 8, 323. [Google Scholar] [CrossRef] [PubMed]
- Ho, D.T.; Park, S.D.; Kwon, S.Y.; Park, K.; Kim, S.Y. Negative Poisson’s Ratios in Metal Nanoplates. Nat. Commun. 2014, 5, 3255. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Wang, S.; Zhan, S.; Yuan, S.J.; Yang, B.; Chen, H. Highly Negative Poisson’s Ratio in a Flexible Two-Dimensional Tungsten Carbide Monolayer. Phys. Chem. Chem. Phys. 2018, 20, 18924–18930. [Google Scholar] [CrossRef] [PubMed]
- Hao, F.; Liao, X.; Li, M.; Xiao, H.; Chen, X. Oxidation-Induced Negative Poisson’s Ratio of Phosphorene. J. Phys. Condens. Matter 2018, 30, 315302. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Li, Q.; Gao, Y.; Miao, F.; Zhou, X.F.; Wan, X.G. Strain Effects on Borophene: Ideal Strength, Negative Possion’s Ratio and Phonon Instability. New J. Phys. 2016, 18, 073016. [Google Scholar] [CrossRef]
- Wang, H.; Li, X.; Li, P.; Yang, J. δ-Phosphorene: A Two-Dimensional Material with High Negative Poisson’s Ratio. Nanoscale 2017, 9, 850–855. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.F.; Jones, T.E.; Li, W.; Zhou, Y.C. Extreme Poisson’s Ratios and their Electronic Origin in B2 CsCl-type AB Intermetallic Compounds. Phys. Rev. B 2012, 85, 134108. [Google Scholar] [CrossRef]
- Colmenero, F. Anomalous Mechanical Behavior of the Deltic, Squaric, and Croconic Acids. Rep. Progr. Phys 2018. under review. [Google Scholar]
- Colmenero, F.; Cobos, J.; Timón, V. Negative Linear Compressibility in Uranyl Squarate Monohydrate. J. Phys. Cond. Matter. 2018. under review. [Google Scholar]
- Colmenero, F. Mechanical Properties of Anhydrous Oxalic Acid and Oxalic Acid Dihydrate. Mater. Horiz. under review.
- Schmidt, A.J.; Delegard, C.H. Assessment of K Basin Sludge Volume Expansion Resulting from Uranium Corrosion During Storage; Report of the U.S. Department of Energy, Pacific Northwest National Laboratory PNNL-13786; Pacific Northwest National Laboratory: Richland, WA, USA, 2002. Available online: https://www.pnnl.gov/main/publications/external/technical_reports/PNNL-13786.pdf (accessed on 3 November 2018).
- Delegard, C.H.; Schmidt, A.J.; Chenault, J.W. Mechanical Properties of K Basin Sludge Constituents and Their Surrogates; Report of the U.S. Department of Energy, Pacific Northwest National Laboratory PNNL-14947; Pacific Northwest National Laboratory: Richland, WA, USA, 2004. Available online: https://www.pnnl.gov/main/publications/external/technical_reports/PNNL-14947.pdf (accessed on 3 November 2018).
- Fritz, I. Elastic properties of UO2 at high pressure. J. Appl. Phys. 1976, 47, 4353–4358. [Google Scholar] [CrossRef]
- Ibrahim, M.; Castelier, E.; Palancher, H.; Bornert, M.; Care, S.; Micha, J.S. Mechanical behaviour near grain boundaries of He-implanted UO2 ceramic polycrystals. J. Nucl. Mater. 2017, 483, 13–20. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Debelle, A.; Boulle, A.; Garrido, F.; Thomas, L.; Demange, V. Mechanical response of UO2 single crystals submitted to low-energy ion irradiation. J. Nucl. Mater. 2015, 467, 505–511. [Google Scholar] [CrossRef]
- Swedish Nuclear Fuel and Waste Management Co., SKB. Final Disposal of Spent Nuclear Fuel. Importance of the Bedrock for Safety; SKB Report 92-20; Swedish Nuclear Fuel and Waste Management Co., SKB: Stockholm, Sweden, 1992; Available online: http://www.skb.se/upload/publications/pdf/TR92-20.pdf (accessed on 3 November 2018).
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef] [PubMed]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Kristallogr. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- MaterialsStudio. Available online: http://accelrys.com/products/materials-studio (accessed on 20 June 2018).
- Troullier, N.; Martins, J.L. Efficient Pseudopotentials for Plane-Wave Calculations. Phys. Rev. B 1991, 43, 1993–2006. [Google Scholar] [CrossRef]
- Pfrommer, B.G.; Cote, M.; Louie, S.G.; Cohen, M.L. Relaxation of Crystals with the Quasi-Newton Method. J. Comput. Phys. 1997, 131, 233–240. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integration. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Yu, R.; Zhu, J.; Ye, H.Q. Calculations of single-crystal elastic constants made simple. Comput. Phys. Commun. 2010, 181, 671–675. [Google Scholar] [CrossRef]
- Nye, J.F. The Physical Properties of Crystals: Their Representation by Tensors and Matrices; Oxford University Press: New York, NY, USA, 1985; ISBN 9780198511656. [Google Scholar]
- Weck, P.F.; Kim, E.; Buck, E.C. On the Mechanical Stability of Uranyl Peroxide Hydrates: Implications for Nuclear Fuel Degradation. RSC Adv. 2015, 5, 79090–79097. [Google Scholar] [CrossRef]
- Mouhat, F.; Coudert, F.-X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 2014, 90, 224104. [Google Scholar] [CrossRef]
- Voigt, W. Lehrbuch der Kristallphysik; Teubner: Leipzig, Germany, 1962; ISBN 978-3-663-15884-4. [Google Scholar]
- Reuss, A. Berechnung der Fliessgrenze von Mischkristallen auf Grund der Plastizitatsbedingung fur Einkristalle. Z. Angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. Lond. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Pugh, S.F. XCII. Relations between the Elastic Moduli and the Plastic Properties of Polycrystalline Pure Metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Niu, H.; Wei, P.; Sun, Y.; Chen, C.-X.; Franchini, C.; Li, D.; Li, Y. Electronic, Optical, and Mechanical Properties of Superhard Cold-Compressed Phases of Carbon. Appl. Phys. Lett. 2011, 99, 031901. [Google Scholar] [CrossRef]
- Bouhadda, Y.; Djella, S.; Bououdina, M.; Fenineche, N.; Boudouma, Y. Structural and Elastic Properties of LiBH4 for Hydrogen Storage Applications. J. Alloys Compd. 2012, 534, 20–24. [Google Scholar] [CrossRef]
- Ravindran, P.; Fast, L.; Korzhavyi, P.A.; Johansson, B.; Wills, J.; Eriksson, O. Density Functional Theory for Calculation of Elastic Properties of Orthorhombic Crystals: Application to TiSi2. J. Appl. Phys. 1998, 84, 4891–4904. [Google Scholar] [CrossRef]
- Evans, K.E.; Nkansah, M.A.; Hutchinson, M.I.; Rogers, S.C. Molecular Network Design. Nature 1991, 353, 124. [Google Scholar] [CrossRef]
- Weck, P.F.; Kim, E. Uncloaking the Thermodynamics of the Studtite to Metastudtite Shear-Induced Transformation. J. Phys. Chem. C 2016, 120, 16553–16560. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).