Deep Forest Reinforcement Learning for Preventive Strategy Considering Automatic Generation Control in Large-Scale Interconnected Power Systems
Abstract
1. Introduction
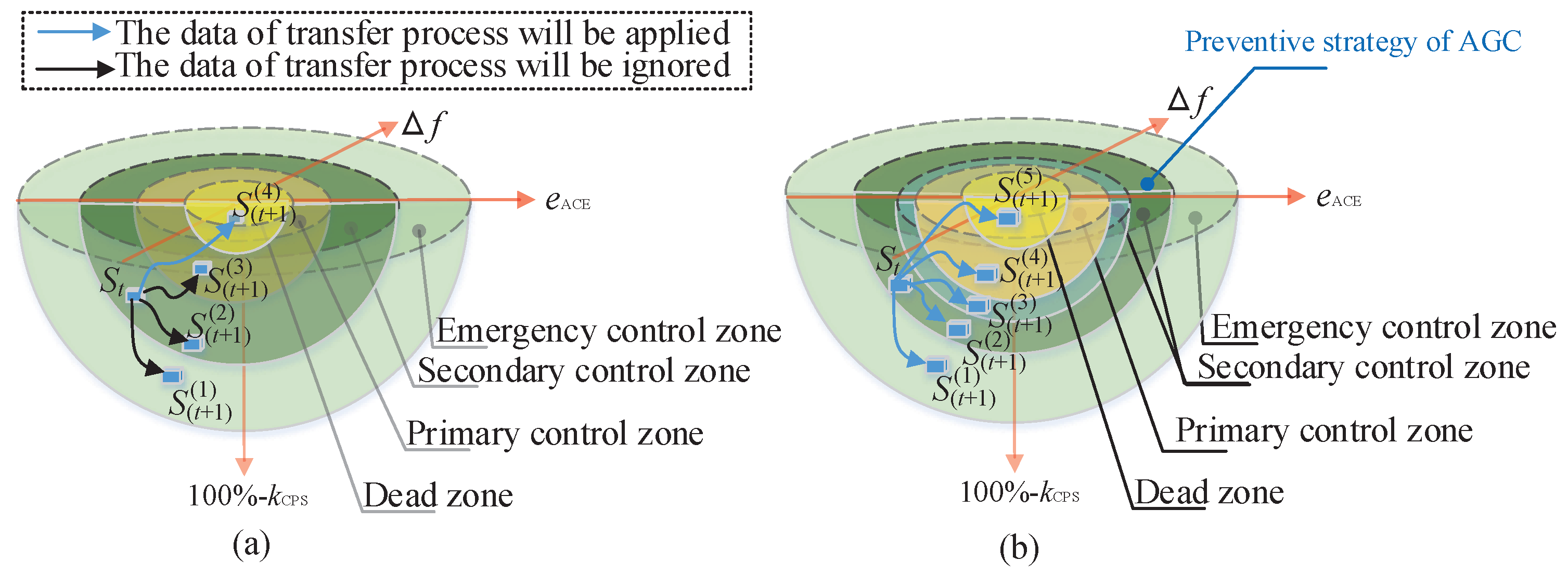
- The strategy should predict the next systemic state of the power system, and it should learn the feature of systemic frequency in the interconnected power system. That is to say, the preventive strategy should know whether the next state of the power system is an emergency state or a normal state, whereas conventional AGC without a preventive strategy cannot determine the next systemic state.
- The strategy should provide an advanced generation command to the AGC unit with the prediction of the next systemic state, which includes the emergency state and normal state.
- Since reinforcement learning is applied to DFRL, DFRL can update its control strategy online.
- The systemic states of a power system, including emergency states and normal states, can be predicted by the deep forest of DFRL using low-dimensional data.
- Since both the Q-value matrix and the action set of reinforcement learning are split into those of an emergency situation and a normal situation, calculation memory is reduced. Thus, the curse of dimensionality is mitigated.
2. Emergency State and Automatic Generation Control
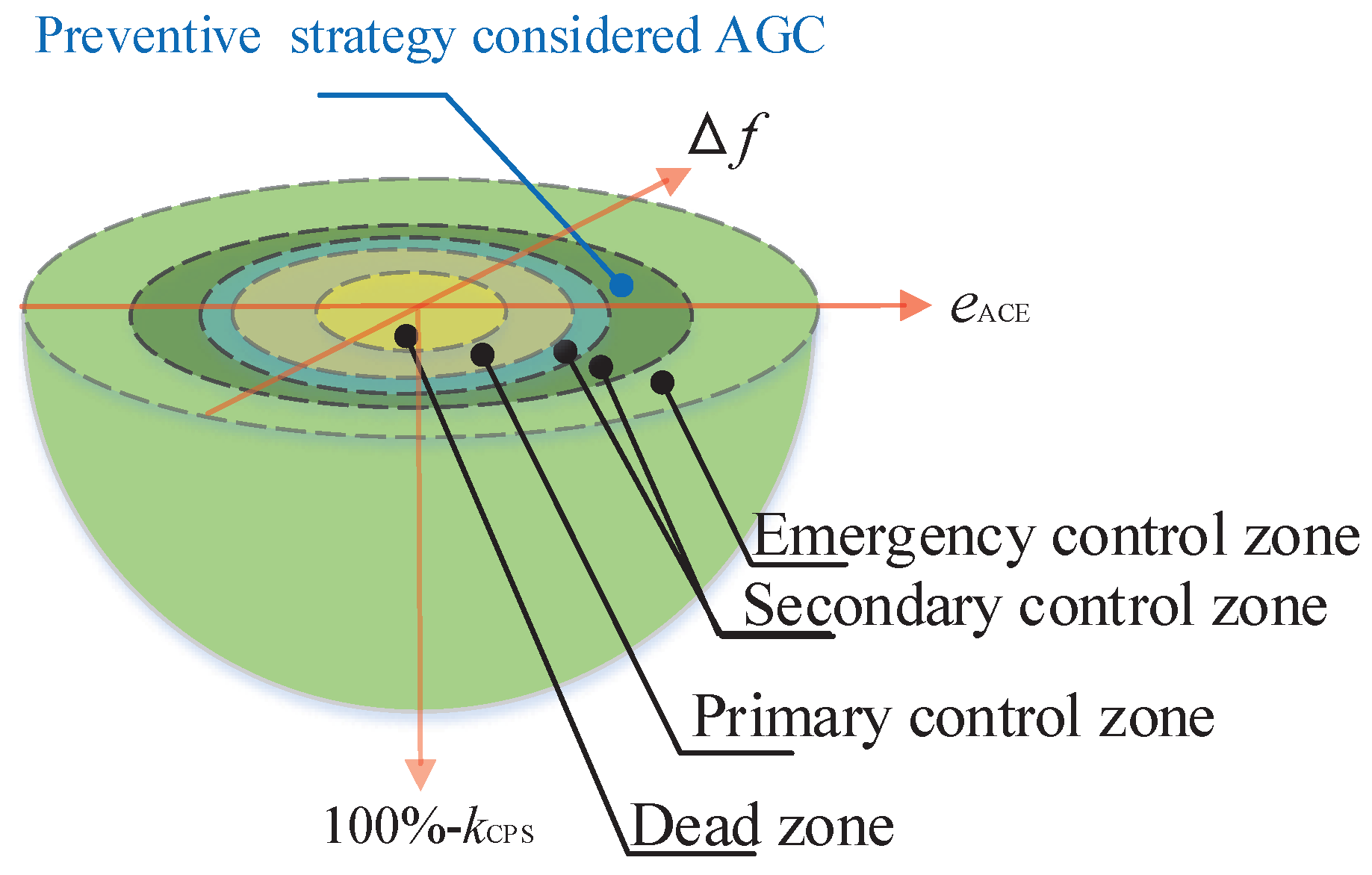
2.1. Emergency State
- The range of the frequency deviation for the dead zone is from to , where the frequency deviation is set to 0.025 Hz; The range of the CPS index for the dead zone is from to 100%, where the CPS index is set to 99% in this paper.
- The range of the frequency deviation for primary control is from to , where the frequency deviation is set to 0.1 Hz; The range of the CPS index for primary control is from to , where the CPS index is set to 95% in this paper.
- The range of the frequency deviation for secondary control is from to , where the frequency deviation is set to 0.5 Hz; The range of the CPS index for secondary control is from to , where the CPS index is set to 85% in this paper.
- The range of the frequency deviation for emergency control is from to , where the frequency deviation is set to ∞ Hz; The range of the CPS index for emergency control is from to , where the CPS index is set to 0% in this paper.
2.2. Framework of Automatic Generation Control
- The controller should provide generation commands to the AGC unit to balance the real-time active power flow between the generator and system loads;
- The controller should reduce the frequency deviation in the control area;
- The controller should decrease the scheduled tie-line power deviation between any two areas, i.e., mitigate the value of the ACE.
2.3. Control Objective of Automatic Generation Control
3. Deep Forest Reinforcement Learning and Preventive Strategy
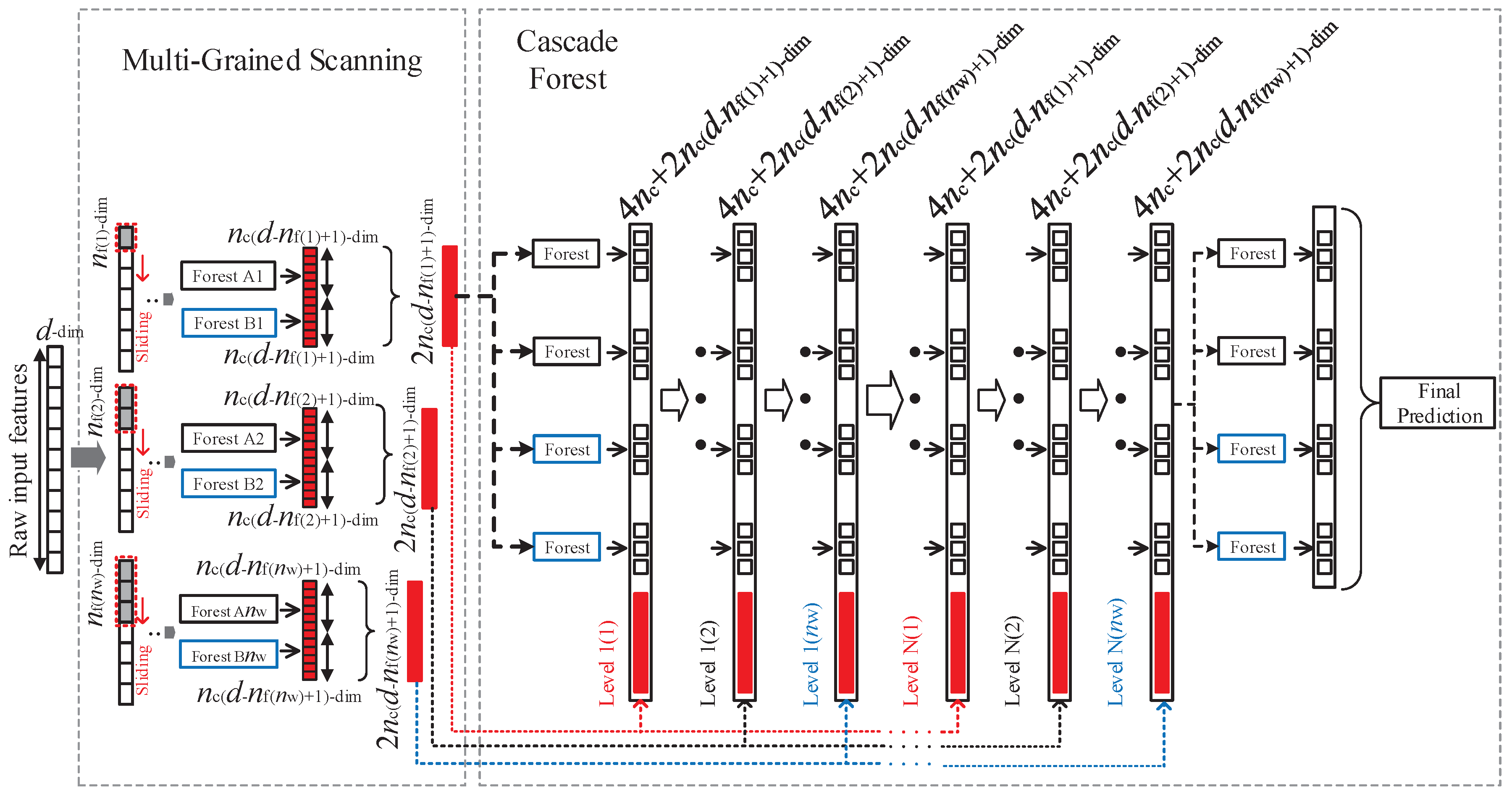
3.1. Deep Forest
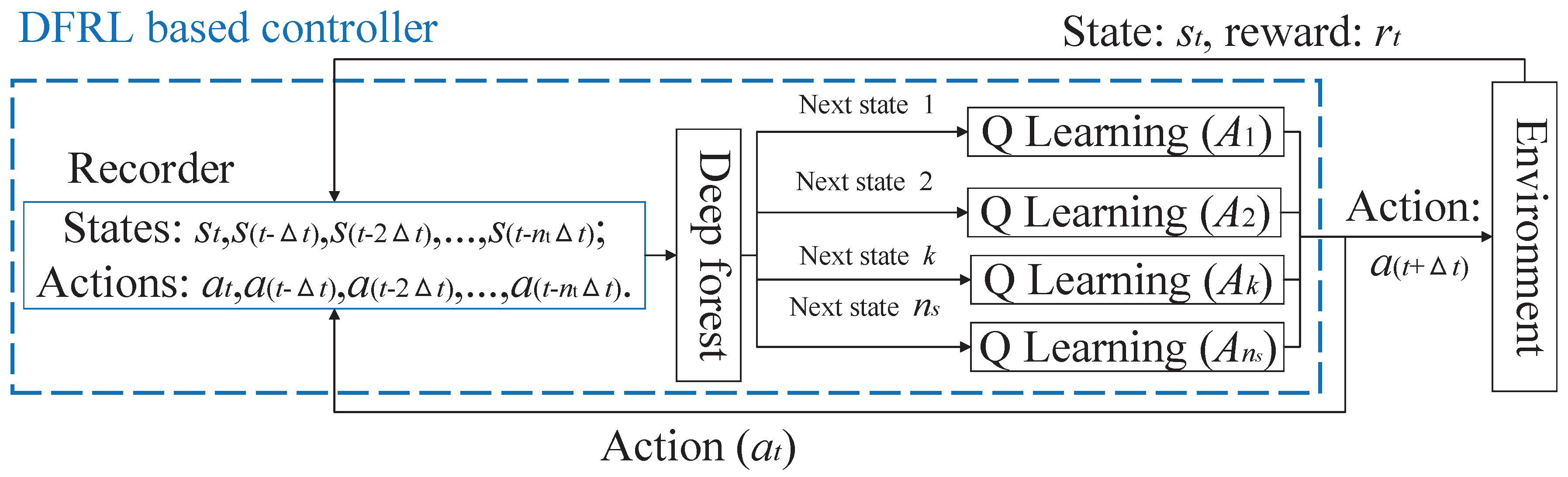
3.2. Reinforcement Learning
3.3. Deep Forest Reinforcement Learning
- Since the calculation memory is reduced because of the split matrices , , and , the curse of dimensionality is reduced and a more accurate control performance can be obtained; thus, the number of actions in the action set and the number of states in the state set of the reinforcement learning of DFRL can be increased to obtain an accurate control action.
- The next systemic state can be predicted more accurately by the deep forest of DFRL with diachronic states and actions.
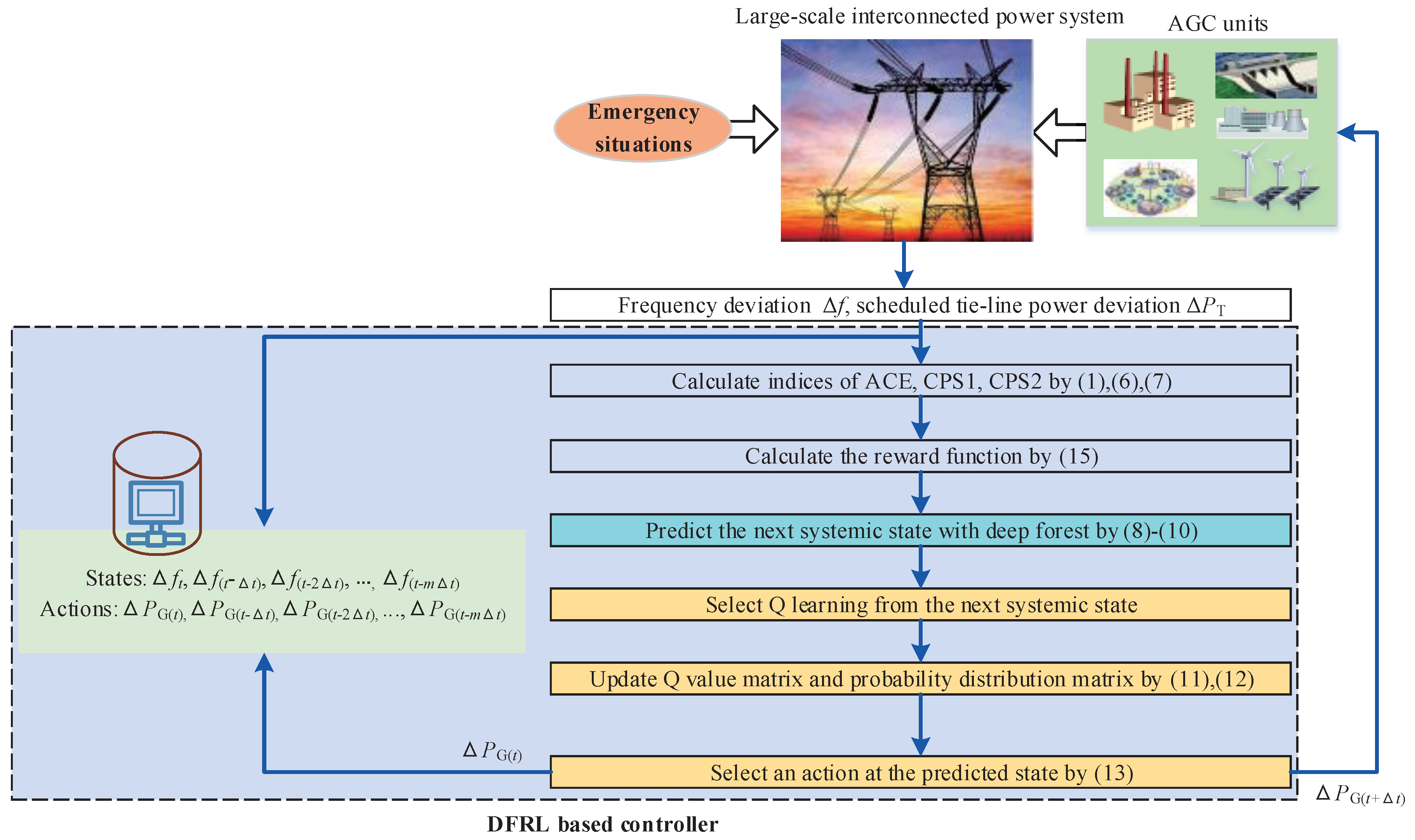
3.4. Deep Forest Reinforcement Learning as a Preventive Strategy for Automatic Generation Control
| Algorithm 1 Pseudo-code of the proposed deep forest reinforcement learning for the preventive strategy for automatic generation control | |
| 1: | Initial parameters of Q learning of the DFRL, i.e., |
| 2: | Initial system state s |
| 3: | Initial Q-value matrix and probability distribution matrix |
| 4: | while loop: do |
| 5: | Obtain the system state s from the environment as Equations (1), (6), and (7) |
| 6: | Save the system state s to the recorder of the DFRL |
| 7: | Calculate the reward value as Equation (15) |
| 8: | Select Q learning from the next systemic state as Equations (8)–(10) |
| 9: | Update Q-value matrix and probability distribution matrix as Equations (11) and (12), respectively |
| 10: | Select the output action by and a random probability as Equation (13) |
| 11: | Given the selected output action to the AGC unit and the recorder of the DFRL |
| 12: | return loop |
3.5. Pre-Training Process of Deep Forest Reinforcement Learning
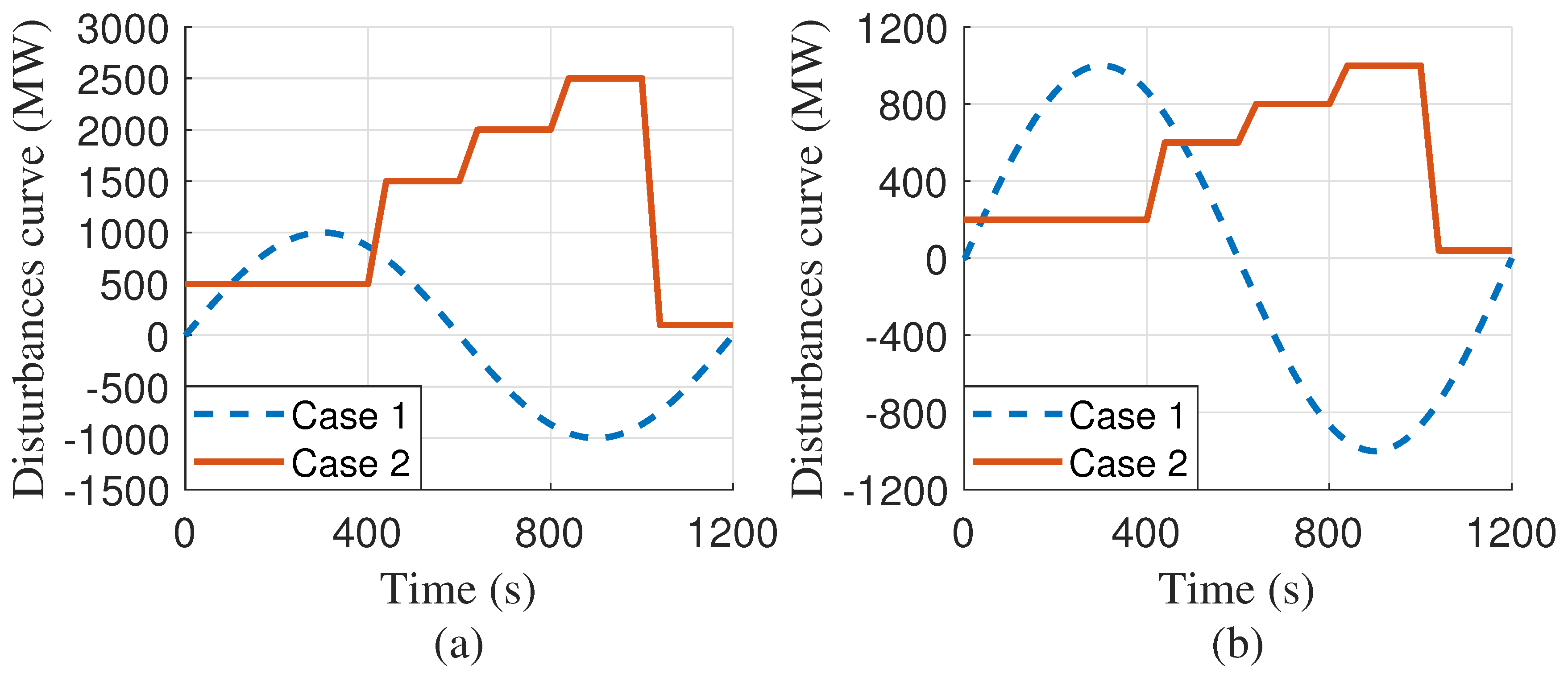
4. Case Study
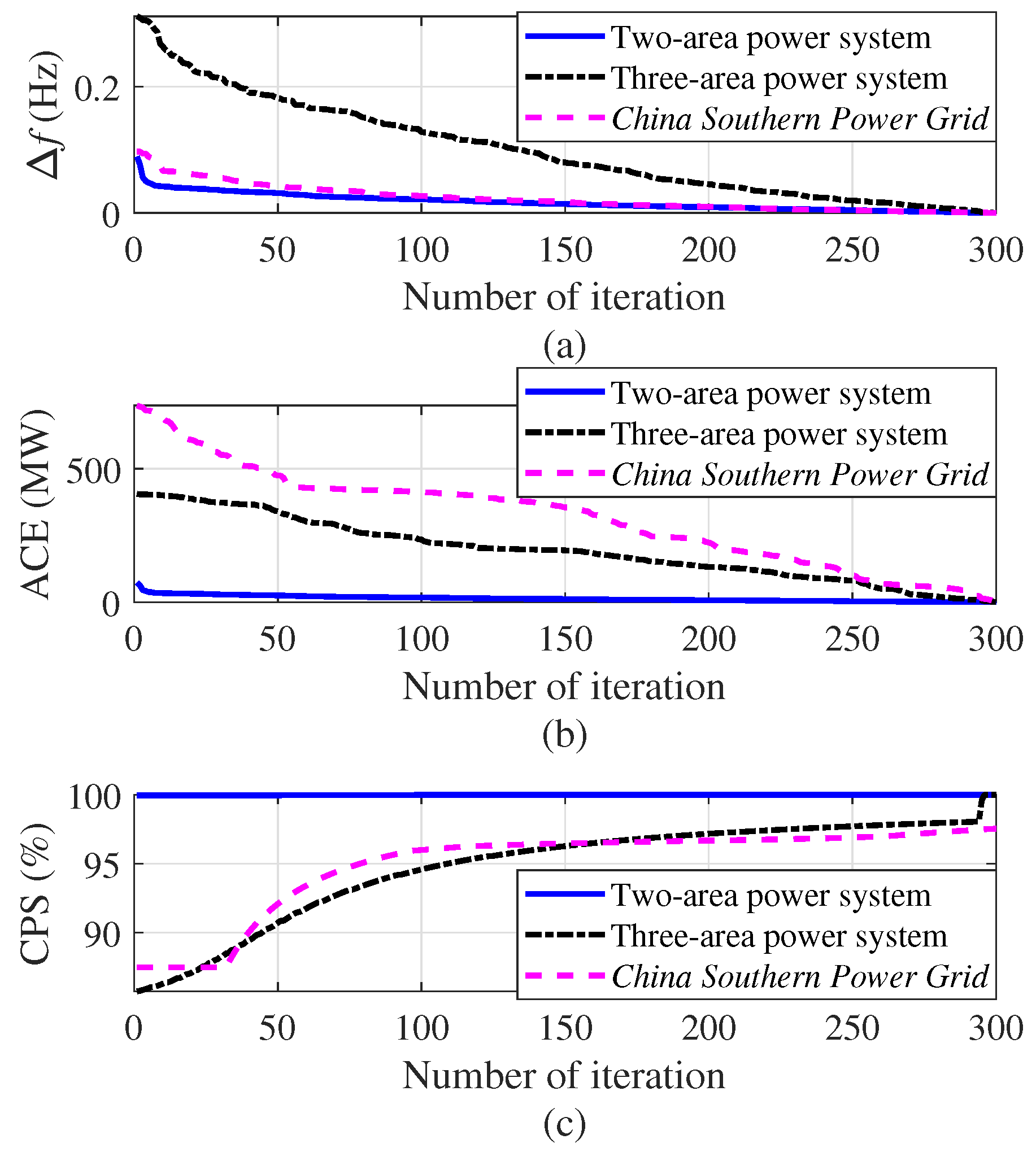
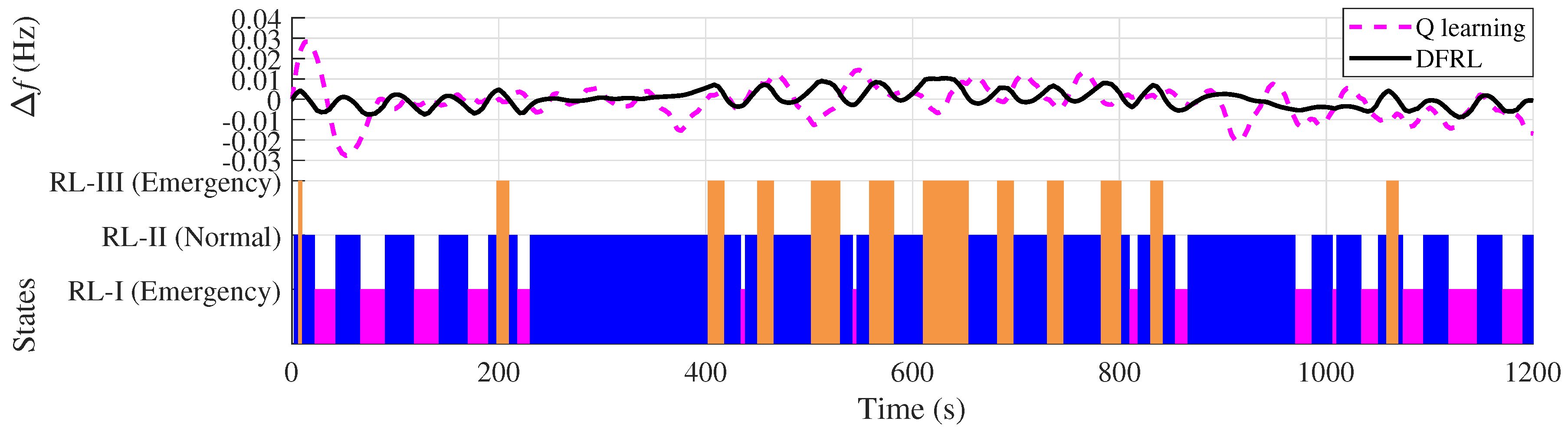
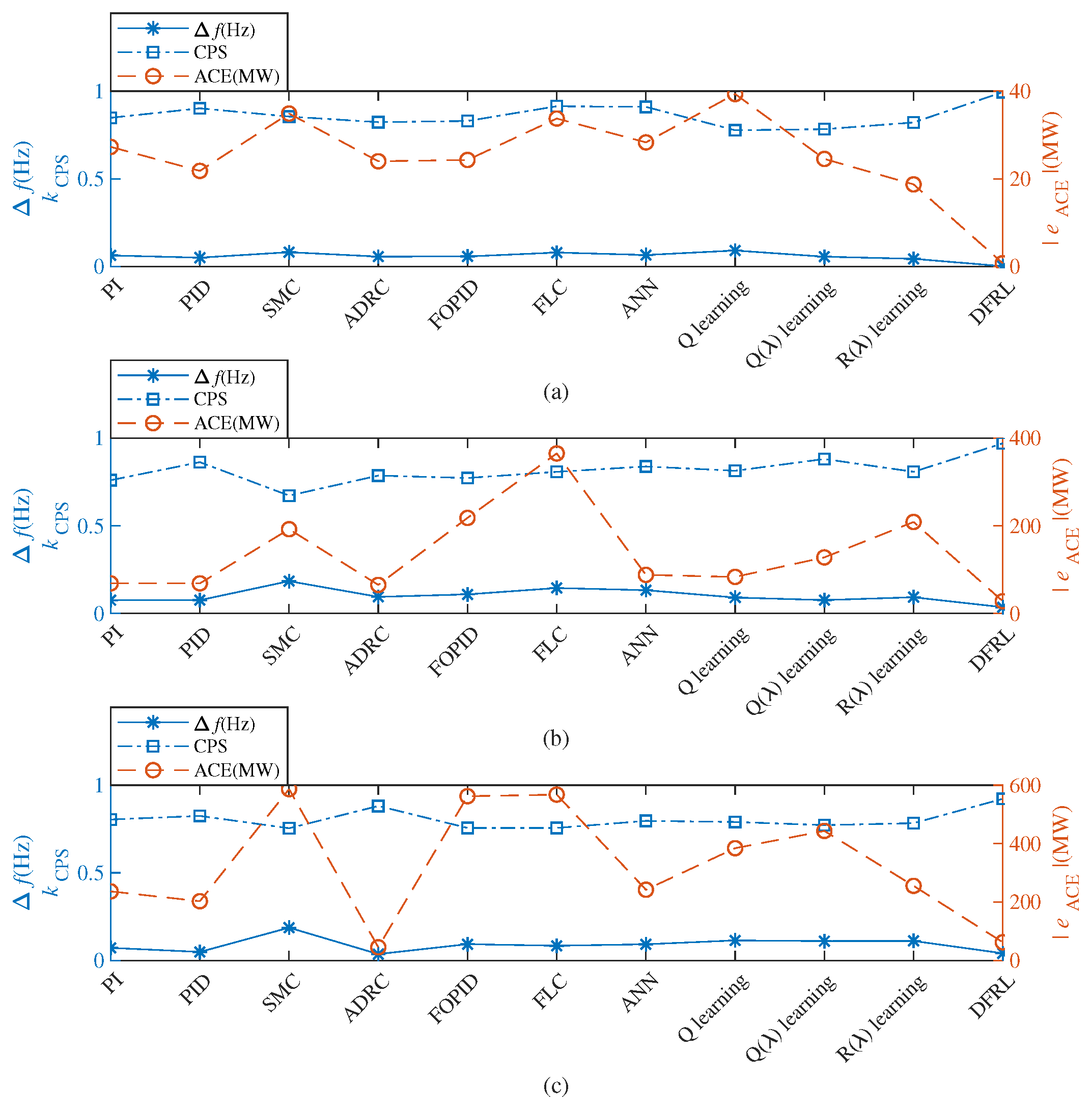
- The average absolute values of the frequency deviations obtained by DFRL are less than (i.e., 0.1 Hz), while the average absolute values of the frequency deviations obtained by 10 conventional AGC algorithms may larger than 0.1 Hz in both Case 1 and Case 2 (Table 2); Therefore, the emergency situation of a large-scale interconnected power system and the curse of dimensionality can simultaneously be reduced by the proposed DFRL.
- Compared to 10 conventional AGC algorithms, DFRL can obtain the highest control performance with a smaller absolute value of frequency deviation and larger CPS index (Figure 11).
- Since the deep forest of DFRL can perform representation learning for the states of the power system, the preventive strategy for AGC can be considered effective for a large-scale interconnected power system.
5. Conclusions
- After the pre-training process using the data of reinforcement learning, the deep forest of DFRL can effectively forecast the next state of a power system. Different from the conventional applications of deep forest, the deep forest of DFRL is incorporated into the control algorithm;
- Since the subsidiary reinforcement learning algorithms of DFRL can update their strategies online, the DFRL can effectively provide generation commands to the controller as a preventive strategy for AGC in power systems. Compared to conventional AGC, the preventive strategy for AGC can predict the next systemic state of the power system;
- Since the next systemic state can be predicted and the calculation memory can be reduced by the DFRL method, the proposed DFRL-based controller can effectively reduce occurrences of emergency situations in large-scale interconnected power systems and simultaneously mitigate the curse of dimensionality. The conventional framework of reinforcement learning can be divided into multiple subsidiary structures for mitigating the curse of dimensionality.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AGC | Automatic generation control |
| DFRL | Deep forest reinforcement learning |
| PI | Proportional-integral |
| PID | Proportional-integral-derivative |
| SMC | Sliding mode controller |
| ADRC | Active disturbance rejection controller |
| LFC | Load frequency control |
| ANN | Artificial neural network |
| FOPID | Freedom fractional order PID |
| FLC | Fuzzy logic control |
| ACE | Area control error |
| CPS | Control performance standard |
Appendix A. Parameters of Conventional AGC Algorithms
- PI, two-area: proportional = −0.882, integral = −0.10; three-area: = −402.63, = −747.86; China Southern Power Grid: = −2527.60, = −559.42;
- PID, two-area: = −0.584, = −0.275, derivative = −0.01; three-area: = −415.12, = −780.46, = −0.001; China Southern Power Grid: = −6640.60, = −658.77, = −0.005;
- SMC, switch on/off point 0.3 Hz; two-area: output when on/off = 1000 (MW); three-area = 45,000 (MW); China Southern Power Grid: = 40,000 (MW);
- ADRC, extended state observer , , , , = 1, two-area: = −1040, = 1, = 10; three-area: = −668.11, = 734.67, = −374.53; China Southern Power Grid: = −851.95, = 161.64, = 428.63;
- FOPID, two-area: = −0.89639, = −0.2071, = 0.33636, = −0.52061, = 0.51401; three-area: = −83500, = −0.005, = 0, = −0.1, = 0.1; China Southern Power Grid: = −6.7573, = −6.7002, = −9.7831, = 0.86527, = 0.61834;
- FLC, X (input, ) 21 grids from −0.2 to 0.2 (Hz), Y (input, ) 21 grids from −1 to 1 (Hz), two-area: Z (output, ) is 441 grids from −256 to 256 (MW); three-area: Z from −91,285 to 91,285 (MW); China Southern Power Grid: Z from −58,527 to 58,527 (MW);
- ANN, layer size L = 8, epochs E = 2;
- Q learning, learning rate = 0.1, the constant of probability distribution method = 0.05, the discounted rate of future reward = 0.9, state set S = {}, two-area: action set A = {}; three-area: A = {}; China Southern Power Grid: A = {};
- Q() learning, = 0.9, , , , A are the same as that of Q learning algorithm;
- R() learning, = 0.9, = 0, , , , A are the same as that of Q learning algorithm.
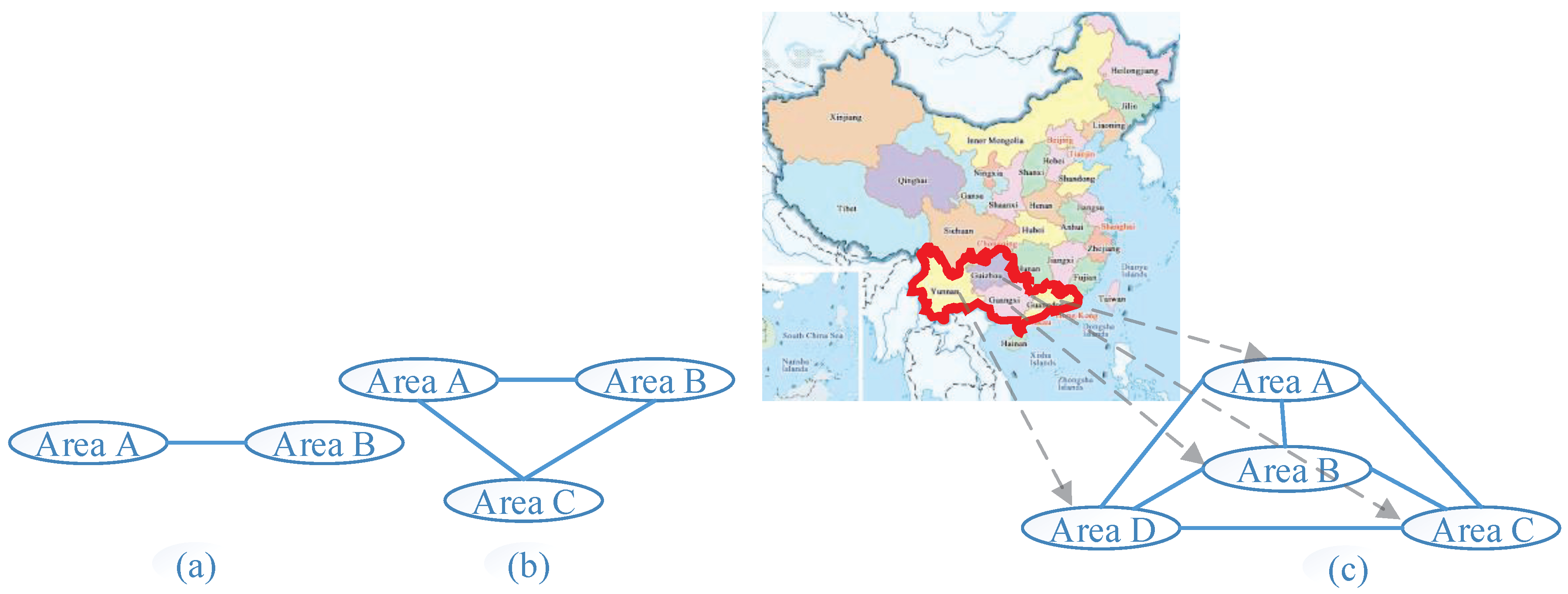
Appendix B. Parameters of IEEE Two-Area Power System
Appendix C. Parameters of Three-Area Power System
Appendix D. Parameters of China Southern Power Grid
References
- Maleki, A.; Hafeznia, H.; Rosen, M.A.; Pourfayaz, F. Optimization of a grid-connected hybrid solar-wind-hydrogen CHP system for residential applications by efficient metaheuristic approaches. Appl. Therm. Eng. 2017, 123, 1263–1277. [Google Scholar] [CrossRef]
- Allison, J. Robust multi-objective control of hybrid renewable microgeneration systems with energy storage. Appl. Therm. Eng. 2017, 114, 149–1506. [Google Scholar] [CrossRef]
- Yin, L.; Yu, T.; Zhang, X.; Yang, B. Relaxed deep learning for real-time economic generation dispatch and control with unified time scale. Energy 2018, 149, 11–23. [Google Scholar] [CrossRef]
- Yang, B.; Yu, T.; Shu, H.; Dong, J.; Jiang, L. Robust sliding-mode control of wind energy conversion systems for optimal power extraction via nonlinear perturbation observers. Appl. Energy 2018, 210, 711–723. [Google Scholar] [CrossRef]
- Dahiya, P.; Sharma, V.; Naresh, R. Automatic generation control using disrupted oppositional based gravitational search spell optimized sliding mode controller under deregulated environment. IET Gener. Transm. Distrib. 2016, 10, 3995–4005. [Google Scholar] [CrossRef]
- Liu, F.; Li, Y.; Cao, Y.; She, J.; Wu, M. A Two-Layer Active Disturbance Rejection Controller Design for Load Frequency Control of Interconnected Power System. IEEE Trans. Power Syst. 2016, 31, 3320–3321. [Google Scholar] [CrossRef]
- Debbarma, S.; Saikia, L.C.; Sinha, N. Automatic generation control using two degree of freedom fractional order PID controller. Int. J. Electr. Power Energy Syst. 2014, 58, 120–129. [Google Scholar] [CrossRef]
- Rahman, A.; Saikia, L.C.; Sinha, N. AGC of dish-Stirling solar thermal integrated thermal system with biogeography based optimized three degree of freedom PID controller. IET Renew. Power Gener. 2016, 10, 1161–1170. [Google Scholar] [CrossRef]
- Jeyalakshmi, V.; Subburaj, P. PSO-scaled fuzzy logic to load frequency control in hydrothermal power system. Soft Comput. 2016, 20, 2577–2594. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Vu Quynh, N.; Duong, M.Q.; Van Dai, L. Modified Differential Evolution Algorithm: A Novel Approach to Optimize the Operation of Hydrothermal Power Systems while Considering the Different Constraints and Valve Point Loading Effects. Energies 2018, 11, 540. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Dinh, B.H.; Quynh, N.V.; Duong, M.Q.; Dai, L.V. A Novel Algorithm for Optimal Operation of Hydrothermal Power Systems under Considering the Constraints in Transmission Networks. Energies 2018, 11, 188. [Google Scholar] [CrossRef]
- Yu, T.; Zhou, B.; Chan, K.W.; Chen, L.; Yang, B. Stochastic Optimal Relaxed Automatic Generation Control in Non-Markov Environment Based on Multi-Step Q(λ) Learning. IEEE Trans. Power Syst. 2011, 26, 1272–1282. [Google Scholar] [CrossRef]
- Yu, T.; Wang, H.; Zhou, B.; Chan, K.; Tang, J. Multi-agent correlated equilibrium Q(λ) learning for coordinated smart generation control of interconnected power grids. IEEE Trans. Power Syst. 2015, 30, 1669–1679. [Google Scholar] [CrossRef]
- Xi, L.; Yu, T.; Yang, B.; Zhang, X.; Qiu, X. A wolf pack hunting strategy based virtual tribes control for automatic generation control of smart grid. Appl. Energy 2016, 178, 198–211. [Google Scholar] [CrossRef]
- Yu, T.; Zhou, B.; Chan, K.; Yuan, Y.; Yang, B.; Wu, Q. R(λ) imitation learning for automatic generation control of interconnected power grids. Automatica 2012, 48, 2130–2136. [Google Scholar] [CrossRef]
- Watkins, C.J.C.H. Learning from Delayed Rewards. Ph.D. Thesis, Unpublished doctoral dissertation. Cambridge University, Cambridge, UK, 1989. [Google Scholar]
- Yin, L.; Yu, T.; Zhou, L. Design of a Novel Smart Generation Controller Based on Deep Q Learning for Large-Scale Interconnected Power System. J. Energy Eng. 2018, 144, 04018033. [Google Scholar] [CrossRef]
- Si, Y.L.; Jin, Y.G.; Yong, T.Y. Determining the Optimal Reserve Capacity in a Microgrid With Islanded Operation. IEEE Trans. Power Syst. 2015, 31, 1369–1376. [Google Scholar]
- Hu-Ling, A.Y.; Fu-Suo, B.L.; Wei, T.C.L.; Guo-Yi, D.J.; Hao, E.H.; Hai-Bo, F.L.; Li, G.F. A coordination and optimization method of preventive control to improve the adaptability of frequency emergency control strategy in high-capacity generators and low load grid. In Proceedings of the 2014 International Conference on Power System Technology, Chengdu, China, 20–22 October 2014; pp. 485–490. [Google Scholar] [CrossRef]
- Amani, A.M.; Gaeini, N.; Afshar, A.; Menhaj, M. A New Approach to Reconfigurable Load Frequency Control of Power Systems in Emergency Conditions. IFAC Proc. Vol. 2013, 46, 526–531. [Google Scholar] [CrossRef]
- Bevrani, H.; Ledwich, G.; Ford, J.J.; Dong, Z.Y. On feasibility of regional frequency-based emergency control plans. Energy Convers. Manag. 2009, 50, 1656–1663. [Google Scholar] [CrossRef]
- Sarker, B.R.; Faiz, T.I. Minimizing maintenance cost for offshore wind turbines following multi-level opportunistic preventive strategy. Renew. Energy 2016, 85, 104–113. [Google Scholar] [CrossRef]
- Huang, G.; Wang, J.; Chen, C.; Qi, J.; Guo, C. Integration of Preventive and Emergency Responses for Power Grid Resilience Enhancement. IEEE Trans. Power Syst. 2017, 32, 4451–4463. [Google Scholar] [CrossRef]
- Pertl, M.; Weckesser, T.; Rezkalla, M.; Heussen, K.; Marinelli, M. A decision support tool for transient stability preventive control. Electr. Power Syst. Res. 2017, 147, 88–96. [Google Scholar] [CrossRef]
- Liu, W.; Qin, G.; He, Y.; Jiang, F. Distributed Cooperative Reinforcement Learning-Based Traffic Signal Control That Integrates V2X Networks’ Dynamic Clustering. IEEE Trans. Veh. Technol. 2017, 66, 8667–8681. [Google Scholar] [CrossRef]
- Yin, L.; Yu, T.; Zhou, L.; Huang, L.; Zhang, X.; Zheng, B. Artificial emotional reinforcement learning for automatic generation control of large-scale interconnected power grids. IET Gener. Transm. Distrib. 2017, 11, 2305–2313. [Google Scholar] [CrossRef]
- Zhou, Z.; Feng, J. Deep Forest: Towards An Alternative to Deep Neural Networks. arXiv, 2017; arXiv:1702.08835. [Google Scholar]
- Utkin, L.V.; Ryabinin, M.A. Discriminative Metric Learning with Deep Forest. arXiv, 2017; arXiv:1705.09620. [Google Scholar]
- Utkin, L.V.; Ryabinin, M.A. A Deep Forest for Transductive Transfer Learning by Using a Consensus Measure. In Artificial Intelligence and Natural Language; Springer International Publishing: Cham, Switzerland, 2018; pp. 194–208. [Google Scholar]
- Li, M.; Zhang, N.; Pan, B.; Xie, S.; Wu, X.; Shi, Z. Hyperspectral Image Classification Based on Deep Forest and Spectral-Spatial Cooperative Feature. In Image and Graphics; Zhao, Y., Kong, X., Taubman, D., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 325–336. [Google Scholar]
- Zhang, Y.; Zhou, J.; Zheng, W.; Feng, J.; Li, L.; Liu, Z.; Li, M.; Zhang, Z.; Chen, C.; Li, X.; Zhou, Z. Distributed Deep Forest and its Application to Automatic Detection of Cash-out Fraud. arXiv, 2018; arXiv:1805.04234. [Google Scholar]
- Utkin, L.V.; Ryabinin, M.A. A Siamese Deep Forest. arXiv, 2017; arXiv:1704.08715. [Google Scholar]
- Wen, S.; Yu, X.; Zeng, Z.; Wang, J. Event-Triggering Load Frequency Control for Multiarea Power Systems with Communication Delays. IEEE Trans. Ind. Electron. 2016, 63, 1308–1317. [Google Scholar] [CrossRef]
- Yao, M.; Shoults, R.R.; Kelm, R. AGC logic based on NERC’s new Control Performance Standard and Disturbance Control Standard. IEEE Tran. Power Syst. 2000, 15, 852–857. [Google Scholar] [CrossRef]
- Jaleeli, N.; VanSlyck, L.S. NERC’s new control performance standards. IEEE Trans. Power Syst. 1999, 14, 1092–1099. [Google Scholar] [CrossRef]
- Nie, J.; Haykin, S. A Dynamic Channel Assignment Policy Through Q-Learning. IEEE Trans. Neural Netw. 1999, 10, 1443–1455. [Google Scholar] [PubMed]
- Zhou, H.; Su, Y.; Chen, Y.; Ma, Q.; Mo, W. The China Southern Power Grid: Solutions to Operation Risks and Planning Challenges. IEEE Power Energy Maga. 2016, 14, 72–78. [Google Scholar] [CrossRef]

| Pow. | Stat. | Value |
|---|---|---|
| All | StaI. | |
| All | StaII. | |
| All | StaIII. | |
| 2 | ActI. | {10, 19, 28, 37, 46, 55, 64, 73, 82, 91, 100} |
| 2 | ActII. | {−10, −8, −6, −4, −2, 0, 2, 4, 6, 8, 10} |
| 2 | ActIII. | {−100, −91, −82, −73, −64, −55, −46, −37, −28, −19, −10} |
| 3 | ActI. | {300, 570, 840, 1110, 1380, 1650, 1920, 2190, 2460, 2730, 3000} |
| 3 | ActII. | {−300, −240, −180, −120, −60, 0, 60, 120, 180, 240, 300} |
| 3 | ActIII. | {−3000, −2730, −2460, −2190, −1920, −1650, −1380, −1110, −840, −570, −300} |
| 4 | ActI. | {510, 561, 612, 663, 714, 765, 816, 867, 918, 969, 1020} |
| 4 | ActII. | {−510, −408, −306, −204, −102, 0, 102, 204, 306, 408, 510} |
| 4 | ActIII. | {−1020, −969, −918, −867, −816, −765, −714, −663, −612, −561, −510} |
| Power Systems | Algorithms | (Hz) | (MW) | (%) |
|---|---|---|---|---|
| Two-area | PI | 0.063 | 27 | 84.82 |
| PID | 0.050 | 22 | 90.23 | |
| SMC | 0.081 | 35 | 85.54 | |
| ADRC | 0.056 | 24 | 82.34 | |
| FOPID | 0.066 | 28 | 83.29 | |
| FLC | 0.079 | 34 | 91.40 | |
| ANN | 0.065 | 28 | 91.06 | |
| Q learning | 0.091 | 39 | 77.72 | |
| Q() learning | 0.056 | 25 | 78.33 | |
| R() learning | 0.044 | 19 | 82.14 | |
| DFRL | 0.002 | 1 | 99.48 | |
| Three-area | PI | 0.075 | 69 | 76.03 |
| PID | 0.076 | 69 | 86.33 | |
| SMC | 0.184 | 192 | 67.24 | |
| ADRC | 0.095 | 65 | 78.66 | |
| FOPID | 0.188 | 209 | 78.78 | |
| FLC | 0.145 | 365 | 80.82 | |
| ANN | 0.133 | 88 | 83.87 | |
| Q learning | 0.091 | 83 | 81.41 | |
| Q() learning | 0.076 | 128 | 88.13 | |
| R() learning | 0.093 | 209 | 80.84 | |
| DFRL | 0.036 | 28 | 97.07 | |
| China Southern Power Grid | PI | 0.072 | 237 | 80.43 |
| PID | 0.049 | 203 | 82.49 | |
| SMC | 0.187 | 587 | 75.45 | |
| ADRC | 0.059 | 48 | 88.22 | |
| FOPID | 0.093 | 562 | 75.65 | |
| FLC | 0.084 | 568 | 75.62 | |
| ANN | 0.093 | 242 | 79.65 | |
| Q learning | 0.114 | 384 | 79.03 | |
| Q() learning | 0.111 | 443 | 77.23 | |
| R() learning | 0.111 | 256 | 78.36 | |
| DFRL | 0.041 | 62 | 92.23 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, L.; Zhao, L.; Yu, T.; Zhang, X. Deep Forest Reinforcement Learning for Preventive Strategy Considering Automatic Generation Control in Large-Scale Interconnected Power Systems. Appl. Sci. 2018, 8, 2185. https://doi.org/10.3390/app8112185
Yin L, Zhao L, Yu T, Zhang X. Deep Forest Reinforcement Learning for Preventive Strategy Considering Automatic Generation Control in Large-Scale Interconnected Power Systems. Applied Sciences. 2018; 8(11):2185. https://doi.org/10.3390/app8112185
Chicago/Turabian StyleYin, Linfei, Lulin Zhao, Tao Yu, and Xiaoshun Zhang. 2018. "Deep Forest Reinforcement Learning for Preventive Strategy Considering Automatic Generation Control in Large-Scale Interconnected Power Systems" Applied Sciences 8, no. 11: 2185. https://doi.org/10.3390/app8112185
APA StyleYin, L., Zhao, L., Yu, T., & Zhang, X. (2018). Deep Forest Reinforcement Learning for Preventive Strategy Considering Automatic Generation Control in Large-Scale Interconnected Power Systems. Applied Sciences, 8(11), 2185. https://doi.org/10.3390/app8112185






