A Space-Variant Deblur Method for Focal-Plane Microwave Imaging
Abstract
1. Introduction
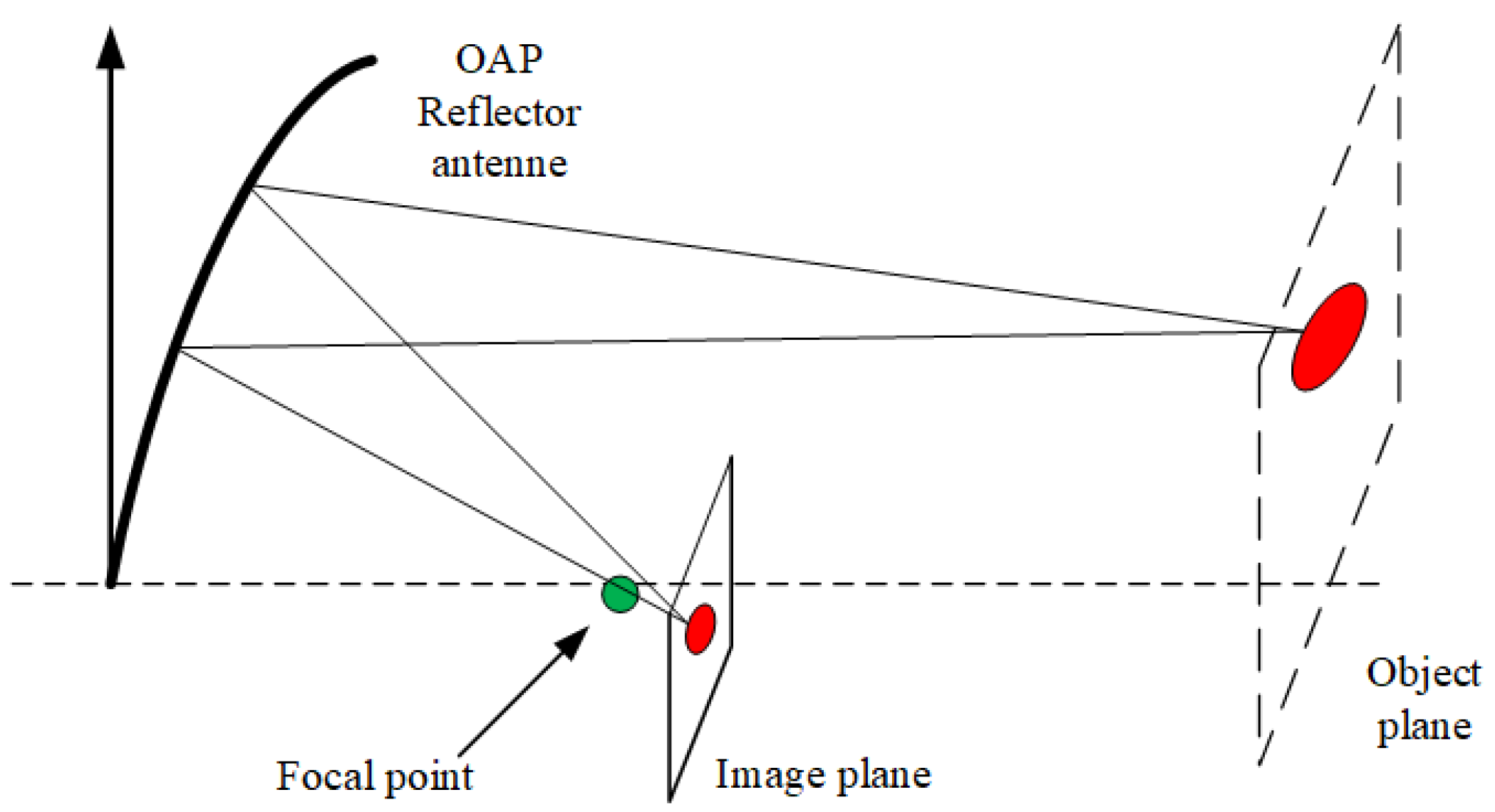
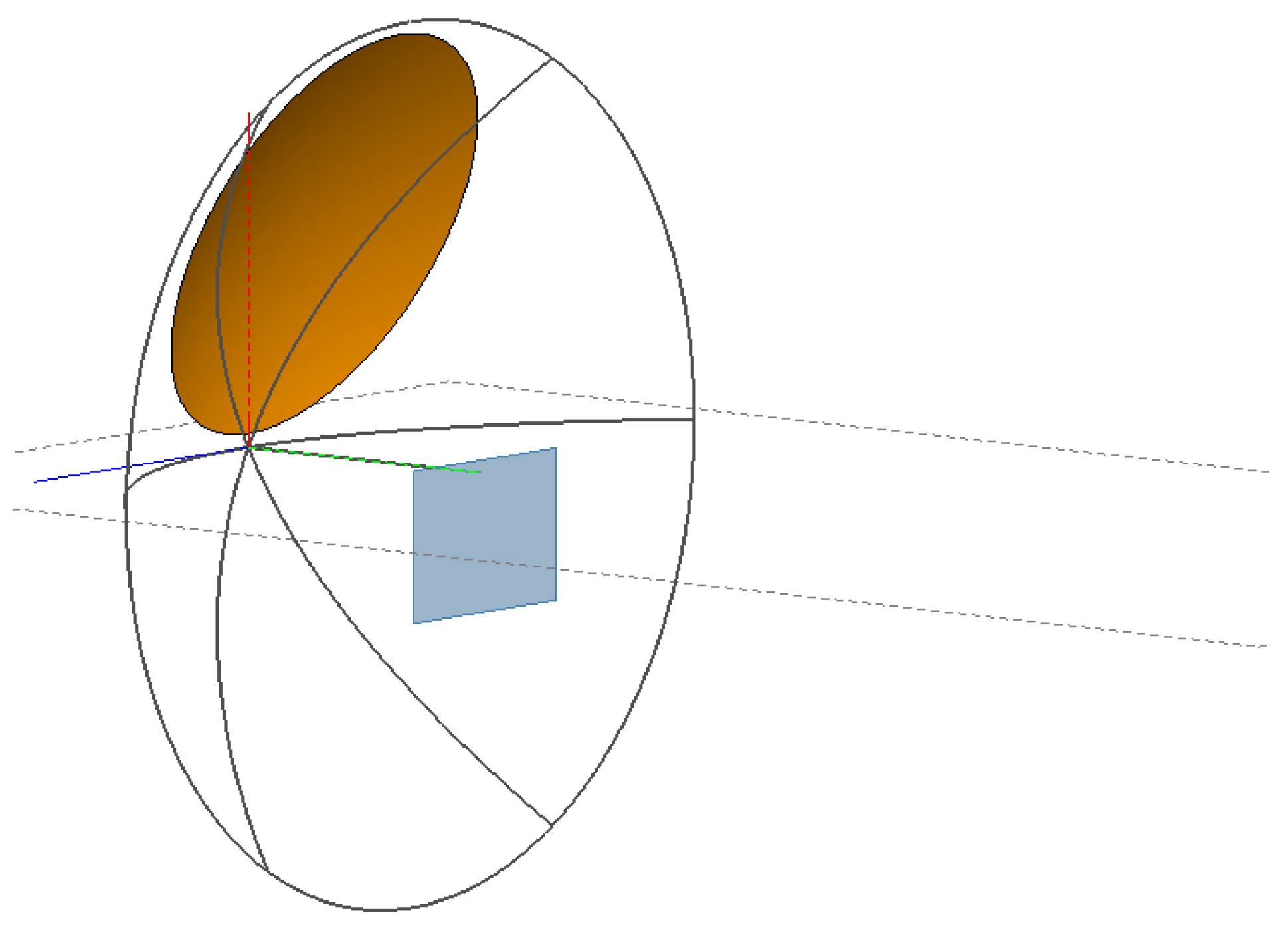
2. Space-Variant PSF of OAP System
2.1. Space-Variance Correction in the Angular Direction
2.2. Space Variance Correction in the Radial Direction
3. Methods
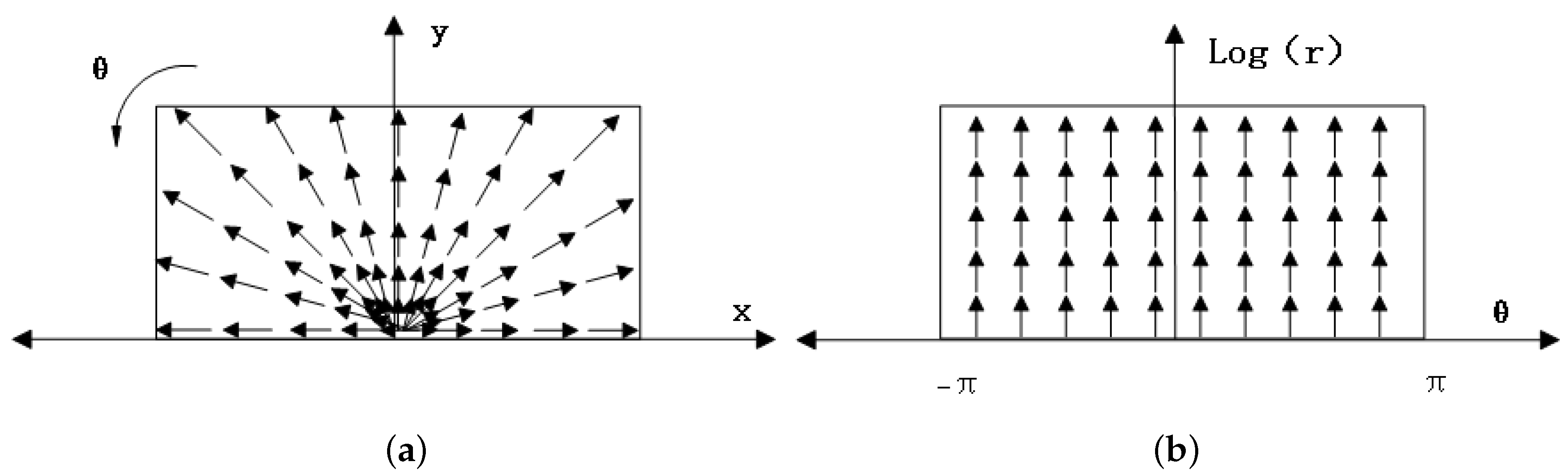
3.1. Log-Polar Transformation
- Step 1 Obtain the image data of M*N by photoelectric sensors and the point spread function of M*N by simulation of the ideal point source in FEKO.
- Step 2 Transform the image data and coordinate into the polar-coordinate to get the new image and the new Equation (8), and interpolate the new image using the bicubic interpolation method.
- Step 3 Use the Lucy–Richardson algorithm with and to reconstruct the high-resolution image .
- Step 4 Inverse transform into the Cartesian coordinate system and interpolate it by the bicubic method to obtain the final result with resolution recovery.
3.2. Lucy–Richardson Iterative Algorithm
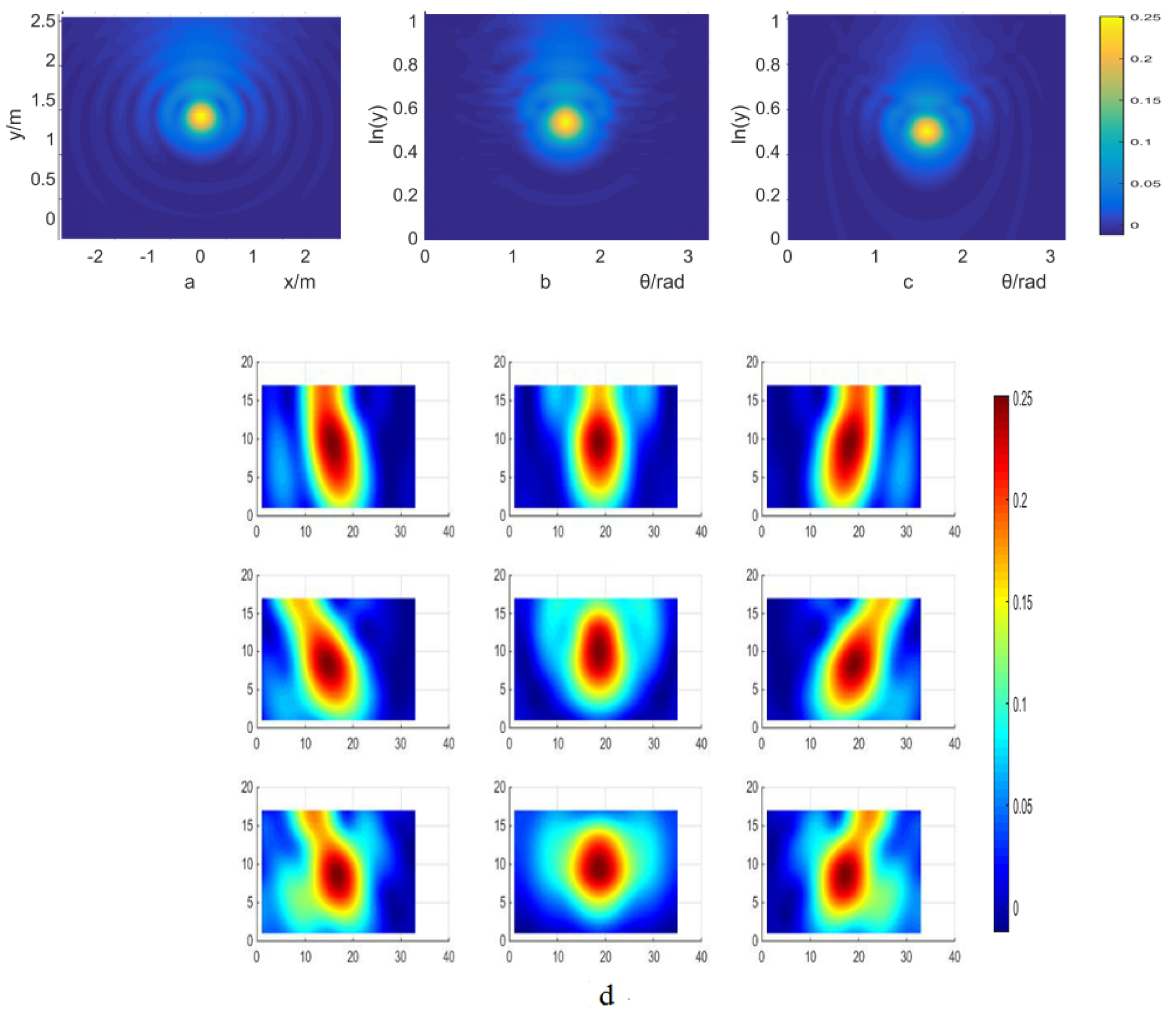
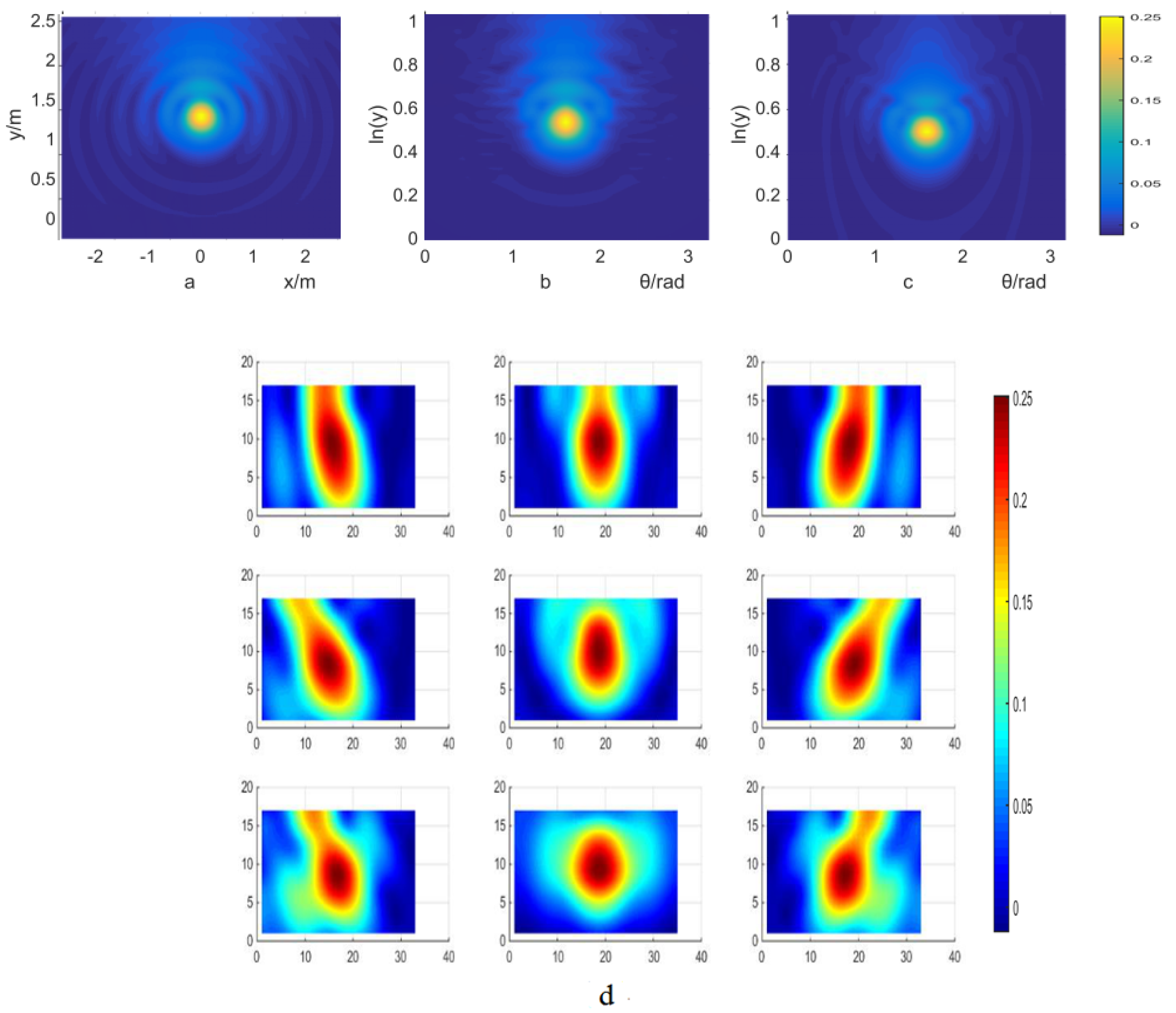
4. Results and Analysis
4.1. PSF Used for the Results
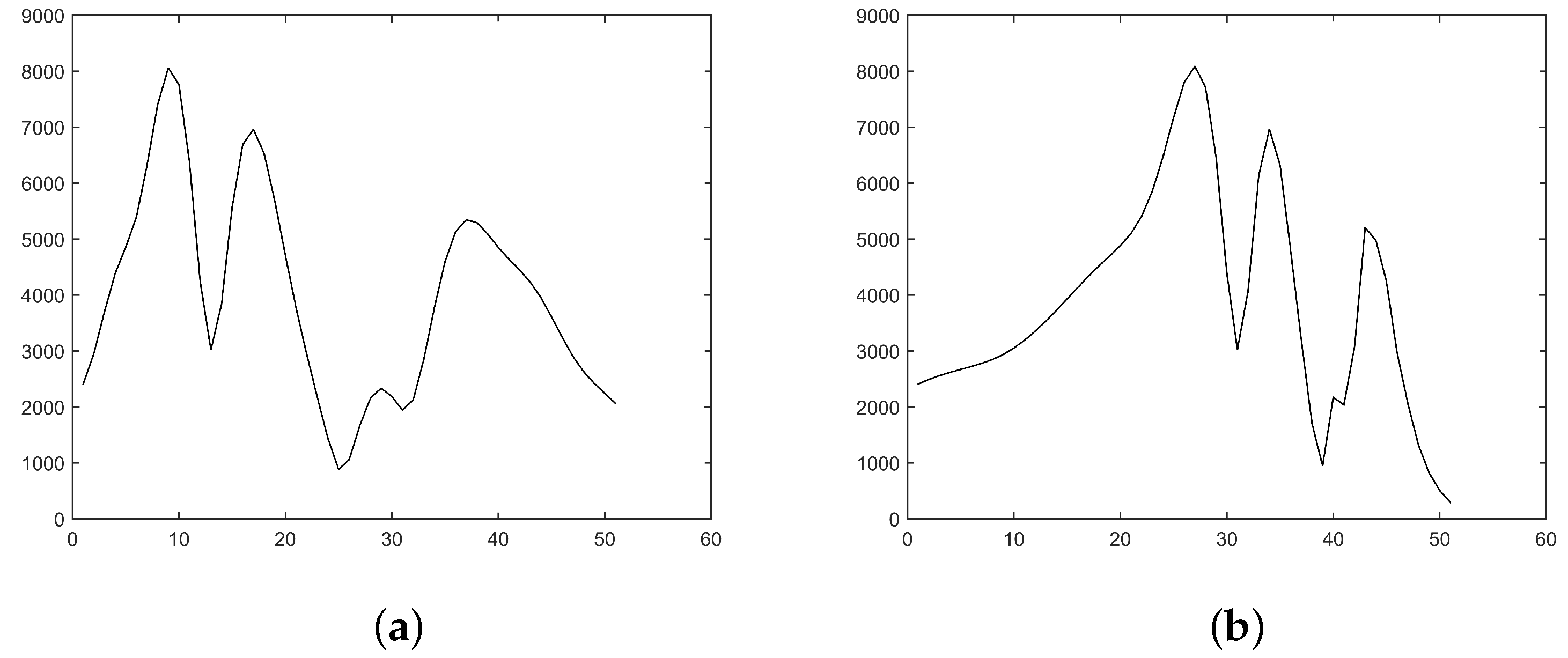
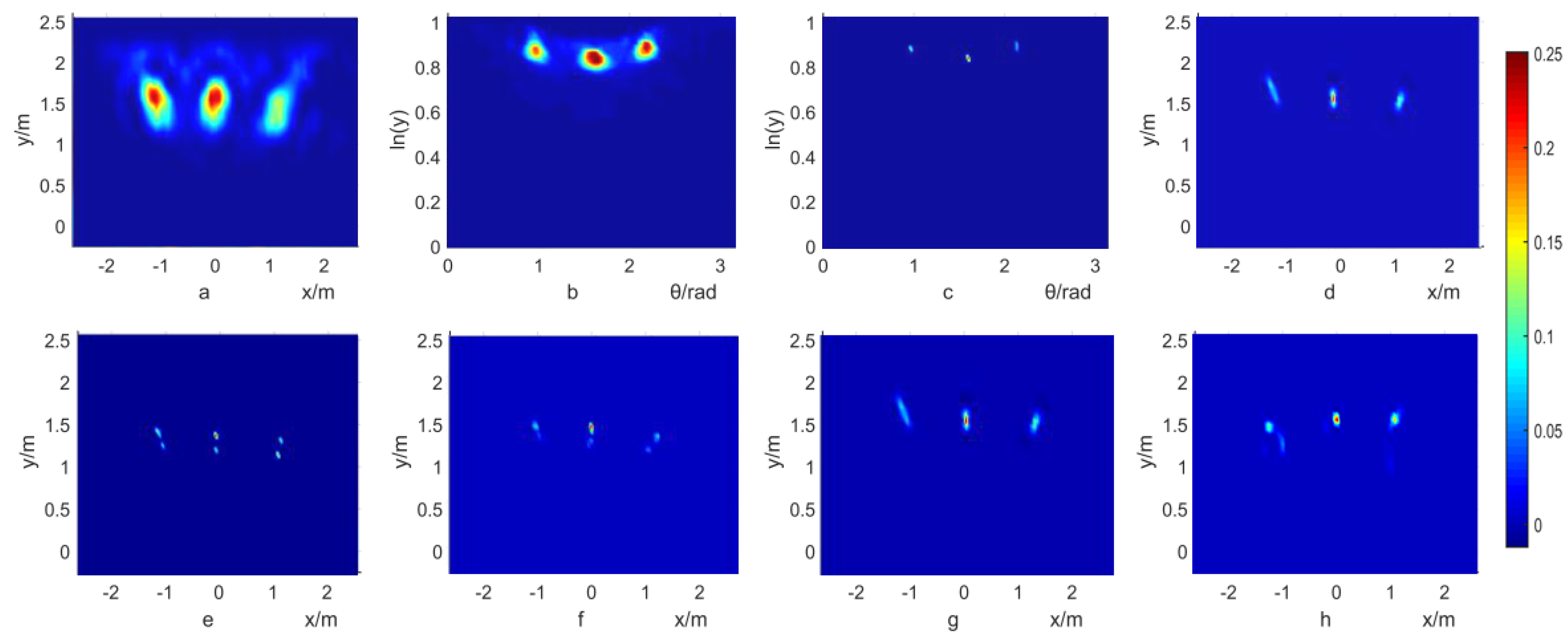
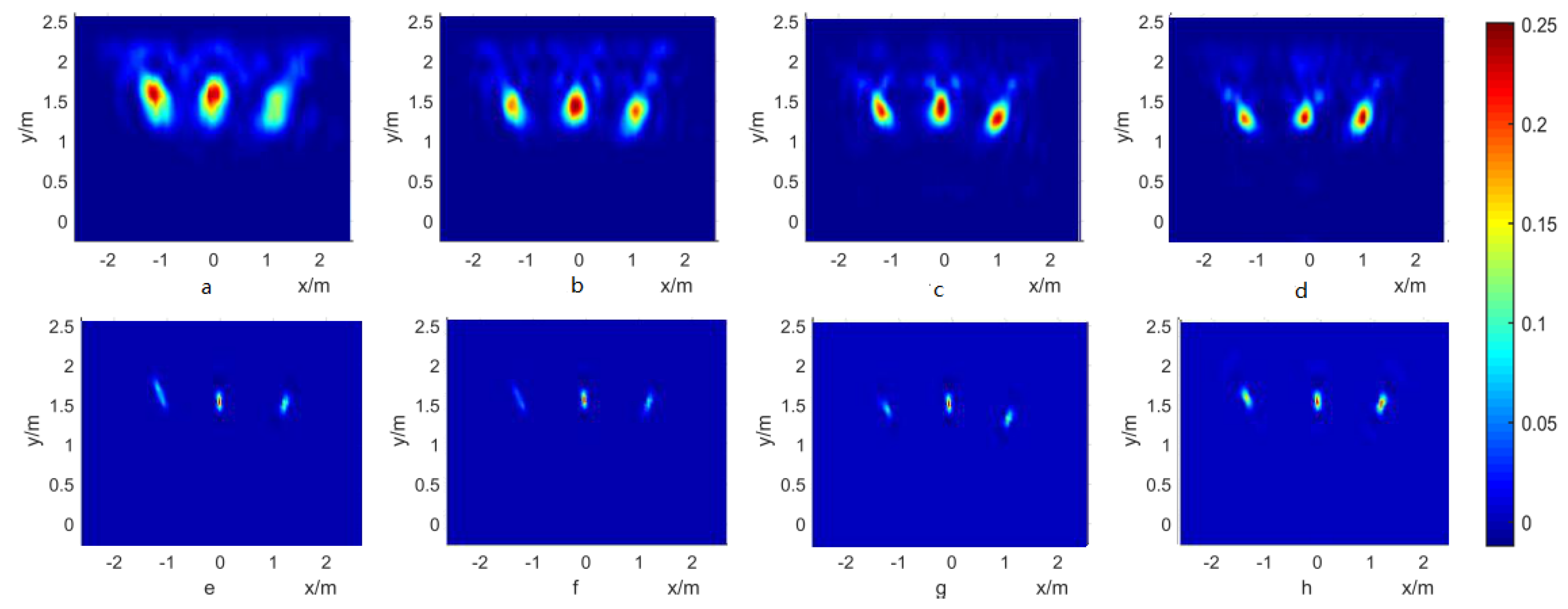
4.2. Deblur of Simulation Results
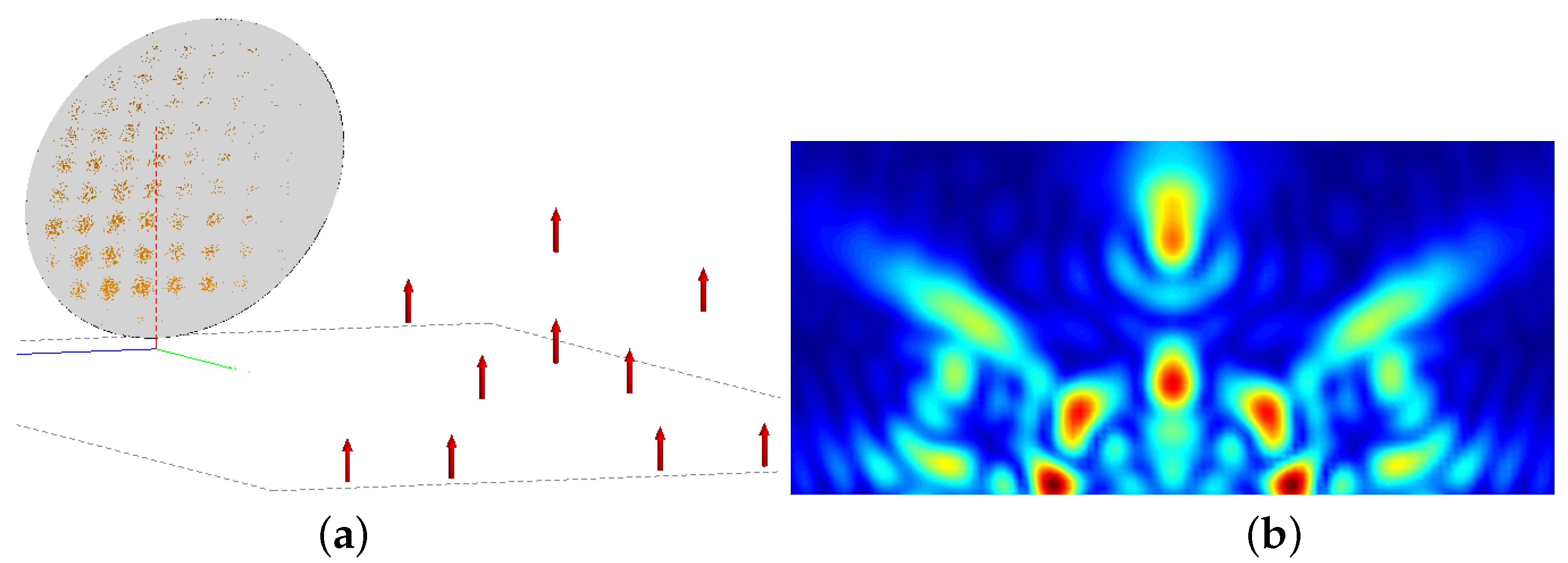
4.3. Deblur of Experiment Results
- Step 1 Convert the z-axis of the image matrix into a dB area by log operation.
- Step 2 Mark the pixel as 1 if its value is larger than the peak subtracted by 6 dB and 0 if not.
- Step 3 Calculate the number of 1 in the whole image as the −6 dB beamwidth.
5. Conclusions
Author Contributions
Funding
References
- Angel, E.S.; Jain, A.K. Restoration of images degraded by spatially varying pointspread functions by a conjugate gradient method. Appl. Opt. 1978, 17, 2186. [Google Scholar] [CrossRef] [PubMed]
- Woods, J.; Radewan, C. Kalman Filtering in Two Dimensions; IEEE Press: Piscataway, NJ, USA, 1977. [Google Scholar]
- Woods, J. Correction to Kalman Filtering in Two Dimensions. IEEE Trans. Inf. Theory 2003, 25, 628–629. [Google Scholar] [CrossRef]
- Ozkan, M.K.; Tekalp, A.M.; Sezan, M.I. POCS-based restoration of space-varying blurred images. IEEE Trans. Image Process. 1994, 3, 450–454. [Google Scholar] [CrossRef] [PubMed]
- Fish, D.A.; Grochmalicki, J.; Pike, E.R. Scanning singular-value-decomposition method for restoration of images with space-variant blur. J. Opt. Soc. Am. A 1996, 13, 464–469. [Google Scholar] [CrossRef]
- Nagy, J.G.; O’Leary, D.P. Fast iterative image restoration with a spatially varying PSF. In Proceedings of the Optical Science, Engineering and Instrumentation, San Diego, CA, USA, 27 July–1 August 1997; pp. 388–399. [Google Scholar]
- Mikhael, W.B. Restoration of digital images with known space-variant blurs from conventional optical systems. Int. Soc. Opt. Eng. 1999, 3716, 71–79. [Google Scholar]
- Trussell, H.; Hunt, B. Sectioned methods for image restoration. IEEE Trans. Acoust. Speech Signal Process. 1978, 26, 157–164. [Google Scholar] [CrossRef]
- Trussell, H.; Hunt, B. Image restoration of space-variant blurs by sectioned methods. IEEE Trans. Acoust. Speech Signal Process. 1978, 26, 608–609. [Google Scholar] [CrossRef]
- Costello, T.P.; Mikhael, W.B. Efficient restoration of space-variant blurs from physical optics by sectioning with modified Wiener filtering. Digit. Signal Process. 2003, 13, 1–22. [Google Scholar] [CrossRef]
- Guo, Y.P.; Lee, H.P.; Teo, C.L. Blind restoration of images degraded by space-variant blurs using iterative algorithms for both blur identification and image restoration. Image Vis. Comput. 1997, 15, 399–410. [Google Scholar] [CrossRef]
- Du, X.; Xie, S.; Hao, X.; Wang, C. An electromagnetic interference source imaging algorithm of Multi-resolution partitions. High Power Laser Part. Beams 2015, 27, 10. [Google Scholar]
- Sawchuk, A.A.; Peyrovian, M.J. Restoration of astigmatism and curvature of field. J. Opt. Soc. Am. 1975, 65, 712–715. [Google Scholar] [CrossRef]
- Camera, A.L.; Schreiber, L.; Diolaiti, E.; Boccacci, P.; Bertero, M.; Bellazzini, M.; Ciliegi, P. A method for space-variant deblurring with application to adaptive optics imaging in astronomy. Astron. Astrophys. 2015, 579, A1. [Google Scholar] [CrossRef]
- Mourya, R.; Ferrari, A.; Flamary, R.; Bianchi, P.; Richard, C. Distributed approach for deblurring large images with shift-variant blur. In Proceedings of the European Signal Processing Conference, Kos island, Greece, 28 August–2 September 2017; pp. 2463–2470. [Google Scholar]
- Zhang, X.; Wang, R.; Jiang, X.; Wang, W.; Gao, W. Spatially variant defocus blur map estimation and deblurring from a single image. J. Vis. Commun. Image Represent. 2016, 35, 257–264. [Google Scholar] [CrossRef]
- Schuler, C.J.; Hirsch, M.; Harmeling, S.; Scholkopf, B. Learning to Deblur. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 1439–1451. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Cao, W.; Xu, Z.; Ponce, J. Learning a convolutional neural network for non-uniform motion blur removal. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 769–777. [Google Scholar]
- Li, L.; Yang, J.; Wang, J.; Deng, Y. An focal plane array space variant model for PMMW imaging. In Proceedings of the IET International Radar Conference, Guilin, China, 20–22 April 2009; pp. 1–4. [Google Scholar]
- Lee, C.; Xiong, B.; Compiled, T. A Course of Optical Information; Dou, J., Ed.; Publishing House: Beijing, China, 2011; pp. 40–41. [Google Scholar]
- Guoguang, E. Light Field Transformation by Paraboloidal Mirror. Acta Opt. Sin. 1995, 15, 593–599. [Google Scholar]
- Arguijo, P.; Scholl, M.S. Exact ray-trace beam for an off-axis paraboloid surface. Appl. Opt. 2003, 42, 3284–3289. [Google Scholar] [CrossRef] [PubMed]
- Arguijo, P.; Scholl, M.S.; Paez, G. Diffraction patterns formed by an off-axis paraboloid surface. Appl. Opt. 2001, 40, 2909–2916. [Google Scholar] [CrossRef] [PubMed]
- Sawchuk, A.A. Space-variant image restoration by coordinate transformations. J. Opt. Soc. Am. 1974, 64, 138–144. [Google Scholar] [CrossRef]
- Wolberg, G.; Zokai, S. Robust image registration using log-polar transform. In Proceedings of the International Conference on Image Processing, Florence, Italy, 13–19 September 2000; Volume 1, pp. 493–496. [Google Scholar]
- Wang, L.; Li, Y.J.; Zhang, K. Application of target recognition algorithm based on log-polar transformation for imaging guidance. J. Astronaut. 2005, 26, 330–333. [Google Scholar]
- Lucy, L.B. An iterative technique for the rectification of observed distributions. J. Astron. 1974, 79, 745. [Google Scholar] [CrossRef]
- White, R.L. Image restoration using the damped Richardson-Lucy method. In Proceedings of the Instrumentation in Astronomy VIII, International Society for Optics and Photonics, Kona, HI, USA, 21–24 September 1994. [Google Scholar]
- Lu, J.K.; Zhong, S.G.; Liu, S.Q. Analytic Extension. In Introduction to the Theory of Complex Functions; World Scientific Publishing Company: Singapore, 2002; pp. 178–199. [Google Scholar]


| 3 GHz | 4 GHz | 5 GHz | 6 GHz | |
|---|---|---|---|---|
| Left | (36,28) | (32,28) | (32,28) | (34,25) |
| Center | (33,50) | (33,50) | (33,50) | (33,50) |
| Right | (33,73) | (33,73) | (30,71) | (33,73) |
| 3 GHz | 4 GHz | 5 GHz | 6 GHz | |
|---|---|---|---|---|
| Left | 2 | 2 | 2 | 3 |
| Center | 6 | 6 | 6 | 6 |
| Right | 7 | 7 | 8 | 10 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luan, S.; Xie, S.; Wang, T.; Hao, X.; Yang, M.; Li, Y. A Space-Variant Deblur Method for Focal-Plane Microwave Imaging. Appl. Sci. 2018, 8, 2166. https://doi.org/10.3390/app8112166
Luan S, Xie S, Wang T, Hao X, Yang M, Li Y. A Space-Variant Deblur Method for Focal-Plane Microwave Imaging. Applied Sciences. 2018; 8(11):2166. https://doi.org/10.3390/app8112166
Chicago/Turabian StyleLuan, Shenshen, Shuguo Xie, Tianheng Wang, Xuchun Hao, Meiling Yang, and Yuanyuan Li. 2018. "A Space-Variant Deblur Method for Focal-Plane Microwave Imaging" Applied Sciences 8, no. 11: 2166. https://doi.org/10.3390/app8112166
APA StyleLuan, S., Xie, S., Wang, T., Hao, X., Yang, M., & Li, Y. (2018). A Space-Variant Deblur Method for Focal-Plane Microwave Imaging. Applied Sciences, 8(11), 2166. https://doi.org/10.3390/app8112166




