Improving Convolutional Neural Networks’ Accuracy in Noisy Environments Using k-Nearest Neighbors

Abstract

We present a hybrid approach to improve the accuracy of Convolutional Neural Networks (CNN) without retraining the model. The proposed architecture replaces the softmax layer by a k-Nearest Neighbor (kNN) algorithm for inference. Although this is a common technique in transfer learning, we apply it to the same domain for which the network was trained. Previous works show that neural codes (neuron activations of the last hidden layers) can benefit from the inclusion of classifiers such as support vector machines or random forests. In this work, our proposed hybrid CNN + kNN architecture is evaluated using several image datasets, network topologies and label noise levels. The results show significant accuracy improvements in the inference stage with respect to the standard CNN with noisy labels, especially with relatively large datasets such as CIFAR100. We also verify that applying the ${\ell }_2$ norm on neural codes is statistically beneficial for this approach.

1. Introduction

Deep convolutional neural networks are multi-layer architectures designed to extract high-level representations of a given input. They have dramatically improved the state-of-the-art in image, video, speech and audio recognition tasks [1]. When trained for supervised classification, the CNN layers are eventually able to extract a set of features suitable for the task at hand. These features are obtained by forwarding a raw input through the network, in which the last layer merely learns a linear mapping to get the most likely class.

We present a simple and effective technique for accounting for label noise on deep neural networks. Large datasets suffer from this problem, as researchers often resort to non-expert sources such as Amazon’s Mechanical Turk or tags from social networking sites to label massive datasets, resulting in unreliable labels [2]. Large amounts of data (required for deep neural networks) typically contain some wrong labels, and the presence of this kind of noise can drastically degrade learning performance [3,4].

Learning with noisy labels has been studied previously, although not extensively, particularly on deep neural networks. In [5], a noise layer was added to simultaneously learn both the neural network parameters and the noise distribution. The work in [6] included a linear layer after the softmax to model the noise. Other approaches used bootstrapping [7], dropout regularization [2] or a modified loss function [8] to increase the CNN accuracy in the presence of noise.

Unlike the above-mentioned methods, the proposed approach is not performed in the training stage; therefore, it can be used for reliable prediction using existing models that were already trained with noisy labels.

The proposed method is based on a technique that has been extensively used in transfer learning. Due to their high generalization power, transfer learning can be used to apply CNN models trained on a domain to a different task where data are similar, but the classes are different [9]. This transfer can be done by fine-tuning the CNN weights of the pretrained network on the new dataset by continuing the backpropagation [10]. Alternatively, it can also be performed by using the CNN as a feature extractor to obtain mid-level representations, forwarding samples through the network to get the activations from one of the last hidden layers, which is usually a fully-connected or a pooling layer. These representations are also referred to as neural codes [11].

Extracting neural codes and then applying Support Vector Machines (SVM) or k-Nearest-Neighbors (kNN) is a common transfer learning technique [12]. Some previous works also used this strategy on the same domain where the network was trained, replacing the softmax layer by an SVM [13,14,15,16]. They proved that using neural codes extracted from a CNN to train an SVM improves the classification accuracy with respect to using the CNN softmax output directly. In addition, in a remarkable previous work, Reference [17] proposed deep neural decision forests replacing the softmax with differentiable Random Forests (RaF) and training this hybrid approach in a joint manner.

The proposed architecture consists of replacing the softmax by a kNN classifier on inference. To our knowledge, there are no previous works using this technique to address the same task for which the network was trained, although this is a common approach for transfer learning. At the inference stage, neural codes from the last hidden layer are extracted to perform a kNN search on the training set in order to yield the class.

The motivation for using kNN is that it is a non-linear method that may obtain more complex decision boundaries than the common linear mapping used in the softmax layer of a CNN. Taking into account that CNN and kNN are totally complementary in terms of feature extraction and decision boundaries, in a hybrid system, both algorithms could exploit their potential and see their drawbacks mitigated by the other. In addition, CNN are usually trained with large datasets, and as the size of the training set approaches infinity, the NN classifier shows strong guarantees with respect to the Bayes error rate [18], the minimum achievable error rate given the distribution of the data.

Moreover, an interesting feature of kNN is its robustness to label noise in the training set by means of high values of the parameter k. We have performed the evaluation with different levels of induced noise to assess the robustness of the proposed method. Using different image datasets and network topologies, we show that the accuracy combining CNN and kNN outperforms consistently that of the softmax layer with noisy labels.

The rest of the paper is structured as follows: the proposed hybrid method, the datasets and the network topologies considered are described in Section 2; the evaluation is done in Section 3 using different label noise levels and performing statistical significance tests; finally, conclusions and future work are described in Section 4.

2. Materials and Methods

The presented work has an eminently experimental nature. Our hypothesis is that a hybrid CNN + kNN can outperform the predictive power of the widely-considered CNN + softmax in noisy environments. To assess this, we compare the results of a CNN trained for a classification task with the learned neural codes of the same CNN, but applying a kNN classifier to the last hidden layer output.

In addition, we consider the ${\ell }_2$ norm for the normalization of the neural codes [13,19]. Let x be a vector of size n, which represents the neural codes; the ${\ell }_2$ norm is defined as:

$$\left|x\right|=\sqrt{\sum _{k=1}^n{\left|x_k\right|}^2}$$

After training a CNN with standard backpropagation, four configurations are evaluated in the inference stage (see Figure 1):

• Use of the CNN softmax layer.
• Use of the last hidden CNN layer (before the softmax) to get the neural codes, which are fed to a kNN that compares them to the training set prototypes using Euclidean distance in order to get the most likely class.
• Similar to the previous configuration, but normalizing with ${\ell }_2$ the neural codes before the kNN.
• Using directly the kNN on the raw data without any representation learning.

The presented configurations are evaluated with different datasets selected to depict different numbers of features and samples. Specifically, our evaluation comprises the following seven datasets of images (summarized in

Table 1. Description of the image datasets used in the experimentation. HOMUS, Handwritten Online Musical Symbol.

Name	Instances	Classes	Shape
USPS	9298	10	$1\times 16\times 16$
MNIST	70,000	10	$1\times 28\times 28$
Landsat	6435	6	$4\times 3\times 3$
HOMUS	15,200	32	$1\times 40\times 40$
NIST	44,951	26	$1\times 32\times 32$
CIFAR10	60,000	10	$3\times 32\times 32$
CIFAR100	60,000	100	$3\times 32\times 32$

):

• United States Postal Office (USPS) [20] and MNIST [21] are datasets of handwritten digits with binary images.
• Landsat is a dataset from the UCI repository [22]. It comprises $3\times 3$ windows in the four spectral bands depicting images of satellites. Each window is labeled as regards the information of the central pixel of the window.
• Handwritten Online Musical Symbol (HOMUS) [23] depicts binary images of isolated handwritten music symbols collected from 100 different musicians.
• NIST Special Database 19 (NIST) of the National Institute of Standards and Technology [24] consists of a huge dataset of isolated characters. For this work, a subset of the upper case characters was selected.
• CIFAR-10 and CIFAR-100 [25] are standard object recognition datasets for the computer vision community. They consist of $32\times 32$ color images extracted from the 80 million tiny images dataset [26] and containing 10 and 100 different categories, respectively.

As regards preprocessing of the input data, the values of the pixels from MNIST, HOMUS and NIST images are divided by 255 for normalization, whereas the mean image is subtracted from CIFAR images. The USPS and Landsat datasets are already normalized in origin.

Furthermore,

Table 2. CNN architectures evaluated with each image dataset. Conv($f\times w\times h$) stands for a layer with f convolution operators with $w\times h$ kernel; MaxPool($w\times h$) stands for the max-pooling operator with $w\times h$ kernel; UpSamp($w\times h$) stands for an up-sampling operator with $w\times h$ kernel; Drop(d) refers to dropout with ratio d; and FC(n) mean a fully-connected layer with n neurons.

Dataset	Layer 1	Layer 2	Layer 3	Layer 4	Layer 5	Layer 6	Layer 7
USPS	Conv ($32\times 3\times 3$)	Conv ($32\times 3\times 3$) MaxPool ($2\times 2$) Drop (0.25)	FC (128) Drop (0.5)
MNIST	Conv ($32\times 3\times 3$)	Conv ($32\times 3\times 3$) MaxPool ($2\times 2$) Drop (0.25)	FC (128) Drop (0.5)
Landsat	Conv ($64\times 1\times 1$) UpSamp ($2\times 2$) Drop (0.3)	Conv ($64\times 2\times 2$) UpSamp ($2\times 2$) Drop (0.3)	Conv ($64\times 2\times 2$) MaxPool ($2\times 2$) UpSamp ($2\times 2$) Drop (0.3)	FC (256) Drop (0.3)	FC (128) Drop (0.3)
HOMUS	Conv ($256\times 3\times 3$) MaxPool ($2\times 2$) Drop (0.2)	Conv ($128\times 3\times 3$) MaxPool ($2\times 2$) Drop (0.2)	Conv ($128\times 3\times 3$) Drop (0.2)	Conv ($64\times 3\times 3$) Drop (0.2)	FC (512) Drop (0.1)	FC (256) Drop (0.1)	FC (128) Drop (0.1)
NIST	Conv ($256\times 3\times 3$) MaxPool ($2\times 2$) Drop (0.2)	Conv ($128\times 3\times 3$) MaxPool ($2\times 2$) Drop (0.2)	Conv ($128\times 3\times 3$) Drop (0.2)	Conv ($64\times 3\times 3$) Drop (0.2)	FC (512) Drop (0.1)	FC (256) Drop (0.1)	FC (128) Drop (0.1)
CIFAR10	VGG16 [27]
CIFAR100	ResNet50 [28] scaling input images to $224\times 224$

shows the evaluated network topologies for each dataset. The selected CNN architectures are designed to obtain close to state-of-the-art results on the target task. Custom models have been designed for USPS, MNIST, Landsat, HOMUS and NIST, whereas the CIFAR datasets were trained using the well-known VGG16 [27] and the 50-layered ResNet [28] models.

The CNN training is carried out by means of stochastic gradient descent [29] considering the adaptive learning rate method proposed by Zeiler [30]. A 128 mini-batch size is used, and the networks have been trained with a maximum of 200 epochs, with early stopping if the loss does not decrease during 10 epochs.

A five-fold cross-validation scheme is followed to provide more robust figures with respect to the variance of the training data. That is, each dataset is divided into 5 equal parts. In each iteration, 4 of these folds are used as the training set (80%) and the remaining one as the test set (20%). After performing the experiments, average results are provided. In addition, these folds have been organized preserving the original distribution of the number of samples per class in the dataset.

Since some of these datasets are not evenly balanced, the performance metric used for evaluation is the weighted average of the $F_1$ scores of each class. The $F_1$ is defined as:

$$F_1=\frac{2·\mathrm{TP}}{2·\mathrm{TP}+\mathrm{FN}+\mathrm{FP}}$$

where TP denotes the number of True Positives, FP denotes the number of False Positives and FN denotes the number of False Negatives.

3. Experiments

The four configurations (kNN, CNN + softmax, CNN + kNN and CNN + ${\ell }_2$ + kNN) have been evaluated with and without adding synthetic noise to the data by swapping the labels of pairs of randomly-chosen prototypes. The percentages of prototypes that change their label are 10%, 20%, 30% and 40% since these are the common values in this kind of experimentation [31]. It is important to remark that each CNN has been trained separately for each noise level, from 0% to 40%. Then, the weights obtained at each noise level were used as a basis for evaluating the different CNN configurations at that noise level.

Different numbers of neighbors k (from 1 to 50) have also been tested for the kNN algorithm. Additionally, in the hybrid approach, the neural codes of the last hidden layer have been ${\ell }_2$-normalized to compare their performance with the unnormalized values.

Table 3. $F_1$ (%) accuracy for each image dataset, classification method and label noise level considered. In the kNN methods, the best value of k is shown between parentheses (unless in the average row).

Dataset	Method	Noise (%)
		0	10	20	30	40
USPS	kNN	97.11 (1)	96.48 (5)	95.75 (9)	95.33 (15)	94.54 (15)
	CNN + softmax	98.71	98.00	96.71	96.22	93.53
	CNN + kNN	98.60 (5)	97.83 (9)	96.26 (11)	93.50 (11)	88.22 (20)
	CNN + ${\ell }_2$ + kNN	98.53 (3)	98.01 (7)	97.40 (11)	96.40 (25)	94.49 (40)
MNIST	kNN	97.22 (1)	96.83 (7)	96.59 (9)	96.24 (15)	95.81 (20)
	CNN + softmax	99.00	98.66	97.95	97.70	95.25
	CNN + kNN	99.21 (5)	98.73 (15)	98.34 (20)	96.88 (40)	92.24 (50)
	CNN + ${\ell }_2$ + kNN	99.29 (3)	98.78 (11)	98.50 (11)	97.62 (30)	95.63 (50)
Landsat	kNN	89.16 (3)	88.42 (7)	87.85 (9)	86.97 (20)	85.46 (20)
	CNN + softmax	93.00	91.04	88.08	83.57	78.35
	CNN + kNN	90.95 (7)	89.19 (11)	87.63 (20)	85.10 (30)	81.02 (50)
	CNN + ${\ell }_2$ + kNN	91.23 (1)	89.43 (15)	87.77 (25)	85.11 (40)	81.33 (50)
HOMUS	kNN	66.52 (1)	61.17 (7)	59.56 (7)	58.12 (9)	56.1 (15)
	CNN + softmax	94.00	89.18	82.57	74.90	69.28
	CNN + kNN	94.63 (3)	90.20 (9)	83.99 (7)	78.67 (9)	71.07 (9)
	CNN + ${\ell }_2$ + kNN	94.66 (1)	91.28 (7)	86.88 (15)	83.01 (25)	77.20 (15)
NIST	kNN	79.67 (5)	78.66 (5)	77.58 (7)	76.53 (9)	75.01 (15)
	CNN + softmax	98.00	95.75	93.64	90.72	88.5
	CNN + kNN	98.00 (1)	95.75 (50)	93.52 (50)	90.96 (50)	87.22 (50)
	CNN + ${\ell }_2$ + kNN	98.03 (1)	96.22 (40)	94.64 (50)	92.77 (50)	90.35 (50)
CIFAR10	kNN	34.28 (1)	31.7 (9)	30.87 (9)	29.95 (15)	29 (30)
	CNN + softmax	86.50	81.66	75.49	69.22	61.00
	CNN + kNN	86.70 (5)	81.30 (5)	75.77 (20)	69.07 (30)	61.69 (15)
	CNN + ${\ell }_2$ + kNN	86.79 (7)	81.26 (7)	75.78 (5)	69.04 (20)	61.54 (7)
CIFAR100	kNN	17.11 (1)	15.41 (1)	13.76 (1)	12.62 (11)	12.11 (20)
	CNN + softmax	62.60	46.80	31.80	22.20	14.20
	CNN + kNN	63.93 (25)	48.30 (50)	35.21 (50)	24.28 (50)	15.56 (50)
	CNN + ${\ell }_2$ + kNN	64.23 (11)	48.85 (20)	35.46 (40)	25.27 (50)	16.51 (50)
Average	kNN	68.62	66.63	65.83	64.88	63.83
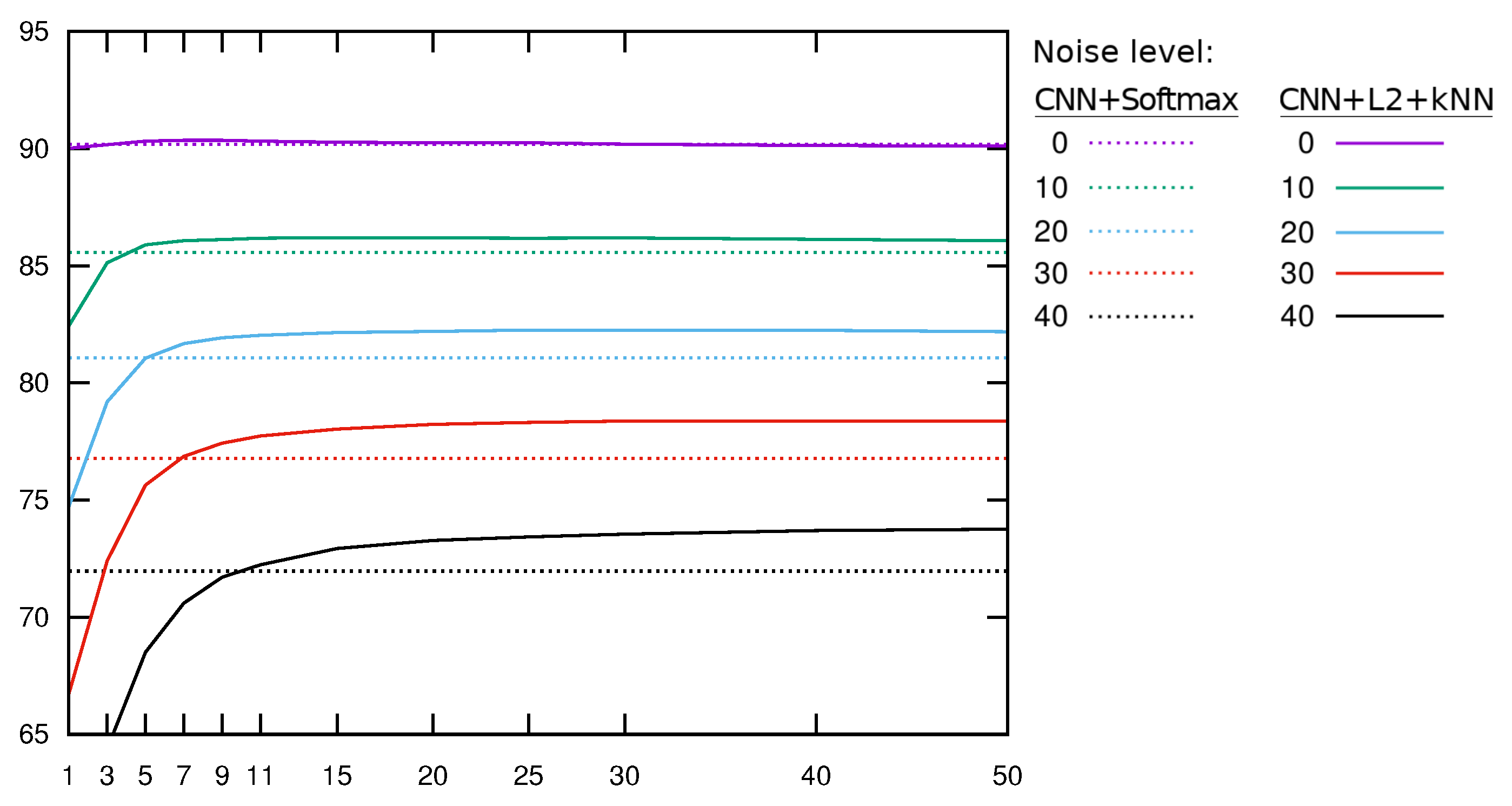
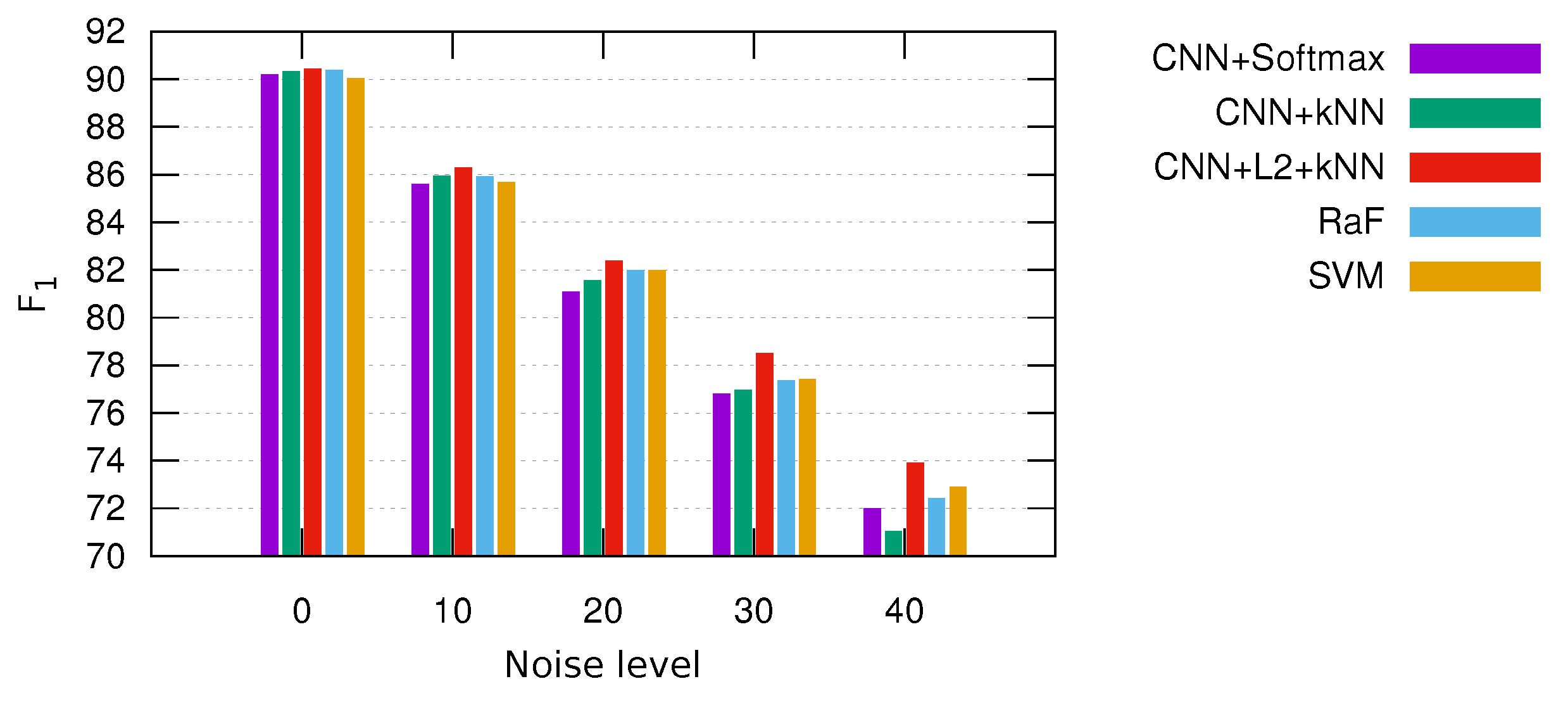
	CNN + softmax	90.17	85.56	81.06	76.77	71.97
	CNN + kNN	90.20	85.70	81.16	76.39	70.37
	CNN + ${\ell }_2$ + kNN	90.35	86.20	82.25	78.37	73.76

reports the detailed results with the image datasets evaluated. In addition, Figure 2 illustrates the accuracy curves as the level of induced label noise is increased. In an overall sense, using kNN over the raw input data obtains a lower average accuracy than the CNN-based methods, especially with the most challenging datasets. Analogously, accuracy is strongly affected by the level of induced label noise in the dataset. All figures depict a noticeable accuracy drop as this level is increased.

For simple datasets such as USPS, MNIST or Landsat (those in which kNN achieves good results), we observe that CNN-based approaches worsen their performance in a much more pronounced way than kNN as the level of noise label is increased. In fact, for high noise levels, the kNN eventually outperforms these approaches. In the remaining datasets (NIST, HOMUS, CIFAR10, CIFAR100), the kNN is far away from the results obtained with the CNN approaches. In the case of NIST, it turns out that CNN + softmax is less accurate in the original scenario, but shows a greater noise robustness even with the lowest noise levels considered. Hybrid approaches, however, depict a more pronounced degradation curve. Furthermore, results reported in the rest of the datasets reflect a similar behavior: hybrid approaches achieve better results than the CNN + softmax, which also degrades generally faster as the noise is increased. Although differences are not especially remarkable with and without the ${\ell }_2$ norm, it can be seen that the former is less sensitive to noise.

An interesting remark is that higher values of k are needed in the hybrid approach, even without the presence of induced noise. This might indicate that neural codes are somehow noisy in the closest neighborhood (when k is low), although this condition can be mitigated considering more neighbors during classification. This means that the proposed technique can benefit from large amounts of annotated data. In this sense, we observe that the ${\ell }_2$ usually needs a lower value of the parameter k, which indicates that this normalization leads to a higher robustness of the neural codes.

Figure 3 shows the impact on the average $F_1$ when using different values of k. As can be seen, the inclusion of kNN is more beneficial when the noise is higher. In addition, the value of k for outperforming the softmax depends on the amount of noise. The higher the noise, the higher k should be, but in all cases, this is a relatively small value (lower than 15). Therefore, the value of k is not so decisive to improve the results of the base CNN + softmax as long as it has been increased enough to surpass the elbow of the curve.

As a general conclusion, the proposed approach consistently outperforms the CNN + softmax even with low noise levels. The accuracy improvement is especially remarkable with challenging datasets such as CIFAR. In addition, it is observed that adding the ${\ell }_2$ norm consistently improves the accuracy with respect to using the raw neural codes, both with or without noise.

On the other hand, no unequivocal conclusions can be drawn with very high levels of noise, as in some cases, the hybrid approach outperforms the CNN (such as in CIFAR100), whereas in others (such as CIFAR10), that is not the case. However, there is a trend towards greater robustness to noise from the classical scheme (CNN + softmax) than from the hybrid schemes, contrary to what could be expected because of the use of kNN. A possible explanation is that training a network with noisy labels forces it to map the features onto an incorrect position of the neural space, making kNN misclassify them. That is, label noise might generate noise at the feature level, which prevents a correct kNN classification. The softmax, however, seems to palliate this phenomenon better because a lower degradation is observed as the induced noise is increased.

The addition of a kNN stage slightly increases the computational cost, but given the success of recent fast kNN methods [32,33,34], it might be more efficient than increasing the number of parameters of the CNN in order to achieve similar results as those obtained with a simpler CNN plus a kNN classifier. For instance, using the approach proposed in [34], a query on a dataset of five million prototypes with a 128-dimensional feature vector (the size of the Neural Code (NC) considered in this work) takes around 0.1 ms.

3.1. Statistical Significance Tests

The previous section has presented the evaluation results, which serve to analyze the general trend of our proposal. However, in this section, statistical tests are performed for comparing the results objectively [35]. Specifically, Wilcoxon signed-rank tests are used, which allow a pairwise comparison of the methods.

We did 4 tests, corresponding to the comparison between CNN + softmax and kNN, between CNN + kNN and CNN + softmax, between CNN + ${\ell }_2$ + kNN and CNN + softmax and between CNN + ${\ell }_2$ + kNN and CNN + kNN. The first one is done to verify that, even in the cases with greater noise, the selected CNN are good predictors. The second and third tests are those that verify the goodness of the proposal of this work: the use of a kNN algorithm instead of the softmax of the network. Finally, the last test is focused on measuring the statistical improvement when using ${\ell }_2$ normalization.

Table 4. Results obtained for the statistical significance tests with respect to the synthetic noise induced in the data. The symbol ✓ states the test is significantly accepted, whereas ✗ states that the test is accepted in the other way. No symbol is depicted otherwise. Significance has been set to $p<0.05$.

Noise	Test
	CNN + softmax > kNN	CNN + kNN > CNN + softmax	CNN + ${\mathit{\ell }}_2$ + kNN > CNN + softmax	CNN + ${\mathit{\ell }}_2$ + kNN > CNN + kNN
0	✓			✓
10	✓		✓	✓
20	✓	✗	✓	✓
30	✓	✗	✓	✓
40	✓	✗	✓	✓

reports the results of such tests, with significance established at a p-value $<0.05$. The symbol ✓ states that the test is significantly accepted, whereas ✗ states that the test is accepted in the other way. No symbol is depicted otherwise.

These tests reflect that CNN + softmax significantly outperforms kNN for all noise levels, as may be expected. Furthermore, the statistical test only recommends using CNN + softmax instead of the hybrid model without normalization in one case (label noise level of 40%), yet it never does when normalization is considered. Consequently, adding ${\ell }_2$ is always statistically beneficial with respect to the original neural codes.

3.2. Comparison with Other Classifiers

One must also address the question of whether the improvement in the results is due to either the good robustness of the kNN against noise or the replacement of the softmax layer by another supervised classifier. That is why in this section, we analyze the general results of replacing the softmax with other schemes. In particular, we consider the following representative algorithms for supervised classification:

• Support Vector Machine (SVM) [36]: This learns a hyperplane that tries to maximize the distance to the nearest samples (support vectors) of each class. It makes use of kernel functions to handle non-linear decision boundaries. In our case, a radial basis function (or Gaussian) kernel is considered. Typically, SVM also considers a parameter that measures the cost of learning a non-optimal hyperplane, which is usually referred to as parameter c. During preliminary experiments, we tuned this parameter in the range $c\in [1,9]$.
• Random Forest (RaF) [37]: This builds an ensemble classifier by generating several random decision trees at the training stage. The final output is taken by combining the individual decisions of each tree. The number of random trees has been established experimenting in the range $t\in [10,500]$.

For the sake of clarity, we directly provide in Figure 4 the average $F_1$ of these classifiers over all datasets, in comparison to the CNN + softmax, CNN + kNN and CNN + ${\ell }_2$ + kNN schemes. It can be observed that the approach proposed in this work (CNN + ${\ell }_2$ + kNN) attains the best results in all cases, increasing its margin over other schemes as the noise level is higher. Note also that, on average, SVM and RaF also outperform both CNN + softmax and CNN + kNN in the presence of noise, yet they remain noticeably below CNN + ${\ell }_2$ + kNN in terms of accuracy.

4. Conclusions and Future Work

In this work, we have proposed a hybrid method that replaces the softmax layer by a kNN classifier in the inference stage without modifying the training stage. Different datasets, network topologies and noise levels have been evaluated, performing statistical tests to get rigorous conclusions.

We show that replacing softmax by kNN significantly outperforms traditional CNN architectures with noisy labels. The optimal number of neighbors is higher in larger datasets; therefore, the proposed method can benefit from large amounts of annotated data. In these large datasets, the performance gain is remarkable, as can be seen in the CIFAR experiments.

It has been statistically verified that a non-linear classifier such as kNN used on the CNN representations significantly increases the accuracy with low noise levels. However, with high label noise levels, softmax and kNN get similar average results. This is because training with label noise forces the CNN to learn an incorrect transformation of data, which generates noise at the feature level. Although the softmax layer may learn to correct this problem, the noisy features confuse the kNN classifier. It has also been statistically verified that adding ${\ell }_2$ normalization is beneficial at any noise level.

An advantage of using kNN is that, besides the class, the most similar prototypes are also obtained, making it suitable for similarity search tasks. In addition, we observed that replacing the softmax layer by other classifiers such as SVM or RaF is also beneficial in terms of accuracy, yet to a lesser extent than considering kNN. On the other hand, computational cost is higher with kNN, but given the efficiency of the recent approximate methods, this may not be a severe issue.

As future work, the reported results could be improved by using networks that aim to maximize the kNN accuracy by jointly training the CNN with kNN in order to optimize the classification error on training data [38] or introducing metric learning techniques. Furthermore, it would be interesting to compare kNN with other classifiers such as SVM or RaF using neural codes.