Form-Finding Analysis of the Rail Cable Shifting System of Long-Span Suspension Bridges
Abstract
1. Introduction
2. Mechanical Characteristics of the RCS System under the Non-Loading Condition
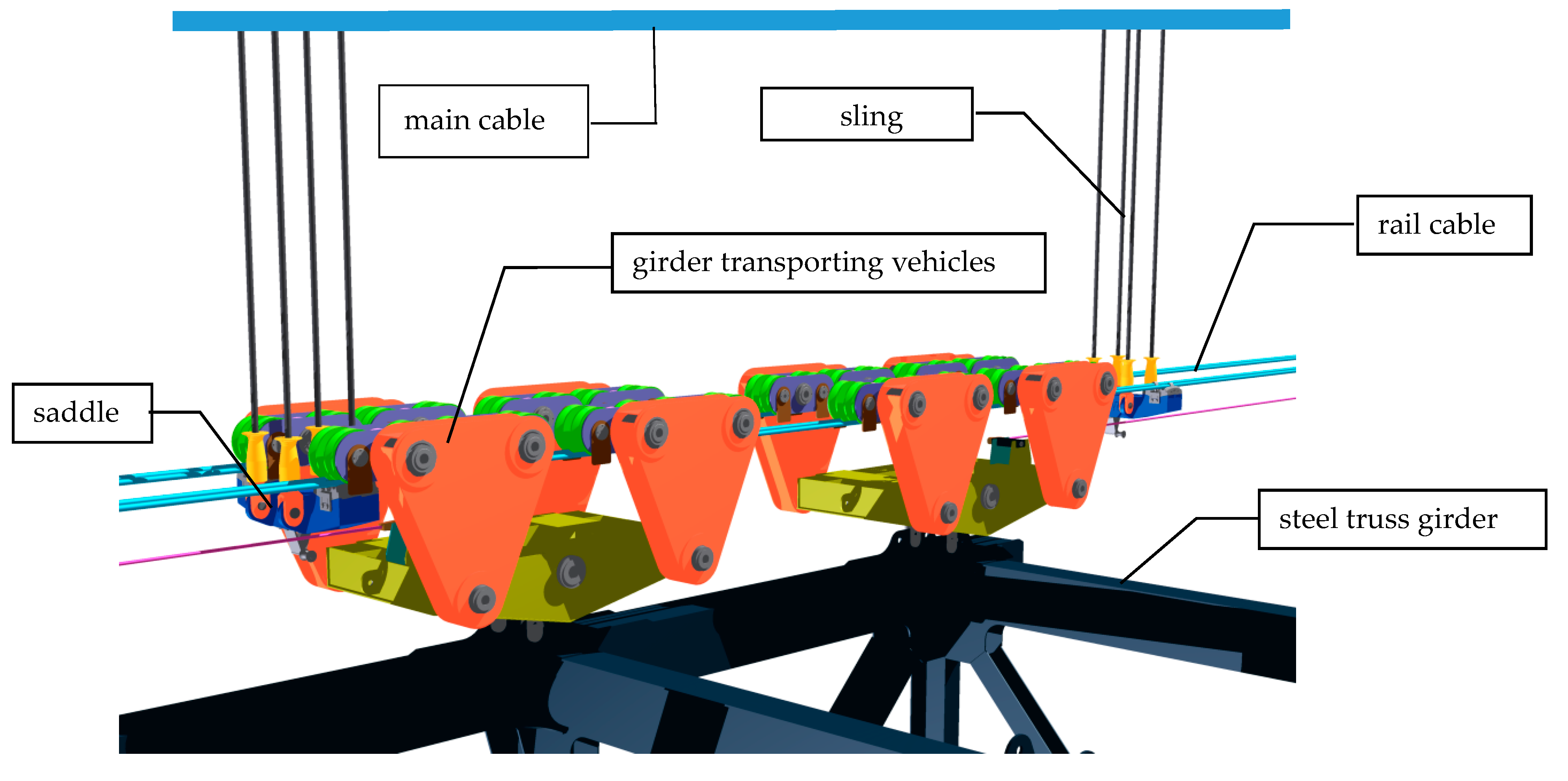
2.1. Brief Introduction to RCS Technology
2.2. Mechanical Model of the RCS System under Non-Loading Condition
- (1)
- The flexible cable can only be tensed but not be pressed or bent.
- (2)
- The stress-strain of the flexible cable is consistent with Hooke’s theorem.
- (3)
- The cross-sectional area before deformation is used for the calculation of the tensile stiffness of the main cable, rail cable, and sling before and after stress.
- (4)
- The friction between the rail cable and the saddle is ignored, and the sling does not tilt after the rail cable tension is completed.
2.2.1. Force Analysis of the Main Cable
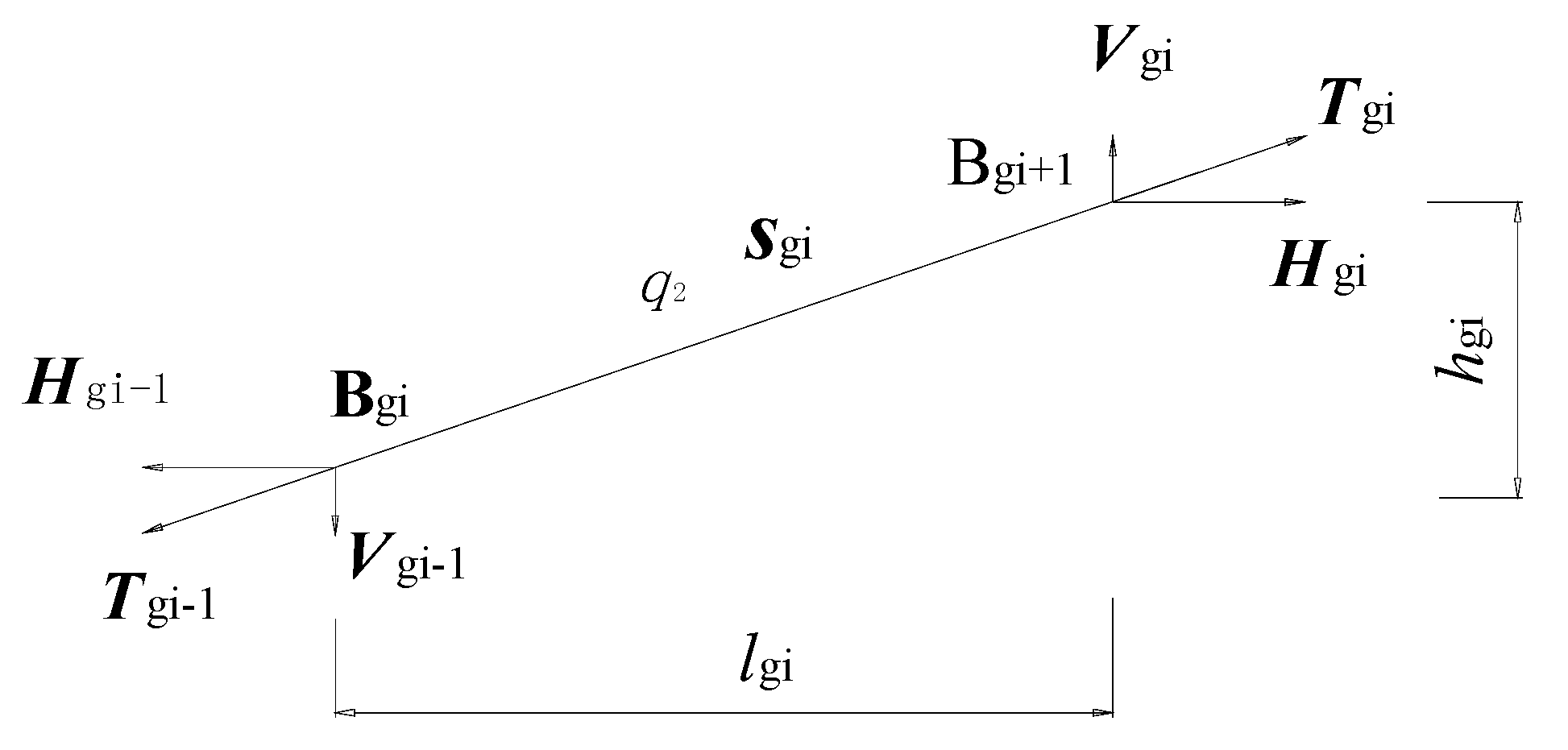
2.2.2. Force Analysis of the Rail Cable
2.2.3. Force Analysis of the Sling
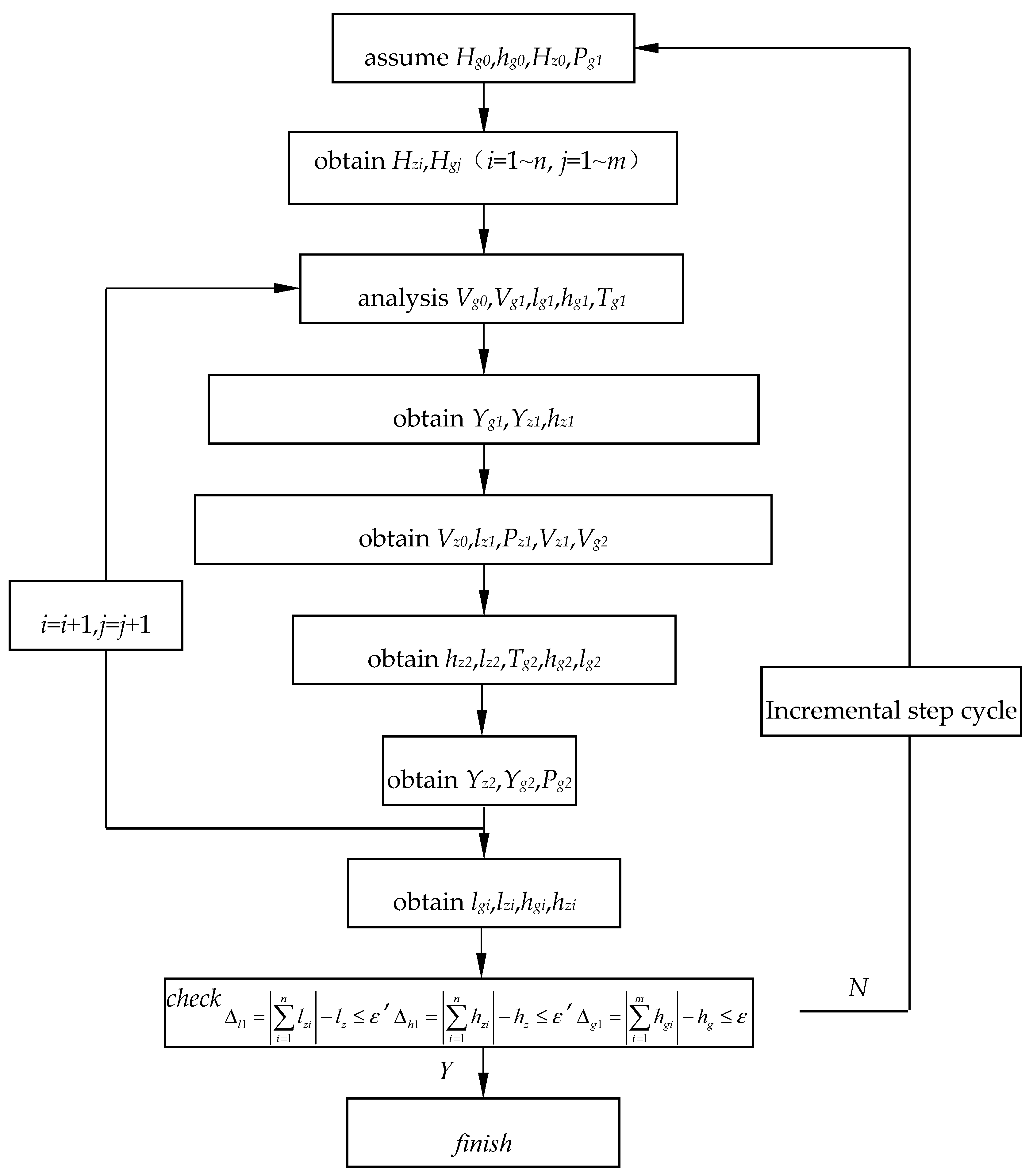
2.3. Solution Analysis of the System
- (1)
- Assume the horizontal force Hg0 and the elevation hg0 at the left support of the rail cable; the horizontal force Hz0 at the left support of the main cable, and the increment of the cable force of the sling Pg1;
- (2)
- Obtain Hgi, Hzi from Equations (4) and (11);
- (3)
- Substitute them into Equations (10), (13), (7), (8), and (9); then Vg0, Vg1, lg1, hg1, and Tg1 are obtained;
- (4)
- From the coordination relation of deformation, Yg1, Yz1 and hz1 are obtained by combing with Equations (15), (17), and (4), respectively;
- (5)
- Substitute Yg1, Yz1 and hz1 into Equations (1) and (2); Vz0 and lz1 can then be obtained;
- (6)
- Substitute Vz0 and lz1 into Equations (16), (6), and (13), Pz1; Vz1 and Vg2 can then be obtained;
- (7)
- Substitute Pz1; Vz1 and Vg2 the results of step 6 into Equations (2), (1), (10), (7), and (8); hz2, lz2, Tg2, lg2, and hg2 can be acquired, respectively;
- (8)
- Substitute them into Equations (4), (15), and (17); Yz2, Yg2, and Pg2 are then obtained;
- (9)
- Following the similar iterative manner, all values of lgi, lzi, hgi and hzi are obtained;
- (10)
- Check convergence conditions Δz1 = ( = 1.0 × 10−6 is the given error limit), Δz2 = , Δg1 = , and Δg2 = . If they are satisfied, go to the next step. If not, let Hz0 = Hz0 + Δz1/DHz, Pg1 = Pg1 + Δz2/DPg, Hg0 = Hg0 + Δg1/DHg and hg0 = hg0 + Δg2/Dhg, and return to step 1, iteratively recalculating, where DHz, DPg, DHg, and Dhg are respectively the first derivatives of Hz0, Pg1, Hg0, and hg0 [38].
3. Global Model Test of the Moving Girder by Rail Cable
4. Testing Results of Model Test
5. Conclusions
- (1)
- The global mechanical analytical model for the main cable, slings, and rail cables of the RCS system under the non-loading condition is established through the theoretical derivation. The equilibrium equation established from the position after structural deformation can be used to perform the geometrical nonlinear analysis of the structural large deformation. The simplified calculation and analysis process of the RCS system achieve sufficient accuracy, which thus can be applied in engineering.
- (2)
- Under the condition that the initial geometric state of the RCS system is unknown, the true internal force and geometry of the rail cable can be iteratively computed by assuming the initial force or configuration of the rail cable.
- (3)
- The designed rail cable tensioning and testing device meets the requirements of the model test. The measured results of the main cable line shape and main cable force in the model test are in good agreement with the theoretical results.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Glossary
| A1 | cross-sectional area of the main cable |
| A2 | cross-sectional area of the rail cable |
| A3 | cross-sectional area of the sling |
| Azi | node locations of main cable segment |
| E1 | elastic modulus of the main cable |
| E2 | elastic modulus of the rail cable |
| E3 | elastic modulus of the sling |
| Hg0 | horizontal force pretension force of the rail cable at the left support |
| hg0 | elevation at the left support of the rail cable |
| hg1 | vertical height between left anchorage points of rail cable and node Ag2 |
| hi | height difference of cable tower |
| Hz0 | horizontal force at the left support of the main cable |
| hz1 | height difference between the top of left cable tower and node Az2 |
| hzi | vertical length of main cable segment |
| lg | longitudinal position of the two anchorage points |
| lg1 | horizontal length between left anchorage points of rail cable and node Ag2 |
| lz | cable tower distance |
| lzi | horizontal length of main cable segment |
| Pg1 | increment of the cable force of the sling |
| Pgi | sling force increment |
| Pzi | force of the sling at Azi node |
| q1 | self-weight per unit length of the main cable |
| q2 | self-weight per unit length of the rail cable |
| q3 | self-weight per unit length of the sling |
| Sdi | unstressed cable length of the sling |
| Sgi | cable length of the rail cable segment |
| Szi | segmental cable length after sling installed to unloaded cable |
| Tg0 | pretension force of the rail cable at the left support |
| Tg1 | vertical force at the left support of the rail cable |
| Vg0 | vertical force pretension force of the rail cable at the left support |
| Vg1 | vertical force between left anchorage points of rail cable and node Ag2 |
| W | constant weight of the saddle |
| Yg1 | vertical displacement between left anchorage points of rail cable and node Ag2 |
| Yz1 | vertical displacement between the top of left cable tower and node Az2 |
| Δg1 | convergence condition |
| Δg2 | convergence condition |
| Δz1 | convergence condition |
| Δz2 | convergence condition |
| ε | given error limit |
References
- Xu, Y.; Øiseth, O.; Moan, T. Time domain simulations of wind- and wave-induced load effects on a three-span suspension bridge with two floating pylons. Mar. Struct. 2018, 58, 434–452. [Google Scholar] [CrossRef]
- Miyata, T.; Okauchi, I.; Shiraishi, N.; Narita, N.; Narahira, T. Preliminary design considerations for wind effects on a very long-span suspension bridge. J. Wind Eng. Ind. Aerodyn. 1988, 29, 379–388. [Google Scholar] [CrossRef]
- Siringoringo, D.M.; Fujino, Y. Observed Along wind Vibration of a Suspension Bridge Tower and Girder. Procedia Eng. 2011, 14, 2358–2365. [Google Scholar] [CrossRef]
- Wang, H.; Li, Ai.; Li, J. Progressive finite element model calibration of a long-span suspension bridge based on ambient vibration and static measurements. Eng. Struct. 2010, 32, 2546–2556. [Google Scholar] [CrossRef]
- Øiseth, O.; Rönnquist, A.; Sigbjörnsson, R. Simplified prediction of wind-induced response and stability limit of slender long-span suspension bridges, based on modified quasi-steady theory: A case study. J. Wind Eng. Ind. Aerodyn. 2010, 98, 730–741. [Google Scholar] [CrossRef]
- Erdoğan, H.; Gülal, E. The application of time series analysis to describe the dynamic movements of suspension bridges. Nonlinear Anal. Real World Appl. 2009, 10, 910–927. [Google Scholar] [CrossRef]
- Miyata, T.; Matsumoto, H.; Yasuda, M. Circumstances of wind-resistant design examinations for very long suspension bridge. J. Wind Eng. Ind. Aerodyn. 1992, 42, 1371–1382. [Google Scholar] [CrossRef]
- Fukumoto, Y. Steel bridge construction in Japan. J. Constr. Steel Res. 1989, 13, 259–267. [Google Scholar] [CrossRef]
- Kim, H.; Lee, M.; Chang, S. Determination of hanger installation procedure for a self-anchored suspension bridge. Eng. Struct. 2006, 28, 959–976. [Google Scholar] [CrossRef]
- Li, S.; An, Y.; Wang, C.; Wang, D. Experimental and numerical studies on galloping of the flat-topped main cables for the long span suspension bridge during construction. J. Wind Eng. Ind. Aerodyn. 2017, 163, 24–32. [Google Scholar] [CrossRef]
- Ko, J.M.; Xue, S.D.; Xu, Y.L. Modal analysis of suspension bridge deck units in erection stage. Eng. Struct. 1998, 20, 1102–1112. [Google Scholar] [CrossRef]
- Adanur, S.; Günaydin, M.; Altunişik, A.C.; Sevim, B. Construction stage analysis of Humber Suspension Bridge. Appl. Math. Model. 2012, 36, 5492–5505. [Google Scholar] [CrossRef]
- Diana, G.; Yamasaki, Y.; Larsen, A.; Rocchi, D.; Portentoso, M. Construction stages of the long span suspension Izmit Bay Bridge: Wind tunnel test assessment. J. Wind Eng. Ind. Aerodyn. 2013, 123, 300–310. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, L.; Ding, Q.; Ge, Y. Flutter performance and improvement for a suspension bridge with central-slotted box girder during erection. J. Wind Eng. Ind. Aerodyn. 2018, 179, 118–124. [Google Scholar] [CrossRef]
- Cho, T.; Kim, T.S. Probabilistic risk assessment for the construction phases of a bridge construction based on finite element analysis. Finite Elem. Anal Des. 2008, 44, 383–400. [Google Scholar] [CrossRef]
- Liu, G.; Peng, Y.; Zhou, P.; Tong, Y. Research on Erection Methods of Steel Stiffening Truss Girder for Baling River Bridge. J. Highw. Transp. Res. Dev. 2010, 4, 50–56. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, Y.; Yu, M.; Hu, H.; Hu, J. Study of the rock foundation stability of the Aizhai suspension bridge over a deep canyon area in China. Eng. Geol. 2015, 198, 65–77. [Google Scholar] [CrossRef]
- Tang, H.; Li, Y.; Wang, Y.; Tao, Q. Aerodynamic optimization for flutter performance of steel truss stiffening girder at large angles of attack. J. Wind Eng. Ind. Aerodyn. 2017, 168, 260–270. [Google Scholar] [CrossRef]
- Huang, G.; Cheng, X.; Peng, L.; Li, M. Aerodynamic shape of transition curve for truncated mountainous terrain model in wind field simulation. J. Wind Eng. Ind. Aerodyn. 2018, 178, 80–90. [Google Scholar] [CrossRef]
- Fang, Z.; Zhang, K.; Tu, B. Experimental investigation of a bond-type anchorage system for multiple FRP tendons. Eng. Struct. 2013, 57, 364–373. [Google Scholar] [CrossRef]
- Yu, S.; Ou, J. Structural health monitoring and model updating of Aizhai suspension bridge. J. Aerosp. Eng. 2016, 30, B4016009. [Google Scholar] [CrossRef]
- Jianhua, H.; Ruili, S. Technical innovations of the Aizhai Bridge in China. J. Bridge Eng. 2014, 19, 04014028. [Google Scholar] [CrossRef]
- Han, Y.; Li, K.; He, X.; Chen, S.; Xue, F. Stress analysis of a long-span steel-truss suspension bridge under combined action of random traffic and wind loads. J. Aerosp. Eng. 2018, 31, 04018021. [Google Scholar] [CrossRef]
- Shen, R.; Yan, Y.; Tang, M.; Zhang, N. Design and Installation of Full-Scale Sectional Model for Testing of Rail Cable Launching Method. Bridge Constr. 2013, 1, 005. (In Chinese) [Google Scholar]
- Huang, J.Z.; Li, D.S.; Li, H.N.; Song, G.B.; Liang, Y. Damage identification of a large cable-stayed bridge with novel cointegrated Kalman filter method under changing environments. Struct. Control Health Monit. 2018, 25, e2152. [Google Scholar] [CrossRef]
- Zhou, P.; Liu, M.; Li, H.; Song, G. Experimental investigations on seismic control of cable-stayed bridges using shape memory alloy self-centering dampers. Struct. Control Health Monit. 2018, 25, e2180. [Google Scholar] [CrossRef]
- Liu, M.; Song, G.; Li, H. Non-model based semi-active vibration suppression of stay cables using Magneto-Rheological (MR) fluid damper. Smart Mater. Struct. 2007, 16, 1447–1452. [Google Scholar] [CrossRef]
- Liu, M.; Sethi, V.; Song, G.; Li, H. Investigation of locking force for stay cable vibration control using magnetorheological fluid damper. J. Vib. Acoust. 2008, 130, 054504. [Google Scholar] [CrossRef]
- Xu, Y.L.; Ko, J.M.; Yu, Z. Modal analysis of tower-cable system of Tsing Ma long suspension bridge. Eng. Struct. 1997, 19, 857–867. [Google Scholar] [CrossRef]
- An, X.; Gosling, P.D.; Zhou, X. Analytical structural reliability analysis of a suspended cable. Struct. Saf. 2016, 58, 20–30. [Google Scholar] [CrossRef]
- Huang, M.-H.; Thambiratnam, D.P.; Perera, N.J. Vibration characteristics of shallow suspension bridge with pre-tensioned cables. Eng. Struct. 2005, 27, 1220–1233. [Google Scholar] [CrossRef]
- Sun, Y.; Zhu, Ho.; Xu, D. A specific rod model based efficient analysis and design of hanger installation for self-anchored suspension bridges with 3D curved cables. Eng. Struct. 2016, 110, 184–208. [Google Scholar] [CrossRef]
- Huang, Y.H.; Fu, J.Y.; Gan, Q.; Wang, R.-H.; Pi, Y.-L.; Liu, A.-R. New method for identifying internal forces of hangers based on form-finding theory of suspension cable. J. Bridge Eng. 2017, 22, 04017096. [Google Scholar] [CrossRef]
- Ma, Q.; Ohsaki, M.; Chen, Z.; Yan, X. Step-by-step unbalanced force iteration method for cable-strut structure with irregular shape. Eng. Struct. 2018, 177, 331–344. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Mokhtari, M.; Amir, R.M. A novel cable element for nonlinear thermo-elastic analysis. Eng. Struct. 2018, 167, 431–444. [Google Scholar] [CrossRef]
- Thai, S.; Kim, Na.; Lee, J.; Kang, J. Optimum design of cable nets by using genetic algorithm. Int. J. Steel Struct. 2017, 17, 1183–1198. [Google Scholar] [CrossRef]
- Li, F.; Wu, P. Dynamic behaviors of pretensioned cable AERORail structure. J. Cent. South Univ. 2015, 22, 2267–2276. [Google Scholar] [CrossRef]
- Lixin, B.A.O. Analysis of Aerobus Transportation System Static and Dynamic Behavior; Southwest Jiaotong University: Chengdu, China, 2007; pp. 21–46. (In Chinese) [Google Scholar]
- Jian, F. The Research on Scale Model Design of Aizhai Suspension Bridge; Changsha University of Science and Technology: Changsha, China, 2010; pp. 23–45. (In Chinese) [Google Scholar]
- Bedon, C.; Dilena, M.; Morassi, A. Ambient vibration testing and structural identification of a cable-stayed bridge. Meccanica 2016, 51, 2777–2796. [Google Scholar] [CrossRef]

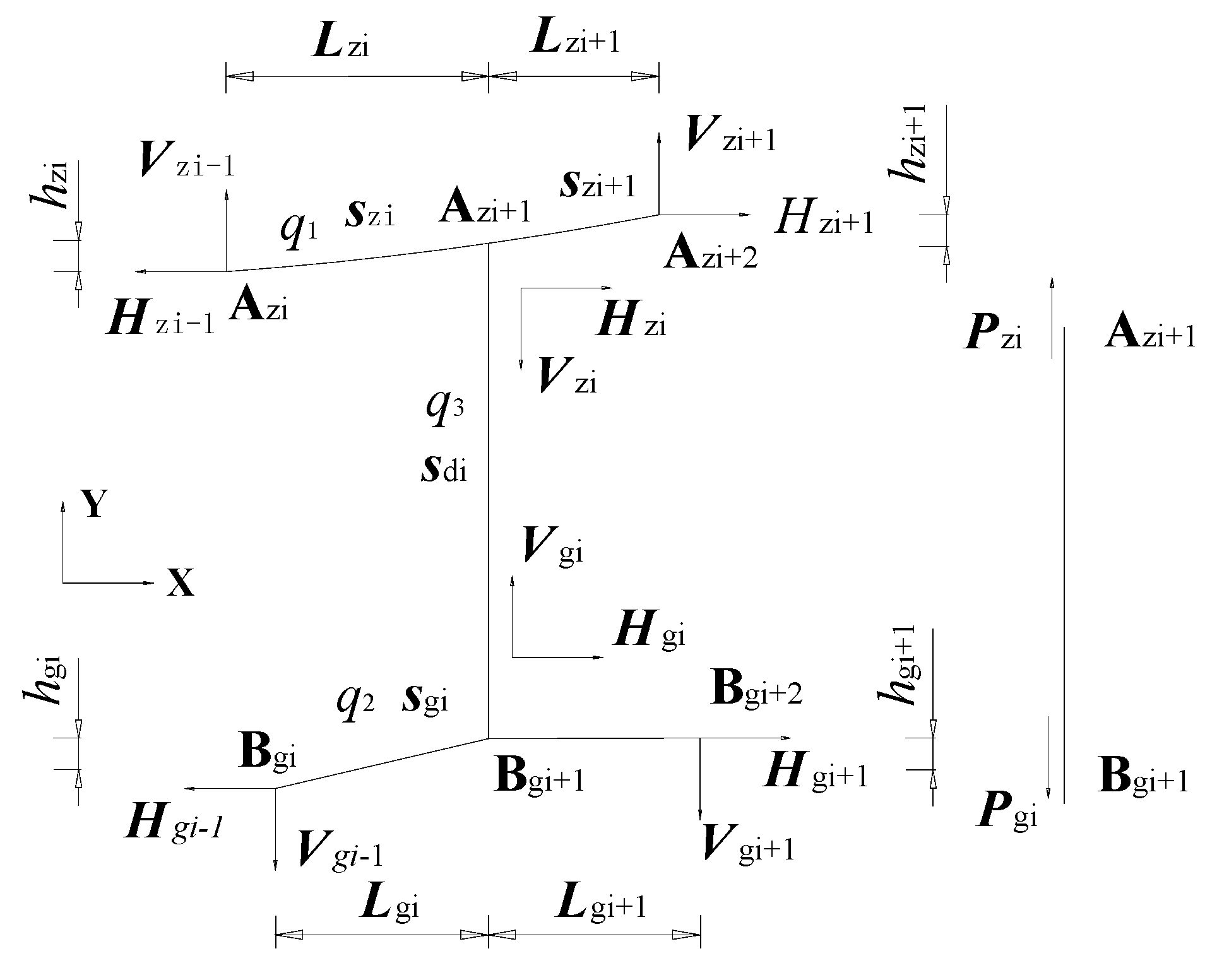

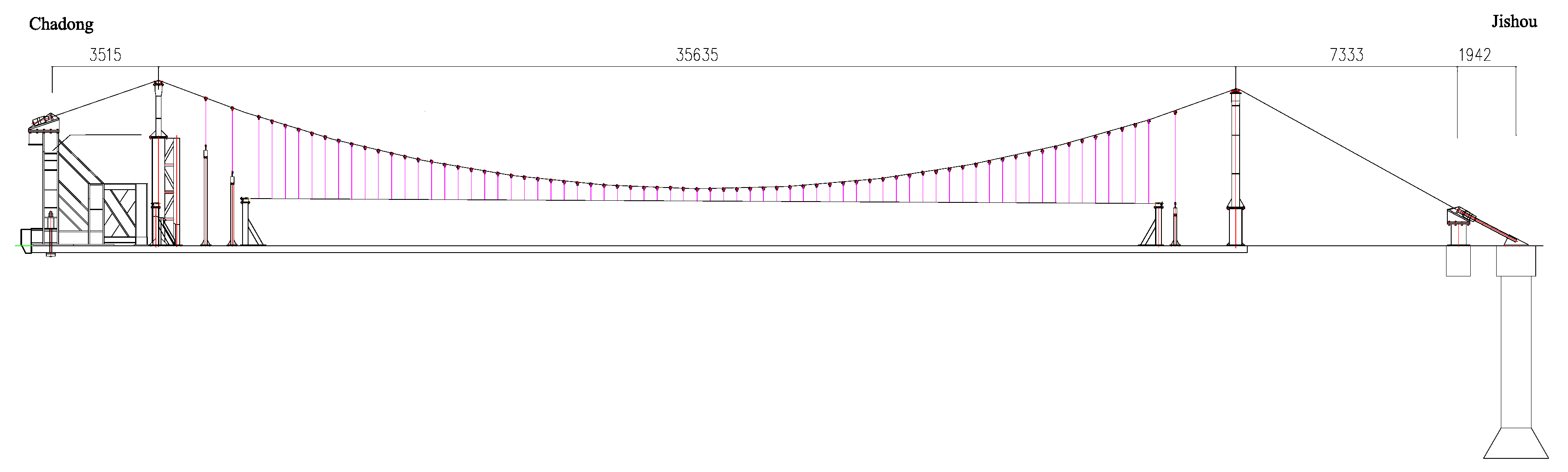
| Items | Main Cable Displacement at Mid-Span | Main Cable Displacement at 1/4 Span on the Jishou Side | Main Cable Displacement at 1/4 Span on the Chadong Side | |||
|---|---|---|---|---|---|---|
| X Direction/mm | Y Direction/mm | X Direction/mm | Y Direction/mm | X Direction/mm | Y Direction/mm | |
| Finite element solution | 1.4 | 28.6 | −0.6 | 9.0 | 3.6 | 7.7 |
| Model test measured value | 1.5 | 27.5 | −0.5 | 8.9 | 3.5 | 7.5 |
| Analytical calculation results | 1.6 | 26.3 | −0.6 | 8.7 | 3.7 | 7.2 |
| Deviation of the finite element solution from the measured value (%) | 6.67 | 4.00 | 20.00 | 1.12 | 2.86 | 2.67 |
| Deviation of the analytical method from the measured value (%) | 6.67 | 4.36 | 20.00 | 2.25 | 5.71 | 4.00 |
| Main Cable Force at the Anchor Point | Finite Element Solution/kN | Model Test Measured Value/kN | Analytical Results/kN | Deviation of the Finite Element Solution from the Measured Value/% | Deviation of the Analytical Method from the Measured Value/% |
|---|---|---|---|---|---|
| Jishou side | 61.7 | 59.9 | 61.3 | 3.01 | 2.34 |
| Chadong side | 58.5 | 57.1 | 58.2 | 2.45 | 1.93 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, Q.; Yan, D.; Yi, Z. Form-Finding Analysis of the Rail Cable Shifting System of Long-Span Suspension Bridges. Appl. Sci. 2018, 8, 2033. https://doi.org/10.3390/app8112033
Pan Q, Yan D, Yi Z. Form-Finding Analysis of the Rail Cable Shifting System of Long-Span Suspension Bridges. Applied Sciences. 2018; 8(11):2033. https://doi.org/10.3390/app8112033
Chicago/Turabian StylePan, Quan, Donghuang Yan, and Zhuangpeng Yi. 2018. "Form-Finding Analysis of the Rail Cable Shifting System of Long-Span Suspension Bridges" Applied Sciences 8, no. 11: 2033. https://doi.org/10.3390/app8112033
APA StylePan, Q., Yan, D., & Yi, Z. (2018). Form-Finding Analysis of the Rail Cable Shifting System of Long-Span Suspension Bridges. Applied Sciences, 8(11), 2033. https://doi.org/10.3390/app8112033




