Abstract
The permissioned blockchain system has recently become popular in a wide range of scenarios, such as artificial intelligence, financial applications and the Internet of things, due to its dominance in terms of distribution, decentralization, reliability and security. However, the Practical Byzantine Fault-Tolerant (PBFT) algorithm, which is currently adopted in such systems, sparks communication bottlenecks when the number of consensus nodes increases sharply, which seriously hinders large-scale applications. In this paper, we propose a scalable dynamic multi-agent hierarchical PBFT algorithm (SDMA-PBFT), which reduces the communication costs from O(n2) to O(). Specifically, SDMA-PBFT forms multiple autonomous systems at each agent node in which message multicasting can be efficiently carried out and the internal voting results can be effectively collected. Therefore, the design of these agent nodes facilitates the in-and-out operations of consensus nodes in the blockchain system. Simulation results show that our proposed algorithm substantially outperforms the PBFT algorithm in terms of latency. Hence, it can be applied to the permissioned blockchain system effectively and efficiently.
1. Introduction
Blockchain, which is also as known distributed ledger and derived from Bitcoin [1], has attracted emerging interest during the last two years. Blockchain is a peer-to-peer distributed system that has the features of high security and dispersive storage with encryption and fault-tolerance technology. It has permeated various sectors of society [2,3], especially digital currency. Permissioned blockchain will be an important development trend in the application of blockchain technology.
A consensus algorithm is the core technology of blockchain, especially permissioned blockchain. In the existing blockchain system, Bitcoin uses the Proof of Work (PoW) consensus and Ethereum adopts the Proof of Stake (PoS) consensus [4], which is constantly being improved. The Hyperledger system employs Practical Byzantine Fault Tolerance (PBFT) [5] to reach agreements, which is developed by IBM. These blockchain systems are public or union systems and have low output performance, e.g., Bitcoin processes 7 transactions per second and Ethererum processes 20 transactions per second. The hyperledger is a union blockchain that provides membership services, including member registration, identity management and auditability, which help it reach high performance in permissioned environments; however, its scalability is insufficient. Consensus technology determines the output performance of the system to a large extent.
The PBFT algorithm is derived from the Byzantine generals’ problem [6]. It can tolerate arbitrary faulty nodes and enhance the availability and reliability using state machine replicated services. The system achieves consensus via a message transfer mechanism and quorum theory in an asynchronous transmission environment. It solves the problem of malicious attacks in the system and has been widely used in distributed computing environments. Furthermore, it has been the main consensus method in the permissioned blockchain system. However, with the increase in blockchain scalability, the communication level reaches O(n2) and the waiting time is substantially increased in an asynchronous environment, which brings great challenges to the output performance of permissioned blockchains.
Although the PBFT algorithm is a satisfactory solution for consensus in a distributed system, it has low consensus speed and scalability. Martin et al. [7] and Braud-Santoni et al. [8] proposed fast Byzantine consensus, which can increase the consensus speed. Paquette et al. [9] and Augustine et al. [10] used a fast broadcast method and a fast Byzantine leader election method separately to increase the speed of consensus. Many scholars have contributed to the scalability of Byzantine Fault-Tolerant (BFT) consensus. Perlman et al. [11] studied the robustness, hierarchy, and scalability problems of Byzantine fault-tolerant consensus. Alchieri et al. [12] proposed an approach that reaches consensus with unknown participants. Distler et al. [13] proposed a resource-efficient Byzantine fault tolerance. Guerraoui et al. [14] discussed highly dynamic distributed computing with Byzantine failures. King et al. [15] discussed scalable Byzantine computation. The application of PBFT has also been considered. Abrardo et al. [16] proposed a game theory framework based on Byzantines. Liu et al. [17] proposed a scalable Byzantine consensus via hardware-assisted secret sharing. Cloud computing environments [18] and digital infrastructures for blockchain [19] applied to PBFT have also been studied. Kraft [20] discussed the difficulty of control for blockchain-based consensus systems. Fault tolerant systems [21], Signatures’ Infrastructure [22], dynamic networks [23], and the speculative Byzantine problem [24] were discussed based on PBFT.
Due to the fault-tolerant nature of PBFT, many experts and scholars apply it to blockchain systems. Luu [25] proposed a computationally scalable Byzantine consensus protocol for blockchains. The honey badger [26] uses PBFT as its core consensus algorithm. The stellar consensus protocol [27] also employs PBFT-based consensus via a federated model for internet-level consensus. In our paper, we take the permissioned blockchain as the research object. In a permissioned blockchain system, scalability and the output performance are relatively large contradictions, and we have tried to resolve the conflict between them to achieve a better balance.
Our contributions: We propose a scalable dynamic multi-agent PBFT consensus (SDMA-PBFT) protocol in this paper, which is implemented effectively in a permissioned blockchain system. The novel method is designed for dynamical hierarchical selection of agent nodes. The PBFT consensus runs in the specified area, which can reduce the traffic of the whole system. The efficiency and latency of our proposed method are demonstrated by the obvious decrease in the latency and the increase in the throughput with multi-agents. This approach enhances the scalability.
The remainder of this paper is organized as follows. Section 2 introduces the preliminaries of blockchain and the consensus protocol. Section 3 describes our model of the SDMA-PBFT structure and presents the details of the process, the traffic analysis and the correctness proof. Section 4 presents the experiments that are conducted to evaluate our proposed approach. Section 5 discusses related works on the application of PBFT in blockchain systems. Section 6 presents the conclusions of this paper and discusses future research directions.
2. Preliminaries
In distributed environments, agreement among multiple computers is essential for applications. Storage, collaborative computing and security protection play important roles in the application of a distributed computing environment. A consensus algorithm can provide fault tolerance and prevent system errors and attacks, thereby providing the system with strong security. In combination with digital signature and other authentication technology, it can provide high security to the system in all directions; therefore, it is used in blockchain technology. Permissioned blockchain is an important application of blockchain. Many famous companies such as IBM conduct research on permissioned blockchain [28,29]. PBFT is based on state machine replication and obtains the correct result via the quorum method. It enables the application of permissioned blockchain.
2.1. Consensus Problem Statement
In a distributed system, reaching agreement is a fundamental problem because all nodes decide on a common outcome. The system requires that the nodes exchange information to negotiate with one another and eventually reach a common agreement before taking application-specific actions [30]. A blockchain is a distributed database system, wherein the nodes collectively decide whether to commit or abort a block in which they participate. For reaching consensus, many famous algorithms have been proposed and applied to all kinds of domains, such as the two-phase commit protocol [31], three-phase commit protocol [32], and paxos protocol [33]. Scholars are exploring the application of these algorithms to blockchain systems.
The communication of a distributed system will be affected by many factors, for example:
Asynchronous communication: In asynchronous communication mode, the system has no clock, no time synchronization, cannot use the timeout mechanism, cannot detect failures, and messages can be arbitrarily delayed or out of order.
Network connectivity: The system has full logical connectivity in which each node can communicate with any other node by direct message passing. However, in practical applications, links may stop carrying or drop messages.
Byzantine faults: The system has malicious behavior such as malicious tampering or attacks. Links in the system may exhibit arbitrary behaviors, which can create and alter messages.
It is impossible to reach a consensus in a distributed environment. Fischer, Lynch and Paterson (FLP) [34] proposed the FLP theorem in 1985. There is no deterministic protocol that solves the consensus problem in a message-passing asynchronous system in which at most one process may fail. In an asynchronous system, a node cannot determine whether a non-faulty node has crashed or is slow.
Based on these considerations, we should consider the fault-tolerance performance of the system in practical applications so that it will not affect the normal output of the system and will allow it to properly function.
We will consider a distributed database with n nodes in a system. Each node i has an input . The consensus problem must guarantee the following:
Definition 1.
Termination. Every non-faulty node eventually decides a value.
Definition 2.
Agreement. All non-faulty nodes decide on the same value in a distributed system.
Definition 3.
Validity. The consensus value must be the input of at least one node and the non-faulty nodes must decide on the same value.
If these three conditions are satisfied [35], the system can work effectively and be applied in practice. Then, we define consensus in a blockchain system.
Definition 4.
Consensus mechanism. In an agreement process, the nodes in a blockchain system must agree on an output to decide whether to append the block to the blockchain. Each node starts with an input message, which comes from the client. At the end of the execution of the algorithm, all nodes output the same result. It is a collaborative computing process in which a majority of the network nodes come to agreement on the state of a ledger.
Definition 5.
Primary-backup. Let p denote the primary node, which is the initiator of the request. The primary node is responsible for tallying the results of voting by other nodes. R = (r1, r2, …, rn) is the set of backup nodes, which record the same information from the primary node. Primary and backup nodes run the consensus algorithm together and record the data of the blockchain.
Definition 6.
Quorum. Assume that N = (n1, n2, …, ni) is the list of all consensus nodes, vi is the value that is received from the sender, vi,j is the value that is forwarded by the sender through the agent, and the polling update uses the following iteration formula:
When the final value satisfies vi ≥ n/2, most nodes are approved and the system accepts the value.
2.2. Blockchain Consensus Comparison
Blockchain systems can be divided into two categories: permissioned blockchain systems in which the identities of users are whitelisted through validation procedures [36], and permissionless systems in which participants are either identified by pseudonymous or anonymous. Bitcoin is designed with permissionless parameters and is the first public and decentralized cryptocurrency system.
Consensus algorithms are widely available for various types of blockchain systems. A permissionless blockchain system, such as Bitcoin, uses a sufficient share of the computational power to reach consensus. The consensus protocol that is used is named Proof of Work (PoW) [1]. PoW is a piece of data which is difficult to produce but easy for others to verify and which satisfies certain requirements. Ethereum uses Proof of State (PoS) as the consensus algorithm. The Hyperledger system employs the practical Byzantine Fault Tolerance to reach agreement, which is developed by IBM [37].
For a permissioned blockchain system, a candidate voting scheme that is based on Replicated State Machine (RSM) provides a better solution. RSM is a general method for implementing a fault-tolerant service by replicating identical states on multiple nodes and coordinating client interactions with those replicas.
We compare the current blockchain consensus algorithms in terms of scalability, latency, throughput, power consumption, fault tolerance, and identity management. The details are listed in Table 1.

Table 1.
Comparison of blockchain consensus protocols. PoS: Proof of State; PoW: Proof of Work; PBFT: Practical Byzantine Fault-Tolerant.
From the table, we conclude the following: First, PoW and PoS have excellent scalability but extremely poor performance in terms of latency and throughput. In contrast, PBFT consensus has limited scalability but extraordinary performance in terms of latency and throughput. Hyperledger consensus shows moderate performance in terms of scalability, latency and throughput. Second, PoW in the Bitcoin system and PoS in Ethereum have no node identity management functions and are open to all users. They require substantial collaborative computing work and run at a high speed; therefore, in terms of power consumption, they waste a lot of energy. Hyperledger and other BFT systems have node identity management functions and know the identities of all the nodes. They perform better in terms of power consumption and attack prevention.
According to the comparison in Table 1, the PBFT algorithm has an extremely large advantage in delay and throughput, but the scalability performance is limited. Therefore, we improved the PBFT algorithm in which agent nodes are added into the system to form a multi-layer scalable PBFT algorithm, which can be applied effectively for the permissioned blockchain system.
2.3. PBFT Consensus in Permissioned Blockchain
The PBFT algorithm is an effective way to solve the Byzantine generals’ problem, which was proposed by Lamport. Since malicious attacks and software errors can cause faulty nodes to exhibit Byzantine behavior, PBFT algorithms are increasingly important in permissioned blockchain systems.
To facilitate understanding, we define notations in Table 2.

Table 2.
Important notations.
PBFT uses cryptographic techniques to prevent spooling and replays, and to detect corrupted messages. Its messages contain public signatures and message digests that are produced by collision-resistant hash functions. A message m that is signed by node i is denoted as , and the digest of message m is denoted as , where is the signature of the message for node i and D is the digest of the message. The execution of the PBFT algorithm is divided into five stages: sending message, pre-prepare, prepare, commit and reply. The execution process is illustrated in Figure 1.
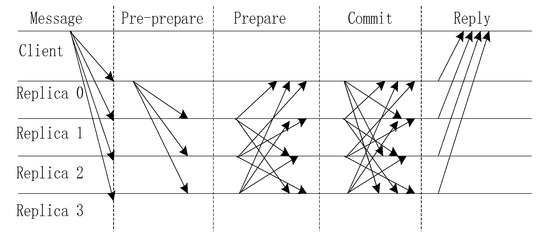
Figure 1.
Basic communication pattern in PBFT (Practical Byzantine Fault-Tolerant).
The algorithm steps are as follows:
- Step 1:
- Sending message. A client sends a request to invoke a service operation to the primary.
- Step 2:
- Pre-prepare. The primary multicasts the request to the backups.
- Step 3:
- Prepare. Replicas execute the request and send a reply to the other replicas.
- Step 4:
- Commit. The primary and replicas send the executed results to other replicas.
- Step 5:
- Reply. The client waits for f + 1 replies from different replicas with the same result; this is the result of the operation.
We assume that the total number of consensus nodes in the system is n and the number of incorrect nodes in the system is f. According to the process, in a distributed system, the message complexity can reach O(n2). In step 1, a client sends n messages; in the pre-prepare stage, the primary sends n-1 messages; in the prepare stage, replicas send (n − 1) × (n − 1) messages; in the commit stage, the primary and replicas send n × (n − 1) messages; and in the reply stage, the client receives n messages. To obtain the consensus results, the total number of messages that must be sent is n + (n − 1) + (n − 1) × (n − 1) + n × (n − 1) + n = 2n2. When the number of nodes reaches 100, the number of messages reaches 20000; this will impose a large burden on the communication network.
For the above reasons, the scalability of PBFT is very poor and it cannot be applied to large-scale blockchain systems. Therefore, we propose an agent-based dynamic multi-level PBFT algorithm that can satisfy the requirement of scalability. The model and process will be described in Section 3.
3. Scalable Dynamic Multi-Agent Byzantine Consensus
In this section, we present the Scalable Dynamic Multi-Agent Byzantine Fault-Tolerant (SDMA-PBFT) consensus algorithm.
First, we will introduce the node types in a blockchain system. In a blockchain system, the following types of nodes are included:
Client node: Records all the transactions and sends the transactions to the consensus nodes. The consensus nodes determine whether each transaction is written into the blockchain.
Consensus nodes: These nodes implement the consensus algorithm and determine the common transactions and whether the blocks are written into the blockchain.
Storage Nodes: The nodes store full backups of the blockchain. When consensus is reached, they append the transaction or block to the blockchain.
3.1. System Model
In large-scale distributed systems, hierarchical technology and agent technology are the basic technologies for large-scale computing and complex communication. In the near future, permissioned blockchains will be applied extensively. First, we propose the SDMA-PBFT model, which is based on the concepts of hierarchical and agent technologies.
In our proposed method, we divide the system into layers, each of which consists of various areas. An agent will serve as the primary in every area. The PBFT consensus algorithm will be conducted in the area. Simultaneously, the level of division is dynamic and the system view may be changed.
The hierarchical dynamic multi-agent model for a permissioned blockchain system is illustrated in Figure 2.
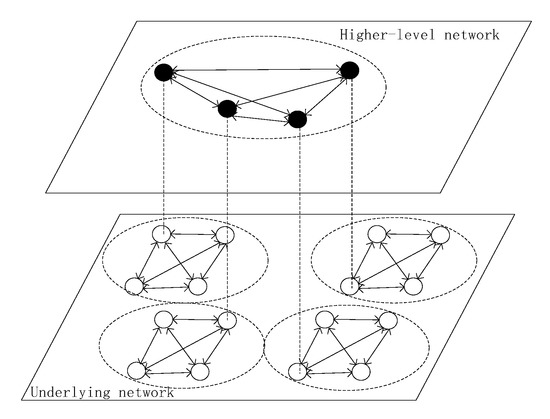
Figure 2.
Multi-agent PBFT model for a blockchain system.
The following questions must be answered when applying this model in practice:
How should the layers be divided? Into how many layers should the system nodes be divided? What are the constraints?
How does the system select agent nodes? Is there a constraint on the selection of agent nodes? What conditions must an agent satisfy?
How large should the area be? In each area, is the size fixed or variable? How is the size determined?
Does the system satisfy the characteristics of a global system? Is it possible to ensure that all nodes participate in voting?
These questions will be answered in the following subsection.
3.2. Process
The PBFT algorithm is a form of state machine replication. Establishing a coincident backup on each node is the final goal. Our SDMA-PBFT approach aims at achieving this goal. Based on the PBFT algorithm, we modify the algorithm in the pre-prepare phase and the reply phase. We assume that the entire network is reachable, that is, each node can transfer a message to any other node conveniently.
3.2.1. Process in Pre-Prepare Stage
A basic feature of blockchain is that all consensus nodes participate in voting and jointly maintain the global characteristics. Therefore, in the pre-prepare stage, all nodes must receive the request message that is issued by the client.
A client c requests the execution of state machine operation o by sending to the first-layer agent. REQUEST is the message that the client sends, o is the detailed operation, c is the client and t is the timestamp. The timestamp is used to ensure exact semantics for the execution of client requests. The timestamp could be the value of the client’s local clock when the request is issued. The PBFT algorithm employs the broadcast approach; however, in our system, we adopt the multicast method to pass the message to the next node.
Our first change to the system is made when the client sends a message to the replicas. Instead of the client broadcasting to all the nodes, the client only sends the message to k nodes, where k is the number of clusters. We define the k nodes as agent nodes. If the total number of consensus nodes n of a blockchain system is less than or equal to k, there is no need to look for agent nodes hierarchically and the blockchain system can use PBFT directly.
Then, the algorithm is executed up to the pre-prepare stage. At this time, agent nodes look for k − 1 peripheral nodes as an autonomous domain. In the autonomous domain, we call these nodes an area. An area has k nodes on which to execute the prepare stage and the commit stage of the PBFT algorithm. The agent nodes will send message to the area, where v is the current view number, n is the sequence number, m is the client’s request message, d is m’s digest, and p is the primary node. When replica i accepts the message, the agents will record the number of agreements with the primary.
Figure 3 illustrates the execution of the SDMA-PBFT algorithm when k is 4.
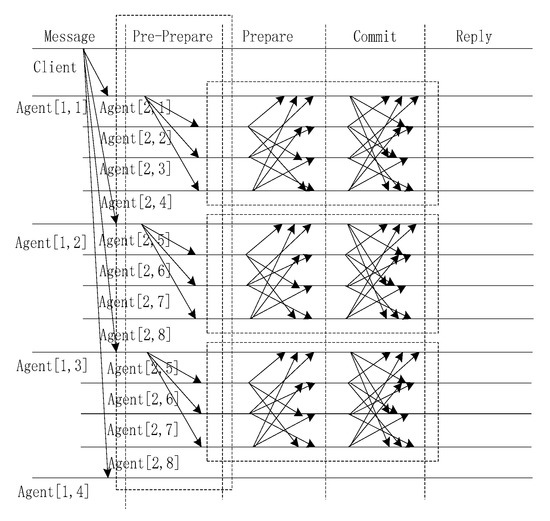
Figure 3.
Pre-preparation process of the scalable dynamic multi-agent hierarchical PBFT algorithm.
Another task of the agent is to send the pre-prepared message to the next layer and record the id of the agent node. All agent nodes perform the same operation until no consensus node exists. The agent nodes are dynamically selected while a multi-fork tree is generated. Each agent node acts as the primary node by broadcasting the message to its area and as an agent by transferring the request message to the next layer.
According to the above concept, we put forward the SDMA-PBFT algorithm in the sending message and pre-prepare stages. The detailed algorithm is presented as Algorithm 1.
According to the above algorithm, the choice and layer of the agent have an important impact on the system performance and implementation. At the same time, agents must recycle the voting results. We use an array agent [layer, number] to represent the agent set, where layer is the number of layers in a blockchain system and number is the total number. To achieve the goal of extension, we use the dynamic spanning tree algorithm and take the root node as the agent node. A schematic diagram of the spanning tree is shown in Figure 4.
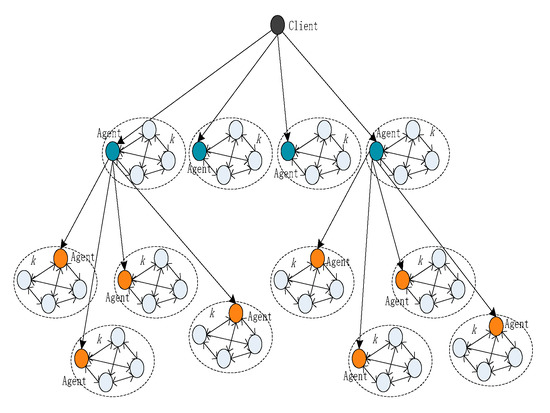
Figure 4.
Spanning tree that is generated for multicasting.
| Algorithm 1. Agent-based layer for SDMA-PBFT. |
| Input: a client node, n consensus nodes, multicast algorithm, the size of the area k Output: agreement results 1: begin // layer processing 2: if k ≥ n 3: run PBFT algorithm directly; 4: else client sent request message to k agent nodes; 5: for i = 1 to n do 6: set agent to be the set of all nodes that can execute at this layer; 7: while agent is not empty 8: do PBFT(areai) for all clusters in this layer; 9: agent sends Pre-prepare message to the next layer; 10: until agent is empty; 11: end while 12: load balance transaction using the method of decomposing clusters, which makes nodes maintain load balance; 13: end for 14: end |
Then, we present a multicast algorithm that meets the PBFT conditions in the multicast application. The detailed algorithm is presented as Algorithm 2.
| Algorithm 2. Spanning tree generation algorithm. |
| Input: n consensus nodes, client c, the size of the area k, identification of all nodes Output: minimum spanning tree for agents 1: begin 2: client c sends a message to the k neighbor nodes; 3: set the client as the root; 4: for (i = 1; i ≤ k, i++) // k area 5: if node i receives the message 6: set node i as agent; 7: set flag = 1 and the layer as the current layer; 8: agent sends k messages to k; 9: while agent cannot find k − 1 nodes 10: The k − 1 nodes will be the leaf nodes; 11: else call line 4; 12: until there are no consensus nodes; 13: end while 14: if a new node enters the system 15: put the node into the nearest area as a leaf node; 16: end if 17: end if 18: end for 19: end |
3.2.2. Process in the Reply Stage
The final step of the algorithm is to return the execution results of all the nodes to the client. The client determines whether the block is written on the chain according to the number of messages that are sent and the number of messages that are recovered. Therefore, the recovery mechanism and counting mechanism of the information request are very important. PBFT allows the system to have [n − 1]/3 non-faulty nodes, and its fault-tolerance rate is 1/3.
In the implementation process, the recycling of the nodes is divided into two steps. First, the internal voting results of an area are returned to the agent. Second, the agent will return the votes inside the area to the client. The agent must record the amount of internal information to return. We assume that if a node agrees to accept the message, the message is sent to the agent. If the node is a non-loyal node or there is a software error or communication timeout, the node does not agree to accept.
In the commit phase, there two types of commit messages, namely, committed-local(m,v,n,i) and committed(m,v,n,i,a), where m is the client’s request message, v is the current view number, n is the sequence number, and a is the agent in an area. The process of committed-local (m,v,n,i) is conducted in an area. Then, the agent will calculate statistics of the voting situation and return the results to the client through the process of committed (m,v,n,i,a).
According to the total number of multicast requests and the total number of received consent messages, the blockchain system can confirm whether the request is received or not. The reply process of the SDMA-PBFT algorithm is illustrated in Figure 5.
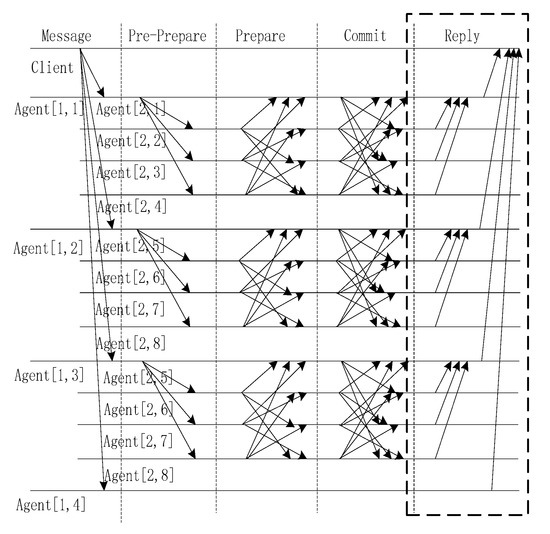
Figure 5.
Reply process of the SDMA-PBFT algorithm.
3.3. Traffic Analysis for SDMA-PBFT
Assume that the total number of consensus nodes in a blockchain system is n and the number in an area is k. In the worst case, each layer has a complete child node and the blockchain consensus nodes constitute a fully branched tree with k nodes. In an asynchronous environment, the number of messages sent can be calculated as follows:
layer 1:
area (layer1) = k
Number (layer1) = K × area (layer1) = k2
Number (layer1) = K × area (layer1) = k2
area (layer2) = Number (layer1) = k2
layer 2:
area (layer2) = Number (layer1) = k2
Number (layer2) = area (layer2) × k = k3
Total (area) = area (layer2) + area (layer1) = k2 + k
Total (Number) = Total (area) × k = k3 + k2
layer 3:
area (layer3) = Number (layer2) = k3
Number (layer3) = area (layer3) × k = k4
Total (area) = area (layer3) + area (layer2) + area (layer1) = k3 + k2 + k
Total (Number) = Total (area) × k = k4 + k3 + k2
Through the above reasoning, we conclude the following:
Total (areai) = area (layeri) + Total (areai−1)
Total (Numberi) = Total (areai) × k
First, we assume that k is 4 and that the size of the message in an area is k2.
When k = 4 and the system has three layers with a full k-branched tree, the number of nodes in the area in the system is 84 and the total number of nodes in the system is 336. The size of the sent message in the system is 84 × 42 = 1344. If the system is not divided into layers, the total size of the message is approximately 3362 = 112,896, which is approximately 84 times larger than in SDMA-PBFT.
If the total number of nodes in the system is fixed, other results will be observed as k is increased. For example, when k is 7 and the total number of nodes is 336, the system only needs to be divided into two layers. The number of nodes in each area is 7, and the complete message is approximately of size 343.
According to the analysis in Section 2.3, in the absence of hierarchy and agents, the total system traffic is 2n2; that is, the communication complexity is O(n2). Assume that the system has n nodes and the size of an area is k. Then, the system satisfies:
Number (layer) = logkn
Number (area) = n/k
The traffic in the multi-agent system is approximately
Traffic = Number (layer) × Number (area) × 2 × k2
That is, the communication complexity of the multi-agent blockchain system is approximately O().
According to the above, the total number of messages that are sent by the system is related to the value of k. At the same time, the delay of the system will be greatly reduced due to the synchronized execution among the autonomous areas. The experimental results are presented in Section 4.
3.4. Correctness Conditions and Proof
In a blockchain system, the consensus nodes can suffer an arbitrary failure; for example, the nodes may stay silent, delay messages or change messages. Therefore, according to the principle of strong consistency, the proposed method is correct only when the system has the following three characteristics:
Termination: Every non-faulty node eventually decides on a value.
Proof: Assuming that the system has a tolerance limit, suppose the tolerance time is T. If the client receives no more than half of the votes that are collected by the agent within time T, the system will forcibly terminate the execution of the request; otherwise, the block is written to the chain.
In the agent multicast process, the agent multicasts the request information to each node according to the global spanning tree algorithm. The system should ensure that all consensus nodes are involved in the system. The agent is responsible for collecting the voting results of the current area and passing them to the upper level. If the agent is a faulty node or a Byzantine node, it is discarded. The system will eventually meet the conditions for entering the termination state.
Agreement: All non-faulty nodes decide on the same value in a distributed system.
Proof: Before the client node sends a request message to the consensus system, all consensus nodes start in the same state. A round in a consensus algorithm consists of the three steps: sending, receiving, and local computation. All nodes send the same messages, receive the same messages, perform the same local computation, and therefore end up in the same state. If a node is a faulty node, it will generate the mistake message, which is not counted by the agent. Therefore, all non-faulty nodes decide on the same value in our blockchain system.
Validity: The consensus value must be the input of at least one node, and the non-faulty nodes must decide on the same consensus value.
Proof: The validity condition implies that if all nodes have the same input x, then the nodes must decide on x. In our SDMA-PBFT algorithm, the input message is sent by the client and transferred by agents. Agents have only added the counting function and did not modify the view, message digest or other attributes; hence, the input is the same. Consensus depends on many parameters of the distributed blockchain system. Although faulty nodes exist, the operation of the system results in either agreement or disagreement in both cases. Therefore, our algorithm is valid.
3.5. Nodes Join and Quit Dynamically and Freely
In practical applications, scalability is an important factor and lack of scalability hinders the application of such systems. According to the characteristics and performance indices of the blockchain system, we define blockchain scalability:
Definition 7.
Scalability. A consensus node can access the blockchain consensus system safely and fast and execute consensus algorithms with other nodes without affecting the current system performance. The consensus time meets the system tolerance conditions, and the output characteristics of the entire system are enhanced as the number of nodes increases.
In our algorithm, when a new node enters, the system judges whether the node accesses the network. If it accesses the network, the node sends the broadcast information to the surrounding nodes. When an agent node receives this broadcast message, the agent judges whether the maximum number of internal nodes in the area has been reached and, if the area is already full, does not process it. If not, the dynamic nodes are put into the area and added to the multicast list. If no agent stores the node, the node is treated as a next-level agent.
The exit mechanism is relatively convenient. The agent will delete the node directly from the multicast list.
To maximize the functionality of the system, an equalization server is utilized. If part of the load is larger, it is transferred to other areas to be processed and the spanning tree is reconstructed.
The interface function should be set in the blockchain system to manage the identities of the nodes for access or termination. Node ID management is a basic guarantee of the permissioned blockchain.
3.6. Safety and Liveness
As a decentralized distributed database, a perfectly correct blockchain system must be able to satisfy two important properties of distributed systems: safety and liveness.
Definition 8.
Safety. The safety property asserts that a system does not exhibit bad behavior. That is to say, nothing bad happens.
The ultimate goal of a consensus algorithm is to achieve consistent results. It encounters Byzantine errors, software errors and other unpredictable circumstances in the course of its work, and thus it must be fault tolerant. The fault-tolerance performance of the PBFT algorithm is [n − 1]/3, which means that it can tolerate n/3 error nodes in the system. Our proposed SDMA-PBFT algorithm is based on PBFT, and its fault-tolerance performance also satisfies [n − 1]/3. However, if the agent node is chosen incorrectly, the system fault tolerance is reduced.
In a permissioned blockchain system, assume that n is the total number of nodes in the system, p is the probability of a single node failure, and k is the maximum number of tolerable failures. The fault-tolerance performance formula can be expressed as
Assume that there are n = 50 nodes for consensus and the system has a maximum number of tolerable failures k = 16 and p = 0.05. The probability of failure is approximately 1.46 × 10−9. This demonstrates that the probability of a system error is negligible. Therefore, the safety of the BFT-based fault-tolerant algorithm is very high.
In the meantime, each non-faulty node will eventually return the voting result to the client in the form of 0 or 1 in a blockchain system. The system satisfies the definition of safety.
Definition 9.
Liveness. The liveness property asserts that a system will eventually obtain satisfactory results.
As in a blockchain system, each node starts with an input message. At the end of the execution of the algorithm, all consensus nodes output the same results. If the number of nodes that agree exceeds 2/3, the blocks or transactions of clients will be accepted.
We assume that the phase property guarantees that specific events will eventually occur. We define the phase property as follows: phase P = {p1, p2, p3, …, pn} asserts that in an infinite execution of a blockchain system, at least one of the actions will be executed infinitely often.
In a blockchain system, consensus nodes participate in the voting. The main objective of voting is to check the integrity of local data and whether the message has been tampered with. In the consensus process, if any steps are not executed or timed out, the node’s voting result is regarded as disagreement. Therefore, within a certain period of time, the result will be returned to the client.
Regardless of whether the final result is agreement or disagreement, it is treated as the correct result. Therefore, the system satisfies the definition of liveness in a distributed environment.
3.7. Fault-Tolerance Analysis for SDMA-PBFT
We will discuss the fault-tolerance performance of our SDMA-PBFT algorithms in this subsection. We discuss the fault tolerance in two situations:
3.7.1. No Faulty Nodes Are Agent Nodes
In this scenario, there are two possibilities: One is that the faulty nodes are evenly distributed in each area and the number of faulty nodes that are running within an area does not exceed 1/3 of the total number of nodes. At this time, the voting result within the area is correct and has no effect on the system output result, and the system’s fault tolerance is:
The second possibility is that faulty nodes are concentrated in an area. After running PBFT in this area, the agent node will produce erroneous output according to the principle of the minority obeying the majority. At this point, the agent sends the results to the previous level. After the upper-level PBFT vote, the agent node is exposed and the agent node is set as an ordinary node and does not participate in voting. The fault tolerance of the system in this case is:
3.7.2. An Agent Node is a Faulty Node
The agents may be faulty nodes, it can be seen in Figure 6. In this case, the faulty agent node will affect all the nodes in the area, thereby resulting in the voting results of the area being incorrect. If the agent nodes are faulty in more than one-third of the total area, the system crashes.
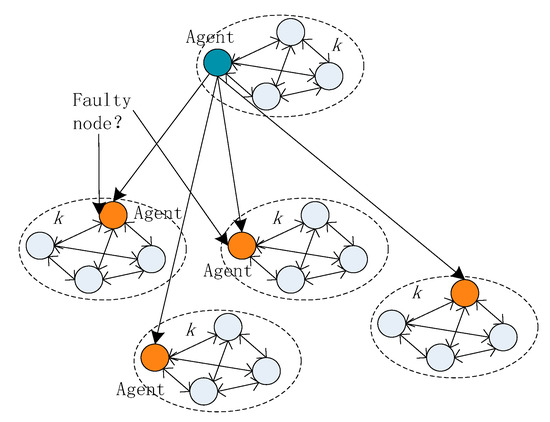
Figure 6.
When the agents are faulty nodes.
In this case, the fault tolerance of the system is:
According to the above analysis, if the faulty nodes are evenly distributed, the fault-tolerance performance of the system is not changed. If a faulty node is an agent node, the system’s fault tolerance performance is reduced. To improve the fault tolerance, we have limited the choice of agent nodes.
To ensure the security of the system and improve the fault tolerance, the choice of agent is very important. For example, if an agent is a malicious node, all the nodes for which this agent is responsible can be viewed as faulty. As a result, it will substantially reduce the security of the system. Therefore, in our system, the choice of agent is changed periodically. When a new node joins or the view changes, the system reselects the agent node, runs a dynamic spanning-tree algorithm, and sets up new agent nodes. At the same time, a reputation mechanism is added to the system. If a node is found to be a malicious node, the node will be punished, the reputation value of the node will be halved, and it will be blocked from participating in the next round of voting. The incorporation of the reputation mechanism can effectively prevent the emergence of faulty agents.
4. Experiments
In this section, we have conducted experiments on traffic simulation, latency and throughput in permissioned blockchain.
Our experiments are conducted in wide area network (WAN). Each node runs SDMA-PBFT algorithms, and the permissioned blockchain system is BHchain, which is developed by our team. The bandwidth can reach 1000 Mb/s in the laboratory environment and 100 Mb/s in WAN. The nodes of a blockchain system use the desktop to run the algorithm, which is configured under the main frequency of 3.6 Ghz with two cores, and the RAM is 4 GB.
4.1. Traffic Simulation
Traffic is an important indicator of system performance. The more messages a system broadcasts or multicasts, the longer it takes. Therefore, to improve the performance of the system, reducing traffic is an option.
According to the hierarchical and clustering features of SDMA-PBFT, we set the area values to 1, 4, 7 and 10. When k = 1, the system is not hierarchical, which is equivalent to all the nodes being on the same layer, and the PBFT algorithm is run directly. When k = 4, 7, or 10, hierarchical clustering is performed. The results of traffic messages are shown in Figure 7.
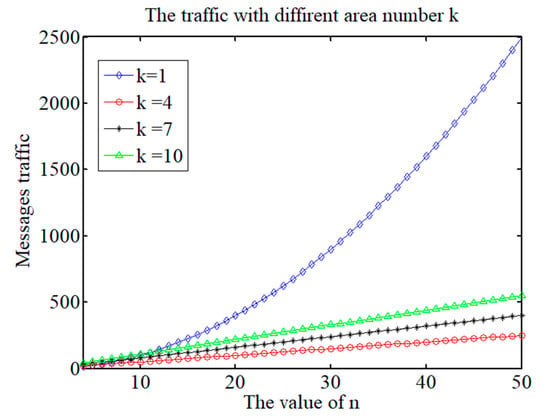
Figure 7.
Traffic for various values of k.
According to Figure 7, after the agent nodes were selected to form hierarchical areas, the traffic decreased substantially. At the same time, the value of k also has an impact on the traffic. In practice, selecting the optimal value of k is the main issue that requires further discussion.
4.2. Latency
Our SDMA-PBFT algorithms rely on timeouts to guarantee liveness. However, in some cases, inappropriate values of timeouts and network congestion will make a correct replica suspect or remove a correct primary. Especially for the agent nodes, we set various timeouts to simulate the algorithm.
First, we define latency. The delay for the client node to send the request message to receive the determination result is called the latency. Due the impact of various factors in the real environment, it deviates from the theoretical latency. In our experiments, we first fixed the system n value and area and considered a numerical test system to obtain the latency. The experimental results are shown in Figure 8.
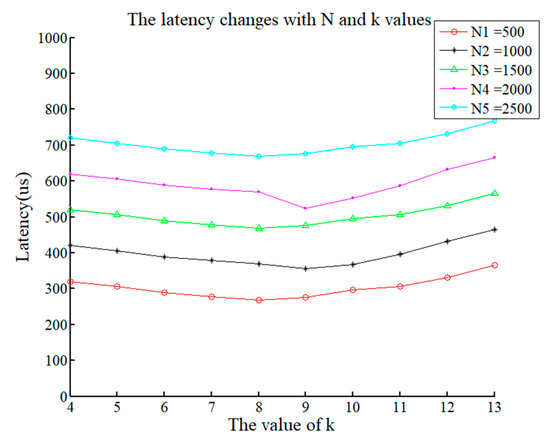
Figure 8.
Latency for various values of k.
According to Figure 8, as n increases, the total system latency increases. This is consistent with the theory. The more nodes there are, the longer the consensus time and the longer the total system latency. When the total number of nodes is 500, the time that is taken to reach a consensus is approximately 300 us, which increases to 700 us when n is 2500. This is far greater than the time it takes PBFT to reach a consensus on the same node. In addition, we tested the latency under various values of k. The value of k has little effect on the system delay, but the overall trend is that with an increase in k, the delay decreases initially and then increases. When the total number of nodes changes, the value if k of the area is dynamic when the system delay is minimal.
In a distributed environment, system congestion or infinite wait is caused by information being affected by network conditions, which results in an increase in system latency. Therefore, we set the timeout for each agent node. If no information of other nodes is received within this time period, the node is regarded as a faulty node. With the timeout, the system will reduce the delay, physical loss, congestion and so on, so the timeout does not wait for the system results but continues the upper data transmission. Figure 8 shows the change in the system delay under various timeout conditions when n is 2500.
According to Figure 9, the latency of the system decreases and then increases with an increase in k. This is because the value of k affects the total system traffic. The same layer area is executed at the same time; the impact on the system is smaller. Voting results at different levels have a greater impact on the system. We fix n to 2500, and the system reaches the minimum delay when k is 8.
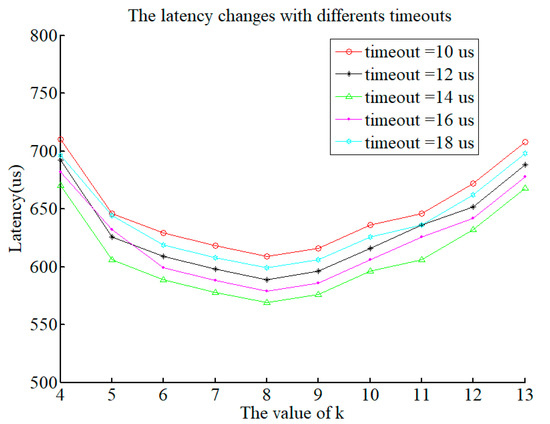
Figure 9.
Latency with various timeouts.
At the same time, as the timeout increases from 10 us to 18 us, there is also a slight increase in system latency. When n is 2500 and the timeout value is 0.14 us, the system’s output performance attains its minimum value.
4.3. Throughput
In a blockchain distributed system, each client node can send a request to a consensus node to determine whether the transaction or block should be executed. We define the throughput of the blockchain system as the number of transactions that are handled per second (tx/s for short). A test was conducted on BHchain to evaluate the system throughput under various values of n.
We now evaluate the throughput that is achieved by various blockchain instantiations. We simulate 500, 1000, 1500, and 2000 consensus nodes in the system; at the same time, the client node provides as many transactions as possible.
In the blockchain test system, we set the values of k to 4, 7, 10, and 13. Then, we examine the relationship between the system throughput and the values of n and k. The detailed output results are shown in Figure 10.
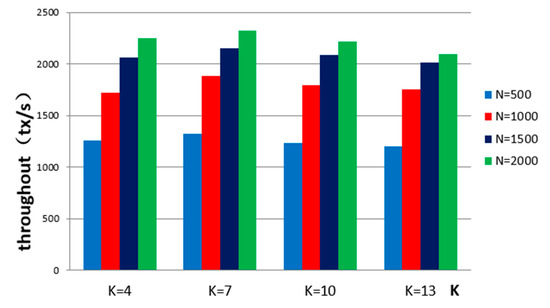
Figure 10.
Throughput for various values of n and k.
According to Figure 10, with an increase in n, the throughput of the system is increased. For example, when n is 500, the number of transactions that the system can process is approximately 1300. When n is increased to 2000, the system can handle approximately 2300 transactions. The system throughput increased significantly. From this point of view, the scalability of the system is achieved; that is, the larger the number of consensus nodes, the greater is the throughput of the system.
The value of k has an impact on the throughput of the system. Analyzing the throughput of the system under the same value of n, when the k value is 7, the system has a larger throughput. This is because the system output is related to the values of k and n.
To test the system’s throughput under various timeouts, we set the timeout on the agent nodes. The timeout has an impact on the system output. In the blockchain test system, we set n to 1000. With a fixed value of n, we obtain the graph that is shown in Figure 11.

Figure 11.
Throughput with various timeouts.
According to Figure 11, varying the timeout changes the output of the system. Due to the existence of an asynchronous transmission environment, to recover information in a timely manner, the system often sets the timeout. The comparison in Figure 11 shows that when the value of the timeout is 12 us, the system can achieve the maximum throughput. The value of k also affects the system’s output performance. The comparison demonstrates that when k is 7, the system can achieve the maximum throughput.
From the above experimental analysis, we conclude that, compared with the PBFT algorithm, the SDMA-PBFT algorithm improves the system’s scalability, reduces the system latency and improves the system throughput. The algorithm has been verified in our blockchain test system.
5. Related Works
The scalability issues and solutions for blockchain have been heatedly discussed, both academically and in industry. In [37], the two most commonly-used methods of PoW-based blockchain and methods that are based on PBFT state machine replication are discussed and compared, highlighting their respective advantages and discussing their limits on scalability. They also discussed the latest technical developments and new directions for development that have been explored recently to overcome these limitations and the lack of scalability. In [38], a decentralized system is proposed in which the transaction is off-blocked in the network where the micro-payment channels are sent. Discussion of the scalability of the bitcoin blockchain, which is currently being solved, is urgently needed. We should consider the problem of the bitcoin block and the effect of its scale concentration. In addition, we should consider the significant cost problem when the block implicitly creates trust.
In [27], a new state machine replication algorithm is described, which can tolerate Byzantine errors and improve the performance of previous algorithms by replacing public-key signatures with vectors of message authentication codes, reducing the size and quantity of messages, and applying incremental checkpoint management techniques. By reducing the number of backups, the system’s response time can be improved; however, as the number of backups decreases, the overall system security will not be guaranteed. In [39], a protocol called Zyzzyva is proposed which uses speculation to reduce costs and simplifies the design of Byzantine fault-tolerant state machine replication. This method can improve the service performance of existing PBFT in throughput and latency. However, this paper only proves its feasibility in theory, we cannot know the effects in a real scenario. Miller et al. [26] put forward an asynchronous BFT protocol called HoneyBadgerBFT, which is based on the BFT to design a new atomic broadcast protocol to achieve the best asymptotic efficiency. Although this protocol has made some improvements in transactions, it needs more response messages with limited bandwidth. In [40], the authors present a hybrid Byzantine fault-tolerant state machine replication protocol called HQ which uses a lightweight arbitration-based when there is no conflict and uses the 3f + 1 copy to tolerate f-faults, providing the best defense against node failures. Although this method reduces the secondary cost of communication between replicas, the cost of communication between copies cannot provide a generic model. In [25], a new blockchain-based Byzantine Coherence Protocol named SCP is designed. The throughput scale is approximately linear in computation. It provides the flexibility to adjustt bandwidth consumption by adjusting computational parameters. Although this method has made many attempts to improve efficiency and trade-off performance, the safety is in bounded computing. In [41], the authors propose a scalable blockchain protocol called Bitcoin-NG. It implements Bitcoin-NG and runs on a large-scale system by using two protocol-invariant clients. They found that if the bandwidth is limited, Bitcoin-NG improves the scalability of blockchain protocols to some point where the network diameter limits consensus latency and the individual node processing power is the throughput bottleneck.
6. Conclusions
In this paper, we propose a scalable PBFT consensus algorithm for dynamic multi-agent hierarchical design, which can be applied to large-scale distributed blockchain systems. The algorithm automatically divides each layer according to the number of consensus nodes in the blockchain and the size of the autonomous region. The agent node is the key node of the system. It acts as the master node by running the PBFT algorithm inside the autonomous region and collecting the execution result. At the same time, the agent node must send requests to the next level according to the number of network nodes and waits for the execution results of all the nodes in the next level.
This design method has the following advantages: First, the system uses a hierarchical design to dynamically determine the size of the autonomous region and the agent node flexibility. Second, when a new consensus node is added to the system, the system can change the view so that the node can become involved in the consensus process as soon as possible, to enhance the scalability. Third, the algorithm does not change the characteristics of the blockchain distributed database without a center and jointly maintains the database and consensus. Moreover, with the increase in the number of consensus nodes, it can obtain better output performance by significantly reducing the system processing time of messages, reducing the delay and increasing system throughput. Finally, the agent node is dynamically selected and reselected after a period of time; hence, the probability of being attacked is relatively low and the security level is high. Experimental results show that this algorithm can be applied to permissioned blockchain systems with high efficiency and that the systems can obtain better output performance under the conditions of larger node size.
This algorithm has two main disadvantages: First, it increases the burden on the agent, which needs to record the number of requests that are sent and the underlying voting results and pass the results to the client. Second, if the agent is a non-loyal node, it will not send a message to the upper layer. The results of all the loyal nodes in the agent range will not be passed to the upper layer, thereby reducing the number of consensus nodes.
Author Contributions
The paper is the result of the intellectual collaboration of all listed authors. L.F. proposed the new ideas, designed the framework, performed the experiments and wrote most part of the manuscript. H.Z. optimized the theories and proposed many useful methods in the process of theoretical analysis. Y.C. and L.L. analyzed the simulation results and revised the paper.
Funding
This work is supported by the National Key Research and Development Program of China (Grant No. 2017YFB1400200) and the National Natural Science Foundation of China (Grant Nos. 61462003 and M1450009).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 31 October 2008).
- Casado-Vara, R.; González-Briones, A.; Prieto, J.; Corchado, J.M. Smart Contract for Monitoring and Control of Logistics Activities: Pharmaceutical Utilities Case Study. In Proceedings of the 13th International Conference on Soft Computing Models in Industrial and Environmental Applications, San Sebasti, Spain, 6–8 June 2018; pp. 509–517. [Google Scholar]
- Casado-Vara, R.; Prieto, J.; De la Prieta, F.; Corchado, J.M. How blockchain improves the supply chain: Case study alimentary supply chain. In Proceedings of the 15th International Conference on Mobile Systems and Pervasive Computing, Gran Canaria, Spain, 13–15 August 2018; pp. 393–398. [Google Scholar]
- Cachin, C. Architecture of the Hyperledger blockchain fabric. In Proceedings of the Workshop on Distributed Cryptocurrencies and Consensus Ledgers, Chicago, IL, USA, 25 July 2016; pp. 1–4. [Google Scholar]
- Castro, M.; Liskov, B. Practical Byzantine fault tolerance. In Proceedings of the 3rd Symposium on Operating Systems Design and Implementation, New Orleans, LA, USA, 22–25 February 1999; pp. 173–186. [Google Scholar]
- Lamport, L.; Shostak, R.; Pease, M. The Byzantine generals problem. ACM Trans. Program. Lang. Syst. 1982, 4, 382–401. [Google Scholar] [CrossRef]
- Martin, J.P.; Alvisi, L. Fast byzantine consensus. IEEE Trans. Depend. Secur. Comput. 2006, 3, 202–215. [Google Scholar] [CrossRef]
- Braud-Santoni, N.; Guerraoui, R.; Huc, F. Fast byzantine agreement. In Proceedings of the 2013 ACM Symposium on Principles of Distributed Computing, Montreal, QC, Canada, 22–24 July 2013; pp. 57–64. [Google Scholar]
- Paquette, M.; Pelc, A. Fast broadcasting with byzantine faults. Int. J. Found. Comput. Sci. 2006, 17, 1423–1439. [Google Scholar] [CrossRef]
- Augustine, J.; Pandurangan, G.; Robinson, P. Fast byzantine leader election in dynamic networks. In Proceedings of the International Symposium on Distributed Computing, Tokyo, Japan, 7–9 October 2015; pp. 276–291. [Google Scholar]
- Perlman, R.; Kaufman, C. Byzantine robustness, hierarchy, and scalability. In Proceedings of the IEEE Conference on Communications and Network Security (CNS), National Harbor, MD, USA, 14–16 October 2013; pp. 242–250. [Google Scholar]
- Alchieri, E.; Bessani, A.; Da Silva Fraga, J.; Greve, F. Byzantine consensus with unknown participants. In Proceedings of the 12th International Conference on Principles of Distributed Systems, Luxor, Egypt, 15–18 December 2008; pp. 22–40. [Google Scholar]
- Distler, T.; Cachin, C.; Kapitza, R. Resource-efficient Byzantine fault tolerance. IEEE Trans. Comput. 2016, 65, 2807–2819. [Google Scholar] [CrossRef]
- Guerraoui, R.; Huc, F.; Kermarrec, A.M. Highly dynamic distributed computing with byzantine failures. In Proceedings of the 2013 ACM symposium on Principles of distributed computing, Montreal, QC, Canada, 22–24 July 2013; pp. 176–183. [Google Scholar]
- King, V.; Saia, J. Scalable byzantine computation. ACM SIGACT News 2010, 41, 89–104. [Google Scholar] [CrossRef]
- Abrardo, A.; Barni, M.; Kallas, K. A game-theoretic framework for optimum decision fusion in the presence of Byzantines. IEEE Trans. Inf. Forensic Secur. 2016, 11, 1333–1345. [Google Scholar] [CrossRef]
- Liu, J.; Li, W.; Karame, G.O. Scalable Byzantine Consensus via Hardware-Assisted Secret Sharing. Available online: https://arxiv.org/abs/1612.04997 (accessed on 15 December 2016).
- Lim, J.B.; Suh, T.; Gil, J.M. Scalable and leaderless Byzantine consensus in cloud computing environments. Inf. Syst. Front. 2014, 16, 19–34. [Google Scholar] [CrossRef]
- Glaser, F. Pervasive decentralisation of digital infrastructures: A framework for blockchain enabled system and use case analysis. In Proceedings of the 50th Hawaii International Conference on System Sciences, Hilton Waikoloa Village, HI, USA, 4–7 January 2017; pp. 1543–1552. [Google Scholar]
- Kraft, D. Difficulty control for blockchain-based consensus systems. Peer-to-Peer Netw. Appl. 2016, 9, 397–413. [Google Scholar] [CrossRef]
- Clemen, A.; Won, E.L.; Alvisi, L. Making Byzantine Fault Tolerant Systems Tolerate Byzantine Faults. In Proceedings of the 6th Symposium on Networked Systems Design and Implementation, Boston, MA, USA, 22–24 April 2009; pp. 153–168. [Google Scholar]
- Emmadi, N.; Narumanchi, H. Reinforcing Immutability of Permissioned Blockchains with Keyless Signatures’ Infrastructure. In Proceedings of the 18th International Conference on Distributed Computing and Networking, Hyderrabad, India, 5–7 January 2017; p. 46. [Google Scholar]
- Augustine, J.; Pandurangan, G.; Robinson, P. Fast byzantine agreement in dynamic networks. In Proceedings of the 2013 ACM Symposium on Principles of Distributed Computing, Montreal, QC, Canada, 22–24 July 2013; pp. 74–83. [Google Scholar]
- Duan, S.; Peisert, S.; Karl, N. hbft: Speculative Byzantine fault toleracnce with minimum cost. IEEE Trans. Depend. Secur. Comput. 2016, 12, 58–71. [Google Scholar] [CrossRef]
- Luu, L.; Narayanan, V.; Baweja, K. SCP: A Computationally-Scalable Byzantine Consensus Protocol for Blockchains. Available online: https://eprint.iacr.org/2015/1168 (accessed on 4 December 2015).
- Miller, A.; Xia, Y.; Croman, K. The honey badger of BFT protocols. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; pp. 31–42. [Google Scholar]
- Mazieres, D. The Stellar Consensus Protocol: A Federated Model for Internet-Level Consensus. Available online: https://www. stellar. org/papers/stellar-consensus-protocol. pdf (accessed on 14 July 2015).
- James, R. Hyperledger Fabric v1.0 Project. Available online: https://github.com/ethereum/wiki/wiki/White-Paper (accessed on 7 August 2017).
- Gupta, H.; Hans, S.; Mehta, S.; Jayachandran, P. On Building Efficient Temporal Indexes on Hyperledger Fabric. In Proceedings of the 11th IEEE International Conference on Cloud Computing, San Francisco, CA, USA, 2–7 July 2018; pp. 294–301. [Google Scholar]
- Li, Z.; Cai, W.; Stellar John, S. Transparent three-phase Byzantine fault tolerance for parallel and distributed simulations. Simul. Model. Pract. Theory 2016, 60, 90–107. [Google Scholar] [CrossRef]
- Lindsa, M.B.; Obermarck, R. Transaction management in the distributed database management system. ACM Trans. Database Syst. 1986, 11, 378–396. [Google Scholar]
- Skeen, D.; Stonebraker, M. A Formal Model of Crash Recovery in a Distributed System. IEEE Trans. Softw. Eng. 1983, 9, 219–228. [Google Scholar] [CrossRef]
- Lamport, L. Paxos Made Simple. ACM SIGACT News 2001, 32, 51–58. [Google Scholar]
- Fischer, J.; Lynch, A.; Paterson, S. Impossibility of Distributed Consensus with One Faulty Process. J. ACM 1985, 32, 374–382. [Google Scholar] [CrossRef]
- Vitalik, B. Notes on Scalable Blockchain Protocols. Available online: https://github.com/vbuterin/scalability_paper (accessed on 17 July 2015).
- Swanson, T. Consensus-as-a-Service: A Brief Report on the Emergence of Permissioned, Distributed Ledger Systems. Available online: https://allquantor.at/blockchainbib/pdf/swanson2015consensus.pdf (accessed on 1 April 2015).
- Vukolić, M. The quest for scalable blockchain fabric: Proof-of-work vs. BFT replication. In Proceedings of the International Workshop on Open Problems in Network Security, Zurich, Switzerland, 29 October 2015; pp. 112–125. [Google Scholar]
- Poon, J.; Thaddeus, D. The Bitcoin Lightning Network: Scalable Off-Chain Instant Payments. Available online: https://lightning.network/lightning-network-paper.pdf (accessed on 14 January 2016).
- Kotla, R.; Alvisi, L.; Dahlin, M. Zyzzyva: Speculative byzantine fault tolerance. ACM Trans. Comput. Syst. 2009, 27, 1–39. [Google Scholar] [CrossRef]
- Cowling, J.; Myers, D.; Liskov, B. HQ replication: A hybrid quorum protocol for Byzantine fault tolerance. In Proceedings of the 7th Symposium on Operating Systems Design and Implementation, Seattle, WA, USA, 6–8 November 2006; pp. 177–190. [Google Scholar]
- Eyal, I.; Gencer, A.E.; Sirer, E.G. Bitcoin-NG: A Scalable Blockchain Protocol. In Proceedings of the 13th Symposium on Networked Systems Design and Implementation, Santa Clara, CA, USA, 16–18 March 2016; pp. 45–59. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).