Mesh Twisting Technique for Swirl Induced Laminar Flow Used to Determine a Desired Blade Shape

Abstract

Swirling flow has been shown to increase heat transfer in heat exchangers. However, producing swirl while not presenting a severe pressure drop can be a challenge. In this paper, a desired shape of guidance blades for laminar swirl flow is determined by numerical simulation in OpenFOAM. Emphasis is on the mesh technique, where a predefined blade shape is formed by mesh twisting, or morphing. The validity of numerical simulations on a twisted mesh is shown by comparing it to the theoretical solution of laminar flow in a pipe without swirl and guidance blades. A sensitivity study shows that a cell size ratio of 0.025 of diameter is sufficient and affects the solution minimally. To determine the desired shape of guidance blades previously found optimal swirl decay and velocity profile for laminar swirling flow are utilized. Three blade shapes are explored: (I) with a twist angle that varies with axial location only; (II) having a deviation angle matching the theoretical deviation angle for laminar swirling flow; (III) same as II but with a hollow center. Simulations are performed for $\mathrm{Re}=100$ and swirl number $S=0.2$. Case II is able to sustain swirl longest while maintaining a low pressure drop and is therefore a desired swirler shape profile as predicted theoretically.

1. Introduction

Swirling flow can by found in many applications: heat exchangers, combustion chambers of jet engines, mixing tanks and more. Swirl increases the friction coefficient and consequently the heat transfer coefficient is increased [1]. Swirling flow in pipes can be produced by active methods (rotating cylinders [2] or rotating propellers [3]) or passive methods (like tangential inlet (e.g., [4,5]), radial/axial swirl blades at the inlet (e.g., [6,7]) or guided swirlers further downstream (more on passive swirl methods in [8,9]). Active methods generate sustained swirl (but require in turn external work) whereas passive methods experience swirl decay downstream unless they cover the entire length of the pipe. Swirl can also be generated by sudden expansion of the pipe (e.g., [10]) and in annular pipes (e.g., [11] and references therein). The most common guided swirlers are twisted tape (generally covering the full length of the pipe e.g., [4,12,13], which then leads to greater pressure drop), either fixed [14] or free to move with the flow, [15] propeller-type or other types of fixed vanes [16].

Most approaches on swirled flow have been aimed at turbulent flow, which is dominant in most heat exchangers, and the literature on laminar swirl flow is sparse. However, laminar swirl flow does also appear in heat exchangers and can be of great interest in the design of microfluidic heat exchangers where laminar flow only occurs. In addition, an ideal velocity profile for laminar swirl flow has been found in [17], where a specific tangential/angular velocity distribution is shown to give the lowest decay of swirl along the flow direction in a circular pipe. Therefore, it is easier to determine if the swirl flow induced is optimal in laminar flow than in turbulent flow, where at present no such ideal flow profile has been determined.

It should be noted that fixed blade swirlers need to have irregular geometry (i.e., they neither follow planes in $xyz$ nor $r\theta z$ coordinate systems) in order to induce swirl flow. Therefore, meshing an irregular geometry for the purpose of numerical simulations can be a challenge. Particularly, when using the finite volume method, it is important that individual cell shapes in the mesh are aligned with flow direction, corresponding to a structured mesh. Traditionally (including structured, unstructured and combined structured/unstructured grids [18]), cells are manually forced to conform to internal walls (blades), often causing increased skewness, loss of orthogonality of the cell walls and more seriously, a rastering of the boundary cells closest to the blades. This rastering will alter the boundary of the computational domain and induce errors in the velocity field of the flow. A mesh twisting/morphing method introduced in this paper is simple and minimizes the rasterizing effect and therefore accurately represents the domain’s size and shape in spite of the cell shape changes during the morphing process.

In this paper, the focus is on exploring a new efficient way of meshing devices that are meant to create a swirling flow. It is well known that a continuous twisted tape creates a too high pressure loss. Hence, short length swirlers are studied; and the shorter, the better. Although a rational approach is described in a previous paper [19], only a few profiles have been studied. Thus, new blade profiles have to be explored. To avoid geometrical meshing limits, it is important to find a “simple” and reliable way to mesh complex shapes that allows the control of the cell dimensions and distribution. The technique presented here consists in twisting an initial straight mesh instead of manually conforming a mesh to already designed blades. With this meshing technique, fixed curved blades are numerically generated from straight blades by this mesh twisting and the mesh automatically conforms to the blades. This efficient mesh generation approach is much less expensive than the conventional technique of generating a CAD and then discretizing the computational domain. It will thus be very easy to integrate it in an optimization loop of the shape of the blades in order to cover a broader parameter field while keeping the qualities of a structured mesh. Furthermore, the “inlet” angle of the swirler can be arbitrarily chosen as it can be set after the beginning of the twisting mesh. This is very useful if a downstream swirler has to be designed in order to reinforce a decayed swirling flow. We show that the errors produced by this twisting are minimal. Furthermore, we use it to search for the desired shape of the guidance blades which can be determined from the fundamental swirling mode described in [17]. The study is performed for a Reynolds number (Re) of 100 and a swirl number (S) of $0.2$, assuming that the swirling device is one diameter in length.

2. Materials and Methods

2.1. Governing Equations

The flow is governed by the Navier–Stokes equations. Furthermore, assuming incompressible flow of Newtonian fluid with constant viscosity and no gravity effects, the governing equations become

$$\begin{array}{c}\nabla ·\mathbf{V}=0,\end{array}$$

(1)

$$\begin{array}{c}\frac{\partial \mathbf{V}}{\partial t}+\left(\mathbf{V}·\nabla \right)\mathbf{V}+\frac{1}{\rho }\nabla p=\nu {\nabla }^2\mathbf{V},\end{array}$$

(2)

where $\mathbf{V}$ is the velocity vector, $\rho$ is density, $\nu$ is kinematic viscosity and p is pressure. Equation (2) is the traditional representation of the Navier–Stokes equation but the advection term, $\left(\mathbf{V}·\nabla \right)\mathbf{V}$, is a pseudovector expression making it variant under coordinate transformation. In pipe flow, cylindrical coordinates are a natural choice (it should be noted that OpenFoam will nonetheless solve the equations in Cartesian coordinates) so an invariant coordinate representation of the Navier–Stokes equation is preferred [20], i.e.,

$$\begin{array}{c}\frac{\partial \mathbf{V}}{\partial t}+\nabla \left(\frac{\mathbf{V}·\mathbf{V}}{2}\right)-\mathbf{V}\times \left(\nabla \times \mathbf{V}\right)+\frac{1}{\rho }\nabla p=-\nu \nabla \times \left(\nabla \times \mathbf{V}\right).\end{array}$$

(3)

When choosing the desired guidance blade shape to be inserted to induce swirling flow, both the resulting velocity field and pressure drop are of interest. Specifically, the axial and tangential velocity components, $v_z$ and $v_{\theta }$, respectively, describe the resulting flow as shown in Figure 1. Note that the axial velocity distribution in fully developed laminar flow is represented by a perfectly parabolic profile,

$$v_z=2\overline{v}\left(1-\frac{r^2}{R^2}\right),$$

(4)

where R is the radius of the pipe, r is the radial coordinate and $\overline{v}$ is the average velocity in the pipe.

The domain under consideration consists of an intake (inlet), an exit (outlet) located 25 diameters from the inlet, and surrounding fixed walls (pipe). The boundary conditions for $\mathbf{V}$ and the kinematic pressure $\frac{p}{\rho }$ used in the study are following:

Inlet: 

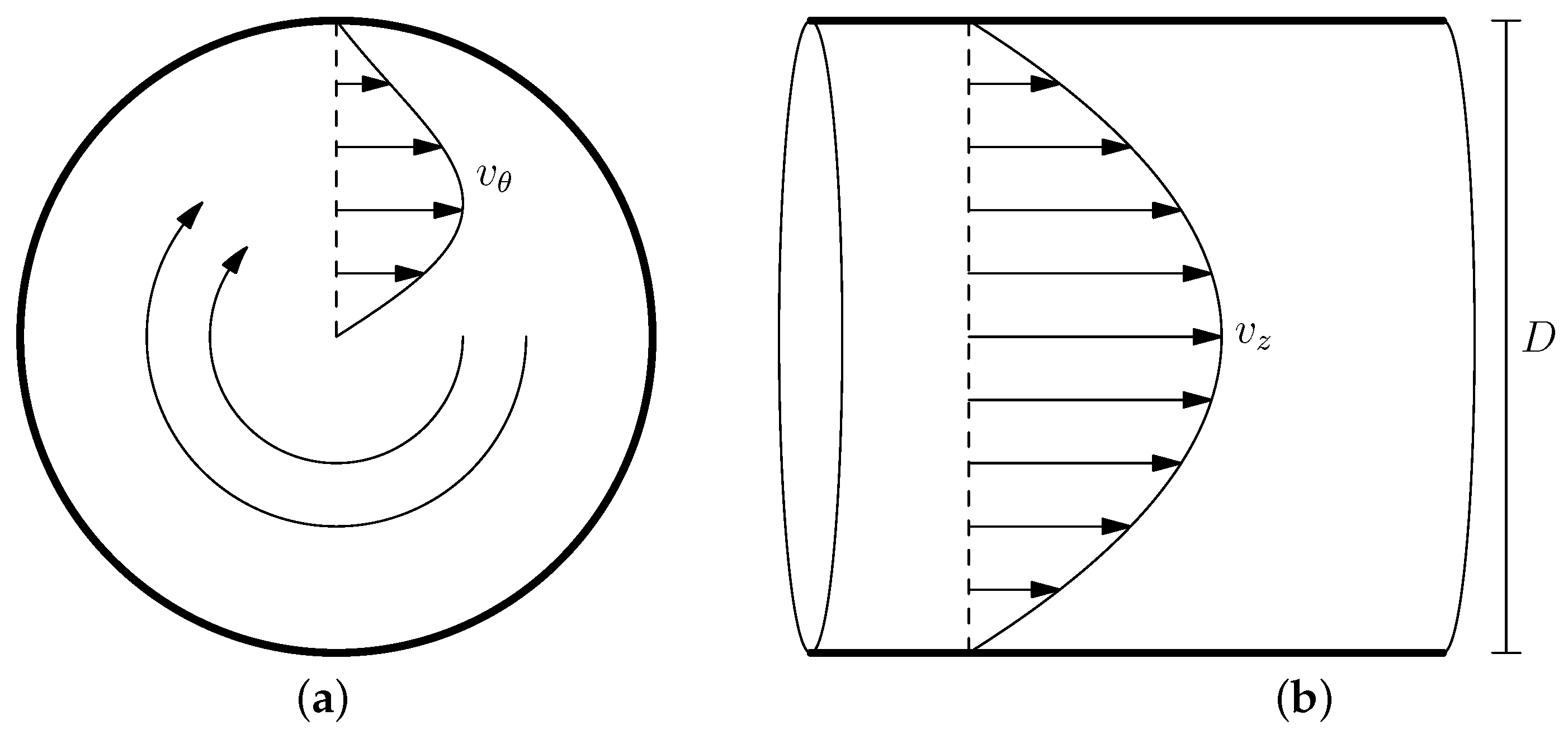
Velocity is purely axial, with a velocity profile specified in accordance with Equation (4) with an average velocity of 1 m/s (corresponding to Re $=100$). The normal gradient of pressure is set to zero, thus $\frac{\partial p}{\partial n}=0$.

Outlet: 

The normal gradient of all velocity components is set to zero. Pressure normal gradient is still zero, but with a fixed average value of 0 which sets a reference pressure for the whole system.

Walls: 

No slip is allowed for the velocity, effectively setting $\mathbf{V}=\mathbf{0}$, and the normal gradient of pressure is zero.

2.2. Swirling Flow

In swirling flow, two velocity components are of main interest, the tangential $v_{\theta }$ and the axial $v_z$. Beaubert et al. [17] found the ideal velocity profile for the tangential velocity for laminar swirl flow. This velocity profile can be seen in Figure 2. Finding the swirler that will behave optimally is finding the one that produces tangential velocity that is as close to this ideal velocity profile as possible.

The swirl number is defined as the ratio of angular momentum flux to axial momentum flux and thus represents swirl intensity (see [21]). A few slightly different versions of the swirl number exist [22], each able to highlight various aspects of the swirl flow. In this paper, the following definition of swirl number, S, is used

$$S=\frac{{\int }_{A}r{v}_{\theta }{v}_{z}dA}{R{\int }_A{v}_z^{2}dA}.$$

(5)

Chen et al. [1] found that the swirl number is dependent on Re for laminar flow but not for turbulent flow. They further concluded that the structure of the velocity profile has the same dependency, which was confirmed in [17].

If the swirler does not cover the entire length of the pipe, swirl decay will be experienced. Swirl decay is often assumed to be exponential downstream of the swirler exit, i.e.,

$$S=\beta e^{-\alpha \frac{z}{R}},$$

(6)

where $\beta$ and $\alpha$ are flow dependent constants, z is the axial distance from the exit of the swirler and R is the radius of the pipe. This assumption is valid for swirl numbers below 0.2 [23], as usually experienced in pipe flows. More accurate approximations of swirl decay in laminar flow can be found in [24]. There, the $\alpha$ and $\beta$ coefficients of Equation (6) depend on Reynolds number. Finally, Figure 3 shows the movement of a single streamline through a swirler, and how the rotational movement decays as suggested in [23]. Figure 3 also shows how a twist angle for the mesh is defined.

2.3. Numerical Approach

Simulations were performed using OpenFOAM^®, an open source object oriented Computational Fluid Dynamics software written in C++ [25]. A second order steady state solver was used, specifically simpleFoam which is part of OpenFOAM version 5.0. A finite volume approach is used for incompressible laminar flow, where pressure and momentum equations are solved iteratively until a specific residual criteria has been reached. A speed up of the solver is achieved by parallelization and by using the fast iterative Generalized Algebraic MultiGrid (GAMG) method for solving critical systems of linear equations.

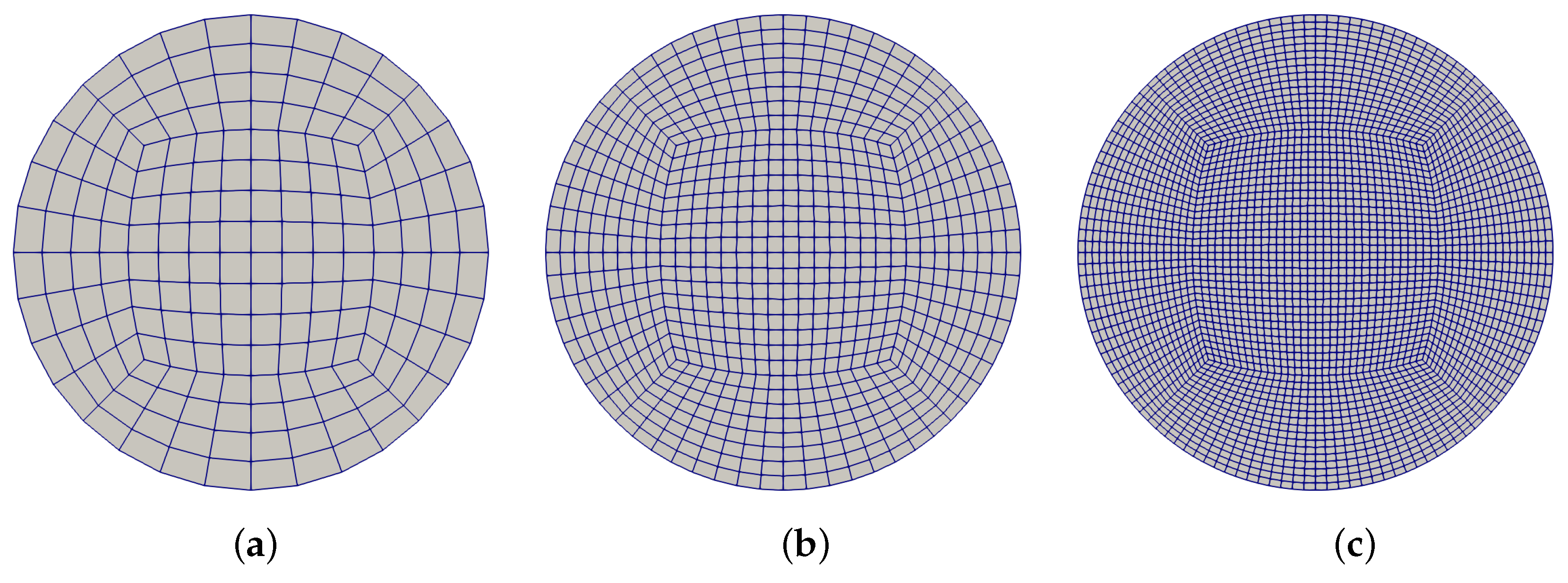
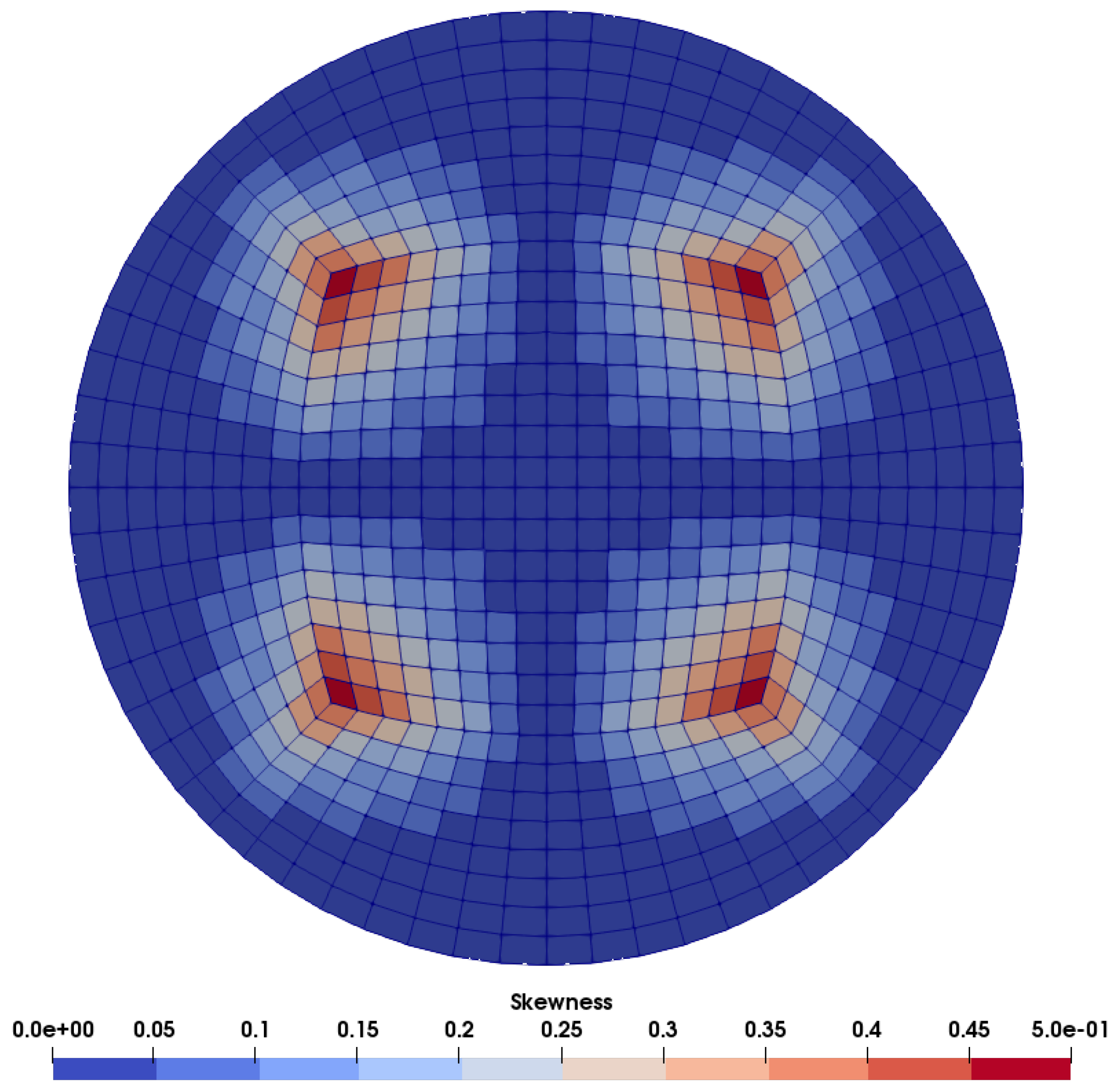
2.4. Mesh Morphing

The interior of the pipe needs to be covered with a spatial three-dimensional mesh. The mesh is constructed of block structured hexahedrals. One can describe the mesh as a rectangular inner core of cells at the center of the cylinder, with radial cells spreading from the rectangular inner core to the outer diameter. A cross section of the mesh without guidance blades can be seen in Figure 4.

It is inevitable that some of the cells in the mesh are skewed, which is most notable at four locations in the mesh (see Figure 4). Skewness is a measure on how equilateral and equiangular a cell is and its value gives a good indication of the quality of the mesh (zero being perfect and 1 being degenerated). The skewness value of the mesh (without blades) is shown in Figure 5.

Most of the mesh has a skewness value below 0.25 which is considered excellent. The maximum skewness value in the mesh is 0.49 which is between 0.25–0.50 and is considered good. Increasing the number of cells does not affect the maximum skewness value. In addition to skewness, the loss of orthogonality of the cell walls can cause numerical errors. The mesh met the constraint required by OpenFOAM and, as shown in Section 3, the mesh did not affect the solution greatly and will, therefore, not be explored further.

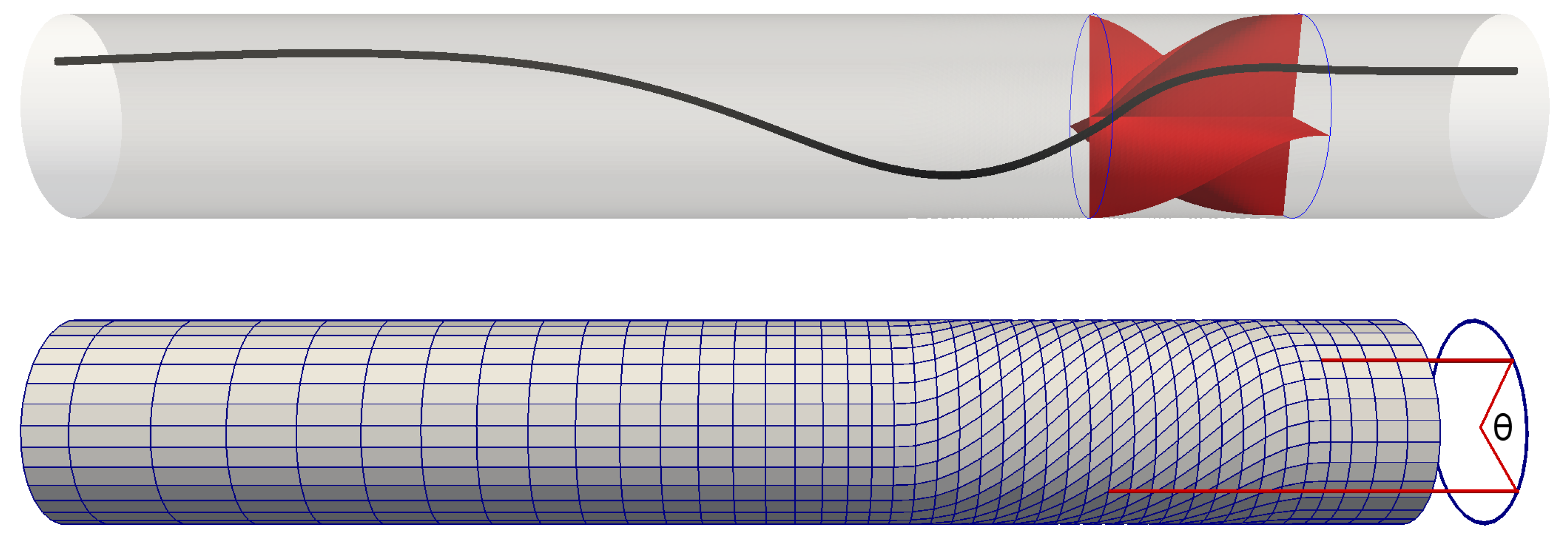
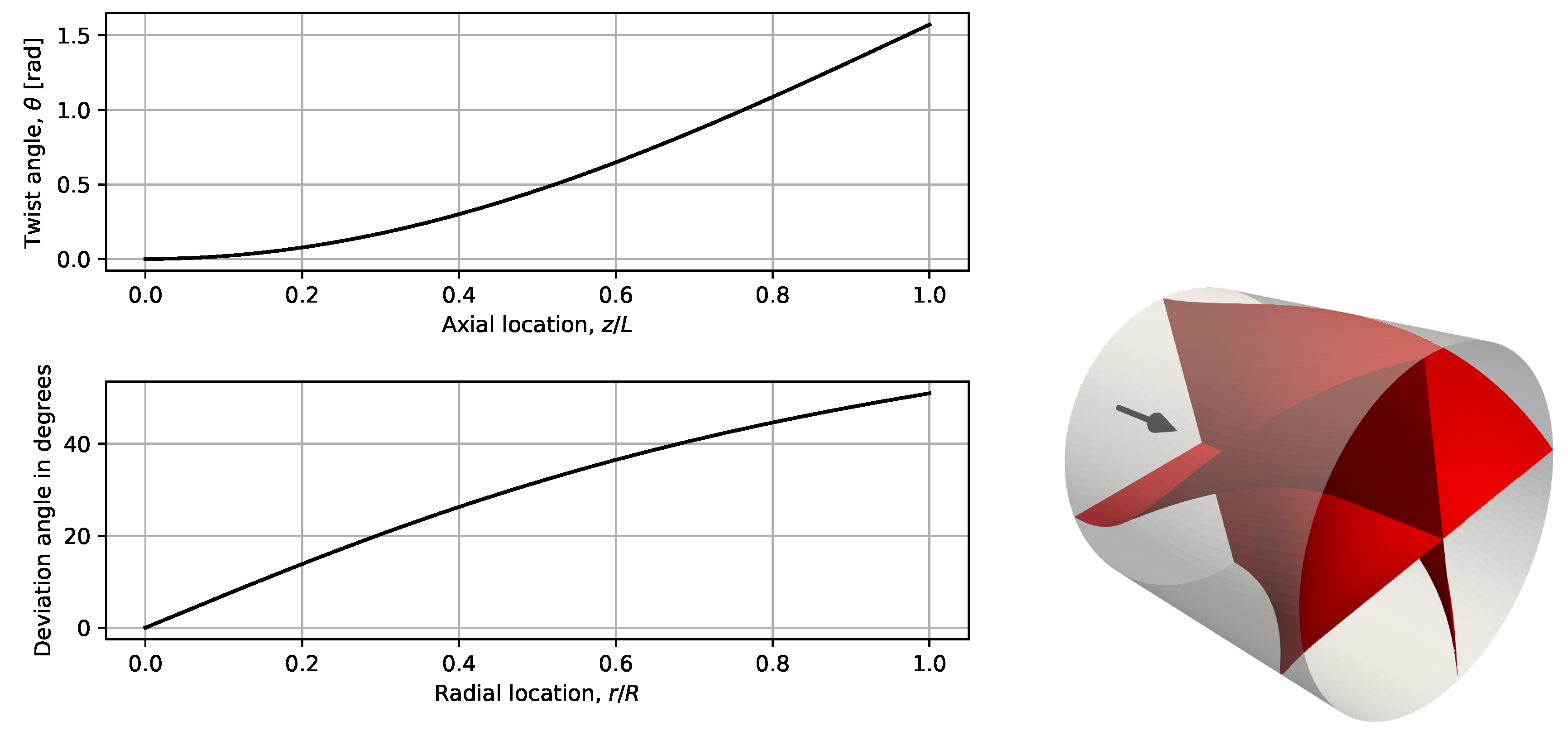
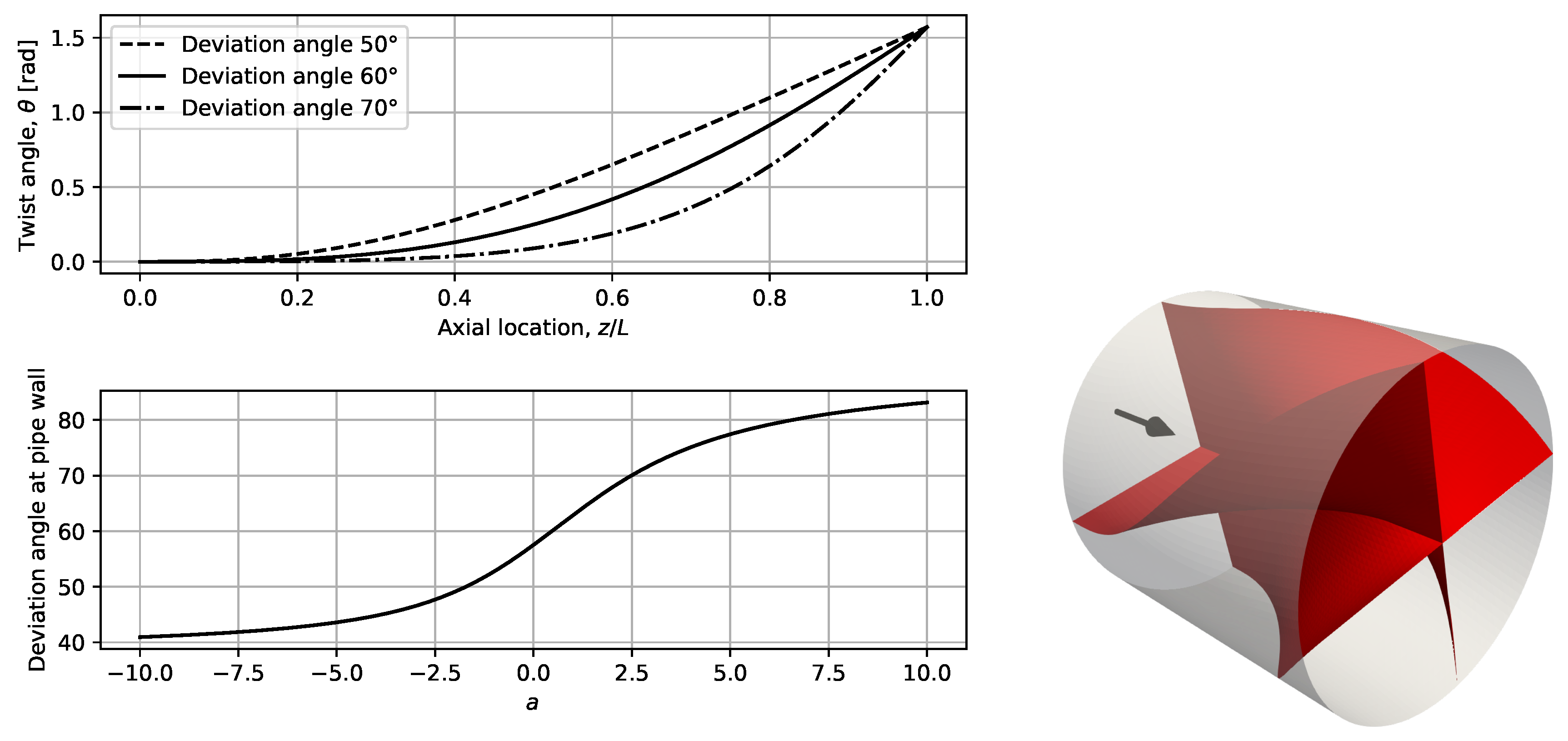
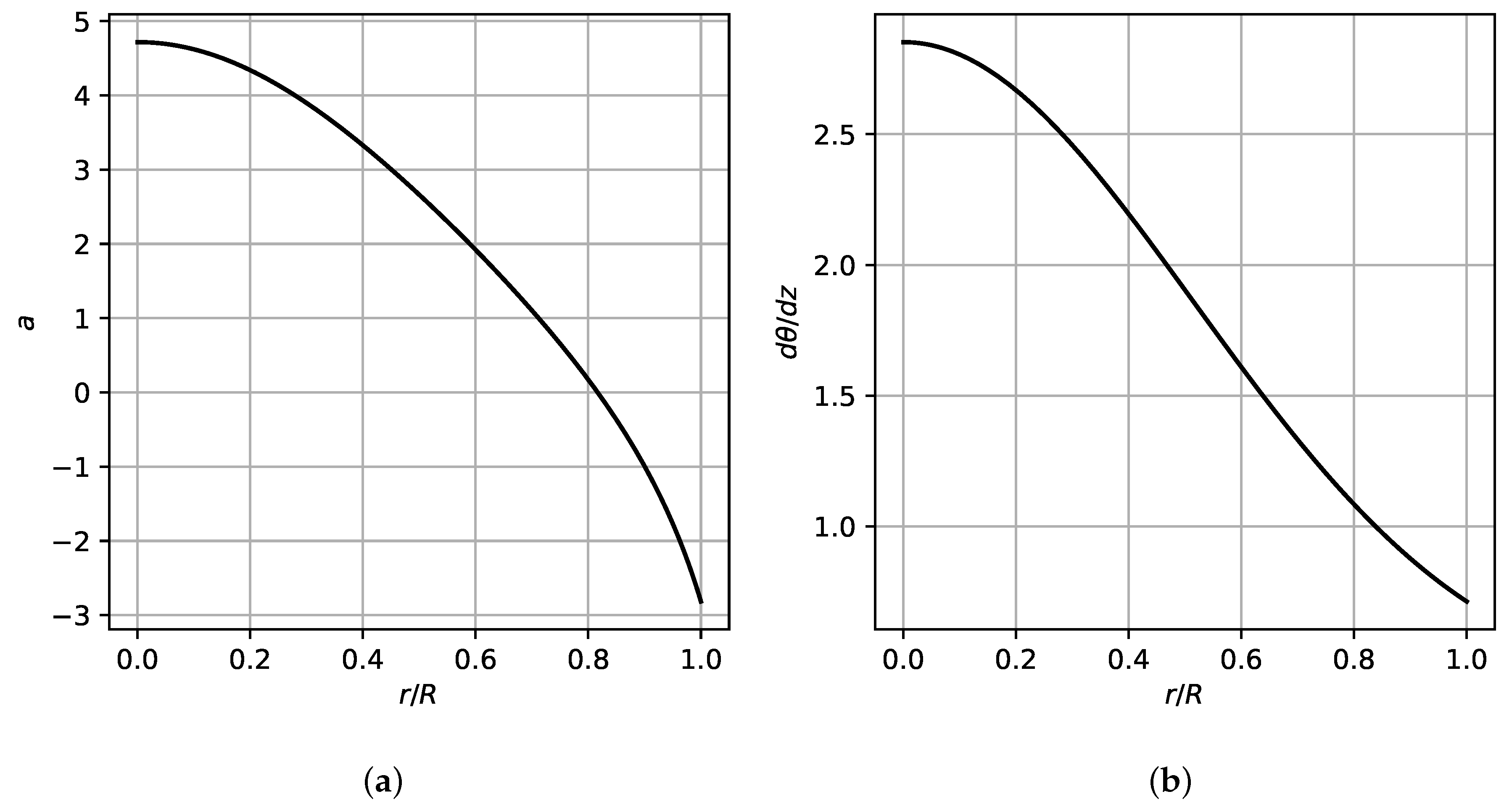
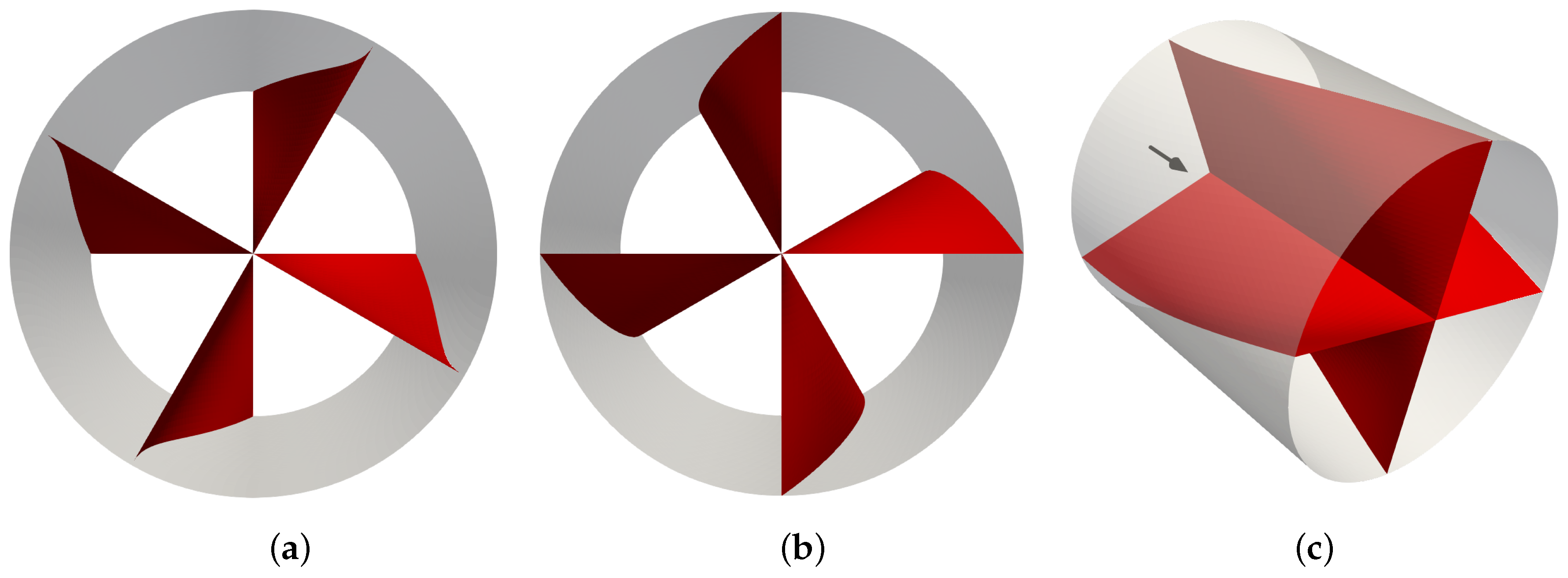
2.5. Constructing Guidance Blades

The general approach in this paper is to use mesh morphing (twisting) to obtain a preferred shape of a guidance blades (vanes) in a swirling device. Thus, the blades, defined as wall patches in OpenFOAM, only need to be specified as straight before the morphing takes place. The aim is to get a distribution of deviation angle as shown in Figure 2, for the flow itself (the flow might not follow the blade’s angle immediately). Thus, the deviation angle ($\varphi =arctan(v_{\theta }/v_z)$) indicates a necessary blade shape.

Three types of blade setups are considered. The twist angle in the mesh is generally a function of radial and axial location, $\theta (z,r)$. The cases are described as follows:

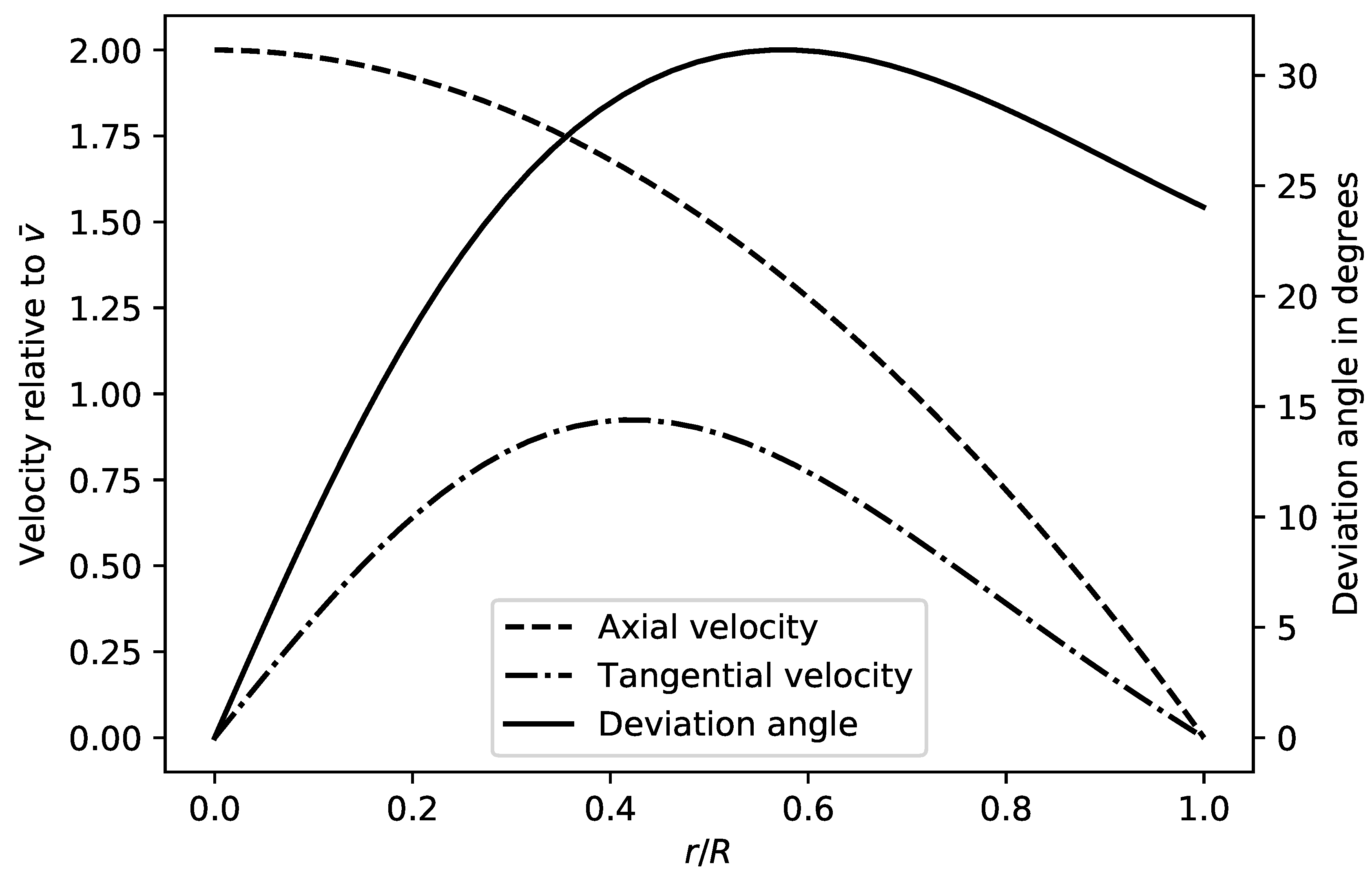
• Blades where $tan(\varphi )$ changes linearly from the center of the pipe to the outer wall, assuming that $\varphi$ is the deviation angle. This is equivalent to constructing a single shape of blade, defined by a twist angle $\theta$ as a function of axial location z but not affected by radial location r.
• Blades where the deviation angle changes along the pipe axis, but also follows at the exit the angle defined in Figure 2, in the radial direction.
• Same blade setup as in Case II, but where 20% of the inner core is removed, thus reducing the flow restriction because of the blade connections in the center.

In all cases, the blade’s inlet was four diameters from the pipe inlet and all swirlers were one pipe diameter in length.

A suitable profile for the twist angle for Case I, where the curvature is zero at the blade exit, is

$$\theta ={\theta }_0\left(1-cos\left(\frac{\pi (z-z_0)}{2(D-z_0)}\right)\right),$$

(7)

where ${\theta }_0$ and $z_0$ are the maximum twist angle and inlet location of the swirler, respectively, and L is the length of the swirler. Figure 6 shows the general blade shape in the axial direction as well as the deviation angle for Case I.

In the second case (Case II), we define a function that is the second derivative of the twist angle formula, but with a parameter a defined,

$${\theta }^{″}(\eta )=K{\theta }_{0}exp(a\eta )\left(1-{\eta }^2\right),$$

(8)

where $\eta =\frac{z-D}{D}$ represents dimensionless axial location ($-1\le \eta \le 1$ from inlet to exit of the swirler) and K is a constant to be determined. This function is closely related to curvature, and it turns out that ${\theta }^{″}$ is zero at the inlet and exit, as well as ${\theta }^{″}$ always being positive. Integration where K is selected in order to get $\theta (1)={\theta }_0$ finally gives a blade profile

$$\theta (\eta )={\theta }_0\frac{exp(a\eta )\left(a^2(1-{\eta }^2)+4a\eta -6\right)+exp(-a)\left(4a+6+2a(a+1)(\eta +1)\right)}{exp(a)\left(4a-6\right)+exp(-a)\left(6+4a(a+2)\right)},$$

(9)

which has the following properties:

• The curvature at the inlet and exit is zero.
• The twist angle is zero at the inlet ($\eta =-1$) and ${\theta }_0$ at the exit ($\eta =1$).
• The slope with respect to $\eta$ (deviation) is zero at the inlet, but is controlled by a at the exit.
• The deviation grows monotonically from the inlet to the exit, regardless of the selection of a.

Figure 7 illustrates the blade shape in the axial direction for three different end deviation angles as well as the relationship between the parameter a and the deviation angle at the pipe wall. The wall is selected as an example, since the deviation angle also changes as a function of radius. In addition, note that these are just examples and not optimized shapes as are presented in the Results section.

It should be noted that the only difference between Case III and Case II is that, in Case III, blades that are within $0.2R$ from the pipe centre are removed, thus removing the axial flow restriction in the middle.

To conclude, the mesh morphing process can be specified as Algorithm 1 which changes the coordinates of each point (vertex) in the mesh, in order to obtain the desired twist and deviation angles. As an example for Case I, the process is as follows:

Algorithm 1: Mesh morphing process.

Require: $\theta (z,r)={\theta }_0\left(1-cos\left(\frac{\pi z}{2}\right)\right)$    for all x,y,z coordinates do   $r\leftarrow \sqrt{x^2+y^2}$     if $z>6$ then    ${\theta }_t\leftarrow 2\theta (1,r)$     else if $z>5$ then    ${\theta }_t\leftarrow 2\theta (1,r)-\theta (6-z,r)$     else if $z>4$ then    ${\theta }_t\leftarrow \theta (z-4,r)$     else    ${\theta }_t\leftarrow \theta (0,r)$     end if     $x_{\mathrm{new}}\leftarrow xcos({\theta }_t)+ysin({\theta }_t)$     $y_{\mathrm{new}}\leftarrow -xsin({\theta }_t)+ycos({\theta }_t)$     $z_{\mathrm{new}}\leftarrow z$    end for

Note that the twisting continues after the blade exit point in order to get a smooth transition from the twisted part to the straight part, hence the definition ${\theta }_t=2\theta (1,r)$ in the algorithm. This is also seen in Figure 3 where $\theta$ covers only the part where the swirl device is present.

3. Results and Discussion

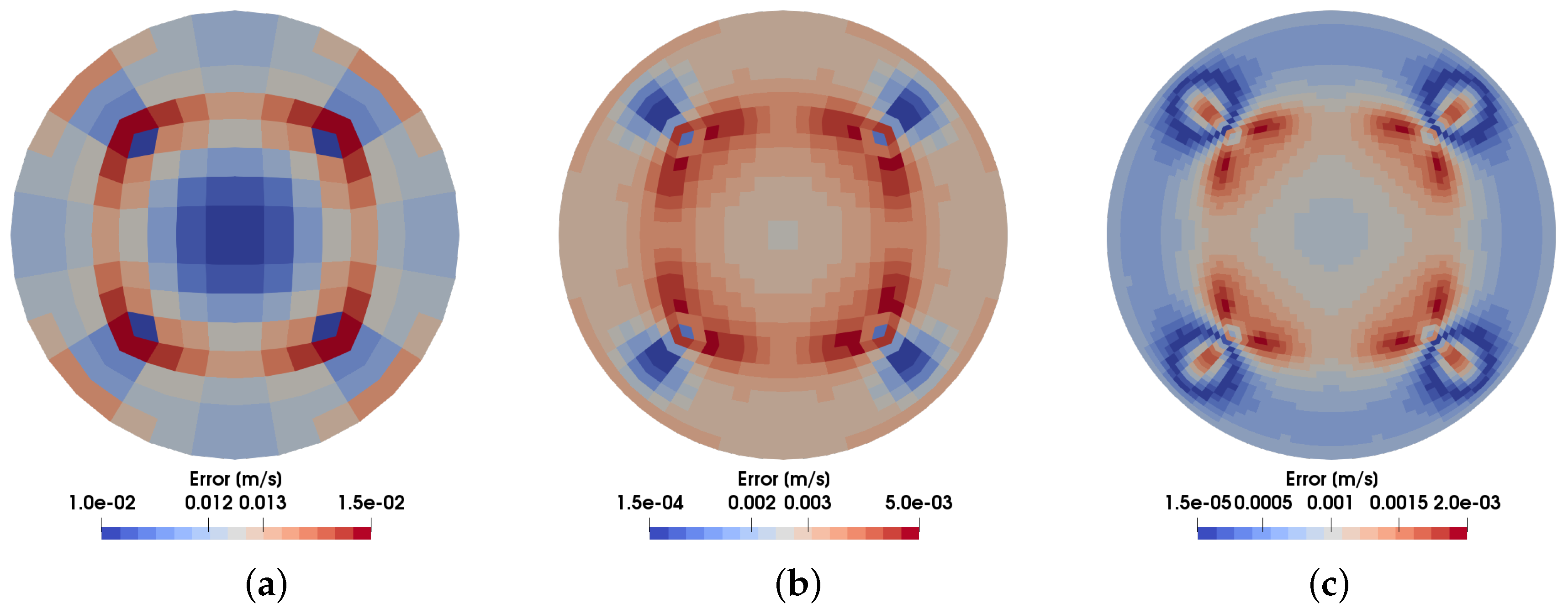
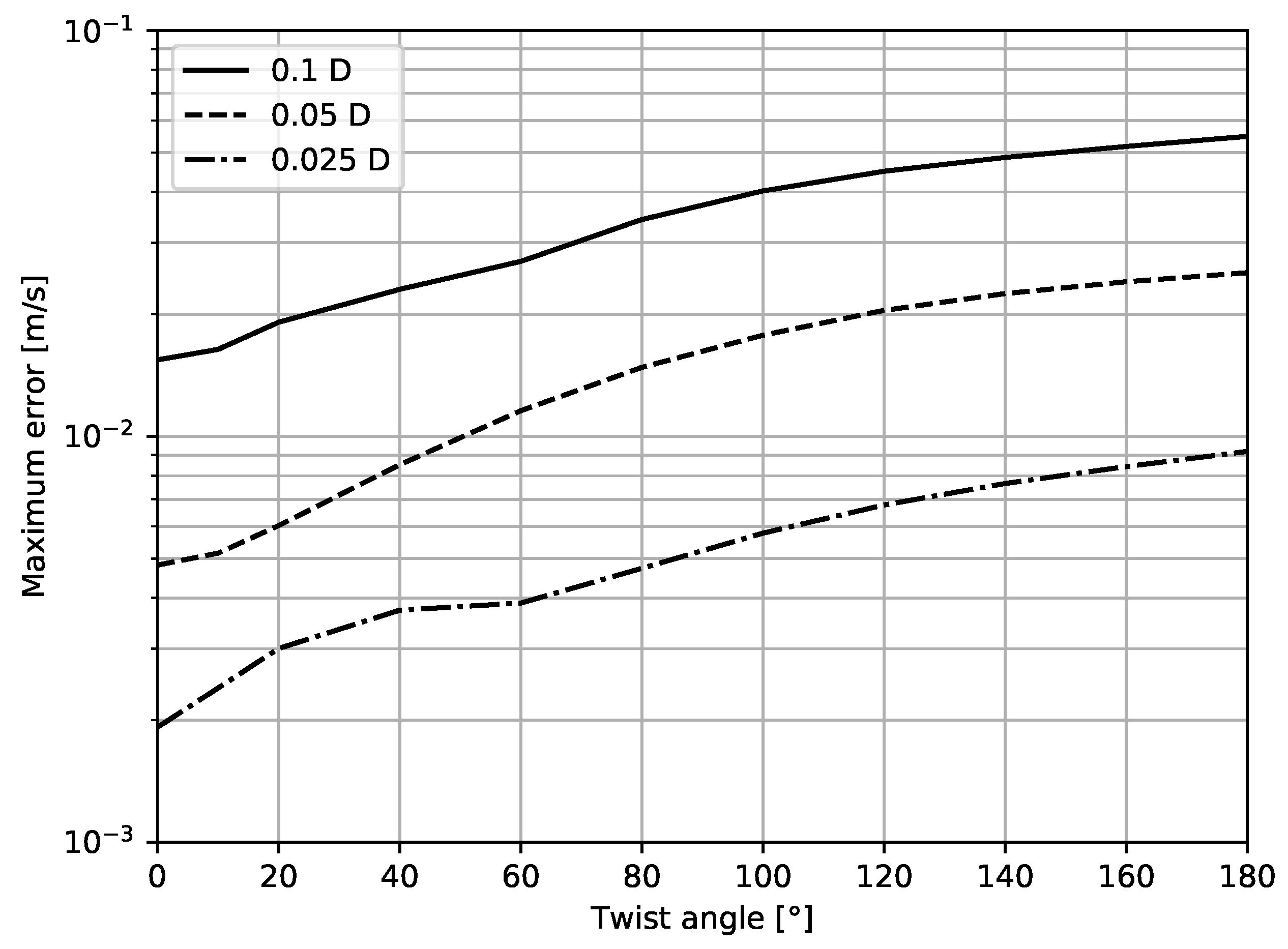
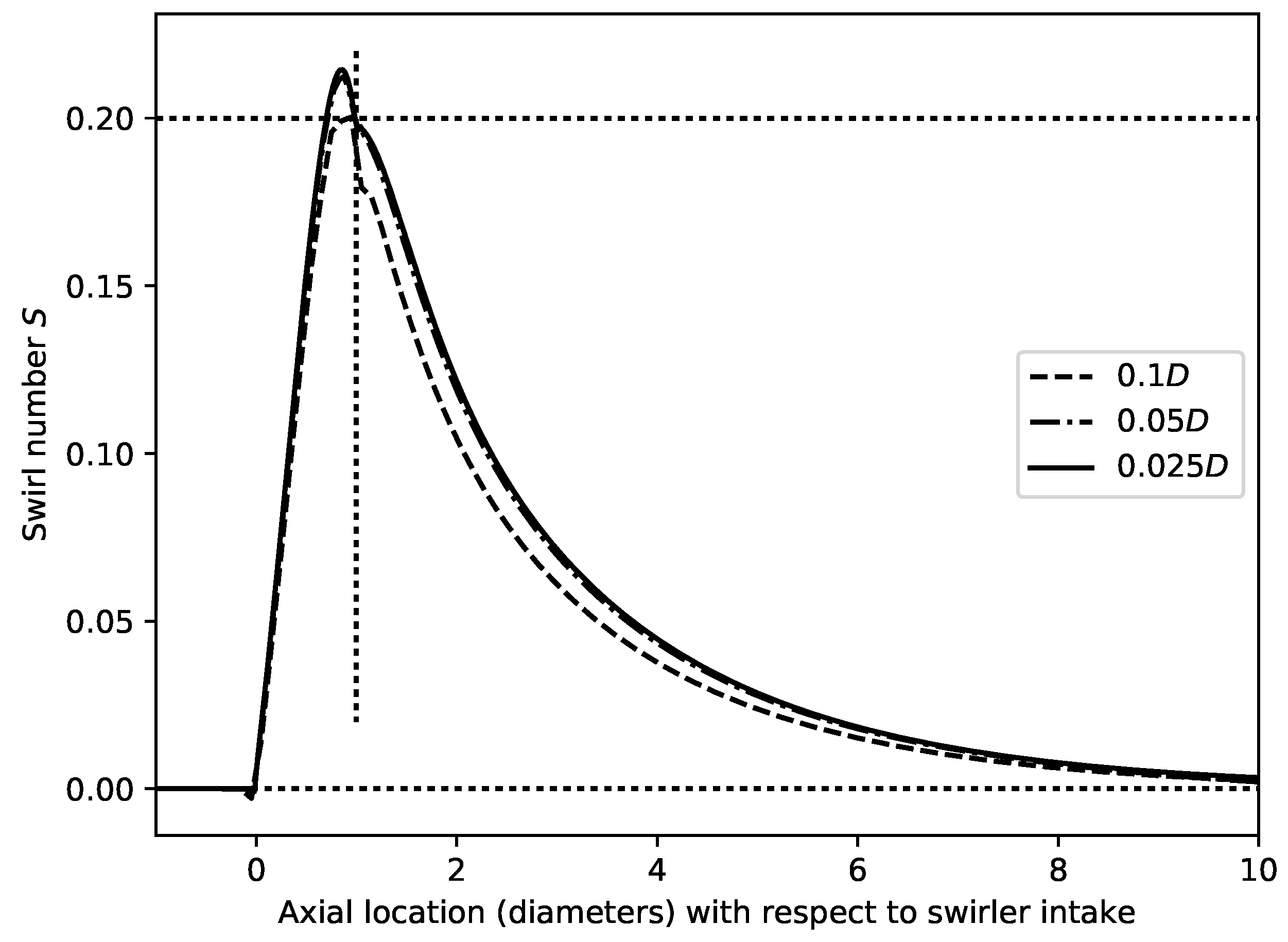
3.1. Mesh Size and Twisting Sensitivity

Twisting the mesh affects the orthogonality of the cells and can increase skewness. Furthermore, the mesh faces deviate slighly from being flat in the twisting region, thus inducing minor errors in area and volume calculations.

Figure 8 shows the error in axial velocity, compared to Equation (4), for three different mesh densities when the mesh is not twisted. The average cell sizes are $0.1$, $0.05$ and $0.025$ diameters for the three different mesh densities. It is clear that the discretization errors decay relatively fast when a finer mesh is used and are of the order of magnitude ${10}^{-3}$ for the finest mesh (for a mean velocity of 1 m/s). This result also indicates which magnitude of error is acceptable for a twisted mesh.

It is important to verify that twisting the mesh does not affect the calculation greatly before implementing it on numerical simulations with guidance blades. Using a mesh twisted according to Equation (7), laminar flow with no guidance blades was compared to a simulation on an equal but untwisted mesh. The velocity profile from those two meshes is also compared to the theoretical solution for laminar flow.

Figure 9 shows the maximum error in velocity for the three mesh densities discussed above. The error grows steadily with twisting angle, indicating the effect of skewness and face distortion in the mesh. However, the effects are moderate and the finest mesh outperforms the coarsest one by a factor two even though it is twisted by $180{}^{\circ }$. In general, twisting by $180{}^{\circ }$ increases the error roughly by a factor of five, but the overall error is still relatively small for the finest mesh.

Finally, a mesh sensitivity study is shown for a case with actual blades present in the pipe, thus giving rise to swirling flow. Figure 10 shows the effect of $180{}^{\circ }$ twisting on the swirl number, along the axial direction of the pipe. The coarsest mesh deviates clearly from the other two and it can be argued that the finest mesh is sufficent for an accurate simulation of the swirling flow, using the mesh twisting technique.

3.2. Guidance Blade Design

After verifying that the mesh twisting minimally affects the solution, this technique can be used to find the desired shape of guidance blades for laminar swirling flow, which approaches the deviation angle shown in Figure 2. Figure 11 shows the results of finding values of a that give a deviation angle distribution as proposed in Figure 2. This distribution uses a total twist angle of $\theta =30{}^{\circ }$ and the deviation angle is equivalent to a swirl number $S=0.2$.

The resulting swirler design is shown in Figure 12, where the deviation angle at the exit exactly follows the profile shown in Figure 2.

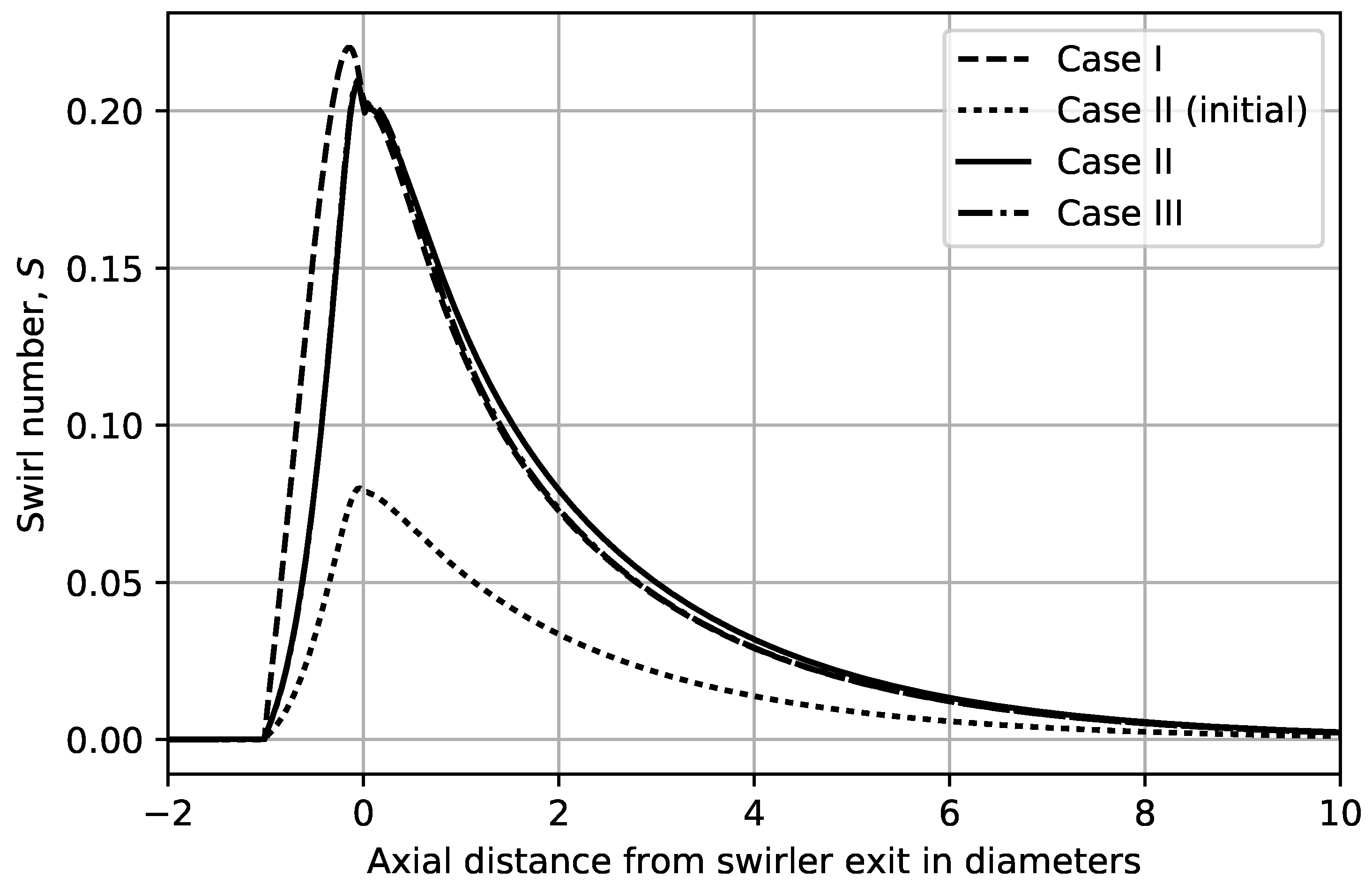
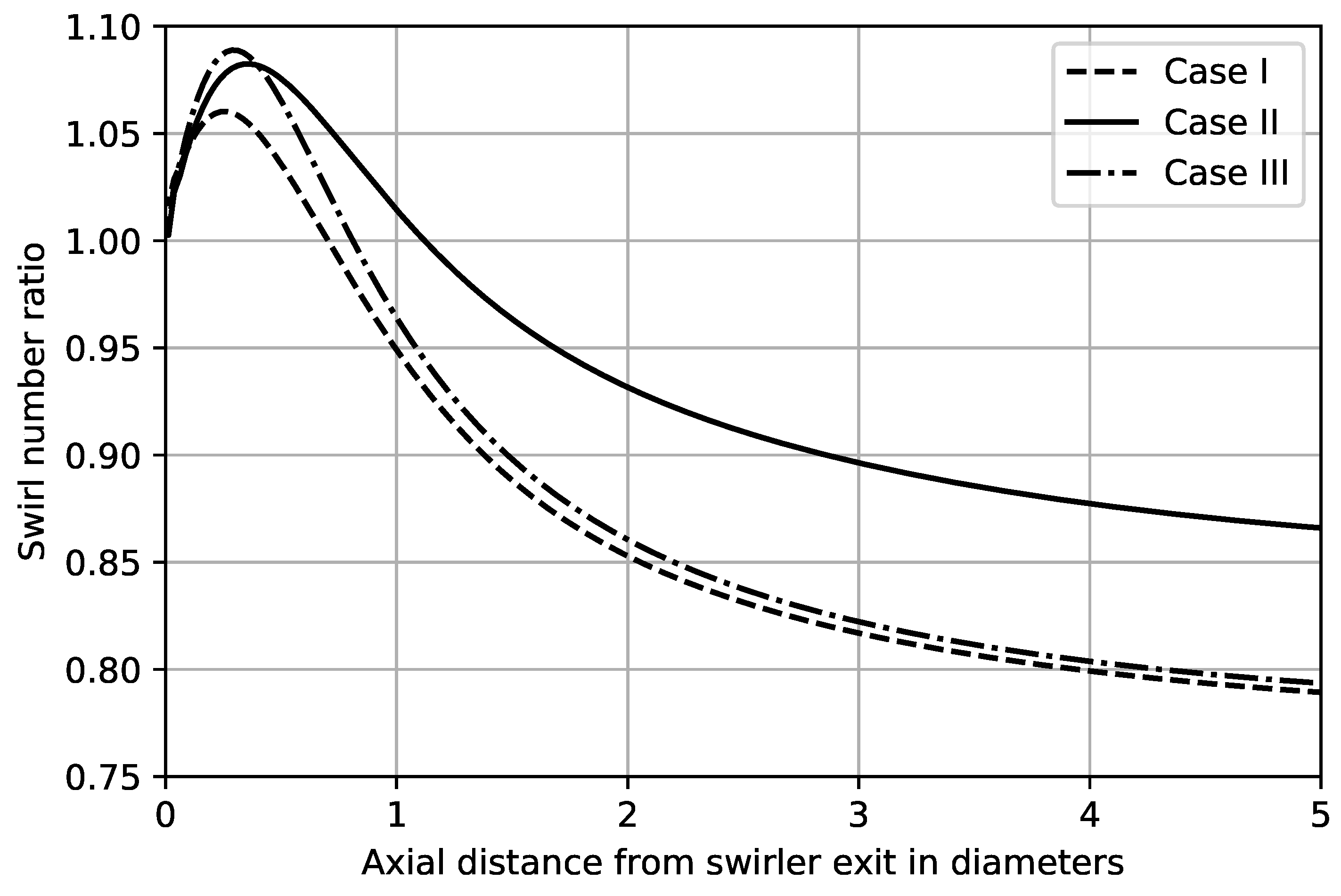
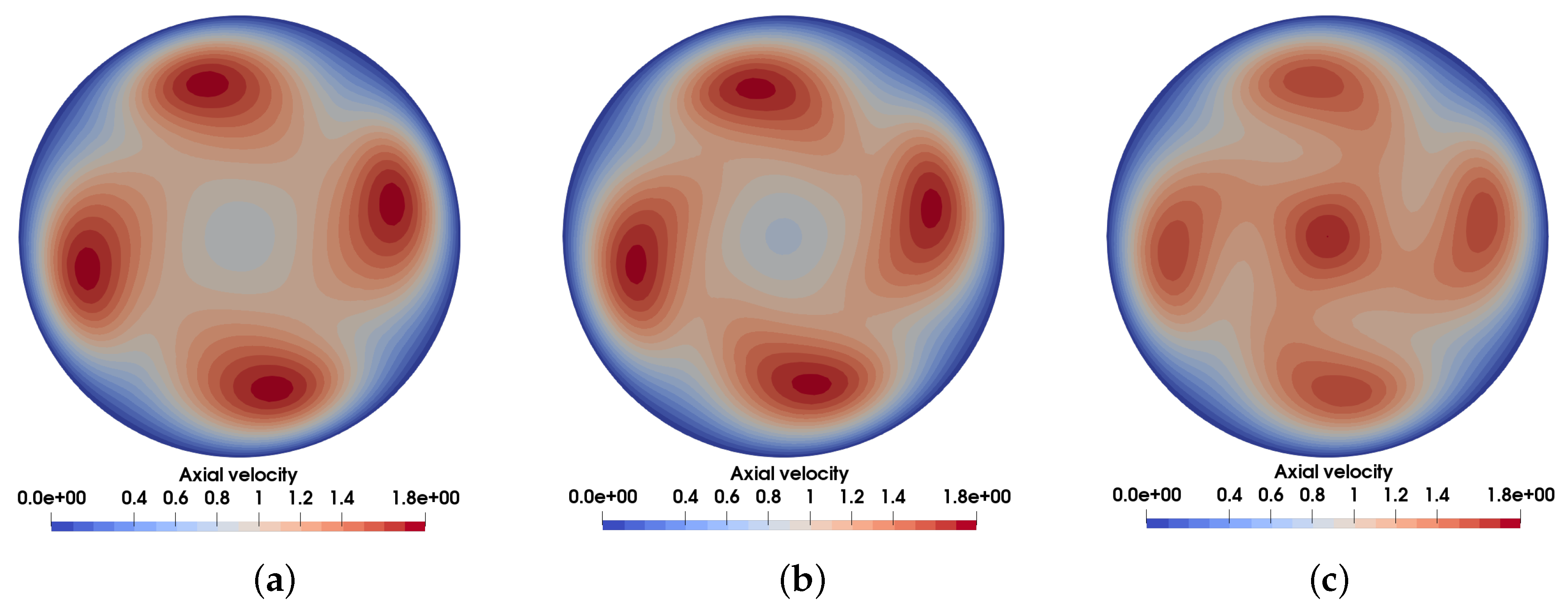
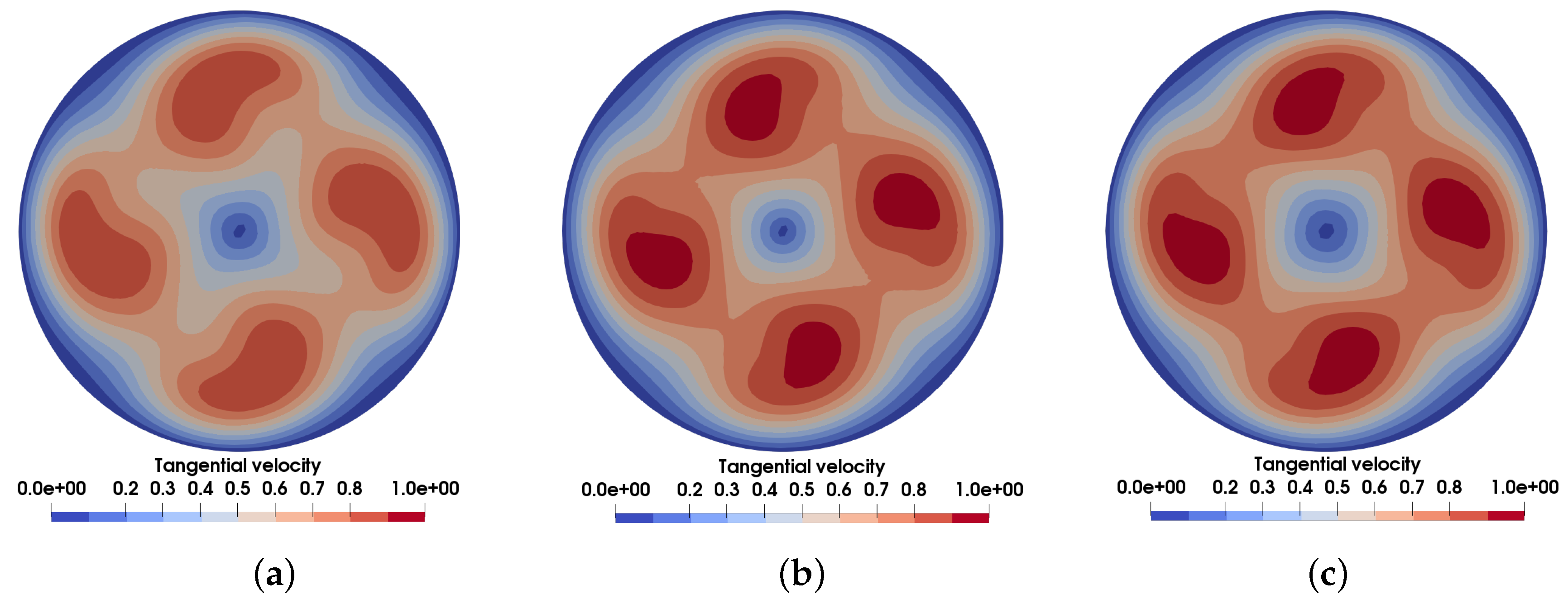
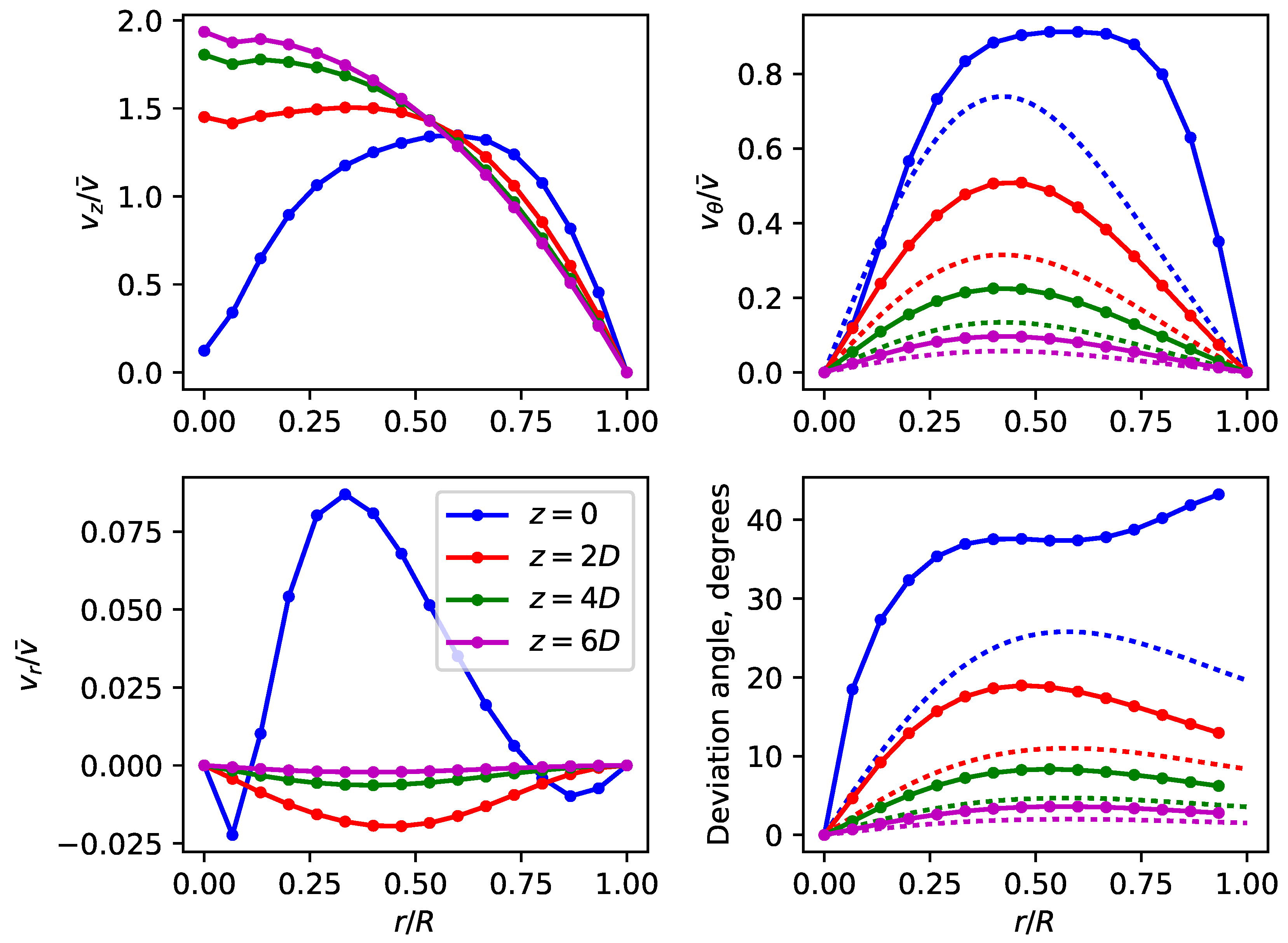
3.3. Case Comparison

Figure 13 shows the results from four different computational cases, with the focus on the swirl number and how it decays along the flow axis. The twist angle is adjusted for all the cases to obtain a swirl number $S=0.2$ at the swirler exit, except for the (initial) case where the theoretical deviation angle shown in Figure 2 is used directly. It is clear that, because of the relatively few guidance blades and the laminar layer forming along the blades, less than half the swirl number is actually obtained when using the (initial) case. It is also noticeable that Case I overshoots the design value $S=0.2$ but is otherwise performing relatively well. The decay profiles are examined further in Figure 14, where they are shown as a ratio to the theoretical decay shown in Equation (6), with $\alpha =0.213179$ obtained from [17]. Case I and Case III (hollow middle) perform similarly, but Case II seems to be superior in terms of keeping the swirling effect along the axis. This confirms that the closer the tangential velocity profile is to the ideal velocity profile, the closer the swirl decay is to the theoretical exponential decay.

Figure 15 shows the additional pressure drop along the axis when compared to standard Hagen–Poiseuille flow (laminar with no swirling). This is useful to compare the cases as well as observe the difference between added pressure drop because of swirling, and because of the swirler device. It turns out that Case III (hollow) is slightly better than Case II (blades are gathered in the center), but both are superior to Case I where the deviation angle at the exit changes linearly with radius. This is shown more clearly in

Table 1. A comparison of added pressure drop and twist angle at the swirler exit for the three cases.

Case:	I	II	III
Added pressure drop [diameters]	$11.47$	$10.44$	$10.25$
Twist angle at swirler exit ${[}^{\circ }]$	$108.9$	$74.5$	$84.8$

along with the necessary maximum twist angles for the cases.

One measure of the performance of different blade setups is how well the axial and tangential velocity profiles conform to the ideal profiles depicted in Figure 2. Figure 16 shows the axial velocity distribution in a cross section half a diameter downsteam of the swirler exit. The results for Cases I and II are very similar; both show the effect of using four blades and thus get an uneven distribution in the angular (tangential) direction. The effect of removing the blades in the centre in Case III is clearly visible, showing a greater axial velocity in the centre of the cross section.

Similarly, Figure 17 shows a comparison of the tangential velocities for the three cases. Here, Cases II and III yield similar results and both result in a more uneven velocity distribution in the tangential direction. All three show the tendency of the flow distribution to follow the theoretical profile for the tangential velocity.

The final result in Figure 18 shows the average axial, tangential and radial velocities as a function of radius, for four cross sections downstream from the blades using Case II as an example. This corresponds to the results in [17] where the profiles are axisymmetrical (not the case here because of the blades) and indicate a clear exponential decay along the flow direction. The deviation angle is furthermore shown for the four cross sections in the figure.

The averaging is performed by taking a plane cut at a given axial z position, followed by a cylindrical cut at a given radius r. Each value is therefore based on an average over a circle.

It is clear that the velocity profiles deviate severely from the theoretical one at the blade exit, but downstream the profiles quickly reach the shape predicted by the fundamental mode. The radial component (assumed zero in [17]) is also quite small and is reduced quickly downstream. The distribution of the deviation angle also quickly reaches the predicted profile, as seen in the lower left part of the figure, two diameters from the blade exit.

4. Conclusions

In this paper, the desired shape design of guidance blades in laminar flow has been sought. In order to produce flow across the guidance blades numerically, a new type of mesh technique was explored. Instead of manually adjusting the mesh to conform to the irregular shaped guidance blades and possibly causing the largest errors where the most accuracy is needed (in the boundary layer close to the blades), a high quality mesh was constructed with blades conforming to the x-, y-, z-axes and the mesh then twisted until the desired shape of the guidance blades was reached. This mesh twisting technique was at first tested on laminar axial flow and was shown to give minimal errors in the axial velocity of order ${10}^{-3}$ m/s compared to a mean velocity of 1 m/s. This was considered acceptable. When deciding on a desired shape of the guidance blades, the deviation angle based on the theoretical optimal velocity profile was used. Three cases were explored all with four blades, swirl number 0.2 and Re 100. Case I is where the twist angle is a function of axial location. Case II is where the deviation angle changes along the pipe axis according to the theoretical value. Case III is like Case II with a hollow center in order to minimize pressure drop. Case II has a lower swirl decay than Cases I and III. The pressure drop for Case III is slightly lower than for Case II but significantly higher for Case I than the other two cases. All cases have a non-uniform axial velocity profile in the angular direction half a diameter downstream from the swirler exit, resulting from the four blade set up. Cases I and II have an axial velocity profile with a closer match to the theoretical axial velocity component for laminar swirl flow than Case III. Case III has a strong axial velocity component in the middle of the pipe due to the hollow center, therefore, deviating from the optimal axial velocity profile for laminar swirl flow. All cases have half a diameter downstream of the swirler a tangential velocity similar to the theoretical laminar swirl flow tangential velocity profile. By comparing the three cases with regard to velocity field, swirl decay and pressure drop, one can conclude that Case II outperforms the other two cases and is therefore the desired blade shape design for a guidance swirler. In a further study, the length of the swirler and the number of swirl blades can be explored, as well as desired blade shape for turbulent flow.