On Minimal Unique Induced Subgraph Queries

Featured Application

MUIS (Minimal Unique Induced Subgraph) query can be used in many potential applications, such as subgraph retrieval, graph visualization, representative subgraph discovery and vertex property exploration.

Abstract

In this paper, a novel type of interesting subgraph query is proposed: Minimal Unique Induced Subgraph (MUIS) query. Given a (large) graph G and a query vertex (position) q in the graph, can we find an induced subgraph containing q with the minimal number of vertices that is unique in G? MUIS query has many potential applications, such as subgraph retrieval, graph visualization, representative subgraph discovery and vertex property exploration. The formal definition of MUIS is given and the properties are discussed in this paper. The baseline and EQA (Efficient Query Answering) algorithms are proposed to solve the MUIS query problem under the filtering-validation framework. In the EQA algorithm, the Breadth First Search (BFS)-based candidate set generation strategy is proposed to ensure the minimality property of MUIS; the matched vertices-based pruning strategy is proposed to prune useless candidate sets and the unnecessary subgraph isomorphism; and the query position-based subgraph isomorphism is proposed to check efficiently the uniqueness of the subgraphs. Experiments are carried on real datasets and synthetic datasets to verify the effectiveness and efficiency of the proposed algorithm under novel measurements. The influencing factors of the process speed are discussed at last in the paper.

1. Introduction

Graphs have been used to model many complex data objects and their relationships in our real world, such as bioinformatics, chemistry, social networks, software, the World Wide Web, and so on [1,2,3,4,5,6]. With the increasing of graph data, graphs have been of extensive concern and deeply studied. The management and mining of graph data can effectively solve the analysis and processing problems of topological data [7,8,9]. One of the most important tasks in graph management is how to effectively answer the various queries in graph databases. For example, medical staff needs to query whether a given compound contains a particular substructure, and scientists want to query the number of specific substructures such as triangle subgraphs in the graph database.

In this paper, a novel type of interesting subgraph query is proposed. Suppose you are searching in the human protein network using query position q (a specific gene at a specific position), and you want to find a suitable subgraph containing the query position in the network for visualization purpose. The subgraph should not be too small to avoid users not being able to distinguish the differences between the neighborhood of the query position and that of other vertices, and the subgraph should not be too large to avoid users getting confused with the returned redundant information. The subgraph should be special and representative. For this demand, this paper presents the Minimal Unique Induced Subgraph (MUIS) query.

MUIS query refers to finding out a unique induced subgraph that contains a minimum number of vertices and the given query position. MUIS query provides a new graph data access and management method that has many potential applications, such as subgraph retrieval, graph visualization, representative subgraph discovery and vertex property exploration.

Answering MUIS query efficiently is far from trivial. There are many academic problems in the research, such as what are the properties of MUIS, how to find MUIS candidate subgraphs, how to prune useless candidate subgraphs as early as possible, how to ensure the minimum number of vertices of MUIS and how to check the uniqueness of candidate graphs.

We summarize the major contributions by the following four ingredients:

• To our best knowledge, we are the first to propose MUIS query, which is a novel type of interesting and useful subgraph query. MUIS query enriches and develops graph data query and management methods;
• For the novel type of subgraph query, the formal definition is given and the properties are discussed in this paper;
• The EQA (Efficient Query Answering) algorithm is proposed to solve the MUIS query problem under the filtering-validation framework. In the EQA algorithm, BFS (Breadth First Search)-based candidate set generation strategy, matched vertices-based pruning strategy and query position-based subgraph isomorphism are proposed to improve the effectiveness and efficiency of MUIS query;
• Through comprehensive experiments on real datasets and synthetic datasets, EQA is demonstrated to outperform the state-of-the-art model to answer MUIS query. Influencing factors of the process speed are also verified by the experiments.

The rest of the paper is organized as follows. We define MUIS and discuss the properties in Section 2, and review the related work briefly in Section 3. Then, we present our model in Section 4. In Section 5, we report the experimental results, and we conclude the paper in Section 6.

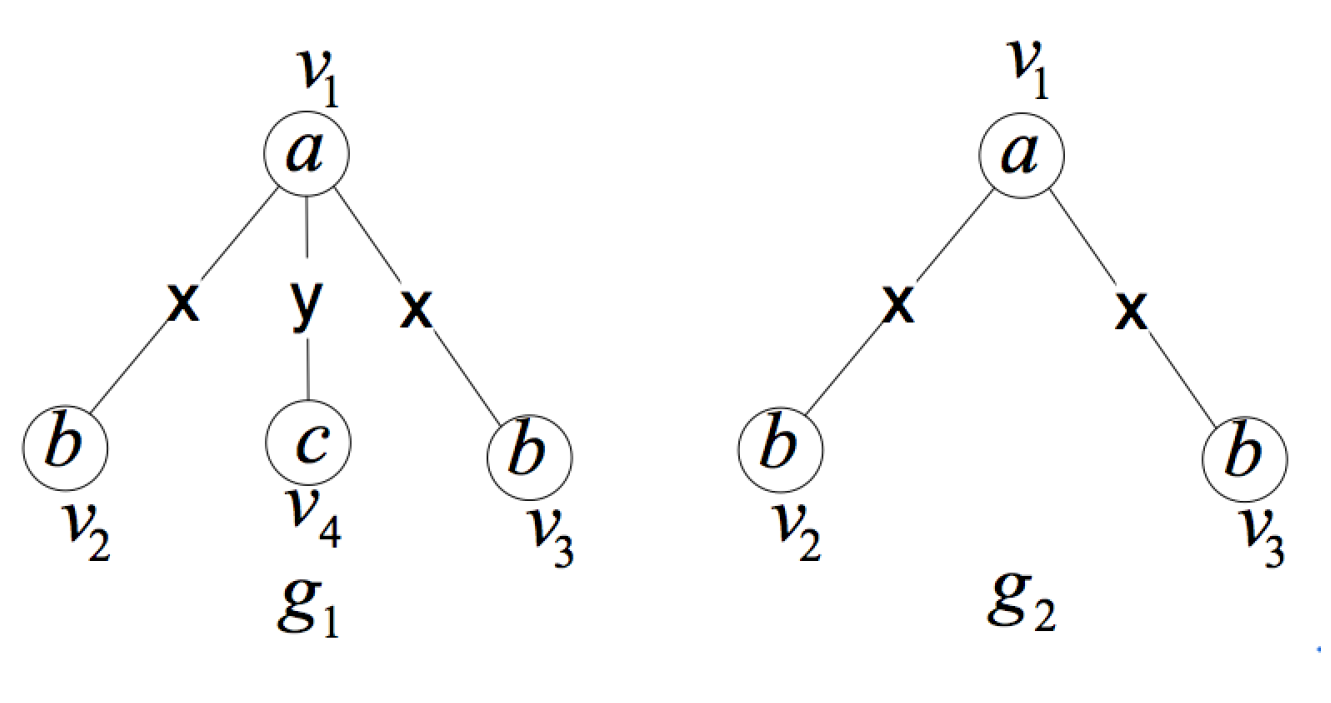
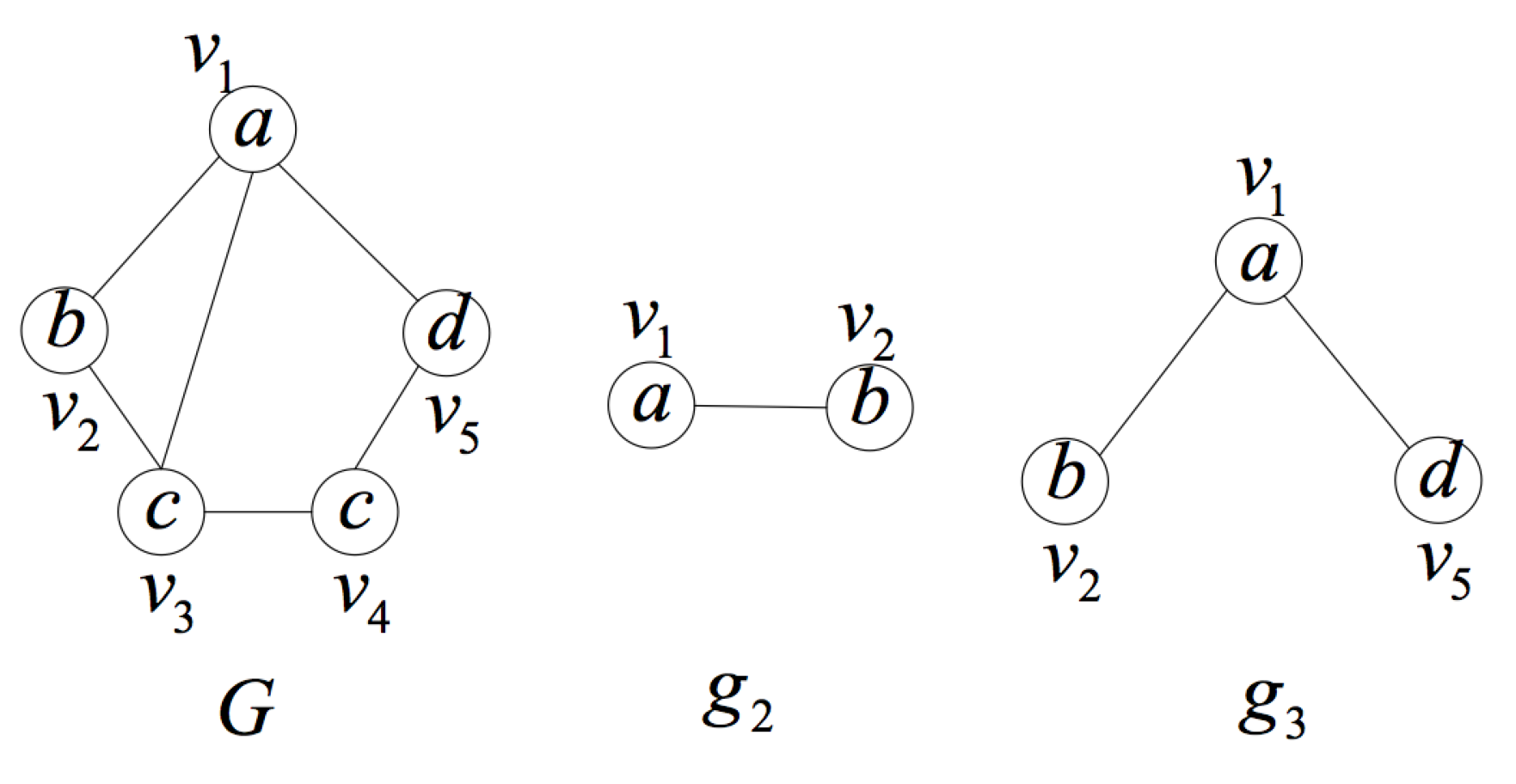
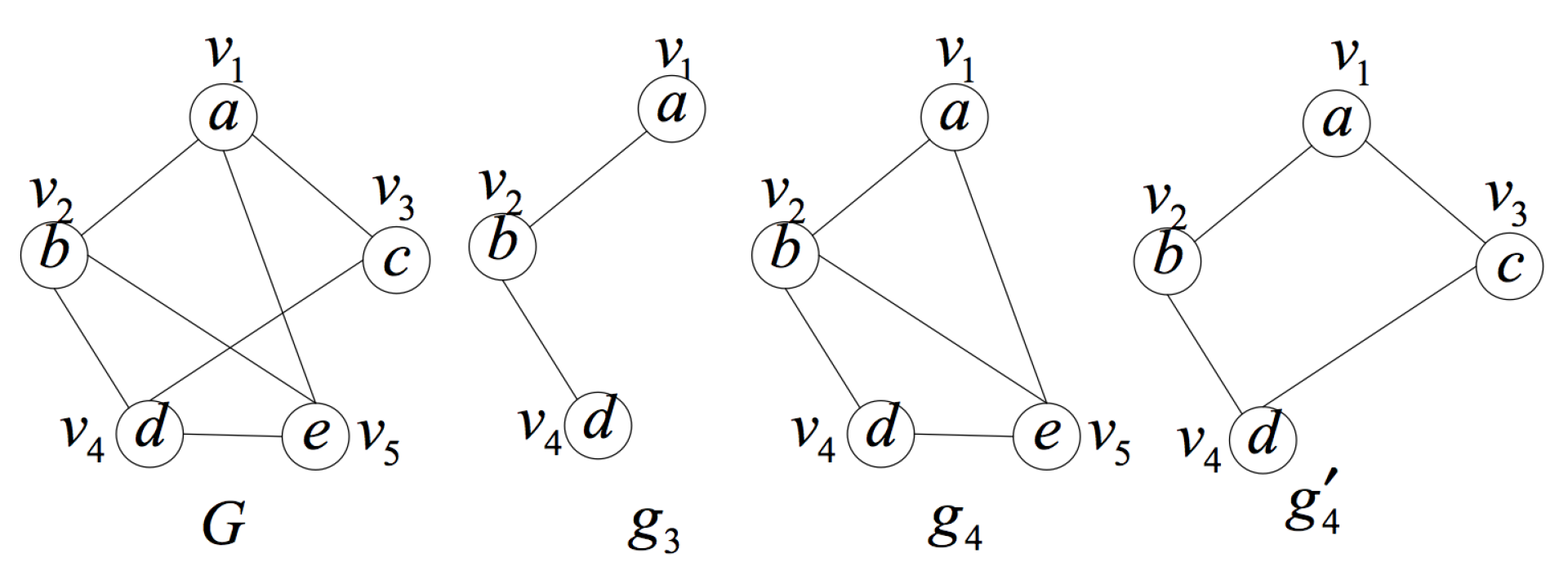
2. Formal Definition and Properties

In this section, we formulate the minimal unique induced subgraph query and discuss the properties of MUIS.

Definition 1.

(Graph) A labeled graph G is defined as $(V,E,l)$ where V is the set of vertices, $E(\subseteq V\times V)$ is the set of edges and l is a label function that maps a vertex or an edge to a set of labels.

Definition 2.

(Subgraph) If a graph $G^{\prime }$ has vertices and edges forming subsets of the vertices and edges of a given graph G, $G^{\prime }$ is a subgraph of G.

Definition 3.

(Induced subgraph) For a graph $G=(V,E)$, an induced subgraph $G^{\prime }=(V^{\prime },E^{\prime })$ of G is the graph whose vertex set $V^{\prime }$ is the subset of V and whose edge set $E^{\prime }$ consists of all the edges in E with both endpoints in $V^{\prime }$.

In Figure 1, the vertex set of $g_2$ is $V_2=\{v_1,v_2,v_3\}$ and the edge set of $g_2$ is $E_2=\{(v_1,v_2),(v_1,v_3)\}$. The vertex set of $g_1$ is $V_1=\{v_1,v_2,v_3,v_4\}$, and the edge set of $g_1$ is $E_1=\{(v_1,v_2),(v_1,v_3),(v_1,v_4)\}$. It is easy to get $V_2\subset V_1$ and $E_2\subset E_1$. Moreover, $l_1\left(v_1\right)=l_2\left(v_1\right)=a$, $l_1\left(v_2\right)=l_2\left(v_2\right)=b$, $l_1\left(v_3\right)=l_2\left(v_3\right)=b$, $l_1(v_1,v_2)=l_2(v_1,v_2)=x$, $l_1(v_1,v_3)=l_2(v_1,v_3)=x$ and $(v_1,v_2)\in E_2,(v_1,v_3)\in E_2\iff (v_1,v_2)\in E_1,(v_1,v_3)\in E_1$. Therefore, $g_2$ is an induced subgraph of graph $g_1$.

Definition 4.

(Graph isomorphism) A labeled graph $G^{\prime }=(V^{\prime },E^{\prime },l^{\prime })$ is isomorphic to another graph $G=(V,E,l)$, denoted by $G^{\prime }\approx G$, iff there exists a bijection $M:V\to V^{\prime }$ such that:

(1)

$\forall u\in V,l\left(u\right)\subseteq l^{\prime }\left(M\left(u\right)\right)$,

(2)

$\forall (u,v)\in E,(M\left(u\right),M\left(v\right))\in E^{\prime }$ and $l(u,v)=l^{\prime }(M\left(u\right),M\left(v\right))$,

The bijection M is called an isomorphism between $G^{\prime }$ and G. We also say that G is isomorphic to $G^{\prime }$ and vice versa.

Definition 5.

(Subgraph isomorphism) A labeled graph $G^{\prime }$ is subgraph isomorphic to a labeled graph G, denoted by $G^{\prime }\subseteq G$, iff there exists a subgraph $G^{″}$ of G such that $G^{\prime }$ is isomorphic to $G^{″}$

In Figure 2, we find subgraphs of data graph g that are isomorphic to query graph q. According to the definition of subgraph isomorphism, there exists two bijections $M_1$ and $M_2$,

$$M_1=\{(u_1,v_3),(u_2,v_5),(u_3,v_9),(u_4,v_6)\}{M}_2=\{(u_1,v_6),(u_2,v_5),(u_3,v_9),(u_4,v_3)\}$$

.

Definition 6.

(Self-isomorphism) If a labeled graph is isomorphic to itself, we call it self-isomorphism.

In Figure 2, query graph q is self-isomorphism. There exists a self-isomorphism bijection $M_0$, $M_0=\{(u_1,u_4),(u_2,u_2),(u_3,u_3),(u_4,u_1)\}$.

It can be seen from the bijection $M_0$ that the vertices $u_1$ and $u_4$ can be interchanged in query graph q. The two vertices can be regarded as equivalent points. Self-isomorphism graphs usually contain equivalent points.

Before the formal definition of MUIS is given, a definition of the Smallest Unique Induced Subgraph (SUIS) that is closely related to the MUIS definition is first given.

Definition 7.

(SUIS) A labeled graph $G_s=(V_s,E_s,l_s)$ is a SUIS of graph $G=(V,E,l)$, such that:

(1)

$G_s$ is a an induced subgraph of G (induced subgraph property).

(2)

$G_s$ is unique in the set of induced subgraphs of G, that is to say, there is no other induced subgraph of graph G isomorphic to $G_s$ except itself (uniqueness property).

(3)

In G, there is no proper subgraph of $G_s$ satisfying (1) and (2) (smallest one property).

Given a vertex q in G, we are interested in the SUIS of graph G containing position q, denoted as SUIS(q), which is closely related to MUIS.

Figure 3 shows an example of SUIS and SUIS(q). Assume $q=v_5$, $G_{s1}$ is not an SUIS of G, but it is an SUIS(q). Below is the verifying process:

First, it is easy to verify that $G_{s1}$ is an induced subgraph of G according to Definition 3. Second, we can verify that $G_{s1}$ is unique according to Definition 4. Third, on the one hand, since {{$v_1$,$v_2$},{($v_1$,$v_2$)}}, an induced subgraph of $G_{s1}$ is also unique, and $G_{s1}$ is not an SUIS. On the other hand, all the induced subgraphs of $G_{s1}$ containing q, except itself, {{$v_5$}, ∅}, {{$v_1$,$v_5$},{($v_1$,$v_5$)}} and {{$v_2$,$v_5$},{($v_2$,$v_5$)}}, are not unique. $G_{s1}$ satisfies the smallest one property when taking into account q, so $G_{s1}$ is an SUIS(q).

$G_{s2}$ is both an SUIS and an SUIS(q) of G, which can also be verified by the same method. The example clearly shows the difference between SUIS and SUIS(q).

Definition 8.

(MUIS) For a graph $G=(V,E,l)$ and a vertex $q(\in V)$, the MUIS subgraph is the induced subgraph in the set of SUIS(q) of G with the minimal number of vertices, denoted as MUIS$\left(q\right)$. More intuitively, MUIS$\left(q\right)$ is the induced subgraph of G containing q with the minimal number of vertices, which is unique.

Vertex q is called the query vertex or query position. Obviously, MUIS is a concept that is closely related to the query position. Similar to SUIS, MUIS has the induced subgraph property, uniqueness property and minimality property. For the same graph, a different query vertex may obtain a different MUIS.

Figure 3 shows an example of MUIS. Suppose $v_5$ is the query vertex. Both $G_{s1}$ and $G_{s2}$ are SUIS(q)s as proven above. The number of vertices of $G_{s2}$ is more than that of $G_{s1}$. Since the number of vertices is not minimal, $G_{s2}$ is not an MUIS. It is easy to find out that the minimal induced subgraph of G containing the query position is {{$v_5$}, ∅}, which is not unique. Furthermore, we can verify that the induced subgraphs of G containing the query position with two vertices are also not unique. Therefore, $G_{s1}$ is an MUIS.

Definition 9.

(Problem definition) Minimal Unique Induced Subgraph Query (MUISQ) is to find an MUIS for the given graph and query position.

We show the induced subgraph property, the uniqueness property and the minimality property of MUIS above. Furthermore, we explore the property related to the number of MUISs below.

Number property. Given a graph $G=(V,E,l)$ and a vertex $q(\in V)$, there exists at least one SUIS, SUIS(q) and MUIS.

Proof: G itself is unique. Therefore, at least one SUIS, or $SUIS\left(q\right)$, or MUIS is itself in extreme cases.

Therefore, there may exist may induced subgraphs satisfying the conditions. MUISQ is a task to find out any one subgraph satisfying the conditions. There is no need to find out all MUISs.

3. Related Works

We will briefly review areas that are relevant to the concept of subgraph query in this section.

3.1. Subgraph Matching Query

Subgraph matching query is the most basic query task in the graph query domain, and it is often the basis of many other query tasks. The subgraph matching query is divided into subgraph isomorphism [10] and similarity matching [11] according to whether strict matching is required. Subgraph isomorphism is defined as follows: for a data graph G and a query graph Q, retrieve all subgraphs of G that are isomorphic to Q, which has been proven to be an NP-complete problem in several papers [12,13]. In recent years, many algorithms such as GraphGrep [14], VF2 [15], QuickSI [16] and TurboISO [17] have been proposed to solve the problem. In the subgraph isomorphism process, when it cannot be strictly matched, the conclusion that the query graph and the subgraphs of data graph are different will be made. However, in real applications, the query graph can be considered to be isomorphic to a subgraph of the data graph within the error tolerance. Depending on the application, the error can have different evaluation criteria. For example, an effective method is to use the edit distance of the graph [18,19].

3.2. Frequent Subgraph Mining

Frequent subgraph mining refers to finding out the subgraphs whose number of occurrences is higher than a given threshold [20,21,22]. The output of frequent subgraph mining can be used to provide support for other graph tasks, such as graph classification or clustering. The core step of frequent subgraph mining is computing subgraph frequencies, which is computationally hard. There are two subgraph enumeration methods: one is the breadth-first search method, such as AGM [23] and FSG [24], and the other is the depth-first search method, such as gSpan [25], FFSM [26] and GASTON [27]. To reduce the computational complexity in large graphs further, new emerging techniques deploy approximate algorithms to find frequent subgraphs.

3.3. Correlation Subgraph Query

Correlation subgraph query aims to find out the subgraphs statistically correlated to query graph Q [28,29]. The work in [30] proposed the CGSearchalgorithm, which adopted the commonly-used Pearson’s correlation coefficient as the correlation measure to take into account the occurrence distributions of graphs. The paper got the subgraph set with Pearson’s correlation coefficient higher than a certain threshold between the subgraph and the query graph. The work in [31] focused on a new subgraph query based on frequent subgraph mining and correlation subgraph query, named frequent correlated subgraph pairs discovery. The paper proposed FCP-Miner, a fast approximate algorithm to solve the problem.

3.4. Network Motif Discovery

The network motif comprises patterns of connectivity that occur significantly more frequently than expected, which was introduced in [32]. Network motif discovery refers to the discovery of subgraphs that are overrepresented, with a p-value higher than a certain threshold. Network motif discovery is a very important research direction in graph query, and it is especially important for the analysis of biological networks. As frequent subgraph mining, computing subgraph frequencies is also an important step for network motif discovery. Many classic algorithms have been proposed to solve the problem, such as Grochow [33] and gTrie [34]. Recently, [35] proposed an analytical method to identify statistically-significant labeled motifs.

Besides the above main subgraph query research, there are also some other interesting graph query problems, such as the classic maximum common subgraphs problem [36], the connected induced subgraph problem [37], similarity search in an XML database [38], and so on. MUIS query enriches and develops graph query technology. Research on the existing subgraph query technology is helpful to solve the MUIS query problem.

4. The Proposed Model

This section presents the proposed model for the MUIS query process. We first show the general filtering-verification framework for the MUIS query problem. Then, we propose a candidate set generation strategy and pruning strategy in the filtering process and the novel subgraph isomorphism method in the verification process. Baseline and EQA algorithms are presented at last.

4.1. The General Framework

This paper adopts the filtering-verification solving strategy, which is commonly used in graph query problems [16,17]. For this novel graph query task, both the filtering process and verification process have new content. In the filtering process, a series of candidate subgraphs is generated by searching the induced subgraph space. The induced subgraph space refers to the set of all the induced subgraphs of the given graph. The generated candidate subgraphs are the points in the induced subgraph space. Then, the candidate subgraphs that do not meet the conditions are filtered out by various pruning methods. In the verification process, the subgraph isomorphism testing is performed to check whether the candidate subgraphs generated in the filtering process are unique or not. Subgraph isomorphism has been proven to be an NP-complete problem in many papers [12,13]. Therefore, the times of subgraph isomorphism testing must be reduced as much as possible due to its high cost. This requires us to design better candidate set generation and pruning strategies.

The above steps ensure the induced subgraph property and uniqueness property of MUIS, but the minimality property cannot be guaranteed. The minimality property requires that the found MUIS has the least number of vertices in all unique induced subgraphs containing the query position. Therefore, we cannot judge whether an induced unique subgraph containing the query position is MUIS before we know that all the induced subgraphs containing the query position with less vertices are not unique.

In Figure 4, considering that $v_1$ is the query position, we can see that the induced subgraph $g_3$ is unique and contains the query positon, but we cannot judge whether $g_3$ is MUIS, as explained above. From the figure, we can also see that the induced subgraph $g_2$ containing the query positon is also unique, and the number of vertices is less than that of $g_3$. Therefore, when searching the induced subgraph space, the search must be performed from the lower layer to the higher layer, that is to say, the induced subgraphs are searched in ascending order of the number of vertices.

The general framework for MUIS query is given in Algorithm 1, which contains a global Boolean variable $Found$ to show whether MUIS has been found. We search the space from the lower layer to the high layer (Lines 2∼3). We then check whether the subgraph is unique in Line 4. Line 5 is a further uniqueness testing for Line 4, which will be explained in detail later. When MUIS is found, we can exit the main loops of the algorithm (Lines 6∼15). If the value of $Found$ is still false after searching all the induced subgraph space, the data graph itself is the MUIS since it is a unique induced subgraph and the number of vertices is minimal in this situation (Lines 16∼17).

Line 5 addresses the self-isomorphism problem, which may cause misjudgment. Figure 5 is a false positive example. Consider data graph G and the query position $v_3$. $g_3$ is an induced graph containing the query position and has the minimal number of vertices. However, it is isomorphic to itself under mapping $M=\{(v_1,v_1),(v_4,v_2),(v_2,v_4)\}$. Since $g_3$ gets an isomorphic induced subgraph, we may judge it to be not unique. However, in fact, there is no other induced subgraph isomorphic to $g_3$ in G. Therefore, $g_3$ is unique. It is necessary to avoid such a misjudgment. If all the vertices of the two induced subgraphs are the same in the original data graph, it is self-isomorphism.

Algorithm 1 The general framework.

Input:   data graph, $G=(V,E,l)$;   query position, q; Output:   MUIS(q); 1: $Found=false$, the number of vertices of induced subgraphs $i=0$; 2: for $i=1$ to $\left|V\right|$ do 3:  for each induced graph $g_i$ with the number of vertices i and containing the vertex q do 4:   isomorphism testing for $g_i$ to judge uniqueness; 5:   check $g_i$ whether is self-isomorphism; 6:   if $g_i$ is unique then 7:    $Found=true$; MUIS(q) = $g_i$; break; 8:   end if 9:  end for 10:  if $Found$ then 11:   Break; 12:  end if 13: end for 14: if $Found$ then 15:   return MUIS(q) 16: else 17:  return G 18: end if

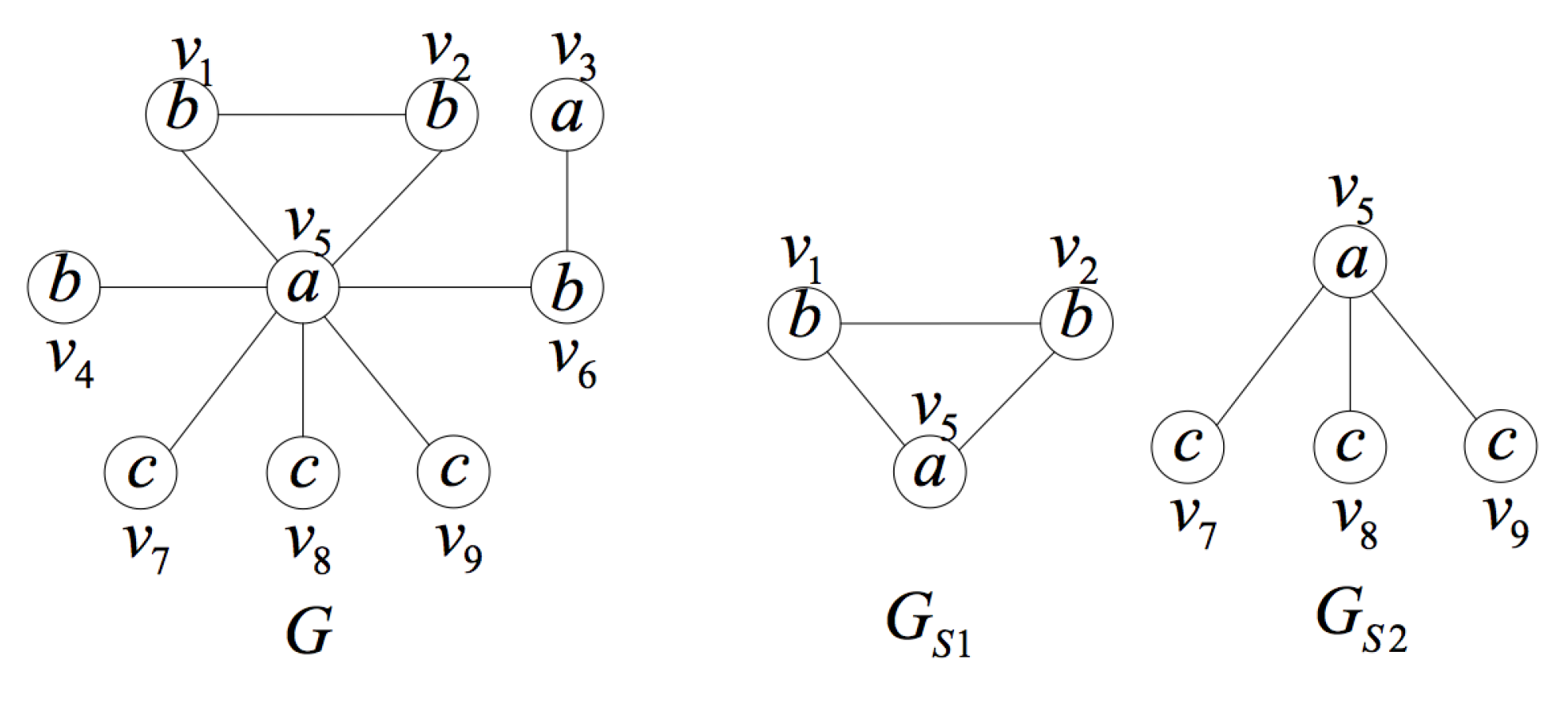
4.2. BFS-Based Candidate Set Generation Strategy

The BFS-based candidate set generation strategy can effectively search the induced subgraph space containing query position q. The strategy mainly contains the following four important ideas:

(1)

Search the induced subgraph space containing query position q in ascending order of the number of vertices. In particular, the first layer of the induced subgraph space is the query position self-constructed induced subgraph $\left\{\right\{q\},\varnothing ,l\}$. Its importance will be explained in detail later.

(2)

Divide all the vertices of the data graph into two subsets. The two subsets are defined as follows:

$V^{in}$ denotes the vertices already contained in the current induced subgraph. Note that it must have query position $q\in V^{in}$.

$V^{out}$ denotes the vertices not contained in the current subgraph. Note that it must have $V^{out}=V-V^{in}$.

(3)

When performing BFS for the $(i+1)$-th layer induced subgraph from the i-th layer induced graph (containing i vertices), select a vertex v from the subset $V^{out}$ of the i-th layer induced subgraph. If vertex v is connected to any vertex of the subgraph, then add vertex v into the vertex set of the subgraph to generate a new induced subgraph (containing $i+1$ vertices).

(4)

We eliminate the generated duplicate induced subgraphs, which have been already obtained by other i-th layer induced subgraphs and vertices in $V^{out}$, which can greatly reduce subsequent computational overhead.

Figure 6 is an example of the induced subgraph space search path. Data graph $G=(V,E,l)$, $V=\{v_1,v_2,v_3,v_4,v_5\}$, $E=\{(v_1,v_2),(v_1,v_3),(v_1,v_5),(v_2,v_4),(v_2,v_5),(v_3,v_4),(v_4,v_5)\}$. Set query position $q=v_2$. $g_3$ is an induced subgraph of graph G with three vertices and containing the query position q. $g_3=(V_3,E_3,l)$, $V_3^{in}=V_3=\{v_1,v_2,v_4\}$, $V_3^{out}=V-V_3^{in}=\{v_3,v_5\}$ in this example. Select a vertex $v_5$ from $V_3^{out}$ and find the existence of edge $(v_1,v_5)$ between vertex $v_5$ and vertex $v_1$ in $V_3^{in}$ after checking. Then, add the vertex $v_5$, the edge $(v_1,v_5)$ and other edges between $v_5$ and other vertices in $V_3^{in}$ ($(v_2,v_5)$ and $(v_4,v_5)$ in this example) to the induced subgraph $g_3$. In this case, we can get the induced subgraph $g_4$ with four vertices and containing the query position q. Similarly, select the vertex $v_3$ from $V_3^{out}$ and obtain another induced subgraph $g_4^{\prime }$.

Algorithm 2 shows the entire process of the BFS-based candidate set generation algorithm. $G_i$ denotes a set of the induced subgraphs with i vertices, and $g_i$ denotes an induced subgraph with i vertices, thus $g_i\in G_i$. Algorithm initialization is extremely important in the algorithm. The induced subgraph composed of the query position q is initialized as the first layer induced subgraph, i.e., $g_1=\{\left\{q\right\},\varnothing ,l\}$, $G_1=g_1$ in Line 1. This initialization can ensure that the subgraphs searched by the algorithm absolutely contain query position q and that all other induced subgraphs not containing query position q are prune off, which makes the candidate set non-repetitive and complete. Then, we search the space from the second layer to the $\left|V\right|$-th layer (Line 2). The details to generate a candidate have been already introduced above and are shown in Lines 3∼9. If $g_i$ does not exist in $G_i$, add $g_i$ to $G_i$ (Lines 10∼12). In addition, it is worth mentioning that there is no need to find all the induced subgraphs containing the query position q. When the MUIS(q) that satisfies the condition is obtained in a certain layer, the search can be stopped.

Algorithm 2 BFS-based candidate set generation algorithm.

Input:   data graph, $G=(V,E,l)$;   query position, q; Output:   induced graphs, $g_i$; 1: initialize the first layer of the induced subgraph space, one vertex induced graph $g_1=\{\left\{q\right\},\varnothing ,l\}$, report $g_1$; 2: for $i=2$ to $\left|V\right|$ do 3:  set i vertices induced subgraph set $G_i$ = ∅; 4:  for each $i-1$ induced graph $g_{i-1}\in G_{i-1}$ do 5:   compute $V^{in}$ and $V^{out}$ of $g_{i-1}$; 6:   for each vertex $v\in V^{out}$ do 7:    if there is an edge between v and vertices in $V^{in}$ then 8:     get all vertices in $V^{in}$ and v to generate induced graph $g_i$, report $g_i$ 9:    end if 10:    if $g_i\notin G_i$ then 11:     add $g_i$ to $G_i$ 12:    end if 13:   end for 14:  end for 15: end for

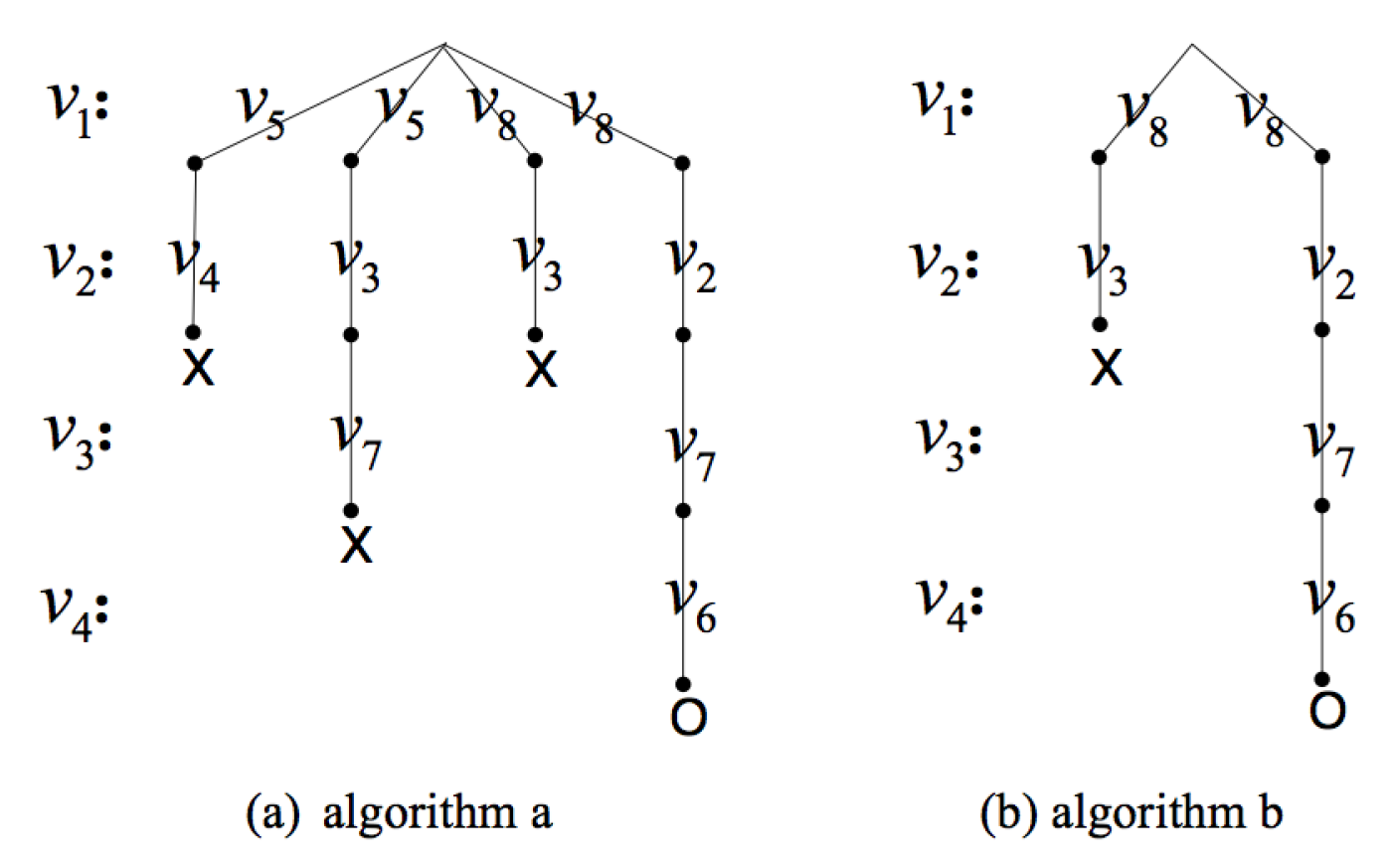
4.3. Matched Vertices-Based Pruning Strategy

The pruning strategy based on the matched vertices can effectively reduce the number of graphs or regions that execute isomorphism testing. The pruning strategy mainly contains the following two important ideas:

(1)

During the isomorphism testing, some vertices in some subgraphs of data graph G are measured not to derive the subgraphs that are isomorphic to the induced subgraph. These vertices can be recorded for pruning.

(2)

Consider graph $g_1=(V,E,l)$, query position $q\in V$ and graph $g_2=(V^{\prime },E^{\prime },l^{\prime })$. In the case of $q^{\prime }(\in V^{\prime })$ corresponding to q, if all the subgraphs containing vertex $q^{\prime }$ of graph $g_2$ are not isomorphic to $g_1$, then any hypergraph of graph $g_1$ and all subgraphs containing vertex $q^{\prime }$ of graph $g_2$ are not isomorphic in this case.

The proposition in (2) can be proven as followings. Under the given conditions, assume that a hypergraph of graph $g_1$ is isomorphic to a subgraph containing vertex $q^{\prime }$ of graph $g_2$. Since vertex q corresponds to vertex $q^{\prime }$, graph $g_1$ must be isomorphic to a subgraph containing vertex $q^{\prime }$ of graph $g_2$, which contradicts the given condition that graph $g_1$ is not isomorphic to any subgraph containing vertex $q^{\prime }$ of graph $g_2$. Therefore, the assumption is not true, and thus, the proposition is true.

The concept of hypergraph used here is a commonly-used concept in graph data research. The hypergraph is relative to the subgraph. If graph $G_1$ is a hypergraph of graph $G_2$, then graph $G_2$ is a subgraph of graph $G_1$.

Figure 7 is an example of the above proposition. In the figure, assuming that the query position is vertex $v_1$ in graph $g_1$ and vertex $v_1$ in graph $g_2$ corresponds to vertex $v_1$ in graph $g_1$, it can be seen from the figure that graph $g_1$ is not isomorphic to any subgraph of graph $g_2$ in this case.

Someone may point out that subgraph $\{\{v_2,v_4\},\left\{(v_2,v_4)\right\}\}$ of graph $g_2$ is isomorphic to graph $g_1$, but this does not satisfy the condition that vertex $v_1$ in graph $g_2$ corresponds to vertex $v_1$ in graph $g_1$. Therefore, it is not considered. The hypergraph $g_h$ of graph $g_1$ shown in the figure is not isomorphic to any subgraph of graph $g_2$ under the condition that vertex $v_1$ in graph $g_2$ corresponds to vertex $v_1$ in graph $g_1$. However, if removing the constraint condition, the hypergraph $g_h$ is isomorphic to the subgraph $\{\{v_1,v_2,v_4\},\{(v_1,v_2),(v_2,v_4)\}\}$ of graph $g_2$. Therefore, the constraint that vertex $v_1$ in the graph $g_2$ corresponds to vertex $v_1$ in graph $g_1$ is extremely important. There is no need to enumerate all hypergraphs of graph $g_1$ infinitely. This example is just for the ease of understanding the above proposition.

The following shows how to use the proposition in (2) for pruning. Considering graph $g=(V,E,l)$ and query position q and setting the query position q as the starting point of isomorphism testing (we do this in this way in our paper), the vertices corresponding to q, denoted by $V_q$, must be the vertices with the same label as q in the set V, i.e., $q\notin V_q$ and $V_q\subset V$. Assuming a vertex $q^{\prime }(\in V_q)$ and in the case of $q^{\prime }$ corresponding to q, the i-th layer induced subgraph $g_i$ containing q is not isomorphic to any subgraphs containing $q^{\prime }$, it can be derived by the proposition that all the $(i+1)$-th layer induced subgraphs (hypergraphs of $g_i$) derived from $g_i$ in the induced subgraph space cannot find their isomorphic subgraphs containing $q^{\prime }$, so that all the branches with $q^{\prime }$ corresponding to q can be pruned off when performing the subgraph isomorphism testing.

Figure 8 shows an example of the matched vertices-based pruning strategy. In the data graph, assuming that the query position q is $v_4$, then the set of vertices corresponding to q is $V_q=\{v_1,v_6,v_8\}$. In the case of $v_4$ corresponding to $v_1$ and $v_8$ in $V_q$, the second layer induced subgraph $g_2=\{\{v_4,v_7\},\left\{(v_4,v_7)\right\}\}$ is not isomorphic to any subgraph containing $v_1$ or $v_8$. Thus, when testing the third layer induced subgraphs $g_3=\{\{v_2,v_4,v_7\},\{(v_2,v_4),(v_4,v_7)\}\}$ derived from $g_2$, do not consider $v_1$ and $v_8$, and only test subgraphs derived from $v_6$.

4.4. Query Position-Based Subgraph Isomorphism

Subgraph isomorphism is used to check the uniqueness of candidate subgraphs in our paper. Most subgraph isomorphism algorithms are implemented with the backtracking strategy [15,16,17], which finds solutions by incrementing partial solutions or abandoning them when it is determined that they cannot be completed until a full match is found. A set of candidate vertices $C\left(u\right)$ for query vertex u is computed at the first step according to specific rules. If $C\left(u\right)$ is empty, that is to say no isomorphic subgraphs, the programs exit. Otherwise, the algorithms invoke the main recursive function $SubgraphSearch$ to match one query vertex with one data vertex one time.

We propose a query positon-based subgraph isomorphism algorithm to improve the testing efficiency for our application. The main ideas is discussed in detail as follows.

(1)

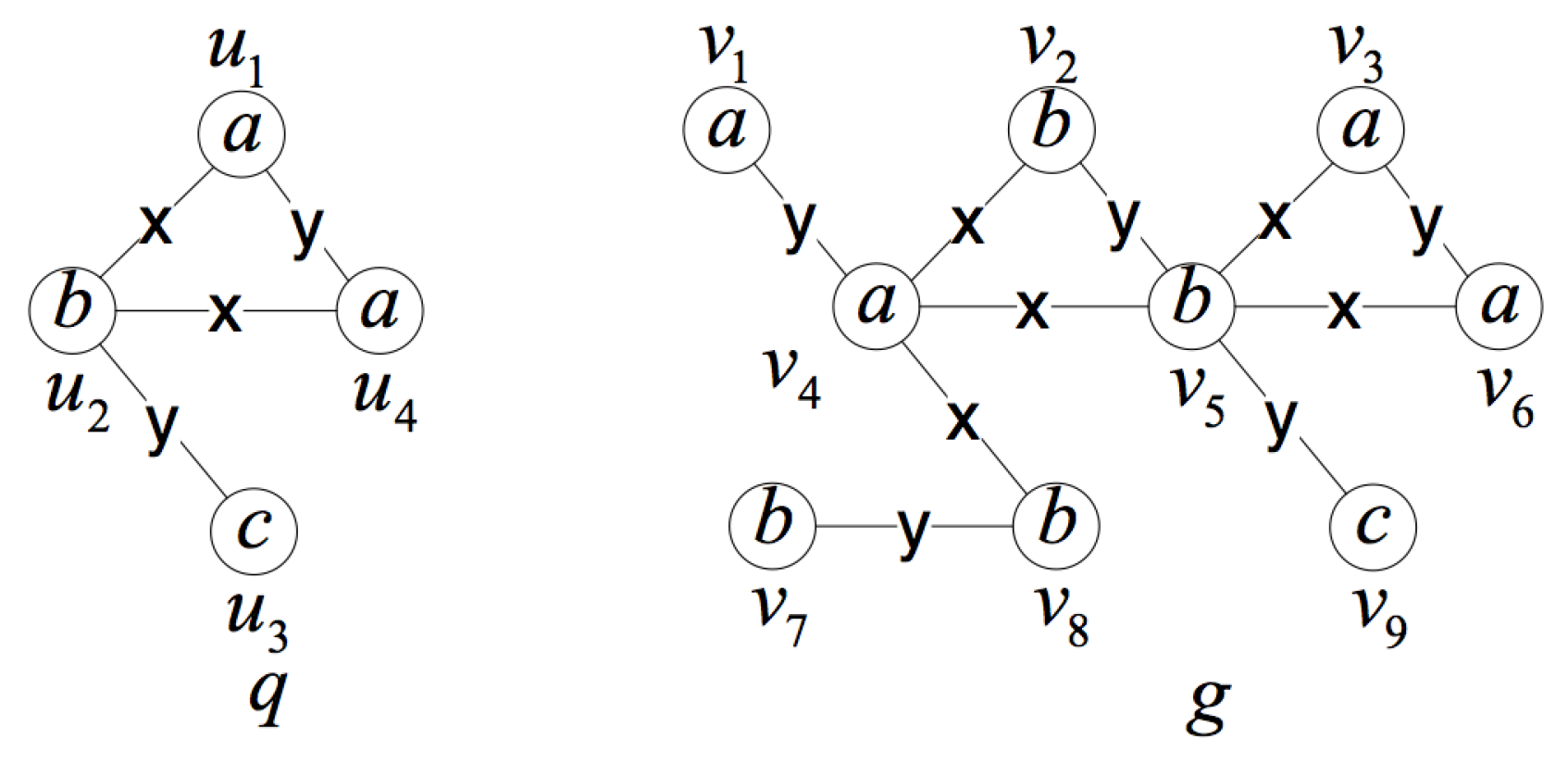
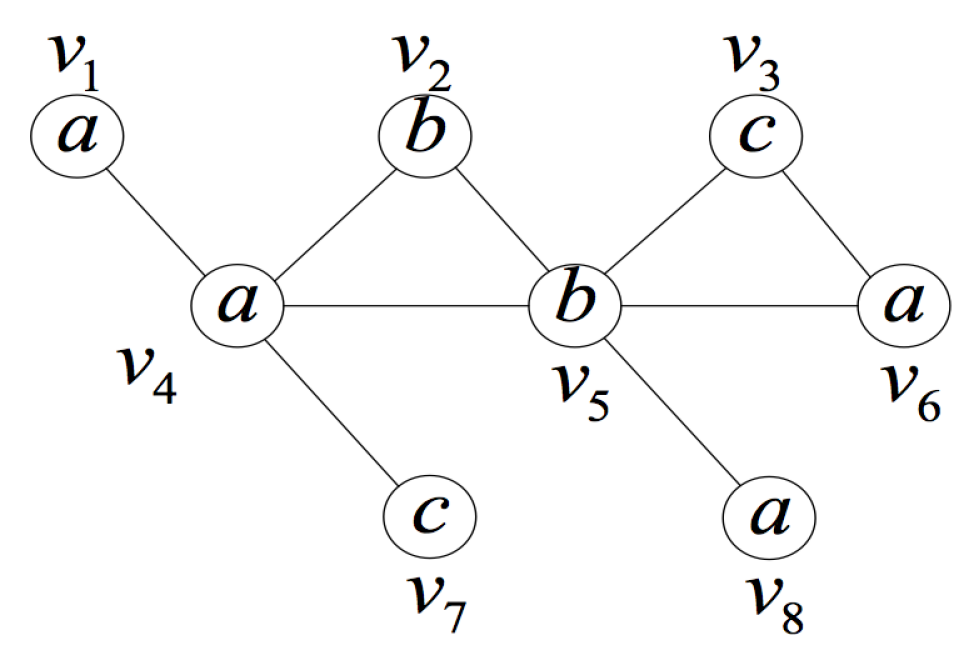
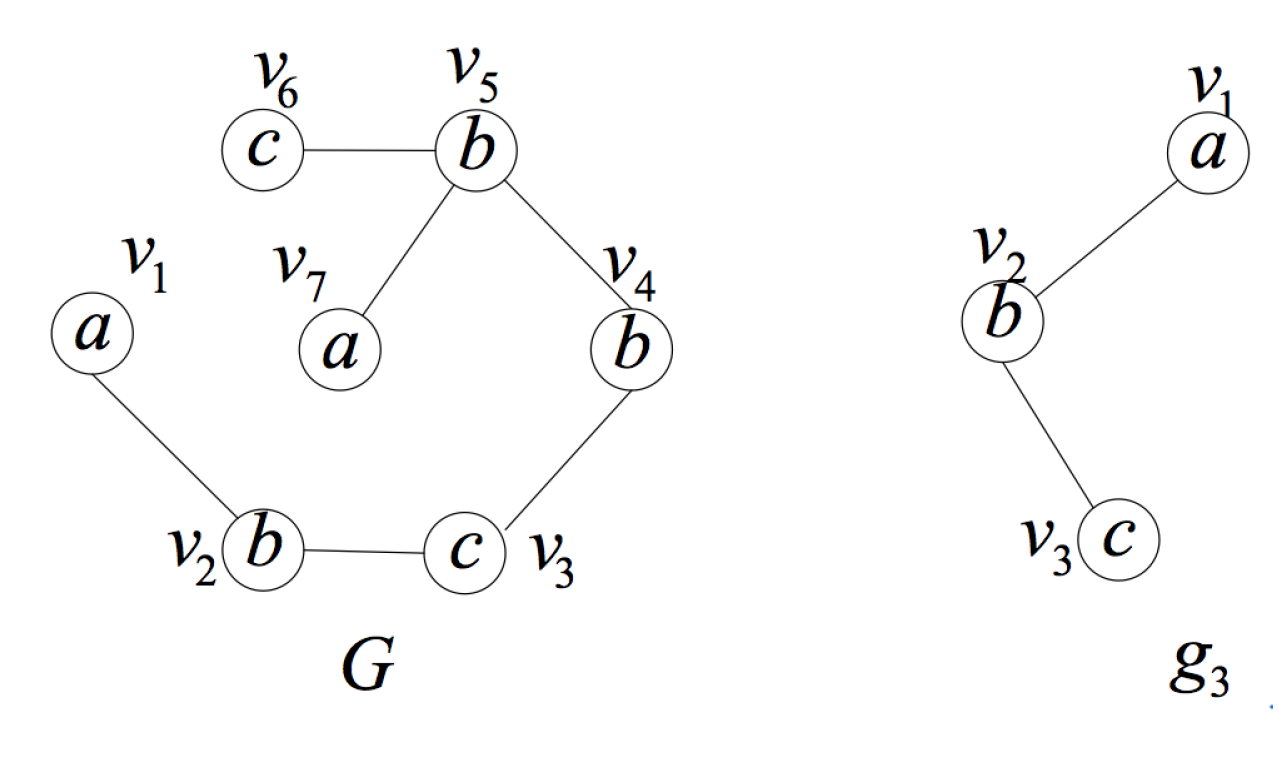
Use the query position as the starting vertex of the isomorphism testing

Using the query position as the starting vertex of the isomorphism testing makes full use of the query position in the data graph, and it is the most important improvement in the isomorphism testing algorithm. When the subgraph isomorphism testing is performed on candidate subgraphs, matching the query position first can avoid invalid and extra isomorphism testing.

Figure 9 is an illustration of the importance of matching the query position first. Considering the data graph G and the query position $v_1$, $g_3$ is an induced subgraph of G containing the query position with three vertices. If we do not use $v_1$ as the first matching vertex, it will be matched in two directions. For the first direction, we can get matched pairs of vertices $(v_3,v_3)$, $(v_2,v_2)$ and $(v_1,v_1)$, where the isomorphic subgraph is $g_3$ itself. For the other direction, we can get matched pairs of vertices $(v_3,v_3)$ and $(v_2,v_4)$ and will stop for the non-matched vertices $v_1$ in $g_3$ and $v_5$ in G. We have to do more testing to judge whether $g_3$ is unique. When using $v_1$ as the first matching vertex, the second direction testing can be avoided.

In fact, much local or partial matching can be avoided when using the query position as the starting vertex of the isomorphism testing, thus judging whether the induced subgraph is unique as soon as possible and improving the efficiency of verification process. In addition, we use the query rewrite method in [17] to rank the other vertices in the query graph and get a matching order according to the ranking value. In this way, we can reduce the candidate regions for performing subgraph isomorphism search and improve the efficiency.

(2)

Sorting the candidate vertices by degree for pruning

For vertex pairs $(u,v)$ in the candidate set P, u represents the vertex from induced subgraph $g_i$, and the set of u can be denoted as $P\left(g_i\right)$, while v represents the vertex from data graph G, and the set of v can be denoted as $P\left(G\right)$.

In the undirected graph, before judging whether vertex pairs $(u,v)$ in P are matched, sort the vertices in $P\left(G\right)$ by degree in descending order. Since u and v are matched only when the degree of v is greater than or equal to the degree of u, when the degree of v is less than the degree of u, it can be pruned. For a given vertex u, if the degree of the vertex v taken from the sorted $P\left(G\right)$ is less than the degree of u, then the degree of the vertices after v in $P\left(G\right)$ must be less than the degree of u, which can be pruned directly without further judgment. The pruning algorithm is denoted as $PruningDegree(u,v)$. In the directed graph, the vertices can be sorted by in degree and out degree. Both can be used for pruning.

Algorithm 3 is a detailed description of the query position-based subgraph isomorphism. The algorithm starts from empty mapping M, and the global Boolean variable $unique$ is set to true value at the beginning in Line 1. The algorithm uses the query position as the starting point of the isomorphism testing in Line 2. The $PruningDegree$ pruning function is called before adding the first vertex mapping pair to maximize the performance (Line 3). Then, we invoke $QueryRewrite$ to get the matching order of the other vertices except the query position (Line 4). For each vertex that matches the query position, the algorithm calls the recursive subroutine $SubgraphSearch$ to find the complete isomorphism mapping (Lines 5∼8).

Algorithm 3 Query position-based subgraph isomorphism.

Input:   data graph, $G=(V,E,l)$;   query position, q;   induced graph, $g_i$ Output:   Boolean variable to answer whether another induced graph in G isomorphic to graph $g_i$, $unique$; 1: $M:=\varnothing$, $unique=true$; 2: get all vertices $w_q$ ($\in P\left(G\right)$) whose label is the same as q, sort $P\left(G\right)$ by degree in descending order; 3: $PruningDegree(q,w_q)$; 4: $O=QueryRewrite(q,g_i)$; 5: for each $w_q\in P\left(G\right)$ do 6:  $M:=M\cup (q,w_q)$; 7:  $subgraphsearch(g_i,G,M,O,\dots )$ 8: end for Subroutine SubgraphSearch 1: if $\left|M\right|=\left|V\left(g_i\right)\right|$ then 2:  $report$ M; 3:  if the isomorphism subgraph of G is $g_i$ itself then 4:   $report$ $self$ $isomorphism$; 5:  else 6:   set $unique=false$, stop all procedures; 7:  end if 8: else 9:  $v:=NextQueryVertex(O,\dots )$; 10:  compute candidate vertices w $(\in W)$ of v; 11:  $PruningDegree(v,w)$; 12:  for each $w\in W$ and w is not yet matched do 13:   if $IsJoinable(g_i,G,M,v,w,\dots )$ then 14:    set $M:=M\cup (v,w)$; 15:    $subgraphsearch(g_i,G,M,O,...)$ 16:   end if 17:  end for 18: end if

In $SubgraphSearch$, Lines 1∼7 present the termination condition of the program. When a full mapping is found (Line 1), we check whether it is self-isomorphism (Line 3). If it is self-isomorphism, we continue to find the real isomorphism subgraph (Line 4). If not, we set $unique$ as false and stop the procedure (Line 6). If $unique$ is true when compared with all other induced subgraphs containing q, all main programs exit, and MUIS is obtained. Lines 8∼18 show how to increase partial mapping. The $NextQueryVertex$ function is invoked to get the next query vertex (Line 9). For the current query vertex v, compute and refine the candidate vertex set W subsequently (Lines 10∼11). Then, for each vertex w in W, the $IsJoinable$ function is invoked to check whether the edges between v and already matched query vertices in query graph $g_i$ have corresponding edges between w and already matched data vertices in data graph G (Lines 12∼13). If w is qualified, add $(v,w)$ to the already matched pairs of vertices (Line 14), and then, continue to invoke $SubgraphSearch$ recursively to match the remaining query vertices and data vertices (Line 15).

4.5. Baseline and EQA Algorithms

The baseline and EQA (Efficient Query Answering) algorithms, to answer MUIS query, are presented after introduction of the general framework and related strategies. Both algorithms use the BFS-based candidate set generation strategy. The baseline algorithm adopts the latest outstanding subgraph isomorphism testing method TurboISO [17] to check the uniqueness of candidate subgraphs, while the EQA algorithm makes use of both the matched vertices-based pruning strategy and the query position-based subgraph isomorphism method. Comparative experiments and results for the two algorithms will be shown in the next section.

5. Results

This section describes the experimental results of the proposed algorithms. All the algorithms were implemented using the C++ programming language. Experiments were run on a Win7 64 system with a 2.7-GHz Intel Core i5 and 4 GB 1333 MHz DDR3 memory. The comparative experiments were conducted on real datasets and synthetic datasets. Novel experimental performance measurements for MUIS query are proposed, and the influencing factors of the query process efficiency are discussed.

5.1. Experimental Performance Measurement

Two experimental performance measurements were used in this paper.

(1)

Average isomorphism time

The running time of each algorithm in this paper contains two parts: the time of filtering and the time of verification. The time of filtering includes the time of searching and pruning in the induced subgraph space. Since the algorithms use the same method to search the induced subgraph space and the time of pruning is negligible relative to the time of searching, the filtering time was almost the same. Therefore, we adopted the verification time as the performance measurement. The verification time is the time of subgraph isomorphism testing.

During the algorithms’ running process, the performance of the computer dynamically changes. Therefore, the average isomorphism time of five experiments was used as a criterion for evaluation. The average isomorphism time is represented by the symbol ${\overline{T}}_{iso}$.

(2)

The times of calling the recursive function

Compared with the isomorphism time, the times of calling the recursive function were more stable and could better reflect the performance of the algorithms. As long as the data graph and query position were given, the times of calling recursive functions were the same for each algorithm and would not change when the PC hardware and software environment change.

The times of calling recursive function are further explained below. In the MUIS query process, when the isomorphism testing was performed, the recursive function is called to determine whether the vertex pairs can join the current partial mapping. A better performing algorithm has a good pruning strategy at every stage to avoid some isomorphism testing or avoid calling recursive functions, so in general, the total number of times to call the recursive function is less. Figure 10 is an example of calling the recursive function and backtracking, where each line represents a calling of the recursive function. Assuming that the vertex set of the candidate induced subgraph is $\{v_1,v_2,v_3,v_4\}$, it can be seen from the figure that Algorithm b utilizes the pruning strategy to avoid the isomorphism testing between the vertex $v_1$ and the vertex $v_5$; thus, the times of calling recursive function were less than those of Algorithm a. The times of the calling recursive function are denoted as $CT$.

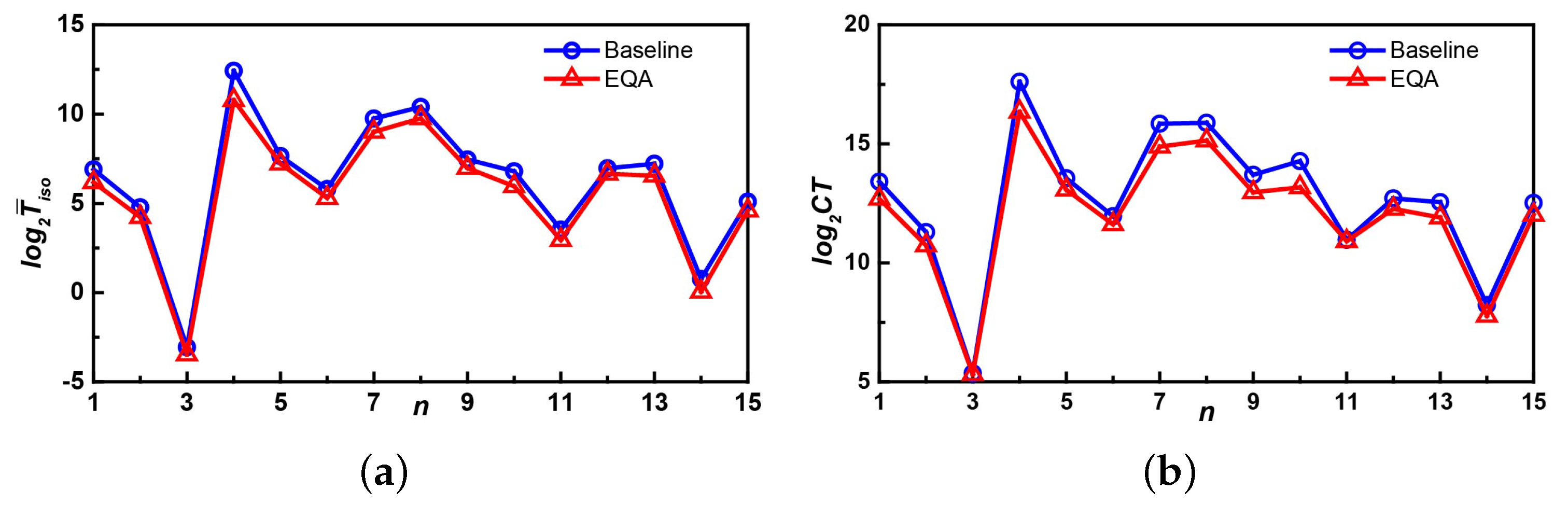
5.2. Experiment on the YEAST Dataset

The YEASTdataset can be downloaded from the official website of Pajek. Pajek is a large-scale complex network analysis tool. The official website also contains many other graph data test sets. The YEAST dataset has been used in [39]. The dataset has 2361 vertices, 7182 edges and 13 different vertex labels. The average degree for each vertex is six, and the maximum degree is 66.

During the process, 15 query points were randomly selected to conduct the experiments. The found MUIS, ${\overline{T}}_{iso}$ and $CT$ were recorded or calculated for each experiment.

Table 1. Experimental results on the yeastdataset.

#	Query Position	Vertex #	MUIS
#1	265	4	257 265 267 991
#2	321	5	81 208 321 522 1024
#3	345	5	146 338 345 400 849
#4	495	4	495 499 1525 1816
#5	620	6	275 303 619 620 625 866
#6	752	4	67 71 752 1040
#7	899	8	186 895 896 891 898 899 900 1280
#8	987	5	368 507 987 1201 1477
#9	1501	4	144 429 1501 1678
#10	1758	5	1483 1526 1724 1725 1758
#11	1895	3	198 1576 1895
#12	1984	5	17 1191 1508 1982 1984
#13	2013	6	1515 1553 1559 1562 1563 2013
#14	2236	4	1442 1617 1885 2236
#15	2300	6	1005 1357 1517 2121 2122 2300

shows the experiment number, the query position number, the number of vertices of found MUIS and the found MUIS. Both the baseline and EQA algorithms can complete the MUIS query process.

Figure 11 shows the comparison of the experimental results of the baseline and EQA algorithms on the YEAST dataset. Figure 11a shows the comparison of ${\overline{T}}_{iso}$, and Figure 11b shows the comparison of $CT$. The X-axis of the figure represents the experiment number, while the Y-axis of Figure 11a represents the logarithm of ${\overline{T}}_{iso}$ to base two, and the Y-axis of Figure 11b represents the logarithm of $CT$ to base two.

As can be seen from Figure 11, the performance of EQA was better than that of the baseline algorithm according to the two criteria. Moreover, in general, the longer ${\overline{T}}_{iso}$, or the more $CT$, the greater advantage of EQA over the baseline algorithm. It can be seen from the figure that the seventh experiment took the most time, and the advantage of the EQA was also the greatest. In addition, it can be seen from the figure that no matter which algorithm, the change trend of ${\overline{T}}_{iso}$ and $CT$ was almost the same, and the efficiency of the MUIS query algorithms can be well evaluated. As mentioned earlier, the measurement $CT$ was more stable, so it is recommended to use $CT$ to evaluate the performance of the algorithms.

5.3. Experiment on the HPRD Dataset

The HPRDdataset is provided by Human Proteinpedia, which was used in [40]. Human Proteinpedia is a community that shares and integrates human protein data. The dataset has 9460 vertices, 37,081 edges and 301 different vertex labels. The average degree for each vertex is seven, and the maximum degree is 249.

During the process, 15 query points were randomly selected to conduct the experiments. Similar information as the YEAST dataset is shown in

Table 2. Experimental results on the HPRDdataset.

#	Query Position	Vertex #	MUIS
#1	1890	4	100 568 723 1890
#2	2155	3	134 2155 2157
#3	2977	2	1098 2977
#4	3434	4	236 2329 3434 6928
#5	3789	3	1144 3789 4832
#6	4334	3	69 4334 4677
#7	4567	4	87 2734 4567 4569
#8	5332	4	77 153 235 5332
#9	5347	5	269 346 347 349 5347
#10	5701	4	659 2255 5701 6596
#11	5734	3	5734 5767 5768
#12	6758	4	419 1282 1818 6758
#13	7345	4	1686 3142 3840 7345
#14	8434	3	127 2959 8434
#15	9147	4	1457 1728 3277 9417

. Both the baseline and EQA algorithms can complete the MUIS query process on the HPRD dataset.

Comparing Table 2 and Table 1, it can be found that the number of vertices of MUIS found on the HPRD dataset was less than that of MUIS found on the YEAST dataset in most cases. That is to say, less layers were searched to find MUIS on the HPRD dataset. This indicates that the time to answer MUIS query on the HPRD dataset was less than that on the YEAST dataset in some sense.

Figure 12a,b shows the comparison of ${\overline{T}}_{iso}$ and $CT$ of the baseline and EQA algorithms separately. The meaning of the X-axis and Y-axis of Figure 12 is the same as that of Figure 11.

According to the two criteria ${\overline{T}}_{iso}$ and $CT$ shown in Figure 12, the performance of EQA was better than that of the baseline algorithm. Comparing Figure 11 with Figure 12, we find that the time to query MUIS on the HPRD dataset was usually less than that on the YEAST dataset, which was the same as the conclusion observed in Table 2. On the HPRD dataset, in many cases, both the baseline and EQA algorithms have less query time, so the performance advantage of EQA was not as obvious as that on the Yeast dataset. This further verifies the above-mentioned conclusion: in the MUIS query process, the longer ${\overline{T}}_{iso}$, or the more $CT$, the greater advantage of EQA over the baseline algorithm.

The reason for this phenomenon is speculated as follows. Although both the number of vertices and the number edges of the HPRD dataset were significantly larger than those of the YEAST dataset, the average degrees of the vertices of the two datasets had little difference. As a result, there was little difference between the number of induced subgraphs generated by the layer with the same number of vertices, as well as the number of candidate MUISs that needed to execute the isomorphism testing. However, the number of vertex labels in the HPRD dataset was significantly more than the number of vertex labels in the YEAST dataset, so on the HPRD dataset, the isomorphism testing was faster, and there were more unique induced subgraphs and a higher probability to obtain MUIS earlier. Therefore, the query time on the HPRD dataset was relatively shorter. Experiments on the synthetic dataset will further verify the above speculation.

5.4. Experiment on the Synthetic Datasets

Experiments were carried out on the synthetic datasets to investigate the influencing factors of EQA process speed. We designed and performed experiments on different sizes of graphs and different numbers of vertex labels and edge labels of graphs. We could also further verify the effectiveness and scalability of EQA algorithms through the experiments.

The synthetic datasets were generated by the graph data simulation generator used in [24]. The parameters of the simulation generator can be set by the users, including the number of edges, the number of vertex labels and the number of edge labels. As mentioned above, ${\overline{T}}_{iso}$ and $CT$ can evaluate the performance of the algorithms, and the trends were almost the same; however, $CT$ was more stable. Therefore, $CT$ was used in the experiments on the synthetic dataset as the evaluation criteria. We randomly selected 100 query positions for each dataset and calculated the average value of $CT$ from the 100 experiments, denoted as $\overline{CT}$.

(1)

Experiments on the increasing number of edges

We investigated the influence of graph size on EQA process speed first. Keep the same number of vertex labels and edge labels, and increase the number of edges. The number of vertices was 3000; the number of edge labels was set as five; the number of vertex labels was set as five; and the number of edges was set as 6000, 7000, 8000 and 9000 separately. The experimental results are shown in

Table 3. Experimental results on the increasing number of edges.

Dataset #	Edge #	Vertex Label #	Edges Label #	$\overline{\mathit{CT}}$
#1	6000	5	5	566,534
#2	7000	5	5	616,321
#3	8000	5	5	685,132
#4	9000	5	5	763,026

. As can be seen from the table, $\overline{CT}$ was increasing with the increasing number of edges, that is to say, the answering speed was decreasing. When the number of vertices in the graph was kept the same and the number of edges was increasing, the average degree of vertices was also increasing. Therefore, when searching the induced subgraph space in ascending order of the number of vertices, more candidate subgraphs would be generated in each layer, and more graphs would participate in the subgraph isomorphism testing; so the query time became longer, and the answering speed decreased.

(2)

Experiments on the increasing number of vertex labels

We investigated the influence of vertex labels on EQA process speed subsequently. Keep the same size of graphs and the same number of edge labels, then increase the number of vertex labels. The graphs contained 3000 vertices and 8000 edges. The number of edge labels was set as five, and the number of vertex labels was set as 10, 30, 50 and 70 separately. The experimental results are shown in

Table 4. Experimental results on the increasing number of vertex labels.

Dataset #	Edge #	Vertex Label #	Edges Label #	$\overline{\mathit{CT}}$
#1	8000	10	5	666,345
#2	8000	30	5	602,654
#3	8000	50	5	538,935
#4	8000	70	5	464,682

. As seen from the table, $\overline{CT}$ was decreasing with the increasing number of vertex labels, that is to say, the answering speed was increasing. Since both the number of vertices and the number of edges in each graph were the same, the number of candidate subgraphs generated had little difference, as well as the number of candidate subgraphs participating in the isomorphism testing. However, with the increasing number of vertex labels, there were more unique induced subgraphs on the dataset and a higher probability to obtain MUIS earlier. Therefore, $CT$ was decreasing, and the answering speed was increasing.

(3)

Experiments on the increasing number of edge labels

We investigated the influence of edge labels on EQA process speed at last. Keep the same size of graphs and the same number of vertex labels, then increase the number of edge labels. All the graphs contained 3000 vertices and 8000 edges. The number of vertex labels was set as five, and the number of edge labels was set as 10, 30, 50 and 70 separately. The experimental results are shown in

Table 5. Experimental results on the increasing number of edge labels.

Dataset #	Edge #	Vertex Label #	Edges Label #	$\overline{\mathit{CT}}$
#1	8000	5	10	675,634
#2	8000	5	30	610,635
#3	8000	5	50	542,684
#4	8000	5	70	476,325

. As seen from the table, $\overline{CT}$ was decreasing with the increasing number of edge labels, that is to say, the answering speed was increasing. Since the size of each graph was the same, the number of candidate subgraphs generated in each graph was also almost the same, that is to say, the number of candidate subgraphs participating in the isomorphism testing also had little difference. However, the number of unique induced subgraphs was increasing in each graph with the increasing number of edge labels, so there was a higher probability to obtain MUIS earlier. Therefore, $CT$ was decreasing, and the answering speed was increasing.

In a summary, the size and labels of graphs were the main influencing factors of the EQA process speed. The answering speed was decreasing when the size of graphs was increasing, while the speed was increasing when the the number of labels was increasing. EQA solved all MUIS queries on the synthetic datasets, which shows its effectiveness and scalability.

6. Conclusions

In this paper, we report a novel type of interesting subgraph query: MUIS query. MUIS query is a graph query technology with high academic value and widespread application prospects. We first give the formal definition of MUIS and discuss the properties. Then, we propose the general filtering-validation framework to solve MUIS query. In the filtering process, the BFS-based candidate set generation strategy is proposed, which searches the induced subgraph space from the lower layer to the higher layer and sets the query position self-constructed one-vertex subgraph as the first layer. In addition, the matched vertices-based pruning strategy is proposed in this process to prune the useless subgraph region, thereby significantly avoiding unnecessary computations. In the validation process, query position-based subgraph isomorphism is proposed to check efficiently whether the candidate subgraphs are unique. The EQA algorithm is devised to answer efficiently MUIS query under the framework and strategies at last. Both synthetic and real datasets are used to test the effectiveness and scalability of the EQA algorithm. The influencing factors of the EQA process speed are also verified by the synthetic dataset experiments.

MUIS query can be used in many potential applications, such as subgraph retrieval, graph visualization, representative subgraph discovery and vertex property exploration. The paper mainly answers MUIS query in single (large) graphs. For graph databases that store more than one graph, our solution may meet problems. We will try to answer MUIS query efficiently in graph databases in future work.