Registration of Dental Tomographic Volume Data and Scan Surface Data Using Dynamic Segmentation
Abstract
1. Introduction
1.1. Backgrounds
1.1.1. Volumetric Computed Tomography (CT) Data
1.1.2. Dental Surface Data
1.2. Related Works
1.3. Motivation and Contribution of the Thesis
2. Proposed Method: MICP
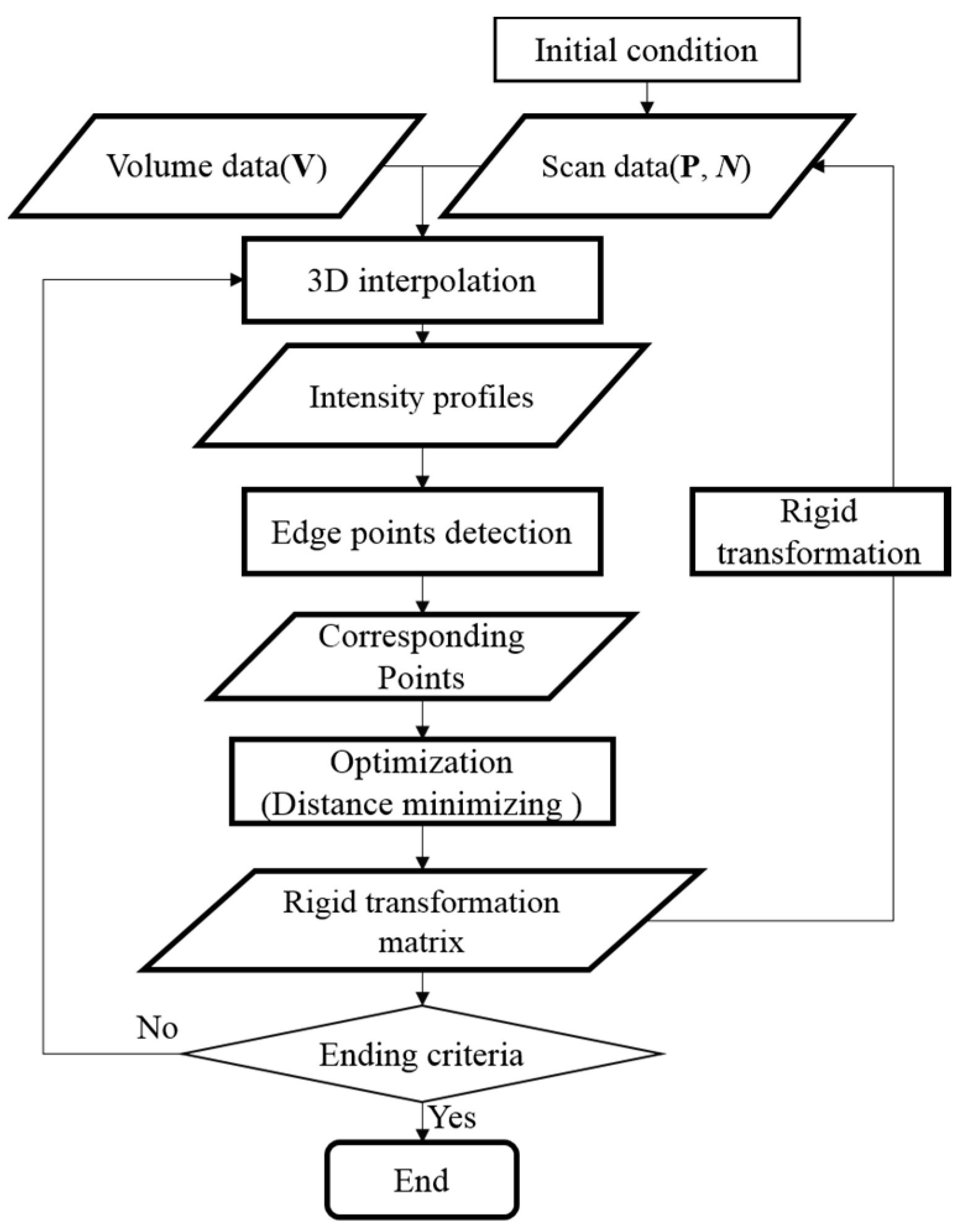
2.1. Overview
| Pseudo-code: The overall process of the proposed method |
| Data: Result: while (e < ending criteria) ← interpolation(V) {E} ← step_edge(V) {M} ← match(E,P′,N) ← minimizing point-to-plane distance metric ← {P} end |
2.2. Automatic Registration Process
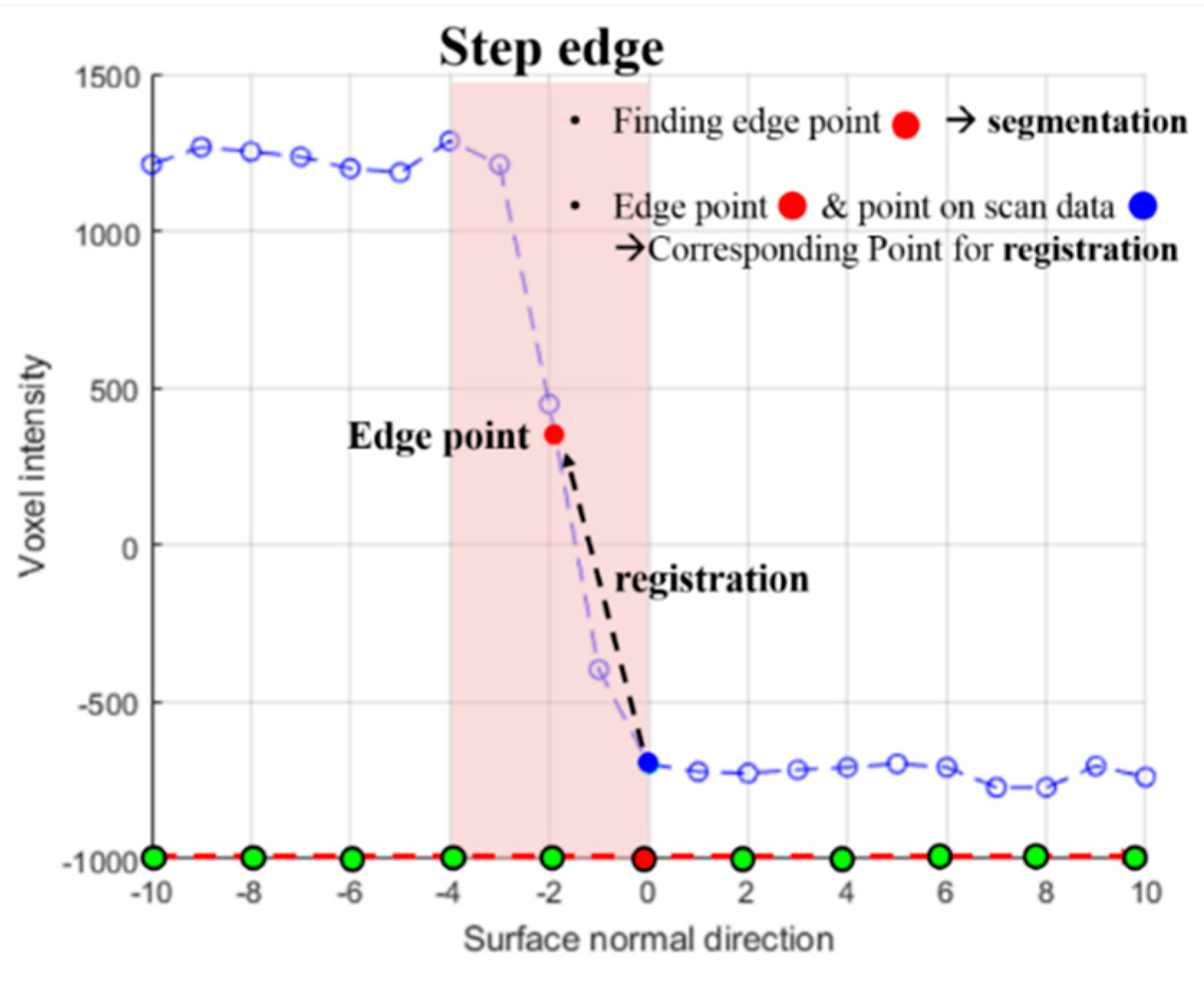
2.2.1. Defining an Edge Point on Intensity Profile
2.2.2. Dynamic Segmentation
2.3. Factors to Consider in Proposed Method
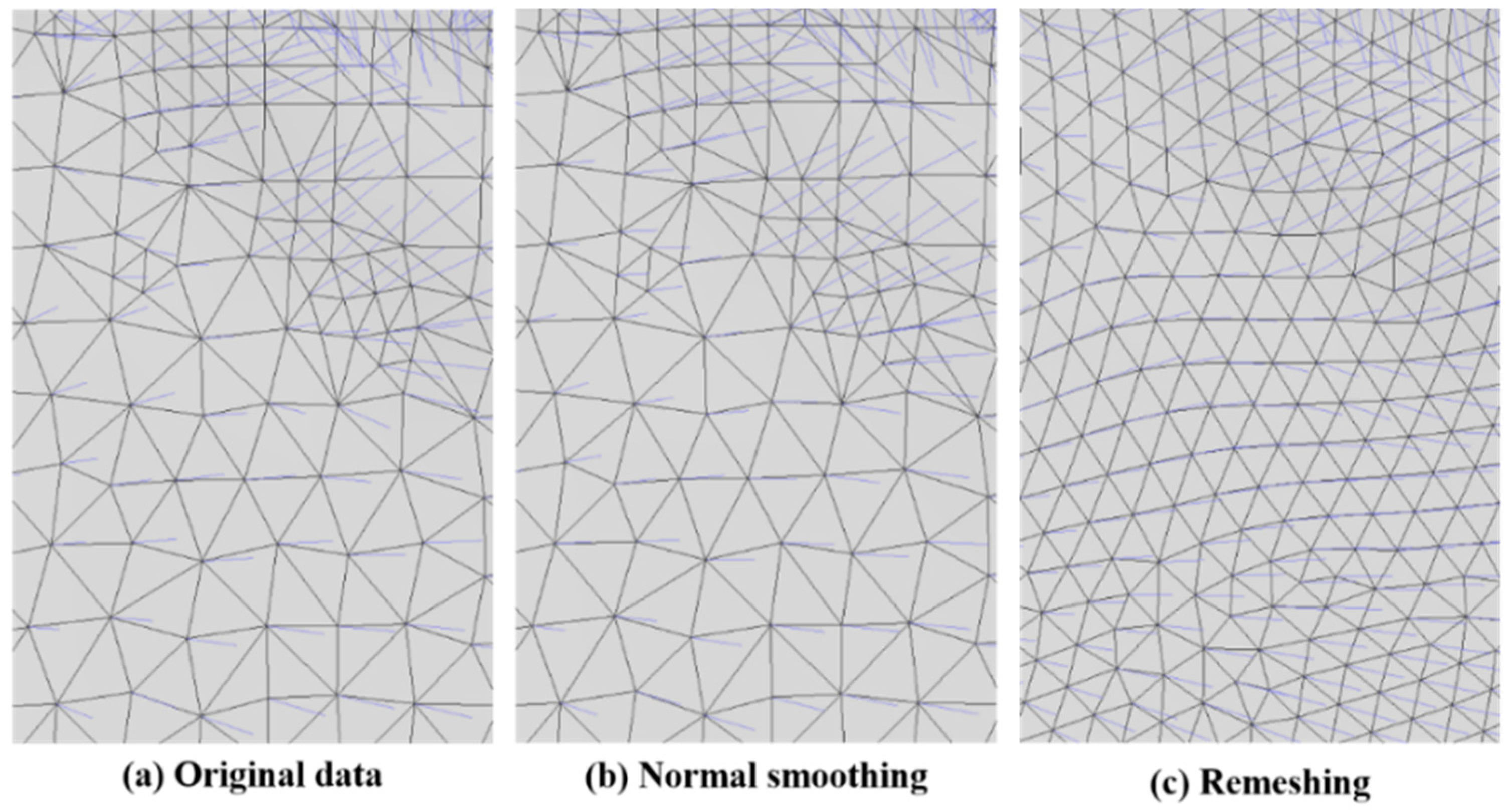
2.3.1. Normal Correction
2.3.2. Length Value to Generate Intensity Profile
2.3.3. Down Sampling
3. Results & Discussion
3.1. Result
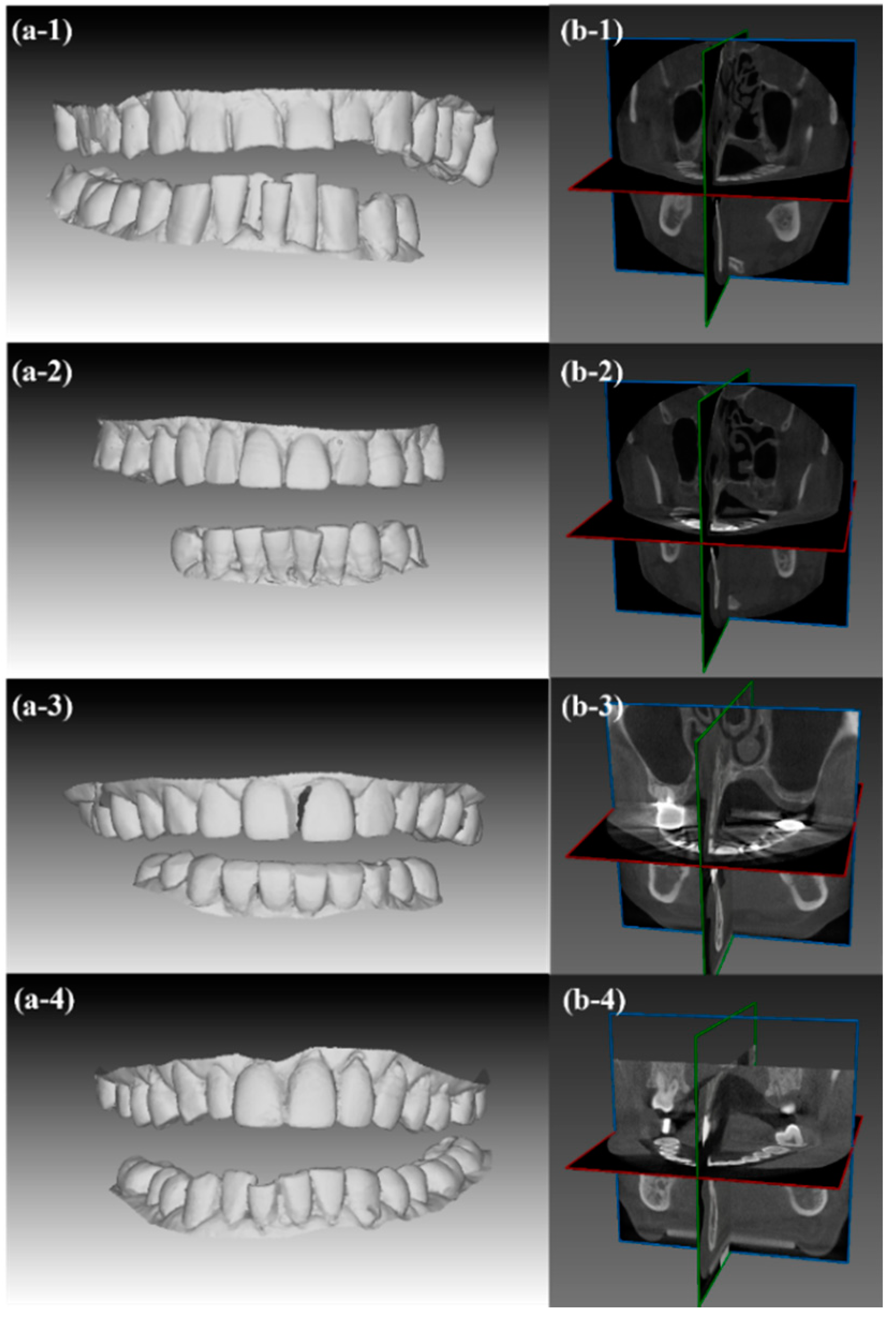
3.1.1. Data Sets
3.1.2. Registration by the Conventional Method
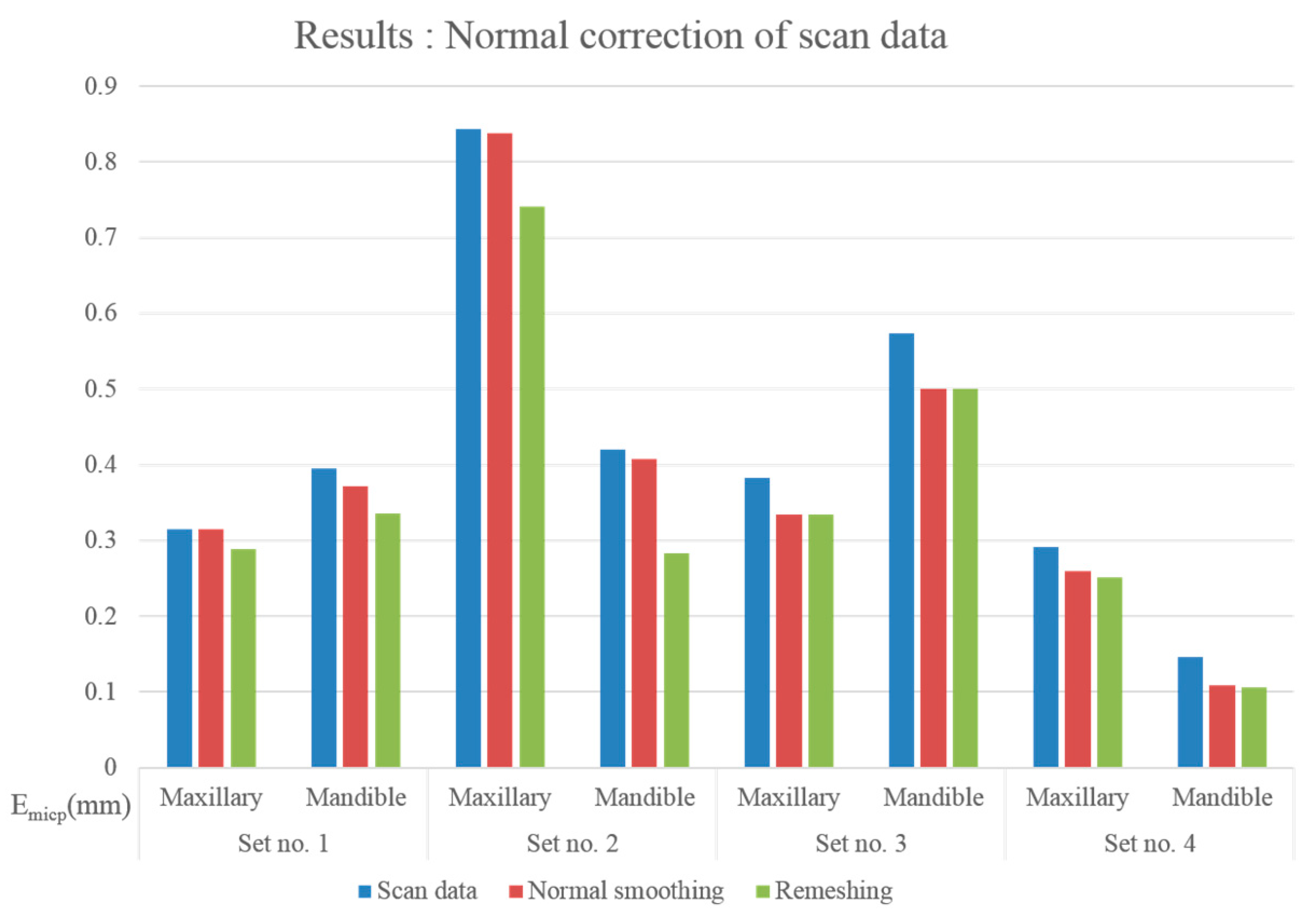
3.1.3. Modified Iterative Closest Point (MICP) Registration Results: Normal Correction
3.1.4. MICP Registration Results: Different Length Values
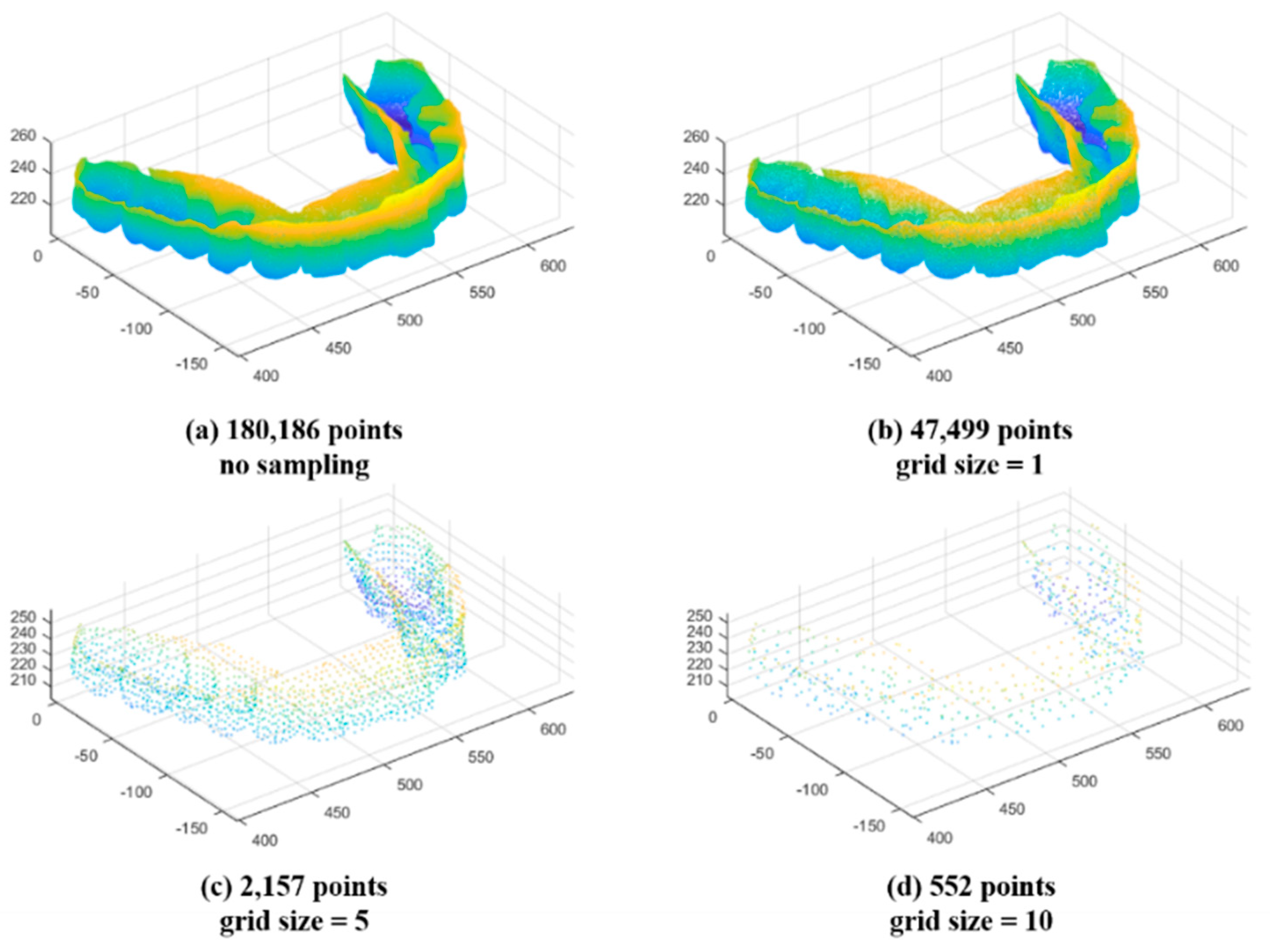
3.1.5. MICP Registration Results: Down Sampling
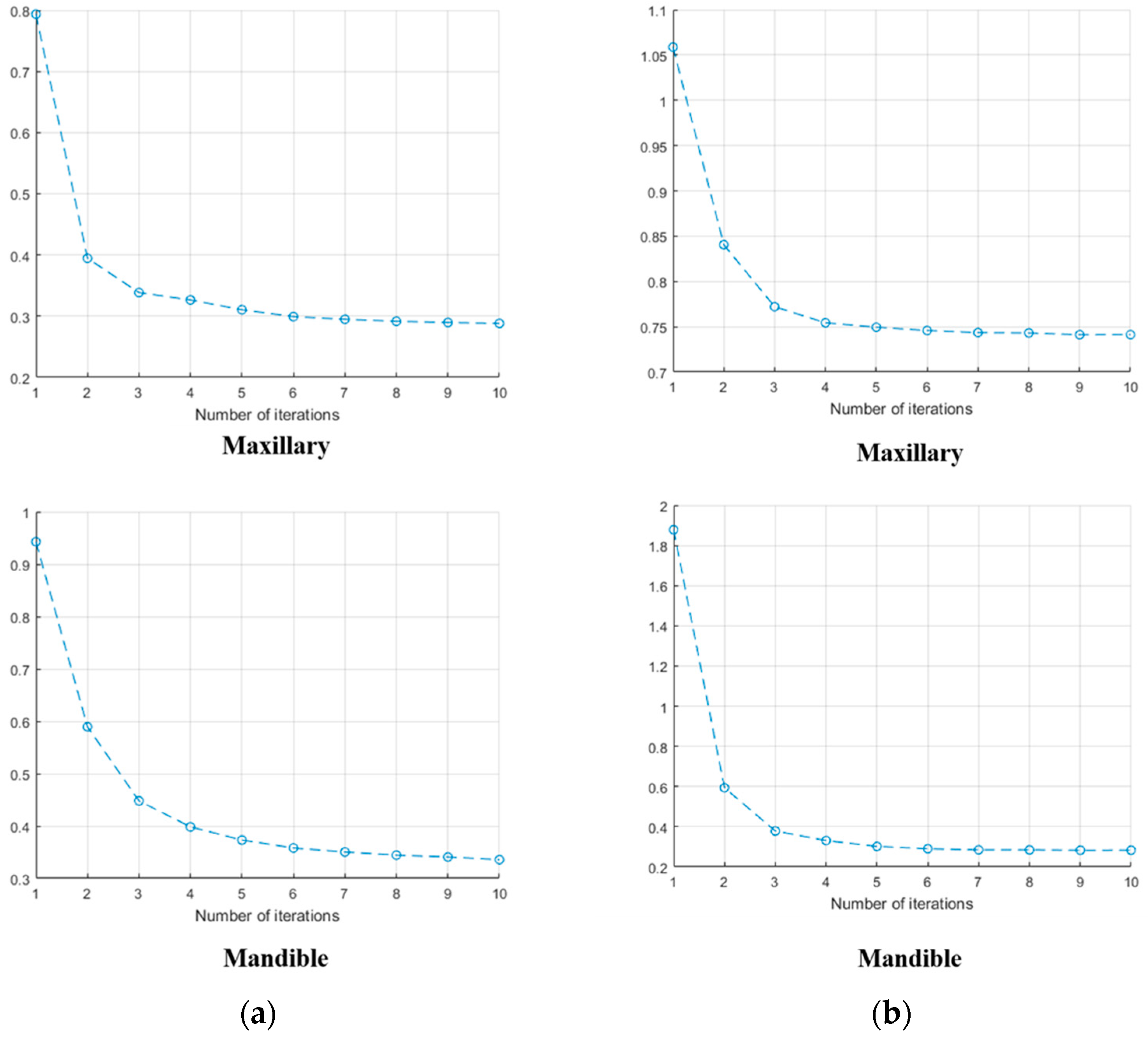
3.1.6. MICP Registration Results
3.2. Discussion
3.2.1. Evaluation of MICP Registration Results
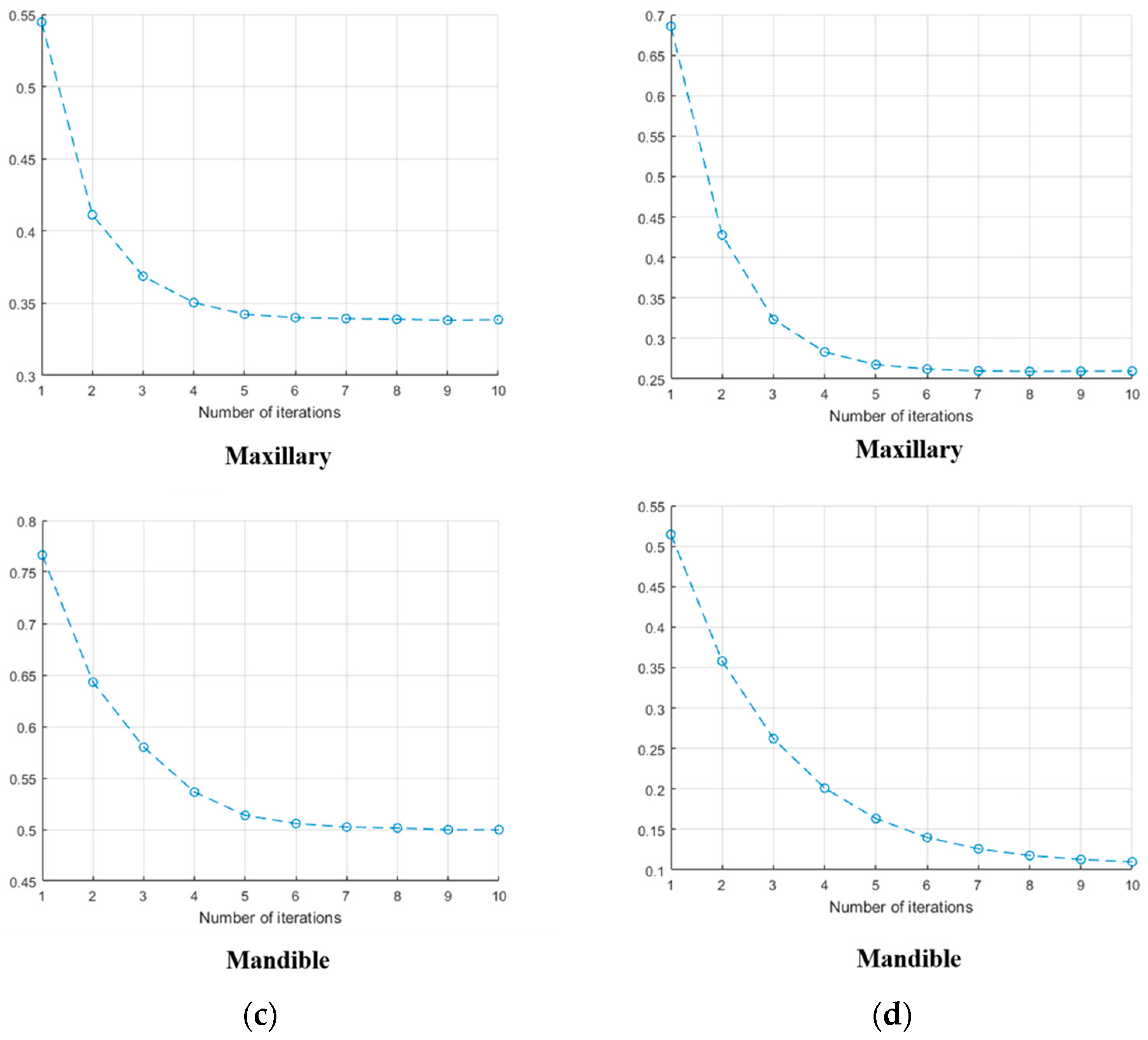
3.2.2. Evaluation of MICP Registration Results by Down Sampling
3.2.3. Limitations
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mildenberger, P.; Eichelberg, M.; Martin, E. Introduction to the DICOM standard. Eur. Radiol. 2002, 12, 920–927. [Google Scholar] [CrossRef] [PubMed]
- Gueld, M.O.; Kohnen, M.; Keysers, D.; Schubert, H.; Wein, B.B.; Bredno, J.; Lehmann, T.M. Quality of DICOM header information for image categorization. Med. Imaging 2002, 4685, 280–288. [Google Scholar]
- Mustra, M.; Delac, K.; Grgic, M. Overview of the DICOM standard. In Proceedings of the 2008 50th International Symposium ELMAR, Zadar, Croatia, 10–12 September 2008; Volume 1, pp. 39–44. [Google Scholar]
- Mozzo, P.; Procacci, C.; Tacconi, A.; Tinazzi Martini, P.; Bergamo Andreis, I.A. A new volumetric CT machine for dental imaging based on the cone-beam technique: Preliminary results. Eur. Radiol. 1998, 8, 1558–1564. [Google Scholar] [CrossRef] [PubMed]
- Scarfe, W.C.; Farman, A.G.; Sukovic, P. Clinical applications of cone-beam computed tomography in dental practice. J. Can. Dent. Assoc. 2006, 72, 75–80. [Google Scholar] [CrossRef] [PubMed]
- Scarfe, W.C.; Farman, A.G. What is Cone-Beam CT and How Does it Work? Dent. Clin. N. Am. 2008, 52, 707–730. [Google Scholar] [CrossRef] [PubMed]
- Suomalainen, A.; Vehmas, T.; Kortesniemi, M.; Robinson, S.; Peltola, J. Accuracy of linear measurements using dental cone beam and conventional multislice computed tomography. Dentomaxillofac. Radiol. 2008, 37, 10–17. [Google Scholar] [CrossRef] [PubMed]
- Hiller, J.D.; Lipson, H. STL 2.0: A Proposal for a Universal Multi-Material Additive Manufacturing File Format. In Proceedings of the 20th Solid Freeform Fabrication Symposium (SFF), Austin, TX, USA, 3–5 August 2009; pp. 266–278. [Google Scholar] [CrossRef]
- Morano, R.A.; Ozturk, C.; Conn, R.; Dubin, S.; Zietz, S.; Nissanov, J. Structured light using pseudorandom codes. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 322–327. [Google Scholar] [CrossRef]
- Salvi, J.; Fernandez, S.; Pribanic, T.; Llado, X. A state of the art in structured light patterns for surface profilometry. Pattern Recognit. 2010, 43, 2666–2680. [Google Scholar] [CrossRef]
- Reza Rokn, A.; Hashemi, K.; Akbari, S.; Javad Kharazifard, M.; Barikani, H.; Panjnoosh, M. Accuracy of Linear Measurements Using Cone Beam Computed Tomography in Comparison with Clinical Measurements. J. Dent. 2016, 13, 333. [Google Scholar]
- Patcas, R.; Müller, L.; Ullrich, O.; Peltomäki, T. Accuracy of cone-beam computed tomography at different resolutions assessed on the bony covering of the mandibular anterior teeth. Am. J. Orthod. Dentofac. Orthop. 2012, 141, 41–50. [Google Scholar] [CrossRef] [PubMed]
- Van Assche, N.; Quirynen, M. Tolerance within a surgical guide. Clin. Oral Implant Res. 2010, 21, 455–458. [Google Scholar] [CrossRef] [PubMed]
- Besl, P.; McKay, N. A Method for Registration of 3-D Shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992. [Google Scholar] [CrossRef]
- Jung, S.; Song, S.; Chang, M.; Park, S. Range image registration based on 2D synthetic images. CAD Comput. Aided Des. 2018, 94, 16–27. [Google Scholar] [CrossRef]
- Gelfand, N.; Mitra, N.J.; Guibas, L.J.; Pottmann, H. Robust global registration. Symp. Geom. Process. 2005, 2, 5. [Google Scholar] [CrossRef]
- Aiger, D.; Mitra, N.J.; Cohen-Or, D. 4-Points Congruent Sets for Robust Pairwise Surface Registration. ACM Trans. Graph. 2008, 27, 1. [Google Scholar] [CrossRef]
- SanthaKumar, R.; Vidhya, S. Three-Dimensional Reconstruction of Cone Beam Computed Tomography Using Splines Interpolation Technique for Dental Application. J. Med Devices 2016, 10, 030927. [Google Scholar] [CrossRef]
- Rumboldt, Z.; Huda, W.; All, J.W. Review of portable CT with assessment of a dedicated head CT scanner. Am. J. Neuroradiol. 2009, 30, 1630–1636. [Google Scholar] [CrossRef] [PubMed]
- Revol, C.; Jourlin, M. A new minimum variance region growing algorithm for image segmentation. Pattern Recognit. Lett. 1997, 18, 249–258. [Google Scholar] [CrossRef]
- Yau, H.T.; Lin, Y.K.; Tsou, L.S.; Lee, C.Y. An adaptive region growing method to segment inferior alveolar nerve canal from 3d medical images for dental implant surgery. Comput. Aided Des. Appl. 2008, 5, 743–752. [Google Scholar] [CrossRef]
- Hosntalab, M.; Aghaeizadeh Zoroofi, R.; Abbaspour Tehrani-Fard, A.; Shirani, G. Segmentation of teeth in CT volumetric dataset by panoramic projection and variational level set. Int. J. Comput. Assist. Radiol. Surg. 2008, 3, 257–265. [Google Scholar] [CrossRef]
- Ji, D.X.; Ong, S.H.; Foong, K.W.C. A level-set based approach for anterior teeth segmentation in cone beam computed tomography images. Comput. Boil. Med. 2014, 50, 116–128. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; Chae, O. Individual tooth segmentation from CT images using level set method with shape and intensity prior. Pattern Recognit. 2010, 43, 2406–2417. [Google Scholar] [CrossRef]
- Pəvəloiu, I.B.; Vasiləţeanu, A.; Goga, N.; Marin, I.; Ilie, C.; Ungar, A.; Pətraşcu, I. 3D dental reconstruction from CBCT data. In Proceedings of the 2014 International Symposium on Fundamentals of Electrical Engineering, Bucharest, Romania, 28–29 November 2014. [Google Scholar] [CrossRef]
- Mortaheb, P.; Rezaeian, M.; Soltanian-Zadeh, H. Automatic dental CT image segmentation using mean shift algorithm. In Proceedings of the 2013 8th Iranian Conference on Machine Vision and Image Processing (MVIP), Zanjan, Iran, 10–12 September 2013; pp. 121–126. [Google Scholar] [CrossRef]
- Thariat, J.; Ramus, L.; Maingon, P.; Odin, G.; Gregoire, V.; Darcourt, V.; Malandain, G. Dentalmaps: Automatic dental delineation for radiotherapy planning in head-and-neck cancer. Int. J. Radiat. Oncol. Boil. Phys. 2012, 82, 1858–1865. [Google Scholar] [CrossRef] [PubMed]
- Schulze, R.; Heil, U.; Groß, D.; Bruellmann, D.D.; Dranischnikow, E.; Schwanecke, U.; Schoemer, E. Artefacts in CBCT: A review. Dentomaxillofac. Radiol. 2011, 40, 265–273. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Snyder, D.L.; O’Sullivan, J.; Vannier, M.W. Iterative Deblurrinf for CT metal artifact reduction. IEEE Trans. Med. Imaging 1996, 15, 657–664. [Google Scholar] [CrossRef] [PubMed]
- Watzke, O.; Kalender, W.A. A pragmatic approach to metal artifact reduction in CT: Merging of metal artifact reduced images. Eur. Radiol. 2004, 14, 849–856. [Google Scholar] [CrossRef] [PubMed]
- Cann, C.E. Quantitative CT for determination of bone mineral density: A review. Radiology 1988, 166, 509–522. [Google Scholar] [CrossRef] [PubMed]
- Norton, M.R.; Gamble, C. Bone classification: An objective scale of bone density using the computerized tomography scan. Clin. Oral Implant Res. 2001, 12, 79–84. [Google Scholar] [CrossRef]
- Turkyilmaz, I.; Ozan, O.; Yilmaz, B.; Ersoy, A.E. Determination of bone quality of 372 implant recipient sites using hounsfield unit from computerized tomography: A clinical study. Clin. Implant Dent. Relat. Res. 2008, 10, 238–244. [Google Scholar] [CrossRef] [PubMed]
- Rafic, M.; Ravindran, P. Evaluation of on-board imager cone beam CT hounsfield units for treatment planning using rigid image registration. J. Cancer Res. Ther. 2015, 11, 690. [Google Scholar] [CrossRef] [PubMed]
- Grimson, W.E.L.; Hildreth, E.C. Comments on “Digital Step Edges from Zero Crossings of Second Directional Derivatives”. IEEE Trans. Pattern Anal. Mach. Intell. 1985, PAMI-7, 121–127. [Google Scholar] [CrossRef]
- Sorkine, O.; Rabinovich, M. Least-Squares Rigid Motion Using SVD. Technical Notes. 2009, pp. 1–6. Available online: http://www.igl.ethz.ch/projects/ARAP/svd_rot.pdf (accessed on 24 February 2009).
- Botsch, M.; Kobbelt, L. An intuitive framework for real-time freeform modeling. ACM Trans. Graph. 2004, 23, 630. [Google Scholar] [CrossRef]
- Kobbelt, L.P.; Bareuther, T.; Seidel, H.P. Multiresolution shape deformations for meshes with dynamic vertex connectivity. Proc. Eurographics 2000 2000, 19, 249–260. [Google Scholar] [CrossRef]
- Gelfand, N.; Ikemoto, L.; Rusinkiewicz, S.; Levoy, M. Geometrically stable sampling for the ICP algorithm. In Proceedings of the Fourth International Conference on 3-D Digital Imaging and Modeling, Banff, AB, Canada, 6–10 October 2003; pp. 260–267. [Google Scholar] [CrossRef]
- Wolf, I.; Vetter, M.; Wegner, I.; Böttger, T.; Nolden, M.; Schöbinger, M.; Meinzer, H.P. The medical imaging interaction toolkit. Med. Image Anal. 2005, 9, 594–604. [Google Scholar] [CrossRef] [PubMed]
- Cignoni, P.; Corsini, M.; Ranzuglia, G. MeshLab: An Open-Source Mesh Processing Tool. In Proceedings of the Eurographics Italian Chapter Conference, Salerno, Italy, 2–4 July 2008; pp. 129–136. [Google Scholar] [CrossRef]
- Schlicher, W.; Nielsen, I.; Huang, J.C.; Maki, K.; Hatcher, D.C.; Miller, A.J. Consistency and precision of landmark identification in three-dimensional cone beam computed tomography scans. Eur. J. Orthod. 2012, 34, 263–275. [Google Scholar] [CrossRef] [PubMed]


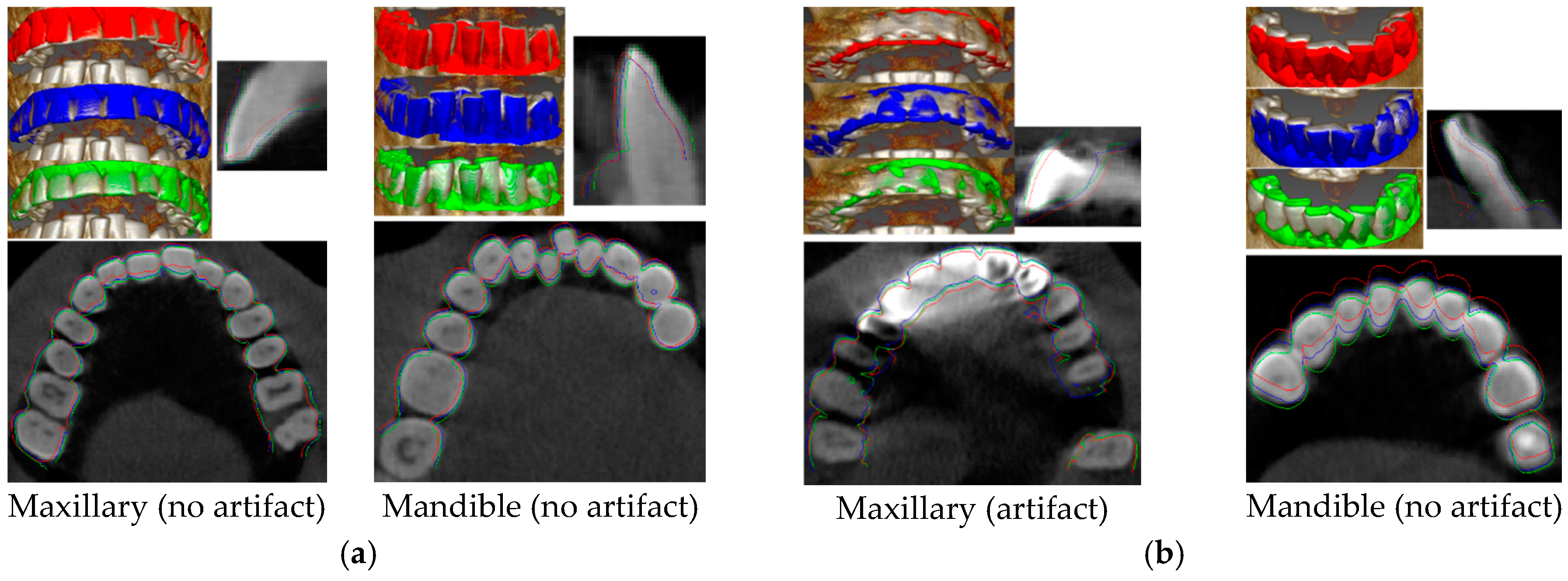
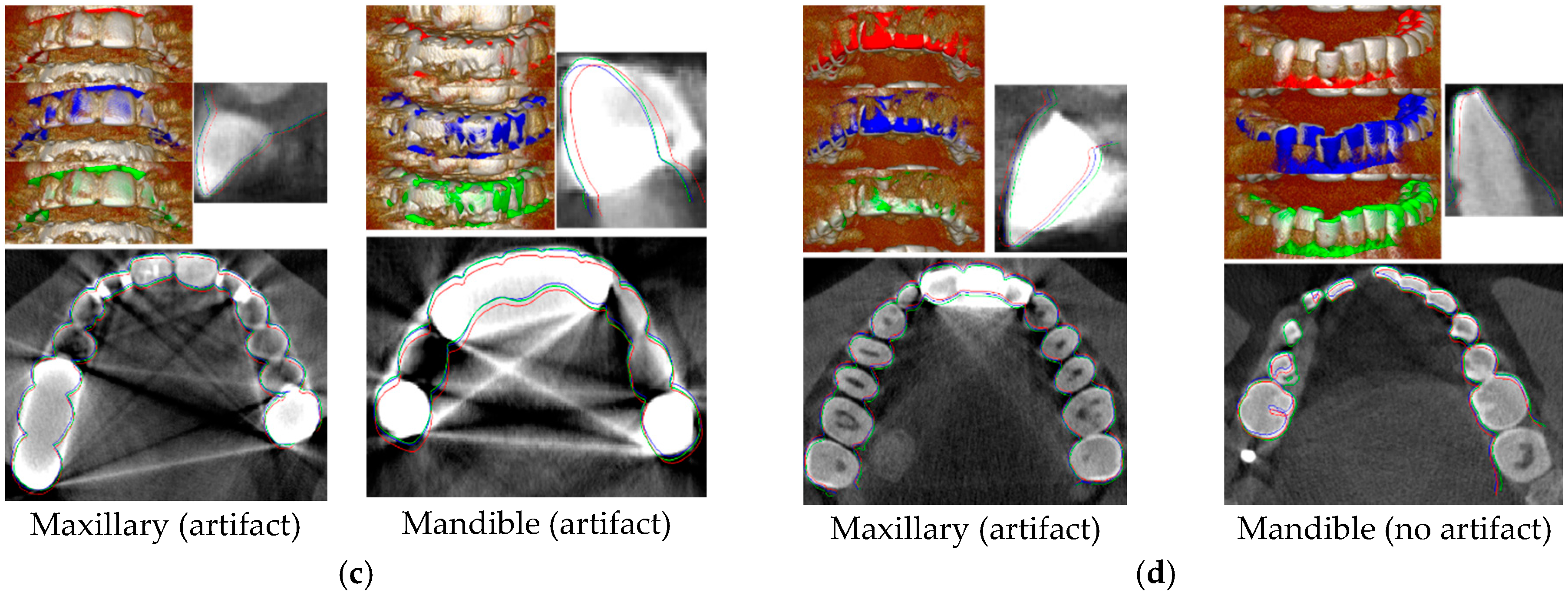
| Input Data | Metal Artifact | (mm) | (mm) | |
|---|---|---|---|---|
| Set no.1 | Maxillary | No | 0.3612 | 0.1308 |
| Mandible | No | 0.3357 | 0.1140 | |
| Set no.2 | Maxillary | Yes | 0.4170 | 0.1574 |
| Mandible | No | 0.3812 | 0.1380 | |
| Set no.3 | Maxillary | Yes | 0.3178 | 0.1242 |
| Mandible | Yes | 0.3464 | 0.1420 | |
| Set no.4 | Maxillary | Yes | 0.5025 | 0.1914 |
| Mandible | no | 0.4834 | 0.1823 | |
| Input Data | Normal Correction | (mm) | (mm) | (mm) | ||
|---|---|---|---|---|---|---|
| Set no.1 | Maxillary | No | 212,125 | 0.3145 | 0.7173 | 0.6178 |
| Normal sampling | 0.3146 | 0.7198 | 0.6172 | |||
| Remeshing | 180,186 | 0.2882 | 0.6703 | 0.6219 | ||
| Mandible | No | 160,112 | 0.3953 | 1.0815 | 1.1811 | |
| Normal sampling | 0.3723 | 1.0094 | 1.1774 | |||
| Remeshing | 131,545 | 0.3357 | 0.9217 | 1.1679 | ||
| Set no.2 | Maxillary | No | 199,456 | 0.8431 | 1.8762 | 1.2145 |
| Normal sampling | 0.8374 | 1.8500 | 1.2461 | |||
| Remeshing | 185,546 | 0.7412 | 1.6113 | 1.2730 | ||
| Mandible | No | 113,333 | 0.4203 | 1.2217 | 1.1116 | |
| Normal sampling | 0.4071 | 1.1760 | 1.1070 | |||
| Remeshing | 95,438 | 0.2830 | 0.8040 | 1.0955 | ||
| Set no.3 | Maxillary | No | 78,442 | 0.3828 | 1.4925 | 0.4458 |
| Normal sampling | 0.3339 | 1.2376 | 0.4350 | |||
| Remeshing | 51,398 | 0.3337 | 1.2289 | 0.4466 | ||
| Mandible | No | 34,081 | 0.5730 | 1.9817 | 0.5957 | |
| Normal sampling | 0.5000 | 1.6143 | 0.5366 | |||
| Remeshing | 78,657 | 0.4998 | 1.6196 | 0.5387 | ||
| Set no.4 | Maxillary | No | 69,563 | 0.2920 | 1.1811 | 0.6204 |
| Normal sampling | 0.2602 | 1.0053 | 0.5959 | |||
| Remeshing | 56,335 | 0.2515 | 0.9704 | 0.5891 | ||
| Mandible | No | 56,817 | 0.1457 | 0.5928 | 0.9164 | |
| Normal sampling | 0.1084 | 0.3837 | 0.9146 | |||
| Remeshing | 44,472 | 0.1059 | 0.3801 | 0.9298 | ||
| Input Data | Metal Artifact | D Value Respect to Length of Intensity Profile | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| Set no.1 | Maxillary | No | X | 0.7009 | 0.5681 | 0.5512 | 0.5409 | 0.5402 | 0.5410 | 0.5442 | 0.5446 | 0.5453 |
| Mandible | No | X | X | 1.1733 | 1.1743 | 1.1735 | 1.1734 | 1.1741 | 1.1776 | 1.1780 | 1.1738 | |
| Set no.2 | Maxillary | Yes | X | 1.0571 | 1.1947 | 1.2525 | 1.0014 | 1.0817 | 1.0813 | 1.3574 | 1.3294 | 1.2866 |
| Mandible | No | X | 1.2707 | 1.1302 | 1.1186 | 1.1215 | 1.1185 | 1.1186 | 1.1185 | 1.1186 | 1.1184 | |
| Set no.3 | Maxillary | Yes | X | 0.7850 | 0.4375 | 0.4101 | 0.4241 | 0.4533 | 0.4557 | 0.4725 | 0.4781 | 0.4817 |
| Mandible | Yes | X | X | 0.5127 | 0.5345 | 0.5482 | 0.5703 | 0.5593 | 0.5508 | 0.5530 | 0.5501 | |
| Set no.4 | Maxillary | Yes | X | X | 0.5614 | 0.5604 | 0.5696 | 0.5844 | 0.5826 | 0.5838 | 0.5717 | 0.5824 |
| Mandible | No | X | X | 0.9393 | 0.9370 | 0.9371 | 0.9371 | 0.9371 | 0.9372 | 0.0973 | 0.9371 | |
| Input Data | Sampling | (mm) | (mm) | (mm) | |||
|---|---|---|---|---|---|---|---|
| Set no.1 | Maxillary | No | 180,186 | 0.2882 | 0.6703 | 0.6219 | 1062.8 |
| 1 | 47,499 | 0.2860 | 0.6622 | 0.6159 | 274.8 | ||
| 5 | 2157 | 0.2528 | 0.5933 | 0.5881 | 12.4 | ||
| 10 | 552 | 0.2434 | 0.5635 | 0.5299 | 3.5 | ||
| Mandible | No | 131,545 | 0.3210 | 0.8730 | 1.1677 | 793.4 | |
| 1 | 34,781 | 0.3131 | 0.8470 | 1.1760 | 210.4 | ||
| 5 | 1593 | 0.2609 | 0.6881 | 1.1882 | 9.9 | ||
| 10 | 395 | 0.2401 | 0.5460 | 1.2847 | 2.9 | ||
| Set no.2 | Maxillary | No | 173,449 | 0.7386 | 1.6003 | 1.2689 | 1142.4 |
| 1 | 46,158 | 0.7279 | 1.5659 | 1.2766 | 307.0 | ||
| 5 | 2155 | 0.6971 | 1.4932 | 1.2698 | 14.1 | ||
| 10 | 539 | 0.5489 | 0.9869 | 1.3935 | 4.0 | ||
| Mandible | No | 84,735 | 0.2716 | 0.7618 | 1.0742 | 550.4 | |
| 1 | 22,285 | 0.2636 | 0.7348 | 1.0698 | 146.4 | ||
| 5 | 1021 | 0.1592 | 0.3407 | 1.0895 | 6.9 | ||
| 10 | 227 | 0.1789 | 0.4136 | 1.1974 | 1.7 | ||
| Set no.3 | Maxillary | No | 163,714 | 0.3386 | 1.2525 | 0.4448 | 1149.0 |
| 1 | 77,997 | 0.3358 | 1.2416 | 0.4464 | 537.8 | ||
| 5 | 3982 | 0.3337 | 1.2247 | 0.4827 | 27.7 | ||
| 10 | 1013 | 0.3210 | 1.1381 | 0.4661 | 7.4 | ||
| Mandible | No | 78,657 | 0.4991 | 1.6165 | 0.5390 | 581.9 | |
| 1 | 40,812 | 0.5004 | 1.6167 | 0.5388 | 303.0 | ||
| 5 | 2097 | 0.4993 | 1.6027 | 0.5468 | 15.9 | ||
| 10 | 543 | 0.5131 | 1.6708 | 0.5920 | 4.3 | ||
| Set no.4 | Maxillary | No | 163,714 | 0.2597 | 1.0095 | 0.5843 | 1092.8 |
| 1 | 82,483 | 0.2589 | 1.0015 | 0.5862 | 580.0 | ||
| 5 | 4232 | 0.2576 | 0.9843 | 0.5753 | 29.4 | ||
| 10 | 1081 | 0.2462 | 0.9398 | 0.5856 | 7.6 | ||
| Mandible | No | 125,617 | 0.1093 | 0.3891 | 0.9128 | 871.6 | |
| 1 | 65,067 | 0.1088 | 0.3857 | 0.9130 | 444.3 | ||
| 5 | 3384 | 0.1067 | 0.3621 | 0.9166 | 23.4 | ||
| 10 | 892 | 0.1248 | 0.4066 | 0.9329 | 6.4 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, K.; Jung, S.; Hwang, I.; Kim, T.; Chang, M. Registration of Dental Tomographic Volume Data and Scan Surface Data Using Dynamic Segmentation. Appl. Sci. 2018, 8, 1762. https://doi.org/10.3390/app8101762
Jung K, Jung S, Hwang I, Kim T, Chang M. Registration of Dental Tomographic Volume Data and Scan Surface Data Using Dynamic Segmentation. Applied Sciences. 2018; 8(10):1762. https://doi.org/10.3390/app8101762
Chicago/Turabian StyleJung, Keonhwa, Sukwoo Jung, Inseon Hwang, Taeksoo Kim, and Minho Chang. 2018. "Registration of Dental Tomographic Volume Data and Scan Surface Data Using Dynamic Segmentation" Applied Sciences 8, no. 10: 1762. https://doi.org/10.3390/app8101762
APA StyleJung, K., Jung, S., Hwang, I., Kim, T., & Chang, M. (2018). Registration of Dental Tomographic Volume Data and Scan Surface Data Using Dynamic Segmentation. Applied Sciences, 8(10), 1762. https://doi.org/10.3390/app8101762




