Finite Difference/Collocation Method for a Generalized Time-Fractional KdV Equation
Abstract
:1. Introduction
2. Preliminaries of Fractional Calculus and Jacobi Polynomials
2.1. Generalized Fractional Calculus
2.2. Jacobi Polynomials
3. Numerical Scheme and Stability Analysis
3.1. Numerical Discretization in the Time Direction
3.2. Numerical Discretization in the Space Direction
3.3. Stability Analysis
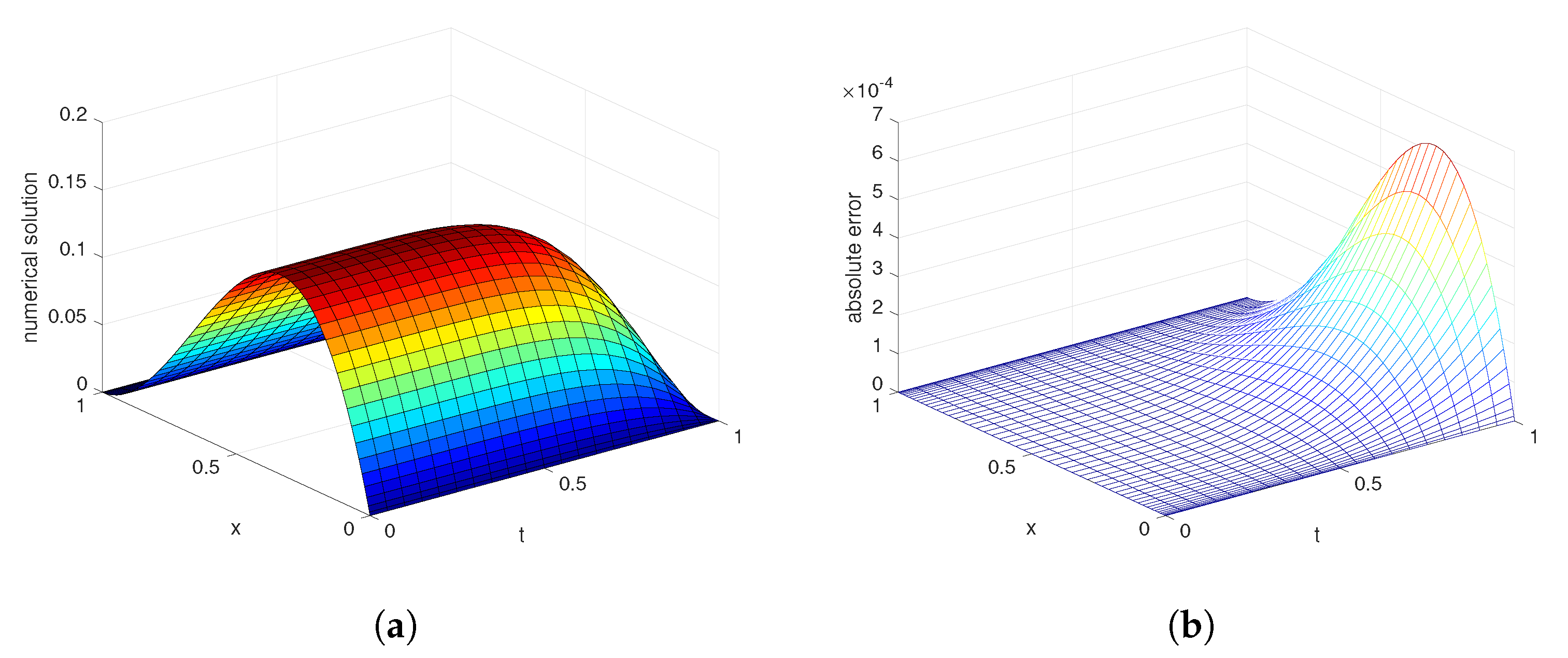
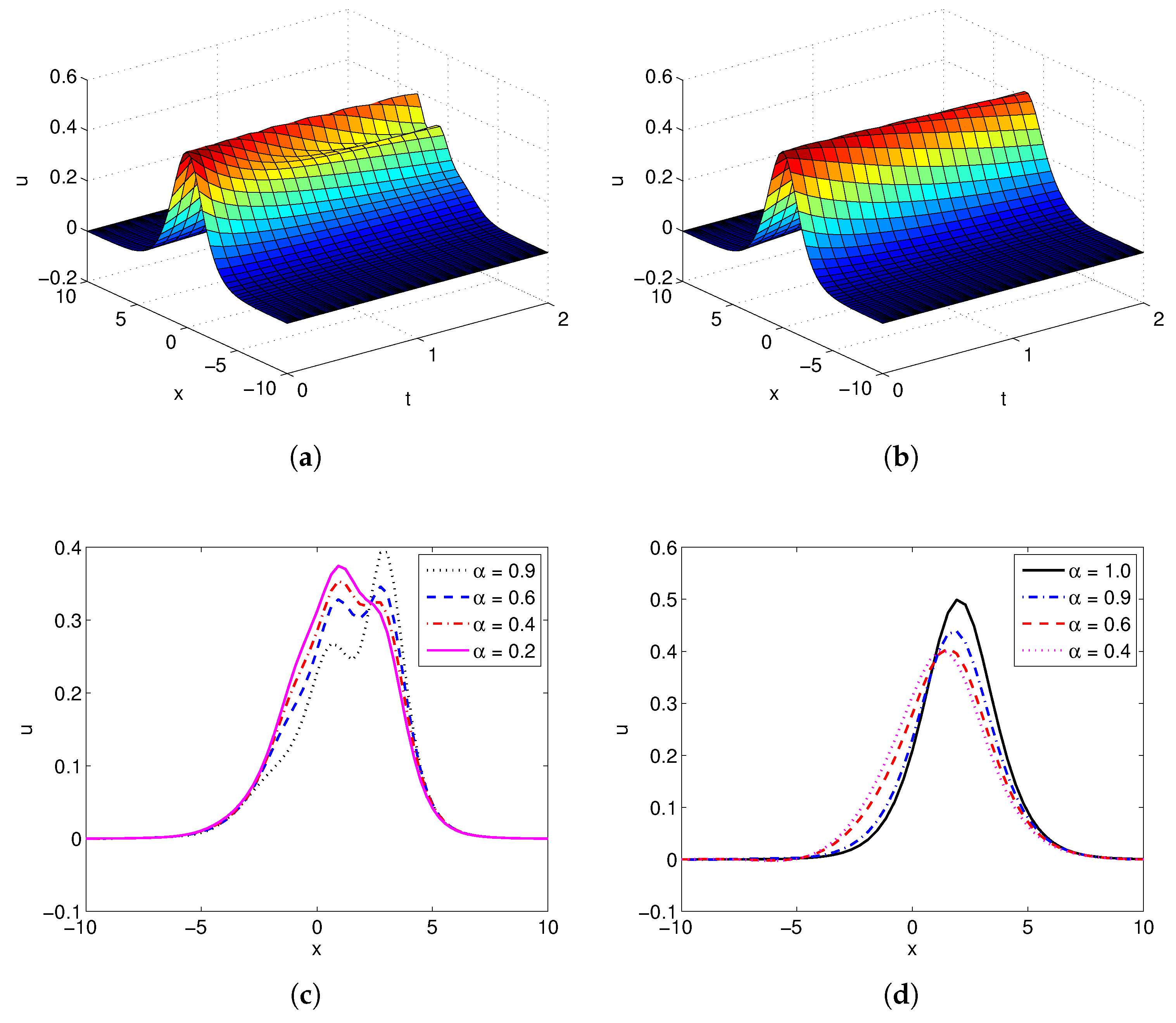
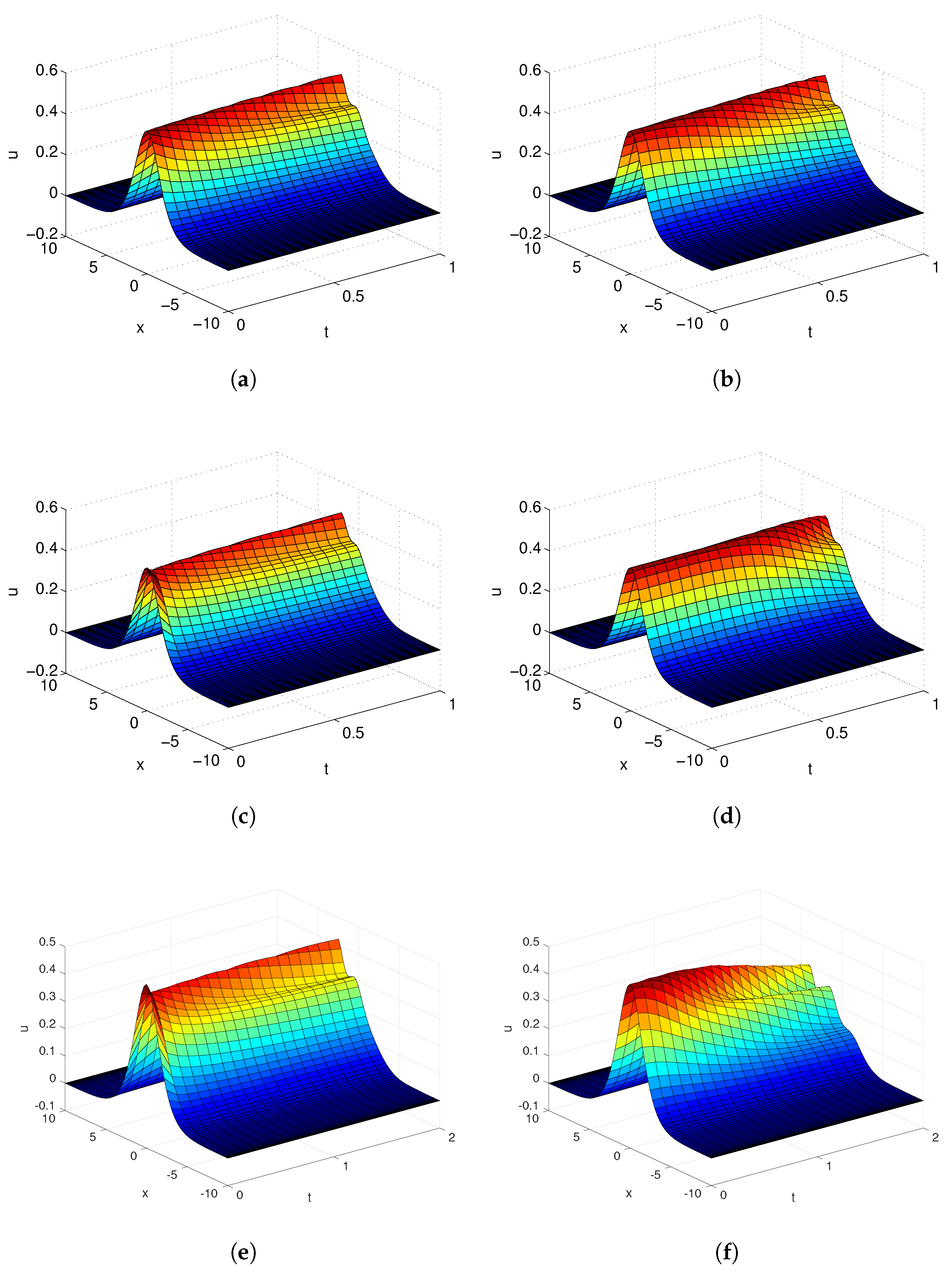
4. Numerical Results and Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Korteweg, D.J.; de Vries, G. On the change of form of long waves and advancing in a rectangular canal and on a new type of long stationary waves. Philos. Mag. 1895, 39, 422–443. [Google Scholar] [CrossRef]
- Tian, B.; Gao, Y.-T. Exact solutions for the Bogoyavlenskii coupled KdV equations. Phys. Lett. A 1995, 208, 193–196. [Google Scholar] [CrossRef]
- Vlieg-Hulstman, M.; Halford, W.D. Exact solutions to KdV equations with variable coefficients and/or nonuniformities. Comput. Math. Appl. 1995, 29, 39–47. [Google Scholar] [CrossRef]
- Senthilkumaran, M.; Pandiaraja, D.; Vaganan, B.M. New exact explicit solutions of the generalized KdV equations. Appl. Math. Comput. 2008, 202, 693–699. [Google Scholar] [CrossRef]
- Akdi, M.; Sedra, M.B. Numerical KdV equation by the adomian decomposition method. Am. J. Mod. Phys. 2013, 2, 111–115. [Google Scholar] [CrossRef]
- Ma, H.; Sun, W. A Legendre-Petrov-Galerkin and Chebyshev collocation method for third-order differential equations. SIAM J. Numer. Anal. 2000, 38, 1425–1438. [Google Scholar] [CrossRef]
- Shen, J. A new Dual-Petrov-Galerkin method for third and high odd-order differential equations: Application to the KdV equation. SIAM J. Numer. Anal. 2003, 41, 1595–1619. [Google Scholar] [CrossRef]
- Guo, J.; Taha, T.R. Parallel implementation of the split-step and the pseudospectral methods for solving higher KdV equation. Math. Comput. Simul. 2003, 62, 41–51. [Google Scholar] [CrossRef]
- An, H.; Chen, Y. Numerical complexiton solutions for the complex KdV equation by the homotopy perturbation method. Appl. Math. Comput. 2008, 203, 125–133. [Google Scholar] [CrossRef]
- Dag, I.; Dereli, Y. Numerical solutions of KdV equation using radial basis functions. Appl. Math. Model. 2008, 32, 535–546. [Google Scholar] [CrossRef]
- Bhatta, D. Use of modified Bernstein polynomials to solve KdV-Burgers equation numerically. Appl. Math. Comput. 2008, 206, 457–464. [Google Scholar] [CrossRef]
- Al-Khaled, K.; Haynes, N.; Schiesser, W.; Usman, M. Eventual periodicity of the forced oscillations for a Korteweg-de Vries type equation on a bounded domain using a sinc collocation method. J. Comput. Appl. Math. 2018, 330, 417–428. [Google Scholar] [CrossRef]
- Xu, Y.; He, Z. The short memory principle for solving Abel differential equation of fractional order. Comput. Math. Appl. 2011, 62, 4796–4805. [Google Scholar] [CrossRef]
- Xu, Q.; Hesthaven, J.S. Stable multi-domain spectral penalty methods for fractional partial differential equations. J. Comput. Phys. 2014, 257, 241–258. [Google Scholar] [CrossRef]
- Zhao, X.; Xu, Q. Efficient numerical schemes for fractional sub-diffusion equation with the spatially variable coefficient. Appl. Math. Model. 2014, 38, 3848–3859. [Google Scholar] [CrossRef]
- Xu, Q.; Hesthaven, J.S. Discontinuous Galerkin method for fractional convection-diffusion equations. SIAM J. Numer. Anal. 2014, 52, 405–423. [Google Scholar] [CrossRef]
- Momani, S. An explicit and numerical solutions of the fractional KdV equation. Math. Comput. Simul. 2005, 70, 110–118. [Google Scholar] [CrossRef]
- Wang, Q. Numerical solutions for fractional KdV-Burgers equation by Adomian decomposition method. Appl. Math. Comput. 2006, 182, 1048–1055. [Google Scholar]
- Song, L.; Zhang, H. Application of homotopy analysis method to fractional KdV-Burgers-Kuramoto equation. Phys. Lett. A 2007, 367, 88–94. [Google Scholar] [CrossRef]
- Odibat, Z.M. Exact solitary solutions for variants of the KdV equations with fractional time derivatives. Chaos Soliton Fractal 2009, 40, 1264–1270. [Google Scholar] [CrossRef]
- El-Ajou, A.; Arqub, O.A.; Momani, S. Approximate analytical solution of the nonlinear fractional KdV-Burgers equation: A new iterative algorithm. J. Comput. Phys. 2015, 293, 81–95. [Google Scholar] [CrossRef]
- Doungmo Goufo, E.F. Application of the Caputo-Fabrizio fractional derivative without singular kernel to Korteweg-de Vries-Burgers Equation. Math. Model. Anal. 2016, 21, 188–198. [Google Scholar] [CrossRef]
- Guo, S.; Mei, L.; He, Y.; Li, Y. Time-fractional Schamel–KdV equation for dust-ion-acoustic waves in pair-ion plasma with trapped electrons and opposite polarity dust grains. Phys. Lett. A 2016, 380, 1031–1036. [Google Scholar] [CrossRef]
- Agrawal, O.P. Some generalized fractional calculus operators and theeir applications in integral equations. Fract. Calc. Appl. Anal. 2012, 15, 700–711. [Google Scholar] [CrossRef]
- Xu, Y.; Agrawal, O.P. Numerical solutions and analysis of diffusion for new generalized fractional Burgers equation. Fract. Calc. Appl. Anal. 2013, 16, 709–736. [Google Scholar] [CrossRef]
- Xu, Y.; He, Z.; Agrawal, O.P. Numerical and analytical solutions of new generalized fractional diffusion equation. Comput. Math. Appl. 2013, 66, 2019–2029. [Google Scholar] [CrossRef]
- Xu, Y.; Agrawal, O.P. Numerical solutions and analysis of diffusion for new generalized fractional advection-diffusion equations. Cent. Eur. J. Phys. 2013, 11, 1178–1193. [Google Scholar] [CrossRef]
- Xu, Y.; Agrawal, O.P. Models and numerical solutions of generalized oscillator equations. J. Vib. Acoust. 2014, 136, 50903. [Google Scholar] [CrossRef]
- Cao, W.; Xu, Y.; Zheng, Z. Existence results for a class of generalized fractional boundary value problem. Adv. Differ. Equ. 2017, in press. [Google Scholar] [CrossRef]
- Shen, J.; Tang, T.; Wang, L.-L. Spectral Methods; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
| M | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| MAE | CO | Time | MAE | CO | Time | MAE | CO | Time | |
| 100 | 1.39 × | - | 7.9 s | 2.67 × | - | 7.1 s | 1.71 × | - | 7.4 s |
| 200 | 4.28 × | 1.70 | 18.7 s | 1.03 × | 1.37 | 17.6 s | 8.04 × | 1.09 | 17.9 s |
| 300 | 2.13 × | 1.72 | 32.1 s | 5.89 × | 1.38 | 30.3 s | 5.16 × | 1.09 | 31.7 s |
| 400 | 1.29 × | 1.73 | 46.3 s | 3.95 × | 1.38 | 47.6 s | 3.76 × | 1.10 | 47.2 s |
| M | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| MAE | CO | Time | MAE | CO | Time | MAE | CO | Time | |
| 100 | 1.77 × | - | 7.9 s | 4.38 × | - | 7.6 s | 3.35 × | - | 7.5 s |
| 200 | 5.42 × | 1.70 | 17.8 s | 1.69 × | 1.37 | 18.2 s | 1.58 × | 1.09 | 17.3 s |
| 300 | 2.70 × | 1.72 | 33.4 s | 9.66 × | 1.38 | 30.9 s | 1.01 × | 1.09 | 30.6 s |
| 400 | 1.64 × | 1.73 | 52.16 s | 6.48 × | 1.39 | 55.4 s | 7.38 × | 1.09 | 51.8 s |
| M | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| MAE | CO | Time | MAE | CO | Time | MAE | CO | Time | |
| 100 | 9.64 × | - | 7.5 s | 1.43 × | - | 7.5 s | 7.52 × | - | 7.3 s |
| 200 | 2.96 × | 1.70 | 18.2 s | 5.50 × | 1.37 | 16.9 s | 3.54 × | 1.09 | 17.6 s |
| 300 | 1.48 × | 1.72 | 31.8 s | 3.14 × | 1.38 | 29.8 s | 2.27 × | 1.09 | 29.7 s |
| 400 | 8.99 × | 1.72 | 46.1 s | 2.11 × | 1.39 | 48.2 s | 1.66 × | 1.10 | 49.1 s |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, W.; Xu, Y.; Zheng, Z. Finite Difference/Collocation Method for a Generalized Time-Fractional KdV Equation. Appl. Sci. 2018, 8, 42. https://doi.org/10.3390/app8010042
Cao W, Xu Y, Zheng Z. Finite Difference/Collocation Method for a Generalized Time-Fractional KdV Equation. Applied Sciences. 2018; 8(1):42. https://doi.org/10.3390/app8010042
Chicago/Turabian StyleCao, Wen, Yufeng Xu, and Zhoushun Zheng. 2018. "Finite Difference/Collocation Method for a Generalized Time-Fractional KdV Equation" Applied Sciences 8, no. 1: 42. https://doi.org/10.3390/app8010042
APA StyleCao, W., Xu, Y., & Zheng, Z. (2018). Finite Difference/Collocation Method for a Generalized Time-Fractional KdV Equation. Applied Sciences, 8(1), 42. https://doi.org/10.3390/app8010042





