1. Introduction
Emerging environmental concerns and attempts to curtail the dependence on fossil fuel resources are bringing renewable energy resources into the mainstream of the electric power sector. Among the various renewable resources, wind power is the most promising from both technical and economic standpoints. The new global total for wind power at the end of 2015 was 432.9 GW, which represents a cumulative market growth of more than 17% [
1]. By 2030, wind power could reach 2110 GW and supply up to 20% of the global electricity [
2]. This large penetration of wind power into the existing grid has introduced some vulnerabilities to the power grid. In order to maintain the stability of the power system and ensure smooth operation, low voltage ride through (LVRT) requirements have been imposed around the world [
3]. In the event of a fault, LVRT mandates that wind farms (WFs) stay connected to the grid in order to support the grid in the same manner as conventional synchronous generators (SGs).
Most wind turbines are constructed using fixed-speed wind turbines with squirrel cage induction generators (FSWT-SCIGs). SCIGs have some advantageous characteristics, such as simplicity, robust construction, low cost, and operational simplicity [
4]. However, FSWT-SCIGs are connected directly to the grid and have no LVRT capabilities during voltage dips [
4]. Moreover, the FSWT-SCIG requires a large reactive power in order to recover air gap flux when a short circuit fault occurs in the power system. If sufficient reactive power is not supplied, the electromagnetic torque of the SCIG decreases significantly. As a result, the rotor speed of the SCIG increases significantly and can make the power system unstable [
4]. Reactive power compensation is a major issue, especially for FSWT-SCIGs. A capacitor bank is usually used to meet the reactive power compensation requirement of an SCIG. However, the SCIG requires more reactive power during fault conditions than in the steady state, and the capacitor bank is not able to supply more reactive power during transient conditions.
A static synchronous compensator (STATCOM) [
5], superconducting magnetic energy storage (SMES) [
6], and an energy capacitor system (ECS) [
7], for example, are installed in WFs with FSWT-SCIGs in order to improve the LVRT capability during a fault condition. However, the overall system cost increases.
On the other hand, variable-speed wind turbines with doubly fed induction generators (VSWT-DFIGs) have some advantageous characteristics, such as light weight, higher output power and efficiency, lower cost, variable-speed operation, and smaller size. In addition to the lower power electronic converter rating required by the DFIG, compared to permanent magnet synchronous generators (PMSGs) [
8], the recent price upsurge of permanent magnet materials has given the DFIG another advantage over the PMSG [
9]. In addition, the DFIG has better system stability characteristics than the SCIG during fault conditions, because of its capability for independent control of active and reactive power delivered to the grid [
10]. By taking advantage of DFIG reactive power control, it is possible to stabilize the SCIG in a WF. Thus, reactive power compensation can be implemented at lower cost. The partial converter is connected to the rotor terminal of the DFIG via slip rings. The converter consists of a rotor-side converter (RSC) and a grid-side converter (GSC). As reported in previous studies [
10,
11,
12], various control strategies can be adopted for both the RSC and the GSC. However, the design procedure of the RSC is very crucial because it is controlling active and reactive power delivered to the grid.
Some auxiliary hardware circuits have been used to help the DFIG to improve the LVRT requirement. For example, the rotor crowbar circuit is used in the rotor terminals to isolate the RSC from the rotor circuit [
13,
14]. However, the rotor crowbar circuit converts the DFIG to a simple induction machine, which absorbs reactive power from the grid. A chopper circuit and parallel capacitors are used to smooth the DC-link voltage by dissipating the excessive power in the DC-link circuit [
15,
16]. Dynamic braking resistors connected to the stator [
17] and a bridge type fault current limiter [
18] are used to limit the stator and rotor overcurrents. A series-connected converter [
19] and a dynamic voltage restorer [
20] are used to keep the stator voltage constant under grid faults. In previous studies [
21,
22], static VAR compensators or STATCOMs were used to supply extra reactive power to the grid during grid faults. Although the LVRT capability is enhanced through various types of equipment [
13,
14,
15,
16,
17,
18,
19,
20,
21,
22], this equipment requires additional converters or equipment, which increases the complexity and cost of the wind turbine system and decreases its reliability.
The cascaded control system for the RSC described in [
23] is also used to improve LVRT capability, where several PI controllers are used in the inner and outer loops. However, due to changes in the parameters of the grid during fault conditions, the conventional PI controller with a fixed gain is not sufficient to ensure the system stability of a large power system. The setting of the parameters of the PI controllers used in cascaded control is cumbersome, especially in power system applications that are difficult to express as a mathematical model or a transfer function. In [
23], a Taguchi approach for optimum design of PI controllers in a cascaded control scheme was presented. However, this cascaded control strategy with the conventional PI controller in the inner loop cannot provide a large amount of reactive power. Thus, the strategy can stabilize only lower ratings of the SCIG. Therefore, using an fuzzy logic controller (FLC) in the inner loop of the rotor-side controller to more efficiently provide reactive power during fault periods is convenient. The FLC can handle nonlinear systems very effectively because it offers variable gain during transient conditions. Thus, the DFIG controlled by the FLC can stabilize a larger amount of SCIG. Moreover, the overall system cost can be decreased by incorporating a lower rating of the DFIG along with a higher rating of the SCIG. This is one of the novel features of the present paper.
Therefore, the main contribution of the present paper is the design of a new control strategy based on fuzzy logic in the inner loop of the rotor-side controller for the DFIG to improve the LVRT capability and increase the capacity of the SCIG-based WF. Detailed modeling and control strategies of the overall system are presented. In order to evaluate the effectiveness of the proposed controller, transient and dynamic analyses are performed. Real wind-speed data measured on Rishiri Island, Hokkaido, Japan are considered in the dynamic analysis.
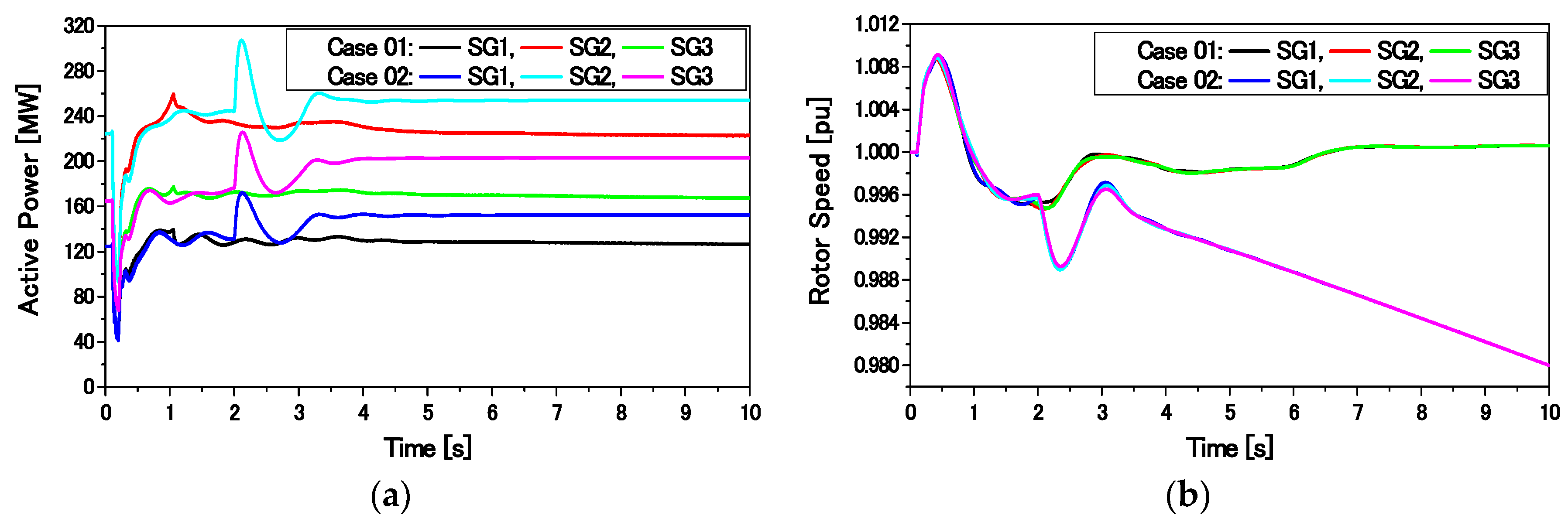
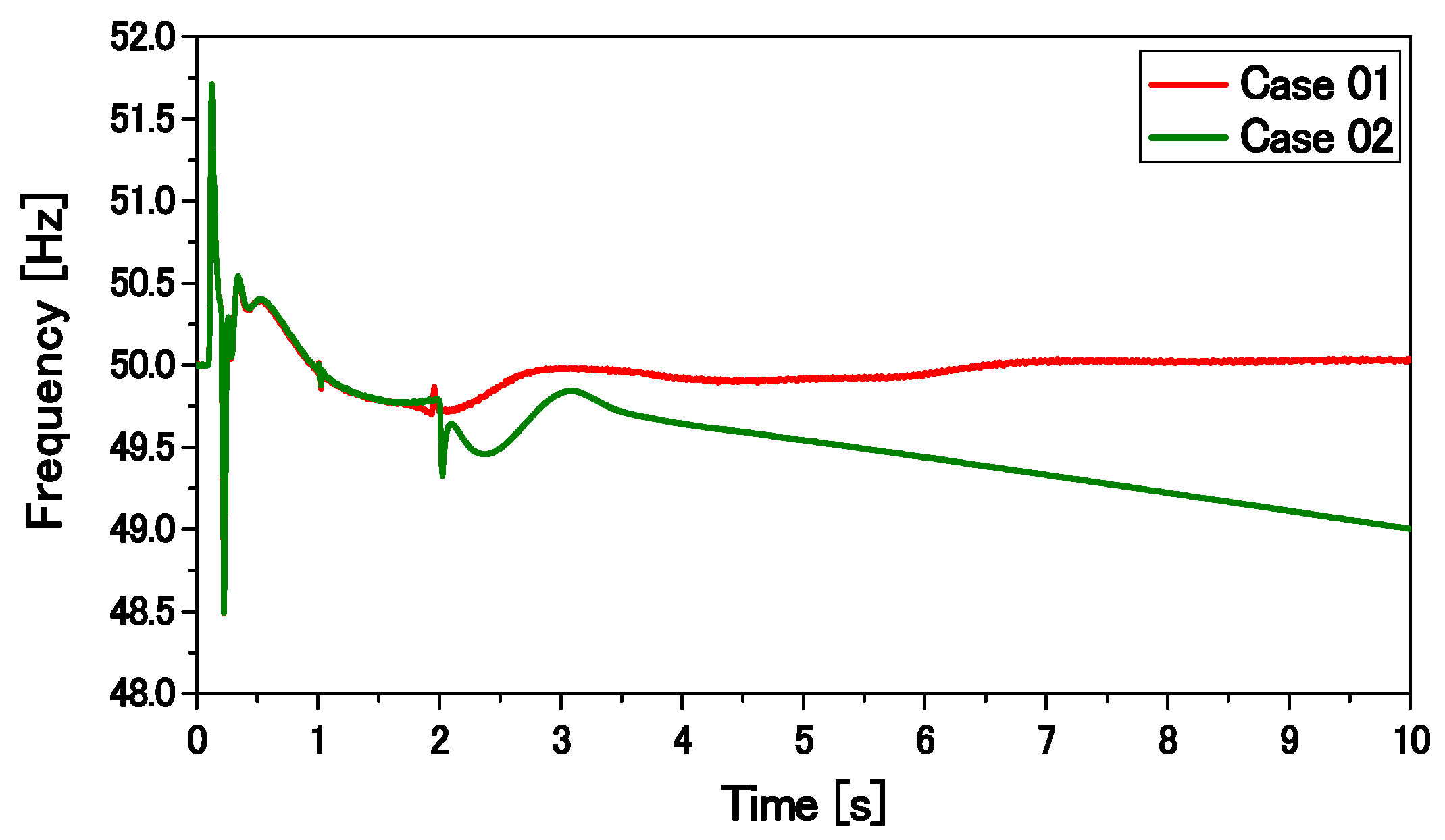
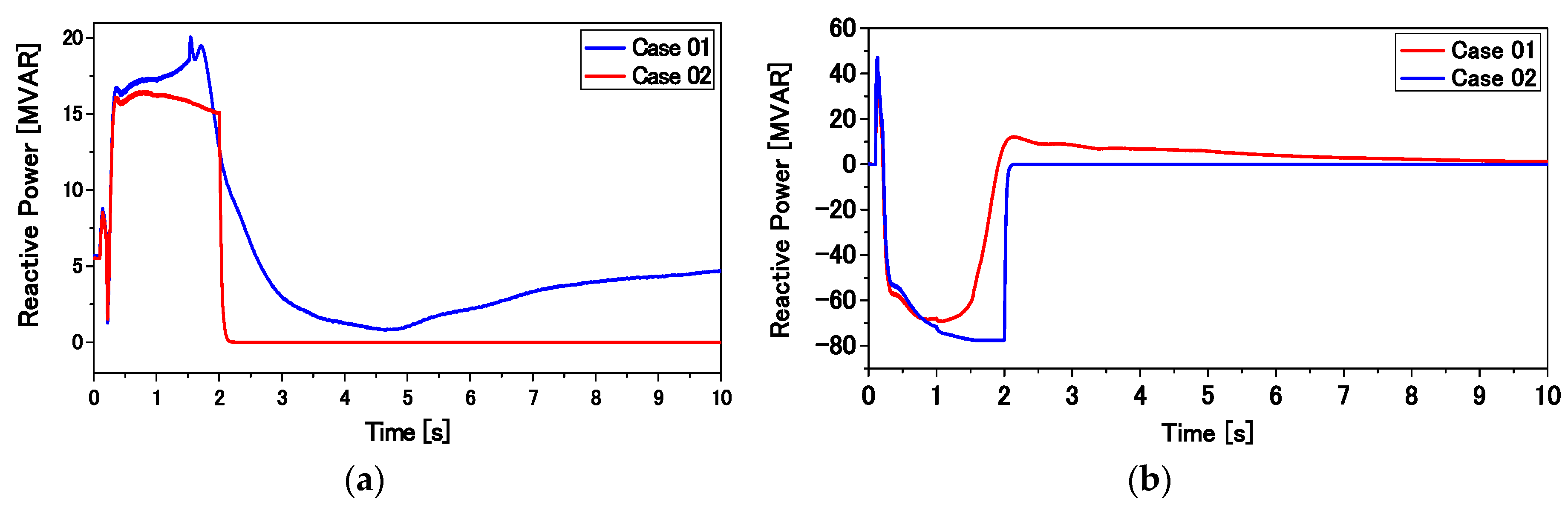
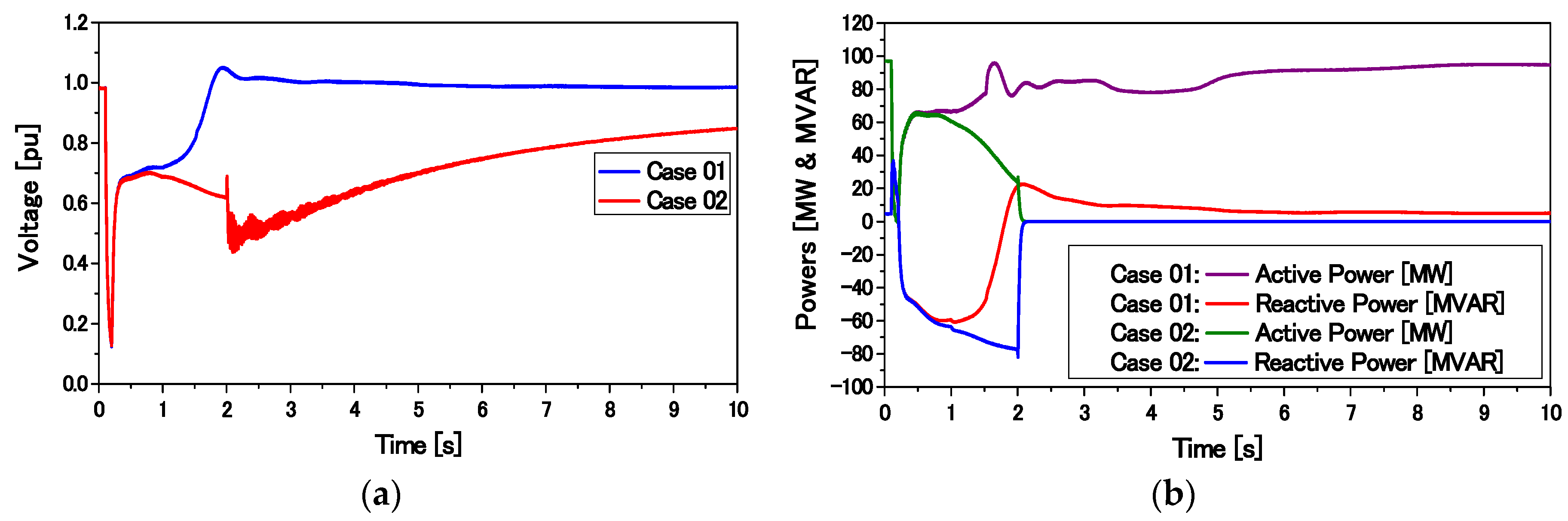
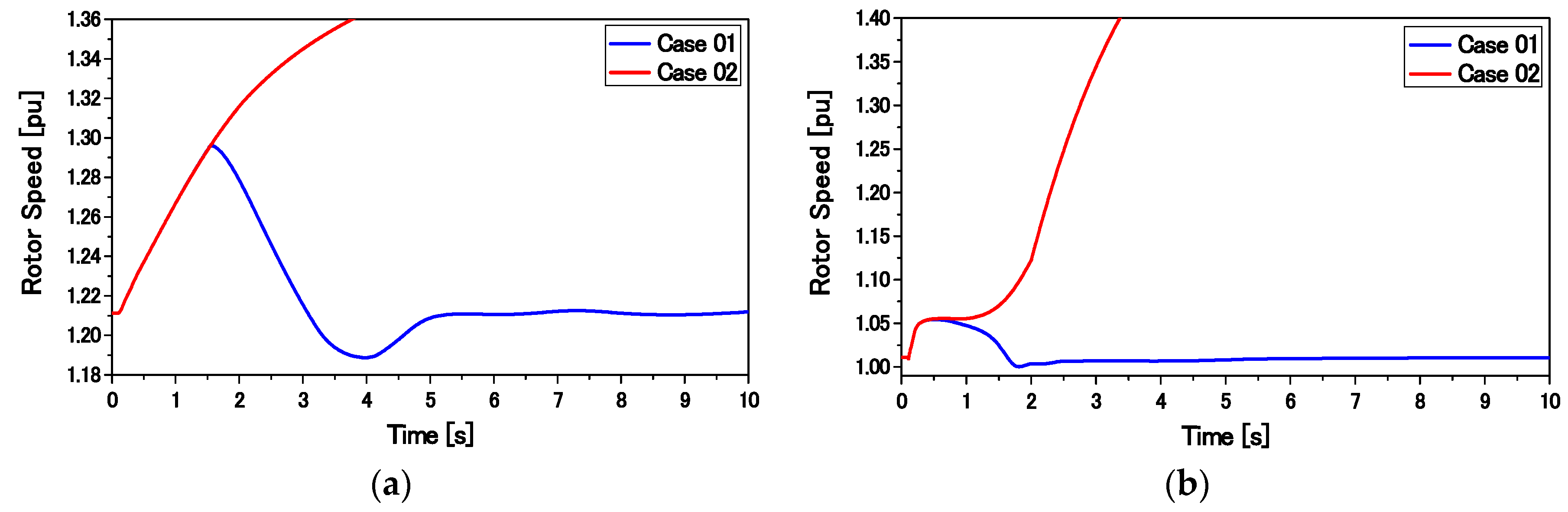
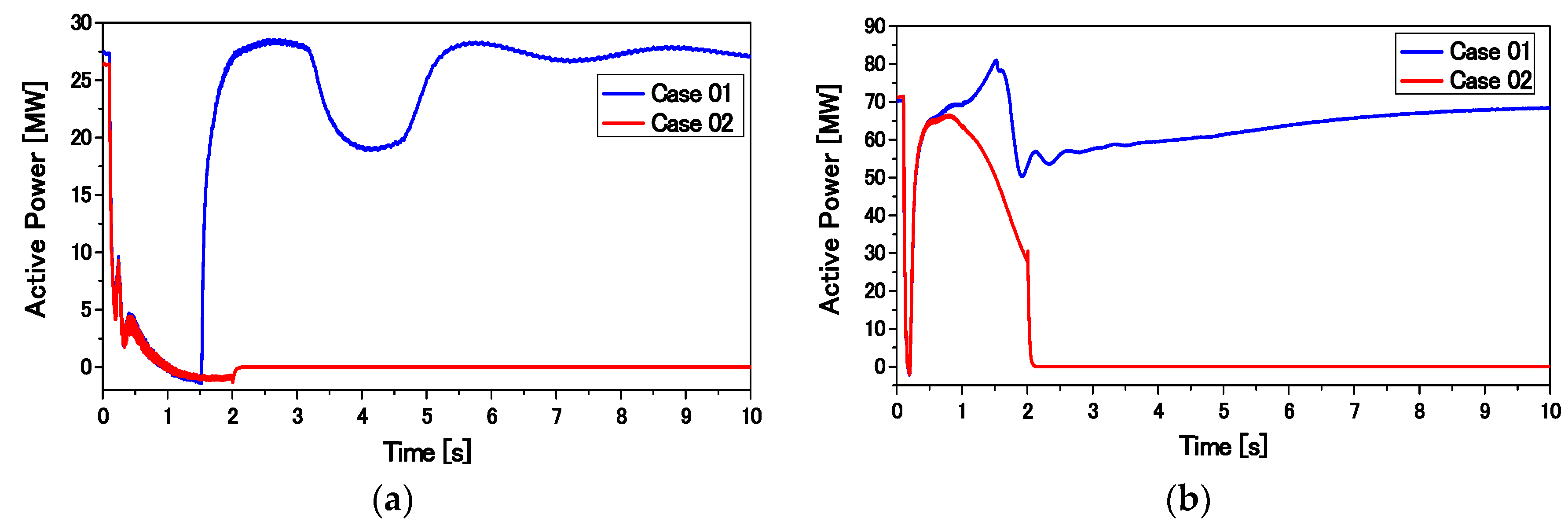
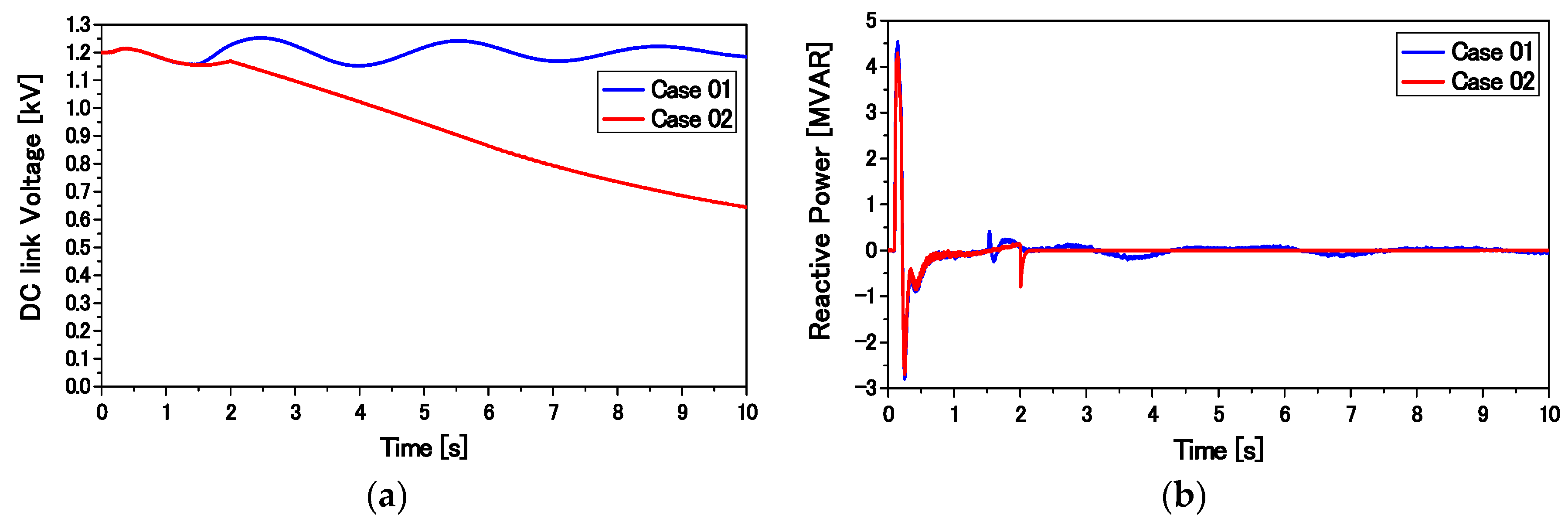
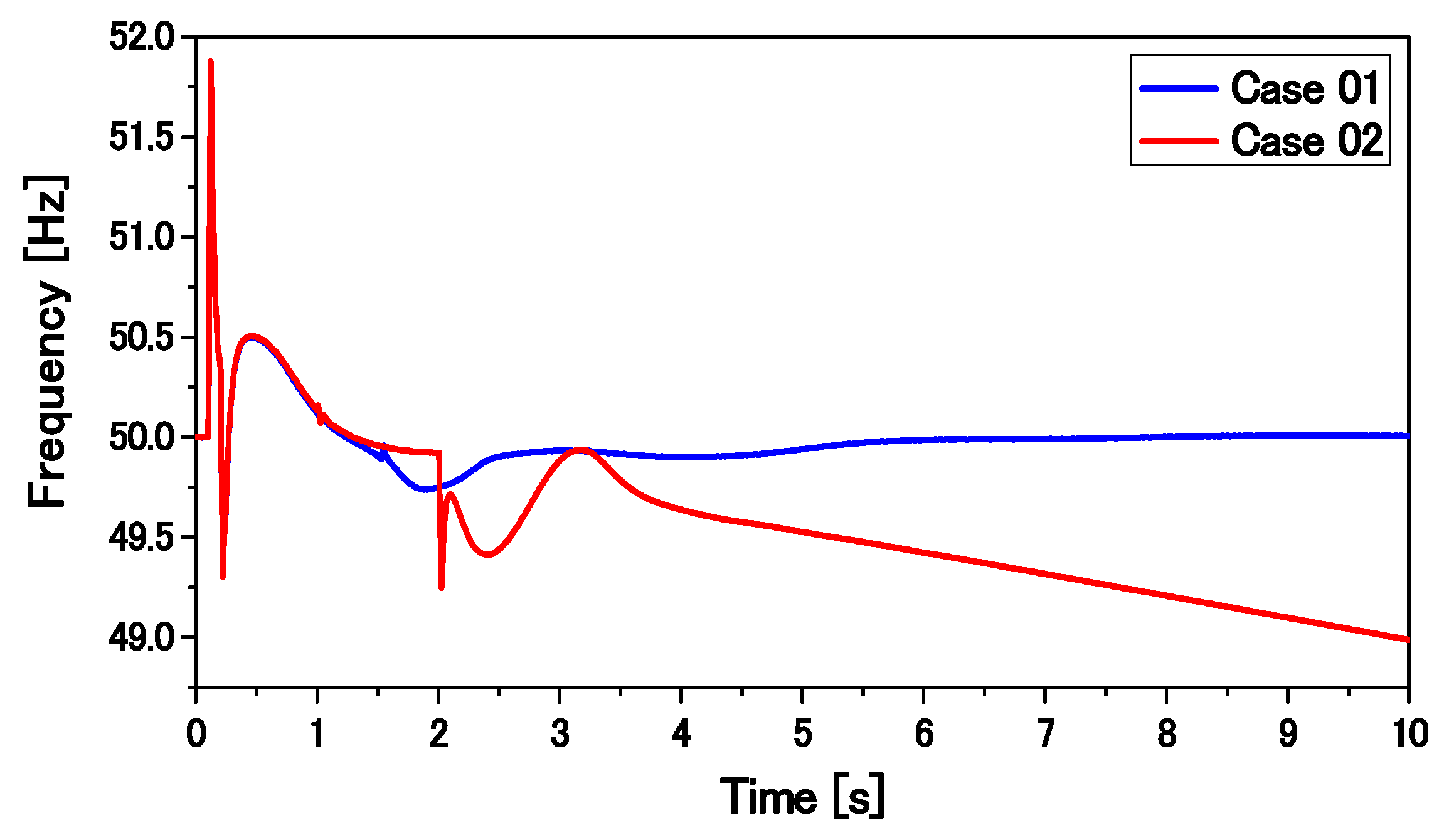
The transient performance of the overall system composed of SGs, an FLC-controlled DFIG, and an SCIG is compared with that composed of a DFIG with the conventional PI-controlled RSC presented in [
23]. Finally, the proposed control strategy is found to be very effective for ensuring the stability of a large power system. Moreover, the capacity of the installed SCIG can be increased.
The remainder of the present paper is organized as follows.
Section 2 presents the wind turbine model.
Section 3 presents the DFIG model, and the design procedure of the proposed FLC is introduced in
Section 4.
Section 5 deals with the power system model.
Section 6 briefly describes the LVRT requirements for wind power. The simulation results and a discussion of the performance of the proposed and conventional methods are presented in
Section 7. Finally,
Section 8 summarizes the findings and concludes the paper.
2. Wind Turbine Model
In the wind turbine model, the aerodynamic power output is given as follows [
4]:
where
Pw is the captured wind power,
ρ is the air density (KG/m
3),
R is the radius of the rotor blade (m),
Vw is the wind speed (m/s), and
Cp is the power coefficient.
The value of
Cp can be calculated as follows [
10]:
where
Tw is the wind turbine torque,
β is the pitch angle, and
λ is the tip speed ratio. Moreover,
c1 through
c6 are the characteristic coefficients of the wind turbine (
c1 = 0.5176,
c2 = 116,
c3 = 0.4,
c4 = 5,
c5 = 21, and
c6 = 0.0068) [
24], and
ωr is the rotational speed of the wind turbine (rad/s).
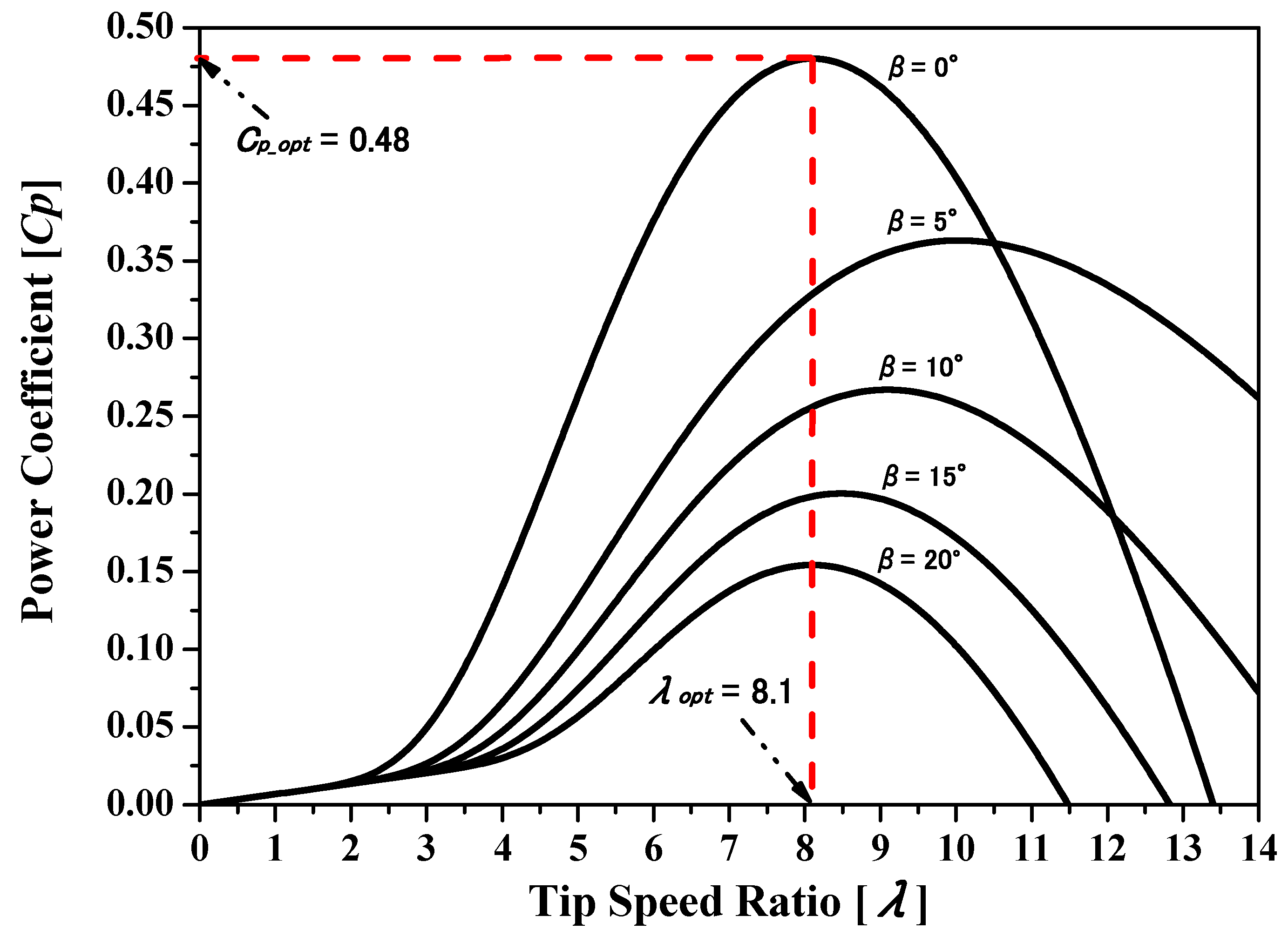
The
Cp vs
λ characteristics shown in
Figure 1 are obtained using Equation (2) with different values of the pitch angle (
β). When
β is equal to zero degrees, the optimum power coefficient (
Cpopt) is 0.48, and the optimum tip speed ratio (
λopt) is 8.1.
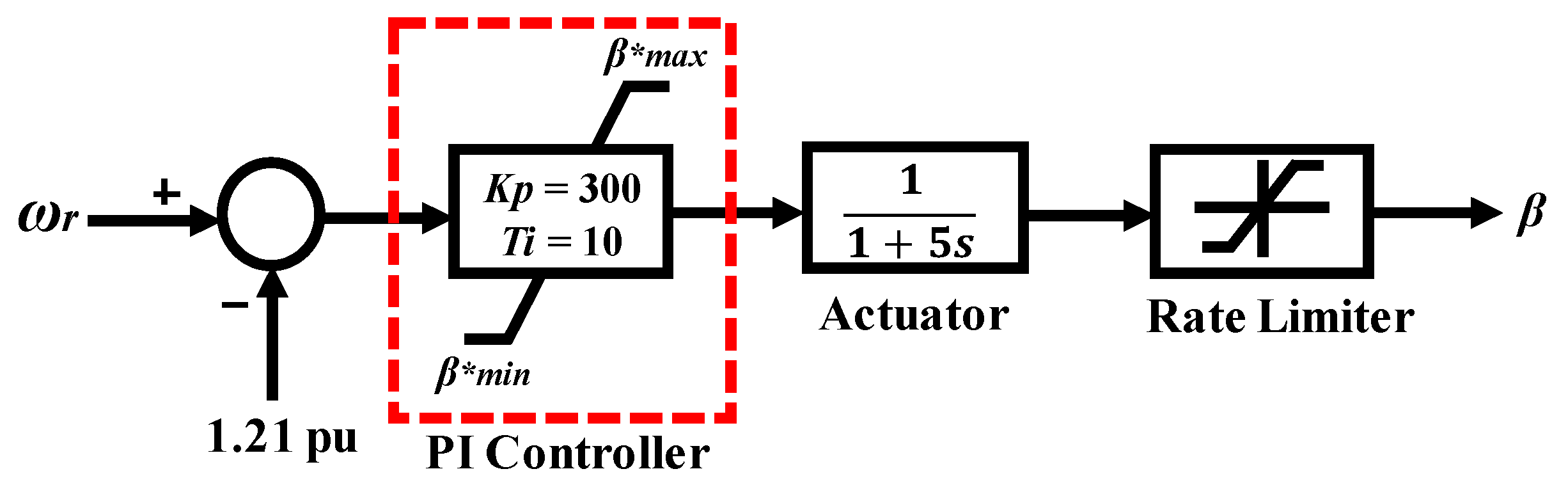
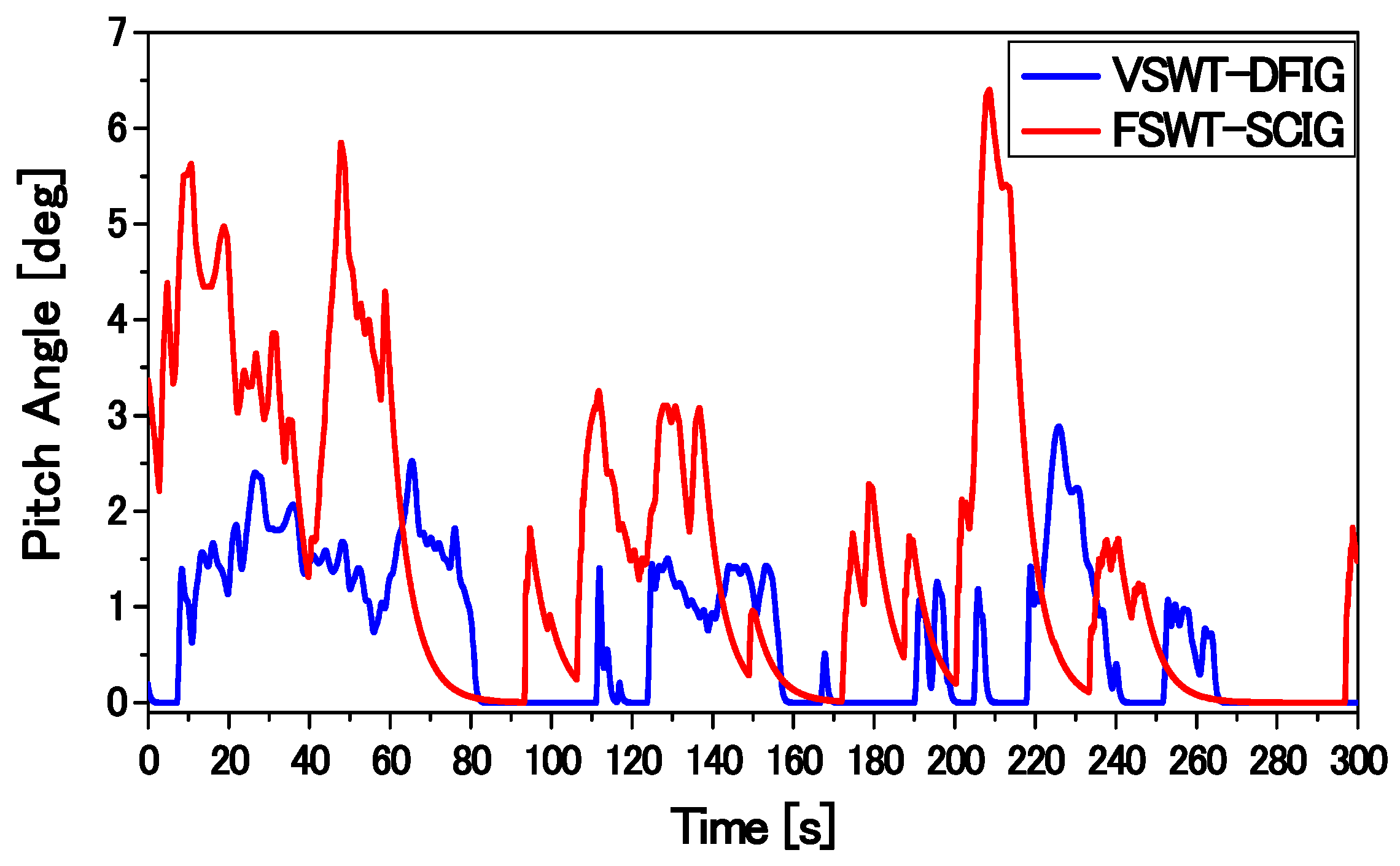
Figure 2 and
Figure 3 show the models of the blade pitch control system for FSWT and VSWT [
25], respectively. In FSWT, the pitch control system is used to control the power output of the SCIG so as not to exceed the rated power. In VSWT, the rotor speed of DFIG is regulate by the pitch controller so as not to exceed the rated speed. The control loop of the pitch actuator is represented by a first-order transfer function with a pitch rate limiter. A PI controller is used to manage the tracking error.
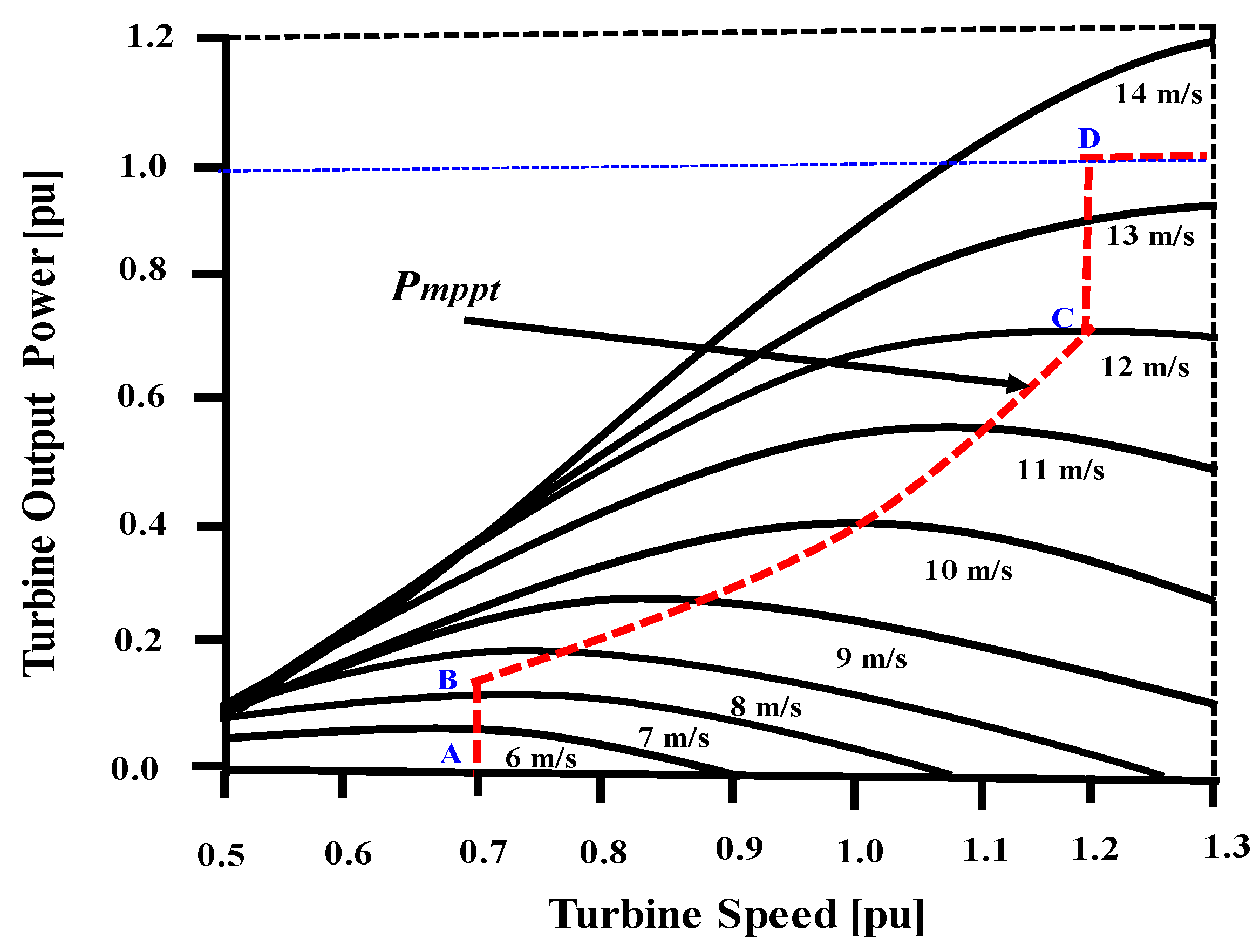
Figure 4 shows the maximum power point tracking (MPPT) curve for the VSWT-DFIG.
3. DFIG Model
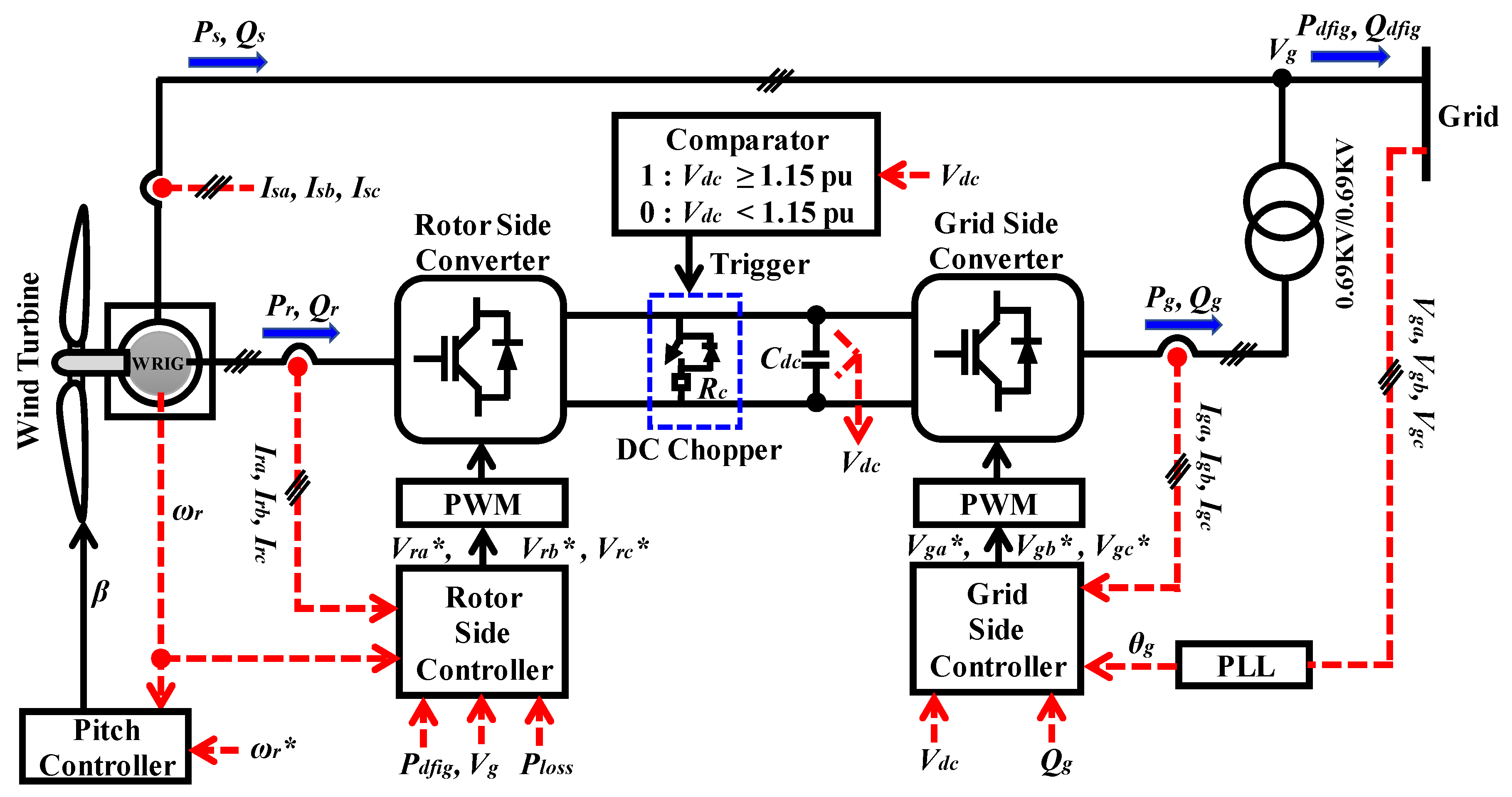
The configuration of the VSWT-DFIG system, along with its control system, is shown in
Figure 5. The model consists of a wind turbine model with aerodynamic characteristics, a pitch controller, a wound rotor induction generator (WRIG), and an AC/DC/AC converter based on two levels of insulated gate bipolar transistors (IGBTs), which are controlled by the rotor-side controller and the grid-side controller, respectively.
The wind turbine drives the WRIG to convert wind power into electrical power. The rotational speed (
ωr) is obtained from the rotor of the WRIG. A pitch controller is used to control the blade pitch angle of the wind turbine in order to reduce the output power when the rotational speed exceeds the rated speed. The WRIG model available in the PSCAD library is used in the present study [
26]. The rotor position (
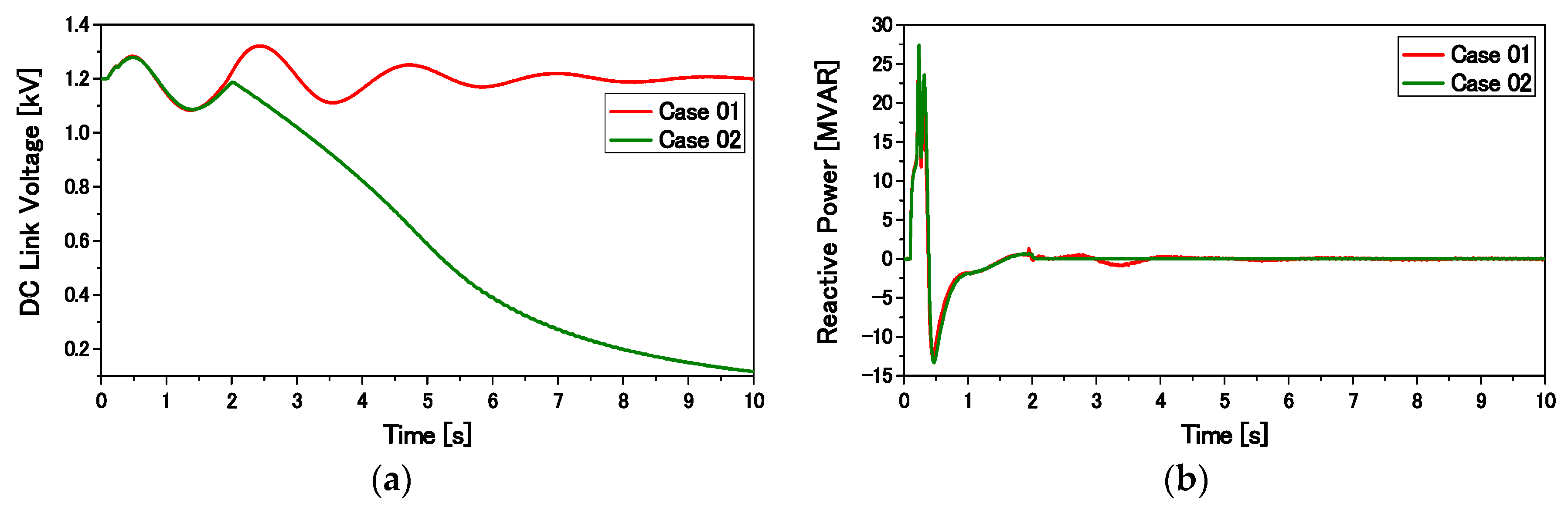
θr) is derived from the rotor of the WRIG. As indicated by the configuration of the VSWT-DFIG system, the stator terminal is directly connected to the grid system. The AC/DC/AC converter is installed between the rotor of the WRIG and the grid system. The rating of the converter is 30% of the WRIG rating. The pulse width modulation (PWM) technique is used to generate the necessary gate pulses for driving the AC/DC/AC converter. The carrier frequency is taken as 3.0 kHz. The RSC is connected to the rotor winding of the WRIG, which provides variable frequency excitation depending on the wind-speed condition. The GSC is connected to the grid system through a transformer. A protection system with a DC chopper is installed in the DC-link circuit. The DC chopper is controlled by the comparator block, which triggers the DC chopper switch when the DC-link voltage becomes greater than or equal to the predefined limit (
Vdc ≥ 1.15 pu).
3.1. Conventional Rotor-Side Controller
The conventional cascaded controller for the RSC is presented in [
23]. This controller consists of four conventional PI controllers to compensate different error signals. The reference reactive power (
Qdfig*) is set to zero for unity power factor operation. The active power and reactive power delivered to the grid are controlled using q-axis and d-axis rotor currents, respectively.
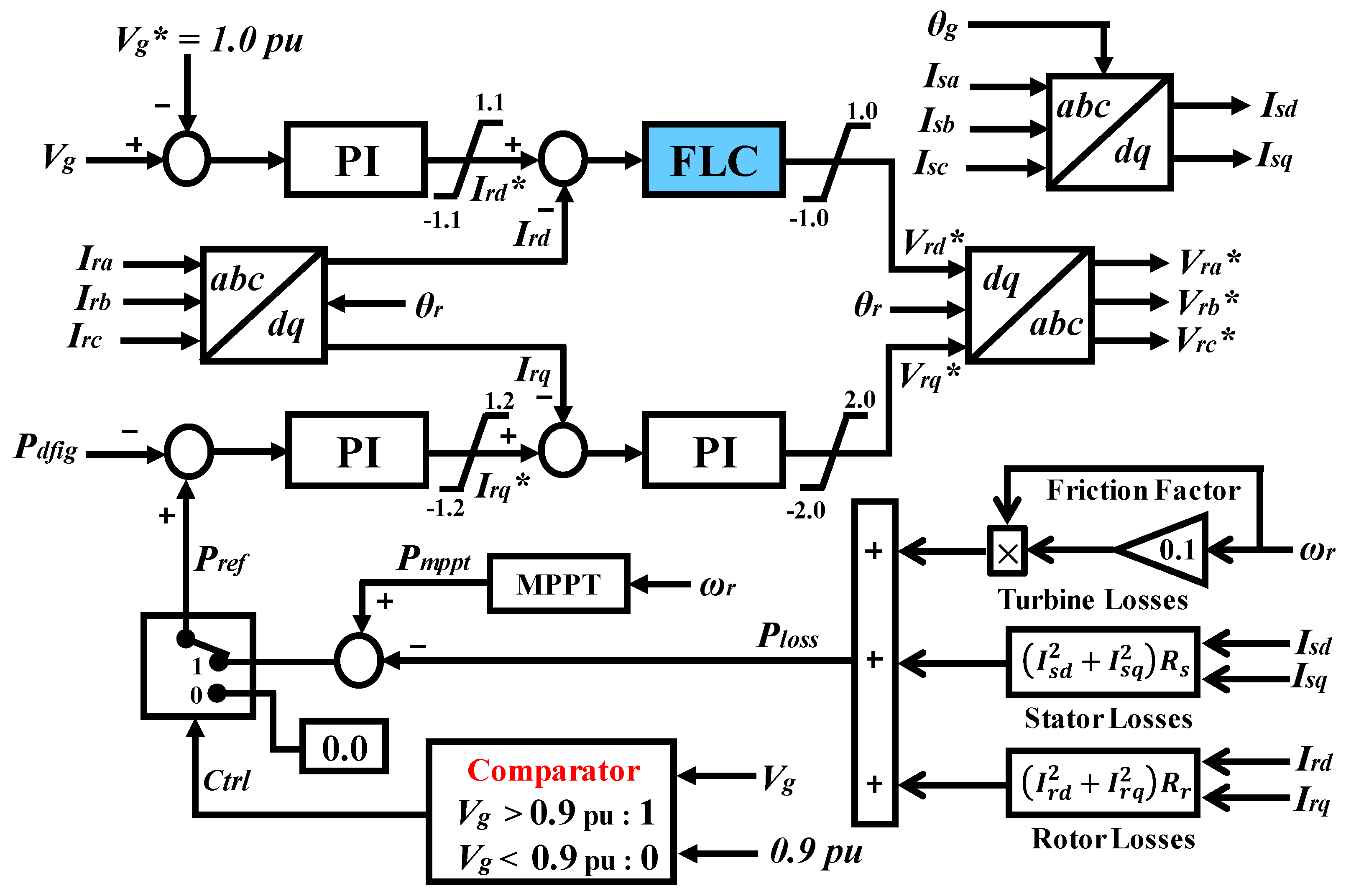
3.2. Proposed Rotor-Side Controller
The proposed controller for the RSC is depicted in
Figure 6. This controller consists of three PI controllers and one FLC. The main motivation behind using one FLC in the inner loop of the cascaded controller is maximization of the reactive power injection. The FLC offers variable gain depending on the system parameters. Due to the variable gain, the FLC can inject reactive power (
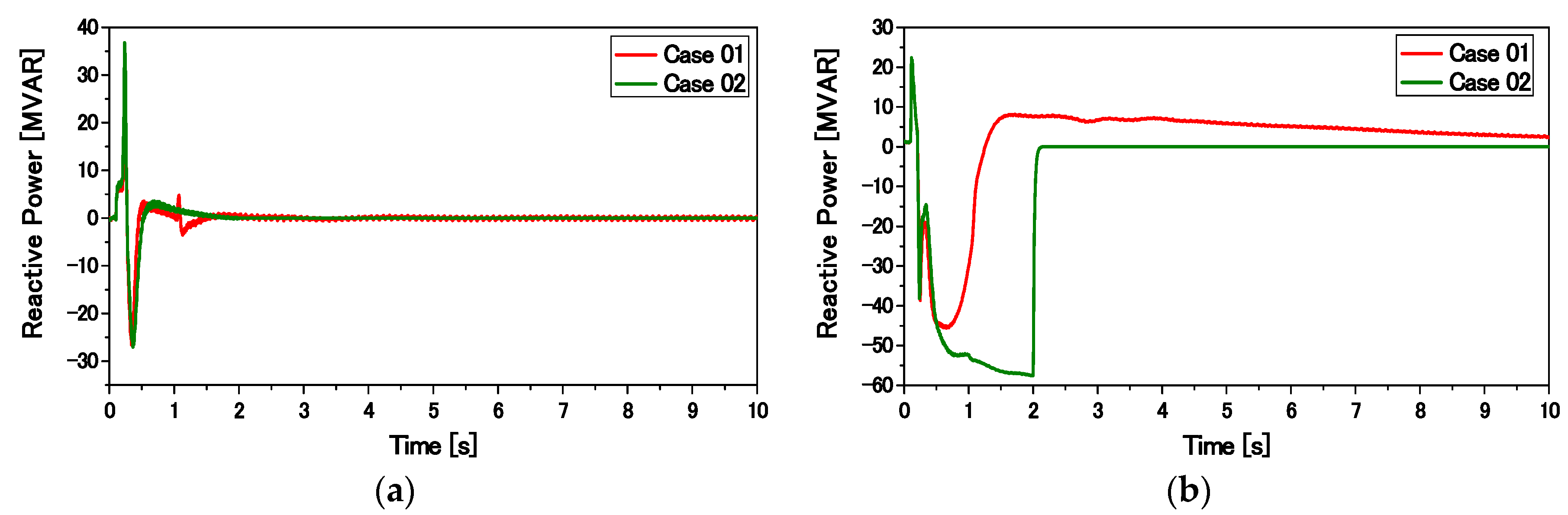
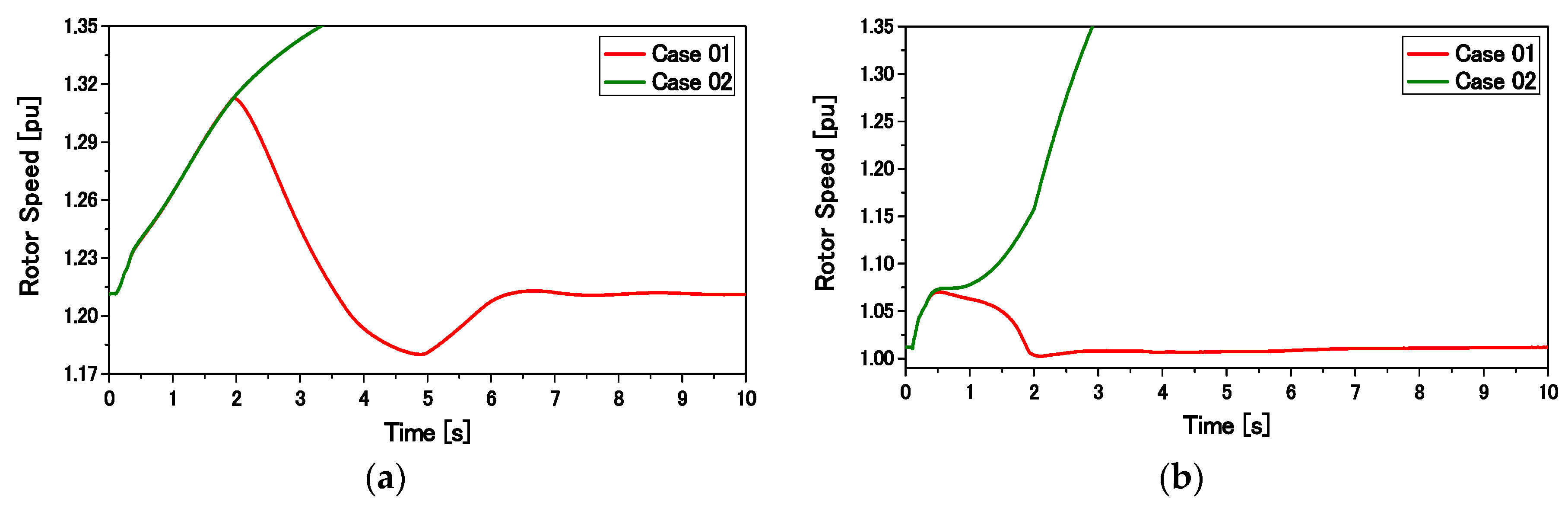
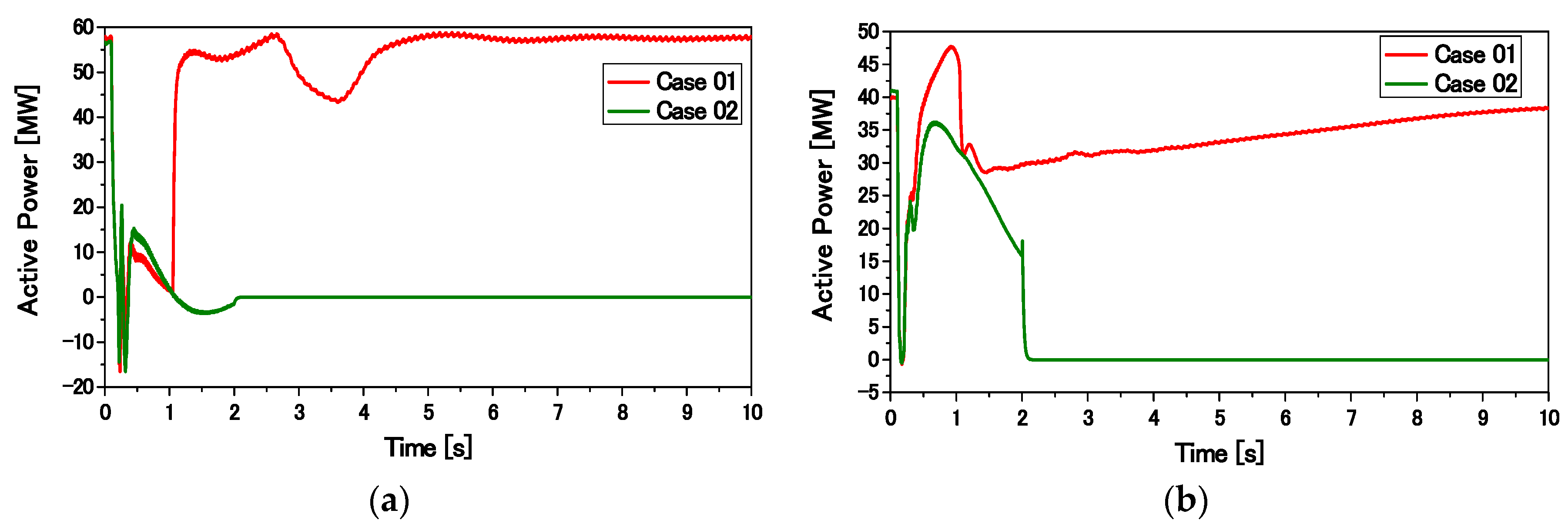
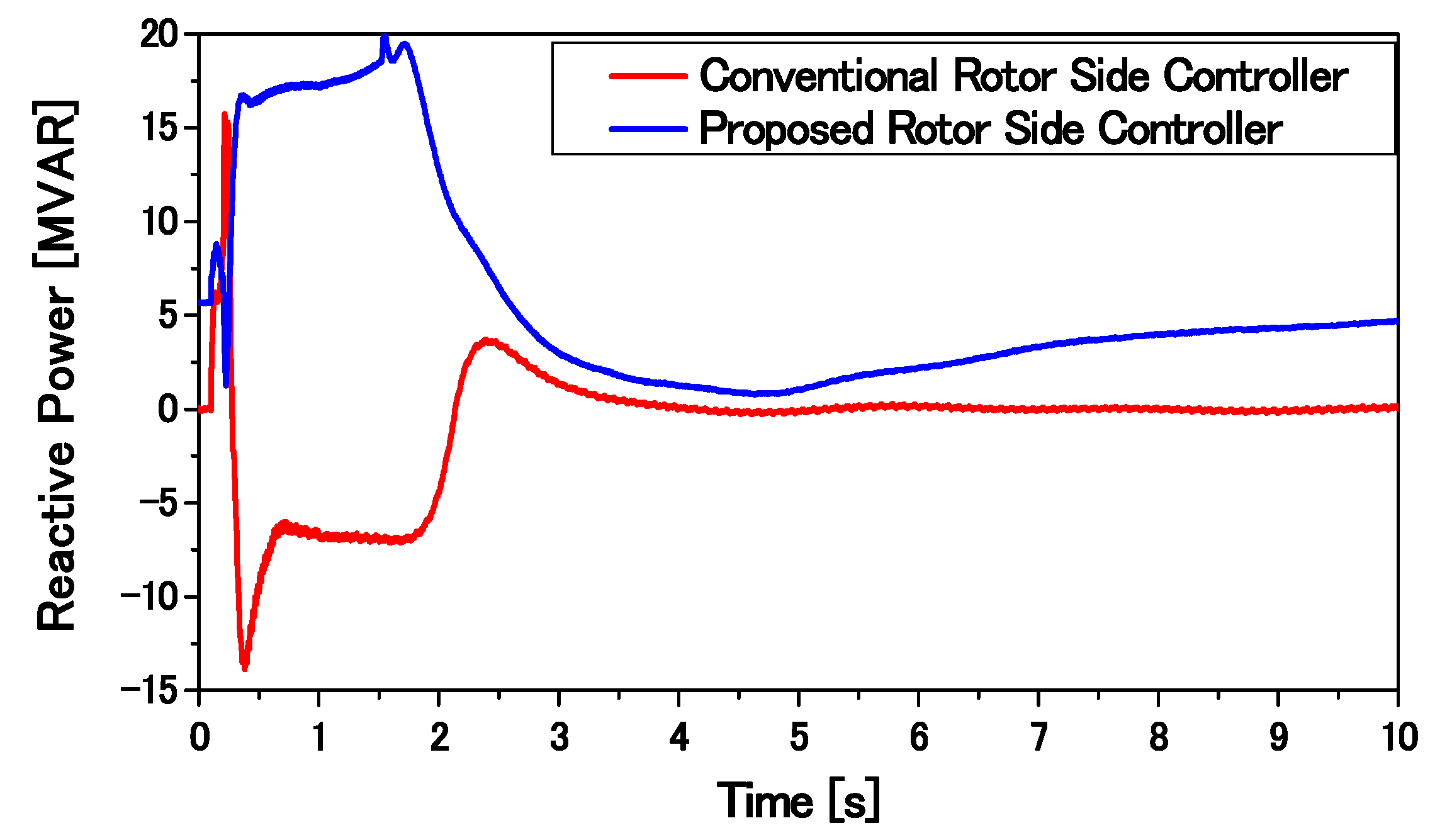
Qdfig) more effectively in the fault condition. Thus, the grid voltage can quickly be retraced back to the nominal value. Moreover, the FLC can stabilize a higher rating of the SCIG as compared to the conventional PI-based controller of the RSC in the inner loop.
The active power (Pdfig) and reactive power (Qdfig) outputs of the DFIG are controlled by regulating the rotor winding current. The reference active power (Pref) is calculated by subtracting the losses (Ploss) from the MPPT output (Pmppt). In the upper loop portion, the grid voltage (Vg) is taken as feedback to regulate the terminal voltage constant at 1.0 pu. The q-axis current (Irq) controls the active power delivered to the grid, and the d-axis current (Ird) controls the reactive power delivered to the grid.
In the normal operating condition (Vg > 0.9 pu), the RSC regulates the active power delivered to the grid. During a fault condition (Vg < 0.9 pu), a comparator sends a signal so that active power transfer to the grid becomes zero. By controlling the power in this manner, the reactive power injected to the grid can be maximized.
The detailed design procedure of the FLC will be discussed in
Section 4.
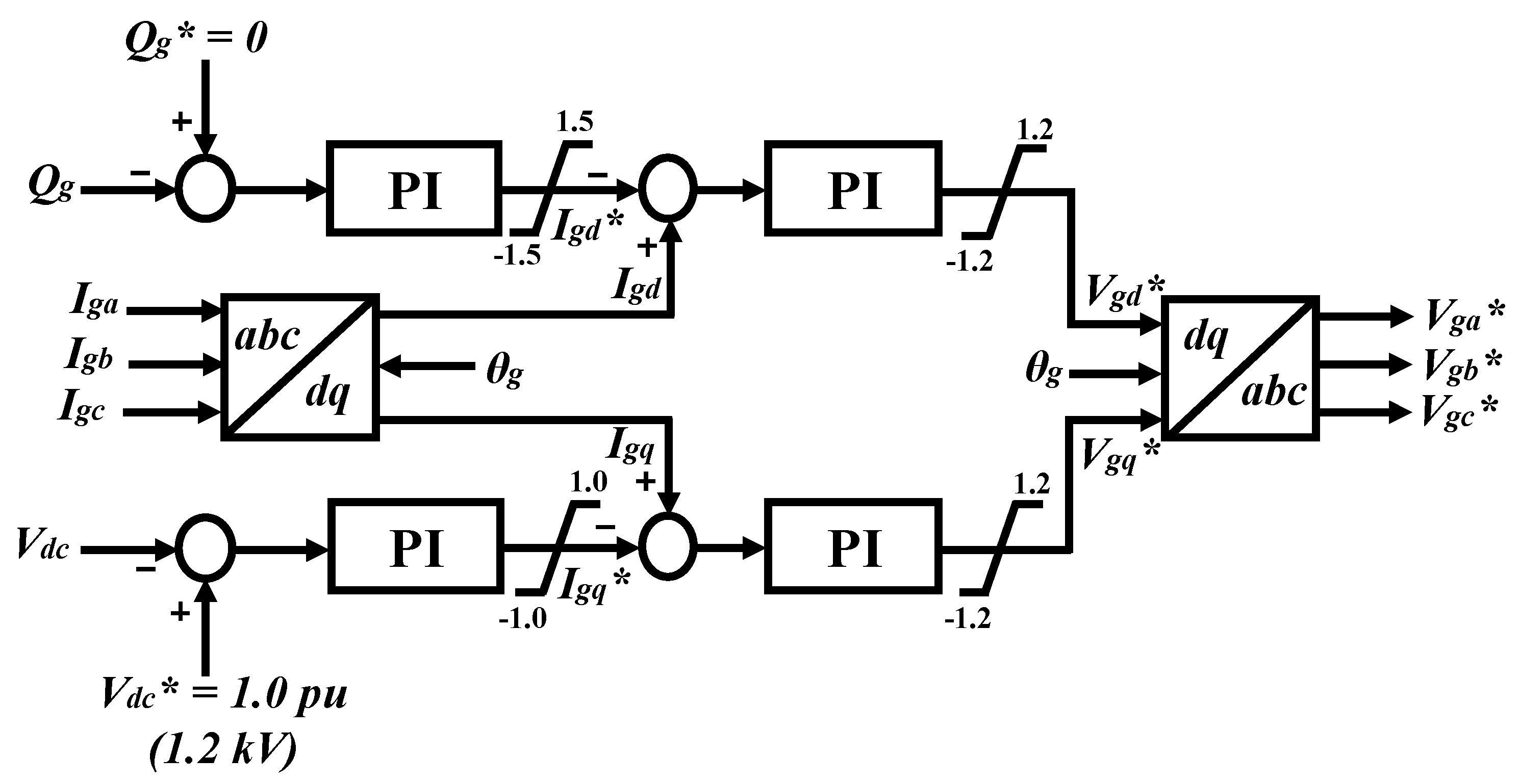
3.3. Grid-Side Controller
The controller for the GSC is depicted in
Figure 7. This controller consists of four PI controllers to compensate different error signals. The GSC reactive power (
Qg) and DC-link voltage (
Vdc) are controlled through d-axis (
Igd) and q-axis (
Igq) current components, respectively. The reactive power reference is set to zero, and the DC-link voltage reference is set to 1.0 pu (1.2 kV).
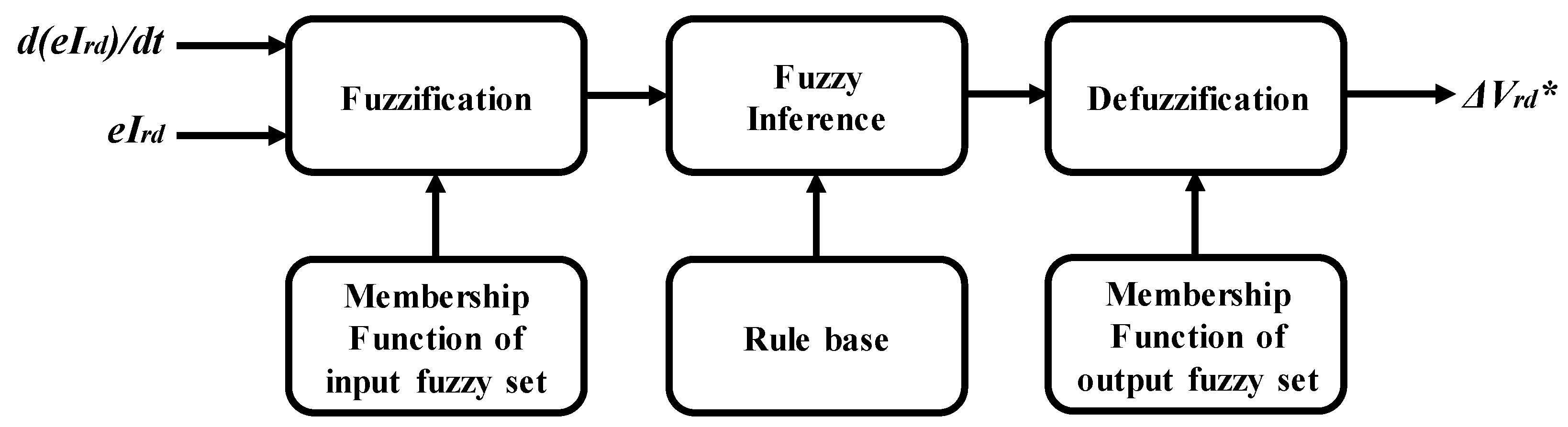
4. Fuzzy Logic Controller Design
Figure 8 shows a block diagram of the proposed FLC. The FLC is composed of fuzzification, a membership function, a rule base, a fuzzy inference, and defuzzification, as shown in
Figure 9.
In order to design the proposed FLC, the error of the rotor d-axis current (
eIrd) and rate of change of the
eIrd (
d[eIrd]/dt) are considered as the controller inputs. The reference rotor d-axis voltage (
Vrd*) is chosen as the controller output. In
Figure 8,
1/z is one sampling time delay.
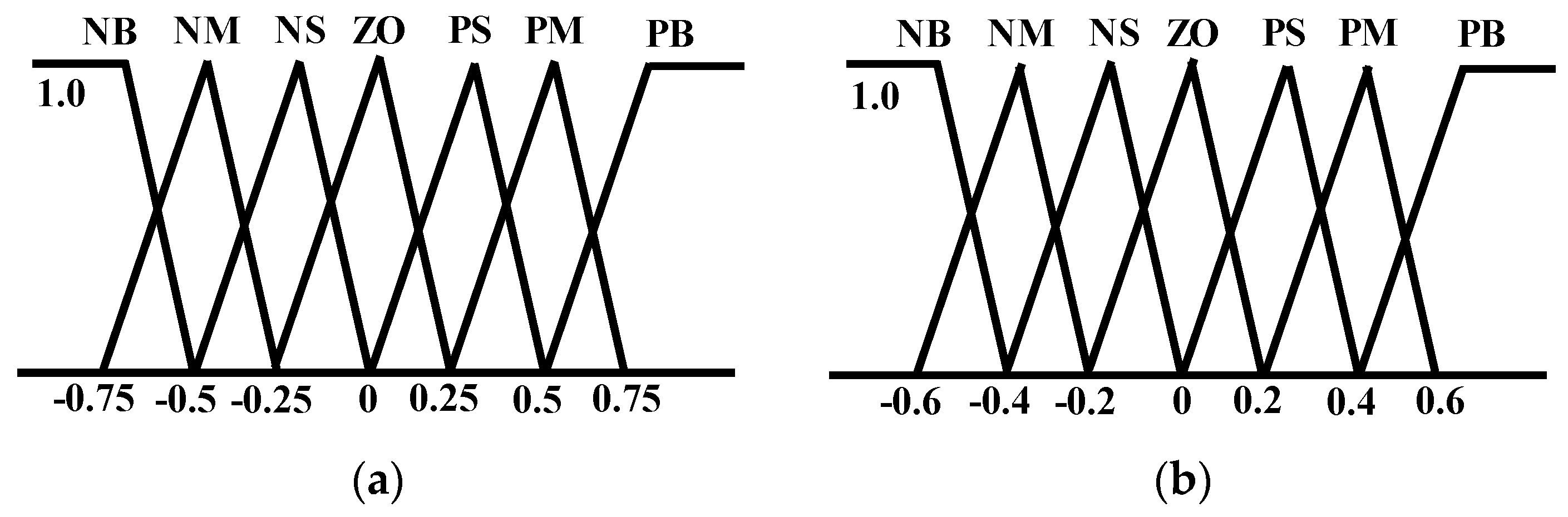
The triangular membership functions with overlap used for the input and output fuzzy sets are shown in
Figure 10, where linguistic variables are indicated as NB (Negative Big), NM (Negative Medium), NS (Negative Small), ZO (Zero), PS (Positive Small), PM (Positive Medium), and PB (Positive Big).
The rules of fuzzy mapping of the input variables to the output are given in the following form:
IF <eIrd is PB> and <d(eIrd)/dt is NS> THEN <Vrd* is PS>
IF <eIrd is NM> and <d(eIrd)/dt is NS> THEN <Vrd* is NB>
The entire rule base is listed in
Table 1, which includes a total of 49 rules.
In the present study, Mamdani’s max-min method is used as the inference mechanism [
27]. The center of gravity method is used for defuzzification in order to obtain
Vrd* [
28].
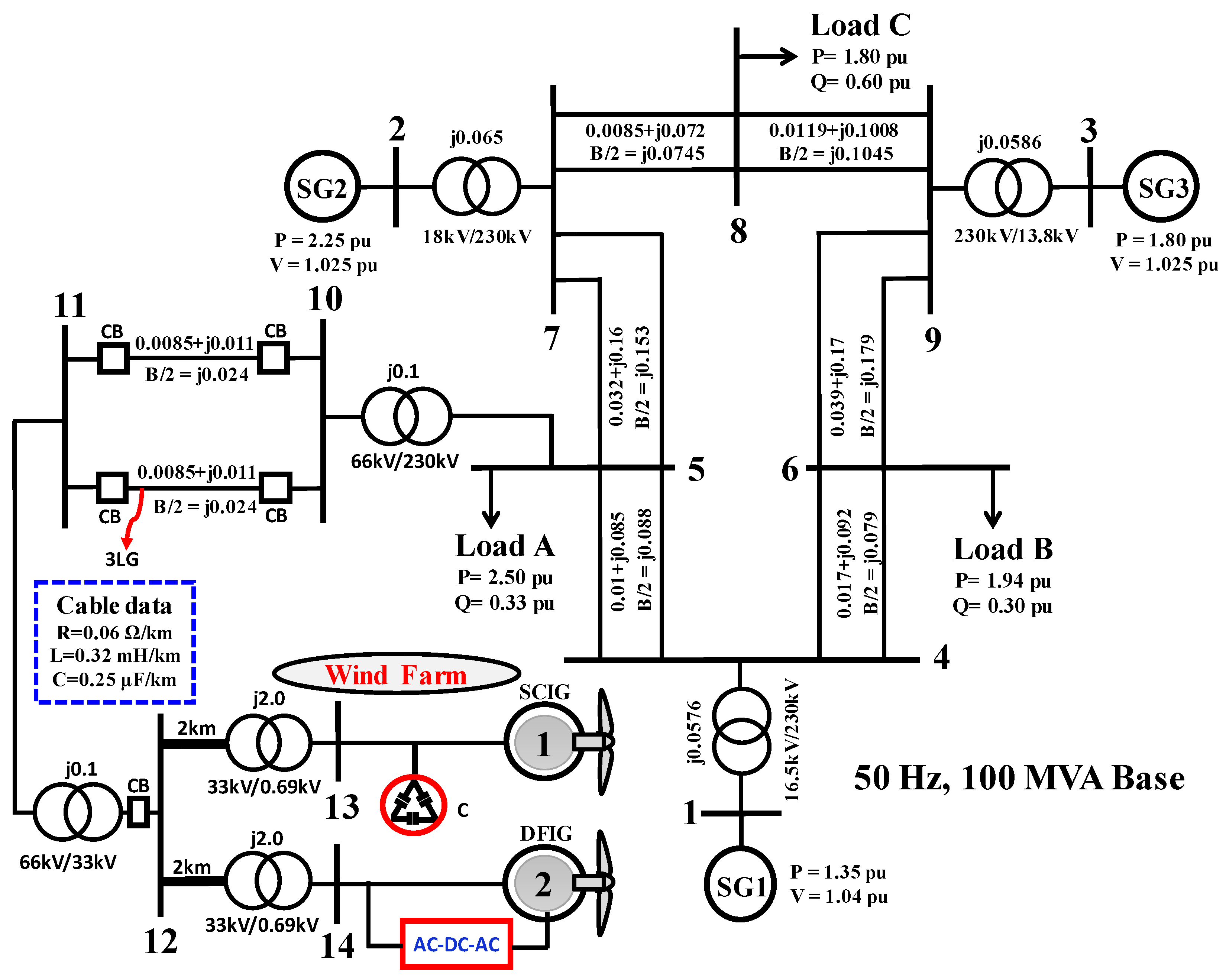
5. Power System Model
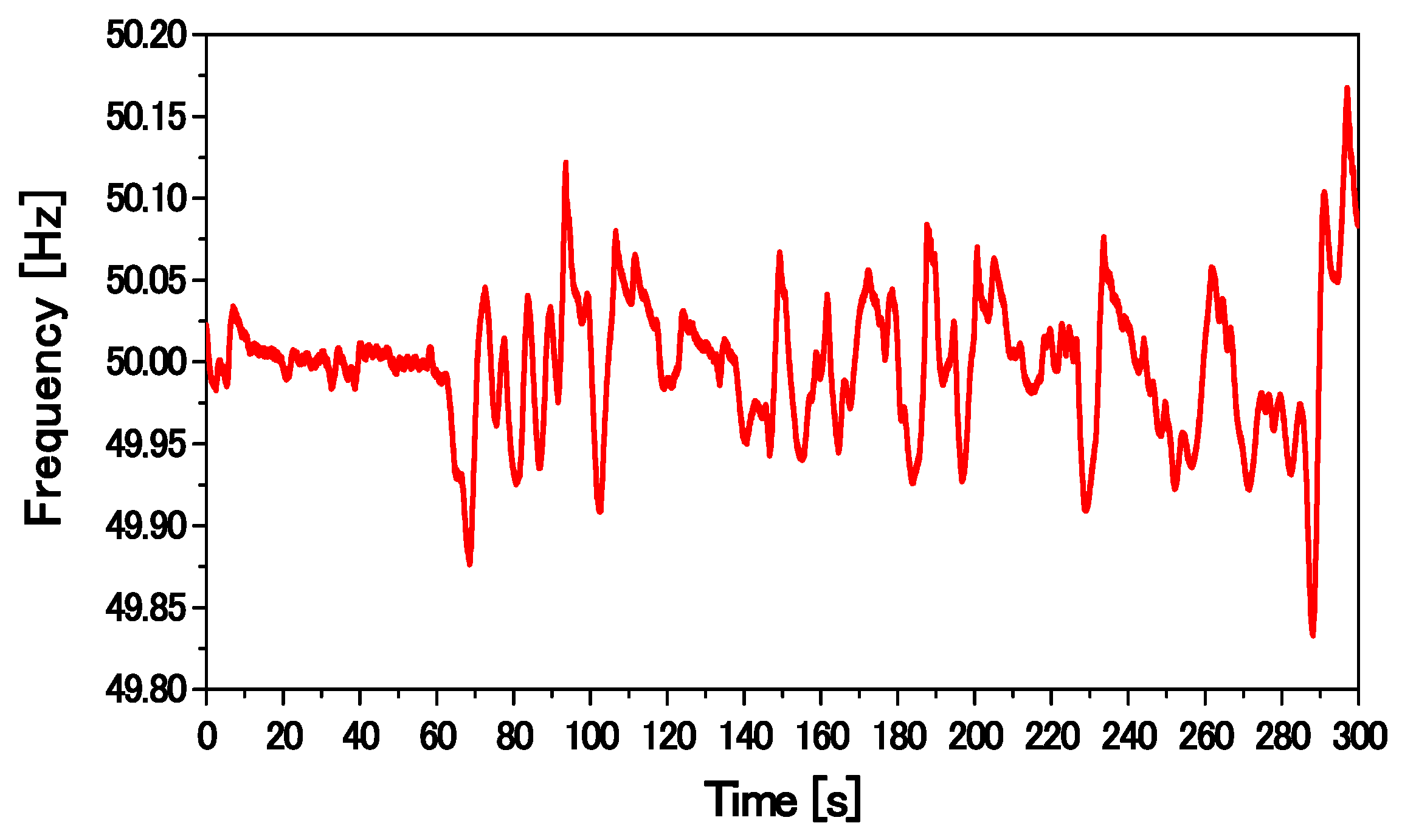
The power system model used for transient stability analysis is shown in
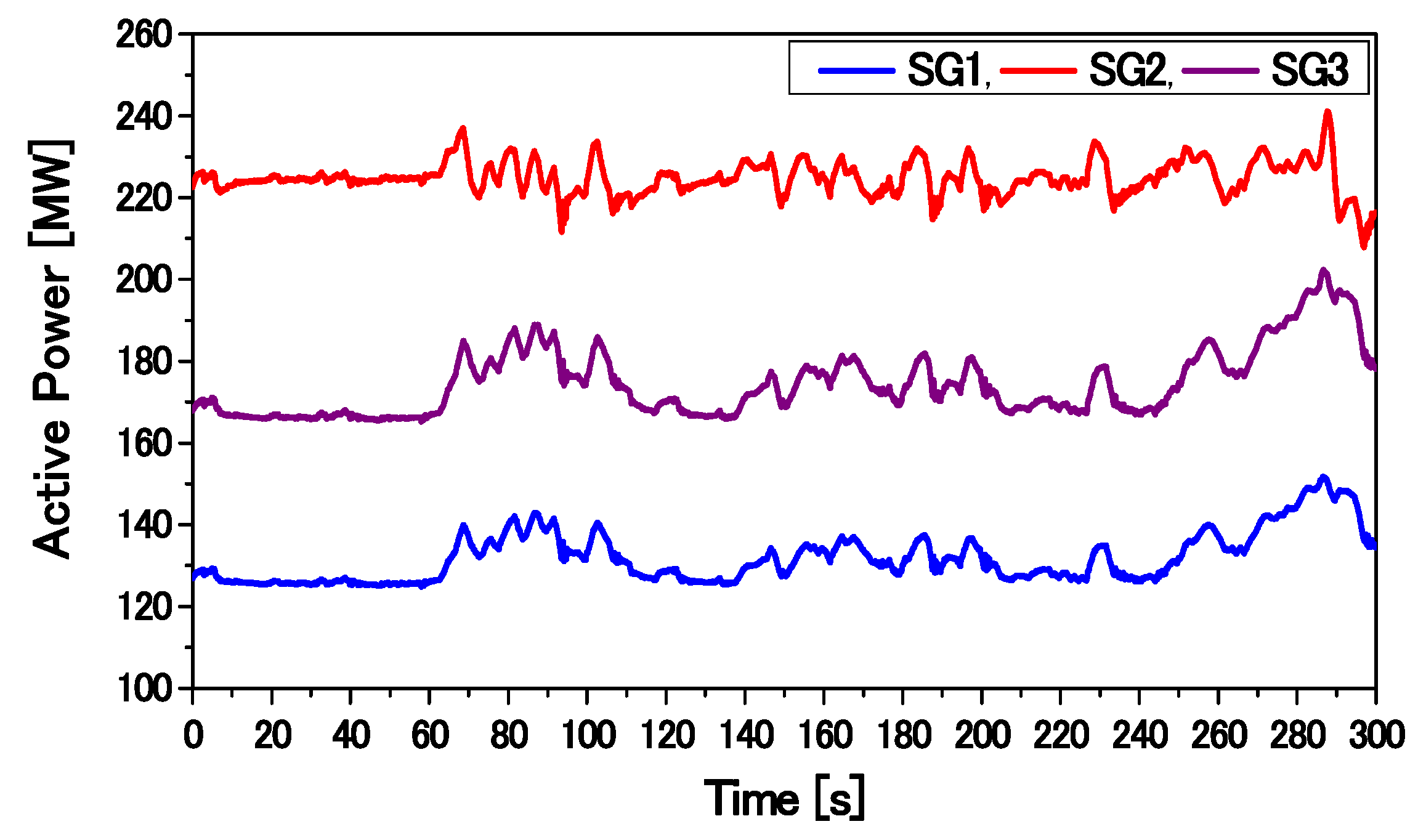
Figure 11. The model is composed of a nine-bus main system [
29] and a WF. The main system is composed of three conventional power plants: two thermal power plants (SG1 and SG2) and one hydropower plant (SG3). Both SG1 and SG3 are operated under automatic generation control (AGC), and SG2 is operated under governor-free (GF) control. The parameters of the SGs are listed in
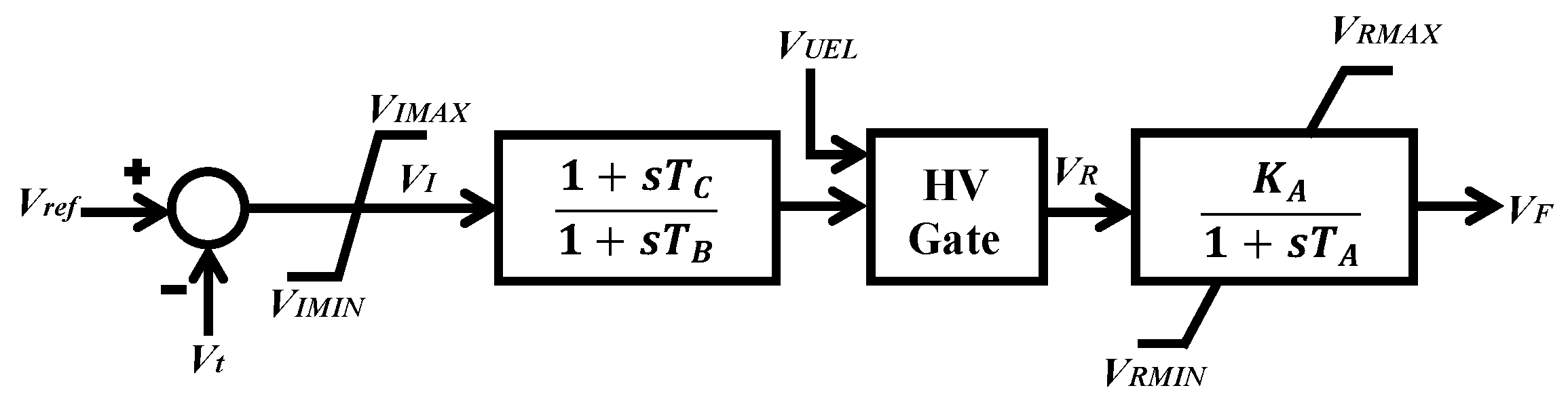
Table 2. The IEEE type AC4A excitation system model shown in
Figure 12 is considered for all SGs [
30].
Table 3 lists the parameters taken from [
30].
Figure 13 shows a block diagram of the reheat steam turbine governor system used in the thermal power plants (SG1 and SG2) [
30]. The hydro turbine governor model system used for the hydropower plant (SG3) is shown in
Figure 14 [
30]. The parameters of both turbine systems are presented in
Table 4 [
30]. For AGC operation, an integral controller is installed on the governor system for both SG1 and SG3.
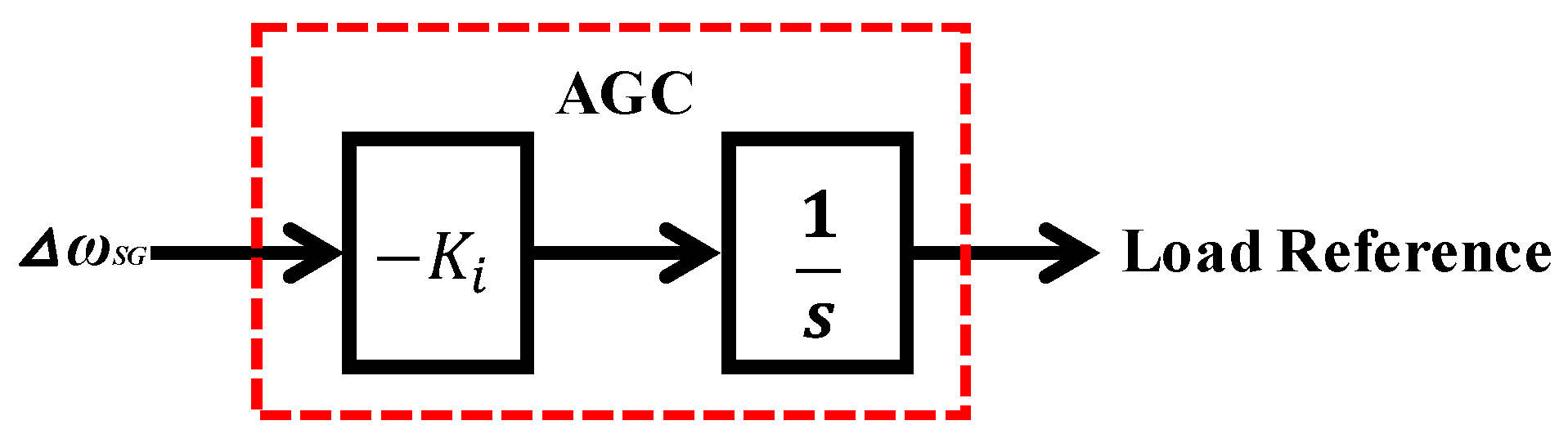
The integral controller on selected units for AGC is shown in
Figure 15 [
30]. The output of the AGC supplies the power load reference of the governor system depending on the speed deviation of the SG (
Δωsg). The integral gain
Ki is set to 6.
A WF is connected to the main system at bus 5, as shown in
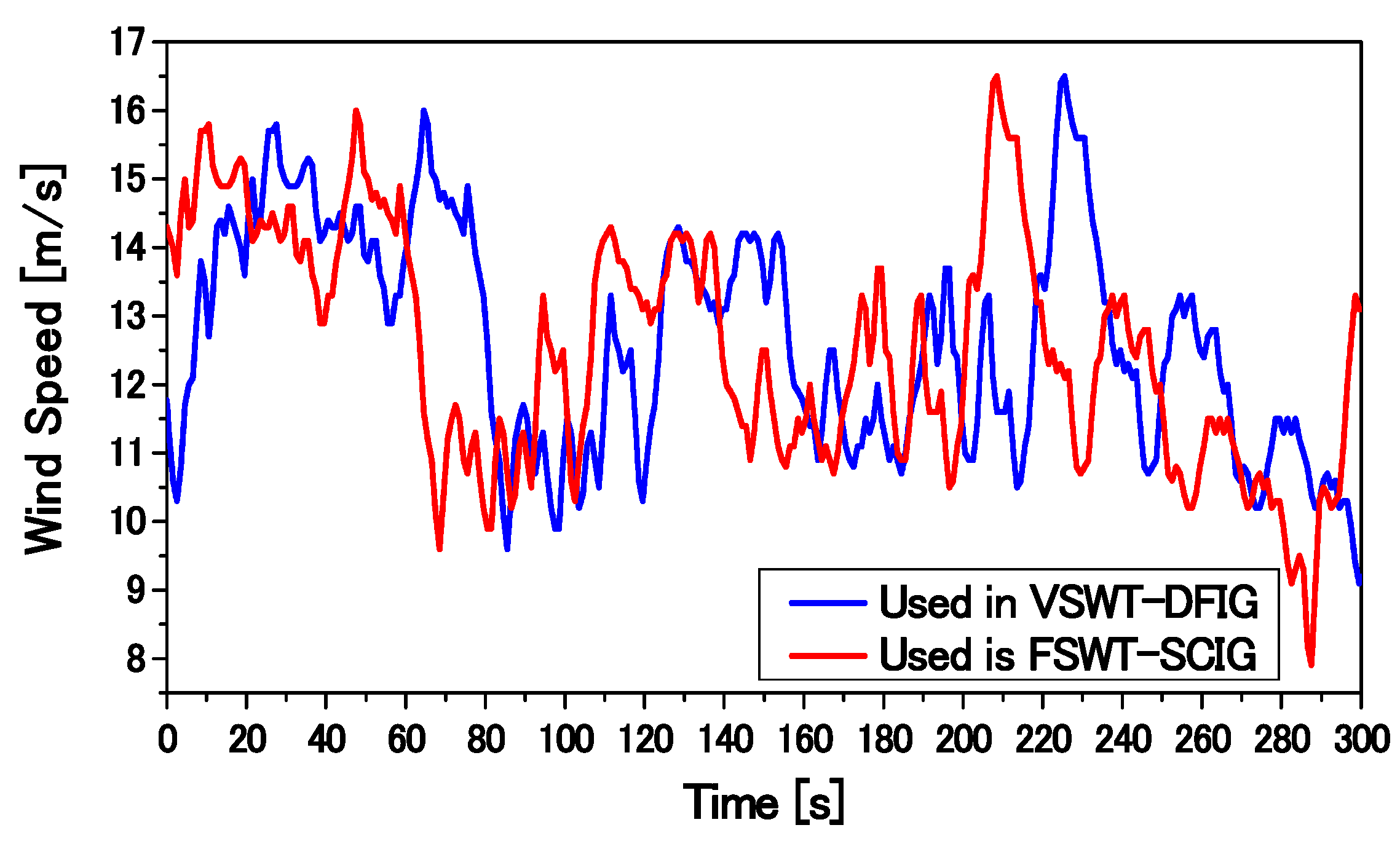
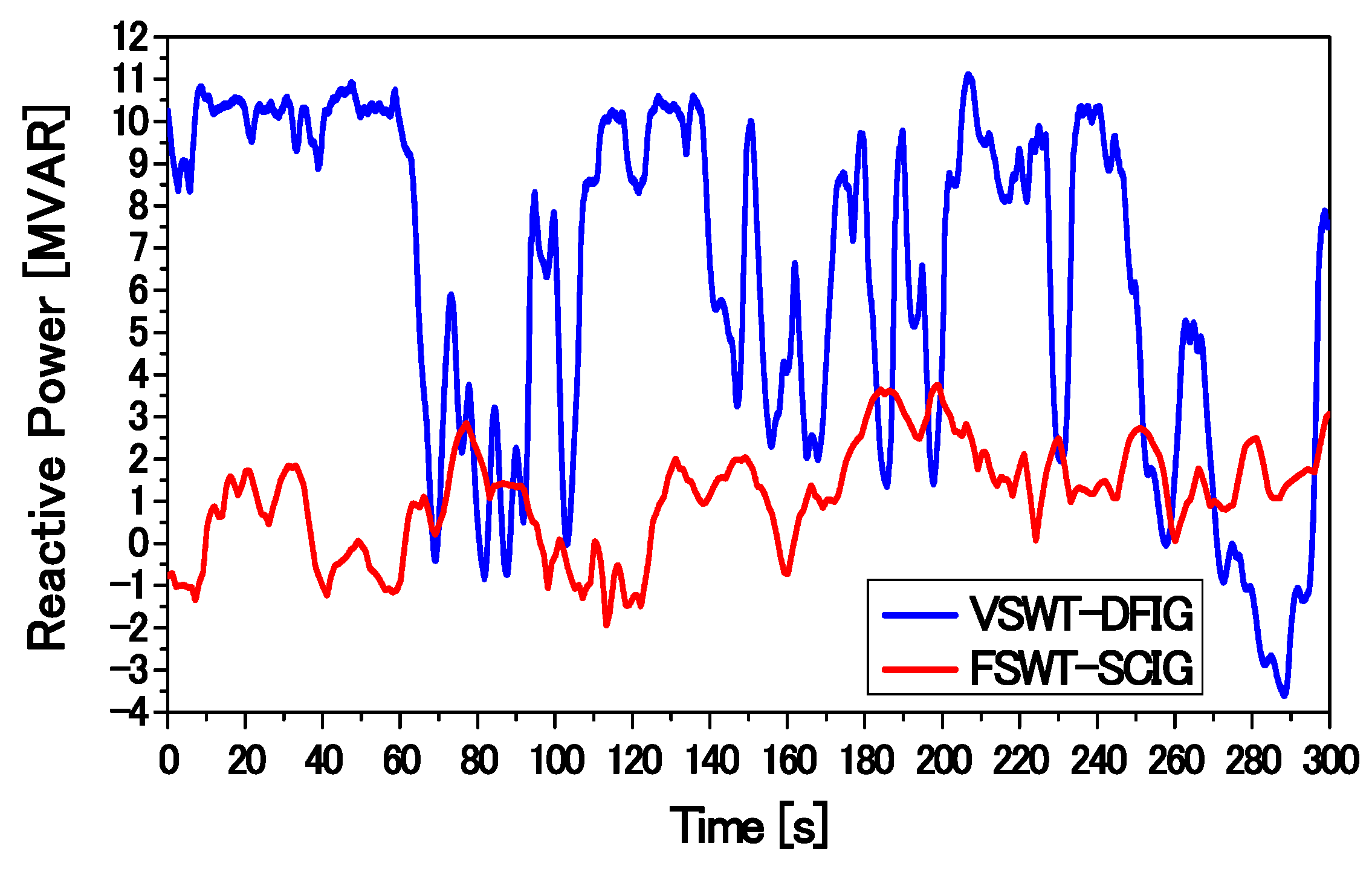
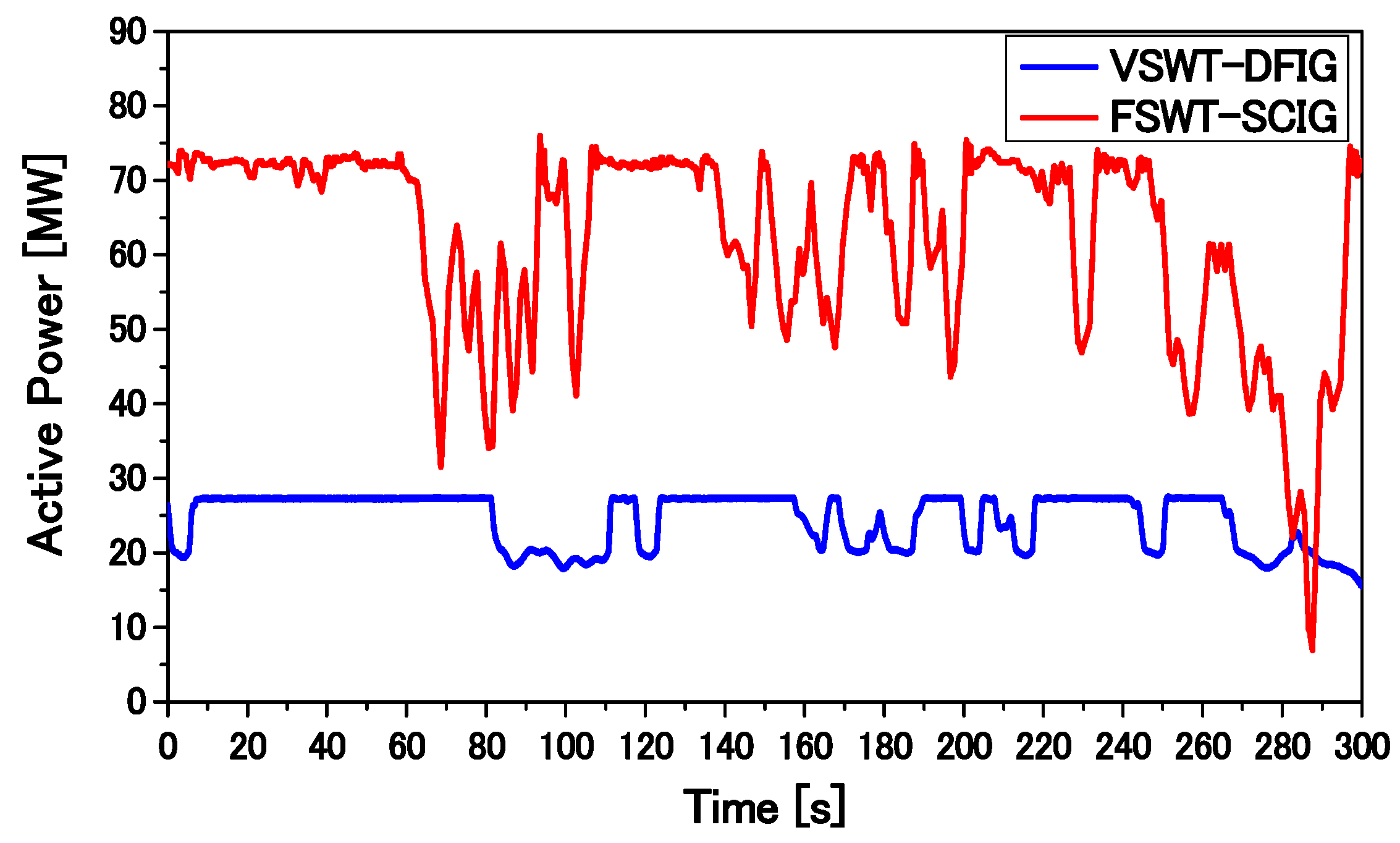
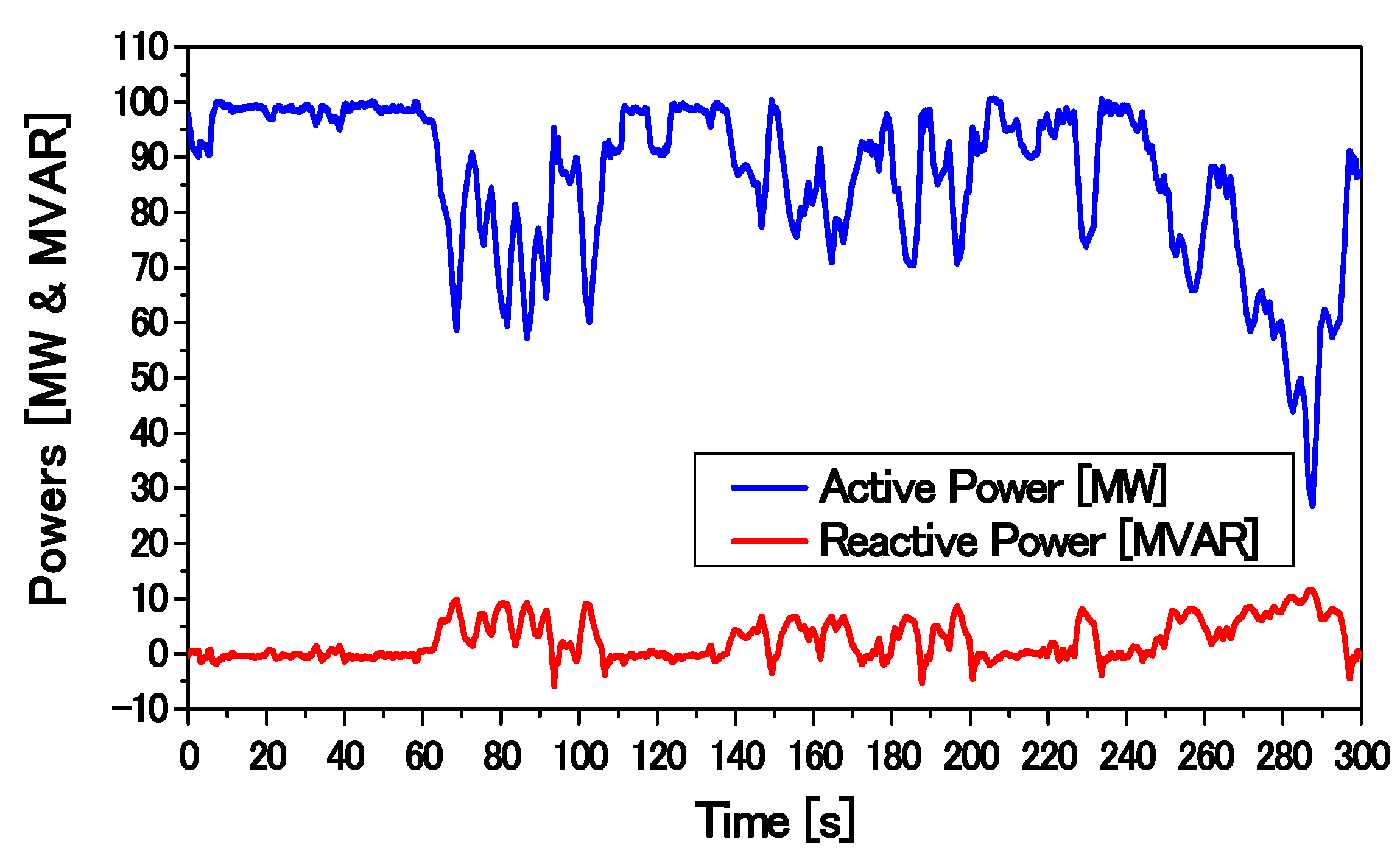
Figure 11, and consists of one VSWT-DFIG and one FSWT-SCIG. In order to reduce computational time, each wind generator is represented as an aggregated equivalent single machine [
31,
32]. The total capacity of the WF is 100 MW. A capacitor bank (C) is used for reactive power compensation of the SCIG. The value of C is chosen such that the power factor of the SCIG-based wind generator becomes unity at the rated operating condition. The base power of the system is 100 MVA, and the rated frequency is 50 Hz. The parameters of the DFIG and the SCIG are presented in
Table 5.