Research on Model-Based Fault Diagnosis for a Gas Turbine Based on Transient Performance
Abstract
1. Introduction
- The accuracy of the algorithm should be increased;
- The diagnostic result based on steady-state data and dynamic data should be compared;
- The diagnostic method based on transient process data should be used to analyze field data.
2. Methodology
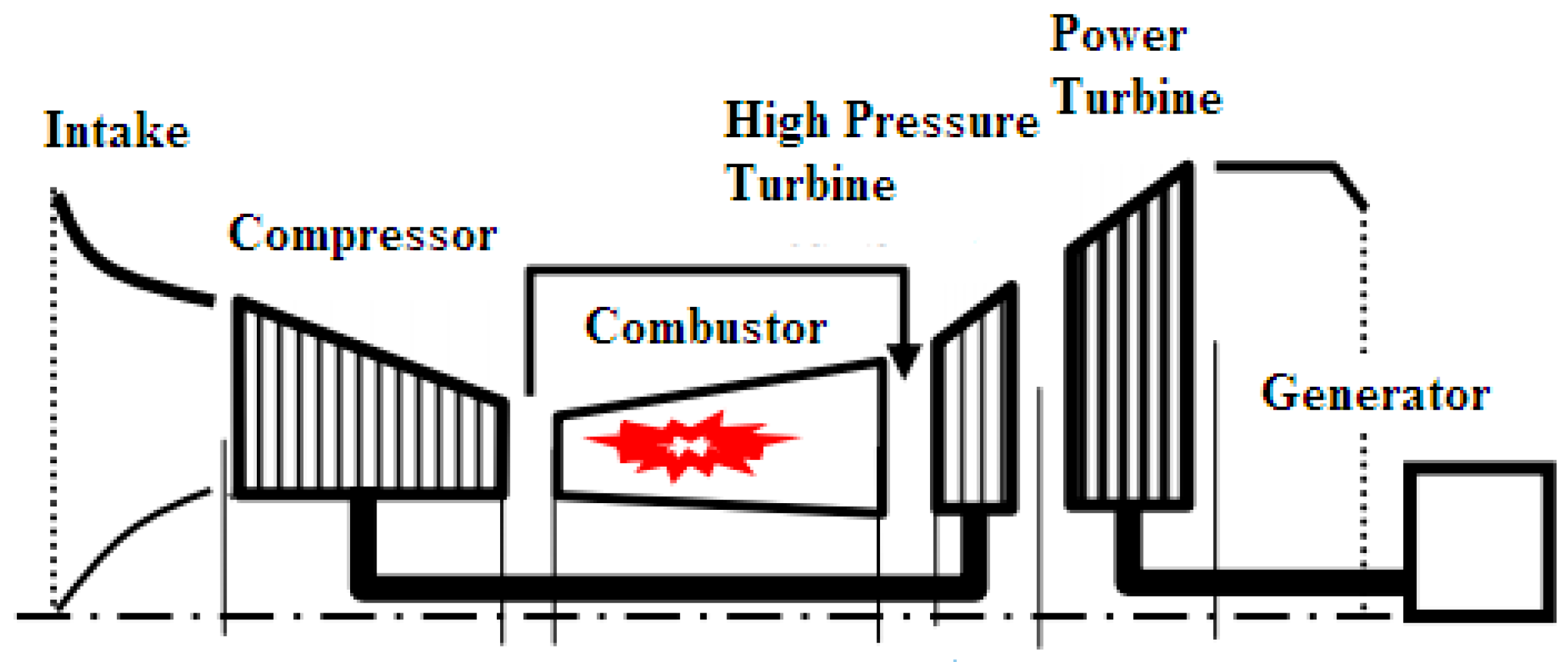
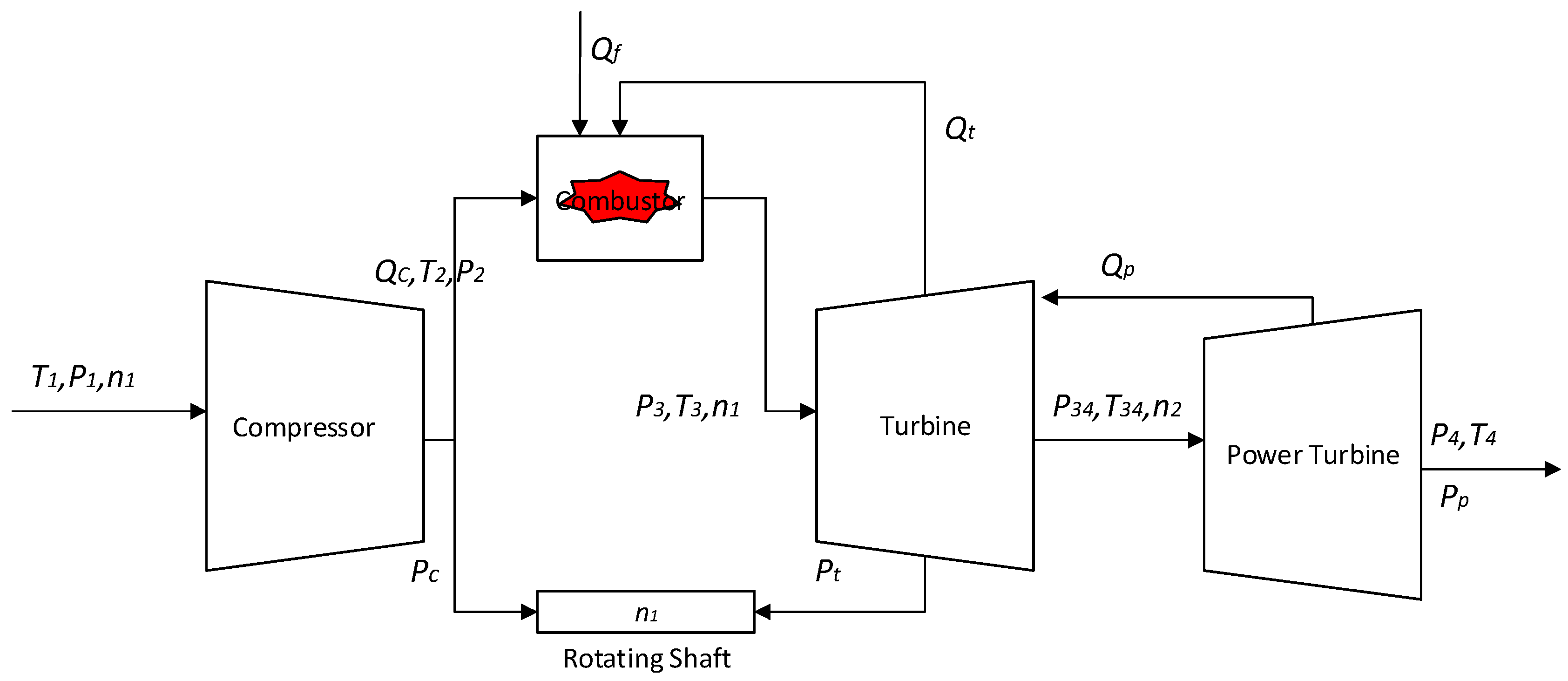
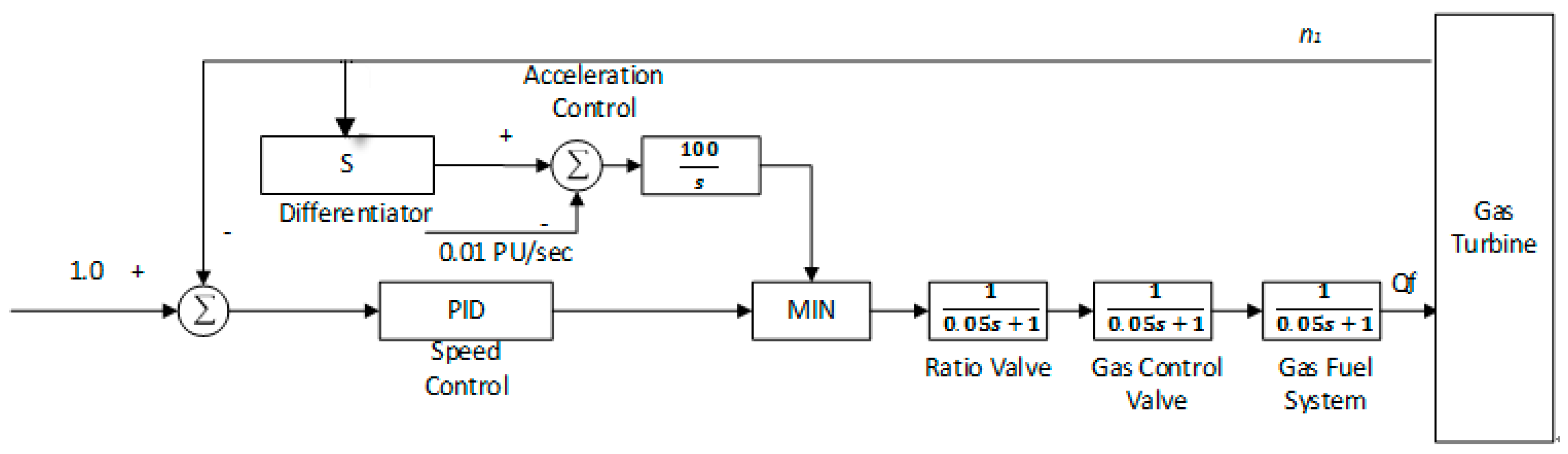
2.1. Modeling of Gas Turbine
2.2. Cuckoo Search Algorithm
- A cuckoo lays one egg at a time, and selects a bird’s nest to hatch it randomly;
- In a randomly selected group of bird’s nests, the best bird’s nest will be retained to the next generation.
- The number n of available bird’s nests is fixed and the probability that an owner of a bird’s nest can find an exotic birds’ eggs is Pa ∈ [0, 1]. Based on the three ideal states, the updating formula of path and location is as follows, when the cuckoo finds a nest:where X(t)i is the next location number in the cuckoo generation t, α represents the step control variable and L(λ) represents the Levy random search path. Levy flight is a random movement process, the step of its flight distance obeys Levy distribution. The following formula is used to produce a Levy random number:u and ν obey standard normal distribution and λ is the distribution factor, In this paper, it equals 1.5 [27]. The formula of φ is as follows:
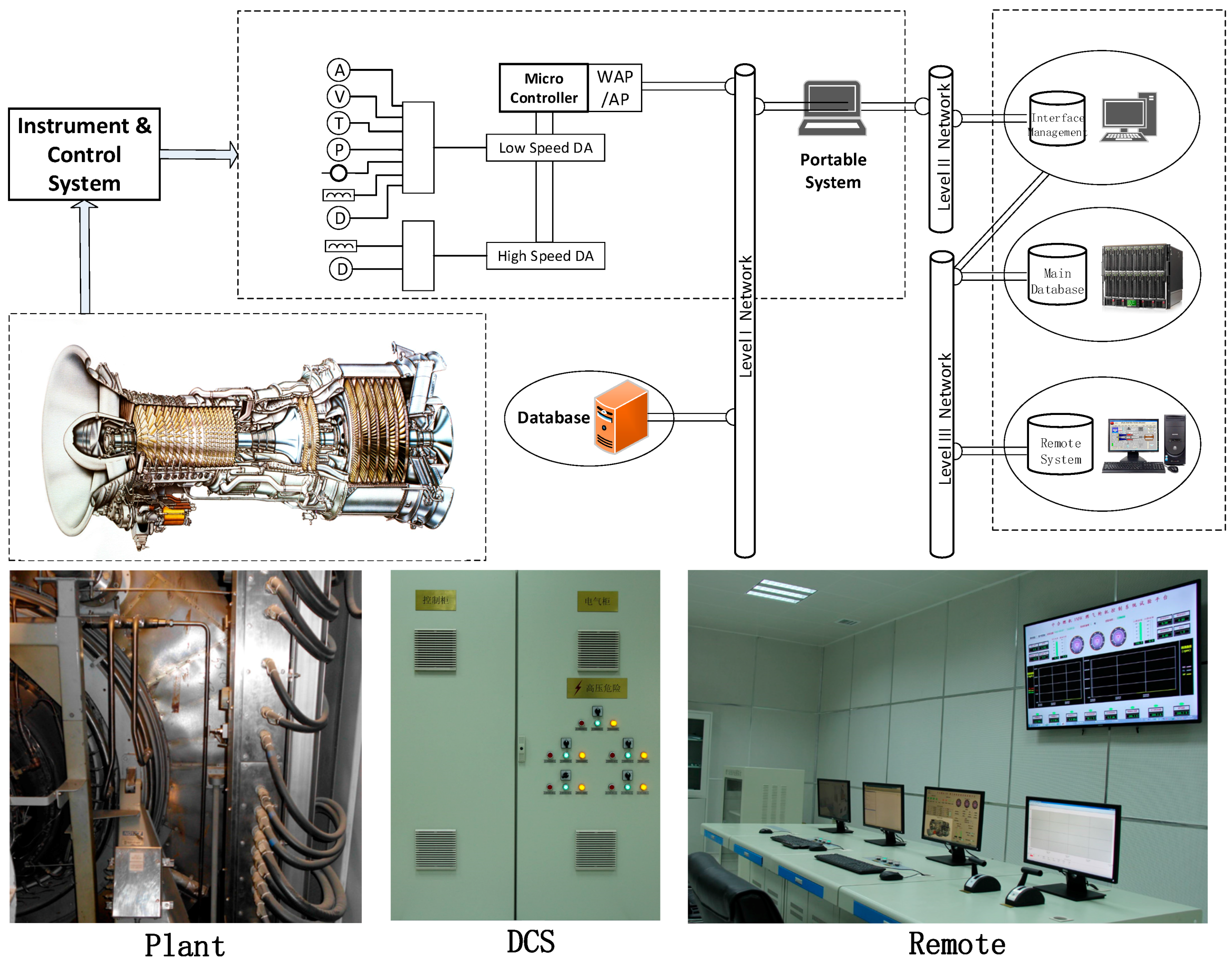
2.3. Diagnostic System
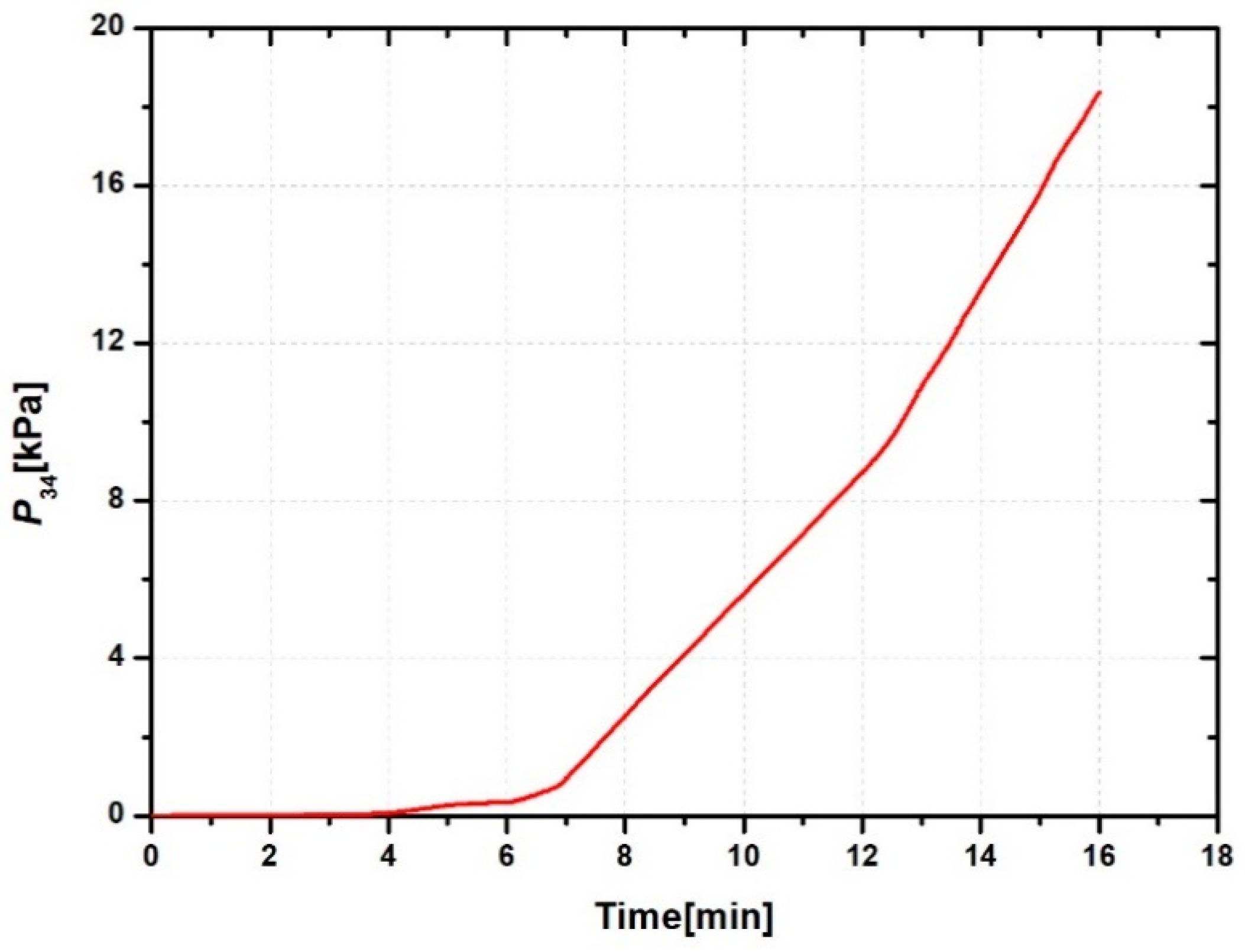
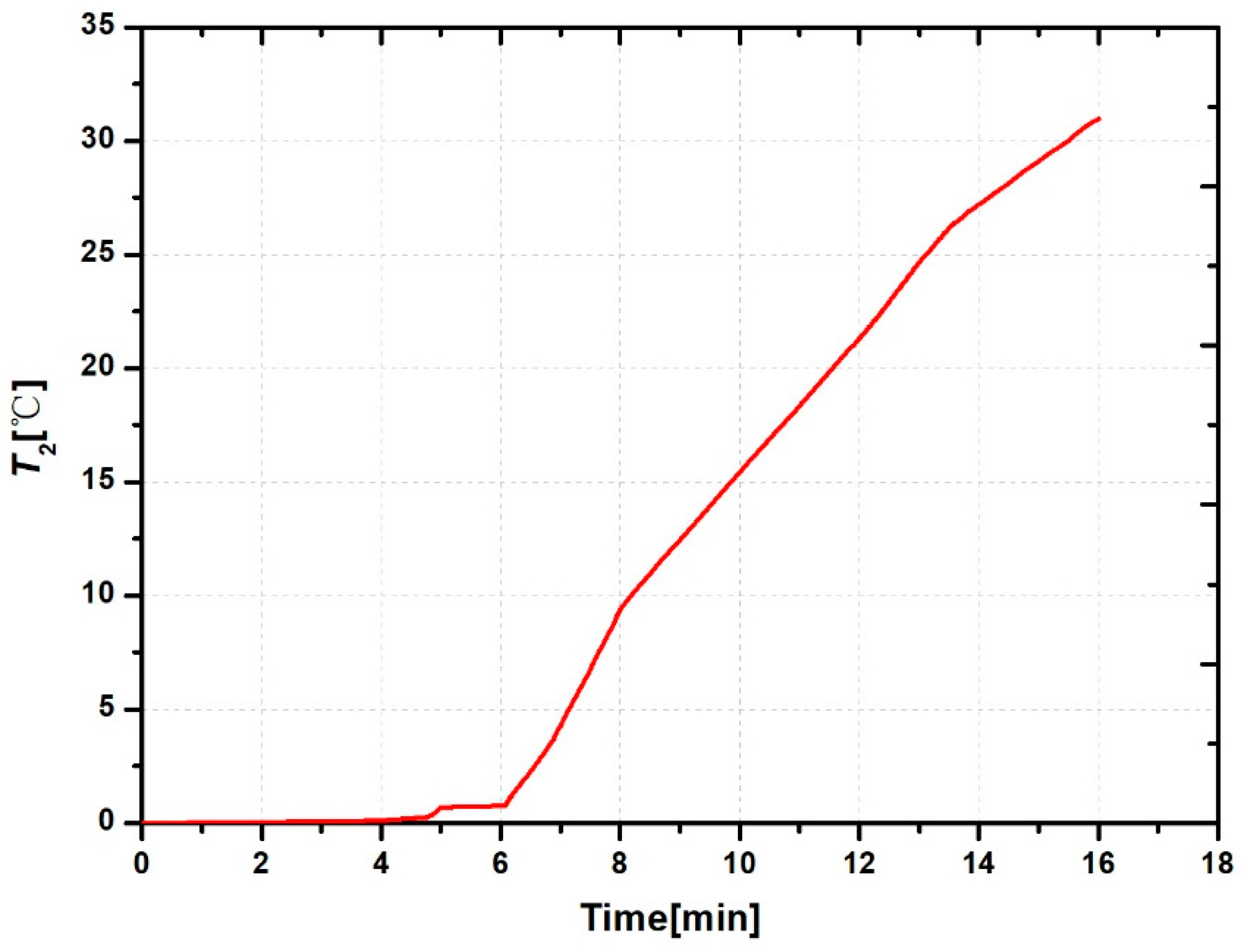
3. Case Study
3.1. Overall Performance Test Rig
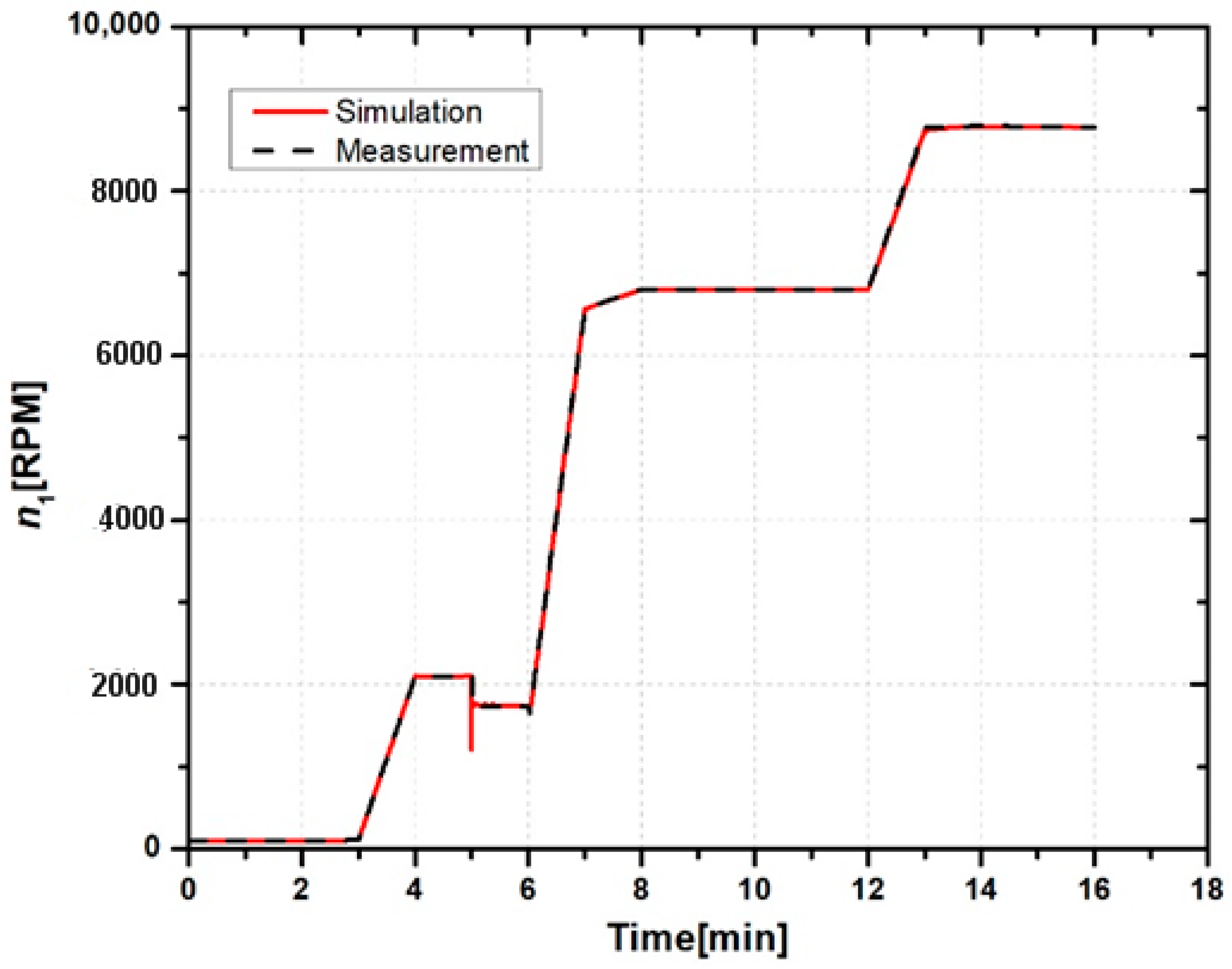
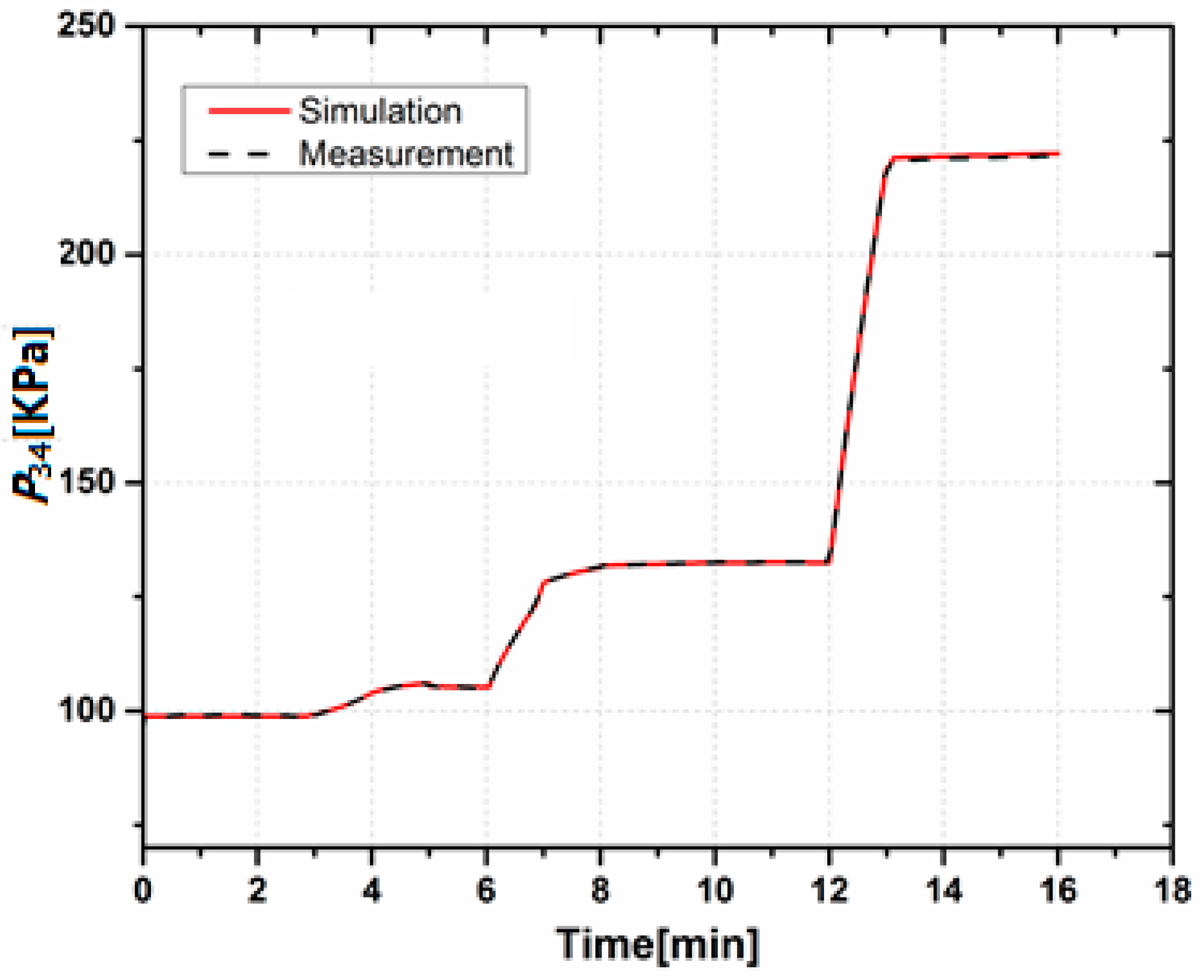
3.2. Simulation Model Validation
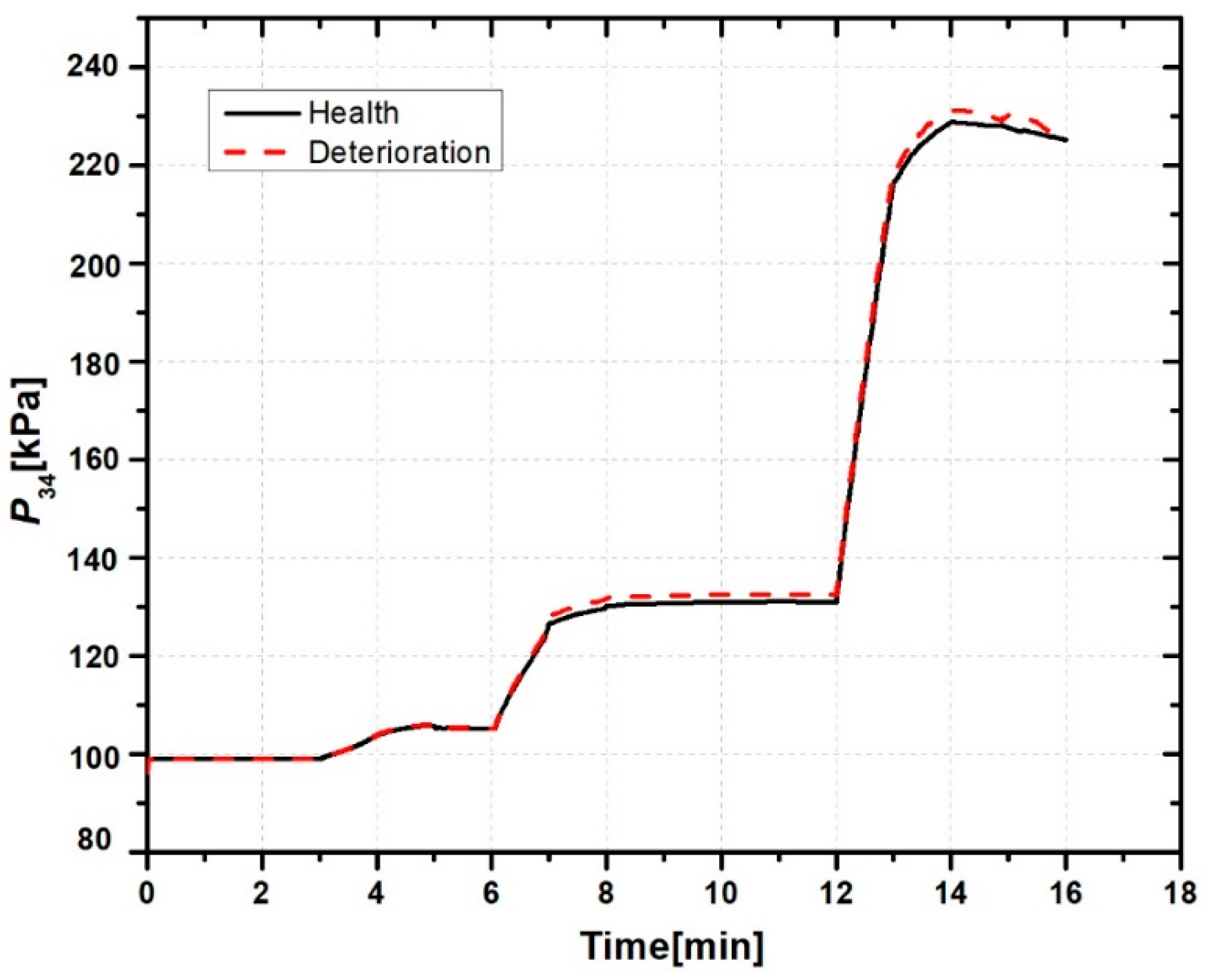
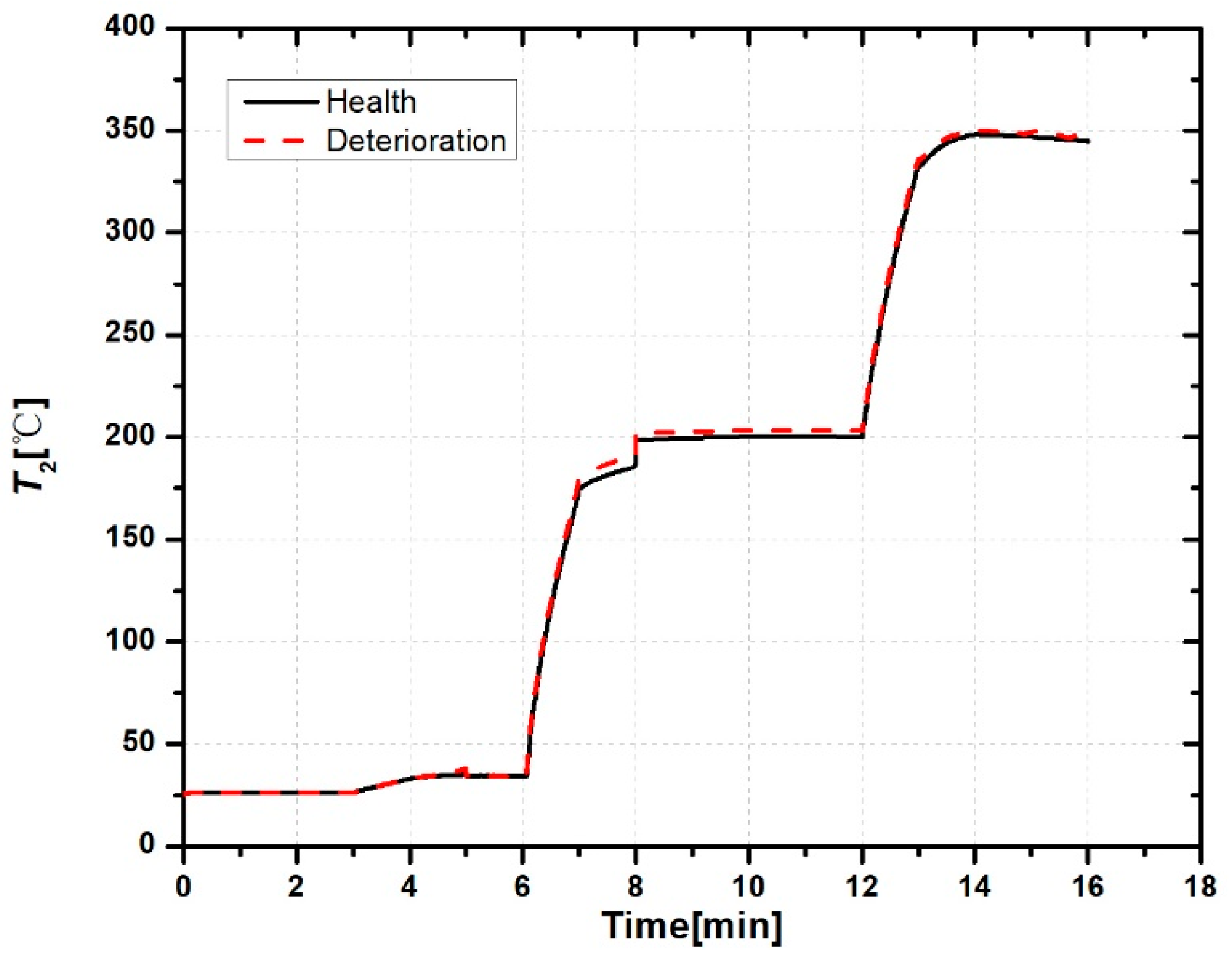
3.3. Simulation with Component Degradation
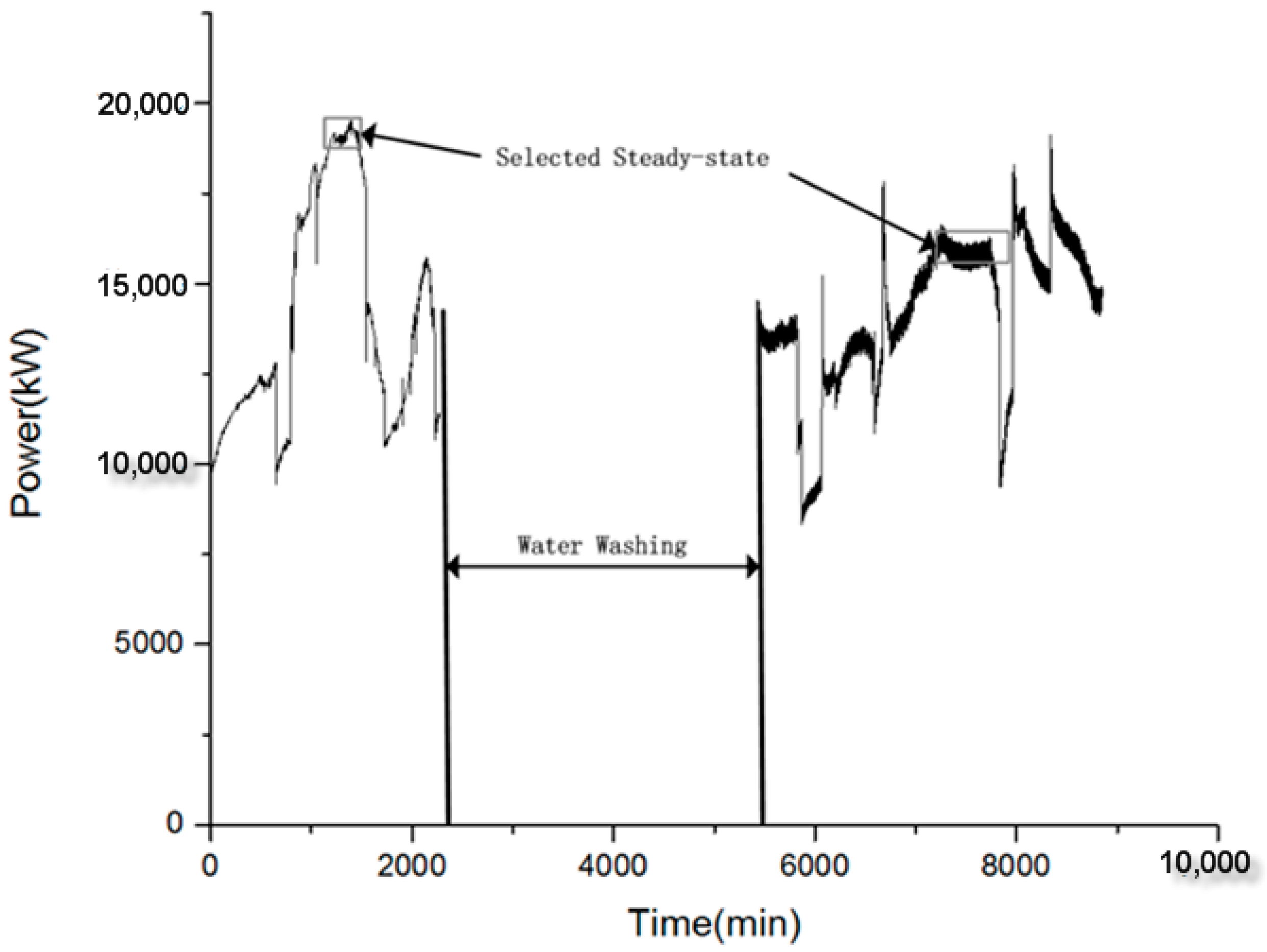
3.4. Comparative Study
- The improvement of the compressor flow rate degradation is 13 times the value of its efficiency degradation based on Method A. It does not meet the theoretical value of three. The result of Method B is 1.96, closer to the theoretical value.
- These ratios for high pressure turbines are 3.86 and 5.33. It seems that Method A is more accurate than Method B for high-pressure turbines. Thus, the health condition of high-pressure turbines can be monitored by both Method A and Method B. However, washing decisions are usually made by compressor degradation. This means that Method B is more suitable for supporting maintenance scheduling.
- There is not any maintenance work being carried out for power turbines in this process. Therefore, the improvement of both its flow rate and efficiency should be zero, theoretically. This proves that Method B is more accurate for power turbine diagnosis.
4. Conclusions
- A new, non-linear, model-based diagnostic method, using gas turbine transient measurements and a cuckoo search (CS) algorithm, was tested to diagnose a gas turbine before and after a washing process.
- Diagnosis with transient measurements is more relevant than diagnosis with steady-state measurements, when gas turbine faults contribute little to performance deviation in steady-state conditions or gas turbine output fluctuates greatly.
- Gas turbine component fault diagnosis using transient data can be more effective than using steady state data, owing to magnifying fault signatures and extending the tracking time to eliminate variable uncertainties.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| π | component pressure ratio |
| η | component efficiency |
| T1 | compressor inlet air temperature |
| P1 | compressor inlet air pressure |
| n1 | rotational speed of high pressure turbine |
| Qc | compressor inlet air mass flow |
| T2 | compressor discharge air temperature |
| P2 | compressor discharge air pressure |
| Qf | fuel gas flow |
| T3 | high pressure turbine inlet temperature |
| P3 | high pressure turbine inlet pressure |
| T34 | high pressure turbine discharge temperature |
| P34 | high pressure turbine discharge pressure |
| Qt | high pressure turbine mass flow |
| T4 | power turbine discharge temperature |
| P4 | power turbine discharge pressure |
| Qp | power turbine mass flow |
| Pc | power consumption of compressor |
| Pt | power generation of high pressure turbine |
| Pp | power generation of power turbine |
References
- Kagermann, H.; Helbig, J.; Hellinger, A.; Wahlster, W. Recommendations for Implementing the Strategic Initiative INDUSTRIE 4.0: Securing the Future of German Manufacturing Industry. Final Report of the Industrie 4.0 Working Group. Available online: http://forschungsunion.de/pdf/industrie_4_0_final_report.pdf (accessed on 16 January 2018).
- Brynjolfsson, E.; McAfee, A. Race against the Machine: How the Digital Revolution is Accelerating Innovation, Driving Productivity, and Irreversibly Transforming Employment and the Economy; Digital Frontier Press: Lexington, MA, USA, 31 January 2012. [Google Scholar]
- Isermann, R.; Ballé, P. Trends in the application of model-based fault detection and diagnosis of technical processes. Control Eng. Pract. 1997, 5, 709–719. [Google Scholar] [CrossRef]
- Zhang, J. Multi-source remote sensing data fusion: Status and trends. Int. J. Image Data Fusion 2010, 1, 5–24. [Google Scholar] [CrossRef]
- Lu, F.; Zheng, W.; Huang, J.; Feng, M. Life cycle performance estimation and in-flight health monitoring for gas turbine engine. J. Dyn. Syst. Meas. Control 2016, 138, 091009. [Google Scholar] [CrossRef]
- Li, Y.G. Performance-analysis-based gas turbine diagnostics: A review. Proc. Inst. Mech. Eng. Part A J. Power Energy 2002, 216, 363–377. [Google Scholar] [CrossRef]
- Sampath, S.; Gulati, A.; Singh, R. Fault diagnostics using genetic algorithm for advanced cycle gas turbine. In Proceedings of the ASME Turbo Expo 2002: Power for Land, Sea, and Air, Amsterdam, The Netherlands, 3–6 June 2002; American Society of Mechanical Engineers: New York, NY, USA, 2002; pp. 19–27. [Google Scholar]
- Li, Y.G. A gas turbine diagnostic approach with transient measurements. Proc. Inst. Mech. Eng. Part A J. Power Energy 2003, 217, 169–177. [Google Scholar] [CrossRef]
- Merrington, G.L. Fault Diagnosis of Gas Turbine Engine from Transient Data. J. Eng. Gas Turbine Power 1989, 111, 237–243. [Google Scholar] [CrossRef]
- Merrington, G.L. Identification of dynamic characteristics for fault isolation purposes in a gas turbine using closed-loop measurements. In Proceedings of the Advisory Group for Aerospace Research and Development (AGARD) Conference, Quebec, QC, Canada, 30 May–3 June 1988; Volume 36, pp. 1–13. [Google Scholar]
- Urban, L.A. Gas Turbine Engine Parameter Interrelationships; Hamilton Standard Division of United Aircraft Corporation: Hartford, Connecticut, 1969. [Google Scholar]
- Naderi, E.; Khorasani, K. Data-driven fault detection, isolation and estimation of aircraft gas turbine engine actuator and sensors. In Proceedings of the IEEE 30th Canadian Conference on Electrical and Computer Engineering (CCECE), Windsor, ON, Canada, 30 April–3 May 2017; pp. 1–6. [Google Scholar]
- Meher-Homji, C.B.; Bhargarva, R. Condition Monitoring and Diagnostic Aspects of Gas Turbine Transient Response. Int. J. Turbo Jet-Engines 1994, 11, 99–111. [Google Scholar] [CrossRef]
- Henry, J.R. CF-18/F404 transient performance trending. In Proceedings of the Advisory Group for Aerospace Research and Development (AGARD) Conference, Quebec, QC, Canada, 30 May–3 June 1988; Volume 37, pp. 1–13. [Google Scholar]
- Merrington, G.; Kwon, O.K.; Goodwin, G.; Carlsson, B. Fault detection and diagnosis in gas turbines. J. Eng. Gas Turbines Power 1991, 113, 276–282. [Google Scholar] [CrossRef]
- Simani, S.; Fantuzzi, C. Dynamic system identification and model-based fault diagnosis of an industrial gas turbine prototype. Mechatronics 2006, 16, 341–363. [Google Scholar] [CrossRef]
- Simani, S.; Patton, R.J. Fault diagnosis of an industrial gas turbine prototype using a system identification approach. Control Eng. Pract. 2008, 16, 769–786. [Google Scholar] [CrossRef]
- Lu, F.; Jiang, C.; Huang, J.; Wang, Y.; You, C. A novel data hierarchical fusion method for gas turbine engine performance fault diagnosis. Energies 2016, 9, 828. [Google Scholar] [CrossRef]
- Kim, J.H.; Song, T.W.; Kim, T.S.; Ro, S.T. Model development and simulation of transient behavior of heavy duty gas turbines. J. Eng. Gas Turbines Power 2001, 123, 589–594. [Google Scholar] [CrossRef]
- Schobeiri, M.T.; Attia, M.; Lippke, C. GETRAN: A generic, modularly structured computer code for simulation of dynamic behavior of aero-and power generation gas turbine engines. J. Eng. Gas Turbines Power 1994, 116, 483–494. [Google Scholar] [CrossRef]
- Muir, D.E.; Saravanamuttoo, H.I.H.; Marshall, D.J. Health monitoring of variable geometry gas turbines for the Canadian Navy. J. Eng. Gas Turbines Power 1989, 111, 244–250. [Google Scholar] [CrossRef]
- Blinstrub, J.; Li, Y.G.; Newby, M.; Zhou, Q.; Stigant, G.; Pilidis, P.; Hönen, H. Application of gas path analysis to compressor diagnosis of an industrial gas turbine using field data. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014; American Society of Mechanical Engineers: New York, NY, USA, 2014; p. V03AT07A008. [Google Scholar]
- Zhou, D.; Zhang, H.; Weng, S. A new gas path fault diagnostic method of gas turbine based on support vector machine. J. Eng. Gas Turbines Power 2015, 137, 102605. [Google Scholar] [CrossRef]
- Yang, X.; Deb, S. Cuckoo search via L’evy flights. In Proceedings of the IEEE World Congress on Nature & Biologically Inspired Computing. Piscataway, Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Civicioglu, P.; Besdok, E. A conceptual comparison of the Cuckoo-search, particle swarm optimization, differential evolution and artificial bee colony algorithms. Artif. Intell. Rev. 2011, 39, 315–346. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Engineering optimization by cuckoo search. Int. J. Math. Model. Numer. Optim. 2010, 1, 330–343. [Google Scholar]
- Nguyen, T.T.; Vo, D.N.; Dinh, B.H. Cuckoo search algorithm for combined heat and power economic dispatch. Int. J. Electr. Power Energy Syst. 2016, 81, 204–214. [Google Scholar] [CrossRef]
- Diakunchak, I.S. Performance deterioration in industrial gas turbines. J. Eng. Gas Turbines Power 1992, 114, 161–168. [Google Scholar] [CrossRef]
- Joly, R.B.; Ogaji, S.O.T.; Singh, R.; Probert, S.D. Gas-turbine diagnostics using artificial neural-networks for a high bypass ratio military turbofan engine. Appl. Energy 2004, 78, 397–418. [Google Scholar] [CrossRef]
- Mohammadi, E.; Montazeri-Gh, M. Simulation of full and part-load performance deterioration of industrial two-shaft gas turbine. J. Eng. Gas Turbines Power 2014, 136, 092602. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Pressure ratio | 24.1 |
| Exhaust mass flow | 84.31 kg/s |
| Power output | 31.4 MW |
| Efficiency of compressor | 85% |
| Measurement Parameter | Symbol |
|---|---|
| Rotational Speed | n1 |
| Discharge Temperature of Compressor | T2 |
| Discharge Pressure of Compressor | P2 |
| Discharge Temperature of High Pressure Turbine | T34 |
| Discharge pressure of High Pressure Turbine | P34 |
| Compressor efficiency degradation | DEC |
| Compressor flow rate degradation | DGC |
| High pressure turbine efficiency degradation | DET |
| High pressure turbine flow rate degradation | DGT |
| Power Turbine efficiency degradation | DEP |
| Power Turbine flow rate degradation | DGP |
| Time | Process | DGC | DEC | DGC/DEC | DGT | DET | DGT/DET | DGP | DEP |
|---|---|---|---|---|---|---|---|---|---|
| Before Washing | Steady-state | 5.79 | 1.70 | - | 4.85 | 2.03 | - | 0.88 | 1.53 |
| Transient process | 7.83 | 4.62 | - | 5.71 | 2.10 | - | 3.28 | 1.89 | |
| After Washing | Steady-state | 2.02 | 1.48 | - | 2.03 | 1.30 | - | −0.17 | 1.07 |
| Transient process | 1.54 | 1.41 | - | 2.56 | 1.42 | - | 2.95 | 1.76 | |
| Improvement | Steady-state | 3.77 | 0.29 | 13.0 | 2.82 | 0.73 | 3.86 | 1.05 | 0.44 |
| Transient process | 6.29 | 3.21 | 1.96 | 3.15 | 0.57 | 5.53 | 0.33 | 0.13 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, D.; Zhou, D.; Tan, C.; Jiang, B. Research on Model-Based Fault Diagnosis for a Gas Turbine Based on Transient Performance. Appl. Sci. 2018, 8, 148. https://doi.org/10.3390/app8010148
Zeng D, Zhou D, Tan C, Jiang B. Research on Model-Based Fault Diagnosis for a Gas Turbine Based on Transient Performance. Applied Sciences. 2018; 8(1):148. https://doi.org/10.3390/app8010148
Chicago/Turabian StyleZeng, Detang, Dengji Zhou, Chunqing Tan, and Baoyang Jiang. 2018. "Research on Model-Based Fault Diagnosis for a Gas Turbine Based on Transient Performance" Applied Sciences 8, no. 1: 148. https://doi.org/10.3390/app8010148
APA StyleZeng, D., Zhou, D., Tan, C., & Jiang, B. (2018). Research on Model-Based Fault Diagnosis for a Gas Turbine Based on Transient Performance. Applied Sciences, 8(1), 148. https://doi.org/10.3390/app8010148




