Incoherent Digital Holography: A Review
Abstract
:1. Introduction
2. Principle of OSH
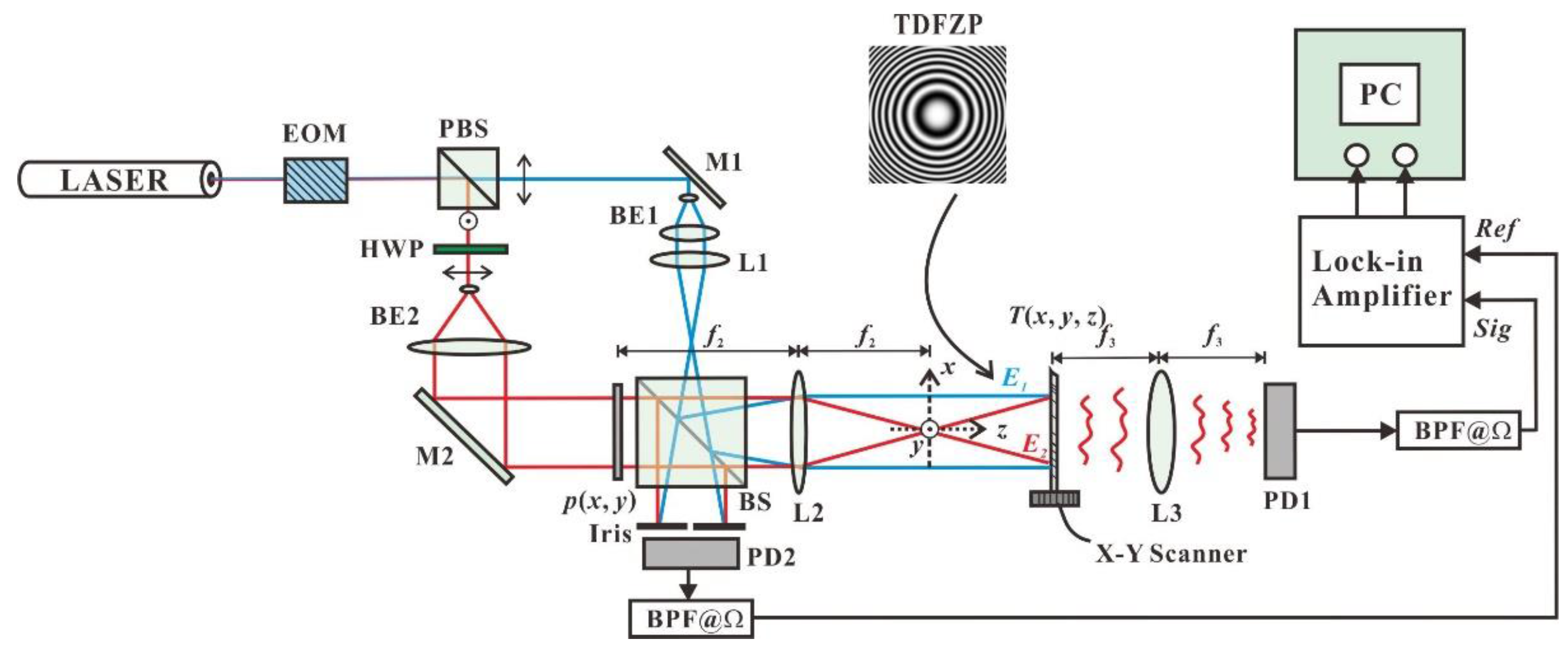
2.1. Setup of OSH
2.2. Mathematical Model of OSH
2.3. Point Spread Function and Pupil Engineering
3. Principle of FINCH
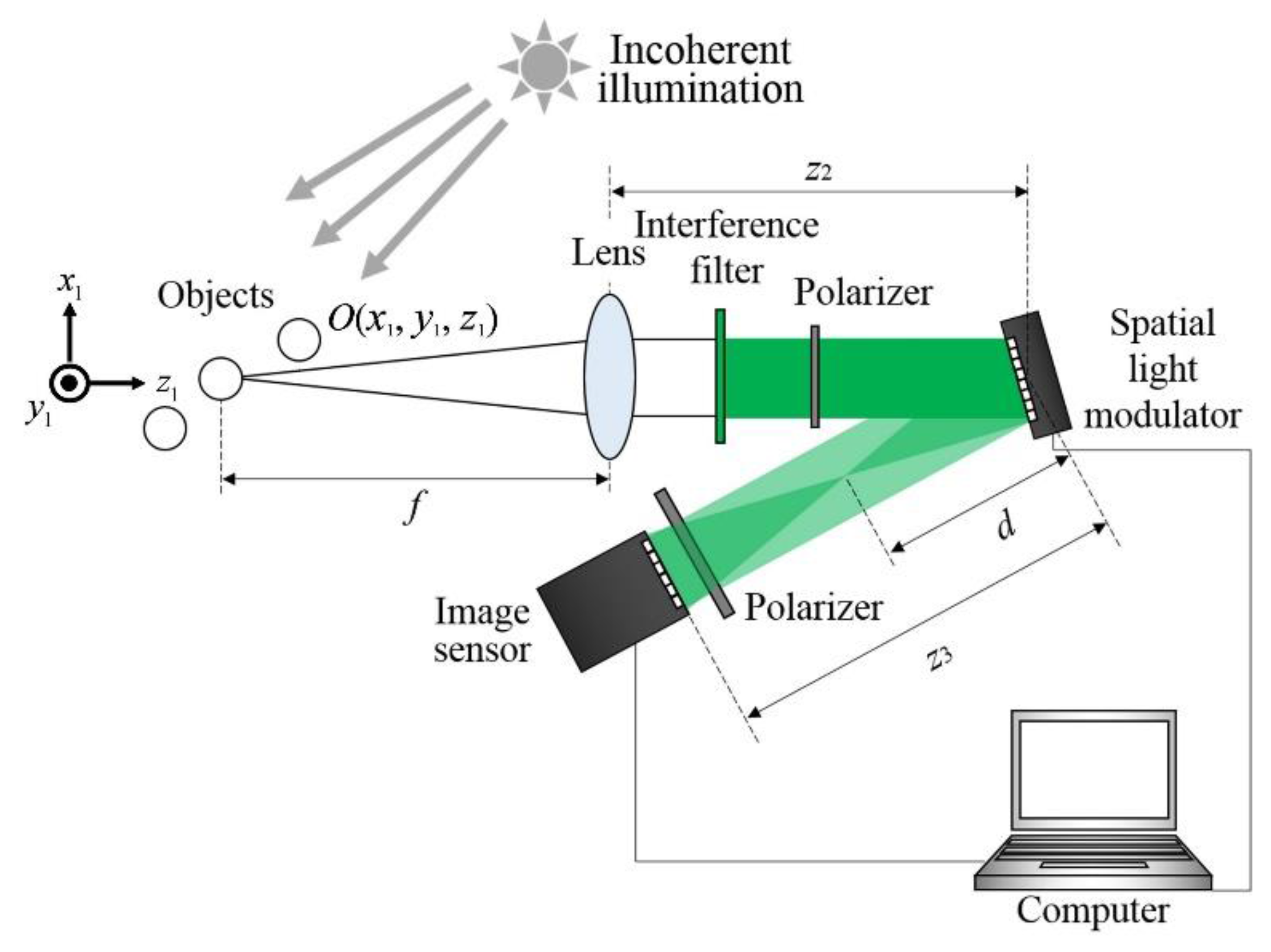
3.1. Setup of FINCH
3.2. Mathematical Model of FINCH
3.3. Point Spread Function
4. Special Topics and Applications
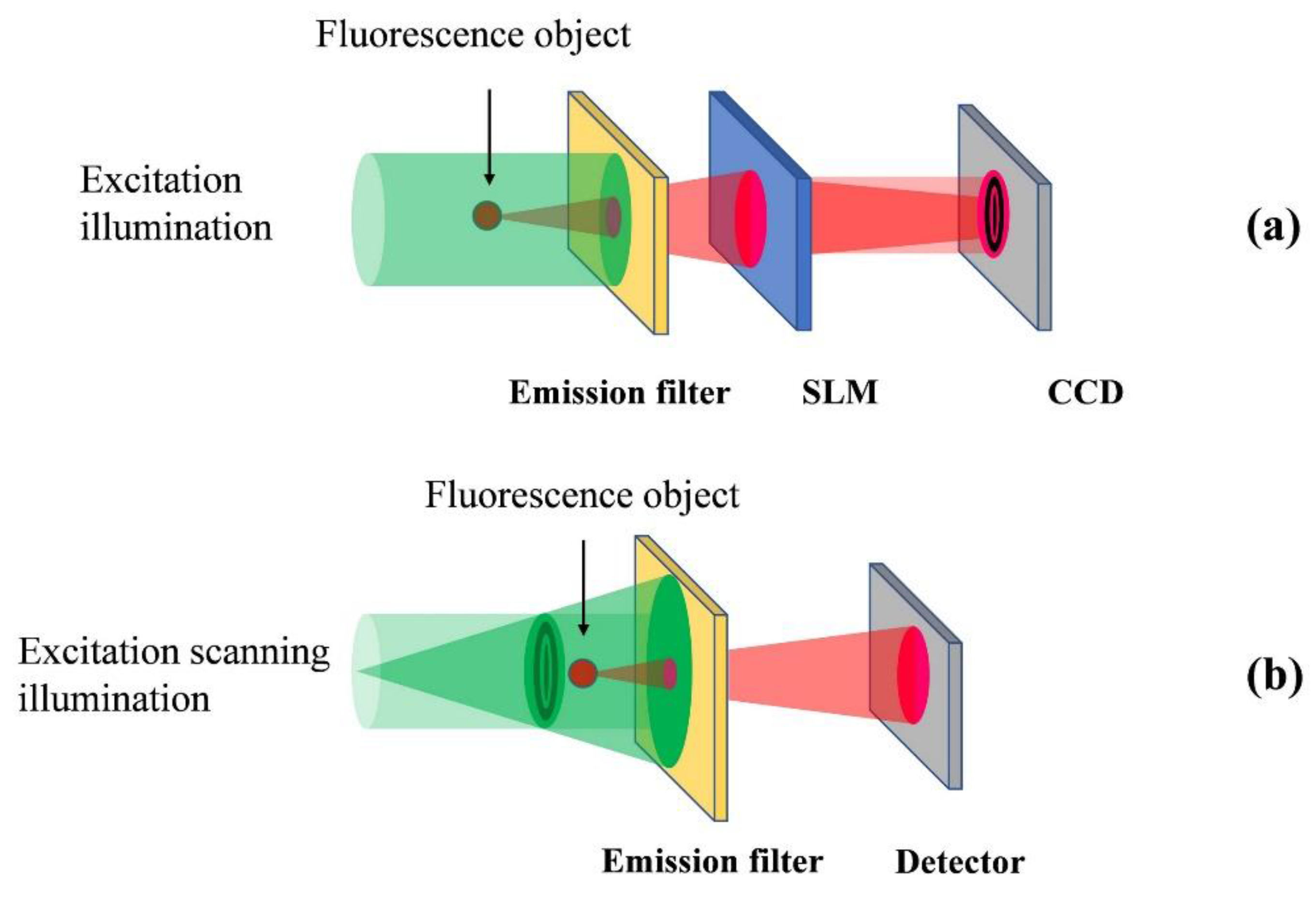
4.1. Fluorescence Holography
4.2. Optical Display of Incoherent Hologram
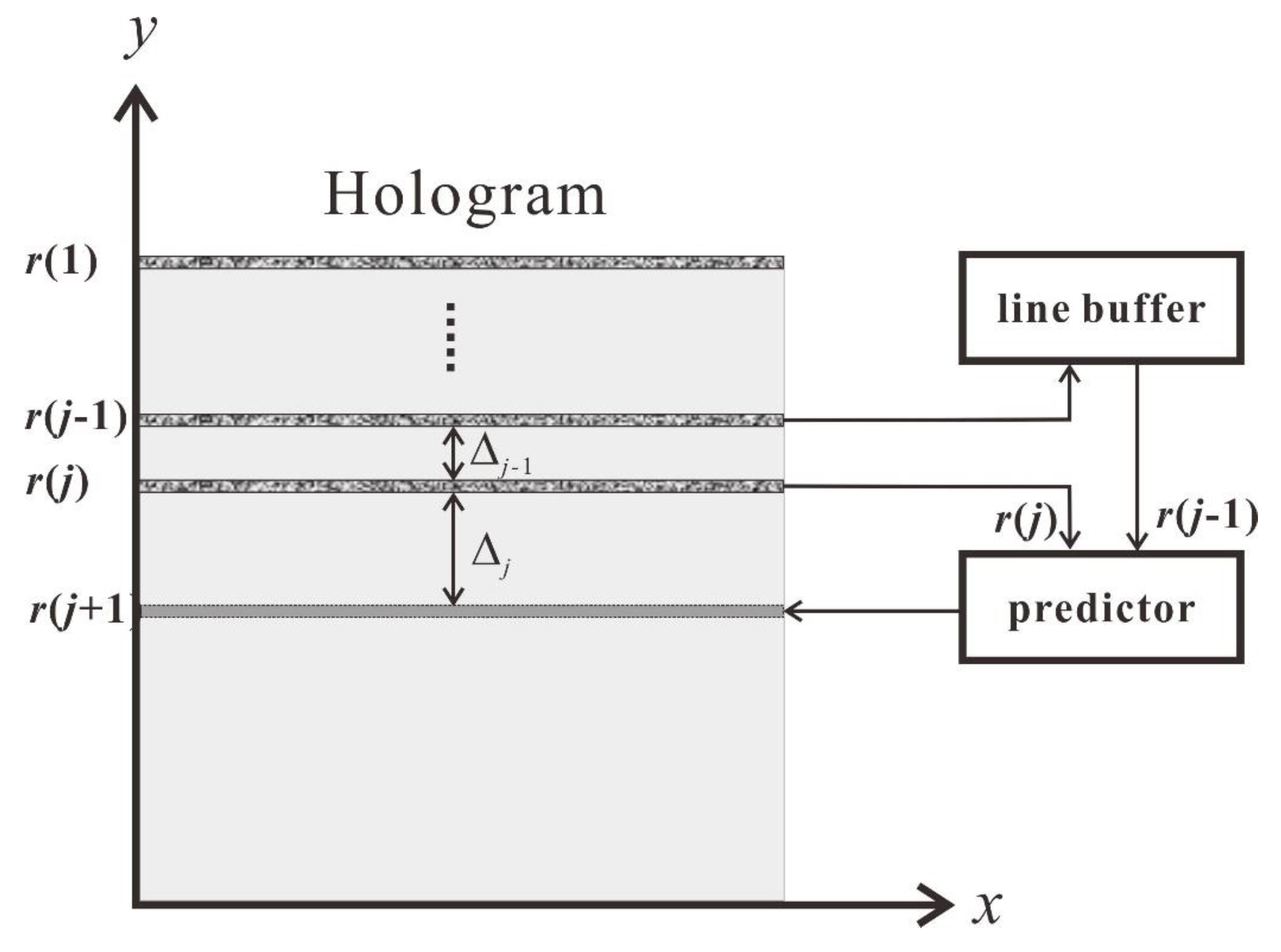
4.3. Reduction of Scanning Speed and Recorded Data in OSH
4.4. Single-Shot Imager for the Aim of Capturing High-Speed Incoherent 3D Objects
4.5. Coded Aperture Correlation Holography (COACH)
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Watanabe, T.M.; Sato, T.; Gonda, K.; Higuchi, H. Three-dimensional nanometry of vesicle transport in living cells using dual-focus imaging optics. Biochem. Biophys. Res. Commun. 2007, 359, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Tanida, J.; Kumagai, T.; Yamda, K.; Miyatake, S.; Ishida, K.; Morimoto, T.; Kondou, N.; Miyazaki, D.; Ichioka, Y. Thin observation module by bound optics (TOMBO), concept and experimrntalverification. Appl. Opt. 2001, 40, 1806–1819. [Google Scholar] [CrossRef] [PubMed]
- Ozeki, Y.; Umemura, W.; Otsuka, Y.; Satoh, S.; Hashimoto, H.; Sumimura, K.; Nishizawa, N.; Fukui, K.; Itoh, K. High-speed molecular spectral imaging of tissue with stimulated raman scattering. Nat. Photonics 2012, 6, 845–851. [Google Scholar] [CrossRef]
- Horisaki, R.; Ogura, Y.; Aino, M.; Tanida, J. Single-shot phase imaging with a coded aperture. Opt. Lett. 2014, 39, 6466–6469. [Google Scholar] [CrossRef] [PubMed]
- Gabor, D. A new microscopic principle. Nature 1948, 161, 777–778. [Google Scholar] [CrossRef] [PubMed]
- Poon, T.-C. Digital Holography and Three-Dimensional Display; Springer: Berlin, Germany, 2006. [Google Scholar]
- Poon, T.-C.; Liu, J.-P. Introduction to Modern Digital Holography with MATLAB®; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Indebetouw, G.; Klysubun, P. Imaging through scattering media with depth resolution by use of low-coherence gating in spatiotemporal digital holography. Opt. Lett. 2000, 25, 212–214. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.-C.; Cheng, C.-J.; Poon, T.-C. Optical sectioning with a low-coherence phase-shifting digital holographic microscope. Appl. Opt. 2011, 50, B25–B30. [Google Scholar] [CrossRef] [PubMed]
- Pham, Q.D.; Hasegawa, S.; Kiire, T.; Barada, D.; Yatagai, T.; Hayasaki, Y. Selectable-wavelength low-coherence digital holography with chromatic phase shifter. Opt. Express 2012, 20, 19744–19756. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.S.G.; Schmoll, T.; Javidi, B.; Leitgeb, R.A. In-line reference-delayed digital holography using a low-coherence light source. Opt. Lett. 2012, 37, 2631–2633. [Google Scholar] [CrossRef] [PubMed]
- Monemhaghdoust, Z.; Montfort, F.; Cuche, E.; Emery, Y.; Depeursinge, C.; Moser, C. Full field vertical scanning in short coherence digital holographic microscope. Opt. Express 2013, 21, 12643–12650. [Google Scholar] [CrossRef] [PubMed]
- Poon, T.-C. Optical Scanning Holography with Matlab; Springer: NewYork, NY, USA, 2007. [Google Scholar]
- Poon, T.-C.; Korpel, A. Optical transfer function of an acousto-optic heterodyning image processor. Opt. Lett. 1979, 4, 317–319. [Google Scholar] [CrossRef] [PubMed]
- Poon, T.-C. Method of two-dimensional bipolar incoherent image processing by acousto-optic two-pupil synthesis. Opt. Lett. 1985, 10, 197–199. [Google Scholar] [CrossRef] [PubMed]
- Poon, T.-C. Scanning holography and two-dimensional image processing by acousto-optic two-pupil synthesis. J. Opt. Soc. Am. A 1985, 2, 521–527. [Google Scholar] [CrossRef]
- Klysubun, P.; Indebetouw, G.; Kim, T.; Poon, T.-C. Accuracy of three-dimensional remote target location using scanning holographic correlation. Opt. Commun. 2000, 184, 357–366. [Google Scholar] [CrossRef]
- Kim, T.; Poon, T.-C.; Indebetouw, G. Depth detection and image recovery in remote sensing by optical scanning holography. Opt. Eng. 2002, 41, 1331–1338. [Google Scholar]
- Poon, T.-C.; Kim, T.; Doh, K. Optical scanning cryptography for secure wireless transmission. Appl. Opt. 2003, 42, 6496–6503. [Google Scholar] [CrossRef] [PubMed]
- Yan, A.; Poon, T.-C.; Hu, Z.; Zhang, J. Optical image encryption using optical scanning and fingerprint keys. J. Mod. Opt. 2016, 63, S38–S43. [Google Scholar] [CrossRef]
- Yan, A.; Wei, Y.; Hu, Z.; Zhang, J.; Tsang, P.W.M.; Poon, T.-C. Optical cryptography with biometrics for multi-depth objects. Sci. Rep. 2017, 7, 12933. [Google Scholar] [CrossRef] [PubMed]
- Schilling, B.W.; Poon, T.-C.; Indebetouw, G.; Storrie, B.; Shinoda, K.; Suzuki, Y.; Wu, M.H. Three-dimensional holographic fluorescence microscopy. Opt. Lett. 1997, 22, 1506–1508. [Google Scholar] [CrossRef] [PubMed]
- Indebetouw, G.; El Maghnouji, A.; Foster, R. Scanning holographic microscopy with transverse resolution exceeding the Rayleigh limit and extended depth of focus. J. Opt. Soc. Am. A 2005, 22, 892–898. [Google Scholar] [CrossRef]
- Indebetouw, G. A posteriori quasi-sectioning of the three-dimensional reconstructions of scanning holographic microscopy. J. Opt. Soc. Am. A 2006, 23, 2657–2661. [Google Scholar] [CrossRef]
- Indebetouw, G.; Tada, Y.; Leacock, J. Quantitative phase imaging with scanning holographic microscopy: An experimental assesment. Biomed. Eng. Online 2006, 5, 63. [Google Scholar] [CrossRef] [PubMed]
- Indebetouw, G.; Zhong, W. Scanning holographic microscopy of three-dimensional fluorescent specimens. J. Opt. Soc. Am. A 2006, 23, 1699–1707. [Google Scholar] [CrossRef]
- Indebetouw, G.; Tada, Y.; Rosen, J.; Brooker, G. Scanning holographic microscopy with resolution exceeding the Rayleigh limit of the objective by superposition of off-axis holograms. Appl. Opt. 2007, 46, 993–1000. [Google Scholar] [CrossRef] [PubMed]
- Lam, E.Y.; Zhang, X.; Vo, H.; Poon, T.-C.; Indebetouw, G. Three-dimensional microscopy and sectional image reconstruction using optical scanning holography. Appl. Opt. 2009, 48, H113–H119. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.-P.; Luo, D.-Z.; Lu, S.-H. Spatial–temporal demodulation technique for heterodyne optical scanning holography. Opt. Lasers Eng. 2015, 68, 42–49. [Google Scholar] [CrossRef]
- Liu, J.-P.; Wang, S.-Y. Stereo-lighting reconstruction of optical scanning holography. IEEE Trans. Ind. Inform. 2016, 12, 1664–1669. [Google Scholar] [CrossRef]
- Liu, J.-P.; Wang, S.-Y.; Tsang, P.W.M.; Poon, T.-C. Nonlinearity compensation and complex-to-phase conversion of complex incoherent digital holograms for optical reconstruction. Opt. Express 2016, 24, 14582–14588. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.S.; Kim, T.; Woo, S.S.; Kang, H.; Poon, T.-C.; Zhou, C. Speckle-free digital holographic recording of a diffusely reflecting object. Opt. Express 2013, 21, 8183–8189. [Google Scholar] [CrossRef] [PubMed]
- Rosen, J.; Brooker, G. Digital spatially incoherent fresnel holography. Opt. Lett. 2007, 32, 912–914. [Google Scholar] [CrossRef] [PubMed]
- Rosen, J.; Brooker, G. Fluorescence incoherent color holography. Opt. Express 2007, 15, 2244–2250. [Google Scholar] [CrossRef] [PubMed]
- Rosen, J.; Brooker, G. Non-scanning motionless fluorescence three-dimensional holographic microscopy. Nat. Photonics 2008, 2, 190–195. [Google Scholar] [CrossRef]
- Brooker, G.; Siegel, N.; Wang, V.; Rosen, J. Optimal resolution in fresnel incoherent correlation holographic fluorescence microscopy. Opt. Express 2011, 19, 5047–5062. [Google Scholar] [CrossRef] [PubMed]
- Rosen, J.; Siegel, N.; Brooker, G. Theoretical and experimental demonstration of resolution beyond the Rayleigh limit by finch fluorescence microscopic imaging. Opt. Express 2011, 19, 26249–26268. [Google Scholar] [CrossRef] [PubMed]
- Siegel, N.; Lupashin, V.; Storrie, B.; Brooker, G. High-magnification super-resolution finch microscopy using birefringent crystal lens interferometers. Nat. Photonics 2016, 10, 802–808. [Google Scholar] [CrossRef] [PubMed]
- Bryngdahl, O.; Lohmann, A. One-dimensional holography with spatially incoherent light. J. Opt. Soc. Am. 1968, 58, 625–628. [Google Scholar] [CrossRef]
- Itoh, K.; Inoue, T.; Yoshida, T.; Ichioka, Y. Interferometric supermultispectral imaging. Appl. Opt. 1990, 29, 1625–1630. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.K. Full color natural light holographic camera. Opt. Express 2013, 21, 9636–9642. [Google Scholar] [CrossRef] [PubMed]
- Yanagawa, T.; Abe, R.; Hayasaki, Y. Three-dimensional mapping of fluorescent nanoparticles using incoherent digital holography. Opt. Lett. 2015, 40, 3312–3315. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, K.; Nomura, T. Recording spatially incoherent fourier hologram using dual channel rotational shearing interferometer. Appl. Opt. 2015, 54, A18–A22. [Google Scholar] [CrossRef] [PubMed]
- Obara, M.; Yoshimori, K. 3D spatial resolution and spectral resolution of interferometric 3D imaging spectrometry. Appl. Opt. 2016, 55, 2489–2497. [Google Scholar] [CrossRef] [PubMed]
- Naik, D.N.; Pedrini, G.; Takeda, M.; Osten, W. Spectrally resolved incoherent holography: 3D spatial and spectral imaging using a mach-zehnder radial-shearing interferometer. Opt. Lett. 2014, 39, 1857–1860. [Google Scholar] [CrossRef] [PubMed]
- Wan, Y.; Man, T.; Wang, D. Incoherent off-axis Fourier triangular color holography. Opt. Express 2014, 22, 8565–8573. [Google Scholar] [CrossRef] [PubMed]
- Lohmann, A.W. Wavefront reconstruction for incoherent objects. J. Opt. Soc. Am. 1965, 55, 1555_1-1556. [Google Scholar] [CrossRef]
- Sirat, G.; Psaltis, D. Conoscopic holography. Opt. Lett. 1985, 10, 4–6. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Kim, Y.S.; Kim, T. Full-color optical scanning holography with common red, green, and blue channels [invited]. Appl. Opt. 2016, 55, A17–A21. [Google Scholar] [CrossRef] [PubMed]
- Poon, T.-C.; Kim, T.; Indebetouw, G.; Schilling, B.W.; Wu, M.H.; Shinoda, K.; Suzuki, Y. Twin-image elimination experiments for three-dimensional images in optical scanning holography. Opt. Lett. 2000, 25, 215–217. [Google Scholar] [CrossRef] [PubMed]
- Rosen, J.; Indebetouw, G.; Brooker, G. Homodyne scanning holography. Opt. Express 2006, 14, 4280–4285. [Google Scholar] [CrossRef] [PubMed]
- Swoger, J.; Martinez-Corral, M.; Huisken, J.; Stelzer, E.H.K. Optical scanning holography as a technique for high-resolution three-dimensional biological microscopy. J. Opt. Soc. Am. A 2002, 19, 1910–1918. [Google Scholar] [CrossRef]
- Poon, T.-C.; Indebetouw, G. Three-dimensional point spread functions of an optical heterodyne scanning image processor. Appl. Opt. 2003, 42, 1485–1492. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.-P. Spatial coherence analysis for optical scanning holography. Appl. Opt. 2015, 54, A59–A66. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.-P.; Guo, C.-H.; Hsiao, W.-J.; Poon, T.-C.; Tsang, P.W.M. Coherence experiments in single-pixel digital holography. Opt. Lett. 2015, 40, 2366–2369. [Google Scholar] [CrossRef] [PubMed]
- Indebetouw, G.; Klysubun, P.; Kim, T.; Poon, T.-C. Imaging properties of scanning holographic microscopy. J. Opt. Soc. Am. A 2000, 17, 380–390. [Google Scholar] [CrossRef]
- Tsang, P.W.M.; Liu, J.-P.; Poon, T.-C. Compressive optical scanning holography. Optica 2015, 2, 476–483. [Google Scholar] [CrossRef]
- Chen, N.; Ren, Z.; Ou, H.; Lam, E.Y. Resolution enhancement of optical scanning holography with a spiral modulated point spread function. Photonics Res. 2016, 4, 1–6. [Google Scholar] [CrossRef]
- Pan, Y.; Jia, W.; Yu, J.; Dobson, K.; Zhou, C.; Wang, Y.; Poon, T.-C. Edge extraction using a time-varying vortex beam in incoherent digital holography. Opt. Lett. 2014, 39, 4176–4179. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.-P.; Lee, C.-C.; Lo, Y.-H.; Luo, D.-Z. Vertical-bandwidth-limited digital holography. Opt. Lett. 2012, 37, 2574–2576. [Google Scholar] [CrossRef] [PubMed]
- Xin, Z.; Dobson, K.; Shinoda, Y.; Poon, T.-C. Sectional image reconstruction in optical scanning holography using a random-phase pupil. Opt. Lett. 2010, 35, 2934–2936. [Google Scholar] [CrossRef] [PubMed]
- Indebetouw, G.; Zhong, W.; Chamberlin-Long, D. Point-spread function synthesis in scanning holographic microscopy. J. Opt. Soc. Am. A 2006, 23, 1708–1717. [Google Scholar] [CrossRef]
- Ou, H.; Poon, T.-C.; Wong, K.K.Y.; Lam, E.Y. Enhanced depth resolution in optical scanning holography using a configurable pupil. Photonics Res. 2014, 2, 64–70. [Google Scholar] [CrossRef]
- Poon, T.-C.; Doh, K.B. On the theory of optical Hilbert transform for incoherent object. Opt. Express 2007, 15, 3006–3011. [Google Scholar] [CrossRef] [PubMed]
- Bruning, J.H.; Herriott, D.R.; Gallagher, J.; Rosenfeld, D.; White, A.; Brangaccio, D. Digital wavefront measuring interferometer for testing optical surfaces and lenses. Appl. Opt. 1974, 13, 2693–2703. [Google Scholar] [CrossRef] [PubMed]
- Yamaguchi, I.; Zhang, T. Phase-shifting digital holography. Opt. Lett. 1997, 22, 1268–1270. [Google Scholar] [CrossRef] [PubMed]
- Tahara, T.; Mori, R.; Arai, Y.; Takaki, Y. Four-step phase-shifting digital holography simultaneously sensing dual-wavelength information using a monochromatic image sensor. J. Opt. 2015, 17, 125707. [Google Scholar] [CrossRef]
- Rosen, J.; Kelner, R. Modified lagrange invariants and their role in determining transverse and axial imaging resolutions of self-interference incoherent holographic systems. Opt. Express 2014, 22, 29048–29066. [Google Scholar] [CrossRef] [PubMed]
- Indebetouw, G.; Kim, T.; Poon, T.-C.; Schilling, B.W. Three-dimensional location of fluorescent inhomogeneities in turbid media by scanning heterodyne holography. Opt. Lett. 1998, 23, 135–137. [Google Scholar] [CrossRef] [PubMed]
- Abe, R.; Hayasaki, Y. Holographic fluorescence mapping using space-division matching method. Opt. Commun. 2017, 401, 35–39. [Google Scholar] [CrossRef]
- Leportier, T.; Park, M.C.; Kim, Y.S.; Kim, T. Converting optical scanning holograms of real objects to binary fourier holograms using an iterative direct binary search algorithm. Opt. Express 2015, 23, 3403–3411. [Google Scholar] [CrossRef] [PubMed]
- Tsang, P.W.M.; Poon, T.-C.; Liu, J.-P. Adaptive optical scanning holography. Sci. Rep. 2016, 6, 21636. [Google Scholar] [CrossRef] [PubMed]
- Tsang, P.W.M.; Poon, T.-C.; Liu, J.-P.; Kim, T.; Kim, Y.S. Low complexity compression and speed enhancement for optical scanning holography. Sci. Rep. 2016, 6, 34724. [Google Scholar] [CrossRef] [PubMed]
- Chan, A.C.S.; Tsia, K.K.; Lam, E.Y. Subsampled scanning holographic imaging (SuSHI) for fast, non-adaptive recording of three-dimensional objects. Optica 2016, 3, 911–917. [Google Scholar] [CrossRef]
- Kelner, R.; Rosen, J. Spatially incoherent single channel digital fourier holography. Opt. Lett. 2012, 37, 3723–3725. [Google Scholar] [CrossRef] [PubMed]
- Hong, J.; Kim, M.K. Single-shot self-interference incoherent digital holography using off-axis configuration. Opt. Lett. 2013, 38, 5196–5199. [Google Scholar] [CrossRef] [PubMed]
- Quan, X.; Matoba, O.; Awatsuji, Y. Single-shot incoherent digital holography using a dual-focusing lens with diffraction gratings. Opt. Lett. 2017, 42, 383–386. [Google Scholar] [CrossRef] [PubMed]
- Tahara, T.; Arai, Y. Hologram Recording Apparatus and Hologram Recording Method. Japanese Patent Application P2013-127829, 18 June 2013. [Google Scholar]
- Tahara, T.; Kanno, T.; Arai, Y.; Ozawa, T. Single-shot phase-shifting incoherent digital holography. J. Opt. 2017, 19, 065705. [Google Scholar] [CrossRef]
- Vijayakumar, A.; Kashter, Y.; Kelner, R.; Rosen, J. Coded aperture correlation holography—A new type of incoherent digital holograms. Opt. Express 2016, 24, 12430–12441. [Google Scholar] [CrossRef] [PubMed]
- Vijayakumar, A.; Rosen, J. Spectrum and space resolved 4D imaging by coded aperture correlation holography (COACH) with diffractive objective lens. Opt. Lett. 2017, 42, 947–950. [Google Scholar] [CrossRef] [PubMed]
- Tahara, T.; Otani, R.; Omae, K.; Gotohda, T.; Arai, Y.; Takaki, Y. Multiwavelength digital holography with wavelength-multiplexed holograms and arbitrary symmetric phase shifts. Opt. Express 2017, 25, 11157–11172. [Google Scholar] [CrossRef] [PubMed]
- Vijayakumar, A.; Rosen, J. Interferenceless coded aperture correlation holography—A new technique for recording incoherent digital holograms without two-wave interference. Opt. Express 2017, 25, 13883–13896. [Google Scholar] [CrossRef] [PubMed]
- Ratnam Rai, M.; Vijayakumar, A.; Rosen, J. Single camera shot interferenceless coded aperture correlation holography. Opt. Lett. 2017, 42, 3992–3995. [Google Scholar] [CrossRef] [PubMed]
- Poon, T.-C. Scan-free three-dimensional imaging. Nat. Photonics 2008, 2, 131–132. [Google Scholar] [CrossRef]





| OSH | FINCH | |
|---|---|---|
| 1. Field of view | Large 1 | Small |
| 2. Pixel pitch | Very small 1 | Small |
| 3. System variety 2 | High | Low |
| 4. Recording time | Slow | Fast |
| 5. Imaging by natural light | No 3 | Yes 4 |
| 6. System complexity | High | Low |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.-P.; Tahara, T.; Hayasaki, Y.; Poon, T.-C. Incoherent Digital Holography: A Review. Appl. Sci. 2018, 8, 143. https://doi.org/10.3390/app8010143
Liu J-P, Tahara T, Hayasaki Y, Poon T-C. Incoherent Digital Holography: A Review. Applied Sciences. 2018; 8(1):143. https://doi.org/10.3390/app8010143
Chicago/Turabian StyleLiu, Jung-Ping, Tatsuki Tahara, Yoshio Hayasaki, and Ting-Chung Poon. 2018. "Incoherent Digital Holography: A Review" Applied Sciences 8, no. 1: 143. https://doi.org/10.3390/app8010143
APA StyleLiu, J.-P., Tahara, T., Hayasaki, Y., & Poon, T.-C. (2018). Incoherent Digital Holography: A Review. Applied Sciences, 8(1), 143. https://doi.org/10.3390/app8010143





