Effects of Order of Expansion for the Exponential Matrix and Number of Mathematical Layers in the Exact 3D Static Analysis of Functionally Graded Plates and Shells
Abstract
:1. Introduction
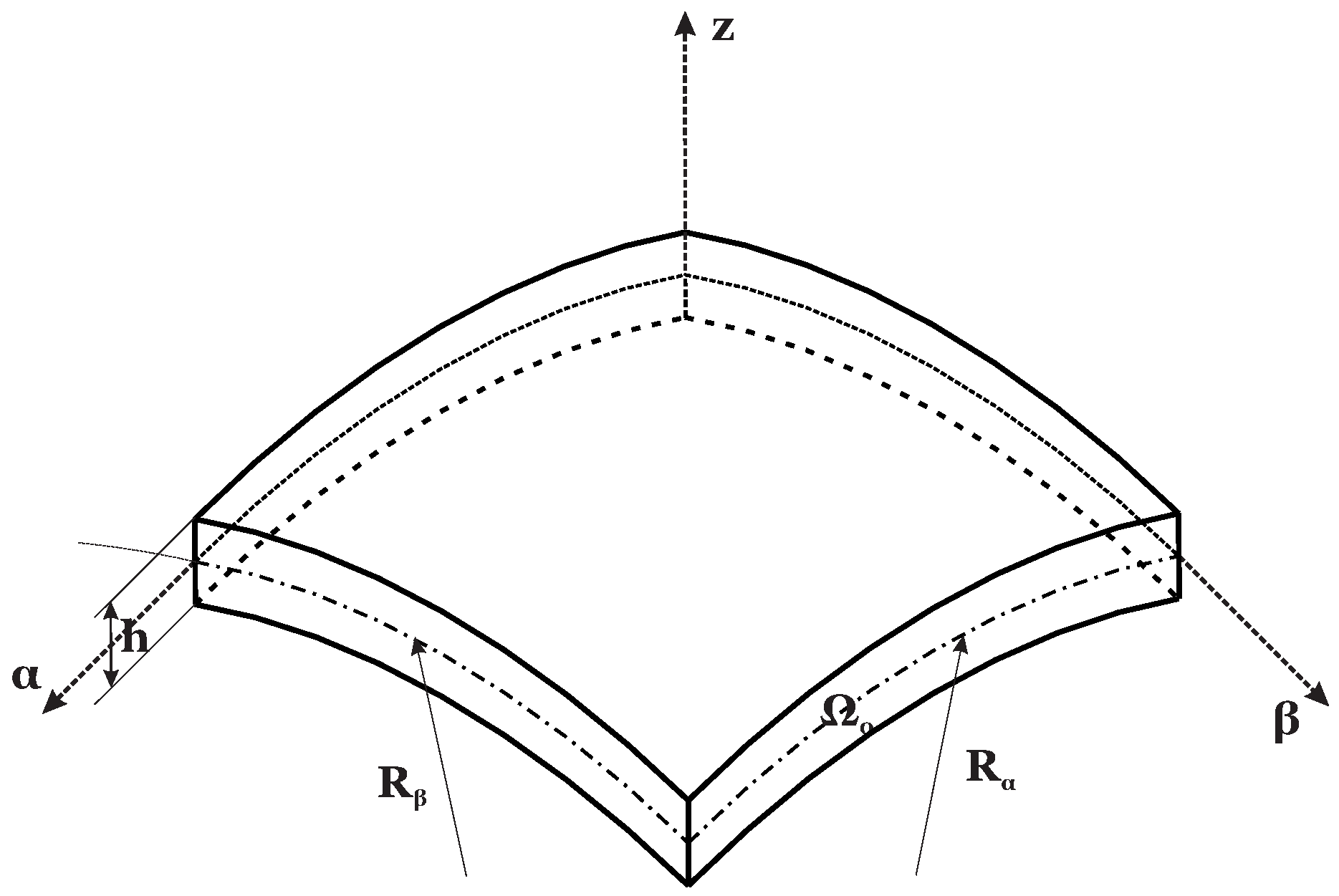
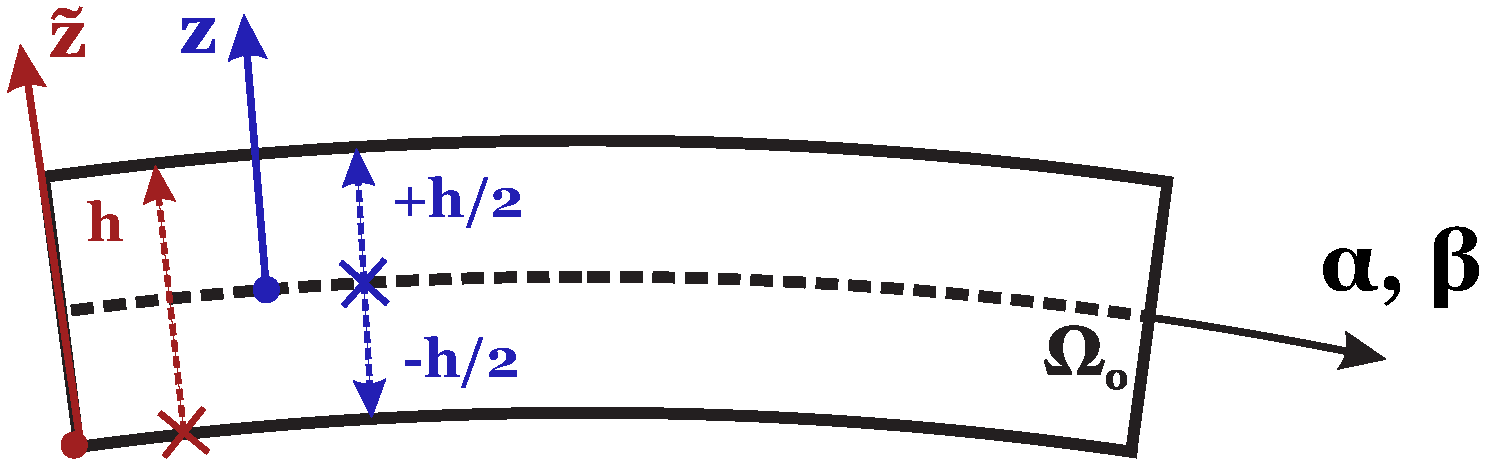
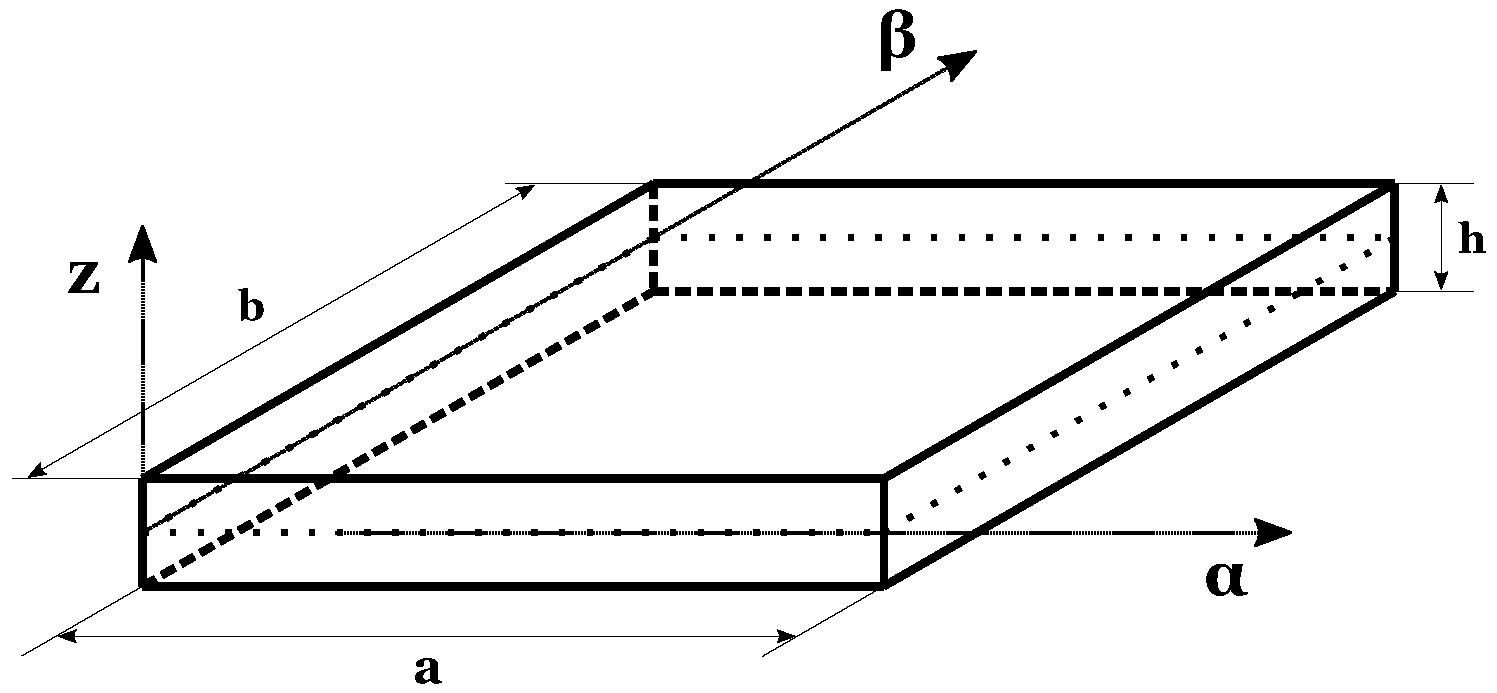
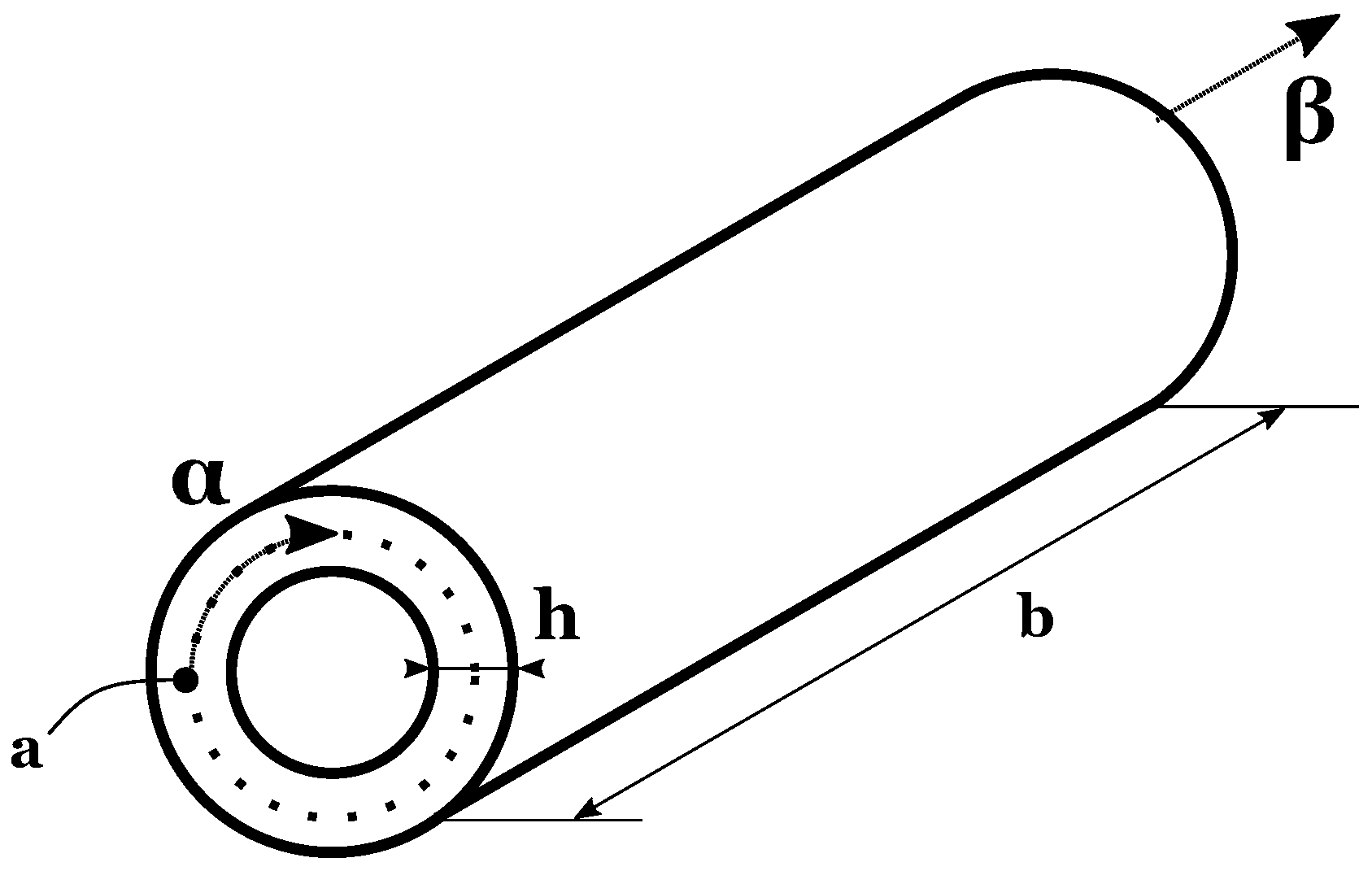
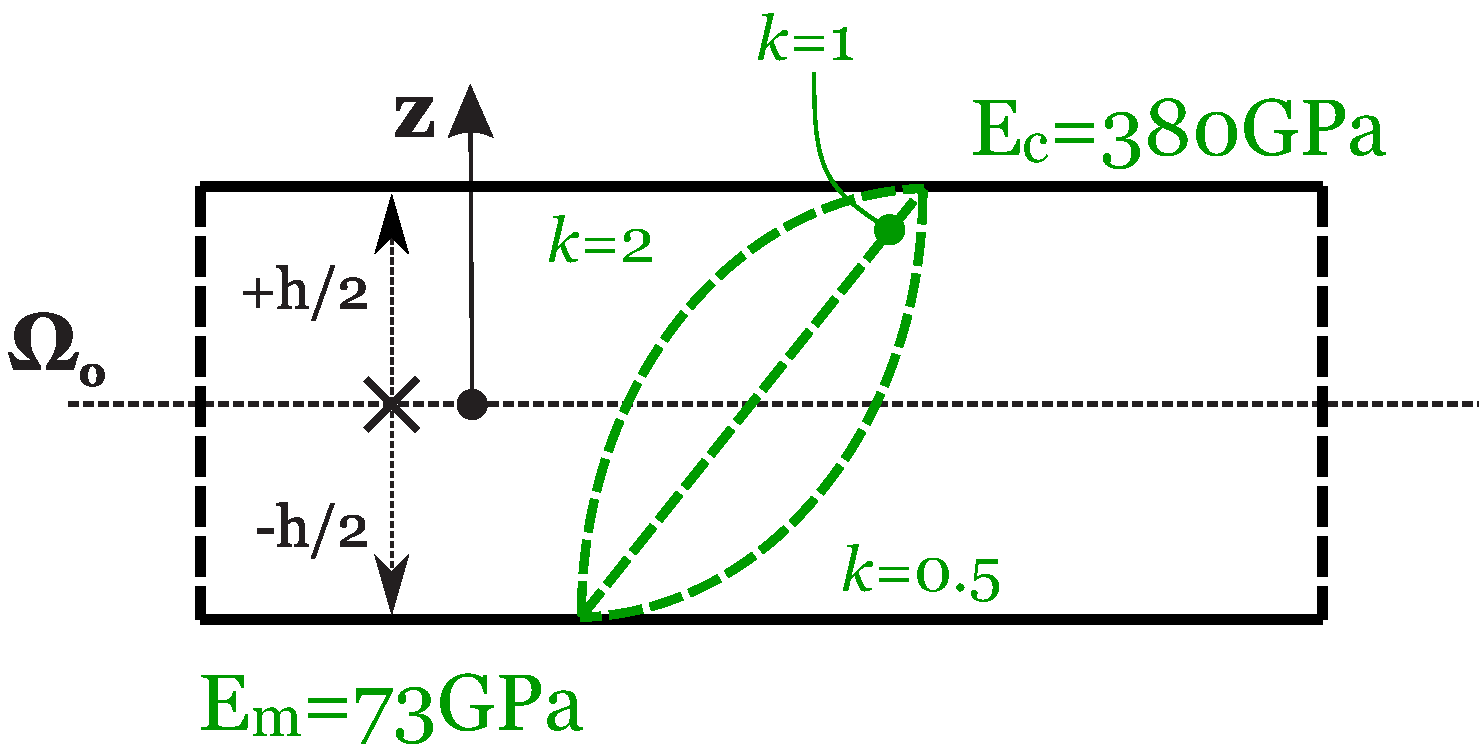
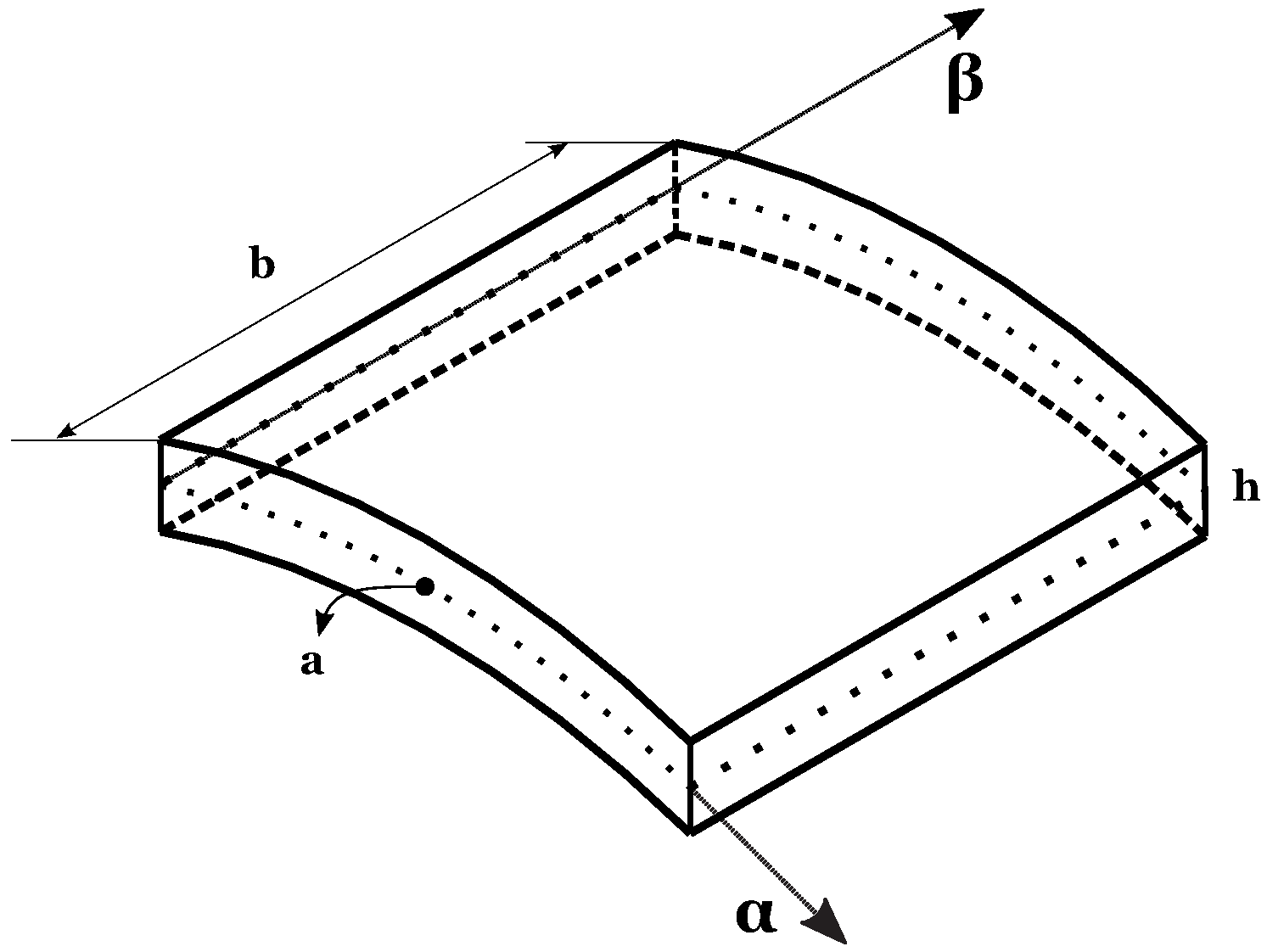
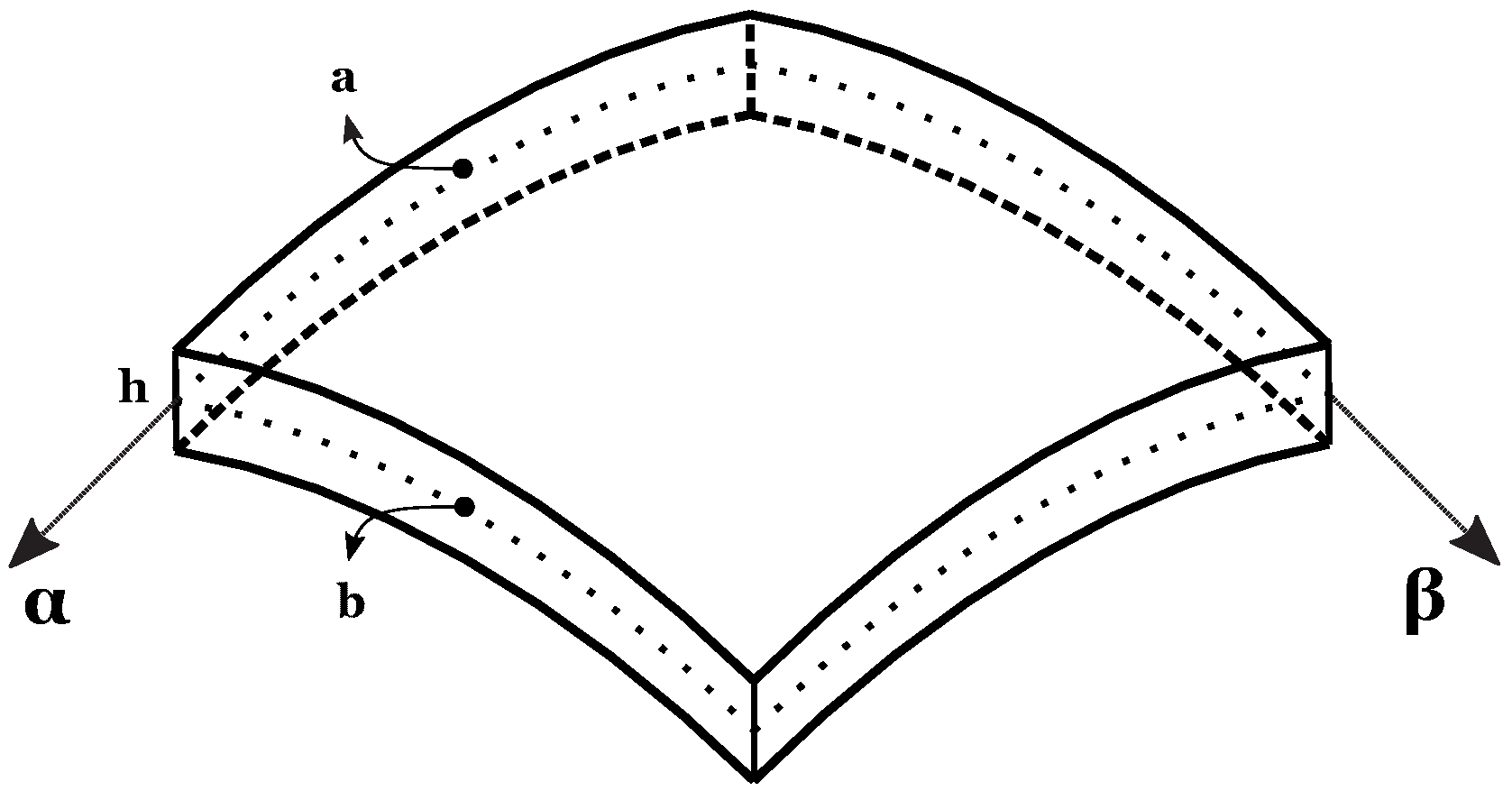
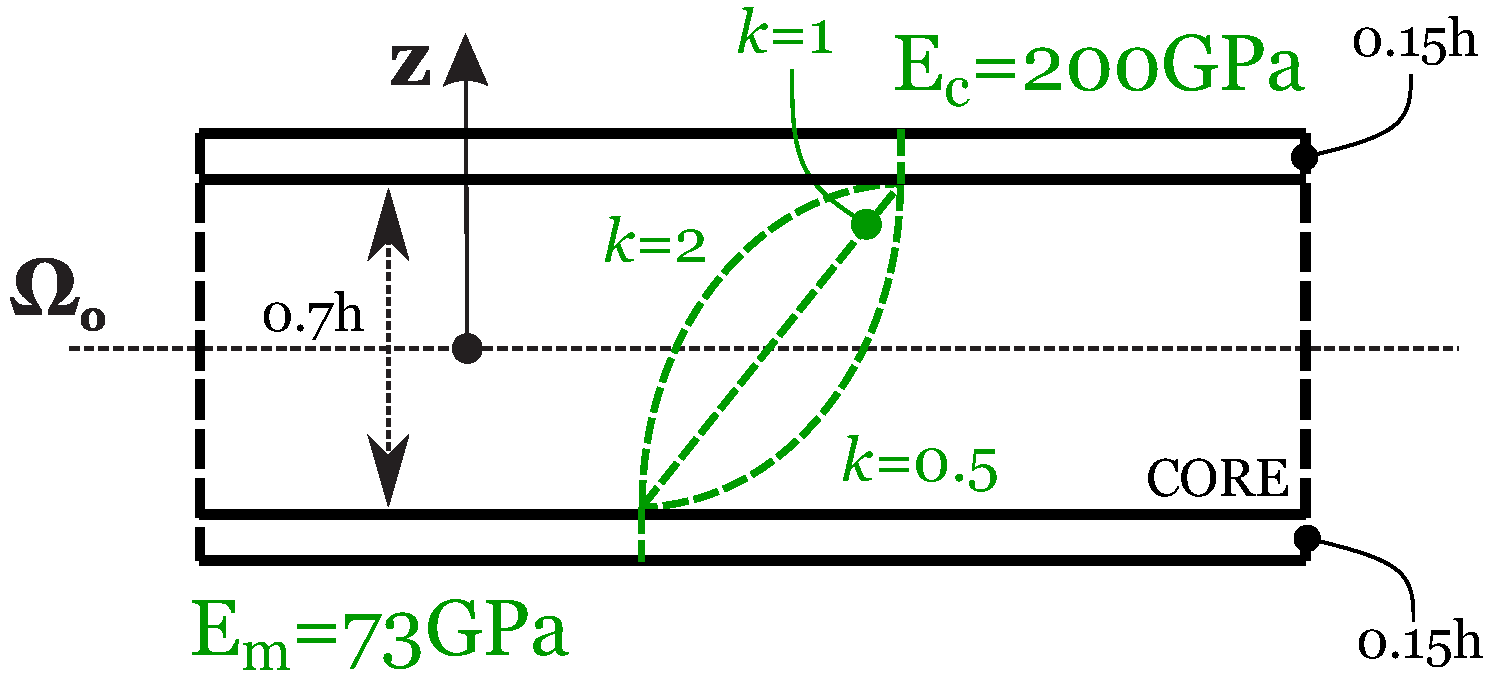
2. 3D Exact Static Analysis of FGM Structures
3. Results
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Wessel, J.K. The Handbook of Advanced Materials; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Mahamood, R.M.; Akinlabi, E.T. Functionally Graded Materials; Springer: Heidelberg, Germany, 2017. [Google Scholar]
- Ichikawa, K. Functionally Graded Materials in the 21st Century; Springer: Heidelberg, Germany, 2001. [Google Scholar]
- Kashtalyan, M. Three-dimensional elasticity solution for bending of functionally graded rectangular plates. Eur. J. Mech. 2004, 23, 853–864. [Google Scholar] [CrossRef]
- Plevako, V.P. On the theory of elasticity of inhomogeneous media. J. Appl. Math. Mech. 1971, 35, 806–813. [Google Scholar] [CrossRef]
- Vel, S.S.; Batra, R.C. Three-dimensional exact solution for the vibration of functionally graded rectangular plates. J. Sound Vib. 2004, 272, 703–730. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, D. Three-dimensional elasticity solution of functionally graded rectangular plates with variable thickness. Compos. Struct. 2009, 91, 56–65. [Google Scholar] [CrossRef]
- Yas, M.H.; Tahouneh, V. 3-D Free vibration analysis of thick functionally graded annular plates on Pasternak elastic foundation via differential quadrature method (DQM). Acta Mech. 2012, 223, 43–62. [Google Scholar] [CrossRef]
- Zhong, Z.; Shang, E.T. Three-dimensional exact analysis of a simply supported functionally gradient piezoelectric plate. Int. J. Solids Struct. 2003, 40, 5335–5352. [Google Scholar] [CrossRef]
- Hosseini-Hashemi, S.; Salehipour, H.; Atashipour, S.R. Exact three-dimensional free vibration analysis of thick homogeneous plates coated by a functionally graded layer. Acta Mech. 2012, 223, 2153–2166. [Google Scholar] [CrossRef]
- Li, Q.; Iu, V.P.; Kou, K.P. Three-dimensional vibration analysis of functionally graded material sandwich plates. J. Sound Vib. 2008, 311, 498–515. [Google Scholar] [CrossRef]
- Zahedinejad, P.; Malekzadeh, P.; Farid, M.; Karami, G. A semi-analytical three-dimensional free vibration analysis of functionally graded curved panels. Int. J. Press. Vessel. Pip. 2010, 87, 470–480. [Google Scholar] [CrossRef]
- Alibeigloo, A.; Kani, A.M.; Pashaei, M.H. Elasticity solution for the free vibration analysis of functionally graded cylindrical shell bonded to thin piezoelectric layers. Int. J. Press. Vessel. Pip. 2012, 89, 98–111. [Google Scholar] [CrossRef]
- Vel, S.S. Exact elasticity solution for the vibration of functionally graded anisotropic cylindrical shells. Compos. Struct. 2010, 92, 2712–2727. [Google Scholar] [CrossRef]
- Dong, C.Y. Three-dimensional free vibration analysis of functionally graded annular plates using the Chebyshev-Ritz method. Mater. Des. 2008, 29, 1518–1525. [Google Scholar] [CrossRef]
- Kashtalyan, M.; Menshykova, M. Three-dimensional elasticity solution for sandwich panels with a functionally graded core. Compos. Struct. 2009, 87, 36–43. [Google Scholar] [CrossRef]
- Barretta, R. Analogies between Kirchhoff plates and Saint-Venant beams under torsion. Acta Mech. 2013, 224, 2955–2964. [Google Scholar] [CrossRef]
- Barretta, R. Analogies between Kirchhoff plates and Saint-Venant beams under flexure. Acta Mech. 2014, 225, 2075–2083. [Google Scholar] [CrossRef]
- Barretta, R.; Luciano, R. Analogies between Kirchhoff plates and functionally graded Saint-Venant beams under torsion. Contin. Mech. Thermodyn. 2014, 27, 449–505. [Google Scholar] [CrossRef]
- Barretta, R. On Cesáro-Volterra Method in Orthotropic Saint-Venant Beam. J. Elast. 2013, 112, 233–253. [Google Scholar] [CrossRef]
- Barretta, R. On the relative position of twist and shear centres in the orthotropic and fiberwise homogeneous Saint–Venant beam theory. Acta Mech. 2012, 49, 3038–3046. [Google Scholar] [CrossRef]
- Brischetto, S. Exact elasticity solution for natural frequencies of functionally graded simply-supported structures. CMES Comput. Mod. Eng. Sci. 2013, 95, 391–430. [Google Scholar]
- Brischetto, S. A general exact elastic shell solution for bending analysis of functionally graded structures. Compos. Struct. 2017, 175, 70–85. [Google Scholar] [CrossRef]
- Brischetto, S. Convergence analysis of the exponential matrix method for the solution of 3D equilibrium equations for free vibration analysis of plates and shells. Compos. Part B Eng. 2016, 98, 453–471. [Google Scholar] [CrossRef]
- Brischetto, S. Exponential matrix method for the solution of exact 3D equilibrium equations for free vibrations of functionally graded plates and shells. J. Sandw. Struct. Mater. 2017. [CrossRef]
- Brischetto, S.; Torre, R. Convergence investigation for the exponential matrix and mathematical layers in the static analysis of multilayered composite structures. J. Compos. Sci. 2017, 1, 19. [Google Scholar] [CrossRef]
- Hildebrand, F.B.; Reissner, E.; Thomas, G.B. Notes on the Foundations of the Theory of Small Displacements of Orthotropic Shells; NACA Technical Note No. 1833; National Advisory Committee for Aeronautics: Washington, DC, USA, 1949. [Google Scholar]
- Soedel, W. Vibration of Shells and Plates; Marcel Dekker, Inc.: New York, NY, USA, 2004. [Google Scholar]
- Tornabene, F. Meccanica delle Strutture a Guscio in Materiale Composito; Società Editrice Esculapio: Bologna, Italy, 2012. [Google Scholar]
- Gustafson, G.B. Systems of Differential Equations. Available online: http://www.math.utah.edu/gustafso/2250systems-de.pdf (accessed on 7 March 2016).
- Boyce, W.E.; DiPrima, R.C. Elementary Differential Equations and Boundary Value Problems; John Wiley & Sons, Ltd.: New York, NY, USA, 2001. [Google Scholar]
- Molery, C.; Van Loan, C. Nineteen dubious ways to compute the exponential of a matrix, twenty-five years later. SIAM Rev. 2003, 45, 1–46. [Google Scholar] [CrossRef]
- Brischetto, S. Exact three-dimensional static analysis of single- and multi-layered plates and shells. Compos. Part B Eng. 2017, 119, 230–252. [Google Scholar] [CrossRef]
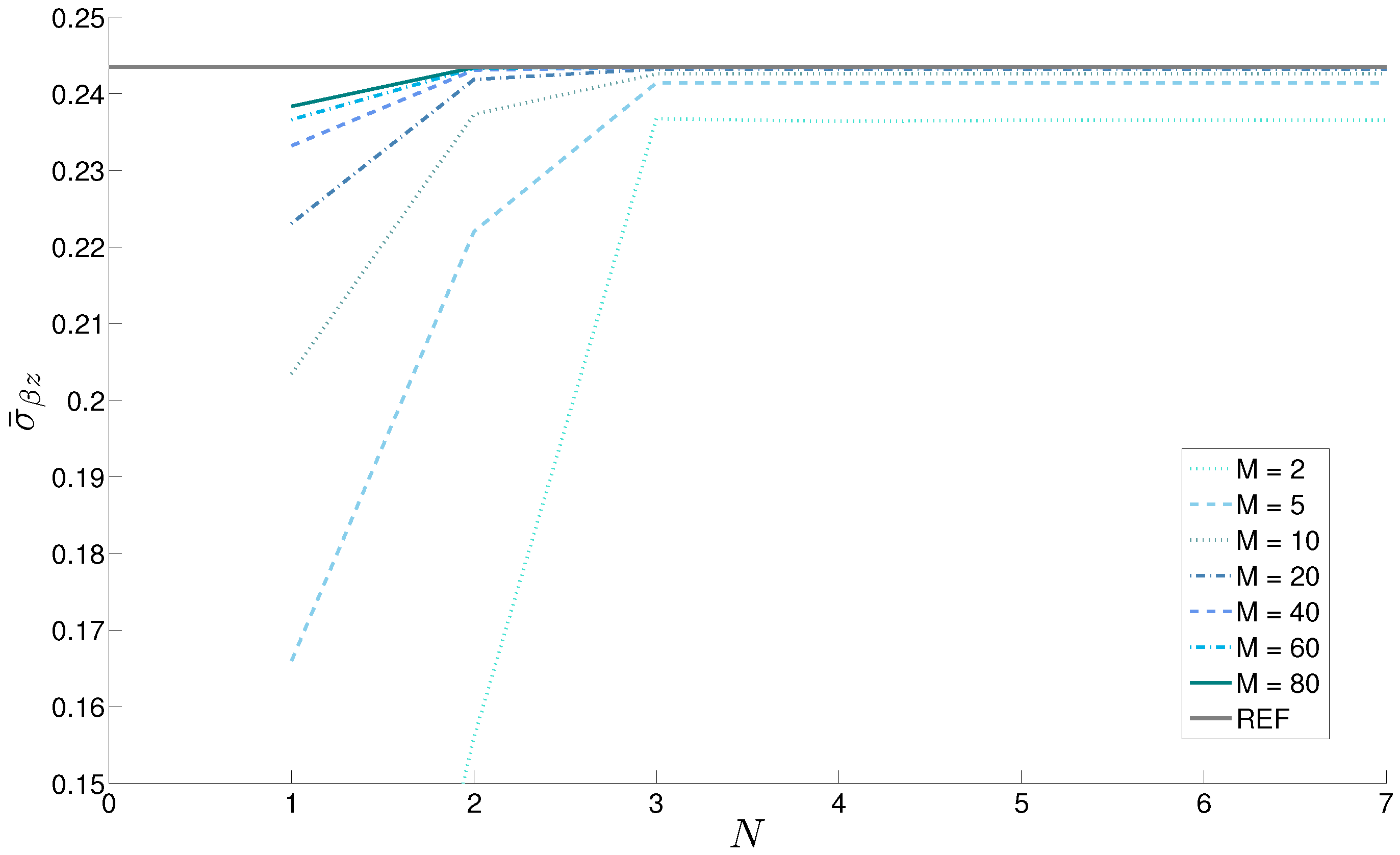
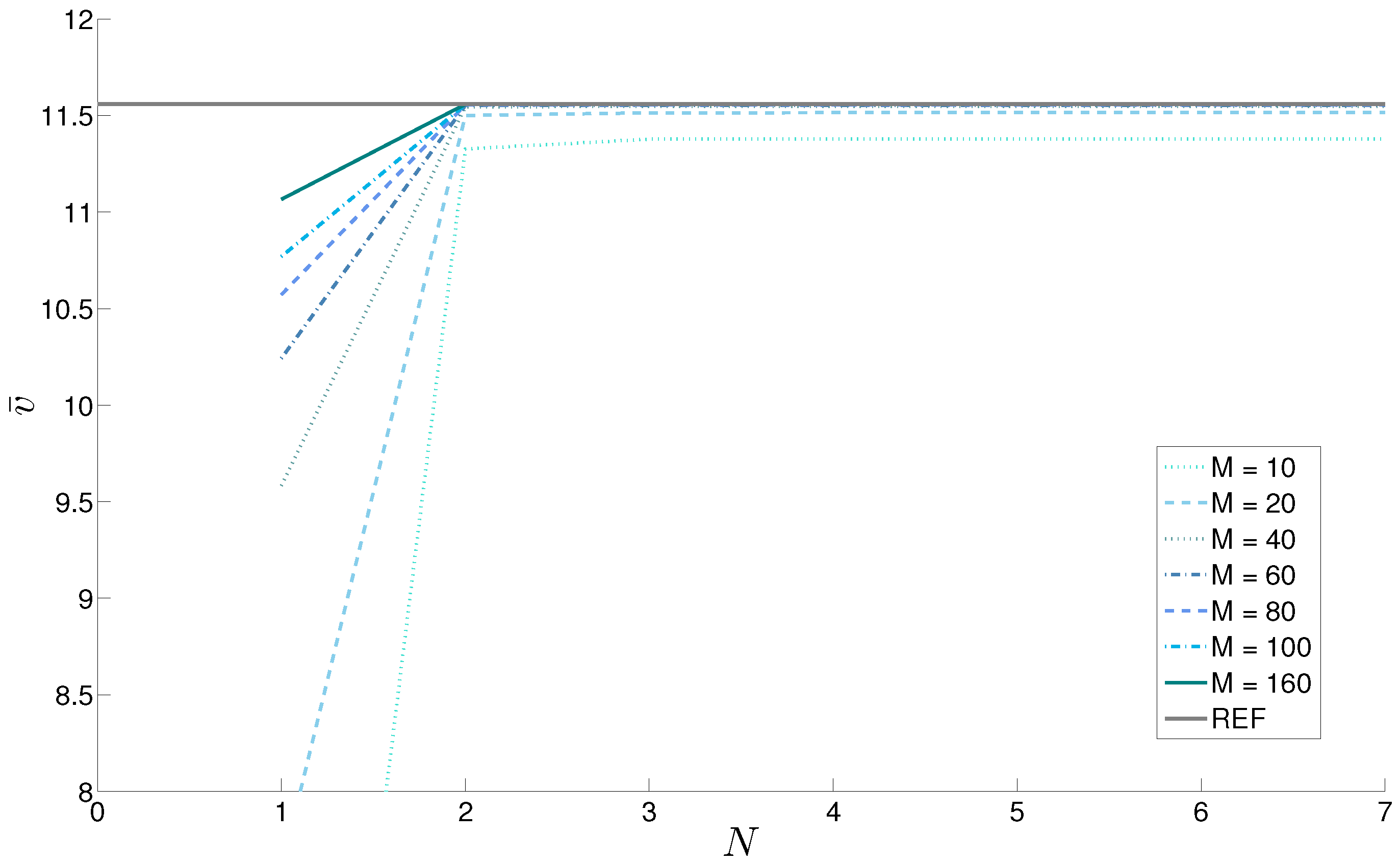
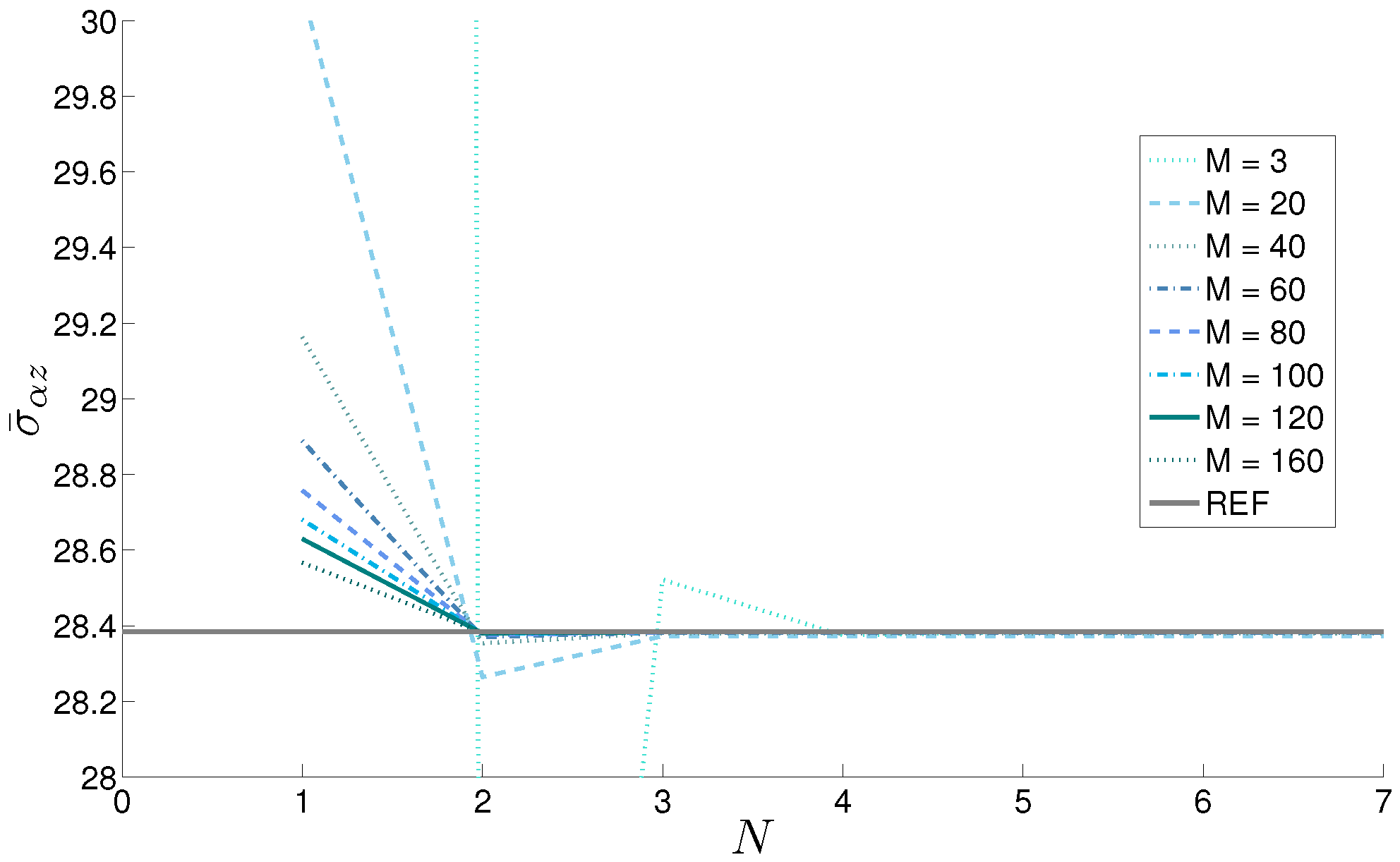
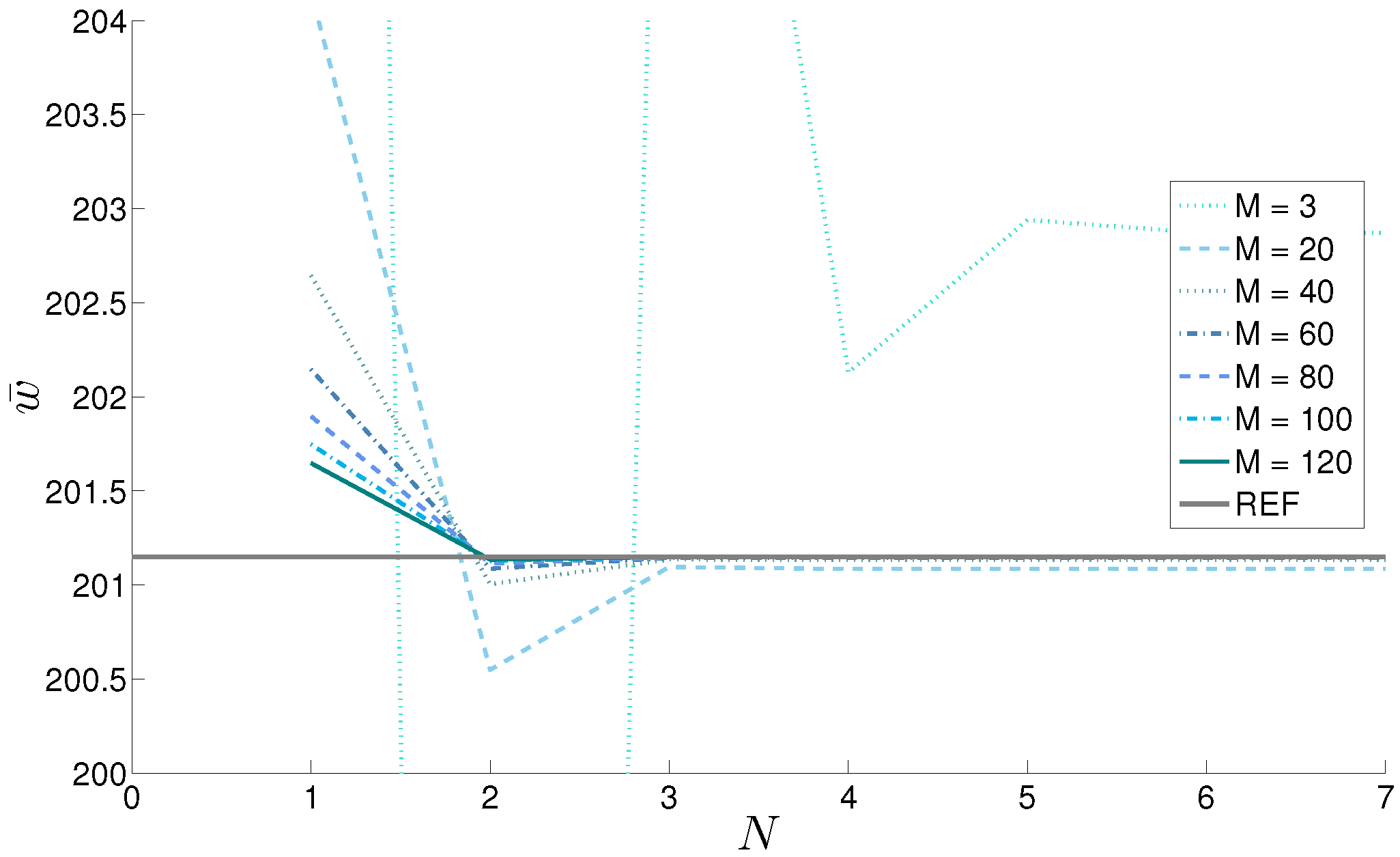
| ; | ||||||||||||
| NaN | 25.06 | 587.80 | 68.89 | 98.26 | 90.80 | 92.36 | 92.15 | 92.18 | 92.18 | 92.18 | 92.18 | |
| 108.43 | 66.33 | 103.67 | 96.70 | 98.32 | 98.22 | 98.23 | 98.23 | 98.23 | 98.23 | 98.23 | 98.23 | |
| 105.18 | 96.78 | 103.35 | 103.18 | 103.22 | 103.22 | 103.22 | 103.22 | 103.22 | 103.22 | 103.22 | 103.22 | |
| 105.54 | 103.06 | 104.77 | 104.76 | 104.77 | 104.77 | 104.77 | 104.77 | 104.77 | 104.77 | 104.77 | 104.77 | |
| 105.66 | 104.92 | 105.35 | 105.35 | 105.35 | 105.35 | 105.35 | 105.35 | 105.35 | 105.35 | 105.35 | 105.35 | |
| 105.70 | 105.45 | 105.56 | 105.56 | 105.56 | 105.56 | 105.56 | 105.56 | 105.56 | 105.56 | 105.56 | 105.56 | |
| 105.70 | 105.56 | 105.61 | 105.61 | 105.61 | 105.61 | 105.61 | 105.61 | 105.61 | 105.61 | 105.61 | 105.61 | |
| 105.70 | 105.61 | 105.63 | 105.63 | 105.63 | 105.63 | 105.63 | 105.63 | 105.63 | 105.63 | 105.63 | 105.63 | |
| 105.69 | 105.63 | 105.65 | 105.65 | 105.65 | 105.65 | 105.65 | 105.65 | 105.65 | 105.65 | 105.65 | 105.65 | |
| 105.69 | 105.64 | 105.65 | 105.65 | 105.65 | 105.65 | 105.65 | 105.65 | 105.65 | 105.65 | 105.65 | 105.65 | |
| 105.69 | 105.65 | 105.66 | 105.66 | 105.66 | 105.66 | 105.66 | 105.66 | 105.66 | 105.66 | 105.66 | 105.66 | |
| 105.69 | 105.66 | 105.66 | 105.66 | 105.66 | 105.66 | 105.66 | 105.66 | 105.66 | 105.66 | 105.66 | 105.66 | |
| 105.68 | 105.66 | 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | |
| 105.68 | 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | |
| 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | |
| 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | 105.67 | |
| ; | ||||||||||||
| NaN | 0.0802 | 0.2448 | 0.2368 | 0.2391 | 0.2391 | 0.2391 | 0.2391 | 0.2391 | 0.2391 | 0.2391 | 0.2391 | |
| 0.0541 | 0.1560 | 0.2367 | 0.2364 | 0.2365 | 0.2365 | 0.2365 | 0.2365 | 0.2365 | 0.2365 | 0.2365 | 0.2365 | |
| 0.1660 | 0.2220 | 0.2414 | 0.2414 | 0.2414 | 0.2414 | 0.2414 | 0.2414 | 0.2414 | 0.2414 | 0.2414 | 0.2414 | |
| 0.2035 | 0.2373 | 0.2426 | 0.2426 | 0.2426 | 0.2426 | 0.2426 | 0.2426 | 0.2426 | 0.2426 | 0.2426 | 0.2426 | |
| 0.2231 | 0.2419 | 0.2432 | 0.2432 | 0.2432 | 0.2432 | 0.2432 | 0.2432 | 0.2432 | 0.2432 | 0.2432 | 0.2432 | |
| 0.2332 | 0.2431 | 0.2434 | 0.2434 | 0.2434 | 0.2434 | 0.2434 | 0.2434 | 0.2434 | 0.2434 | 0.2434 | 0.2434 | |
| 0.2366 | 0.2433 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | |
| 0.2384 | 0.2434 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | |
| 0.2394 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | |
| 0.2403 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | |
| 0.2409 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | |
| 0.2415 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | |
| 0.2419 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | |
| 0.2422 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | |
| 0.2424 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | |
| 0.2425 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | 0.2435 | |
| ; | ||||||||||||
| 0.273 | ||||||||||||
| 6.919 | 6.776 | 7.078 | 7.707 | 7.707 | 7.707 | 7.707 | 7.707 | 7.707 | 7.707 | 7.707 | ||
| 10.601 | 10.759 | 10.776 | 10.776 | 10.776 | 10.776 | 10.776 | 10.776 | 10.776 | 10.776 | 10.776 | ||
| 3.603 | 11.326 | 11.377 | 11.379 | 11.379 | 11.379 | 11.379 | 11.379 | 11.379 | 11.379 | 11.379 | 11.379 | |
| 7.600 | 11.500 | 11.514 | 11.514 | 11.514 | 11.514 | 11.514 | 11.514 | 11.514 | 11.514 | 11.514 | 11.514 | |
| 9.584 | 11.544 | 11.548 | 11.548 | 11.548 | 11.548 | 11.548 | 11.548 | 11.548 | 11.548 | 11.548 | 11.548 | |
| 10.243 | 11.553 | 11.554 | 11.554 | 11.554 | 11.554 | 11.554 | 11.554 | 11.554 | 11.554 | 11.554 | 11.554 | |
| 10.572 | 11.556 | 11.556 | 11.556 | 11.556 | 11.556 | 11.556 | 11.556 | 11.556 | 11.556 | 11.556 | 11.556 | |
| 10.770 | 11.557 | 11.557 | 11.557 | 11.557 | 11.557 | 11.557 | 11.557 | 11.557 | 11.557 | 11.557 | 11.557 | |
| 10.952 | 11.558 | 11.558 | 11.558 | 11.558 | 11.558 | 11.558 | 11.558 | 11.558 | 11.558 | 11.558 | 11.558 | |
| 11.066 | 11.558 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | |
| 11.165 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | |
| 11.244 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | |
| 11.296 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | |
| 11.334 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | |
| 11.362 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | 11.559 | |
| ; | ||||||||||||
| 0.5118 | 0.4456 | 0.4723 | 0.4699 | 0.4701 | 0.4701 | 0.4701 | 0.4701 | 0.4701 | 0.4701 | 0.4701 | 0.4701 | |
| 0.3457 | 0.3292 | 0.3333 | 0.3331 | 0.3331 | 0.3331 | 0.3331 | 0.3331 | 0.3331 | 0.3331 | 0.3331 | 0.3331 | |
| 0.3432 | 0.3376 | 0.3382 | 0.3382 | 0.3382 | 0.3382 | 0.3382 | 0.3382 | 0.3382 | 0.3382 | 0.3382 | 0.3382 | |
| 0.3351 | 0.3326 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | |
| 0.3339 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | |
| 0.3333 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | |
| 0.3331 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | |
| 0.333 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | |
| 0.3329 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | |
| 0.3329 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | |
| 0.3328 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | |
| 0.3328 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | |
| 0.3328 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | |
| 0.3328 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | |
| 0.3328 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | |
| 0.3328 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | 0.3327 | |
| ; | ||||||||||||
| 469.72 | 246.78 | 320.81 | 312.72 | 313.62 | 313.57 | 313.58 | 313.58 | 313.58 | 313.58 | 313.58 | 313.58 | |
| 329.32 | 319.37 | 320.96 | 320.95 | 320.95 | 320.95 | 320.95 | 320.95 | 320.95 | 320.95 | 320.95 | 320.95 | |
| 324.87 | 320.57 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | |
| 323.51 | 320.79 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | |
| 322.85 | 320.87 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | |
| 322.46 | 320.90 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | |
| 322.21 | 320.92 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | |
| 322.03 | 320.93 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | |
| 321.89 | 320.94 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | |
| 321.70 | 320.95 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | |
| 321.58 | 320.95 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | |
| 321.53 | 320.95 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | |
| 321.45 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | |
| 321.40 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | |
| 321.33 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | 320.96 | |
| ; | ||||||||||||
| 191.60 | 24.041 | 28.522 | 28.375 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | |
| 30.081 | 28.265 | 28.373 | 28.373 | 28.373 | 28.373 | 28.373 | 28.373 | 28.373 | 28.373 | 28.373 | 28.373 | |
| 29.163 | 28.354 | 28.381 | 28.381 | 28.381 | 28.381 | 28.381 | 28.381 | 28.381 | 28.381 | 28.381 | 28.381 | |
| 28.889 | 28.371 | 28.382 | 28.382 | 28.382 | 28.382 | 28.382 | 28.382 | 28.382 | 28.382 | 28.382 | 28.382 | |
| 28.758 | 28.376 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | |
| 28.681 | 28.379 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | |
| 28.630 | 28.380 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | |
| 28.594 | 28.381 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | 28.383 | |
| 28.567 | 28.382 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | |
| 28.530 | 28.383 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | |
| 28.505 | 28.383 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | |
| 28.496 | 28.383 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | |
| 28.481 | 28.383 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | |
| 28.469 | 28.383 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | |
| 28.456 | 28.383 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | 28.384 | |
| ; | ||||||||||||
| 228.39 | 172.20 | 208.31 | 202.13 | 202.94 | 202.87 | 202.87 | 202.87 | 202.87 | 202.87 | 202.87 | 202.87 | |
| 204.15 | 200.55 | 201.10 | 201.08 | 201.08 | 201.08 | 201.08 | 201.08 | 201.08 | 201.08 | 201.08 | 201.08 | |
| 202.64 | 201.00 | 201.14 | 201.13 | 201.13 | 201.13 | 201.13 | 201.13 | 201.13 | 201.13 | 201.13 | 201.13 | |
| 202.14 | 201.09 | 201.14 | 201.14 | 201.14 | 201.14 | 201.14 | 201.14 | 201.14 | 201.14 | 201.14 | 201.14 | |
| 201.90 | 201.11 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | |
| 201.75 | 201.13 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | |
| 201.65 | 201.13 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | |
| 201.58 | 201.14 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | |
| 201.52 | 201.14 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | |
| 201.45 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | |
| 201.40 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | |
| 201.38 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | |
| 201.35 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | |
| 201.33 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | |
| 201.30 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | 201.15 | |
| ; | ||||||||||||
| 17.75 | 11.27 | 11.99 | 11.94 | 11.94 | 11.94 | 11.94 | 11.94 | 11.94 | 11.94 | 11.94 | 11.94 | |
| 12.72 | 12.02 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | |
| 12.37 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | |
| 12.26 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | |
| 12.20 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | |
| 12.16 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | |
| 12.14 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | |
| 12.13 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | |
| 12.11 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | |
| 12.10 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | |
| 12.09 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | |
| 12.08 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | |
| 12.07 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | |
| 12.07 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | |
| 12.06 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | 12.03 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brischetto, S.; Torre, R. Effects of Order of Expansion for the Exponential Matrix and Number of Mathematical Layers in the Exact 3D Static Analysis of Functionally Graded Plates and Shells. Appl. Sci. 2018, 8, 110. https://doi.org/10.3390/app8010110
Brischetto S, Torre R. Effects of Order of Expansion for the Exponential Matrix and Number of Mathematical Layers in the Exact 3D Static Analysis of Functionally Graded Plates and Shells. Applied Sciences. 2018; 8(1):110. https://doi.org/10.3390/app8010110
Chicago/Turabian StyleBrischetto, Salvatore, and Roberto Torre. 2018. "Effects of Order of Expansion for the Exponential Matrix and Number of Mathematical Layers in the Exact 3D Static Analysis of Functionally Graded Plates and Shells" Applied Sciences 8, no. 1: 110. https://doi.org/10.3390/app8010110
APA StyleBrischetto, S., & Torre, R. (2018). Effects of Order of Expansion for the Exponential Matrix and Number of Mathematical Layers in the Exact 3D Static Analysis of Functionally Graded Plates and Shells. Applied Sciences, 8(1), 110. https://doi.org/10.3390/app8010110






