Reduction of T2 Relaxation Rates due to Large Volume Fractions of Magnetic Nanoparticles for All Motional Regimes
Abstract
:Featured Application
Abstract
1. Introduction
2. Methods
3. Results
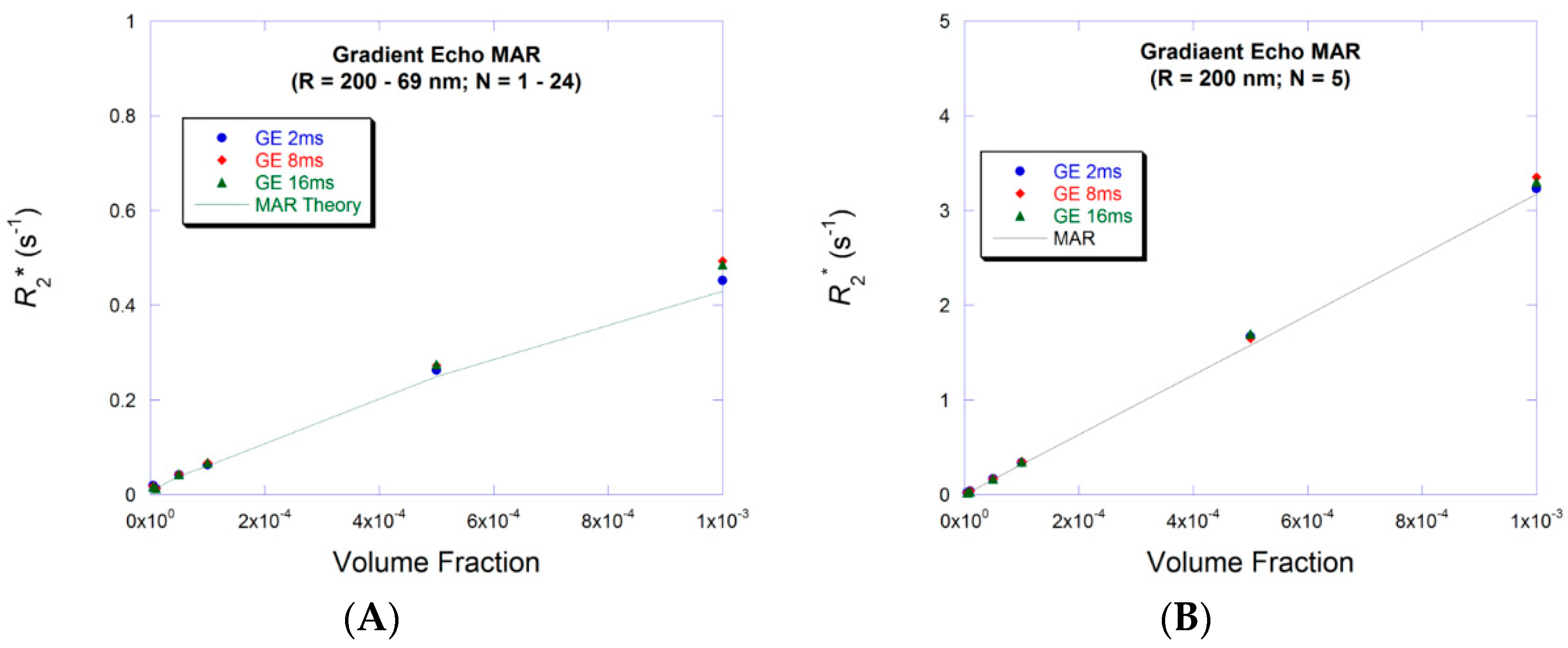
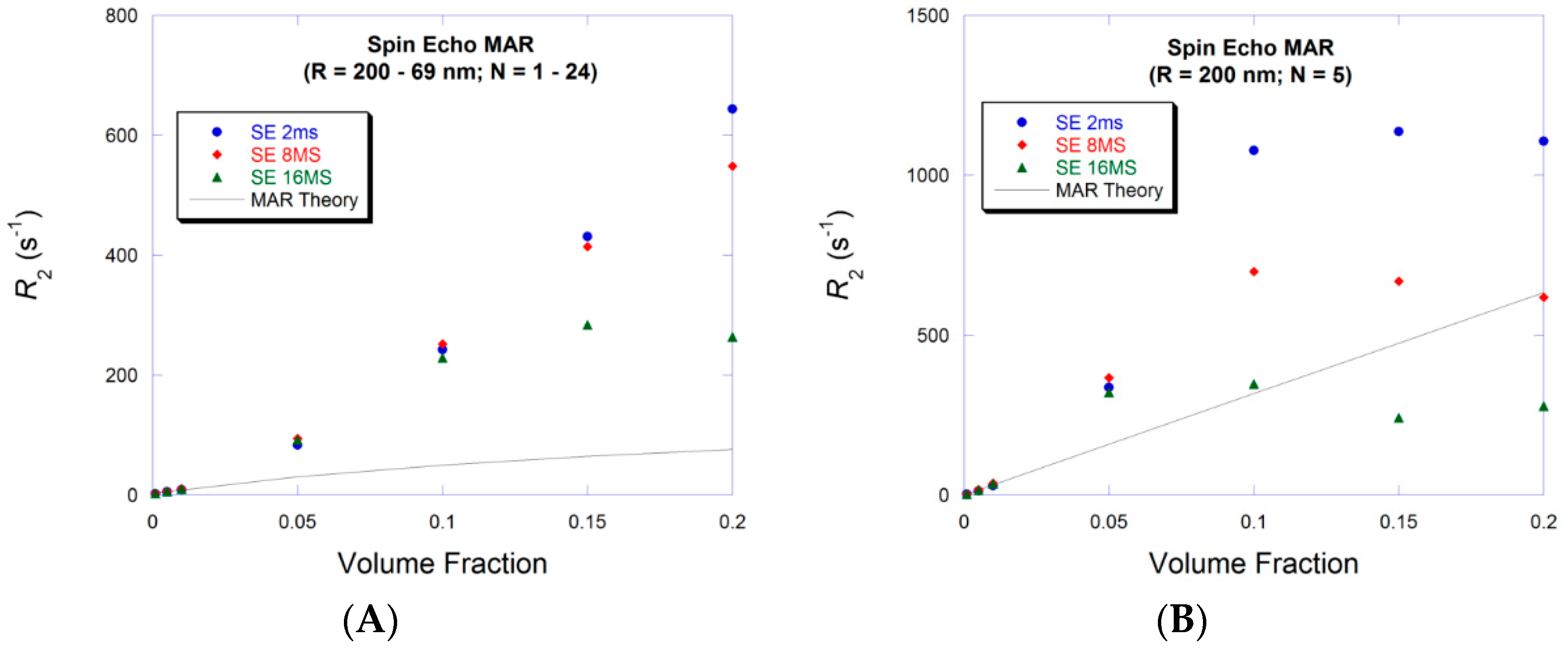
3.1. Small Volume Fraction—MAR
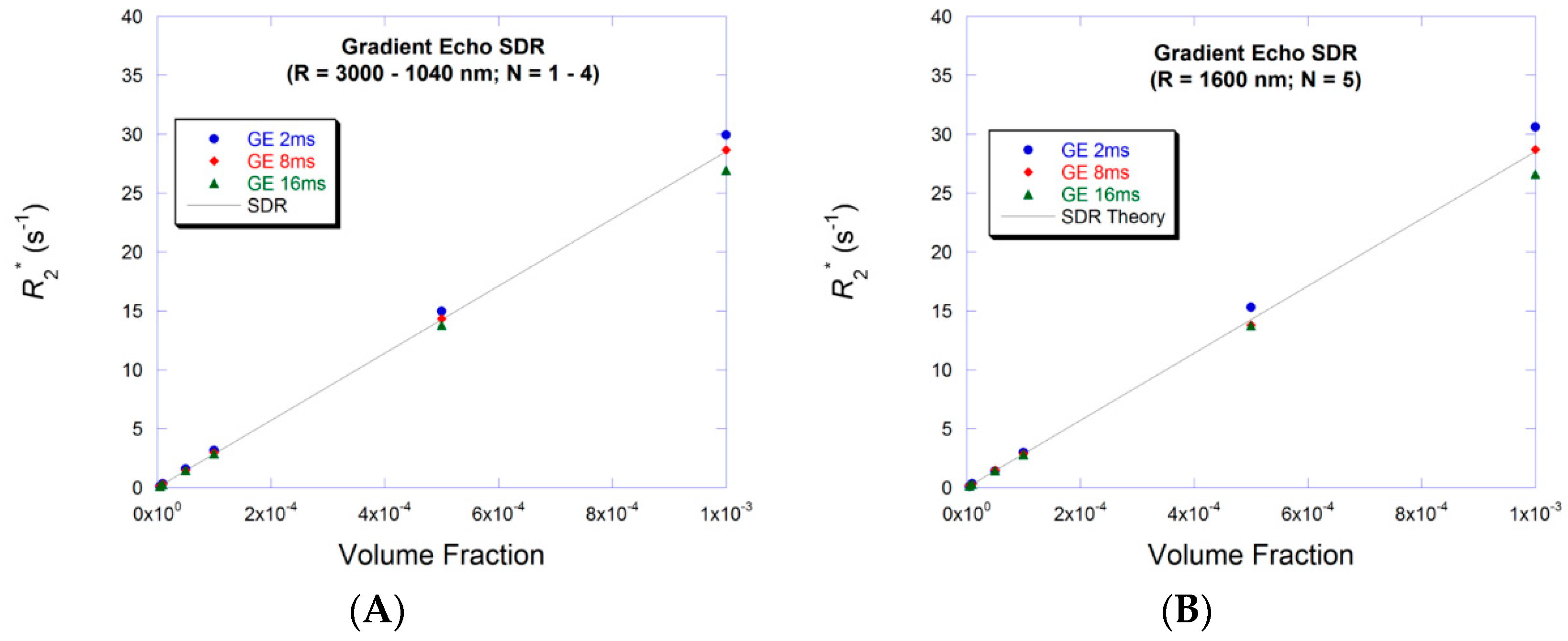
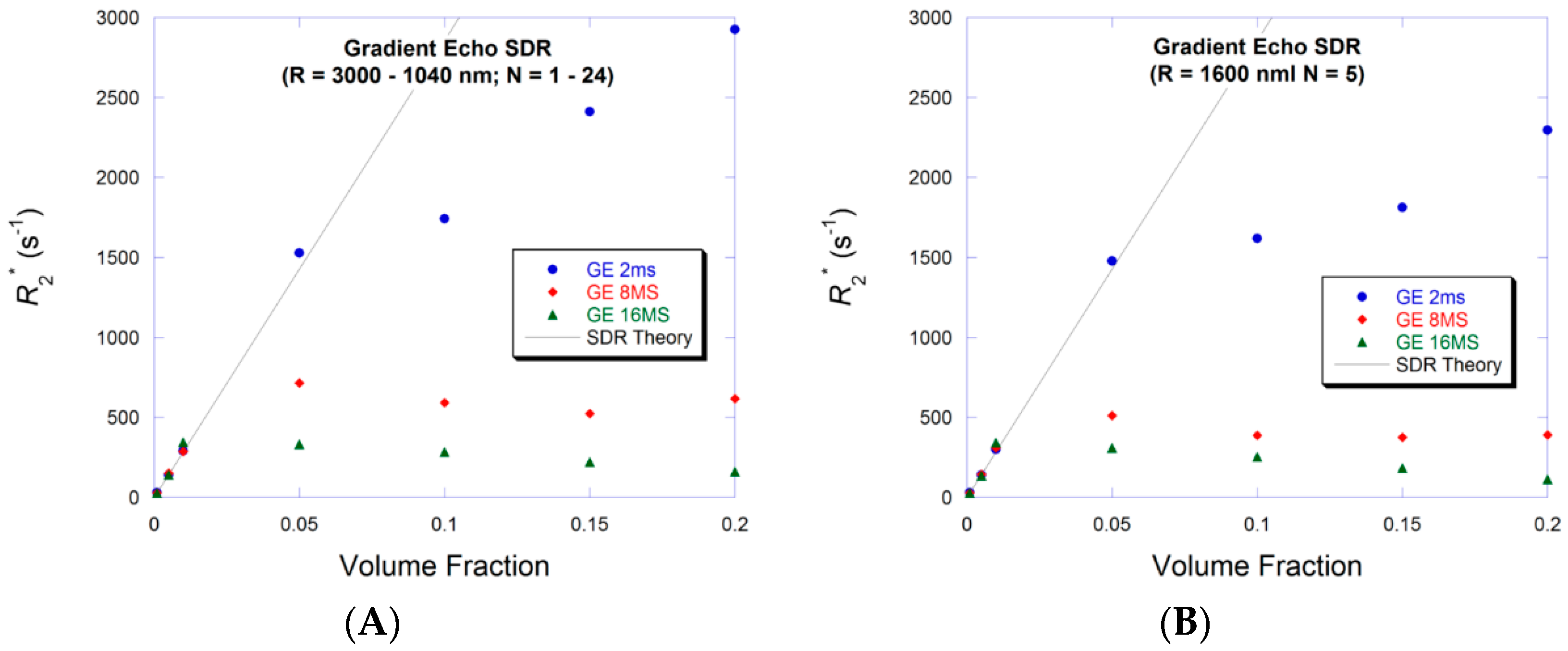
3.2. Small Volume Fraction—SDR
3.3. Large Volume Fraction—MAR
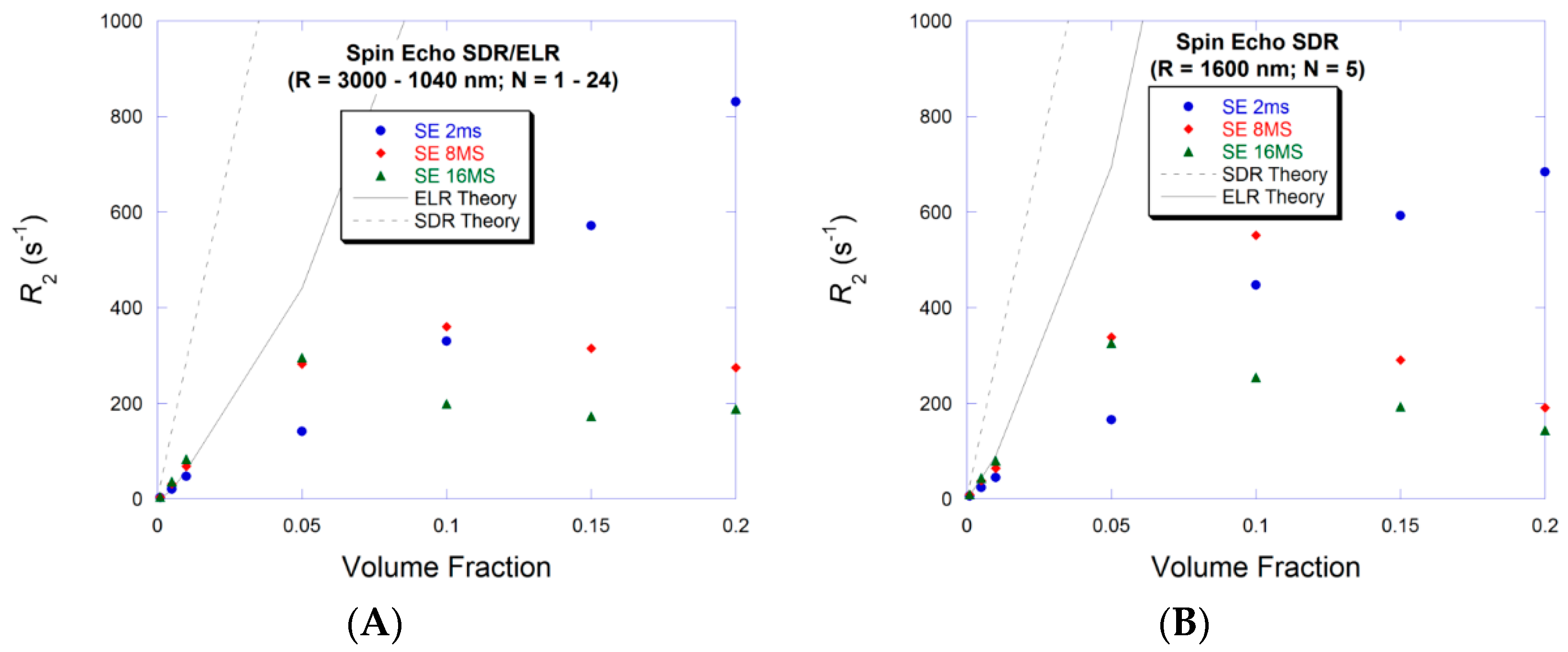
3.4. Large Volume Fraction—SDR
4. Discussion
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Issa, B.; Obaidat, I.M.; Albiss, B.A.; Haik, Y. Magnetic nanoparticles: Surface effects and properties related to biomedicine applications. Int. J. Mol. Sci. 2013, 14, 21266–21305. [Google Scholar] [CrossRef] [PubMed]
- Laurent, S.; Forge, D.; Port, M.; Roch, A.; Robic, C.; Vander Elst, L.; Muller, R.N. Magnetic iron oxide nanoparticles: Synthesis, stabilization, vectorization, physicochemical characterizations, and biological applications. Chem. Rev. 2008, 108, 2064–2110. [Google Scholar] [CrossRef] [PubMed]
- Roch, A.; Muller, R.N.; Gillis, P. Theory of proton relaxation induced by superparamagnetic particles. J. Chem. Phys. 1999, 110, 5403–5411. [Google Scholar] [CrossRef]
- Poperechny, I.S.; Raikher, Y.L.; Stepanov, V.I. Ferromagnetic resonance in a dilute suspension of uniaxial superparamagnetic particles. J. Magn. Magn. Mater. 2017, 424, 185–188. [Google Scholar] [CrossRef]
- Villaraza, A.J.L.; Bumb, A.; Brechbiel, M.W. Macromolecules, dendrimers, and nanomaterials in magnetic resonance imaging: The interplay between size, function, and pharmacokinetics. Chem. Rev. 2010, 110, 2921–2959. [Google Scholar] [CrossRef] [PubMed]
- Saritas, E.U.; Goodwill, P.W.; Croft, L.R.; Konkle, J.J.; Lu, K.; Zheng, B.; Conolly, S.M. Magnetic particle imaging (MPI) for NMR and MRI researchers. J. Magn. Reson. 2013, 229, 116–126. [Google Scholar] [CrossRef] [PubMed]
- Kateb, B.; Chiu, K.; Black, K.L.; Yamamoto, V.; Khalsa, B.; Ljubimova, J.Y.; Ding, H.; Patil, R.; Portilla-Arias, J.A.; Modo, M.; et al. Nanoplatforms for constructing new approaches to cancer treatment, imaging, and drug delivery: What should be the policy? NeuroImage 2011, 54, S106–S124. [Google Scholar] [CrossRef] [PubMed]
- Branquinho, L.C.; Carrião, M.S.; Costa, A.S.; Zufelato, N.; Sousa, M.H.; Miotto, R.; Ivkov, R.; Bakuzis, A.F. Effect of magnetic dipolar interactions on nanoparticle heating efficiency: Implications for cancer hyperthermia. Sci. Rep. 2013, 3, 2887. [Google Scholar] [CrossRef] [PubMed]
- Obaidat, I.; Issa, B.; Haik, Y. Magnetic Properties of Magnetic Nanoparticles for Efficient Hyperthermia. Nanomaterials 2015, 5, 63–89. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Klingeler, R.; Kath, M.; El Gendy, A.A.; Cendrowski, K.; Kalenczuk, R.J.; Borowiak-Palen, E. Magnetic silica nanotubes: Synthesis, drug release, and feasibility for magnetic hyperthermia. ACS Appl. Mater. Interfaces 2012, 4, 2303–2309. [Google Scholar] [CrossRef] [PubMed]
- Issa, B.; Obaidat, I.M.; Hejasee, R.H.; Qadri, S.; Haik, Y. NMR relaxation in systems with magnetic nanoparticles: A temperature study. J. Magn. Reson. Imaging 2014, 39, 648–655. [Google Scholar] [CrossRef] [PubMed]
- Korchinski, D.J.; Taha, M.; Yang, R.; Nathoo, N.; Dunn, J.F. Iron Oxide as an MRI Contrast Agent for Cell Tracking. Magn. Reson. Insights 2015, 8, 15–29. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.-X.; Tang, W.-L.; Wang, X.-X. Superparamagnetic iron oxide nanoparticles may affect endothelial progenitor cell migration ability and adhesion capacity. Cytotherapy 2010, 12, 251–259. [Google Scholar] [CrossRef] [PubMed]
- Kurlyandskaya, G.V.; Novoselova, I.P.; Schupletsova, V.V.; Andrade, R.; Dunec, N.A.; Litvinova, L.S.; Safronov, A.P.; Yurova, K.A.; Kulesh, N.A.; Dzyuman, A.N.; et al. Nanoparticles for magnetic biosensing systems. J. Magn. Magn. Mater. 2017, 431, 249–254. [Google Scholar] [CrossRef]
- García-Arribas, A.; Martínez, F.; Fernández, E.; Ozaeta, I.; Kurlyandskaya, G.V.; Svalov, A.V.; Berganzo, J.; Barandiaran, J.M. GMI detection of magnetic-particle concentration in continuous flow. Sens. Actuators A Phys. 2011, 172, 103–108. [Google Scholar] [CrossRef]
- Blyakhman, F.A.; Safronov, A.P.; Zubarev, A.Y.; Shklyar, T.F.; Makeyev, O.G.; Makarova, E.B.; Melekhin, V.V.; Larrañaga, A.; Kurlyandskaya, G.V. Polyacrylamide ferrogels with embedded maghemite nanoparticles for biomedical engineering. Results Phys. 2017, 7, 3624–3633. [Google Scholar] [CrossRef]
- Van Rijt, S.; Habibovic, P. Enhancing regenerative approaches with nanoparticles. J. R. Soc. Interface 2017, 14. [Google Scholar] [CrossRef] [PubMed]
- Corti, M.; Lascialfari, A.; Micotti, E.; Castellano, A.; Donativi, M.; Quarta, A.; Cozzoli, P.D.; Manna, L.; Pellegrino, T.; Sangregorio, C. Magnetic properties of novel superparamagnetic MRI contrast agents based on colloidal nanocrystals. J. Magn. Magn. Mater. 2008, 320, e320–e323. [Google Scholar] [CrossRef]
- Szpak, A.; Fiejdasz, S.; Prendota, W.; Strączek, T.; Kapusta, C.; Szmyd, J.; Nowakowska, M.; Zapotoczny, S. T1-T2 Dual-modal MRI contrast agents based on superparamagnetic iron oxide nanoparticles with surface attached gadolinium complexes. J. Nanopart. Res. 2014, 16, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Waters, E.A.; Wickline, S. A Contrast agents for MRI. Basic Res. Cardiol. 2008, 103, 114–121. [Google Scholar] [CrossRef] [PubMed]
- Carroll, M.R.J.; Woodward, R.C.; House, M.J.; Teoh, W.Y.; Amal, R.; Hanley, T.L.; St Pierre, T.G. Experimental validation of proton transverse relaxivity models for superparamagnetic nanoparticle MRI contrast agents. Nanotechnology 2010, 21, 35103. [Google Scholar] [CrossRef] [PubMed]
- Weisskoff, R.M.; Zuo, C.S.; Boxerman, J.L.; Rosen, B.R. Microscopic Susceptibility Variation and Transverse Relaxation: Theory and Experiment. Magn. Reson. Med. 1994, 31, 601–610. [Google Scholar] [CrossRef] [PubMed]
- Yablonskiy, D.A.; Haacke, E.M. Theory of NMR Signal Behavior in Magnetic ally Inhomogeneous Tissues: The Static Dephasing Regime. Magn. Reson. Med. 1994, 32, 749–763. [Google Scholar] [CrossRef] [PubMed]
- Ayant, Y.; Belorizky, E.; Alizon, J.; Gallice, J. Calcul Des Densités Spectrales Résultant D’un Mouvement Aléatoire De Translation En Relaxation Par Interaction Dipolaire Magnétique Dans Les Liquides. J. Phys. (Paris) 1975, 36, 991–1004. [Google Scholar] [CrossRef]
- Brooks, R.A.; Moiny, F.; Gillis, P. On T2-Shortening by Weakly Magnetized Particles: The Chemical Exchange Model. Magn. Reson. Med. 2001, 1020, 1014–1020. [Google Scholar] [CrossRef] [PubMed]
- Jensen, J.H.; Chandra, R. NMR relaxation in tissues with weak magnetic inhomogeneities. Magn. Reson. Med. 2000, 44, 144–156. [Google Scholar] [CrossRef]
- Brown, R.J.S. Distribution of fields from randomly placed dipoles: Freeprecession signal decay as result of magnetic grains. Phys. Rev. 1961, 121, 1379–1382. [Google Scholar] [CrossRef]
- Heyn, C.; Bowen, C.V.; Rutt, B.K.; Foster, P.J. Detection threshold of single SPIO-labeled cells with FIESTA. Magn. Reson. Med. 2005, 53, 312–320. [Google Scholar] [CrossRef] [PubMed]
- Hak, S.; Goa, P.E.; Stenmark, S.; Bjerkholt, F.F.; Haraldseth, O. Transverse relaxivity of iron oxide nanocrystals clustered in nanoemulsions: Experiment and theory. Med. Reson. Med. 2014, 74, 858–867. [Google Scholar] [CrossRef] [PubMed]
- Hartung, A.; Lisy, M.R.; Herrmann, K.-H.; Hilger, I.; Schüler, D.; Lang, C.; Bellemann, M.E.; Kaiser, W.A.; Reichenbach, J.R. Labeling of macrophages using bacterial magnetosomes and their characterization by magnetic resonance imaging. J. Magn. Magn. Mater. 2007, 311, 454–459. [Google Scholar] [CrossRef]
- Zhang, J.; Chamberlain, R.; Etheridge, M.; Idiyatullin, D.; Corum, C.; Bischof, J.; Garwood, M. Quantifying iron-oxide nanoparticles at high concentration based on longitudinal relaxation using a three-dimensional SWIFT look-locker sequence. Magn. Reson. Med. 2014, 71, 1982–1988. [Google Scholar] [CrossRef] [PubMed]
- Brooks, R.A. T2-shortening by strongly magnetized spheres: A chemical exchange model. Magn. Reson. Med. 2002, 47, 388–391. [Google Scholar] [CrossRef] [PubMed]
- Gillis, P.; Moiny, F.; Brooks, R. A On T2-shortening by strongly magnetized spheres: A partial refocusing model. Magn. Reson. Med. 2002, 47, 257–263. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.X.; Sun, N.; Huang, Z.J.; Cheng, C.M.; Xu, H.; Gu, H.C. Experimental study on T2 relaxation time of protons in water suspensions of iron-oxide nanoparticles: Effects of polymer coating thickness and over-low 1/T2. J. Magn. Magn. Mater. 2010, 322, 548–556. [Google Scholar] [CrossRef]
- Matsumoto, Y.; Jasanoff, A. T2 relaxation induced by clusters of superparamagnetic nanoparticles: Monte Carlo simulations. Magn. Reson. Imaging 2008, 26, 994–998. [Google Scholar] [CrossRef] [PubMed]
- Boxerman, J.L.; Hamberg, L.M.; Rosen, B.R.; Weisskoff, R.M. Mr contrast due to intravascular magnetic susceptibility perturbations. Magn. Reson. Med. 1995, 34, 555–566. [Google Scholar] [CrossRef] [PubMed]




| Arrangement 1 | Volume Fraction | Arrangement 2 | ||||
|---|---|---|---|---|---|---|
| No. Particles | q (nm) | R (nm) | No. Particles | q (nm) | R (nm) | |
| 1 | 1.89 × 10−5 | 200 | 5.0 × 10−6 | 5 | 3.22 × 10−5 | 200 |
| 4 | 1.50 × 10−5 | 126 | 1.0 × 10−5 | 5 | 2.56 × 10−5 | 200 |
| 8 | 8.75 × 10−6 | 100 | 5.0 × 10−5 | 5 | 1.50 × 10−5 | 200 |
| 12 | 6.95 × 10−6 | 87.4 | 1.0 × 10−4 | 5 | 1.19 × 10−5 | 200 |
| 16 | 4.06 × 10−6 | 79.4 | 5.0 × 10−4 | 5 | 6.95 × 10−6 | 200 |
| 20 | 3.22 × 10−6 | 73.7 | 1.0 × 10−3 | 5 | 5.51 × 10−6 | 200 |
| 24 | 1.89 × 10−6 | 69.3 | 5.0 × 10−3 | 5 | 3.22 × 10−6 | 200 |
| Arrangement 1 | Volume Fraction | Arrangement 2 | ||||
|---|---|---|---|---|---|---|
| No. Particles | q (nm) | R (nm) | No. Particles | q (nm) | R (nm) | |
| 1 | 4.84 × 10−5 | 3000 | 5.0 × 10−6 | 5 | 3.31 × 10−5 | 1200 |
| 4 | 2.83 × 10−5 | 1890 | 1.0 × 10−5 | 5 | 1.93 × 10−5 | 1200 |
| 8 | 2.24 × 10−5 | 1500 | 5.0 × 10−5 | 5 | 1.54 × 10−5 | 1200 |
| 12 | 1.31 × 10−5 | 1310 | 1.0 × 10−4 | 5 | 8.98 × 10−6 | 1200 |
| 16 | 1.04 × 10−5 | 1190 | 5.0 × 10−4 | 5 | 7.13 × 10−6 | 1200 |
| 20 | 9.10 × 10−6 | 1110 | 1.0 × 10−3 | 5 | 6.23 × 10−6 | 1200 |
| 24 | 8.27 × 10−6 | 1040 | 5.0 × 10−3 | 5 | 5.66 × 10−6 | 1200 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Issa, B. Reduction of T2 Relaxation Rates due to Large Volume Fractions of Magnetic Nanoparticles for All Motional Regimes. Appl. Sci. 2018, 8, 101. https://doi.org/10.3390/app8010101
Issa B. Reduction of T2 Relaxation Rates due to Large Volume Fractions of Magnetic Nanoparticles for All Motional Regimes. Applied Sciences. 2018; 8(1):101. https://doi.org/10.3390/app8010101
Chicago/Turabian StyleIssa, Bashar. 2018. "Reduction of T2 Relaxation Rates due to Large Volume Fractions of Magnetic Nanoparticles for All Motional Regimes" Applied Sciences 8, no. 1: 101. https://doi.org/10.3390/app8010101
APA StyleIssa, B. (2018). Reduction of T2 Relaxation Rates due to Large Volume Fractions of Magnetic Nanoparticles for All Motional Regimes. Applied Sciences, 8(1), 101. https://doi.org/10.3390/app8010101






