Inverse Optimal Design for Position Control of a Quadrotor
Abstract
:1. Introduction
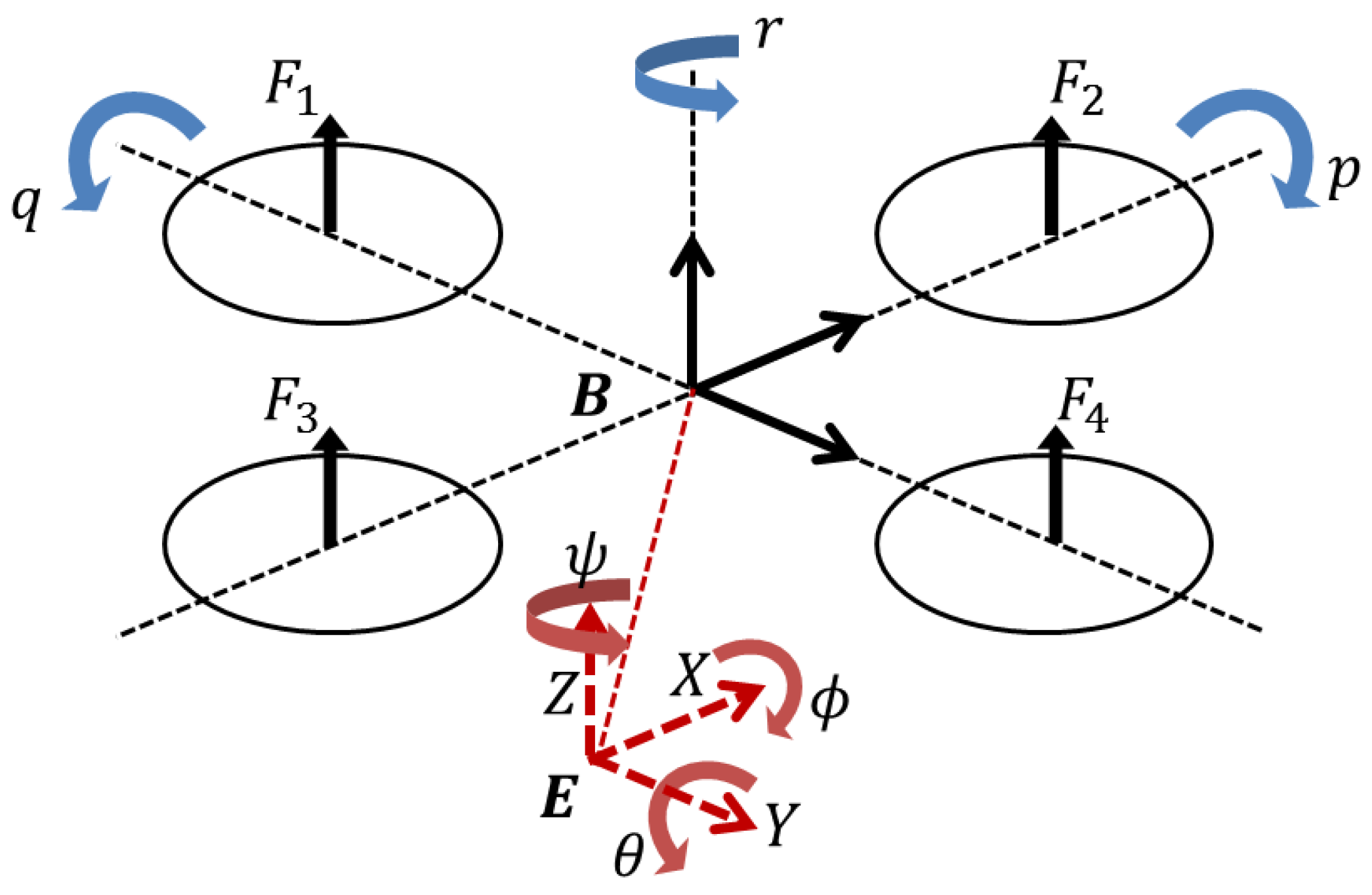
2. Dynamic Model of a Quadrotor
3. Design of Inverse Optimal Position Controller
3.1. Altitude Control of a Quadrotor
3.2. Position Control of a Quadrotor Based on Altitude Control
4. Simulation Results and Analysis
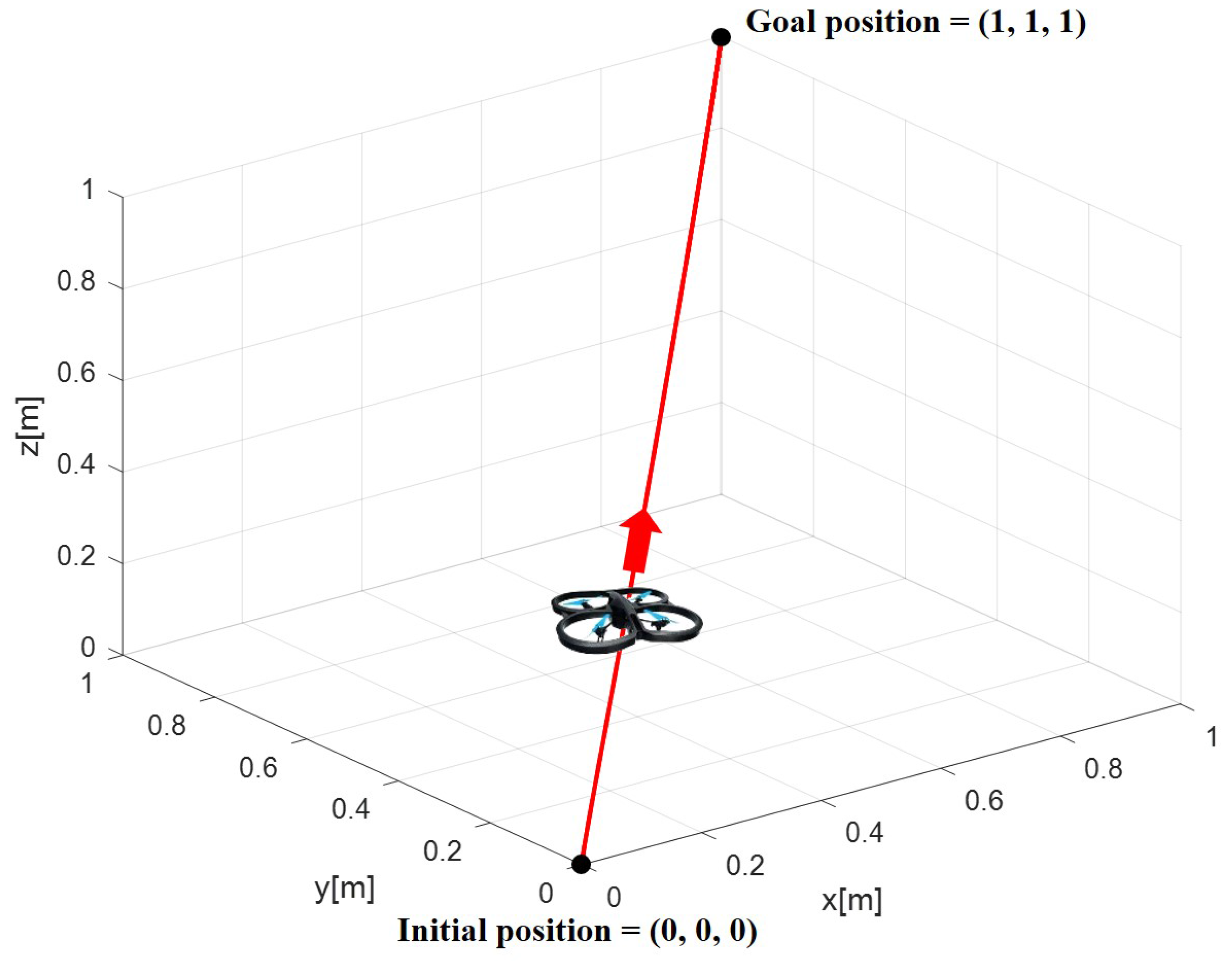
4.1. Testing/Evaluation Methodology
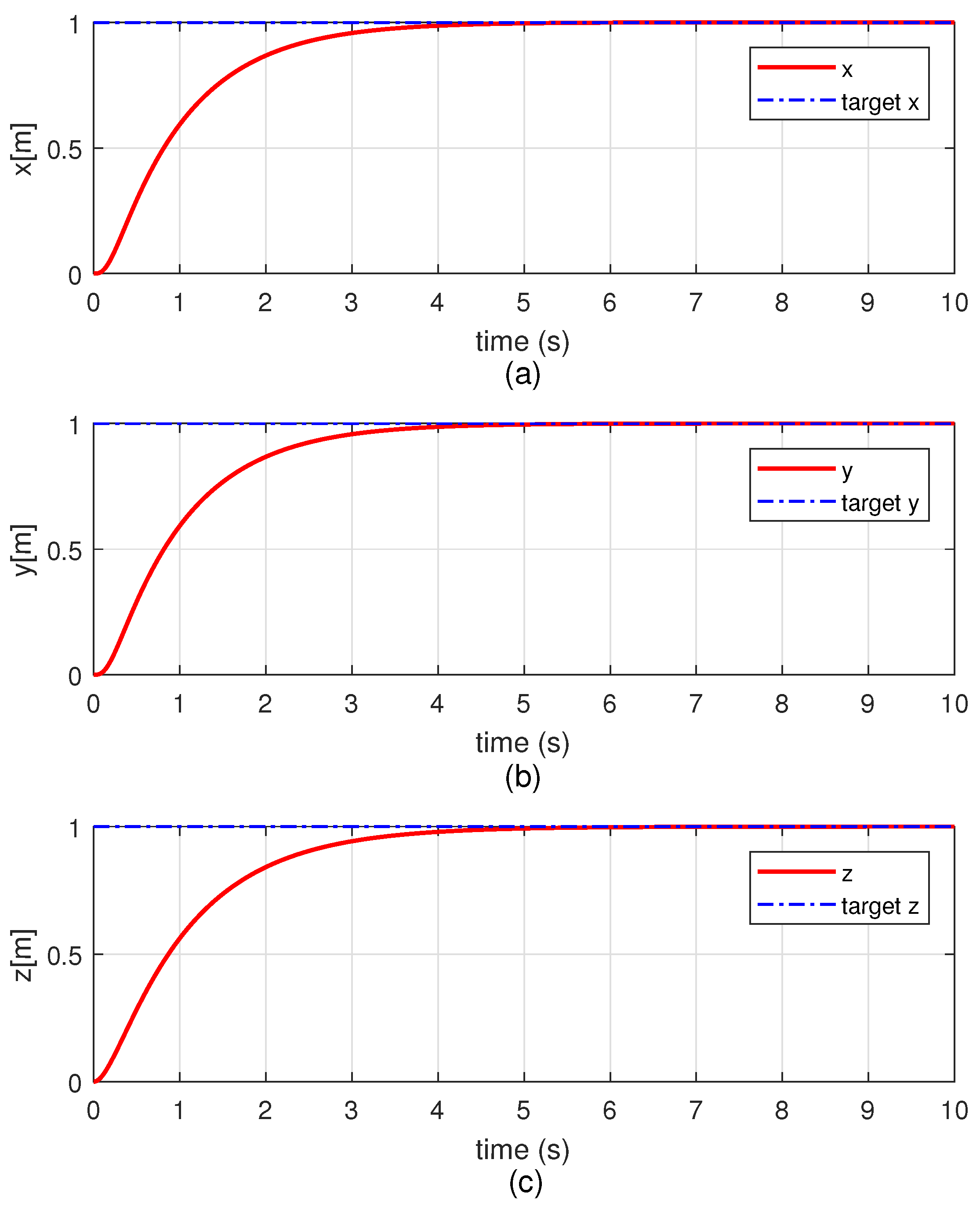
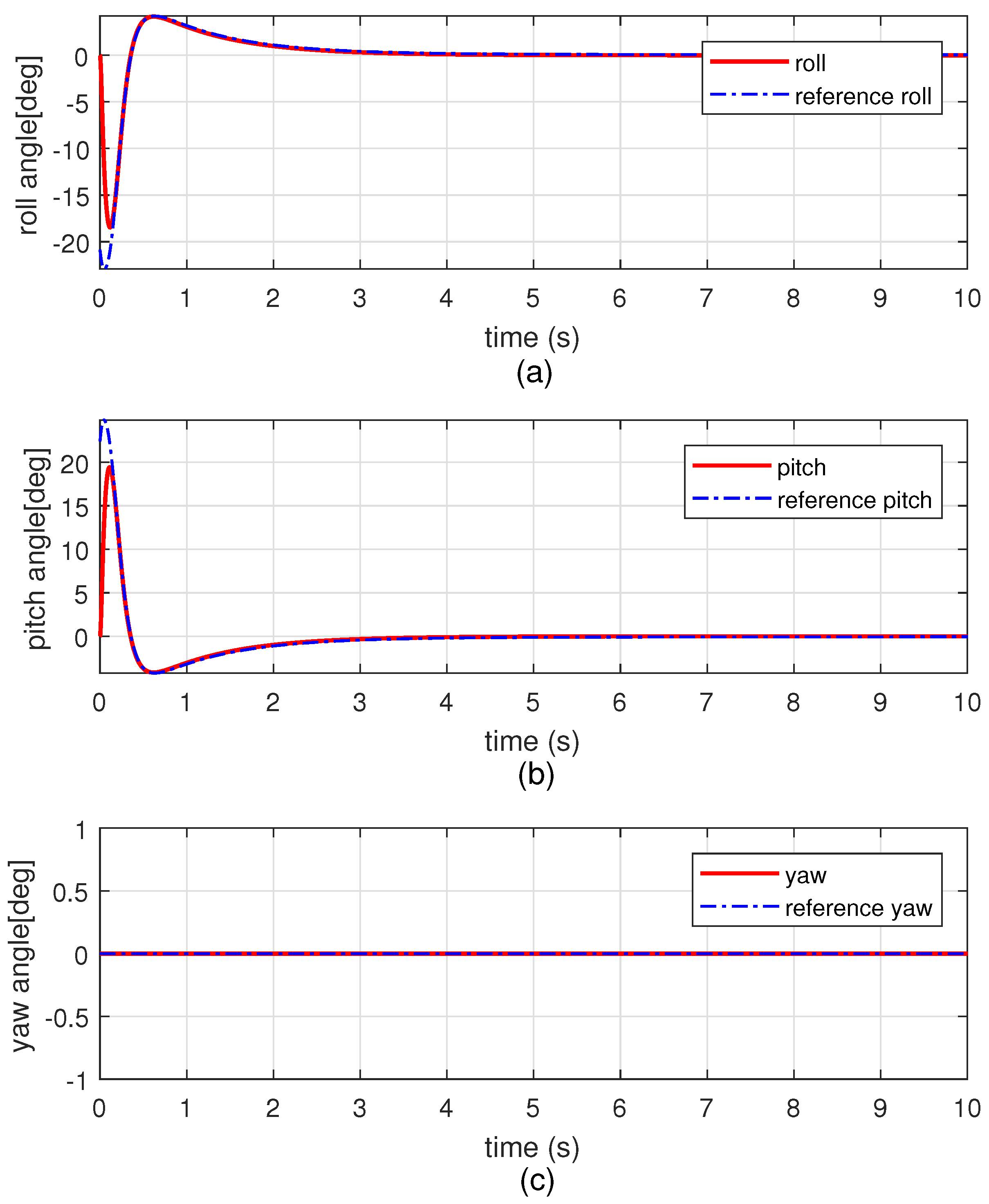
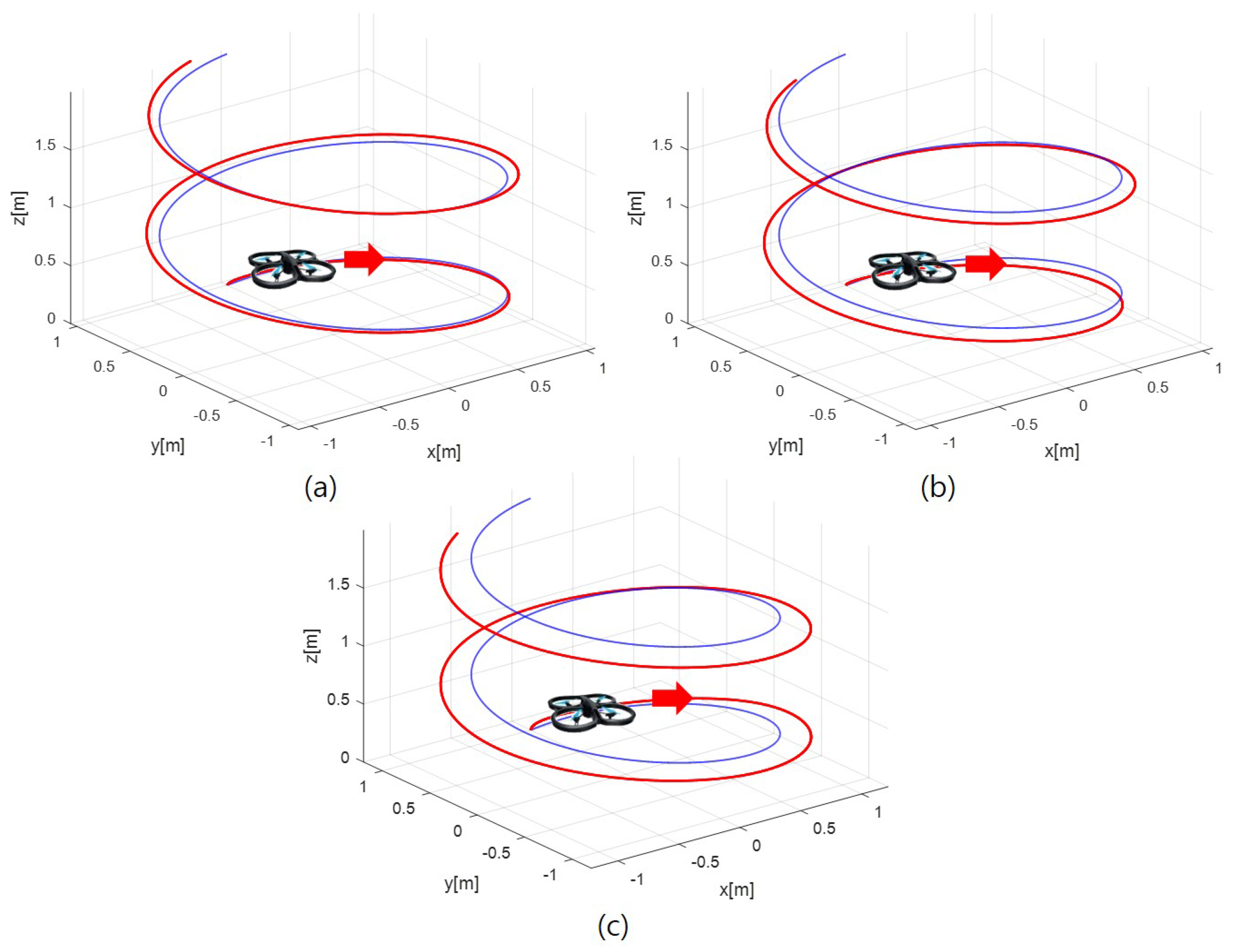
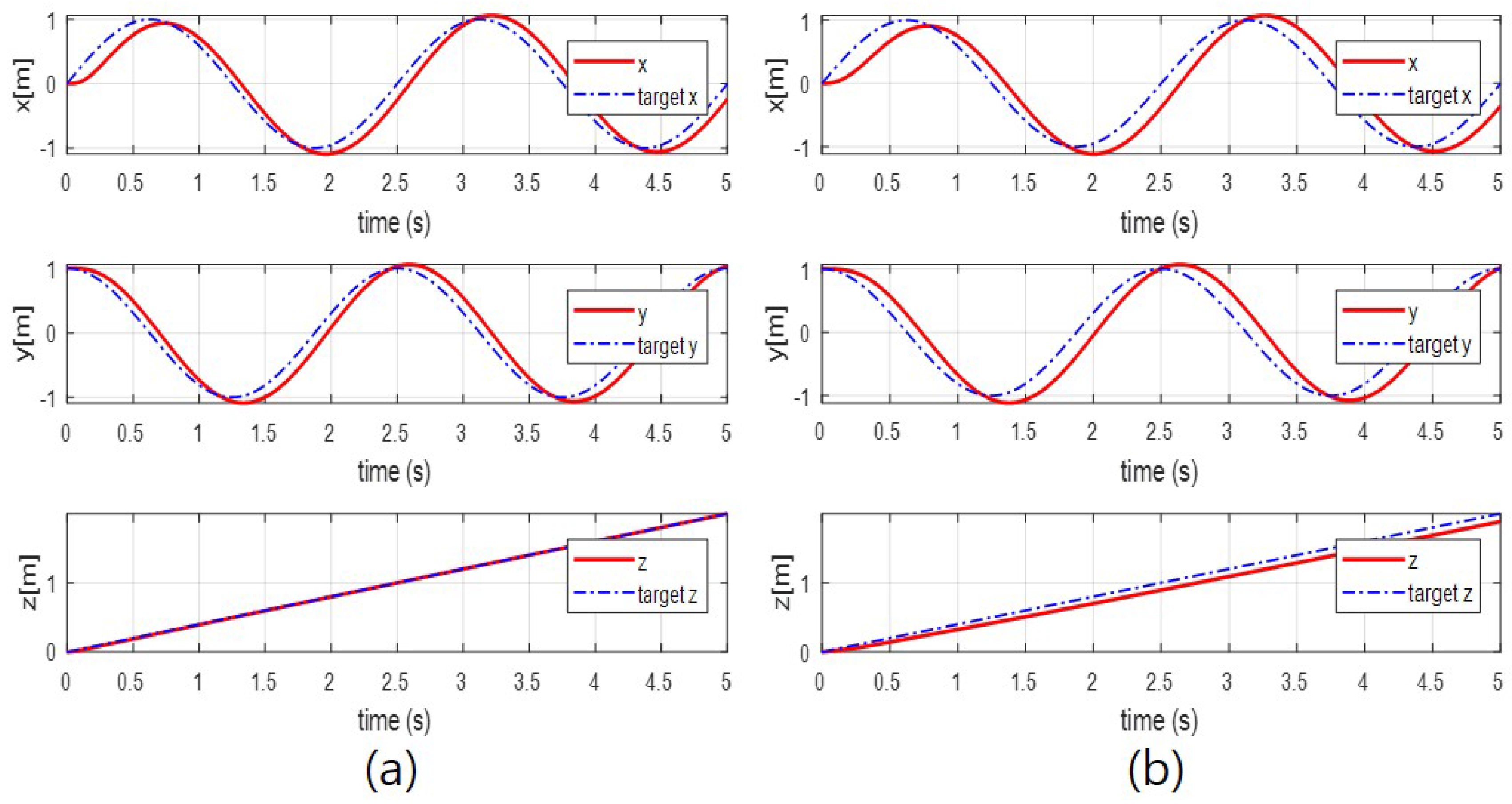
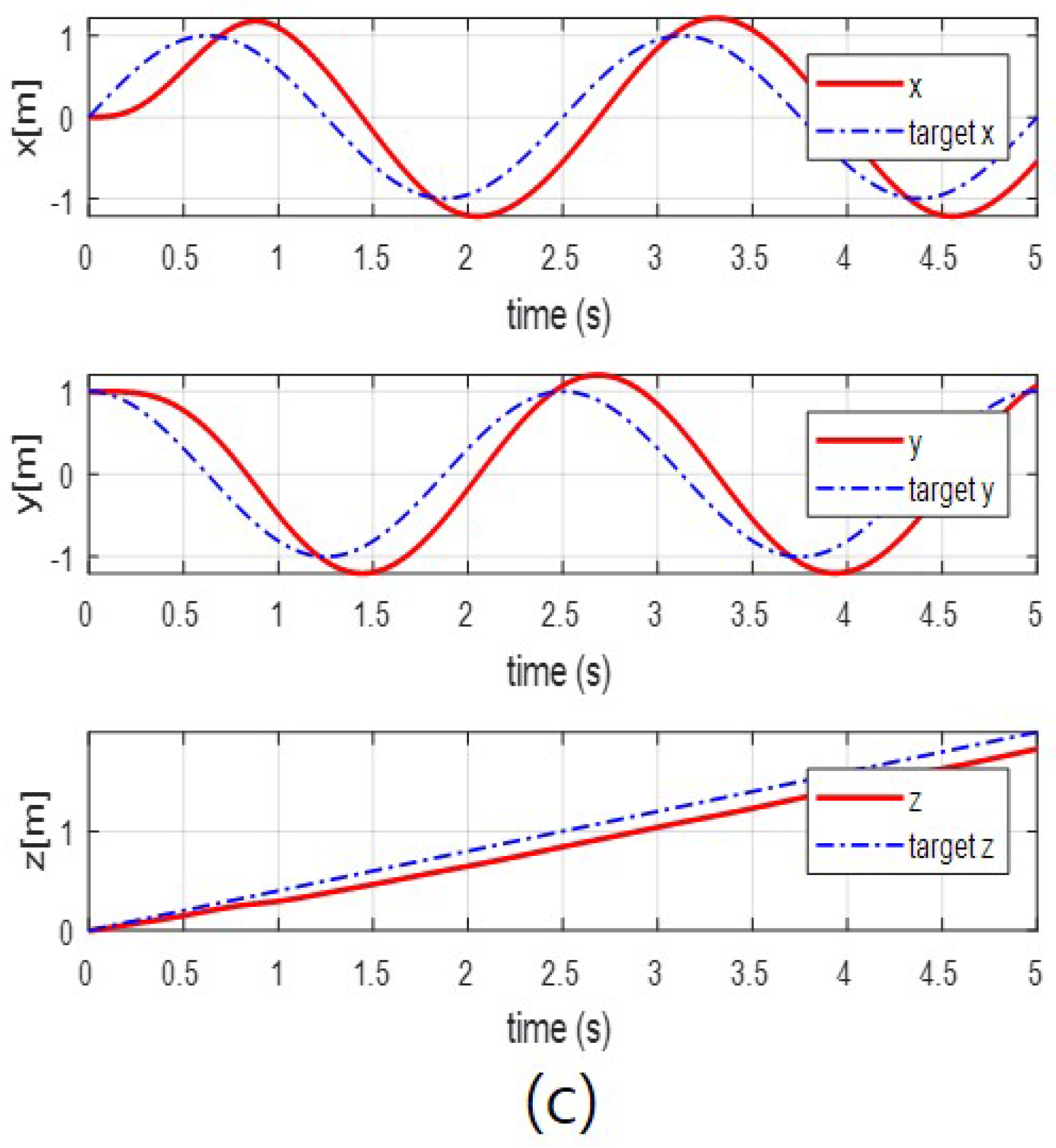
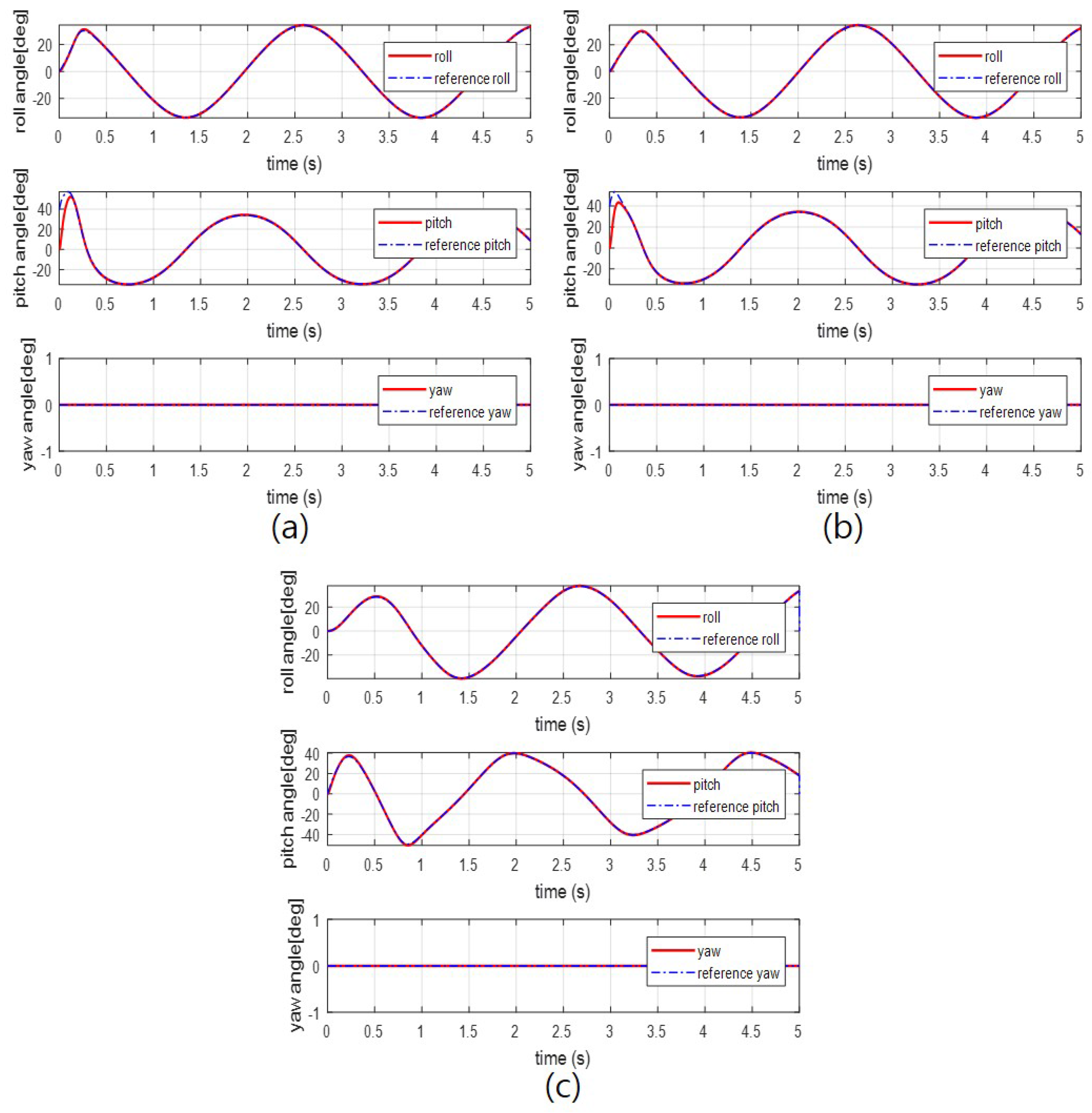
4.2. Simulation Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Erginer, B.; Altug, E. Modeling and PD Control of a Quadrotor VTOL Vehicle. In Proceedings of the 2007 IEEE Intelligent Vehicles Symposium, Istanbul, Turkey, 13–15 June 2007; pp. 894–899. [Google Scholar]
- Oner, K.; Cetinsoy, E.; Unel, M.; Aksit, M.; Kandemir, I.; Gulez, K. Dynamic Model and Control of a New Quadrotor UAV with Tilt-wing Mechanism. IJMME 2008, 2, 12–17. [Google Scholar]
- Castillo, P.; Dzul, A.; Lozano, R. Real-time stabilization and tracking of a four-rotor mini rotorcraft. IEEE Trans. Control Syst. Technol. 2004, 12, 510–516. [Google Scholar] [CrossRef]
- Das, A.; Subbarao, K.; Lewis, F. Dynamic inversion with zero-dynamics stabilisation for quadrotor control. IET Control Theory Appl. 2009, 3, 303–314. [Google Scholar] [CrossRef]
- Bouadi, H.; Bouchoucha, M.; Tadjine, M. Sliding Mode Control Based on Backstepping Approach for an UAV Type-quadrotor. Int. J. Appl. Math. Comput. Sci. 2007, 4, 12–17. [Google Scholar]
- Xu, R.; Ozguner, V. Sliding Mode Control of a class of underactuated systems. Automatica 2008, 44, 233–241. [Google Scholar] [CrossRef]
- Efe, M. Robust Low Altitude Behavior Control of a Quadrotor Rotorcraft Through Sliding Modes. In Proceedings of the 2007 Mediterranean Conference on Control and Automation, Athens, Greece, 27–29 June 2007; pp. 1–6. [Google Scholar]
- Madani, T.; Benallegue, A. Backstepping Control for a Quadrotor Helicopter. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 3255–3260. [Google Scholar]
- Ashfaq, A.; Wang, D. Modelling and Backstepping-based Nonlinear Control Strategy for a 6 DOF Quadrotor Helicopter. Chin. J. Aeronaut. 2008, 21, 261–268. [Google Scholar]
- Das, A.; Lewis, F.; Subbaroa, K. Backstepping approach for controlling a quadrotor using larange form dynamics. J. Intell. Robot. Syst. 2009, 56, 127–151. [Google Scholar] [CrossRef]
- Raffo, G.; Ortega, M.; Rubio, F. An integral predictive/nonlinear control structure for a quadrotor helicopter. Automatica 2010, 46, 29–39. [Google Scholar] [CrossRef]
- Dierks, T.; Jagannathan, S. Output feedback control of a quadrotor UAV using neural networks. IEEE Trans. Neural Netw. 2010, 21, 50–66. [Google Scholar] [CrossRef] [PubMed]
- Alexis, K.; Nikolakopoulos, G.; Tzes, A. Model predictive quadrotor control: Attitude, altitude and position experimental studies. IET Control Theory Appl. 2012, 6, 1812–1827. [Google Scholar] [CrossRef]
- Lai, L.; Yang, C.; Wu, C. Time-Optimal Control of a Hovering Quad-Rotor Helicopter. J. Intell. Robot. Syst. 2006, 45, 115–135. [Google Scholar] [CrossRef]
- Krstic, M.; Tsiotras, P. Inverse Optimal Stabilization of a Rigid Spacecraft. IEEE Trans. Autom. Control 1999, 44, 1042–1049. [Google Scholar] [CrossRef]
- Honglei, A.; Jie, L.; Jian, W.; Jianwen, W.; Hongxu, M. Backstepping-Based Inverse Optimal Atiitude Control of Quadrotor. Int. J. Adv. Robot. Syst. 2013, 10. [Google Scholar] [CrossRef]
- Efe, M. Neural network assisted computationally simple piλdμ control of a quadrotor UAV. IEEE Trans. Ind. Inform. 2011, 7, 354–361. [Google Scholar] [CrossRef]
- Movric, K.; Lewis, F. Cooperative optimal control for multiagent systems on directed graph topologies. IEEE Trans. Autom. Control 2013, 59, 769–774. [Google Scholar] [CrossRef]
- Khalil, H. Nonlinear Systems, 3rd ed.; Prentice Hall: New York, NY, USA, 2002. [Google Scholar]
- Jeong, S.; Seul, J.; Tomizuka, M. Attitude control of a quad-rotor system using an acceleration-based disturbance observer: An empirical approach. In Proceedings of the 2012 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Kachsiung, Taiwan, 11–14 July 2012; pp. 916–921. [Google Scholar]
- Bouabdallah, Samir, A.N.; Siegwart, R. PID vs. LQ control techniques applied to an indoor micro quadrotor. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems, Sendai, Japan, 28 September–2 October 2004; pp. 2451–2456. [Google Scholar]

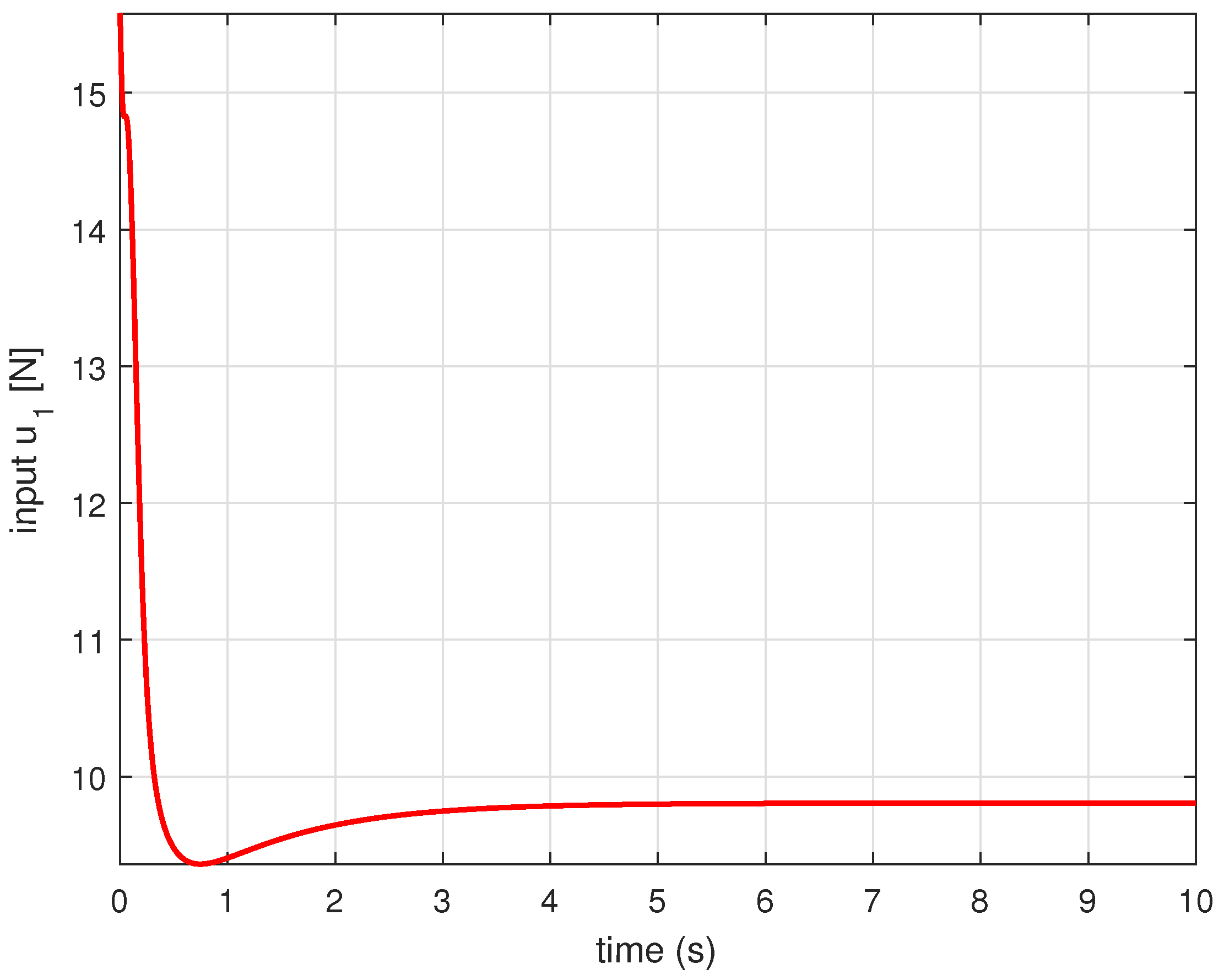
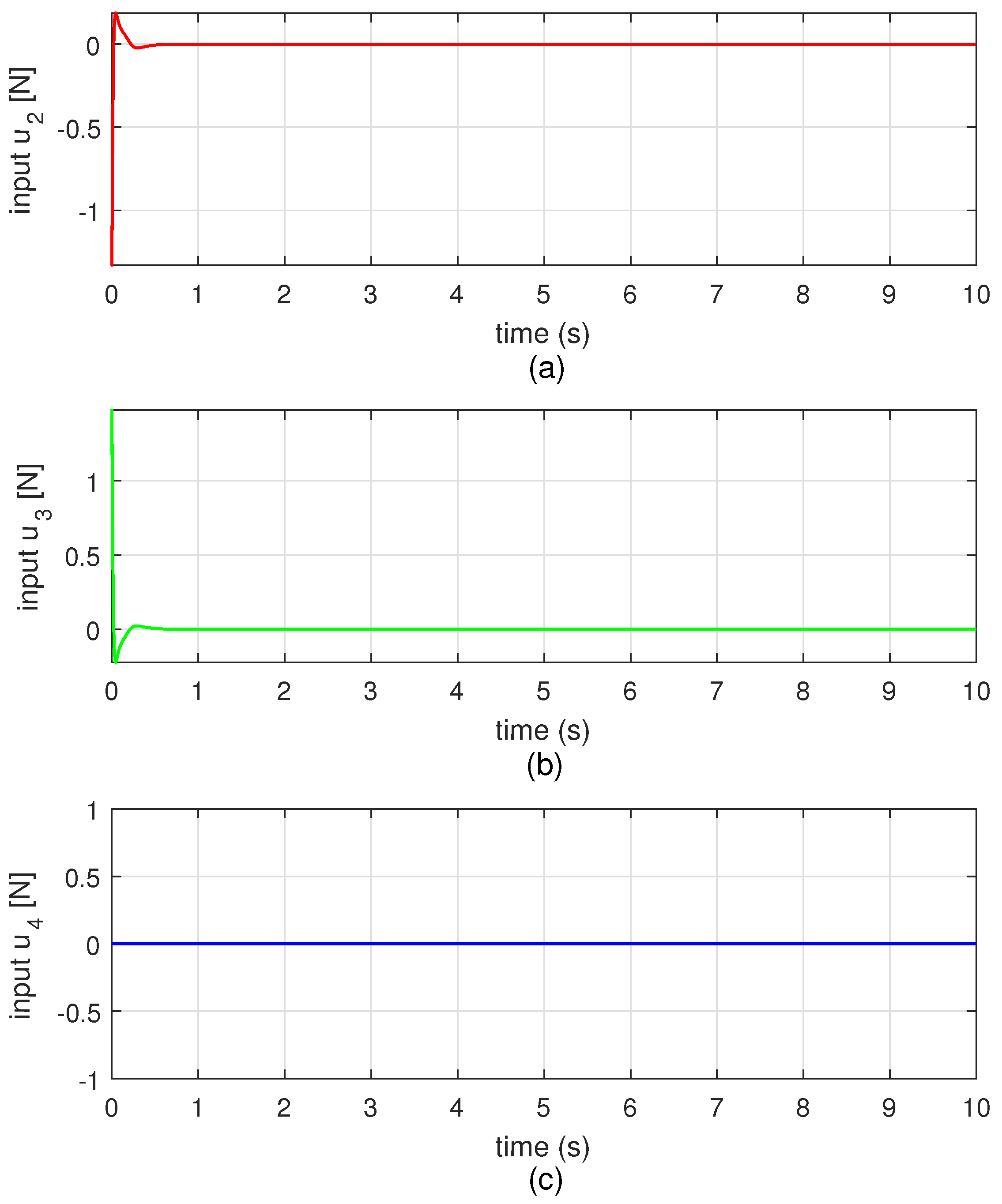
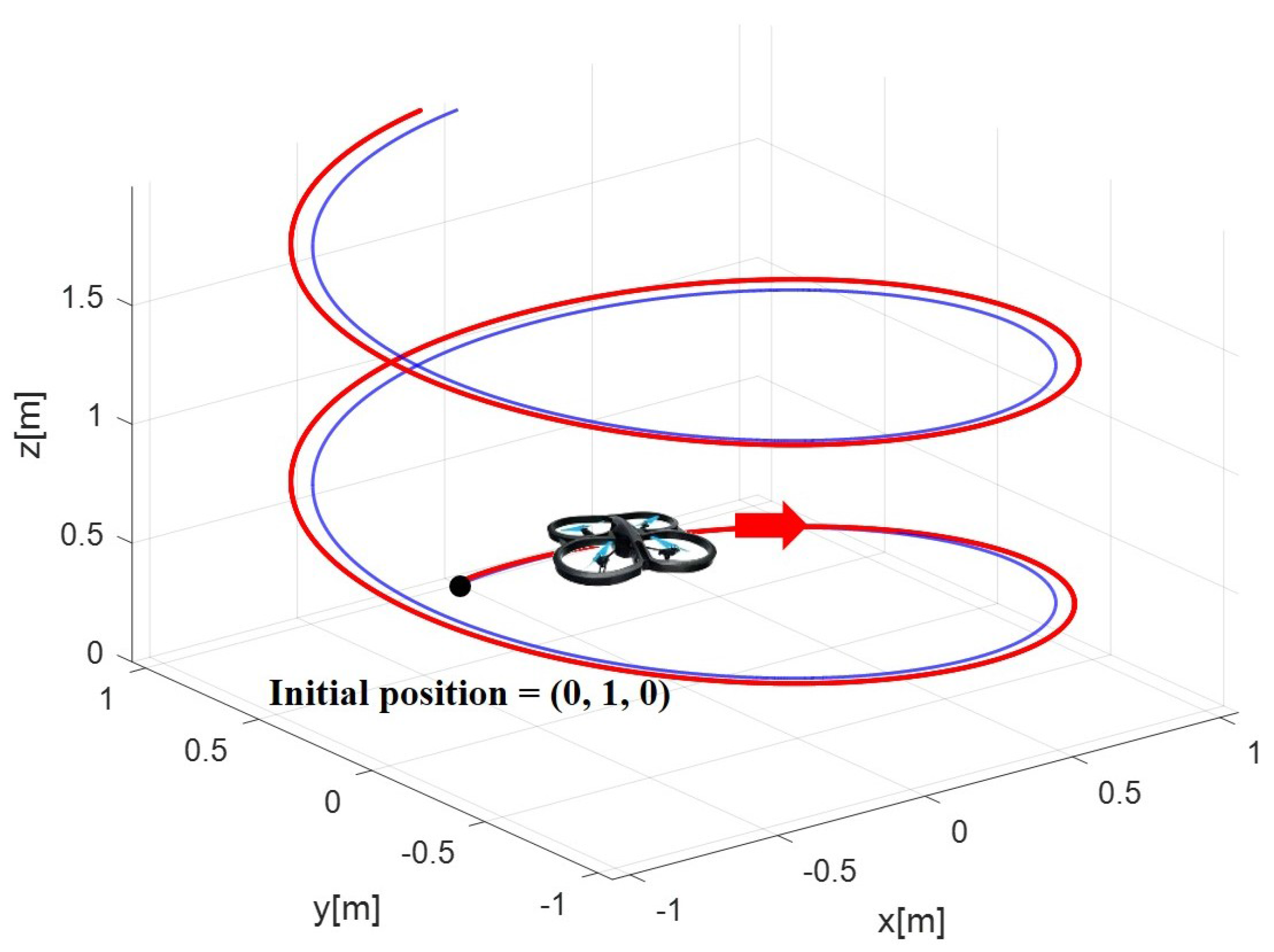
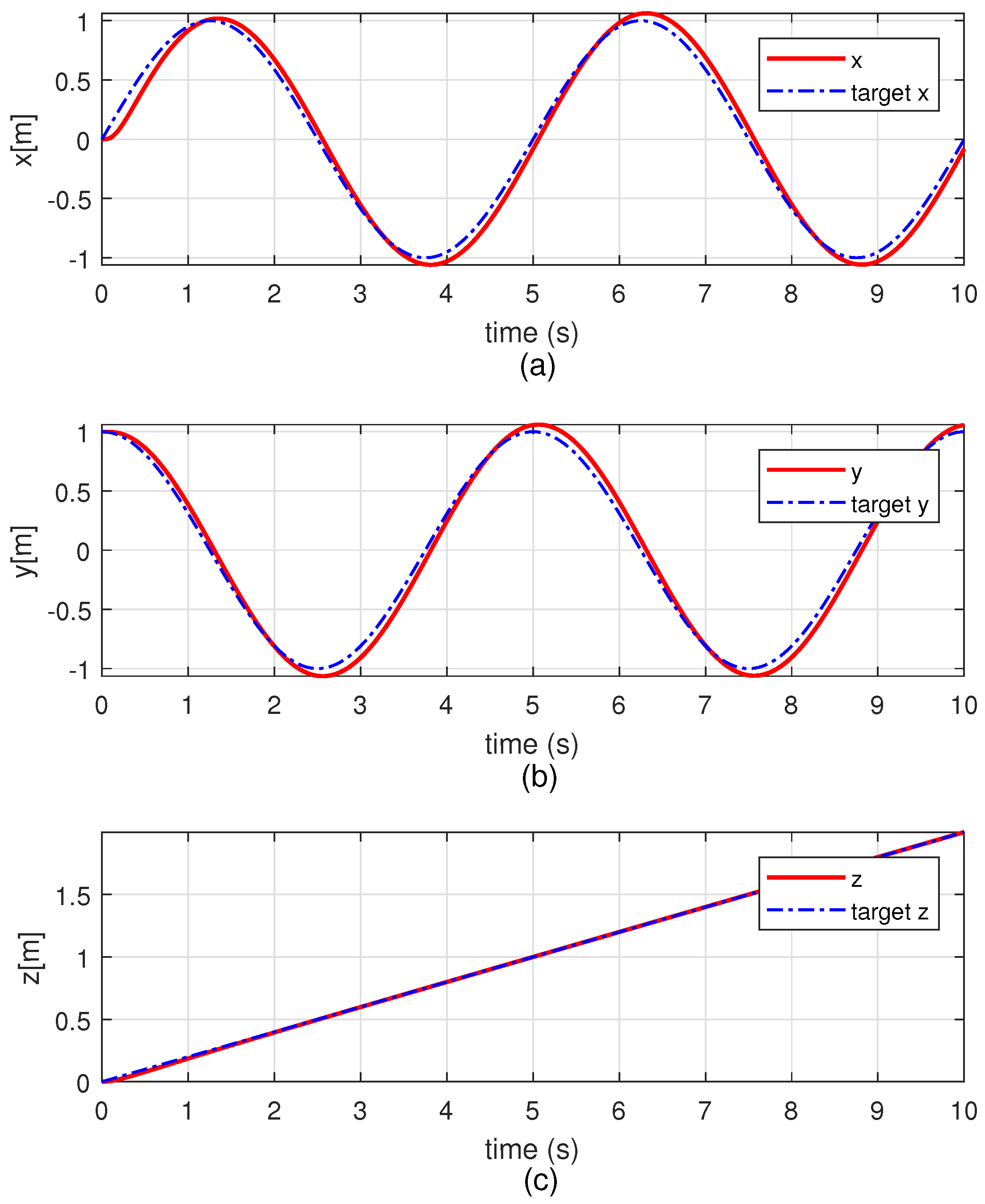

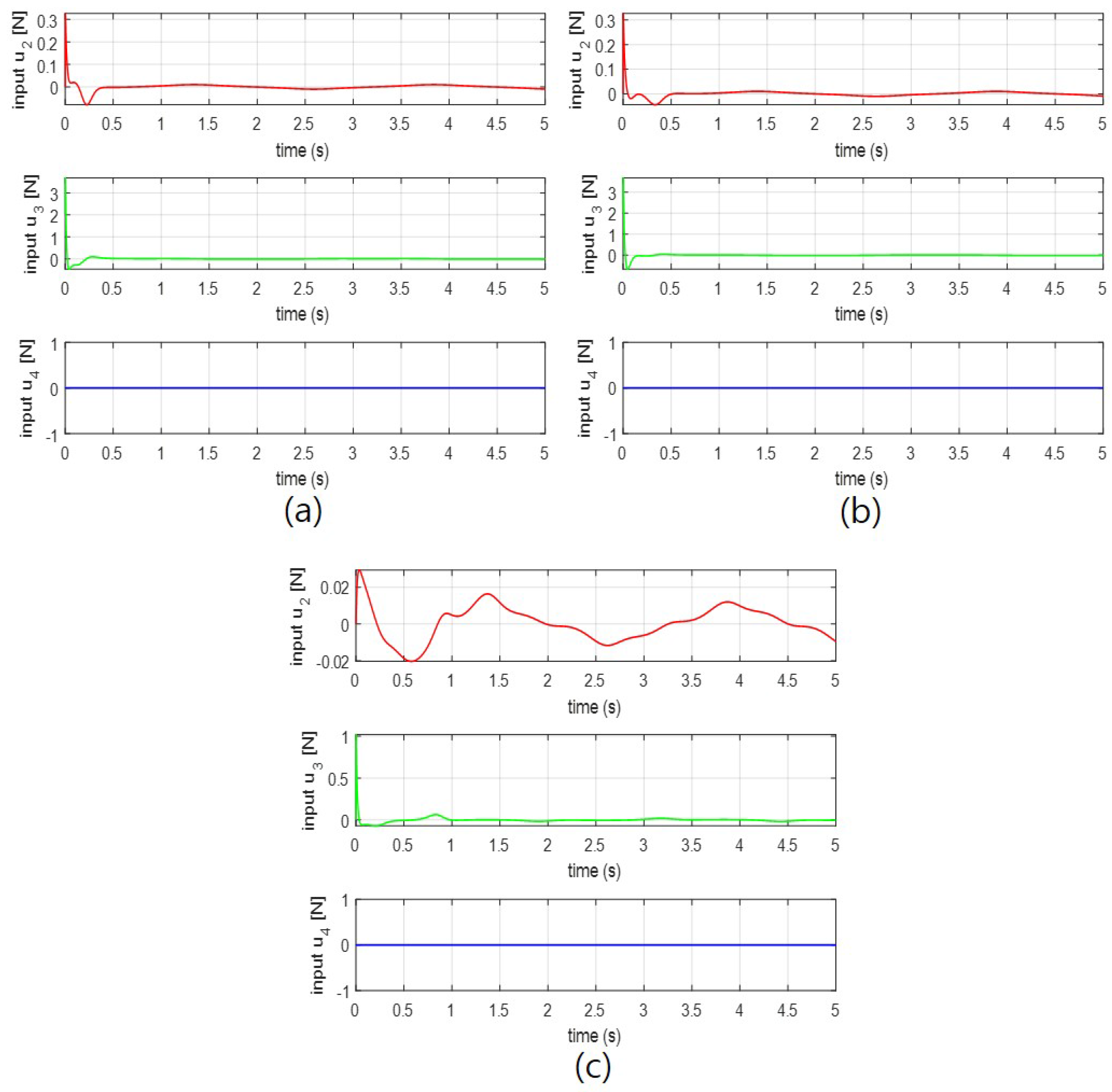
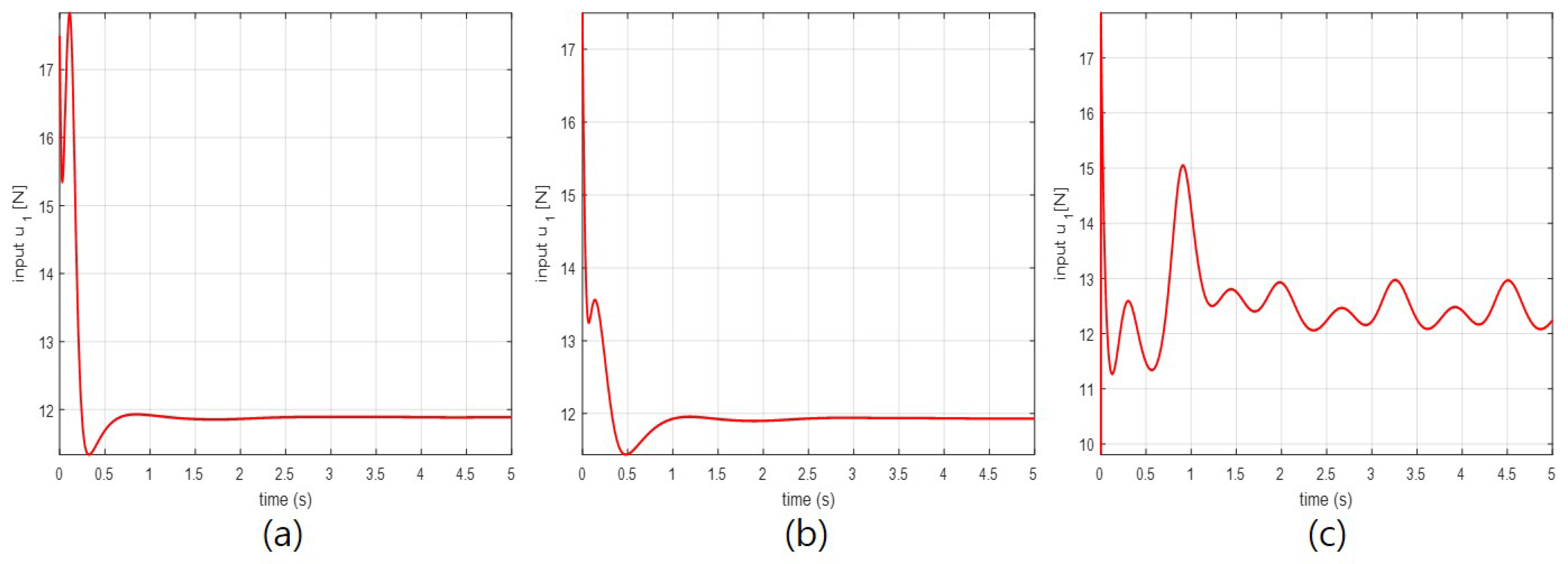
| Feedback gains of the position controller | |||
| 0.03 | |||
| 0.001 | |||
| PID parameters of rotational controller | |||
| 3 | 3 | 3 | |
| 0.3 | 0.3 | 0.3 | |
| 0.2 | 0.2 | 0.2 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, K.U.; Choi, Y.H.; Park, J.B. Inverse Optimal Design for Position Control of a Quadrotor. Appl. Sci. 2017, 7, 907. https://doi.org/10.3390/app7090907
Lee KU, Choi YH, Park JB. Inverse Optimal Design for Position Control of a Quadrotor. Applied Sciences. 2017; 7(9):907. https://doi.org/10.3390/app7090907
Chicago/Turabian StyleLee, Keun Uk, Yoon Ho Choi, and Jin Bae Park. 2017. "Inverse Optimal Design for Position Control of a Quadrotor" Applied Sciences 7, no. 9: 907. https://doi.org/10.3390/app7090907
APA StyleLee, K. U., Choi, Y. H., & Park, J. B. (2017). Inverse Optimal Design for Position Control of a Quadrotor. Applied Sciences, 7(9), 907. https://doi.org/10.3390/app7090907





