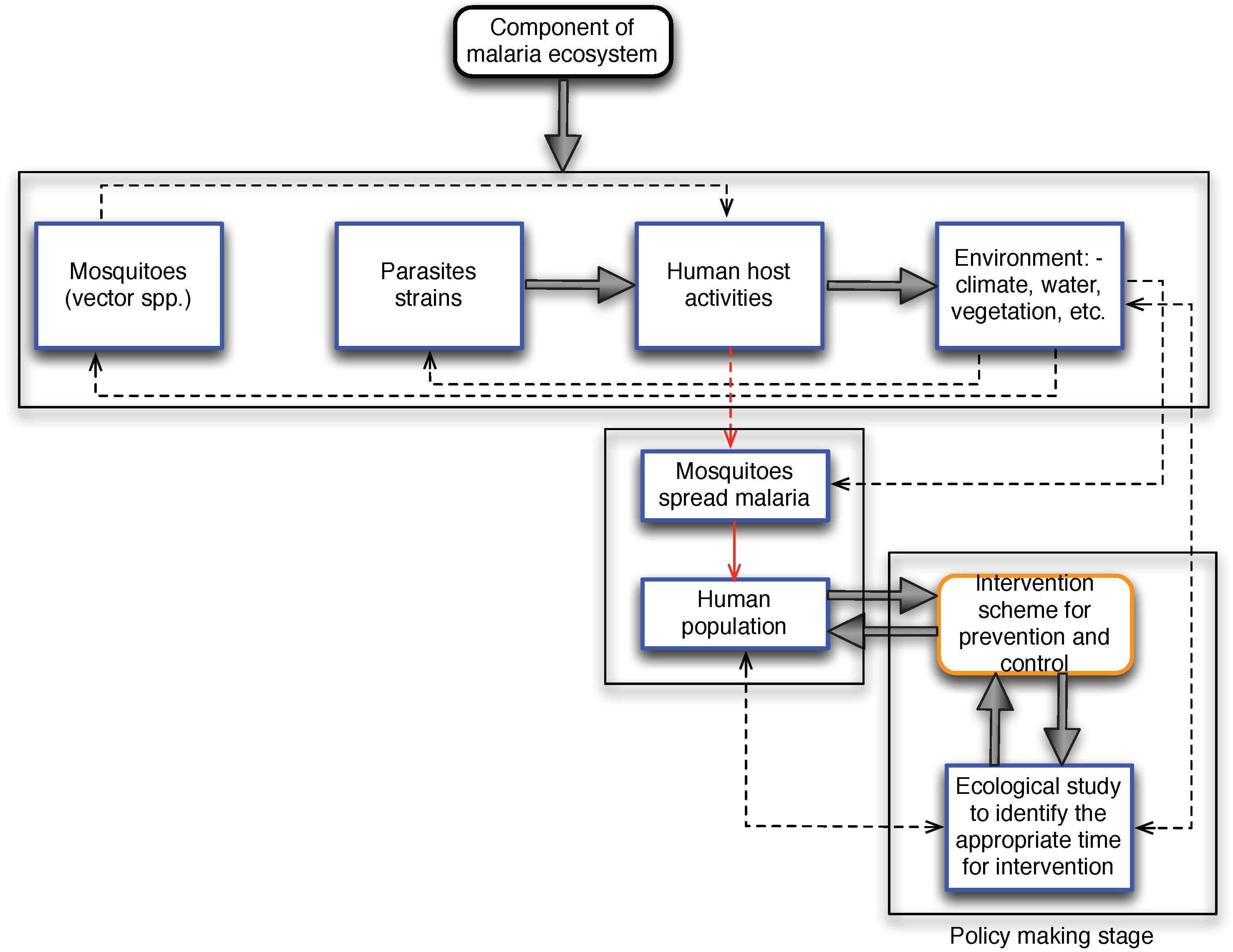
These components are very dynamic in nature due to the inherent characteristics of ecology and the anticipatory change to biodiversity because of global warming. The works by [
15,
16,
17] reported that ecological changes would adversely affect human health in some ways that are both obvious and obscure. However, the growing evidence also suggests that due to the rise in temperature as a result of the anticipated global warming, some previously unexposed regions of malaria transmission would have a 50% chance of experiencing it due to the link between malaria incidence and ecological factors [
18]. The relationship between environmental changes and human health cannot be overemphasized because of the inherent variability and complexity of human nature. In many circumstances, grasslands and forest are converted for agriculture to reduce communicable disease, including wetland drainage for the prevention and control of malaria [
17]. These activities can either lead to unintended negative health effects or succeed in the designed purpose. Also, transforming forest to augment food production may, in the long run, lead to the creation of a suitable environment for disease-causing agents such as mosquitoes for malaria transmission [
19].
2.6. Presentation of Results
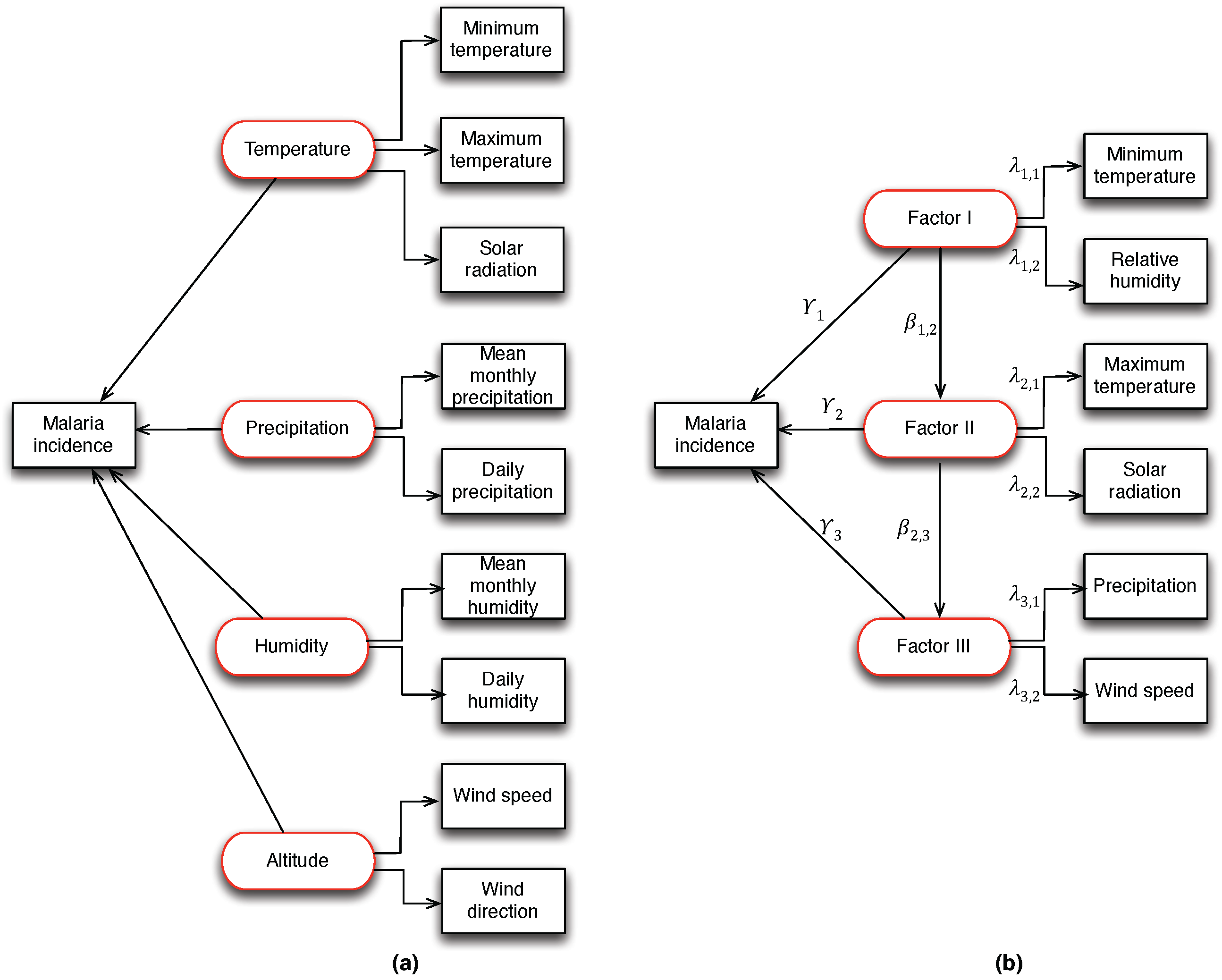
In the application of PLS-SEM, three weighting schemes such as centroid weighting, factorial weighting and path weighting are conceptually used for model specifications and estimations. The conceptual SEM presented in
Figure 3a shows the hypothetical causal relationship between latent (hidden) variables and observed meteorological (manifest) variables to the occurrence of malaria incidence. For the identification of confounding hidden variables, we performed factor analysis using exploratory factor analysis (EFA) [
34]. From the results, three hidden factors were identified: Factor I (related to the minimum temperature and relative humidity), Factor II (related to the maximum temperature and solar radiation) and Factor III (related to precipitation and wind speed). The identified factors accounted for 64% of the total variance, and at
= 5% level of significance,
= 13.91, df = 8, Pvalue = 0.0841. This result provides sufficient evidence to explain malaria incidence in the study area.
We also explored the Guttman–Kaiser Criterion [
35] and Cattell scree plots [
36], to determine the number of factors to extract, the result of which reconfirmed the existence of three hidden ecological factors to the incidence of malaria. In the Guttman–Kaiser Criterion, we have the eigenvalues 2.71, 1.53, 1.02, 0.82, 0.57, 0.29, 0.05 computed using the correlation matrix (see
Table 1); however, the rule for extraction is based on the factors whose eigenvalues are greater than unity. We then discard those factors that have eigenvalues less than unity, and are left with three eigenvalues indicating the number of factors to be considered. Similarly, the Cattell scree plot presented in (
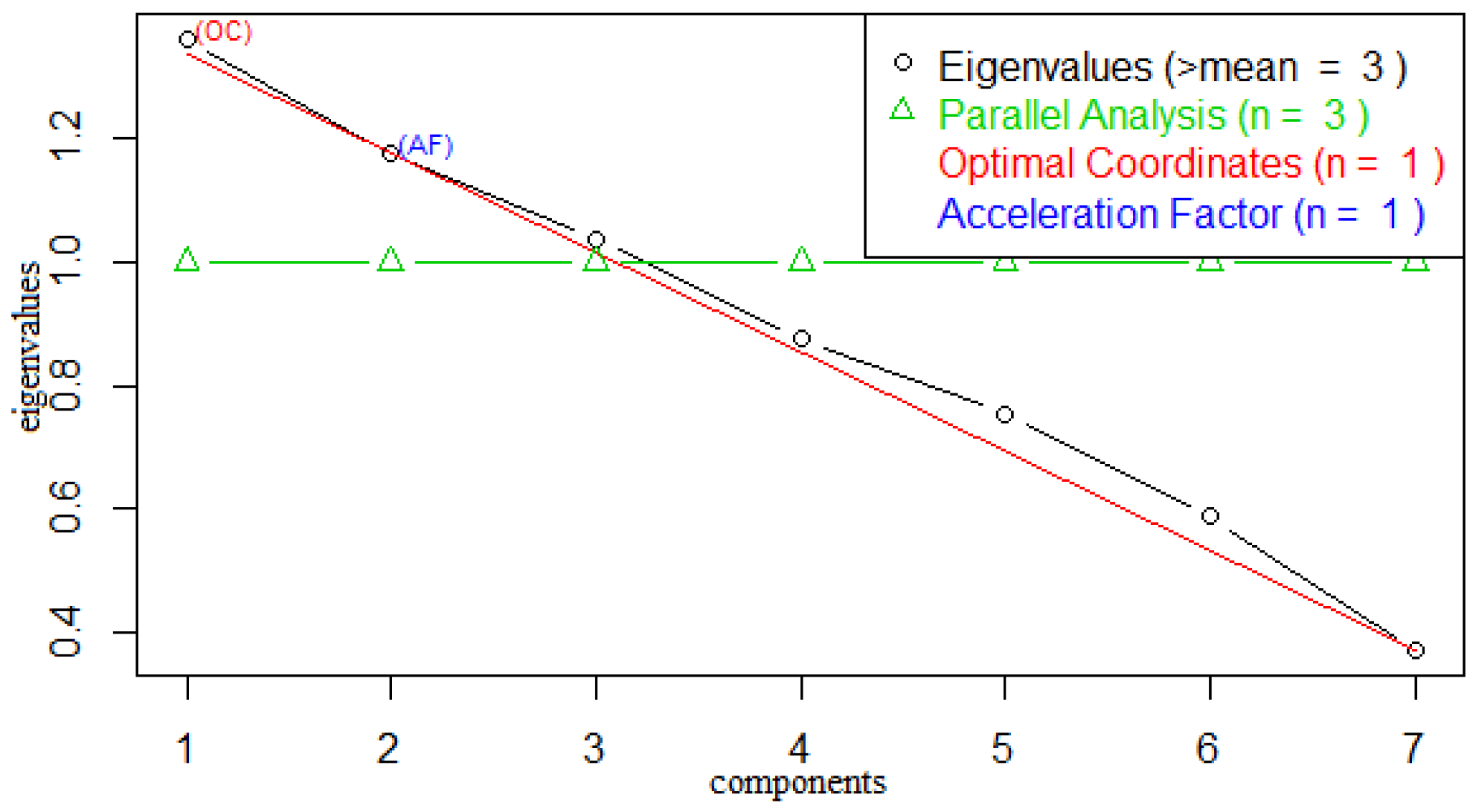
Figure 4) facilitates decisions regarding the number of factors to retain.
By analysing
Table 1, we obtained the scree plot shown in
Figure 4 which represents the relative proportion of variance accounted for by the components. In the scree plot, the eigenvalues of the first three components greater than unity can be seen from the parallel indicator, while the subsequent components below unity also line up beneath the parallel indicator. However, it is important to evaluate the variance accounted for by a few of the eigenvalues regarded as sufficient so that we can focus on them and discard the remaining insufficient factors as noise.
In
Table 2, we present Pearson’s cross-correlation between meteorological variables and occurrence of malaria incidence at various lag effects from 0 to 3 months. The Lag 0, Lag 1 and Lag 2 (e.g., 0 month, 1 month and 2 month) presented in
Table 2 which indicates the lagged correlation effects between climate variables and the incidence of malaria in the study area. We observed that at lag effects of 1 month, the minimum temperature, maximum temperature and relative humidity have positive association with malaria incidence as indicated by 0.321, 0.215 and 0.254 respectively. While the precipitation is negatively correlated with malaria incidence at lag effects of 1 month as indicated by −0.292. This explained that the climate drivers at lag of 1 month would be quite enough for the mosquitoes to reproduce and also complete their incubation periods (EIP) to becomes fully active in transmitting malaria infection. We found that the preceding result is consistent with other relevant studies on the influence of meteorological variables on the malaria incidence [
37]. The 1 month time lag in the study area is sufficient to capture the pattern of malaria transmission for various strains of plasmodium parasites with definite lengths of EIP. This period usually takes about 10–15 days [
38] and temporally varies over location, parasite species and climatic resolution. At Lag 0 and Lag 2, the minimum temperature, precipitation and relative humidity have negative lag effects at 0 month and 2 month except the maximum temperature which has effects of 0.284 and 0.092. These results revealed some clear indications that the malaria transmission in the study area at Lag 0 and Lag 2 suffered a negative effect, which might be attributed to the bi-annual rainfall pattern, low relative humidity—say less than 50%—and inability of mosquitoes completing the EIP cycle. In general, the result showed that maximum temperature, minimum temperature, and relative humidity were related to the malaria incidence at lagged effects of 1 month (i.e., a month in advance) except precipitation which has a negative association in the study area.
Some important summary statistics are presented in
Table 2, which describe the distributional pattern of the climate indicators of malaria incidence and variance inflated factor (VIF). In factor analysis, multicollinearity can be used as a diagnostics check prior to application of regression analysis, whereby variables with high-factor loadings are typically multicollinear. We compute VIF of the climate variables to measure the degrees of multicollinearity and identify those factors that are independent of the magnitude of their VIF. In
Table 2, the minimum temperature and relative humidity have VIF of 8.7919 and 9.0065 that gives a high degree of multicollinearity. The results revealed a high independent predictor of malaria incidence in the study area, and the degree to which they are independent gives evidence to accurately determine the major factors. However, the values of kurtosis (see
Table 2) indicate a high peak of the climate variables with positive values across all the indicators except the wind speed which indicates a flat distribution. Positive values, generally listed in
Table 2, indicate that the peakedness of distribution of the climate variables particularly influences the malaria incidence. Also, the standard error estimates provide information on the statistical accuracy of the climate variables; the larger the standard error, the wider the confidence interval of the statistic and vice-versa.
Non-normality of the dataset is one necessity for adopting PLS-SEM, and it is very robust when used on extremely non-normal data [
39]. We examined the degree to which the data on malaria incidence are non-normal using the Shapiro–Wilk tests by invoking R software (3.4.1, University of Aukland, New Zealand). The results show that the null hypothesis (Ho) is rejected, indicating that the malaria incidence dataset is non-normal as suggested by the following indices W = 0.9486,
p-value = 0.0134 and
= 0.05, respectively. This method is particularly chosen and useful in smaller samples sizes, less than 2000 [
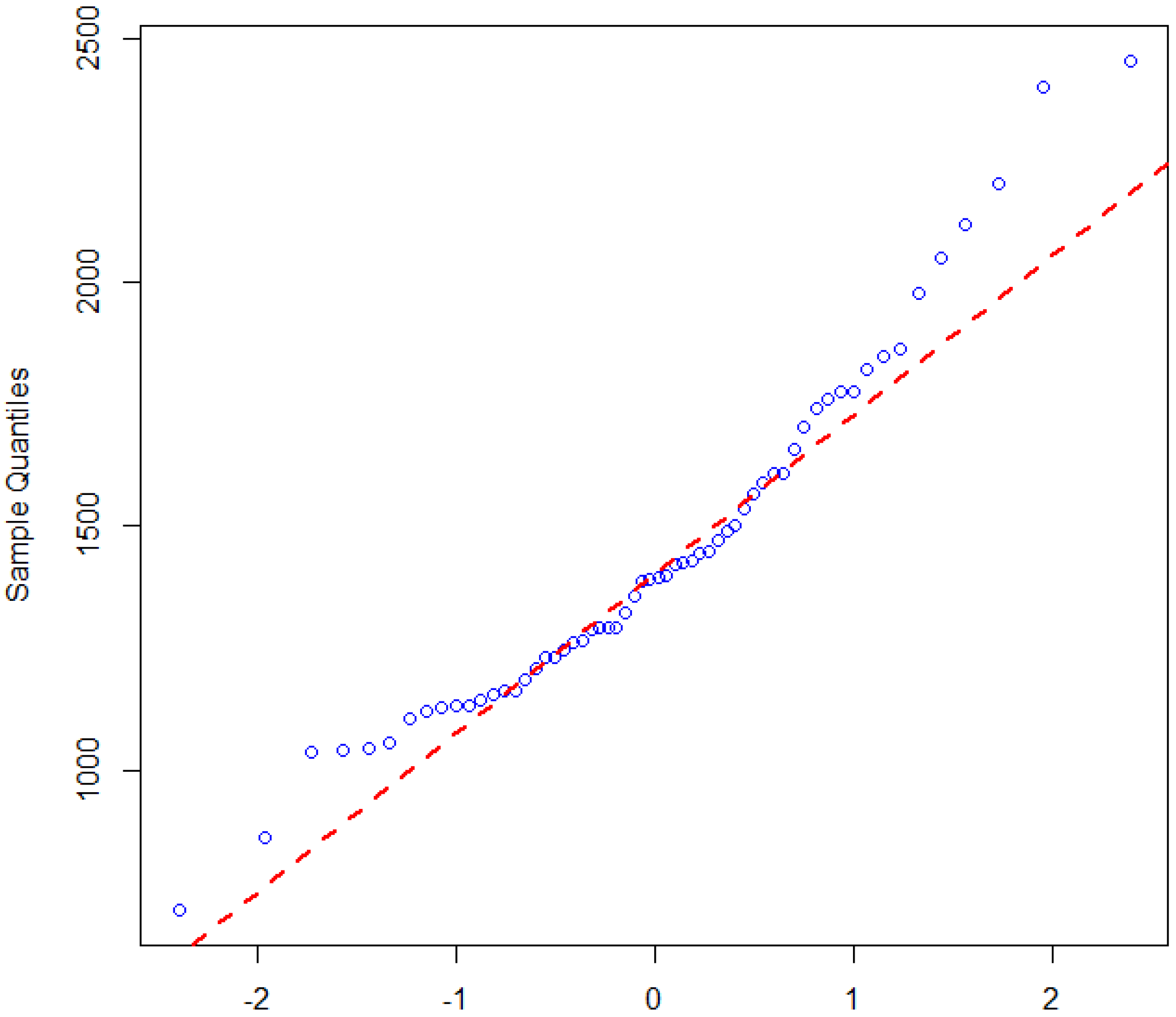
40], and the null hypothesis is that the data are from a normal distribution. Similarly, we used a graphical approach called quantile–quantile (Q–Q) plot [
41] and tested for normality of the dataset in similar fashion. The approach creates a plot from the ranked samples of the dataset against a similar number of ranked theoretical samples from a normal distribution. The plot shown in
Figure 5, clearly indicates that the data points for malaria incidence are deviating from the straight line. Hence, the malaria incidence dataset is therefore not normally distributed using the Q–Q plot.
In
Table 3, we show the results of the factor score estimates for path coefficients of SEM estimated using PLS path modelling, and three different structural model weighting schemes were analysed. We observed that Centroid (A) converges faster after 12 iterations, while factorial (B) and path weighting (C) converge after 15 iterations. The procedure of selecting the best weighting scheme is determined by the maximum number of iterations that will be used for calculating the PLS results and this algorithm did not stop until the maximum number of iterations is reached due to the stop criterion. From
Table 3, we can observe that the B and C weighting schemes converge at the same maximum number of iterations in estimating the parameters of SEM. The weighting scheme provides the highest R
value for endogenous latent variables in the PLS path model specifications and estimations. This result shows that the C weighting scheme is better than A and B, as suggested by [
42] in terms of robustness and also when the path model includes higher-order constructs.
Table 4 presents the results of bootstrapping sampling for outer loadings of the observed variables and path coefficient of the latent variables estimated using PLS-PM. The results also show that all outer loadings and path coefficients are significant at
= 5%, except for the solar radiation with Factor II and wind speed with Factor III that contains zero-point in the bootstrap confidence interval. Furthermore, the interaction effects of the Factors between I and II, II and III were also investigated and the results revealed that none of the Factor combinations is significant in the incidence of malaria in the study area. This result provides sufficient evidence that high malaria incidence in the study area was attributed to the occurrence of minimum temperature and relative humidity which are identified as Factor I.
The decision to select the most influential hidden ecological factor to the incidence of malaria is based on the communality and Dillon–Goldstein’s indices. Furthermore,
Table 5 summarizes the results, indicating some indices for selecting the hidden ecological factors to the high incidence of malaria in the study area. Among the three factors identified by EFA, we find that Factor I, indicated by minimum temperature and relative humidity, influences malaria transmission with communality index (0.94) and Dillon–Goldstein’s
(0.97). This result is also consistent with the finding in [
37], where a positive association exists between temperature and occurrence of dengue. Factor II and Factor III appear to have less influence on the malaria incidence.