Experimental Study on Mechanical Behavior of Shear Connectors of Square Concrete Filled Steel Tube
Abstract
:1. Introduction
2. Specimen Design and Test Scheme
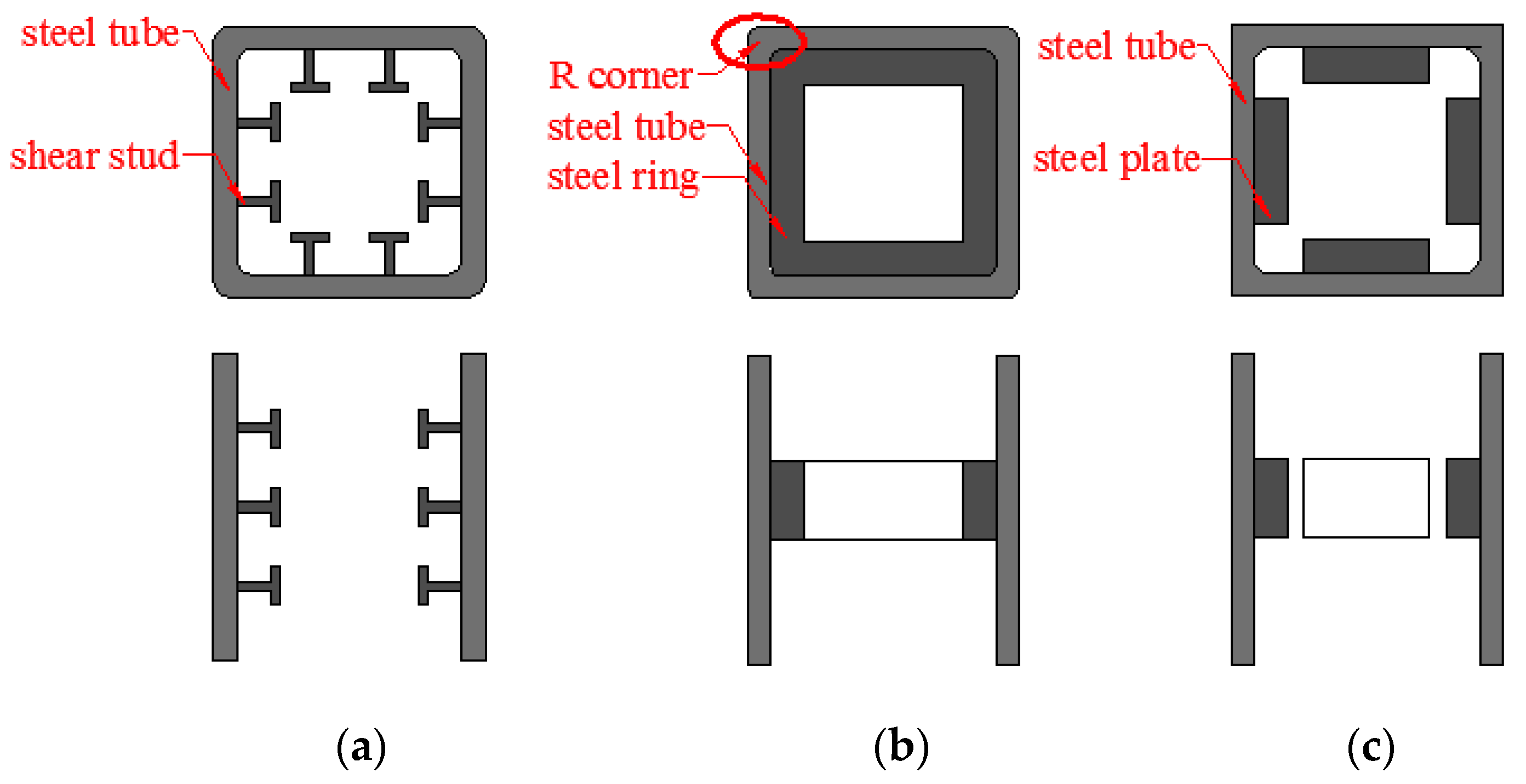
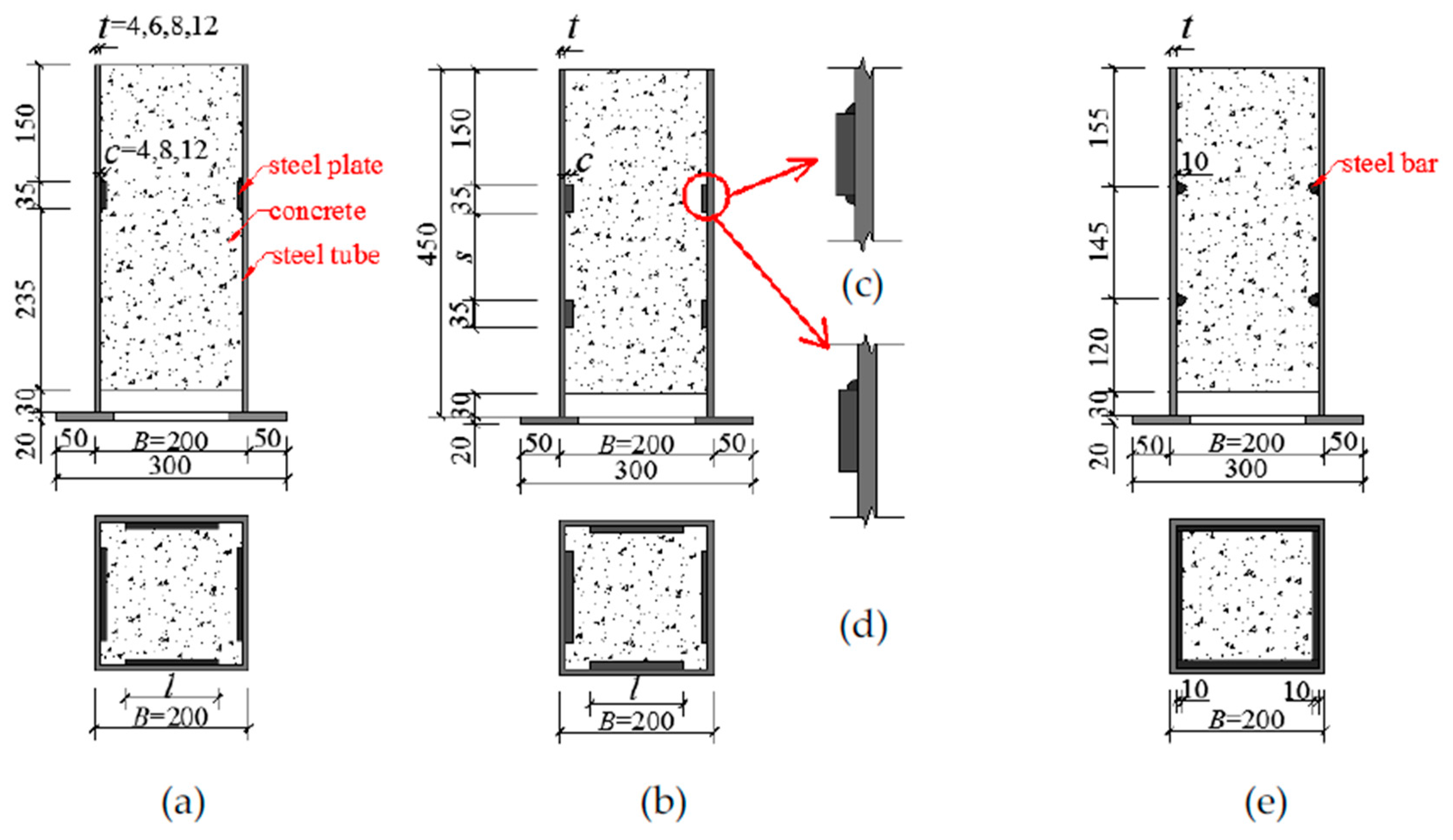
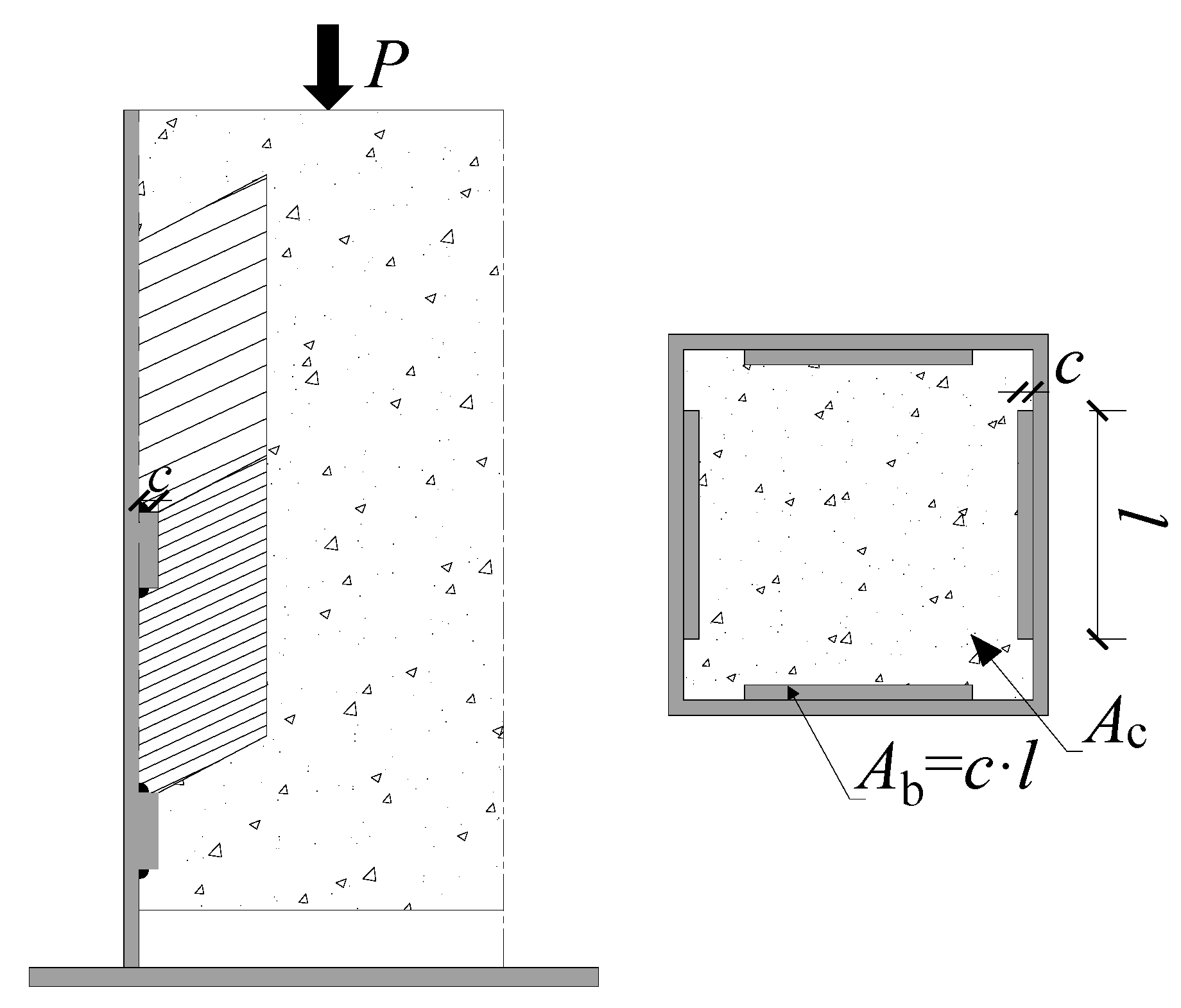
2.1. Specimen Design
2.2. Materials Properties
2.2.1. Concrete
2.2.2. Steel
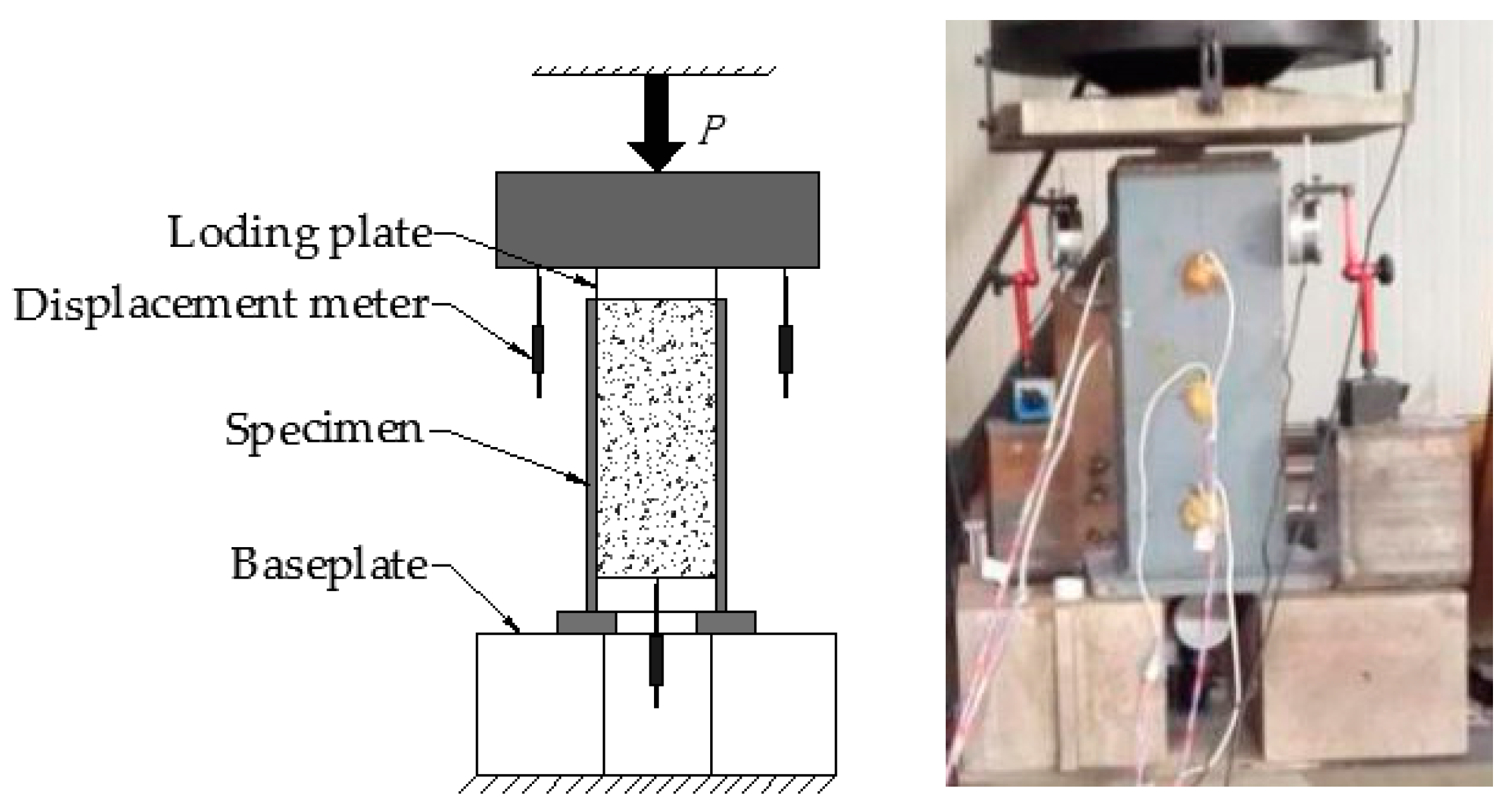
2.3. Test Scheme
2.3.1. Loading Scheme
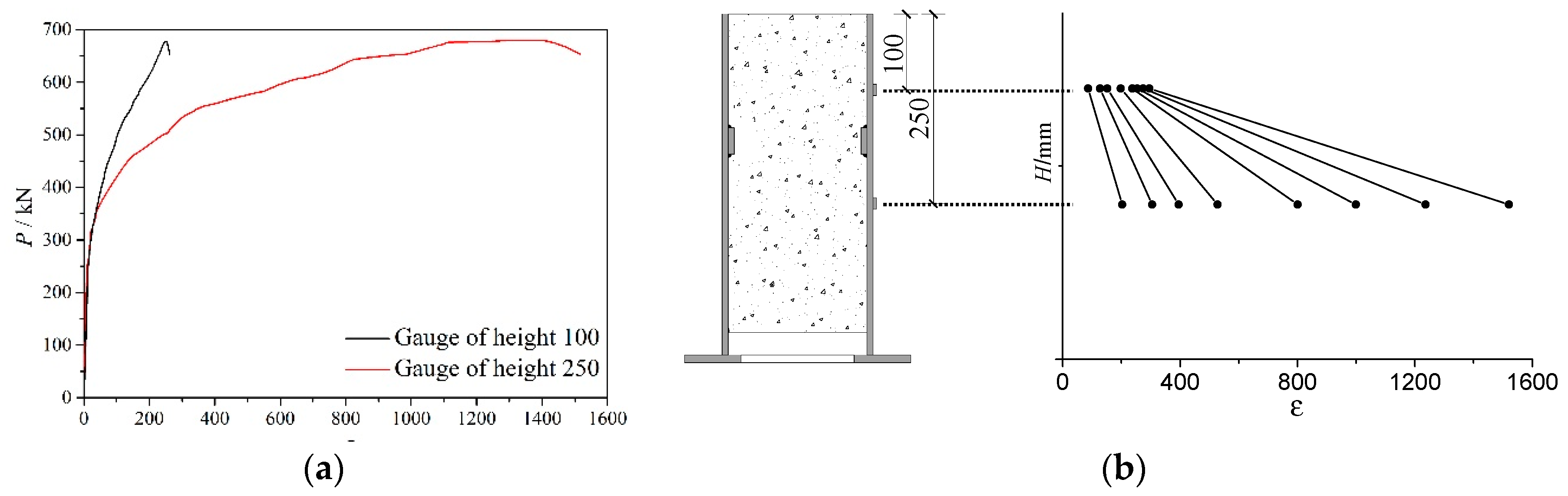
2.3.2. Arrangement of Measurements
3. Test Results and Theoretical Analysis
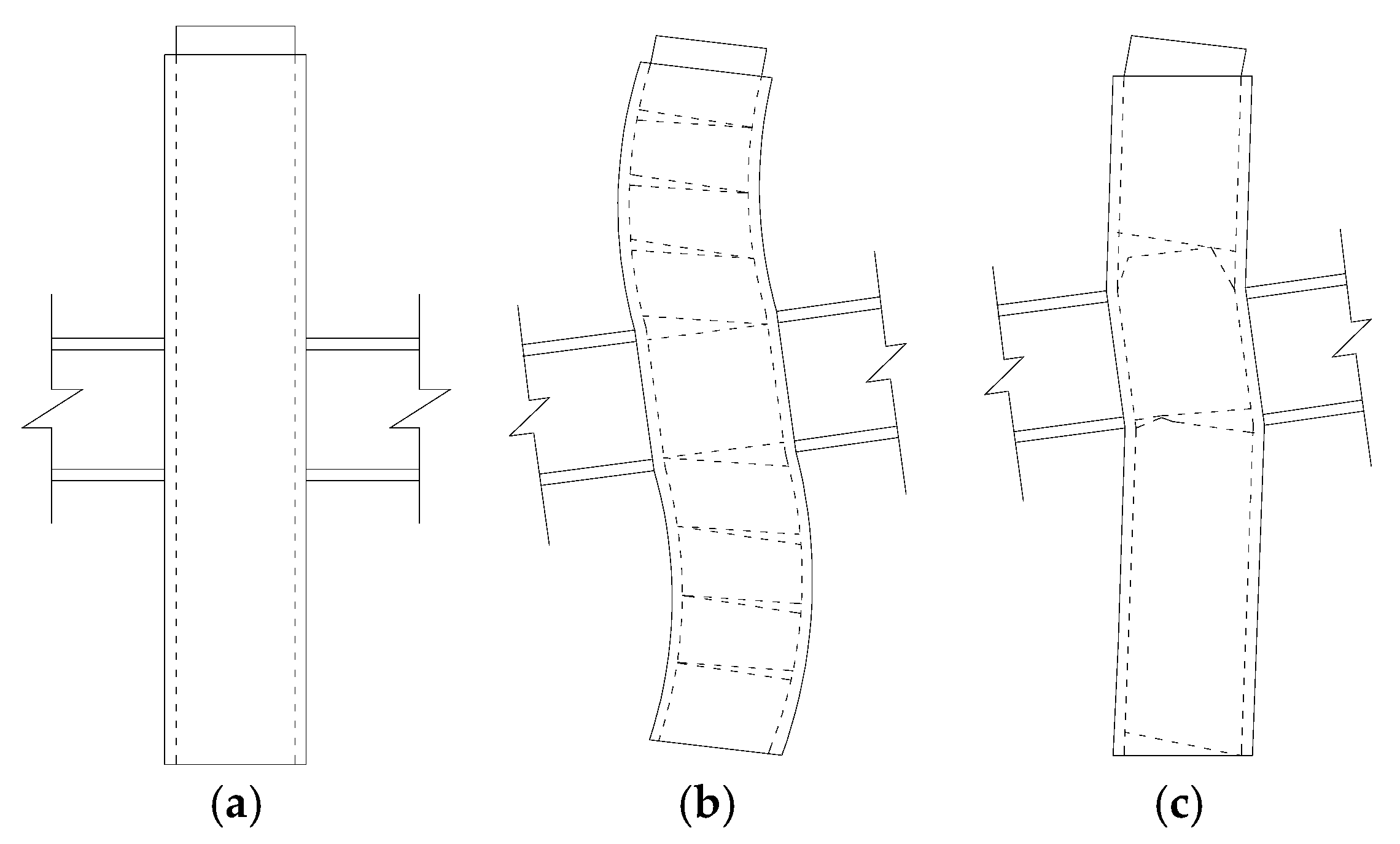
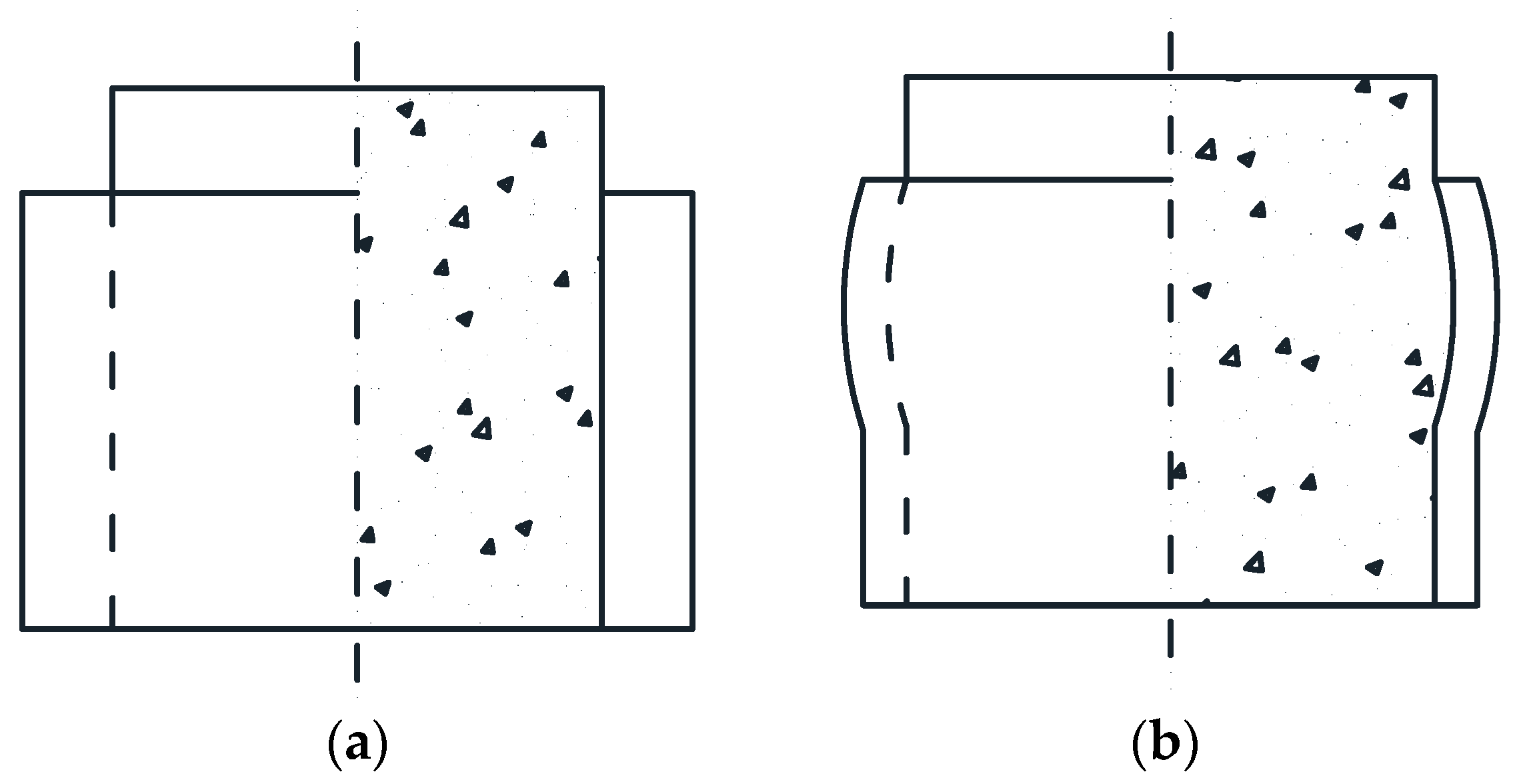
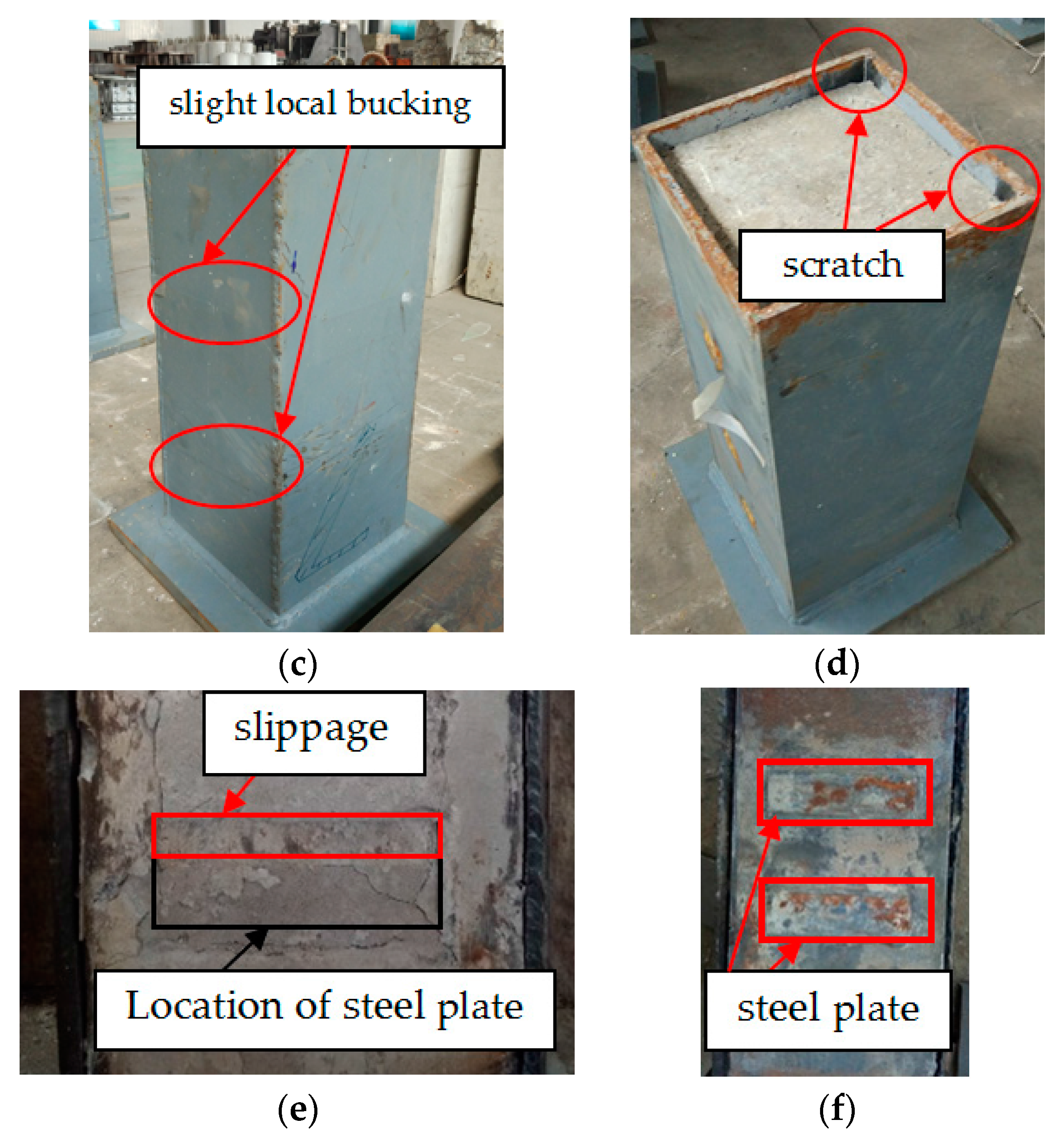
3.1. Failure Mode
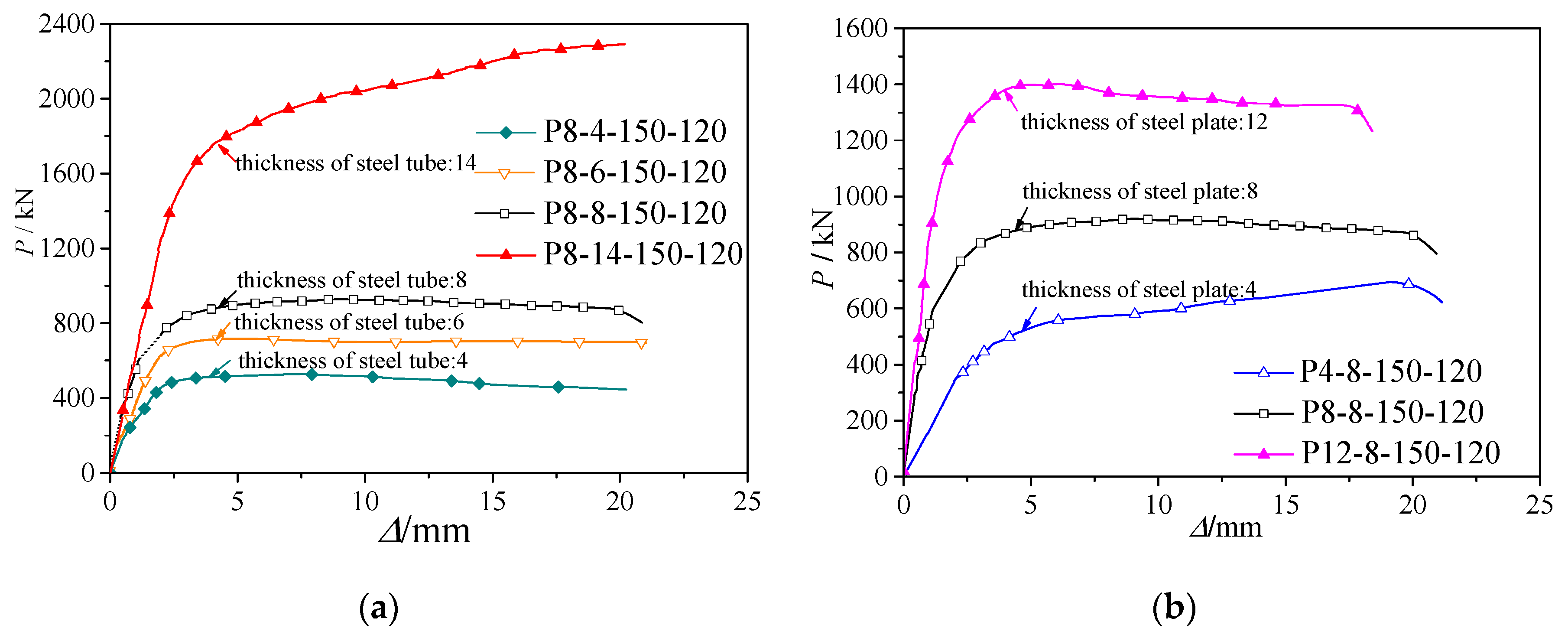
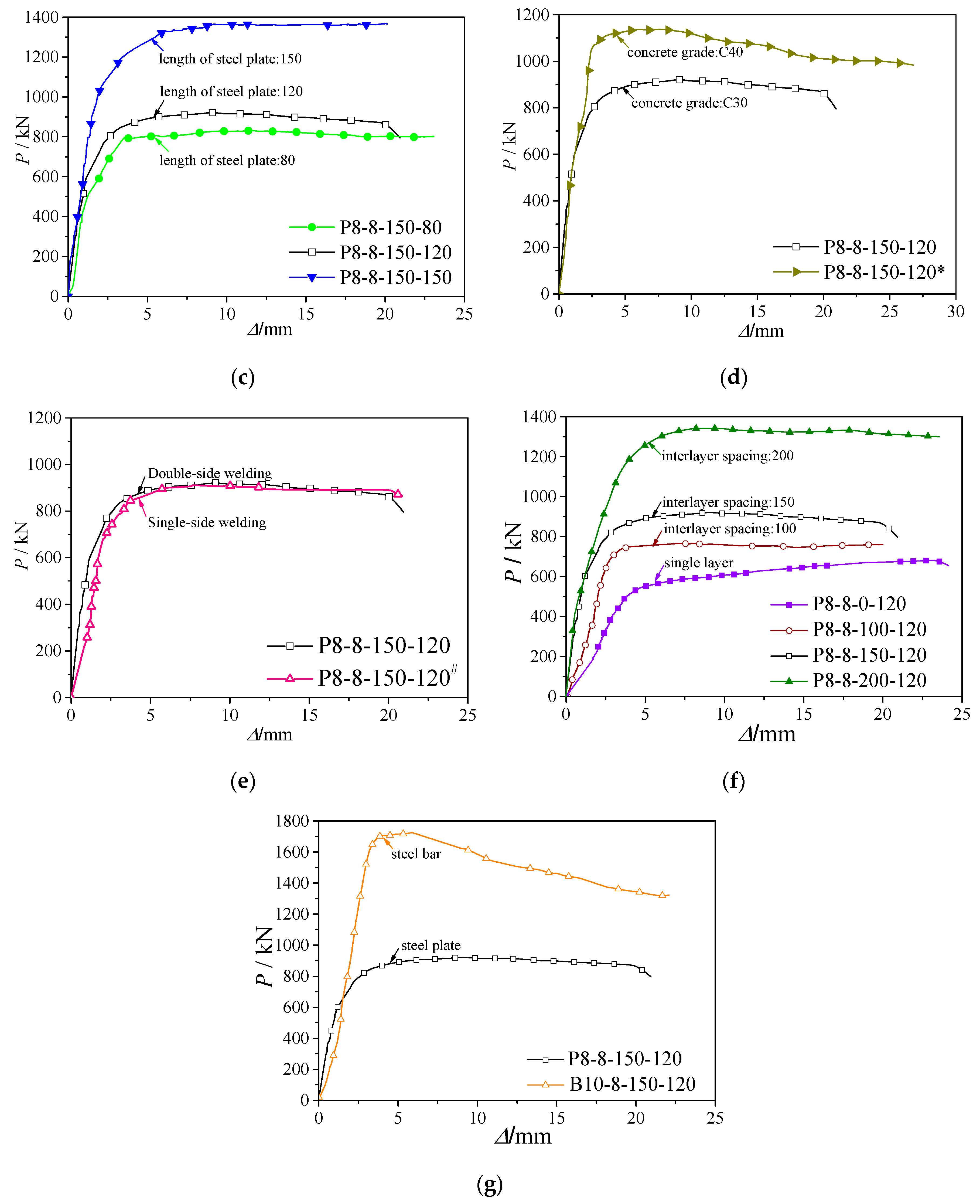
3.2. Load-Displacement Relationships and Parametrical Study
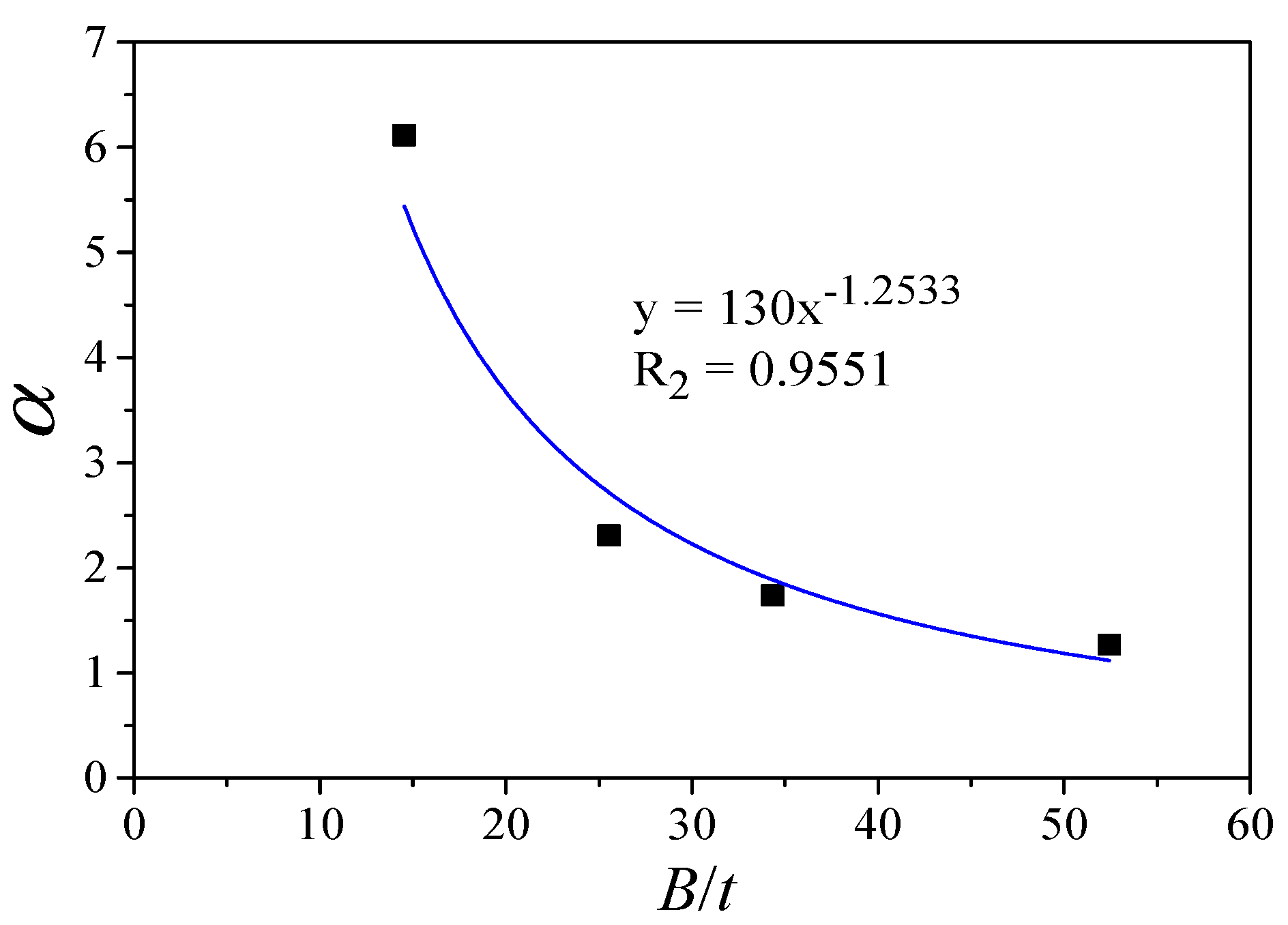
3.2.1. Width to Thickness Ratio of Steel Tube
3.2.2. Thickness of Steel Plate
3.2.3. Length of Steel Plate
3.2.4. Concrete Strength
3.2.5. Welding Condition of Steel Plate
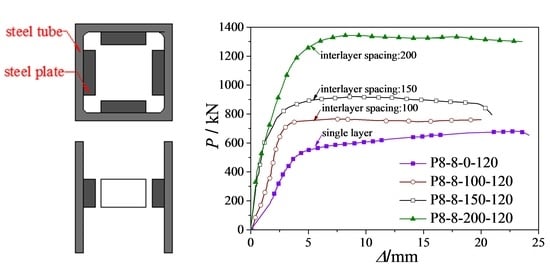
3.2.6. Number of Steel Plate Layer and Interlayer Spacing
3.2.7. Types of Shear Connectors
3.3. Strain Analysis
4. Calculation of the Ultimate Bearing Capacity
5. Conclusions
- (1)
- The steel plate can effectively transmit the load between the steel tube and core concrete, and improve the co-working performance of the steel tube and concrete.
- (2)
- Comparing with single-layer steel plate specimens, the ultimate bearing capacities of the double-layer steel plate specimens are greater, and the increase has a good correlation with the spacing to height ratio s/h ratio. Further, the bigger the s/h ratio of steel plates, the greater the bearing capacity. Therefore, the s/h ratio of the steel plate must be less than 5.9 in engineering design.
- (3)
- The width to thickness ratio of the steel tube, the thickness the length of the steel plate all have significant effects on the ultimate bearing capacity and initial stiffness. The ultimate bearing capacity and the elastic stiffness increase with decreasing width to thickness ratio of the steel tube, and increasing thickness and length of the steel plate.
- (4)
- The concrete strength has a significant effect on the ultimate bearing capacity. Further, with concrete of greater strength, the ultimate bearing capacity is also greater.
- (5)
- The welding condition of the steel plate has no effect on the ultimate bearing capacity. Hence, if the shear connectors are designed to have no shear failure on the steel plate or no local bucking on the steel tube, single-sided welding can be used in real-life engineering projects, which reduces the construction tasks.
- (6)
- In the case of the same amount of steel, the bearing capacity of the steel bar specimen with the same number of layers is 87% greater than that of the steel plate specimen. However, the descending part of the steel bar specimen is steeper than that of the steel plate specimen after reaching the ultimate bearing capacity.
- (7)
- The calculation method is proposed for the ultimate bearing capacity, and the calculated capacities are in good agreement with the test data.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Song, J.Y.; Kwon, Y.B. Structural behavior of concrete-filled steel box sections. In International Conference Report on Composite Construction-Conventional and Innovative; IABSE: Zurich, Switzerland, 1997; pp. 795–801. [Google Scholar]
- Han, L.H. Tests on stub columns of concrete-filled RHS sections. J. Constr. Steel Res. 2002, 58, 353–372. [Google Scholar] [CrossRef]
- Giakoumelisa, G.; Lam, D. Axial capacity of circular concrete-filled tube Columns. J. Constr. Steel Res. 2004, 60, 1049–1068. [Google Scholar] [CrossRef]
- Han, L.H. The influence of concrete compaction on the strength of concrete filled steel tubes. Int. J. Adv. Struct. Eng. 2000, 3, 131–137. [Google Scholar] [CrossRef]
- Roeder, C.W.; Cameron, B.; Brown, C.B. Composite action in concrete filled tubes. J. Struct. Eng. ASCE 1999, 125, 477–484. [Google Scholar] [CrossRef]
- Chang, X.; Huang, C.K.; Jiang, D.C.; Song, Y.C. Push-out test of pre-stressing concrete filled circular steel tube columns by means of expansive cement. Constr. Build. Mater. 2009, 23, 491–497. [Google Scholar]
- Aly, T.; Elchalakani, M.; Thayalan, P.; Patnaikuni, I. Incremental collapse threshold for push-out resistance of circular concrete filled steel tubular columns. J. Constr. Steel Res. 2010, 66, 11–18. [Google Scholar] [CrossRef]
- Uy, B.; Tao, Z.; Han, L.H. Bond strength between the steel tube and concrete in concrete-filled steel columns. In Proceedings of the Inaugural Annual Conference of the Institute for Infrastructure Engineering, Sydney, Australia, 22–23 November 2012. [Google Scholar]
- Shakir-Khalil, H. Push out strength of concrete-filled steel hollow sections. Struct. Eng. 1993, 71, 230–243. [Google Scholar]
- An, L.; Cederwall, K. Push-out Tests on Studs in High Strength and Normal Strength Concrete. J. Constr. Steel Res. 1996, 36, 15–29. [Google Scholar] [CrossRef]
- Shim, C.S.; Lee, P.G.; Yoon, T.Y. Static behavior of large stud shear connectors. Eng. Struct. 2004, 26, 1853–1860. [Google Scholar] [CrossRef]
- Pil-Goo, L.; Chang-Su, S.; Sung-Pil, C. Static and fatigue behavior of large stud shear connectors for steel-concrete composite bridge. J. Constr. Steel Res. 2005, 61, 1270–1285. [Google Scholar]
- Xue, W.; Ding, M.; Wang, H.; Luo, Z. Static behavior and theoretical model of stud shear connectors. J. Bridge Eng. ASCE 2008, 13, 623–634. [Google Scholar] [CrossRef]
- CECS 28-1990: Specification for Design and Construction of Concrete Filled Steel Tubular Structures; China Planning Press: Beijing, China, 1992.
- Recommendations for Design and Construction of Concrete Filled Steel Tubular Structures; Architecture Institute of Japan: Tokyo, Japan, 2008.
- Tao, Z.; Song, T.Y.; Uy, B.; Han, L.H. Bond behavior in concrete-filled steel tubes. J. Constr. Steel Res. 2016, 120, 81–93. [Google Scholar] [CrossRef]
- Lai, M.H.; Ho, J.C.M. Confinement effect of ring-confined concrete-filled-steel-tube columns under uni-axial load. Eng. Struct. 2014, 67, 123–141. [Google Scholar] [CrossRef]
- China Ministry of Construction (CMC). Code for Design of Concrete Structures (GB50010-2010); China Ministry of Construction: Beijing, China, 2010. (In Chinese)
- China Ministry of Construction (CMC). Code for Design of Composite Structure (JB 138-2012); China Ministry of Construction: Beijing, China, 2012. (In Chinese)
- Eurocode 4: Design of Composite Steel and Concrete Structures, Part 1.1: General Rules and Rules for Buildings (Together with United Kingdom National Application Document); Draft for Development Preliminary European Standard (DD ENV); British Standards Institution: London, UK, 1994.
- Miyao, T.; Nakamura, N.; Sugiyama, T. Evaluation of bearing strength of backing rings for concrete filled tube. J. Archit. Build. Sci. 1997, 4, 51–56. [Google Scholar] [CrossRef]
- Xue, L.; Cai, S. Experimental study of shear connector of the concrete-filled steel tube. Build. Sci. 1998, 14, 13–21. (In Chinese) [Google Scholar]


| Specimen | t mm | B/t | c mm | s mm | l mm | Concrete Grade | Shear Connector Type |
|---|---|---|---|---|---|---|---|
| P8-8-0-120 | 8 | 25 | 8 | single layer | 120 | C30 | steel plate |
| P8-4-150-120 | 4 | 50 | 8 | 150 | 120 | C30 | steel plate |
| P8-6-150-120 | 6 | 33.3 | 8 | 150 | 120 | C30 | steel plate |
| P8-8-150-120 | 8 | 25 | 8 | 150 | 120 | C30 | steel plate |
| P8-14-150-120 | 14 | 14.3 | 8 | 150 | 120 | C30 | steel plate |
| P4-8-150-120 | 8 | 25 | 4 | 150 | 120 | C30 | steel plate |
| P12-8-150-120 | 8 | 25 | 12 | 150 | 120 | C30 | steel plate |
| P8-8-100-120 | 8 | 25 | 8 | 100 | 120 | C30 | steel plate |
| P8-8-200-120 | 8 | 25 | 8 | 200 | 120 | C30 | steel plate |
| P8-8-150-120# | 8 | 25 | 8 | 150 | 120 | C30 | steel plate |
| P8-8-150-80 | 8 | 25 | 8 | 150 | 80 | C30 | steel plate |
| P8-8-150-150 | 8 | 25 | 8 | 150 | 150 | C30 | steel plate |
| P8-8-150-120* | 8 | 25 | 8 | 150 | 120 | C40 | steel plate |
| B10-8-150-174 | 8 | 25 | 10 | 150 | 174 | C30 | steel bar |
| Concrete Grade | Water (kg/m3) | Cement (kg/m3) | Fine Aggregates (kg/m3) | Coarse Aggregates (kg/m3) |
|---|---|---|---|---|
| C30 | 185 | 325 | 660 | 1220 |
| C40 | 185 | 420 | 570 | 1270 |
| Concrete Grade | Cubic Compression Strength fcu150 (MPa) | Cylinder Compression Strength fc′ (MPa) | Young’s Modulus (N/mm2) |
|---|---|---|---|
| C30 | 33.0 | 25.0 | 3.00 × 104 |
| C40 | 40.1 | 30.5 | 3.25 × 104 |
| Steel Type | fy (N/mm2) | fu (N/mm2) | δ (%) |
|---|---|---|---|
| Q345, 4 mm | 390 | 521 | 27.6 |
| Q345, 6 mm | 362 | 495 | 26.8 |
| Q345, 8 mm | 381 | 516 | 27.1 |
| Q345, 12 mm | 355 | 530 | 27.5 |
| Q345, 14 mm | 368 | 509 | 27.2 |
| HRB335, steel bar | 389 | 502 | 23.4 |
| Specimen | Pu.exp (kN) | Pu.cal (kN) | Pu.exp/Pu.cal | Failure Mode |
|---|---|---|---|---|
| P8-8-0-120 | 680.2 | 674.9 | 1.008 | A |
| P8-4-150-120 | 527.9 | 505.4 | 1.044 | A, B |
| P8-6-150-120 | 709.3 | 679.1 | 1.044 | A |
| P8-8-150-120 | 921.0 | 913.8 | 1.008 | A |
| P8-14-150-120 | 2284.0 | 2186.8 | 1.044 | A |
| P4-8-150-120 | 694.5 | 615.5 | 1.128 | A |
| P12-8-150-120 | 1401.6 | 1215.4 | 1.153 | A |
| P8-8-100-120 | 766.0 | 742.4 | 1.032 | A |
| P8-8-200-120 | 1342.9 | 1349.8 | 0.995 | A |
| P8-8-150-120# | 1050.5 | - | - | A |
| P8-8-150-80 | 833.0 | 746.1 | 1.116 | A |
| P8-8-150-150 | 1250.0 | 1021.7 | 1.223 | A |
| P8-8-150-120* | 1137.3 | 1114.9 | 1.020 | A |
| B10-8-150-174 | 1725.5 | - | - | A |
| the mean value: | 1.068 | |||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, Q.; Zhang, W.; Qian, Z.; Cao, W.; Liu, W. Experimental Study on Mechanical Behavior of Shear Connectors of Square Concrete Filled Steel Tube. Appl. Sci. 2017, 7, 818. https://doi.org/10.3390/app7080818
Qiao Q, Zhang W, Qian Z, Cao W, Liu W. Experimental Study on Mechanical Behavior of Shear Connectors of Square Concrete Filled Steel Tube. Applied Sciences. 2017; 7(8):818. https://doi.org/10.3390/app7080818
Chicago/Turabian StyleQiao, Qiyun, Wenwen Zhang, Zhiwei Qian, Wanlin Cao, and Wenchao Liu. 2017. "Experimental Study on Mechanical Behavior of Shear Connectors of Square Concrete Filled Steel Tube" Applied Sciences 7, no. 8: 818. https://doi.org/10.3390/app7080818
APA StyleQiao, Q., Zhang, W., Qian, Z., Cao, W., & Liu, W. (2017). Experimental Study on Mechanical Behavior of Shear Connectors of Square Concrete Filled Steel Tube. Applied Sciences, 7(8), 818. https://doi.org/10.3390/app7080818