Probing Physics in Vacuum Using an X-ray Free-Electron Laser, a High-Power Laser, and a High-Field Magnet
Abstract
:1. Introduction
2. Probing the Vacuum Process
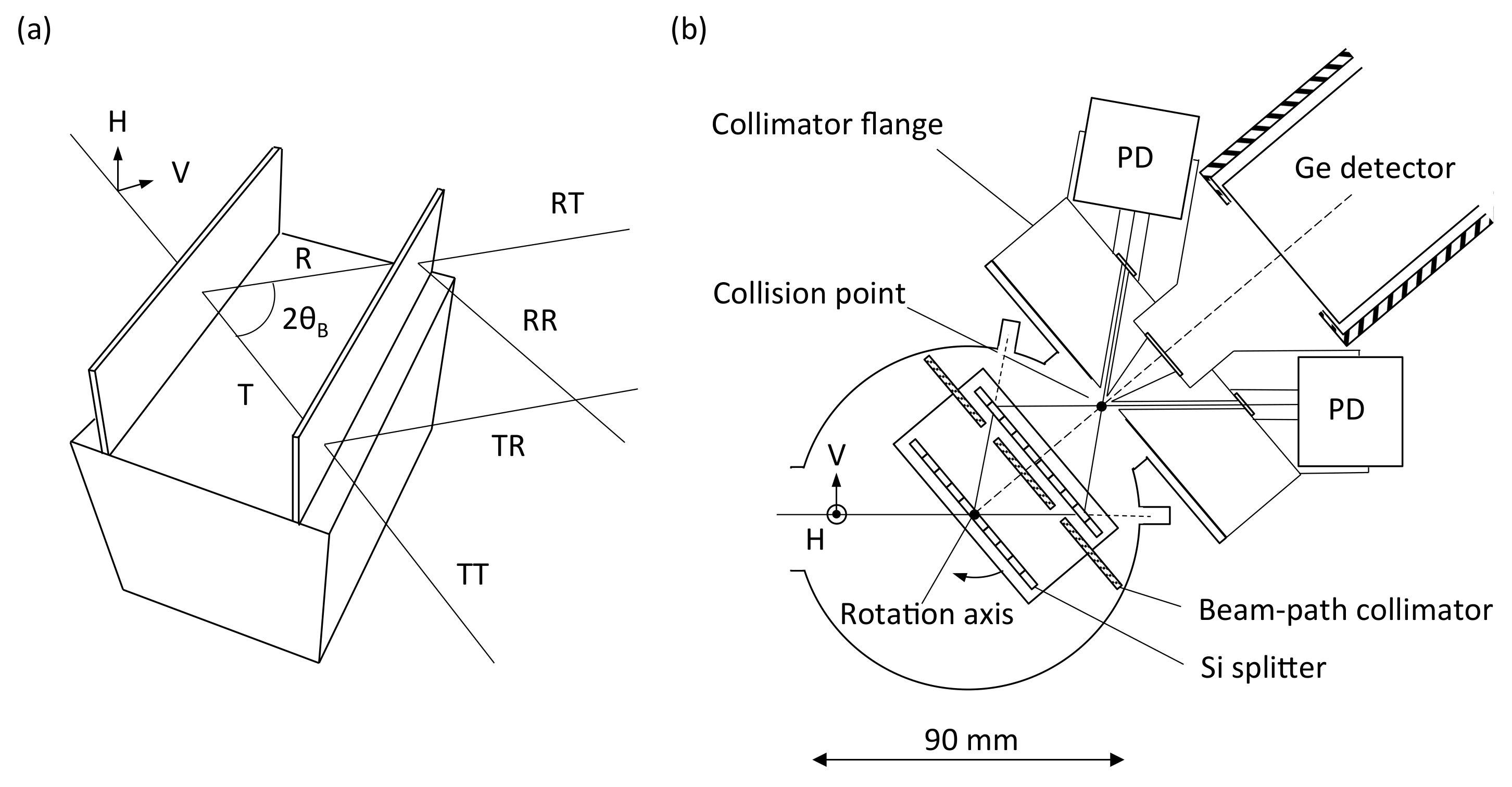
2.1. Elastic Scattering by the Collision of Two X-ray Pulses
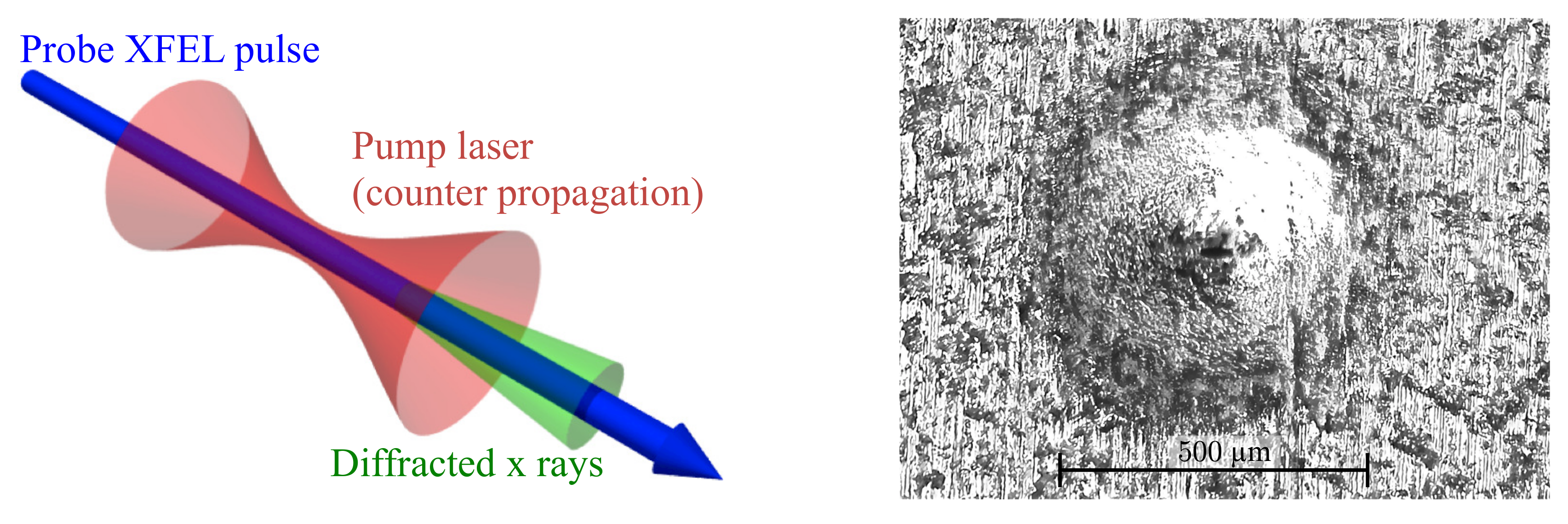
2.2. Laser-Induced Birefringence and Diffraction of X-rays
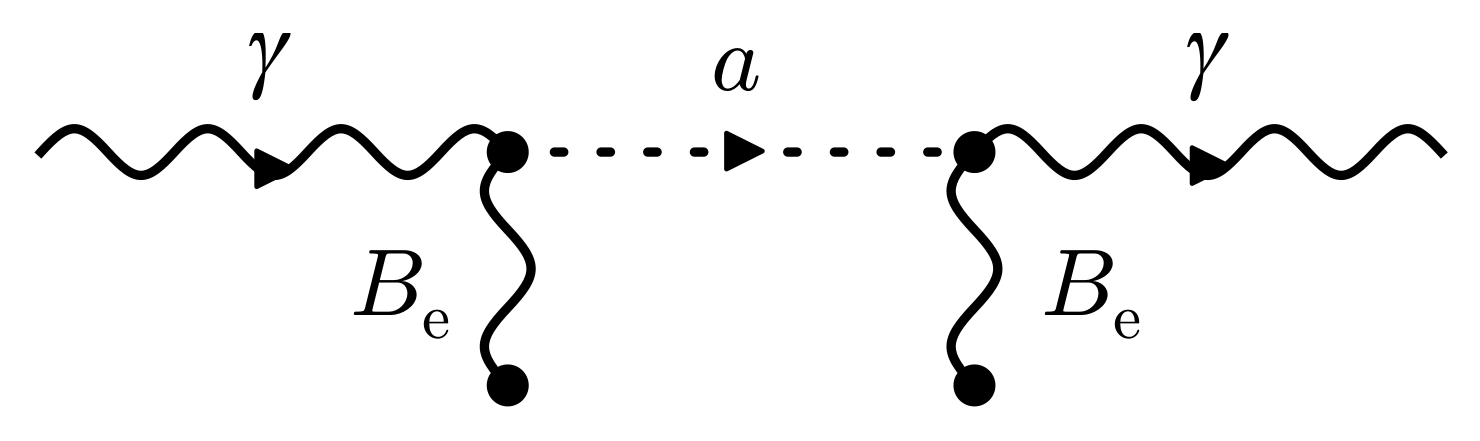
2.3. Birefringence Induced by a High-Field Magnet
3. Searches for Physics Beyond the Standard Model
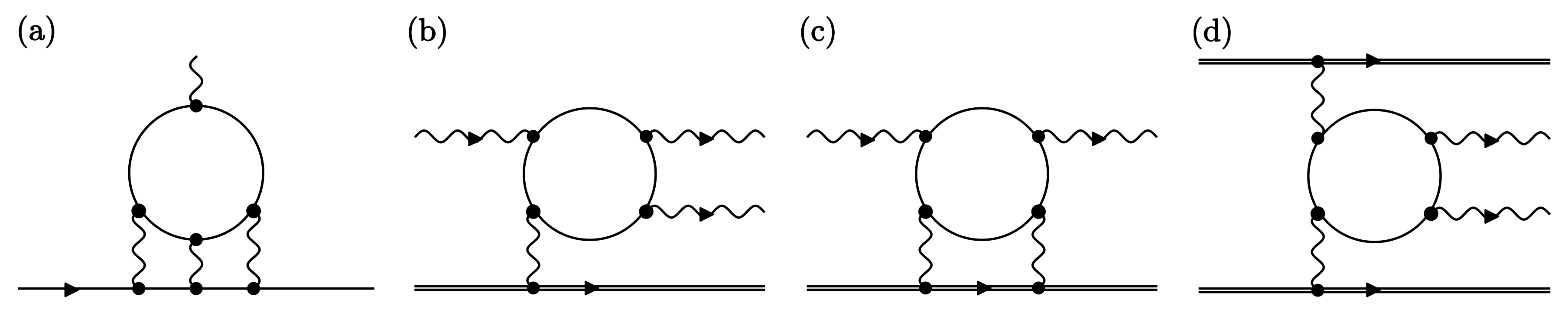
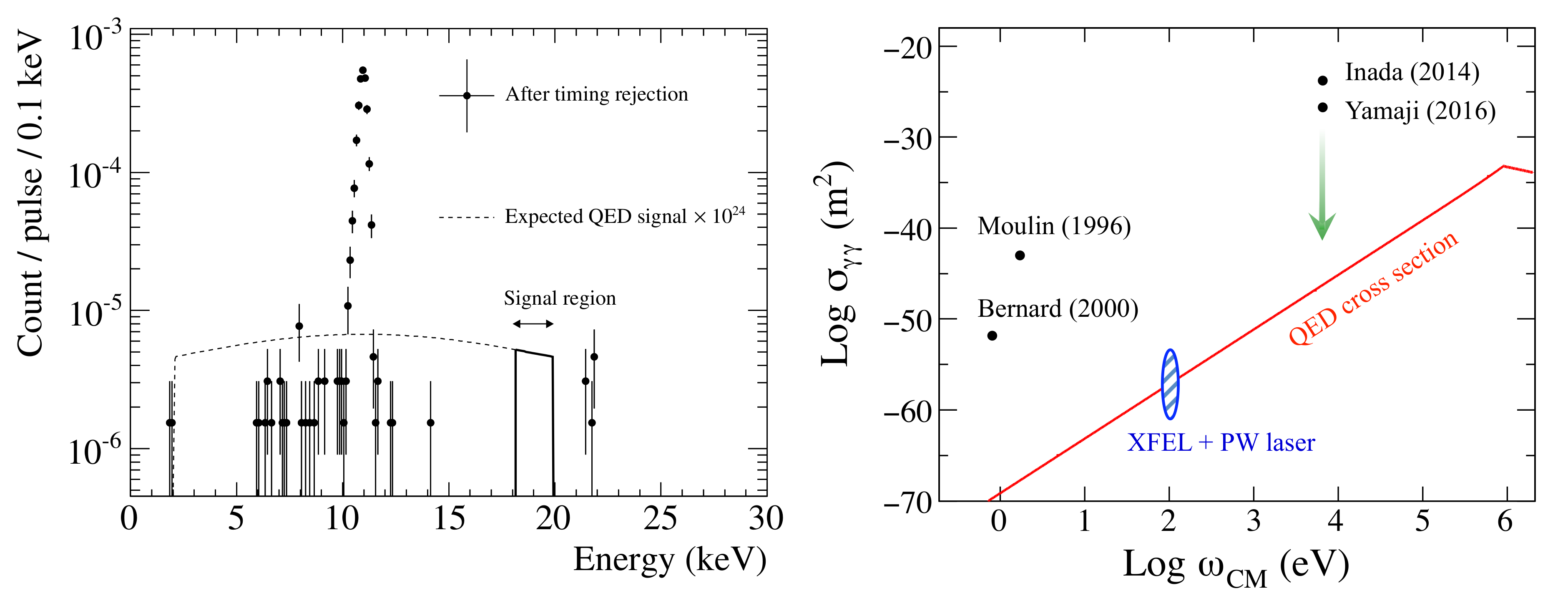
3.1. Exotic Contribution to Photon–Photon Scattering
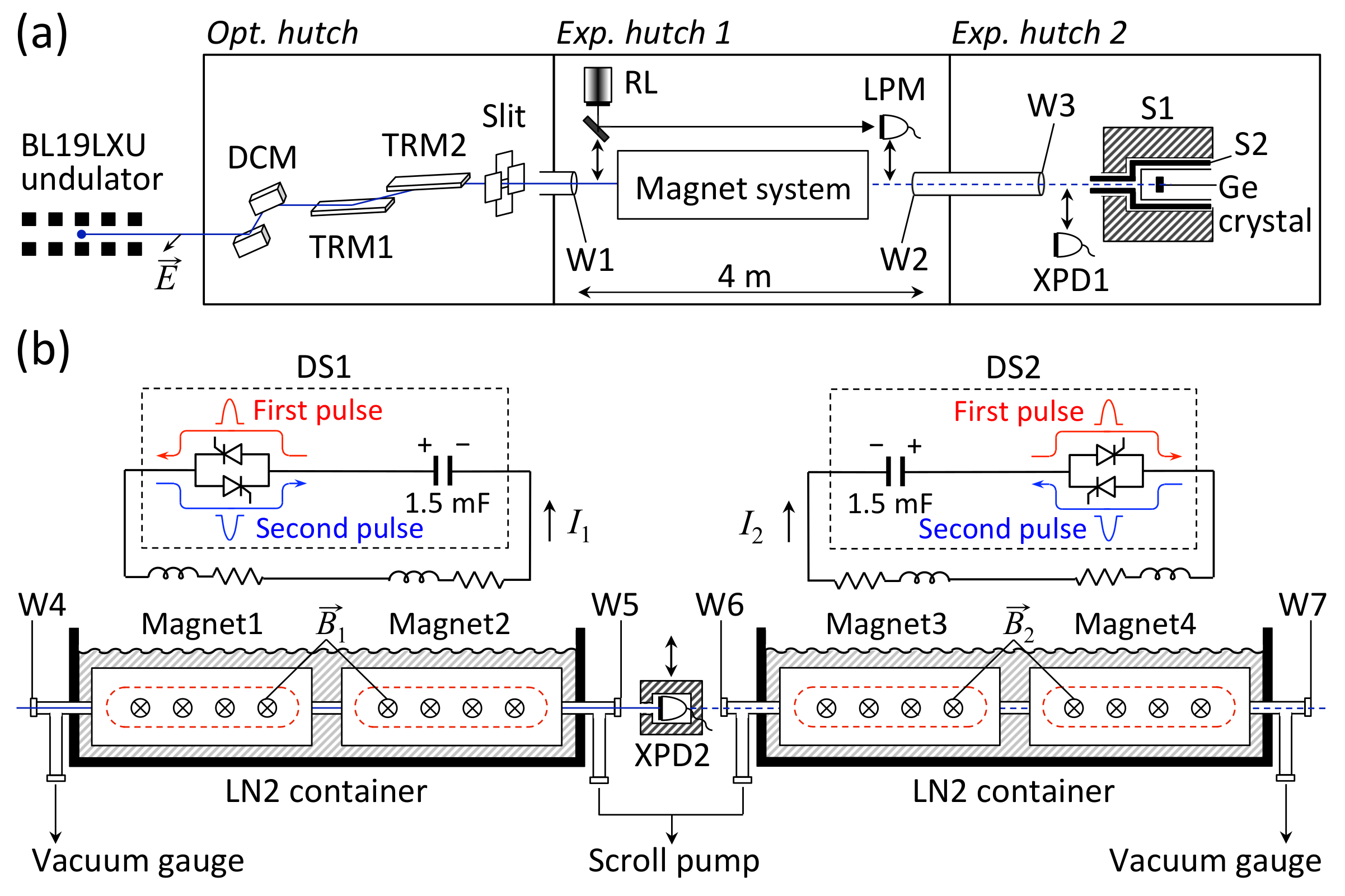
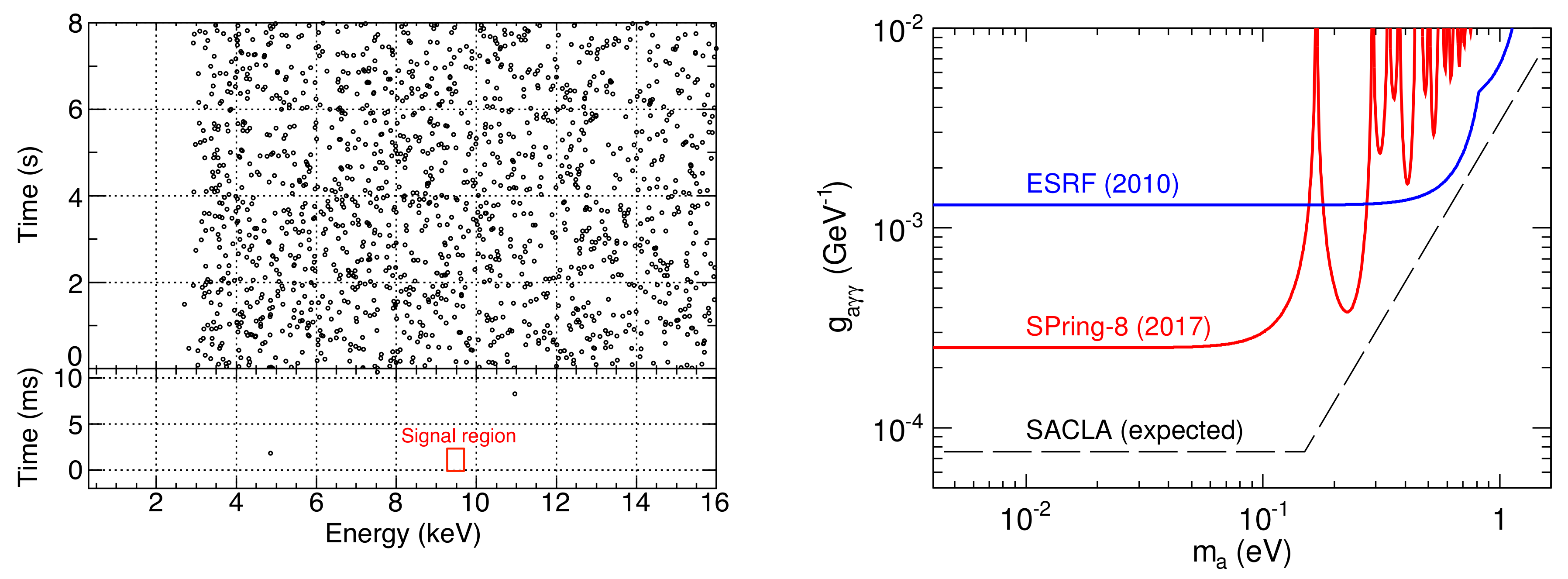
3.2. Dedicated Search for Axion-Like Particles
4. Summary
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Aoyama, T.; Hayakawa, M.; Kinoshita, T.; Nio, M. Tenth-order electron anomalous magnetic moment—Contribution of diagrams without closed lepton loops. Phys. Rev. D 2015, 91, 033006. [Google Scholar] [CrossRef]
- Jegerlehner, F.; Nyffeler, A. The muon g–2. Phys. Rep. 2009, 477, 1–10. [Google Scholar] [CrossRef]
- Hanneke, D.; Fogwell, S.; Gabrielse, G. New Measurement of the Electron Magnetic Moment and the Fine Structure Constant. Phys. Rev. Lett. 2008, 100, 120801. [Google Scholar] [CrossRef] [PubMed]
- Akhmadaliev, S.Z.; Kezerashvili, G.Y.; Klimenko, S.G.; Lee, R.N.; Malyshev, V.M.; Maslennikov, A.L.; Milov, A.M.; Milstein, A.I.; Muchnoi, N.Y.; Naumenkov, A.I.; et al. Experimental Investigation of High-Energy Photon Splitting in Atomic Fields. Phys. Rev. Lett. 2002, 89, 061802. [Google Scholar] [CrossRef] [PubMed]
- Akhmadaliev, S.Z.; Kezerashvili, G.Y.; Klimenko, S.G.; Malyshev, V.M.; Maslennikov, A.L.; Milov, A.M.; Milstein, A.I.; Muchnoi, N.Y.; Naumenkov, A.I.; Panin, V.S.; et al. Delbrück scattering at energies of 140–450 MeV. Phys. Rev. C 1998, 58, 2844. [Google Scholar] [CrossRef]
- ATLAS Collaboration. Light-by-Light Scattering in Ultra-Peripheral Pb+Pb Collisions at sqrt(sNN)=5.02 TeV with the ATLAS Detector at the LHC. ATLAS-CONF-2016-111.
- Di Piazza, A.; Müller, C.; Hatsagortsyan, K.Z.; Keitel, C.H. Extremely high-intensity laser interactions with fundamental quantum systems. Rev. Mod. Phys. 2012, 84, 1177. [Google Scholar] [CrossRef]
- King, B.; Heinzl, T. Measuring vacuum polarization with high-power lasers. High Power Laser Sci. Eng. 2016, 4, e5. [Google Scholar] [CrossRef]
- Schlenvoigt, H.; Heinzl, T.; Schramm, U.; Cowan, T.; Sauerbrey, R. Detecting vacuum birefringence with X-ray free electron lasers and high-power optical lasers: A feasibility study. Phys. Scr. 2016, 91, 023010. [Google Scholar] [CrossRef]
- Della Valle, F.; Ejlli, A.; Gastaldi, U.; Messineo, G.; Milotti, E.; Pengo, R.; Ruoso, G.; Zavattini, G. The PVLAS experiment: Measuring vacuum magnetic birefringence and dichroism with a birefringent Fabry–Perot cavity. Eur. Phys. J. C 2016, 76, 24. [Google Scholar] [CrossRef]
- Dittrich, W.; Gies, H. Probing the Quantum Vacuum; Springer: Berlin, Germany, 2000. [Google Scholar]
- Magnani, R.P.; Testa, V.; González Caniulef, D.; Taverna, R.; Turolla, R.; Zane, S.; Wu, K. Evidence for vacuum birefringence from the first optical-polarimetry measurement of the isolated neutron star RX J1856.5–3754. MNRAS 2017, 465, 492–500. [Google Scholar] [CrossRef]
- Capparelli, L.M.; Maiani, L.; Polosa, A.D. A Note on Polarized Light from Magnetars: QED Effects and Axion-Like Particles. arXiv, 2017; arXiv:1705.01540. [Google Scholar]
- Turolla, R.; Zane, S.; Taverna, R.; Gonzalez Caniulef, D.; Mignani, R.P.; Testa, V.; Wu, K. A Comment on “A Note on Polarized Light from Magnetars: QED Effects and Axion-Like Particles” by L.M. Capparelli, L. Maiani and A.D. Polosa. arXiv, 2017; arXiv:1706.02505. [Google Scholar]
- Essig, R.; Jaros, J.A.; Wester, W.; Hansson Adrian, P.; Andreas, S.; Averett, T.; Baker, O.; Batell, B.; Battaglieri, M.; Beacham, J.; et al. Dark Sectors and New, Light, Weakly-Coupled Particles. Report of the Community Summer Study (Snowmass) Intensity Frontier New, Light, Weakly-Coupled Particles Subgroup. arXiv, 2013; arXiv:1311.0029. [Google Scholar]
- Graham, P.W.; Irastorza, I.G.; Lamoreaux, S.K.; Lindner, A.; van Bibber, K.A. Experimental Searches for the Axion and Axion-Like Particles. Annu. Rev. Nucl. Part. Sci. 2015, 65, 485–514. [Google Scholar] [CrossRef]
- Ishikawa, T.; Aoyagi, H.; Asaka, T.; Asano, Y.; Asano, N.; Bizen, T.; Ego, H.; Fukami, K.; Fukui, T.; Furukawa, Y.; et al. A compact X-ray free-electron laser emitting in the sub-ångström region. Nat. Photonics 2012, 6, 540–544. [Google Scholar] [CrossRef]
- Tono, K.; Togashi, T.; Inubushi, Y.; Sato, T.; Katayama, T.; Ogawa, K.; Ohashi, H.; Kimura, H.; Takahashi, S.; Takeshita, K.; et al. Beamline, experimental stations and photon beam diagnostics for the hard X-ray free electron laser of SACLA. New J. Phys. 2013, 15, 083035. [Google Scholar] [CrossRef]
- Inada, T.; Yamaji, T.; Adachi, S.; Namba, T.; Asai, S.; Kobayashi, T.; Tamasaku, K.; Tanaka, Y.; Inubushi, Y.; Sawada, K.; et al. Search for photon–photon elastic scattering in the X-ray region. Phys. Lett. B 2014, 732, 356–359. [Google Scholar] [CrossRef]
- Yamaji, T.; Inada, T.; Yamazaki, T.; Namba, T.; Asai, S.; Kobayashi, T.; Tamasaku, K.; Tanaka, Y.; Inubushi, Y.; Sawada, K.; et al. An experiment of X-ray photon–photon elastic scattering with a Laue-case beam collider. Phys. Lett. B 2016, 763, 454–457. [Google Scholar] [CrossRef]
- Moulin, F.; Bernard, D.; Amiranoff, F. Photon-photon elastic scattering in the visible domain. Z. Phys. C 1996, 72, 607–611. [Google Scholar] [CrossRef]
- De Tollis, B. Dispersive approach to photon-photon scattering. Nuovo Cim. 1964, 32, 757–768. [Google Scholar] [CrossRef]
- De Tollis, B. The scattering of photons by photons. Nuovo Cim. 1965, 35, 1182–1193. [Google Scholar] [CrossRef]
- Bonse, U.; Hart, M. Principles and design of Laue-case X-ray interferometers. Z. Physik 1965, 188, 154–164. [Google Scholar] [CrossRef]
- Bernard, D.; Moulin, F.; Amiranoff, F.; Braun, A.; Chambaret, J.P.; Darpentigny, G.; Grillon, G.; Ranc, S.; Perrone, F. Search for stimulated photon-photon scattering in vacuum. Eur. Phys. J. D 2000, 10, 141–145. [Google Scholar] [CrossRef]
- Bonse, U.; Hart, M. An X-ray Interferometer. Appl. Phys. Lett. 1965, 6, 155–156. [Google Scholar] [CrossRef]
- Bonse, U.; Hart, M. An X-ray interferometer with Bragg case beam splitting and beam recombination. Z. Physik 1966, 194, 1–17. [Google Scholar] [CrossRef]
- Amann, J.; Berg, W.; Blank, V.; Decker, F.-J.; Ding, Y.; Emma, P.; Feng, Y.; Frisch, J.; Fritz, D.; Hastings, J.; et al. Demonstration of Self-Seeding in a Hard-X-ray Free-Electron Laser. Nat. Photonics 2012, 6, 693–698. [Google Scholar] [CrossRef]
- SACLA Website. Available online: http://xfel.riken.jp/eng/index.html (accssed on 29 June 2017).
- Di Piazza, A.; Hatsagortsyan, K.Z.; Keitel, C.H. Light Diffraction by a Strong Standing Electromagnetic Wave. Phys. Rev. Lett. 2006, 97, 083603. [Google Scholar] [CrossRef] [PubMed]
- Heinzl, T.; Liesfeld, B.; Amthor, K.-U.; Schwoerer, H.; Sauerbrey, R.; Wip, A. On the observation of vacuum birefringence. Opt. Commun. 2006, 267, 318. [Google Scholar] [CrossRef]
- Karbstein, F.; Sundqvist, C. Probing vacuum birefringence using X-ray free electron and optical high-intensity lasers. Phys. Rev. D 2016, 94, 013004. [Google Scholar] [CrossRef]
- Katayama, T.; Owada, S.; Togashi, T.; Ogawa, K.; Karvinen, P.; Vartiainen, I.; Eronen, A.; David, C.; Sato, T.; Nakajima, K.; et al. A beam branching method for timing and spectral characterization of hard X-ray free-electron lasers. Struct. Dyn. 2016, 3, 034301. [Google Scholar] [CrossRef] [PubMed]
- Seino, Y. Search for vacuum diffraction using high power laser and X-ray free electron laser SACLA. Light Driven Nucl.-Part. Phys. Cosmol. 2017, in press. [Google Scholar]
- Rizzo, C.; Rizzo, A.; Bishop, D.M. The Cotton-Mouton effect in gases: Experiment and theory. Int. Rev. Phys. Chem. 1997, 16, 81–111. [Google Scholar] [CrossRef]
- Cadène, A.; Berceau, P.; Fouché, M.; Battesti, R.; Rizzo, C. Vacuum magnetic linear birefringence using pulsed fields: Status of the BMV experiment. Eur. Phys. J. D 2014, 68, 16. [Google Scholar]
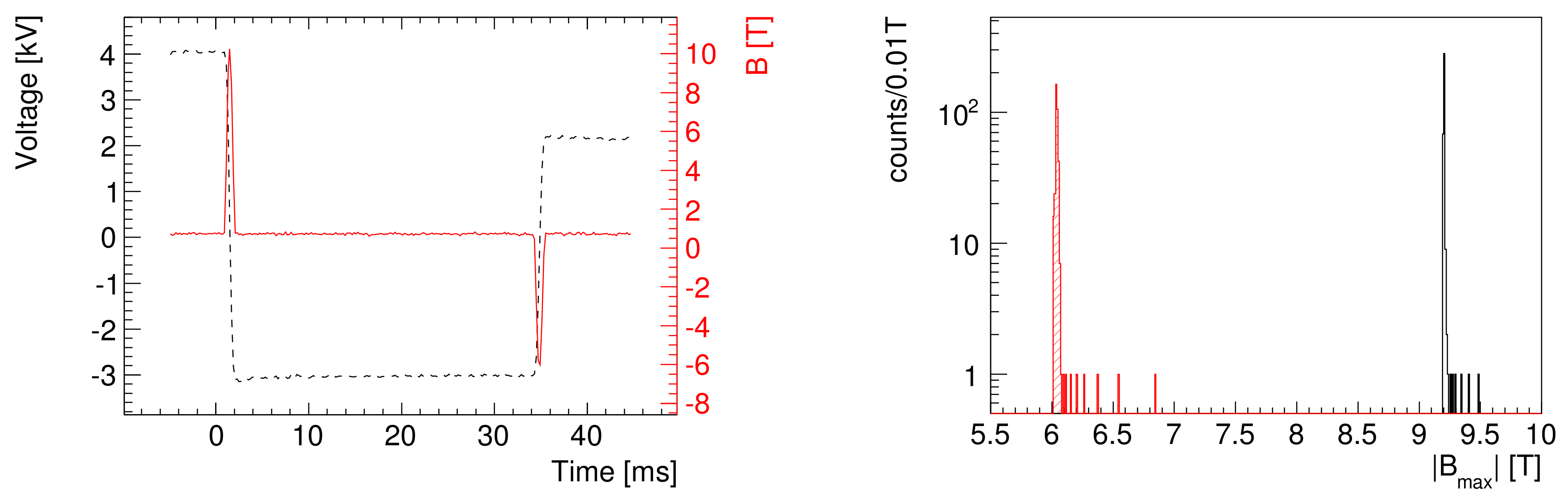
- Yamazaki, T.; Inada, T.; Namba, T.; Asai, S.; Kobayashi, T.; Matsuo, A.; Kindo, K.; Nojiri, H. Repeating pulsed magnet system for axion-like particle searches and vacuum birefringence experiments. Nucl. Instrum. Methods A 2016, 833, 122–126. [Google Scholar] [CrossRef]
- Fan, X.; Kamioka, S.; Inada, T.; Yamazaki, T.; Namba, T.; Asai, S.; Omachi, J.; Yoshioka, K.; Kuwata-Gonokami, M.; Matsuo, A.; et al. The OVAL experiment: A New Experiment to Measure Vacuum Magnetic Birefringence Using High Repetition Pulsed Magnets. arXiv, 2017; arXiv:1705.00495. [Google Scholar]
- ATLAS Collaboration. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 2012, 716, 1. [Google Scholar]
- CMS Collaboration. Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys. Lett. B 2012, 716, 30. [Google Scholar]
- Inada, T.; Namba, T.; Asai, S.; Kobayashi, T.; Tanaka, Y.; Tamasaku, K.; Sawada, K.; Ishikawa, T. Results of a search for paraphotons with intense X-ray beams at SPring-8. Phys. Lett. B 2013, 722, 301–304. [Google Scholar] [CrossRef]
- Inada, T.; Yamazaki, T.; Namba, T.; Asai, S.; Kobayashi, T.; Tamasaku, K.; Tanaka, Y.; Inubushi, Y.; Sawada, K.; Yabashi, M.; et al. Search for Two-Photon Interaction with Axionlike Particles Using High-Repetition Pulsed Magnets and Synchrotron X rays. Phys. Rev. Lett. 2017, 118, 071803. [Google Scholar] [CrossRef] [PubMed]
- Daido, R.; Takahashi, F.; Yin, W. The ALP miracle: Unified inflaton and dark matter. J. Cosmol. Astropart. Phys. 2017, 5, 44. [Google Scholar] [CrossRef]
- Battesti, R.; Fouché, M.; Detlefs, C.; Roth, T.; Berceau, P.; Duc, F.; Frings, P.; Rikken, G.L.J.A.; Rizzo, C. Photon Regeneration Experiment for Axion Search Using X-rays. Phys. Rev. Lett. 2010, 105, 250405. [Google Scholar] [CrossRef] [PubMed]
- Arik, M. Search for Solar Axions by the CERN Axion Solar Telescope with 3He Buffer Gas: Closing the Hot Dark Matter Gap. Phys. Rev. Lett. 2014, 112, 091302. [Google Scholar] [CrossRef] [PubMed]
- Ossendrijver, M. The solar dynamo. Astron. Astrophys. Rev. 2003, 11, 287. [Google Scholar] [CrossRef]
- Yabashi, M.; Mochizuki, T.; Yamazaki, H.; Goto, S.; Ohashi, H.; Takeshita, K.; Ohata, T.; Matsushita, T.; Tamasaku, K.; Tanaka, Y.; et al. Design of a beamline for the SPring-8 long undulator source 1. Nucl. Instrum. Methods A 2001, 467, 678–681. [Google Scholar] [CrossRef]


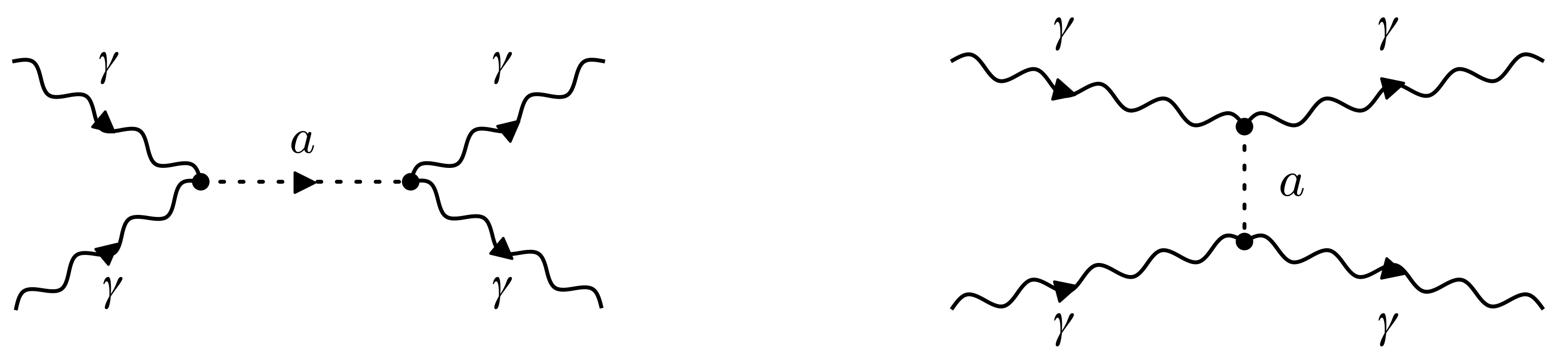
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Inada, T.; Yamazaki, T.; Yamaji, T.; Seino, Y.; Fan, X.; Kamioka, S.; Namba, T.; Asai, S. Probing Physics in Vacuum Using an X-ray Free-Electron Laser, a High-Power Laser, and a High-Field Magnet. Appl. Sci. 2017, 7, 671. https://doi.org/10.3390/app7070671
Inada T, Yamazaki T, Yamaji T, Seino Y, Fan X, Kamioka S, Namba T, Asai S. Probing Physics in Vacuum Using an X-ray Free-Electron Laser, a High-Power Laser, and a High-Field Magnet. Applied Sciences. 2017; 7(7):671. https://doi.org/10.3390/app7070671
Chicago/Turabian StyleInada, Toshiaki, Takayuki Yamazaki, Tomohiro Yamaji, Yudai Seino, Xing Fan, Shusei Kamioka, Toshio Namba, and Shoji Asai. 2017. "Probing Physics in Vacuum Using an X-ray Free-Electron Laser, a High-Power Laser, and a High-Field Magnet" Applied Sciences 7, no. 7: 671. https://doi.org/10.3390/app7070671
APA StyleInada, T., Yamazaki, T., Yamaji, T., Seino, Y., Fan, X., Kamioka, S., Namba, T., & Asai, S. (2017). Probing Physics in Vacuum Using an X-ray Free-Electron Laser, a High-Power Laser, and a High-Field Magnet. Applied Sciences, 7(7), 671. https://doi.org/10.3390/app7070671




