Adaptive Neuro-Fuzzy Inference System Model Based on the Width and Depth of the Defect in an Eddy Current Signal
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Inspection the Calibration Blocks Using a Weld Probe
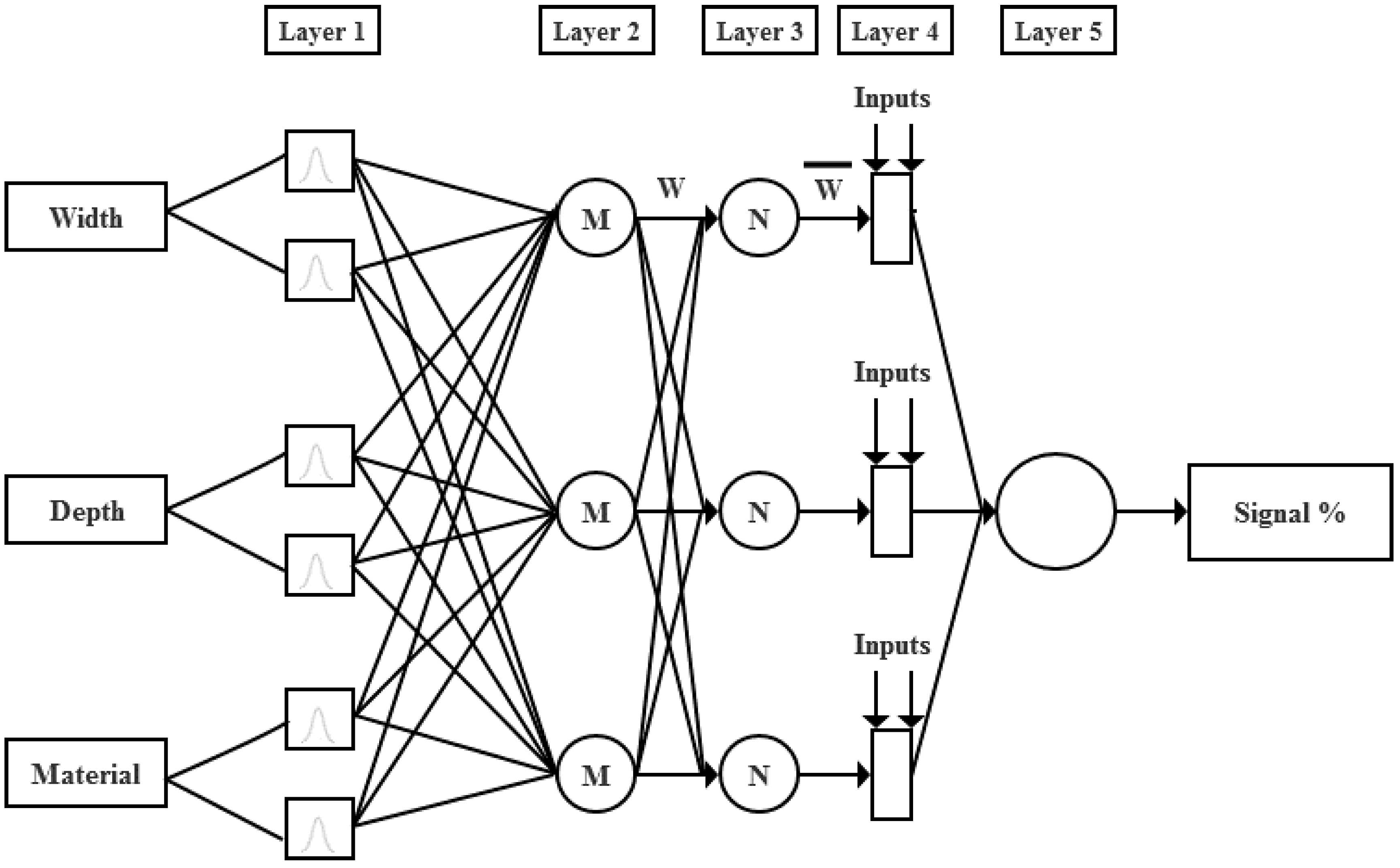
3. Proposed ANFIS Model
4. Experimental Designs
5. Results and Discussion
5.1. Inspection Results for Mild Steel Blocks
5.2. The DOE Analysis
5.2.1. The Effect of the Depth of the Defect and Width of the Defect on the Response
5.2.2. The Effect of Defect Width and the Type of Material on the Response
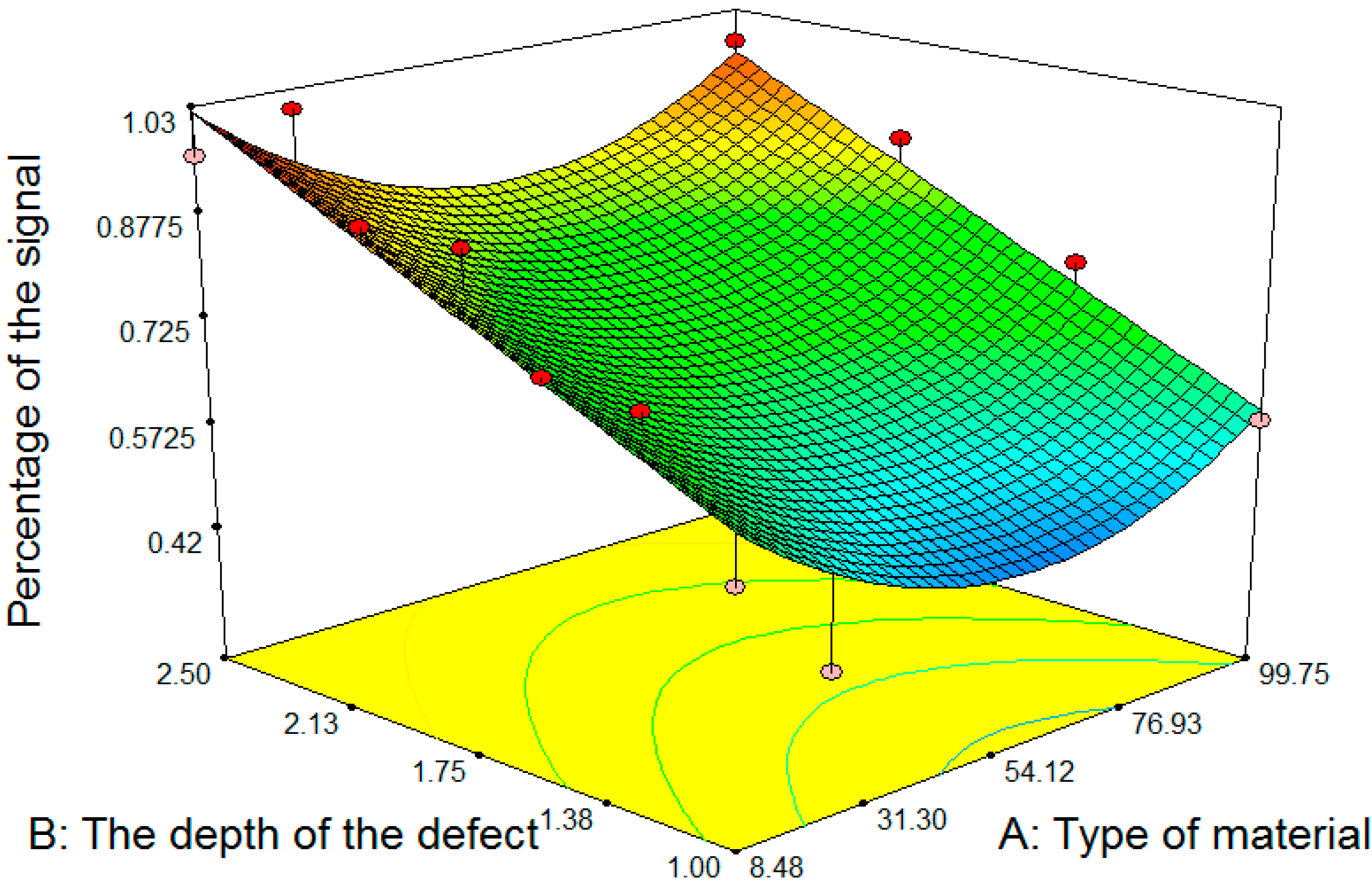
5.2.3. The Effect of Defect Depth and the Type of Material on the Response
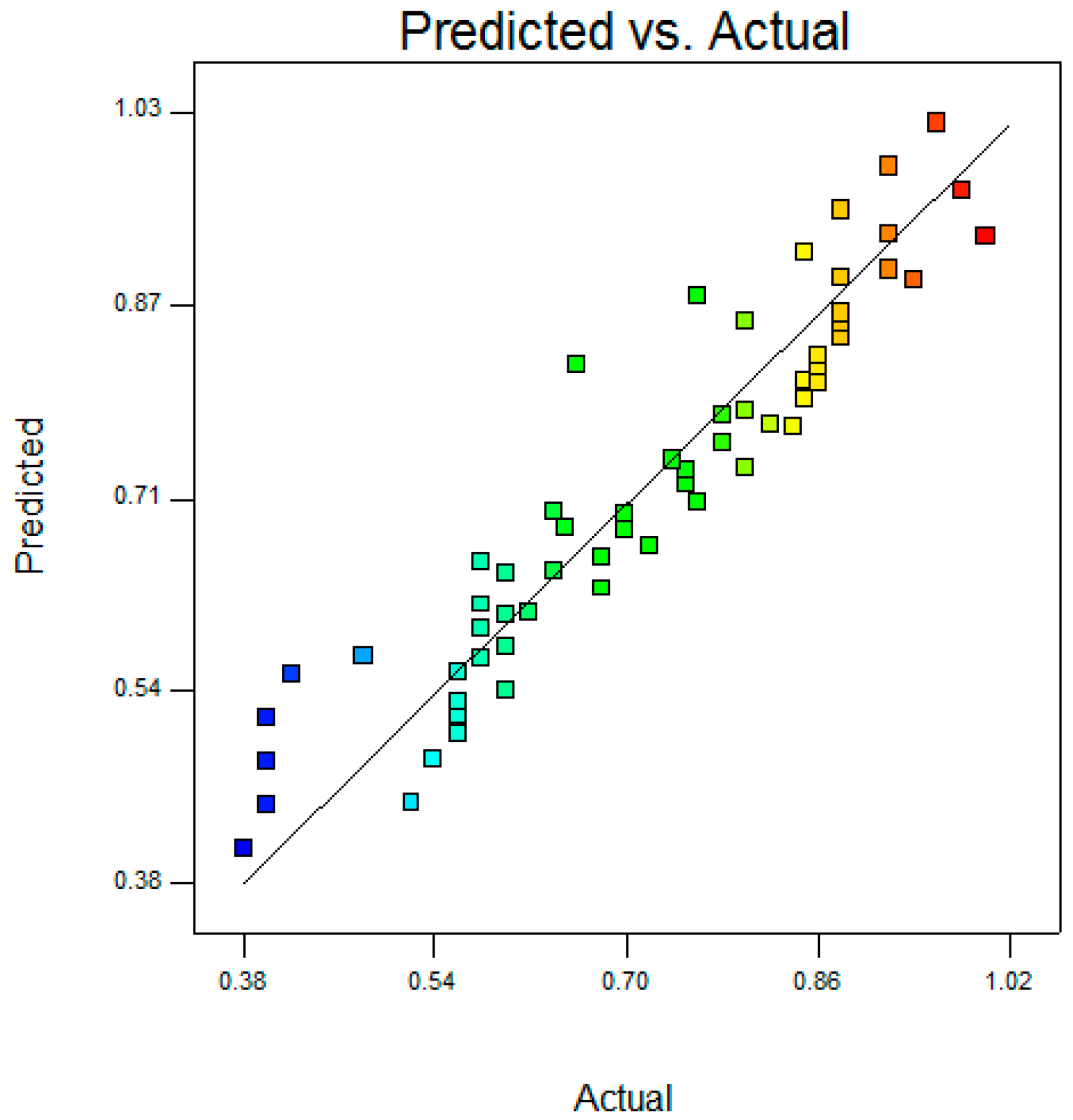
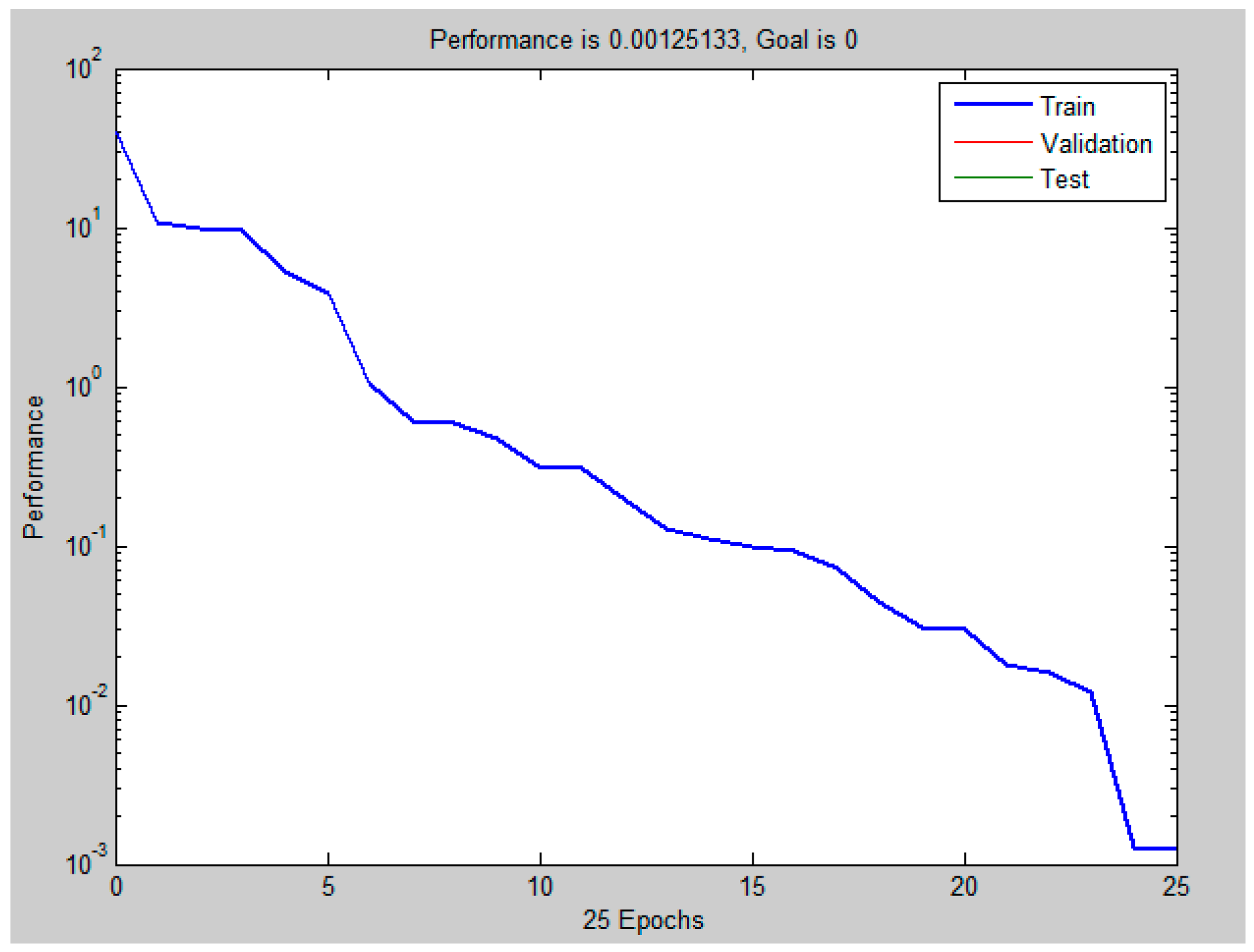
5.3. ANFIS Simulation Results
6. Conclusions
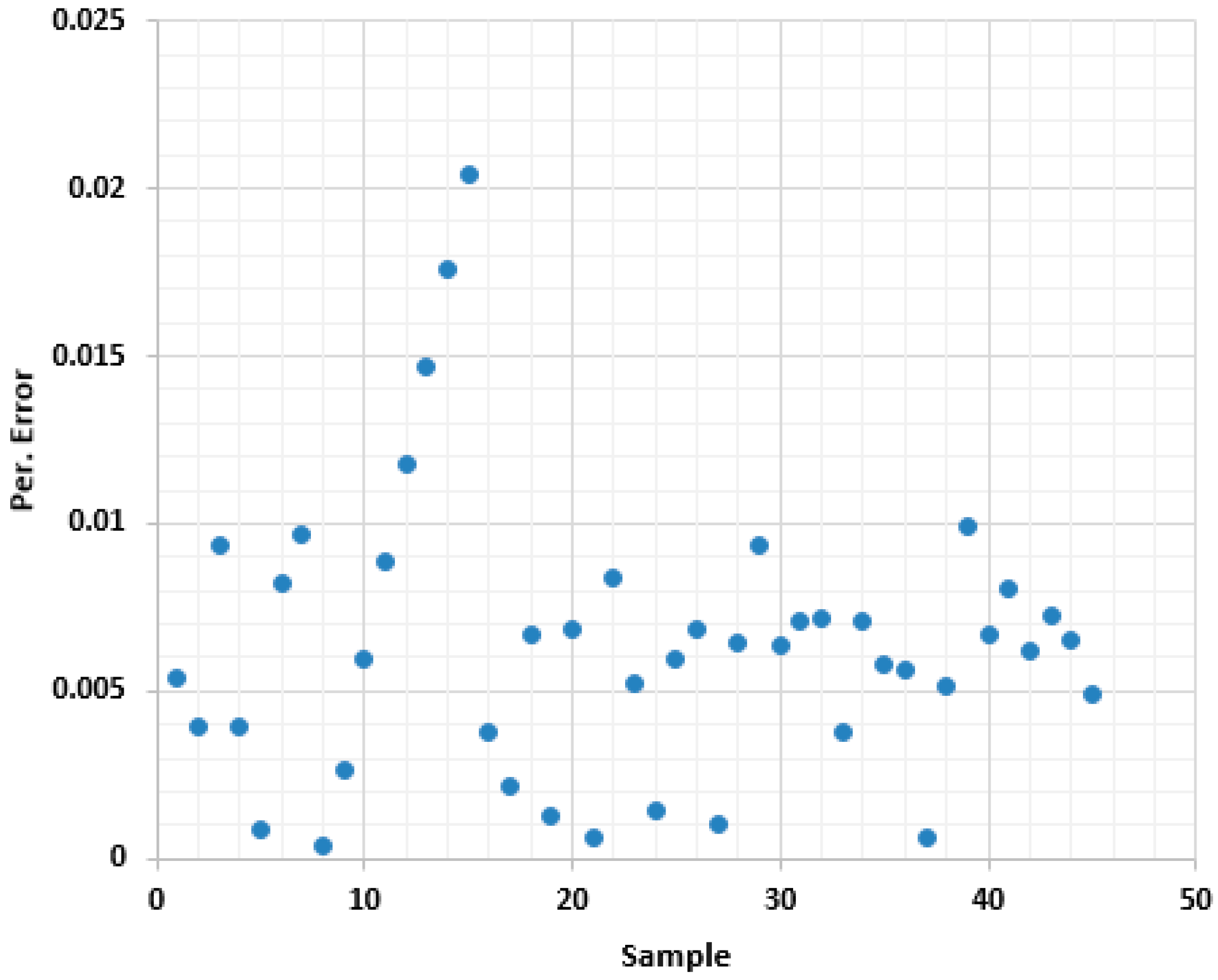
- For the percentage signal, the maximum error for trained and tested values is 0.023%, and the average error is 0.000493 in the ANFIS model.
- The prediction of the averaged percentage signal with the ANFIS models is in good agreement with the experimental result; it also has a smaller error.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rifai, D.; Abdalla, A.N.; Ali, K.; Razali, R. Giant Magnetoresistance Sensors: A Review on Structures and Non-Destructive Eddy Current Testing Applications. Sensors 2016, 16, 298. [Google Scholar] [CrossRef] [PubMed]
- Ali, K.; Abdalla, A.N.; Rifai, D.; Faraj, M. A Review on System Development in Eddy Current Testing and Technique for Defect Classification and Characterization. IET Circuits Devices Syst. 2017. [Google Scholar] [CrossRef]
- Garcia-Martin, J.; Gomez-Gil, J.; Vazquez-Sanchez, E. Non-destructive techniques based on eddy current testing. Sensors (Basel) 2011, 11, 2525–2565. [Google Scholar] [CrossRef] [PubMed]
- Faraj, M.A.; Abdalla, A.N.; Samsuri, F.B.; Rifai, D.; Ali, K. Investigate of the Effect of Width Defect on Eddy Current Testing Signals under Different Materials. Indian J. Sci. Technol. 2017, 10. [Google Scholar] [CrossRef]
- Lee, K.H.; Baek, M.K.; Park, I.H. Estimation of deep defect in ferromagnetic material by low frequency eddy current method. IEEE Trans. Magn. 2012, 48, 3965–3968. [Google Scholar] [CrossRef]
- Biju, N.; Ganesan, N.; Krishnamurthy, C.; Balasubramaniam, K. Optimum frequency variations with coil geometry and defects in tone burst eddy current thermography (TBET). Insight-Non-Destr. Test. Cond. Monit. 2013, 55, 504–509. [Google Scholar] [CrossRef]
- Rosado, L.S.; Janeiro, F.M.; Ramos, P.M.; Piedade, M. Defect characterization with eddy current testing using nonlinear-regression feature extraction and artificial neural networks. IEEE Trans. Instrum. Meas. 2013, 62, 1207–1214. [Google Scholar] [CrossRef]
- Rifai, D.; Abdalla, A.N.; Khamsah, N.; Aizat, M.; Fadzli, M. Subsurface Defects Evaluation using Eddy Current Testing. Indian J. Sci. Technol. 2016, 9. [Google Scholar] [CrossRef]
- Sasayama, T.; Ishida, T.; Matsuo, M.; Enpuku, K. Thickness Measurement of an Iron Plate Using Low-Frequency Eddy Current Testing With an HTS Coil. IEEE Trans. Appl. Superconduct. 2016, 26, 1–5. [Google Scholar] [CrossRef]
- Postolache, O.; Ramos, H.G.; Ribeiro, A.L. Characterization of defects in aluminum plates using GMR probes and neural network signal processing. In Proceedings of the XVI-IMEKO TC4 Symposium, Florence, Italy, 22–24 September 2008. [Google Scholar]
- Bodruzzaman, M.; Zein-Sabatto, S. Estimation of micro-crack lengths using eddy current C-scan images and neural-wavelet transform. In Proceedings of the Southeastcon 2008 IEEE, Huntsville, AL, USA, 3–6 April 2008; pp. 551–556. [Google Scholar]
- Morabito, E.; Versaci, M. A fuzzy neural approach to localizing holes in conducting plates. IEEE Trans. Magn. 2001, 37, 3534–3537. [Google Scholar] [CrossRef]
- Buck, J.A.; Underhill, P.R.; Morelli, J.E.; Krause, T.W. Simultaneous multiparameter measurement in pulsed eddy current steam generator data using artificial neural networks. IEEE Trans. Instrum. Meas. 2016, 65, 672–679. [Google Scholar] [CrossRef]
- Jang, J.S.; Sun, C.T. Neuro-Fuzzy Modeling and Control. Proc. IEEE 1995, 83, 378–406. [Google Scholar] [CrossRef]
- Jang, J.S.R.; Sun, C.T.; Mizutani, E. Neuro-Fuzzy and Soft Computing, a Computational Approach to Learning and Machine Intelligence; Prentice Hall, Inc: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Bunke, H.; Kandel, A. Neuro-Fuzzy Pattern Recognition; World Scientific Publishing Company: Singapore, 2000; Volume 41. [Google Scholar]
- Fausett, L.V. Fundamentals of Neural Networks; Prentice-Hall, Inc: Upper Saddle River, NJ, USA, 1994. [Google Scholar]
- Firatligil-Durmus, E.; Evranuz, O. Response surface methodology for protein extraction optimization of red pepper seed (Capsicum frutescens). LWT-Food Sci. Technol. 2010, 43, 226–231. [Google Scholar] [CrossRef]




| Frequency | Gain | Probe | Persistence | Phase | Spot X/Y |
|---|---|---|---|---|---|
| 100 KHz | 50 dB (approx.) | Bridge | Permanent | Set to 12 o’clock 100% FSH | Centre of the screen |
| The Depth of Defect (mm) | The Width of Defect (mm) | Signal Display | Percentage Signal |
|---|---|---|---|
| 1 | 0.2 |  | 56% |
| 1.5 | 0.4 |  | 72% |
| 2 | 0.6 |  | 86% |
| 2.5 | 0.8 |  | 92% |
| 1.5 | 1 |  | 58% |
| Source | Sum of Square | Df | Mean Square | F Value | p-Value Prob > F |
|---|---|---|---|---|---|
| Model | 1.39 | 4 | 0.35 | 101.58 | <0.0001 |
| A-material | 0.032 | 1 | 0.032 | 9.33 | 0.0035 |
| B-depth | 1.14 | 1 | 1.14 | 332.66 | <0.0001 |
| C-width | 0.16 | 1 | 0.16 | 46.72 | <0.0001 |
| A2 | 0.060 | 1 | 0.086 | 25.15 | <0.0001 |
| Residual | 0.19 | 55 | 3.422 × 10–3 | ||
| Cor Total | 1.58 | 59 |
| Experiment Runs | Type of Material | Depth of Crack | Width of Crack | Percentage of Signal |
|---|---|---|---|---|
| Training data | ||||
| 1 | 1 | 1 | 0.2 | 0.56 |
| 2 | 1 | 1 | 0.4 | 0.6 |
| 3 | 1 | 1 | 0.6 | 0.6 |
| 4 | 1 | 1 | 0.8 | 0.58 |
| 6 | 1 | 1.5 | 0.2 | 0.68 |
| 8 | 1 | 1.5 | 0.6 | 0.76 |
| 9 | 1 | 1.5 | 0.8 | 0.74 |
| 10 | 1 | 1.5 | 1 | 0.78 |
| 12 | 1 | 2 | 0.4 | 0.85 |
| 14 | 1 | 2 | 0.8 | 0.88 |
| 15 | 1 | 2 | 1 | 0.92 |
| 16 | 1 | 2.5 | 0.2 | 0.76 |
| 17 | 1 | 2.5 | 0.4 | 0.85 |
| 18 | 1 | 2.5 | 0.6 | 0.88 |
| 20 | 1 | 2.5 | 1 | 0.96 |
| 21 | 2 | 1 | 0.2 | 0.38 |
| 22 | 2 | 1 | 0.4 | 0.4 |
| 24 | 2 | 1 | 0.8 | 0.4 |
| 25 | 2 | 1 | 1 | 0.42 |
| 26 | 2 | 1.5 | 0.2 | 0.56 |
| 27 | 2 | 1.5 | 0.4 | 0.58 |
| 29 | 2 | 1.5 | 0.6 | 0.6 |
| 30 | 2 | 1.5 | 1 | 0.7 |
| 32 | 2 | 2 | 0.4 | 0.7 |
| 33 | 2 | 2 | 0.6 | 0.75 |
| 34 | 2 | 2 | 0.8 | 0.84 |
| 35 | 2 | 2 | 1 | 0.86 |
| 37 | 2 | 2.5 | 0.4 | 0.86 |
| 38 | 2 | 2.5 | 0.6 | 0.88 |
| 39 | 2 | 2.5 | 0.8 | 0.94 |
| 41 | 3 | 1 | 0.2 | 0.52 |
| 42 | 3 | 1 | 0.4 | 0.54 |
| 43 | 3 | 1 | 0.6 | 0.56 |
| 45 | 3 | 1 | 1 | 0.58 |
| 47 | 3 | 1.5 | 0.4 | 0.62 |
| 48 | 3 | 1.5 | 0.6 | 0.64 |
| 49 | 3 | 1.5 | 0.8 | 0.65 |
| 51 | 3 | 2 | 0.2 | 0.64 |
| 53 | 3 | 2 | 0.6 | 0.82 |
| 54 | 3 | 2 | 0.8 | 0.85 |
| 55 | 3 | 2 | 1 | 0.88 |
| 56 | 3 | 2.5 | 0.2 | 0.66 |
| 57 | 3 | 2.5 | 0.4 | 0.8 |
| 59 | 3 | 2.5 | 0.8 | 0.92 |
| 60 | 3 | 2.5 | 1 | 0.98 |
| Testing data | ||||
| 5 | 1 | 1 | 1 | 0.58 |
| 7 | 1 | 1.5 | 0.4 | 0.72 |
| 11 | 1 | 2 | 0.2 | 0.78 |
| 13 | 1 | 2 | 0.6 | 0.86 |
| 19 | 1 | 2.5 | 0.8 | 0.92 |
| 23 | 2 | 1 | 0.6 | 0.4 |
| 28 | 2 | 1.5 | 0.8 | 0.6 |
| 31 | 2 | 2 | 0.2 | 0.68 |
| 36 | 2 | 2.5 | 0.2 | 0.8 |
| 40 | 2 | 2.5 | 1 | 1 |
| 44 | 3 | 1 | 0.8 | 0.56 |
| 46 | 3 | 1.5 | 0.2 | 0.48 |
| 50 | 3 | 1.5 | 1 | 0.75 |
| 52 | 3 | 2 | 0.4 | 0.8 |
| 58 | 3 | 2.5 | 0.6 | 0.88 |
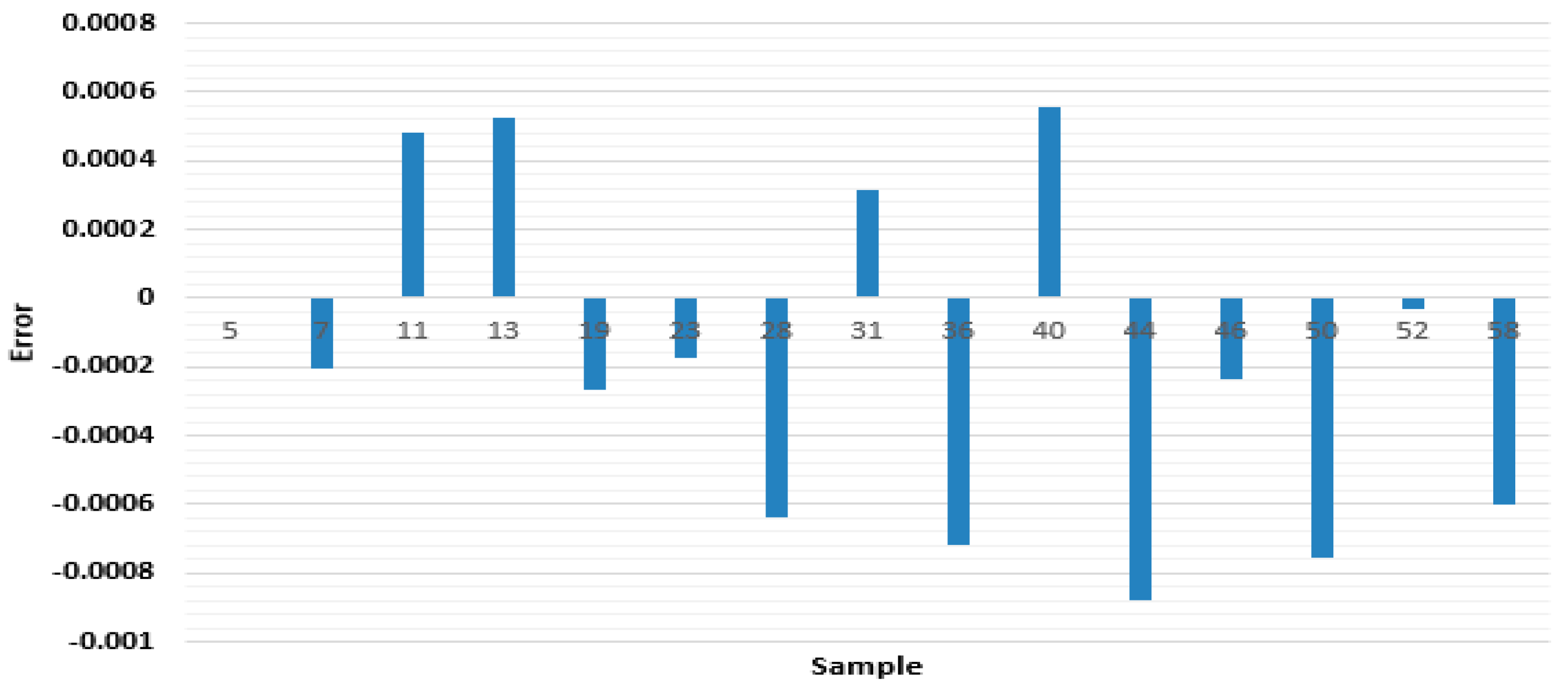
| Exp. Run | Signal % | ANFIS | ER% |
|---|---|---|---|
| 5 | 0.58 | 0.57900165 | −0.001 |
| 7 | 0.72 | 0.71979543 | −0.0002 |
| 11 | 0.78 | 0.78048298 | 0.000483 |
| 13 | 0.86 | 0.86052741 | 0.000527 |
| 19 | 0.92 | 0.91973257 | −0.00027 |
| 23 | 0.4 | 0.39982569 | −0.00017 |
| 28 | 0.6 | 0.59936003 | −0.00064 |
| 31 | 0.68 | 0.68031255 | 0.000313 |
| 36 | 0.8 | 0.79928399 | −0.00072 |
| 40 | 1 | 1.0005583 | 0.000558 |
| 44 | 0.56 | 0.5591191 | −0.00088 |
| 46 | 0.48 | 0.47976182 | −0.00024 |
| 50 | 0.75 | 0.74924405 | −0.00076 |
| 52 | 0.8 | 0.79996763 | −3.2 × 10–5 |
| 58 | 0.88 | 0.87939948 | −0.0006 |
| Maximum | 0.000998 | ||
| ABS Average | 0.000493 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faraj, M.A.; Samsuri, F.; Abdalla, A.N.; Rifai, D.; Ali, K. Adaptive Neuro-Fuzzy Inference System Model Based on the Width and Depth of the Defect in an Eddy Current Signal. Appl. Sci. 2017, 7, 668. https://doi.org/10.3390/app7070668
Faraj MA, Samsuri F, Abdalla AN, Rifai D, Ali K. Adaptive Neuro-Fuzzy Inference System Model Based on the Width and Depth of the Defect in an Eddy Current Signal. Applied Sciences. 2017; 7(7):668. https://doi.org/10.3390/app7070668
Chicago/Turabian StyleFaraj, Moneer A, Fahmi Samsuri, Ahmed N. Abdalla, Damhuji Rifai, and Kharudin Ali. 2017. "Adaptive Neuro-Fuzzy Inference System Model Based on the Width and Depth of the Defect in an Eddy Current Signal" Applied Sciences 7, no. 7: 668. https://doi.org/10.3390/app7070668
APA StyleFaraj, M. A., Samsuri, F., Abdalla, A. N., Rifai, D., & Ali, K. (2017). Adaptive Neuro-Fuzzy Inference System Model Based on the Width and Depth of the Defect in an Eddy Current Signal. Applied Sciences, 7(7), 668. https://doi.org/10.3390/app7070668






