Double-Sided Terahertz Imaging of Multilayered Glass Fiber-Reinforced Polymer
Abstract
:1. Introduction
- non-contact measurement in reflection and transmission arrangement;
- non-ionizing nature;
- inner structure and spectral information is obtainable; and
- fraction of a millimeter resolution.
- low power of THz emitters;
- low speed of examination (need of raster scanning in case of VNA and TDS solutions);
- restriction to nonconductive materials (because of high frequency and skin effect); and
- high cost of VNA and TDS solutions.
2. Materials and Methods
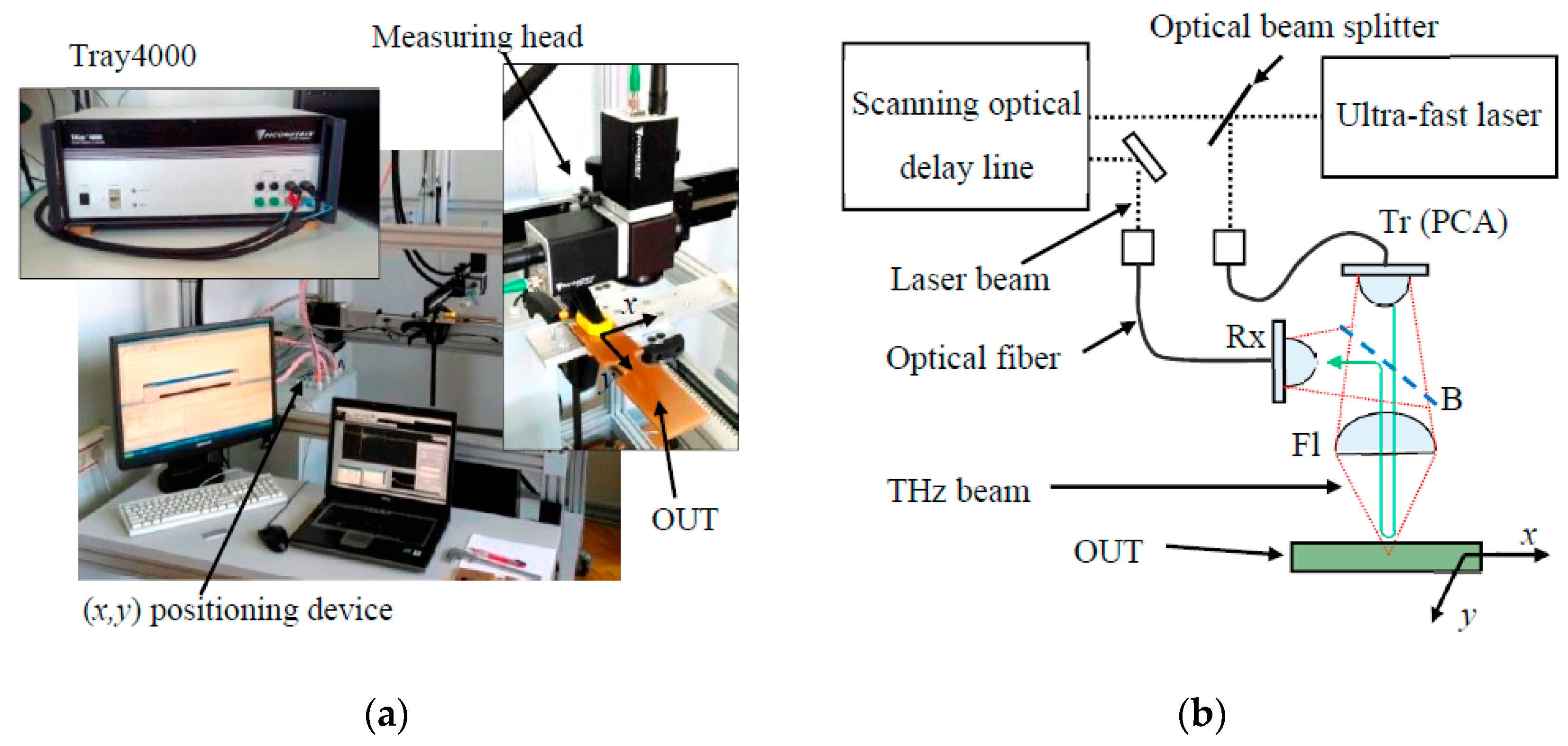
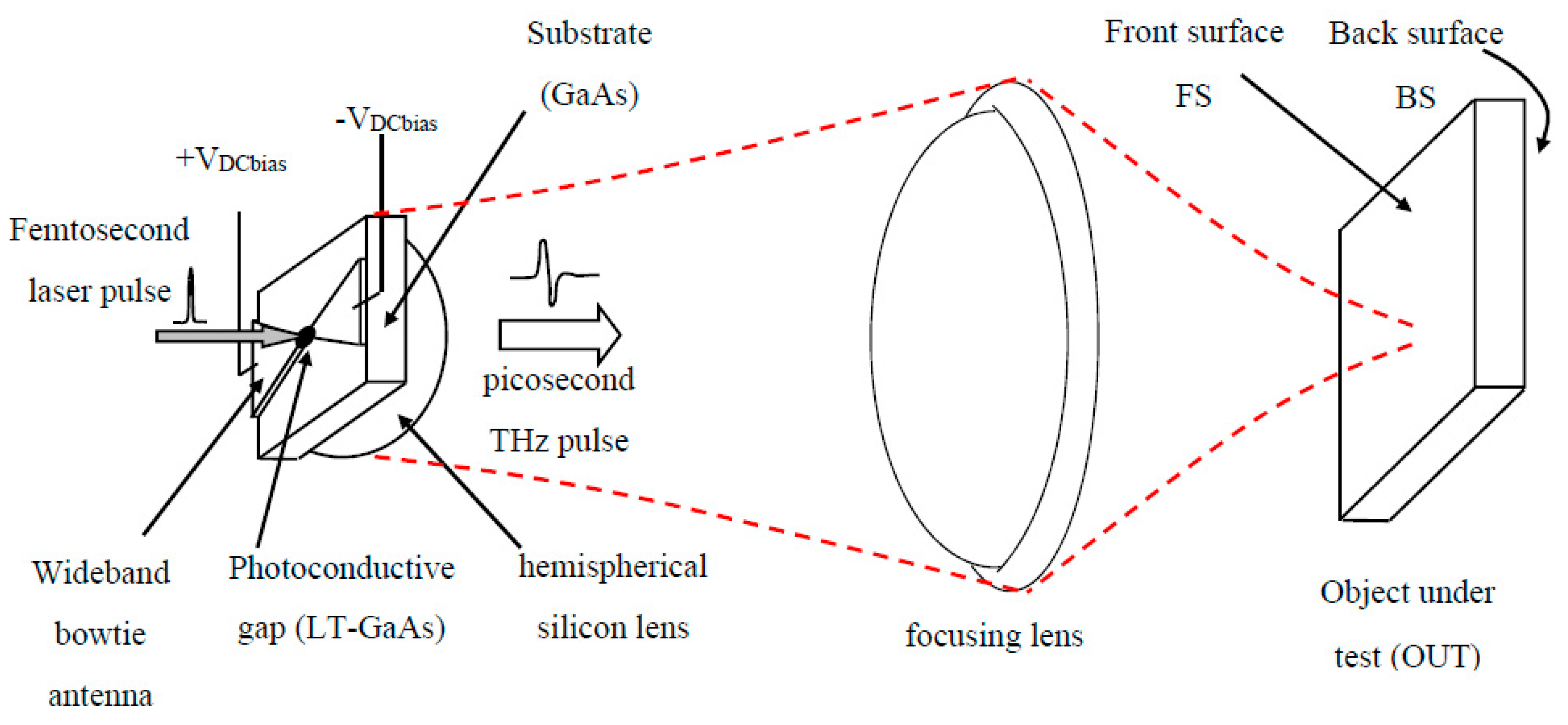
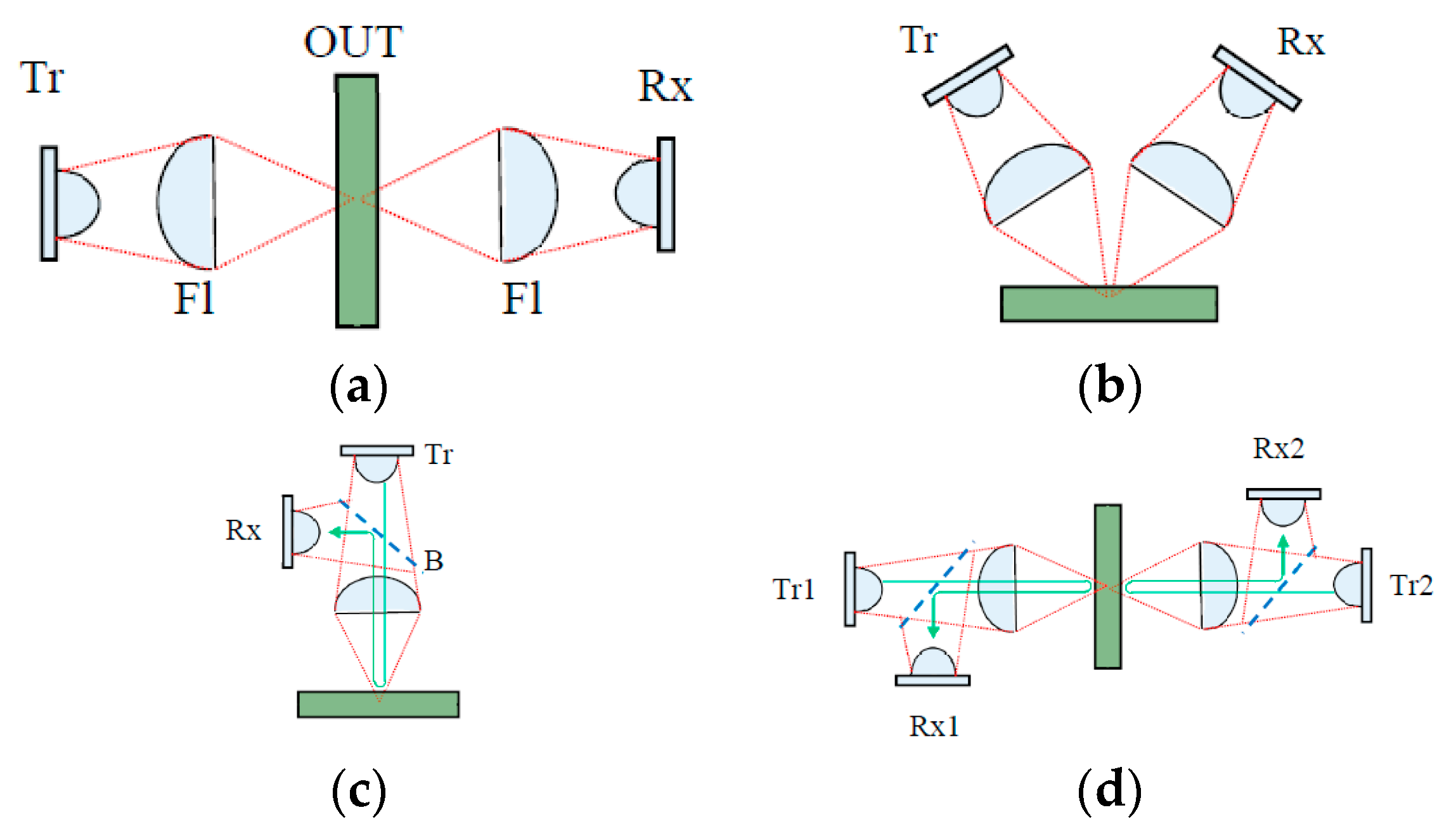
2.1. Pulsed Terahertz Measuring System
2.2. Proposed Algorithm
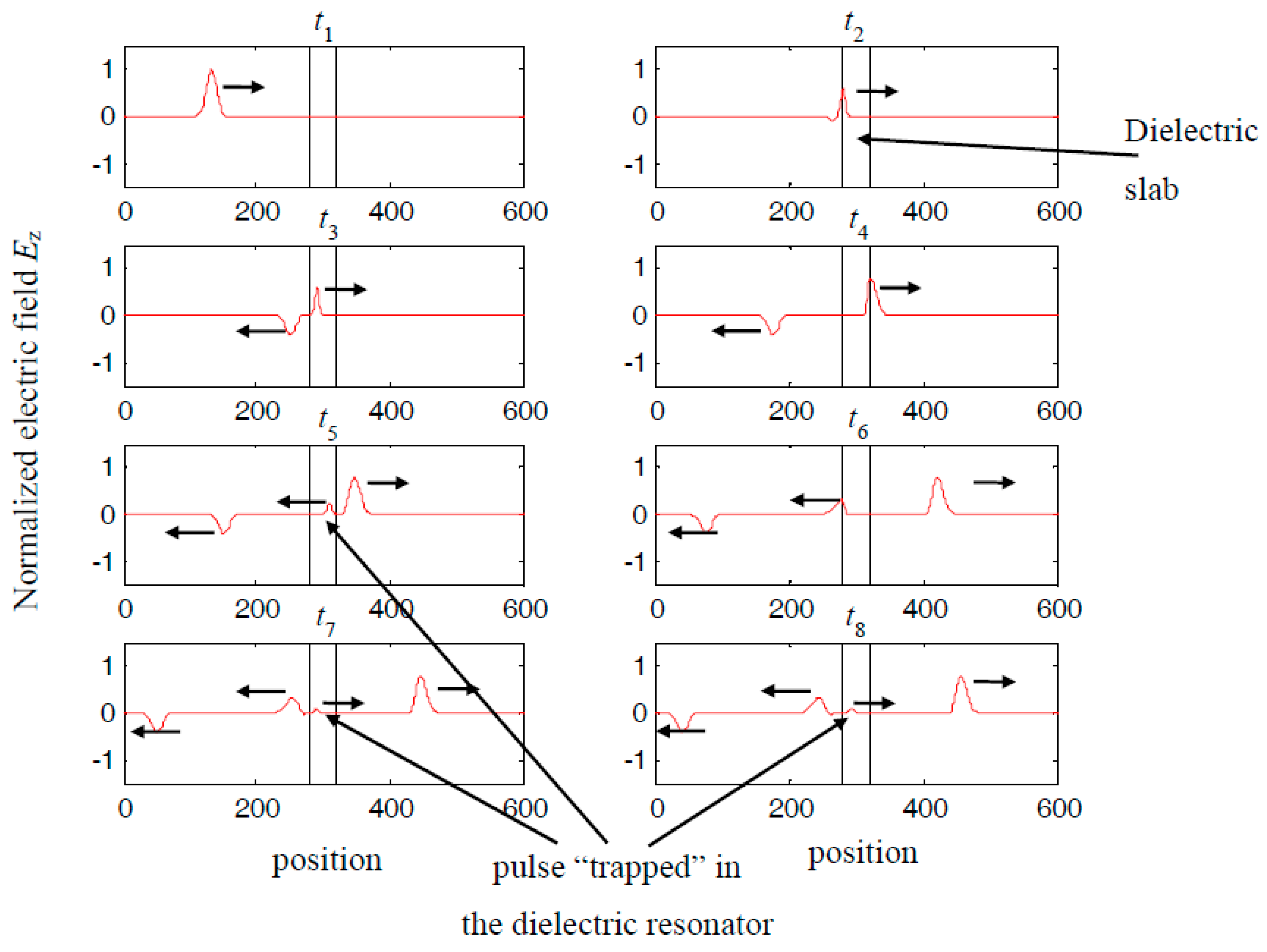
2.3. Analytical Model
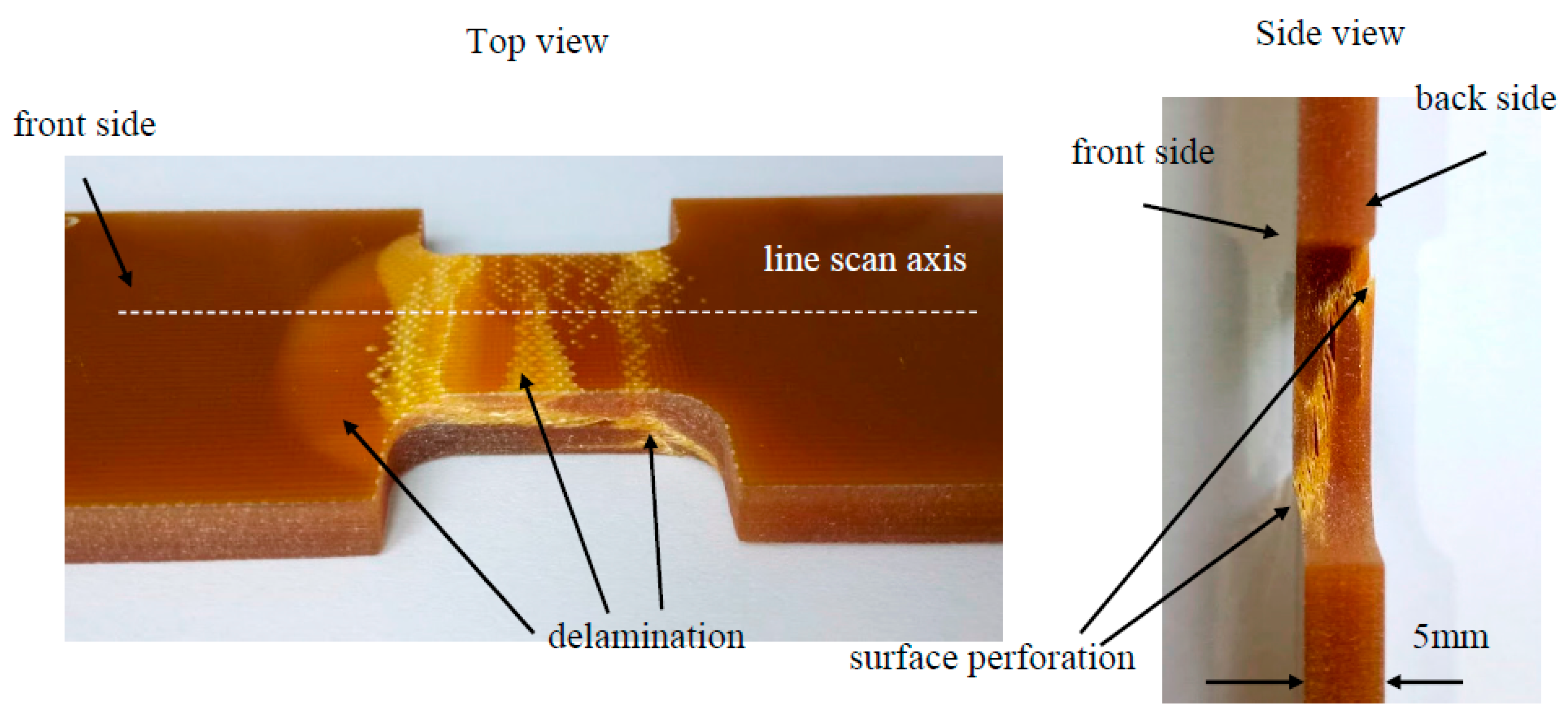
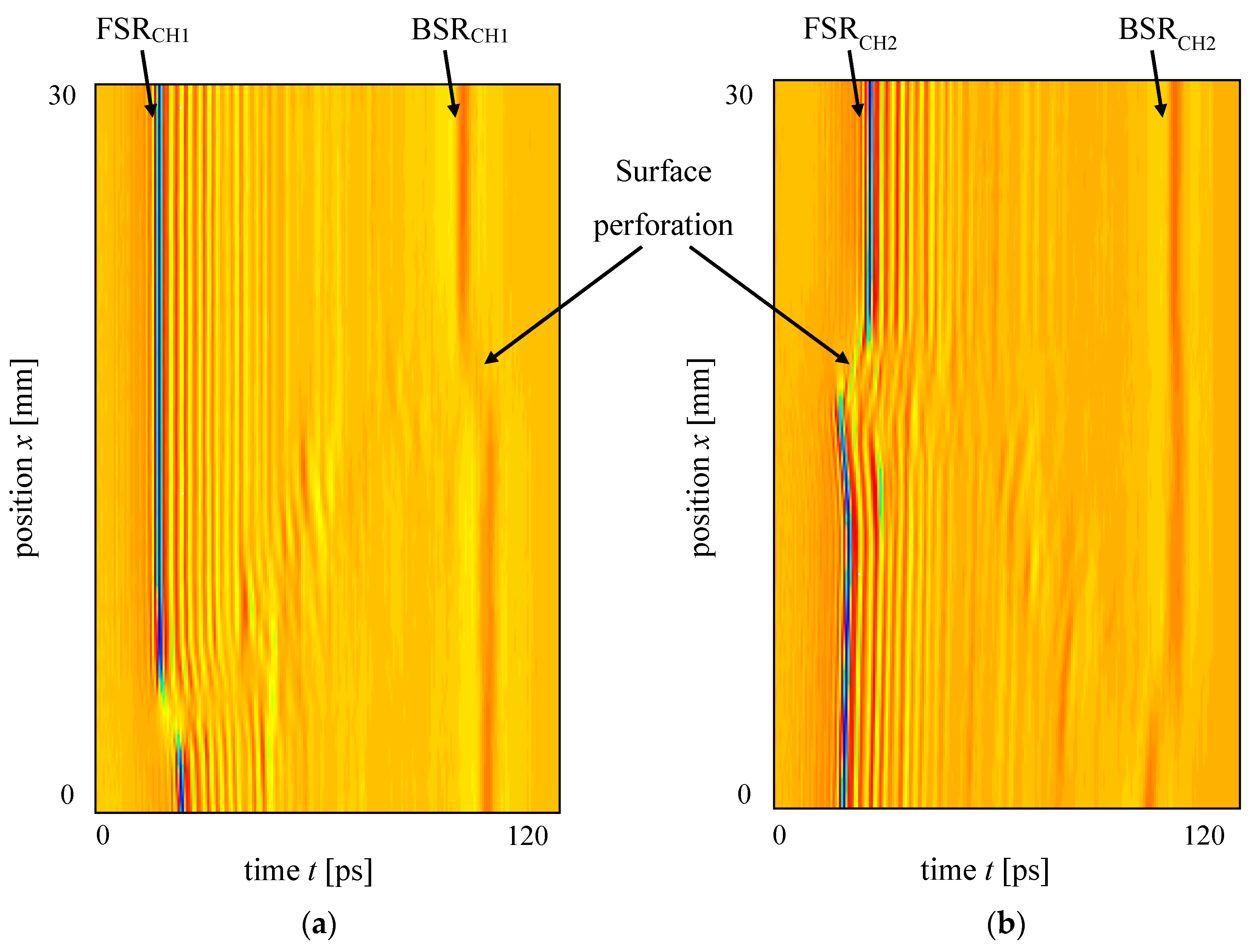
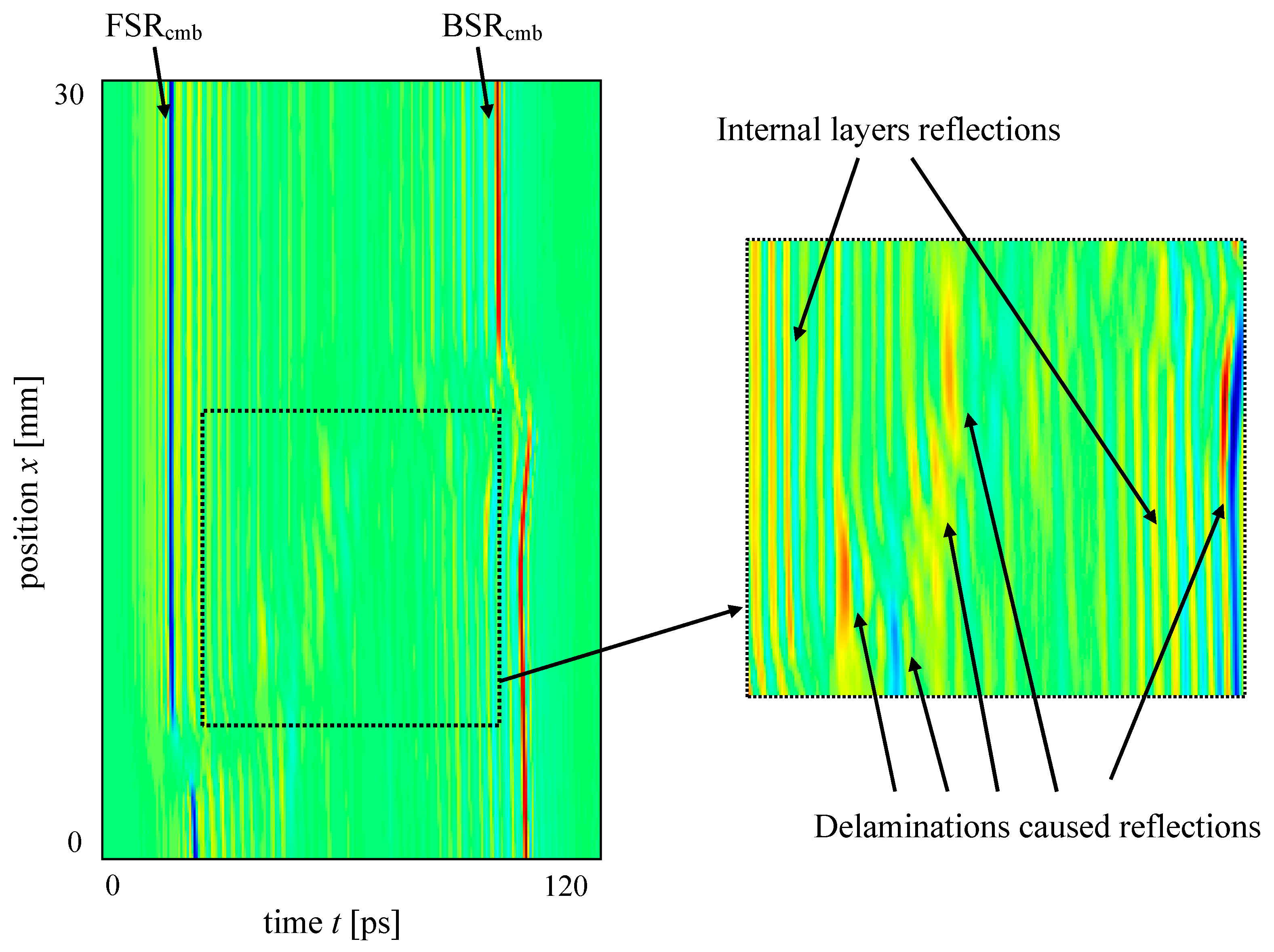
3. Results and Discussion
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Wang, R.M.; Zheng, S.R.; Zheng, Y. Polymer Matrix Composites and Technology, 1st ed.; Woodhead Publishing: Cambridge, UK, 2011. [Google Scholar]
- Lopato, P.; Szymanik, B.; Psuj, G. Nondestructive inspection of thin basalt fiber reinforced composites using combined terahertz imaging and infrared thermography. Adv. Mater. Sci. Eng. 2016. [Google Scholar] [CrossRef]
- Raj, B.; Jayakumar, T.; Thavasimuthu, M. Practical Non-Destructive Testing, 2nd ed.; Woodhead Publishing: Sawston, UK, 2002. [Google Scholar]
- Szymanik, B.; Psuj, G. Infrared and electromagnetic inspection of steel structures under load. Quant. InfraRed Thermogr. J. 2016, 13, 232–241. [Google Scholar] [CrossRef]
- Cheng, L.; Tian, G.Y. Comparison of Nondestructive Testing Methods on Detection of Delaminations in Composites. J. Sens. 2012, 2012, 408437. [Google Scholar] [CrossRef]
- Maldague, X. Theory and Practice of Infrared Technology for Nondestructive Testing; John Wiley and Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Balageas, D.; Maldague, X.; Burleigh, D.; Vavilov, V.P.; Oswald-Tranta, B.; Roche, J.M.; Pradere, C.; Carlomagno, G.M. Thermal (IR) and other NDT techniques for improved material inspection. J. Nondestruct. Eval. 2016, 35, 18. [Google Scholar] [CrossRef]
- Chady, T.; Psuj, G. Data Fusion From Multidirectional Remanent Flux Leakage Transducers for Nondestructive Testing of Stress-and Fatigue-Loaded Steel Samples. IEEE Trans. Magn. 2008, 44, 3285–3288. [Google Scholar] [CrossRef]
- Naftaly, M.; Clake, R.G.; Humphreys, D.A.; Ridler, N.M. Metrology State-of-the-Art and Challenges in Broadband Phase-Sensitive Terahertz Measurements. Proc. IEEE 2017, 105, 1151–1165. [Google Scholar] [CrossRef]
- Naito, K.; Kagawa, Y.; Utsuno, S.; Naganuma, T.; Kurihara, K. Dielectric properties of woven fabric glass fiber reinforced polymer-matrix composites in the THz frequency range. Compos. Sci. Technol. 2009, 69, 2027–2029. [Google Scholar] [CrossRef]
- Wallace, V.P.; Macpherson, E.; Zeitler, J.A.; Reid, C. Three-dimensional imaging of optically opaque materials using nonionizing terahertz radiation. J. Opt. Soc. Am. 2008, 25, 3120–3133. [Google Scholar] [CrossRef]
- Parrott, E.P.; Sy, S.M.; Blu, T.; Wallace, V.P.; Pickwell-MacPherson, E. Terahertz pulsed imaging in vivo: Measurements and processing methods. J. Biomed. Opt. 2011, 16, 106010. [Google Scholar] [CrossRef] [PubMed]
- Mittleman, D.M.; Gupta, M.; Neelamani, R.; Baraniuk, R.G.; Rudd, J.V.; Koch, M. Recent advances in terahertz imaging. Appl. Phys. B 1999, 68, 1085–1094. [Google Scholar] [CrossRef]
- Mittelman, D. Sensing with Terahertz Radiation; Springer: Berlin, Germany, 2010. [Google Scholar]
- Palka, N.; Miedzińska, D. Detailed non-destructive evaluation of UHMWPE composites in the terahertz range. Opt. Quantum Electron. 2014, 46, 515–525. [Google Scholar] [CrossRef]
- Jin, Y.S.; Kim, G.J.; Jeon, S.G. Terahertz dielectric properties of polymers. J. Korean Phys. Soc. 2006, 49, 513–517. [Google Scholar]
- Dolganova, I.; Zaytsev, K.; Metelkina, A.; Yakovlev, E.; Karasik, V.; Yurchenko, S. Combined terahertz imaging system for enhanced imaging quality. Opt. Quant. Electron. 2016, 48, 325. [Google Scholar] [CrossRef]
- Chang, T.; Zhang, X.; Zhang, X.; Cui, H.-L. Accurate determination of dielectric permittivity of polymers from 75 GHz to 1.6 THz using both S-parameters and transmission spectroscopy. Appl. Opt. 2017, 56, 3287–3292. [Google Scholar] [CrossRef] [PubMed]
- Jassim, H.; Abdullah, I.; Shaban, A. THz spectra identification and classification of explosives, illicit drugs, based on BP-ANN and PSO-ANN algorithms. Eur. J. Sci. Res. 2012, 74, 487–494. [Google Scholar]
- Liang, M.; Shen, J.; Wang, G. Identification of illicit drugs by using SOM neural networks. J. Phys. D Appl. Phys. 2008, 41, 135306. [Google Scholar] [CrossRef]
- Ferguson, B.; Wang, S.; Gray, D.; Abbott, D.; Zhang, X. Identification of biological tissue using chirped probe THz imaging. Microelectron. J. 2002, 33, 1043–1051. [Google Scholar] [CrossRef]
- Grootendorst, M.R.; Fitzgerald, A.J.; de Koning, S.G.B.; Santaolalla, A.; Portieri, A.; Van Hemelrijck, M.; Young, M.R.; Owen, J.; Cariati, M.; Pepper, M.; et al. Use of a handheld terahertz pulsed imaging device to differentiate benign and malignant breast tissue. Biomed. Opt. Express 2017, 8, 2932–2945. [Google Scholar] [CrossRef]
- Malinowski, P.; Palka, N.; Opoka, S.; Wandowski, T.; Ostachowicz, W. Moisture detection in composites by terahertz spectroscopy. J. Phys. Conf. Ser. 2015, 628, 012100. [Google Scholar] [CrossRef]
- Zeitler, J.A.; Shen, Y.C. Industrial applications of terahertz imaging. In Terahertz Spectroscopy and Imaging, Springer Series in Optical Sciences; Peiponen, K.E., Zeitler, A., Kuwata-Gonokami, M., Eds.; Springer: Berlin, Germany, 2013; Volume 171, pp. 451–489. [Google Scholar]
- Yakovlev, E.; Zaytsev, K.; Dolganova, I.; Yurchenko, S. Non-destructive evaluation of polymer composite materials at the manufacturing stage using terahertz pulsed spectroscopy. IEEE Trans. Terahertz Sci. Technol. 2015, 5, 810–816. [Google Scholar] [CrossRef]
- El Haddad, J.; Bousquet, B.; Canioni, L.; Mounaix, P. Review in terahertz spectral analysis. Trends Anal. Chem. 2013, 44, 98–105. [Google Scholar] [CrossRef]
- Li, M.; Dai, G.; Chang, T.; Shi, C.; Wei, D.; Du, C.; Cui, H.L. Accurate determination of geographical origin of tea based on terahertz spectroscopy. Appl. Sci. 2017, 7, 172. [Google Scholar] [CrossRef]
- Lopato, P.; Chady, T. Terahertz detection and identification of defects in layered polymer composites and composite coatings. Nondestruct. Test. Eval. 2013, 28, 28–43. [Google Scholar] [CrossRef]
- Yakovlev, E.; Zaytsev, K.; Chernomyrdin, N.; Gavdush, A.; Zotov, A.; Nikonovich, M.; Yurchenko, S. Non-destructive testing of composite materials using terahertz time-domain spectroscopy. Proc. SPIE 2016. [Google Scholar] [CrossRef]
- Ahi, K.; Anwar, M. Advanced terahertz techniques for quality control and counterfeit detection. Proc. SPIE 2016. [Google Scholar] [CrossRef]
- Ahi, K.; Anwar, M. Developing terahertz imaging equation and enhancement of the resolution of terahertz images using deconvolution. Proc. SPIE 2016. [Google Scholar] [CrossRef]
- Ferguson, B.; Wang, S.; Gray, D.; Abbott, D.; Zhang, X.C. Towards functional 3D T-ray imaging. Phys. Med. Biol. 2002, 47, 3735–3742. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Zhang, X.C. Pulsed terahertz tomography. J. Phys. D Appl. Phys. 2004, 37, R1–R36. [Google Scholar] [CrossRef]
- Zimdars, D.; Fichter, G.; Chemovski, A. Time domain terahertz computed axial tomography for nondestructive evaluation. Rev. Quant. Nondestruct. Eval. 2009, 28, 426–433. [Google Scholar]
- Choi, H.; Son, J.H. Terahertz imaging and tomography techniques. In Terahertz Biomedical Science and Technology; Son, J.H., Ed.; CRC Press: Boca Raton, FL, USA, 2014; pp. 47–66. [Google Scholar]
- Guillet, J.P.; Recur, B.; Frederique, L.; Bousquet, B.; Canioni, L.; Manek-Honninger, I.; Desbarats, P.; Mounaix, P. Review of terahertz tomography techniques. J. Infrared Millim. Terahertz Waves 2014, 35, 382–411. [Google Scholar] [CrossRef]
- Hack, E.; Valzania, L.; Gäumann, G.; Shalaby, M.; Hauri, C.P.; Zolliker, P. Comparison of Thermal Detector Arrays for Off-Axis THz Holography and Real-Time THz Imaging. Sensors 2016, 16, 221. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.R.; Lee, W.J.; Han, S.T. Signal-Conditioning Block of a 1x200 CMOS Detector Array for a Terahertz Real-Time Imaging System. Sensors 2016, 16, 319. [Google Scholar] [CrossRef] [PubMed]
- Boukhayma, A.; Dupret, A.; Rostaing, J.P.; Enz, C. A Low-Noise CMOS THz Imager Based on Source Modulation and an In-Pixel High-Q Passive Switched-Capacitor N-Path Filter. Sensors 2016, 16, 325. [Google Scholar] [CrossRef] [PubMed]
- Santamarina, J.; Fratta, D. Discrete Signals and Inverse Problems: An Introduction for Engineers and Scientists; John Wiley & Sons: Chichester, UK, 2005; pp. 249–284. [Google Scholar]
- Collin, R.E. Field Theory of Guided Waves; Wiley-IEEE Press: New York, NY, USA, 1990. [Google Scholar]
- Lopato, P. Estimation of layered materials dielectric parameters using pulsed terahertz technique. Int. J. Appl. Electromagn. Mech. 2013, 43, 161–168. [Google Scholar]
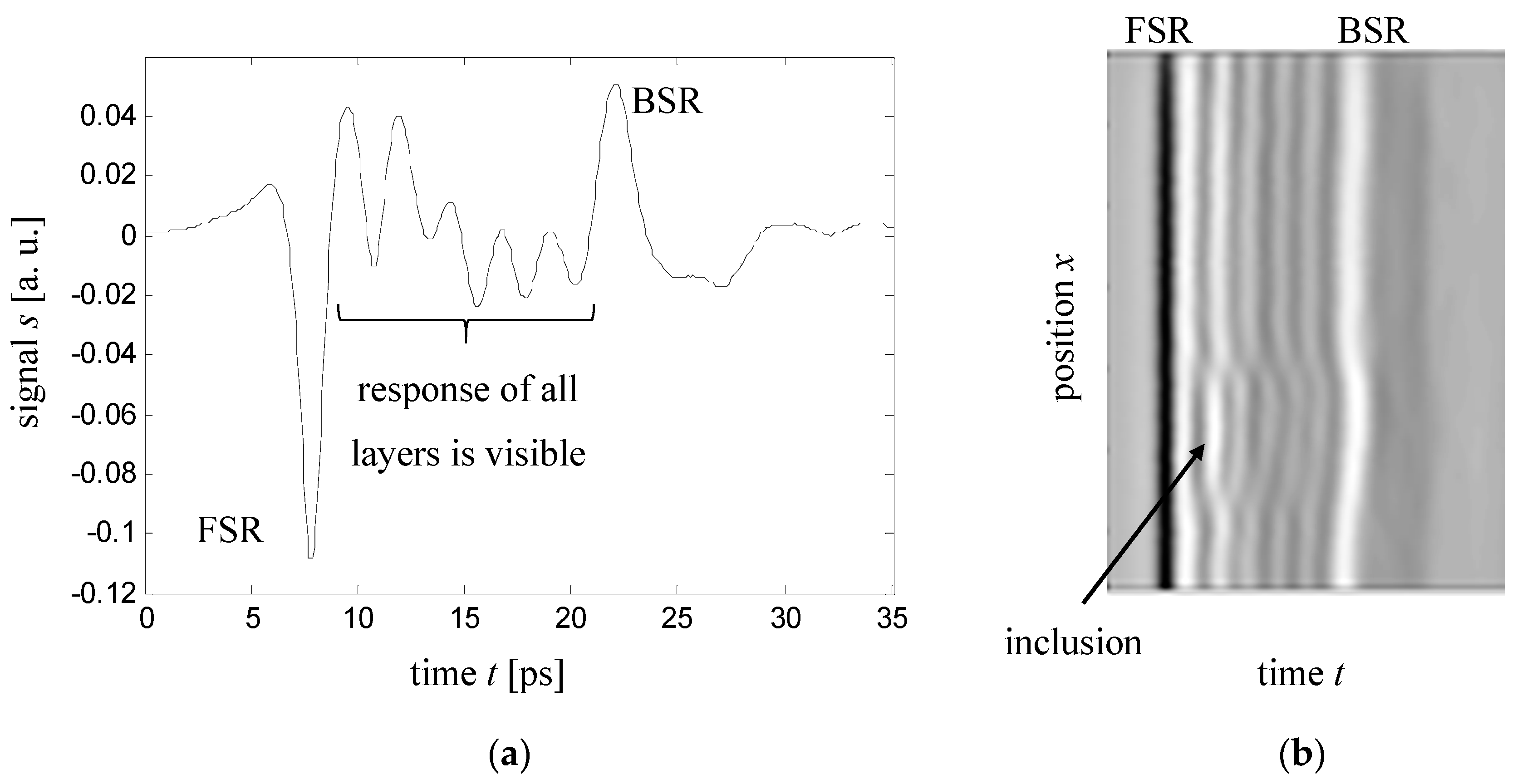
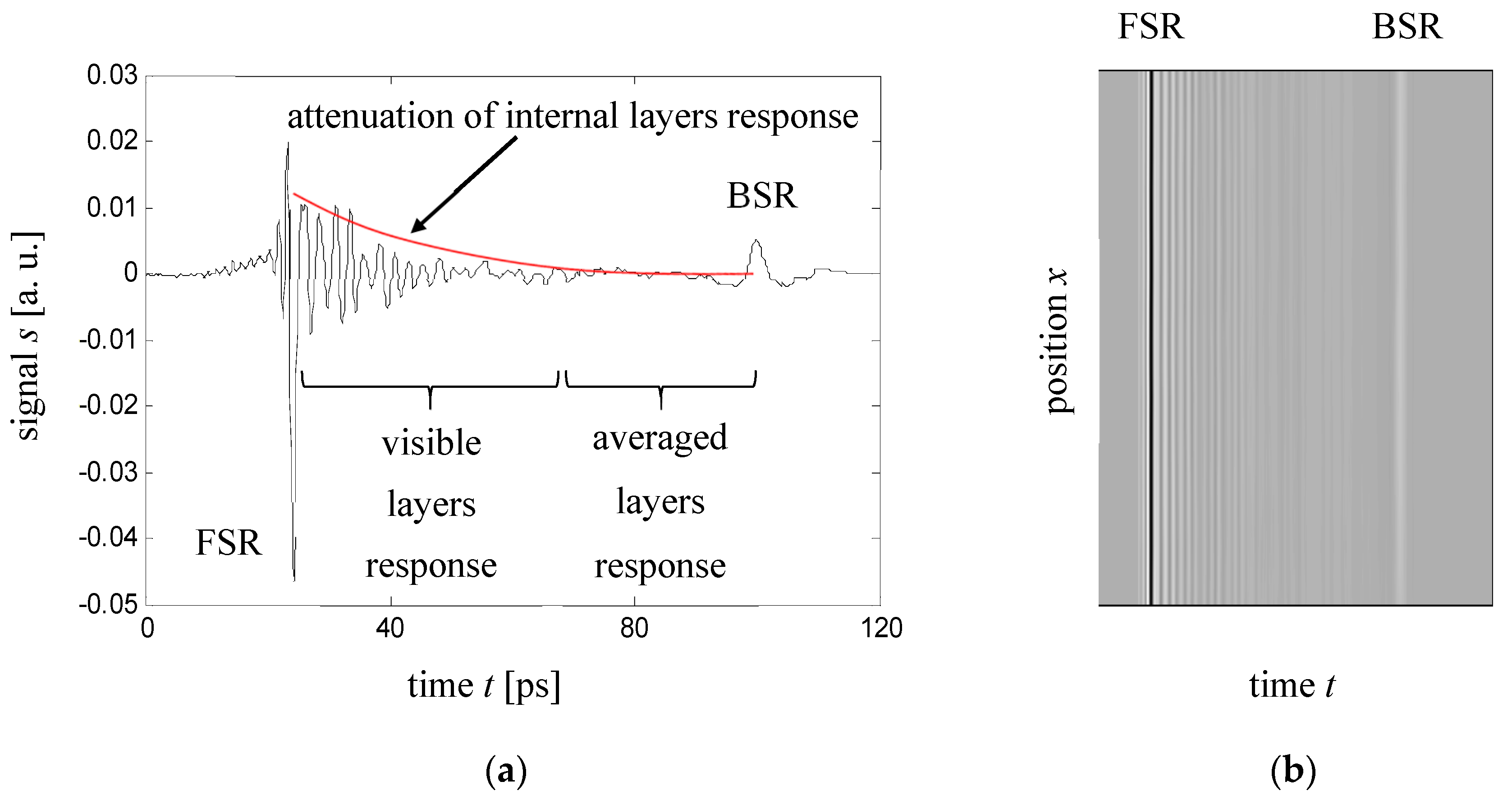
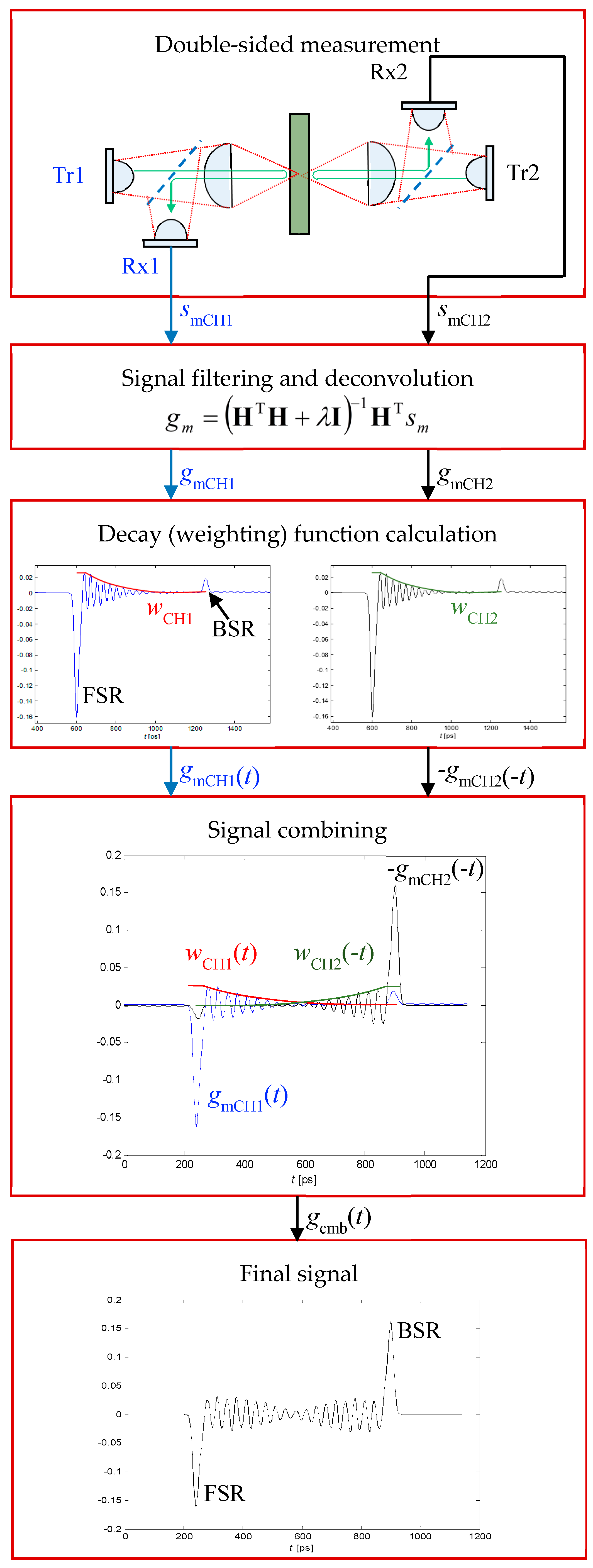
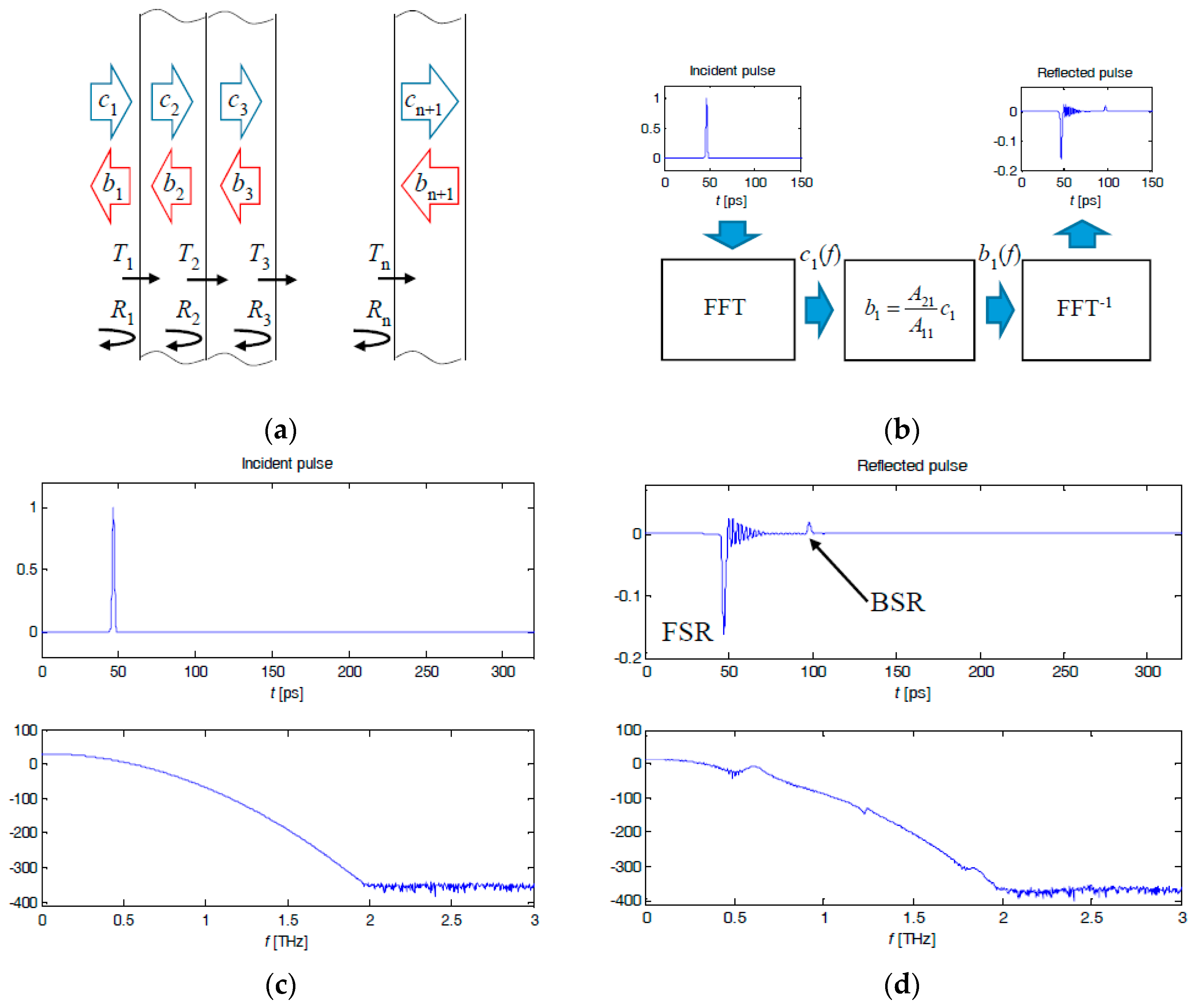


© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lopato, P. Double-Sided Terahertz Imaging of Multilayered Glass Fiber-Reinforced Polymer. Appl. Sci. 2017, 7, 661. https://doi.org/10.3390/app7070661
Lopato P. Double-Sided Terahertz Imaging of Multilayered Glass Fiber-Reinforced Polymer. Applied Sciences. 2017; 7(7):661. https://doi.org/10.3390/app7070661
Chicago/Turabian StyleLopato, Przemyslaw. 2017. "Double-Sided Terahertz Imaging of Multilayered Glass Fiber-Reinforced Polymer" Applied Sciences 7, no. 7: 661. https://doi.org/10.3390/app7070661
APA StyleLopato, P. (2017). Double-Sided Terahertz Imaging of Multilayered Glass Fiber-Reinforced Polymer. Applied Sciences, 7(7), 661. https://doi.org/10.3390/app7070661




