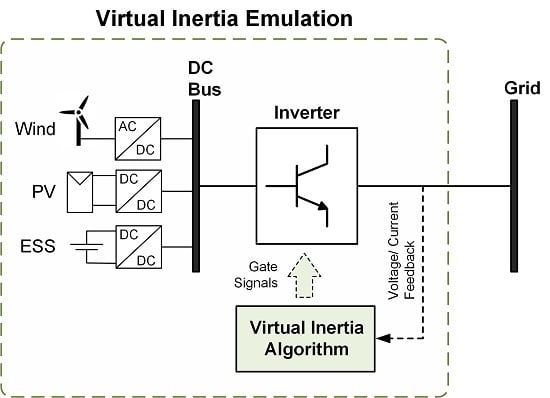
Virtual Inertia: Current Trends and Future Directions
Abstract
:1. Introduction
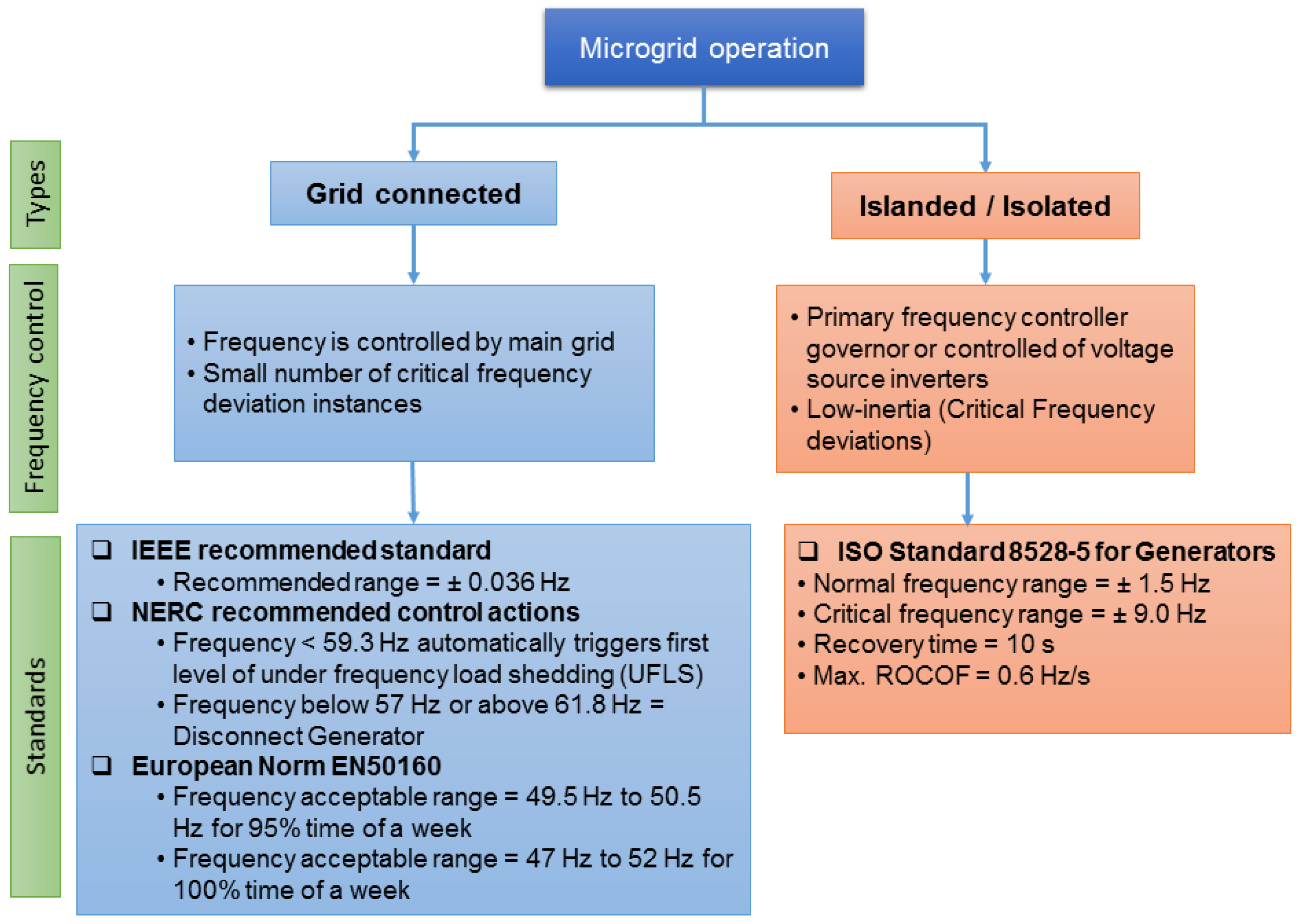
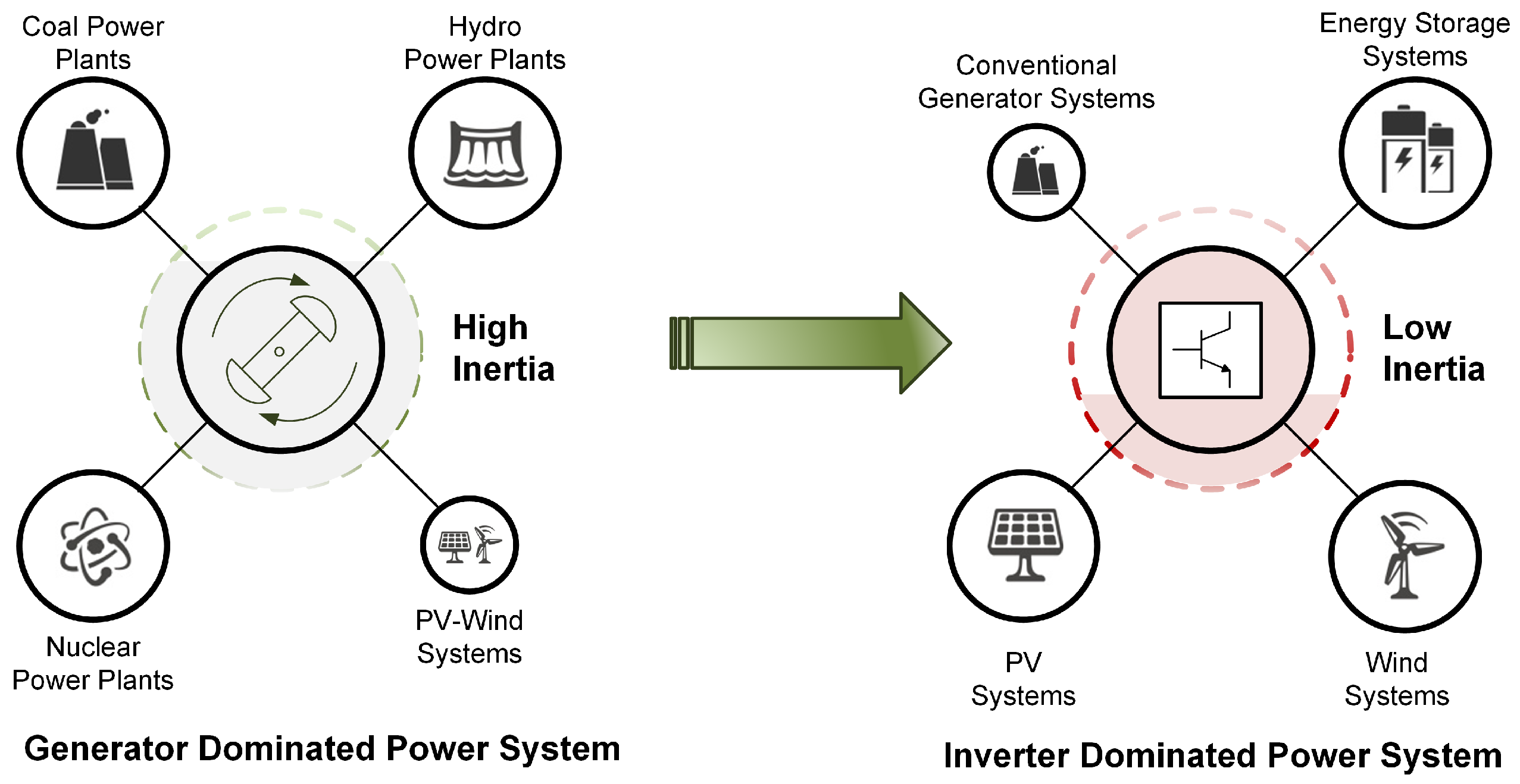
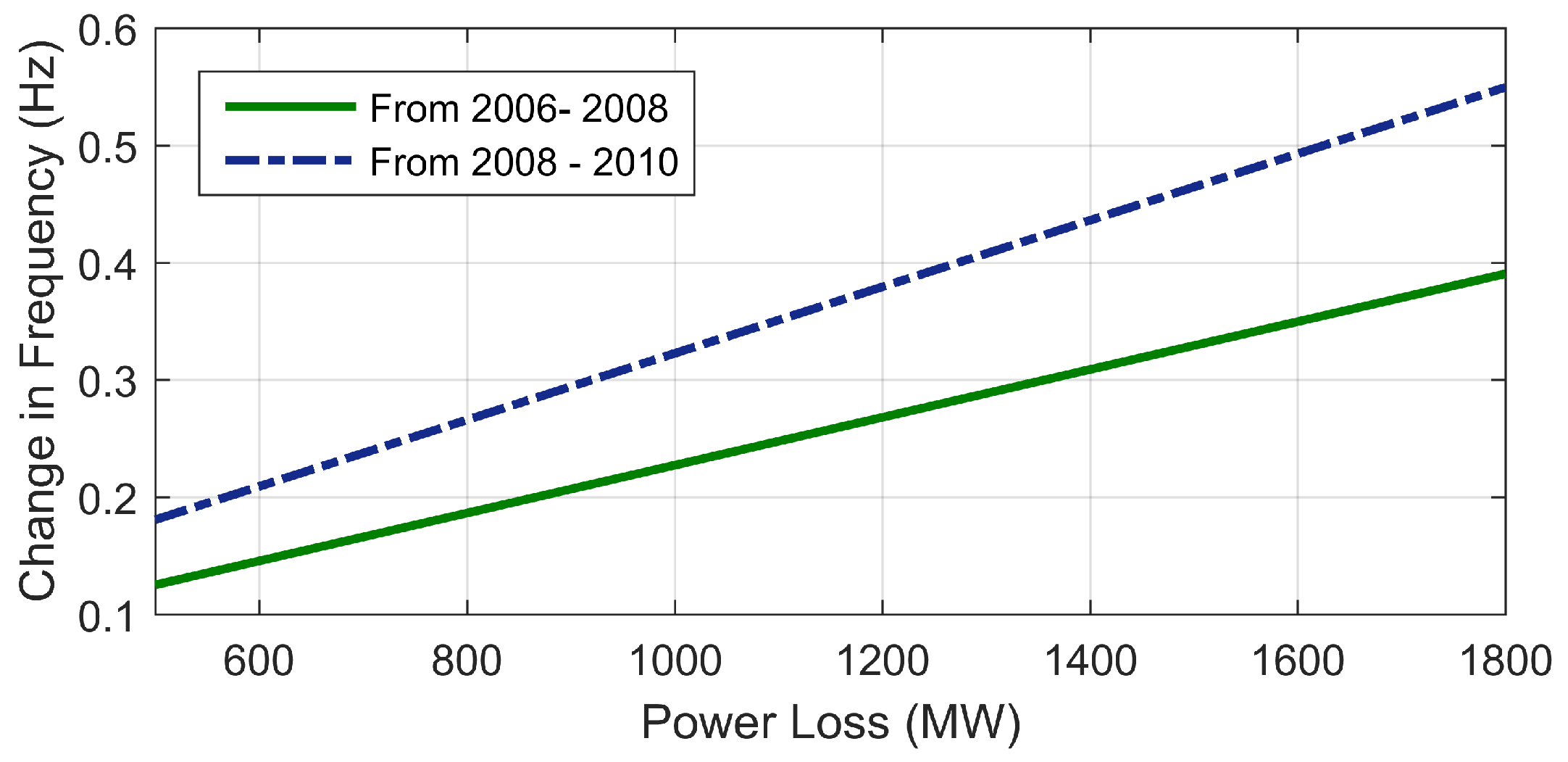
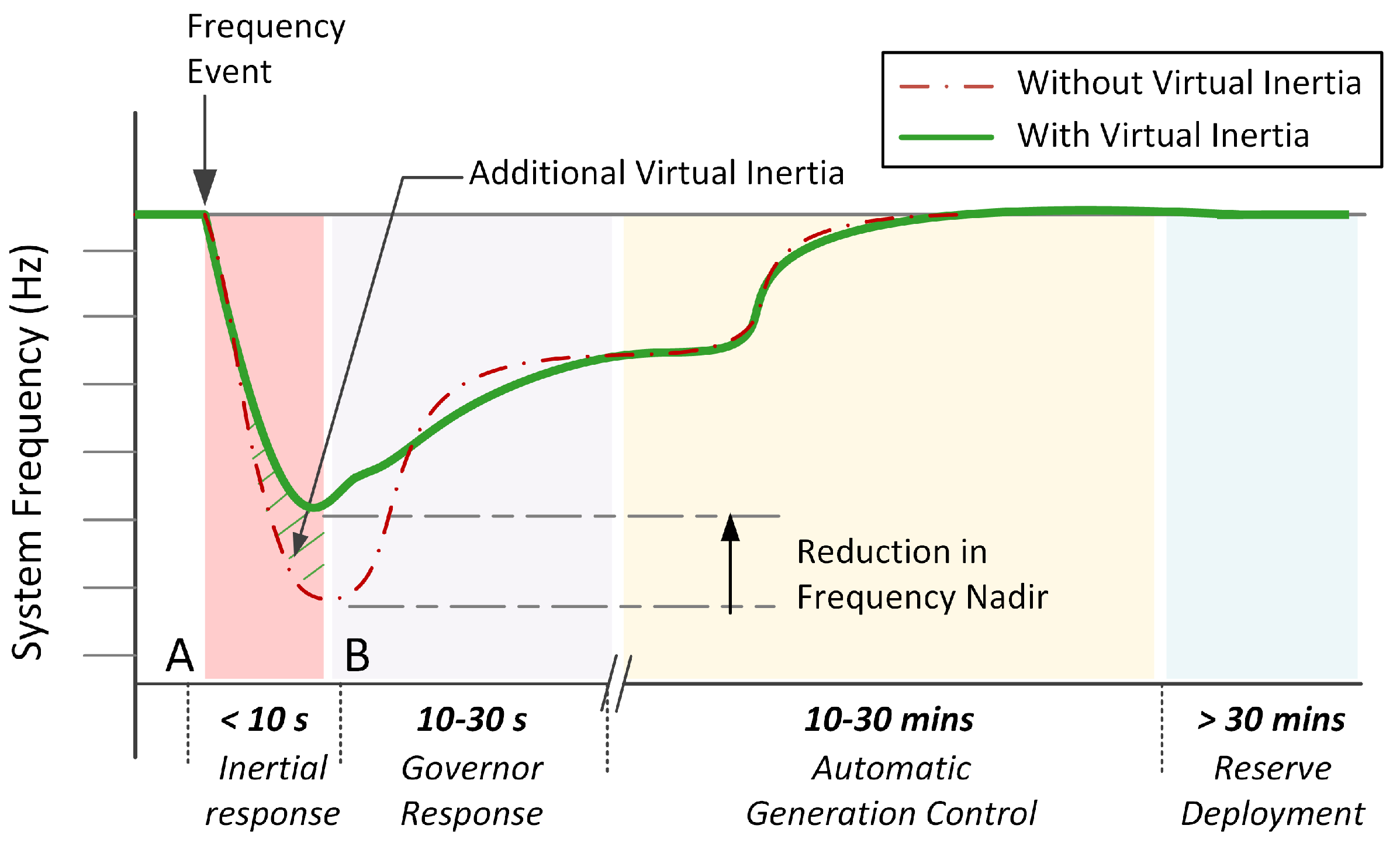
2. Frequency Variations in Weak Power Systems with High Penetration of RES
3. First Generation: Virtual Inertia Topologies
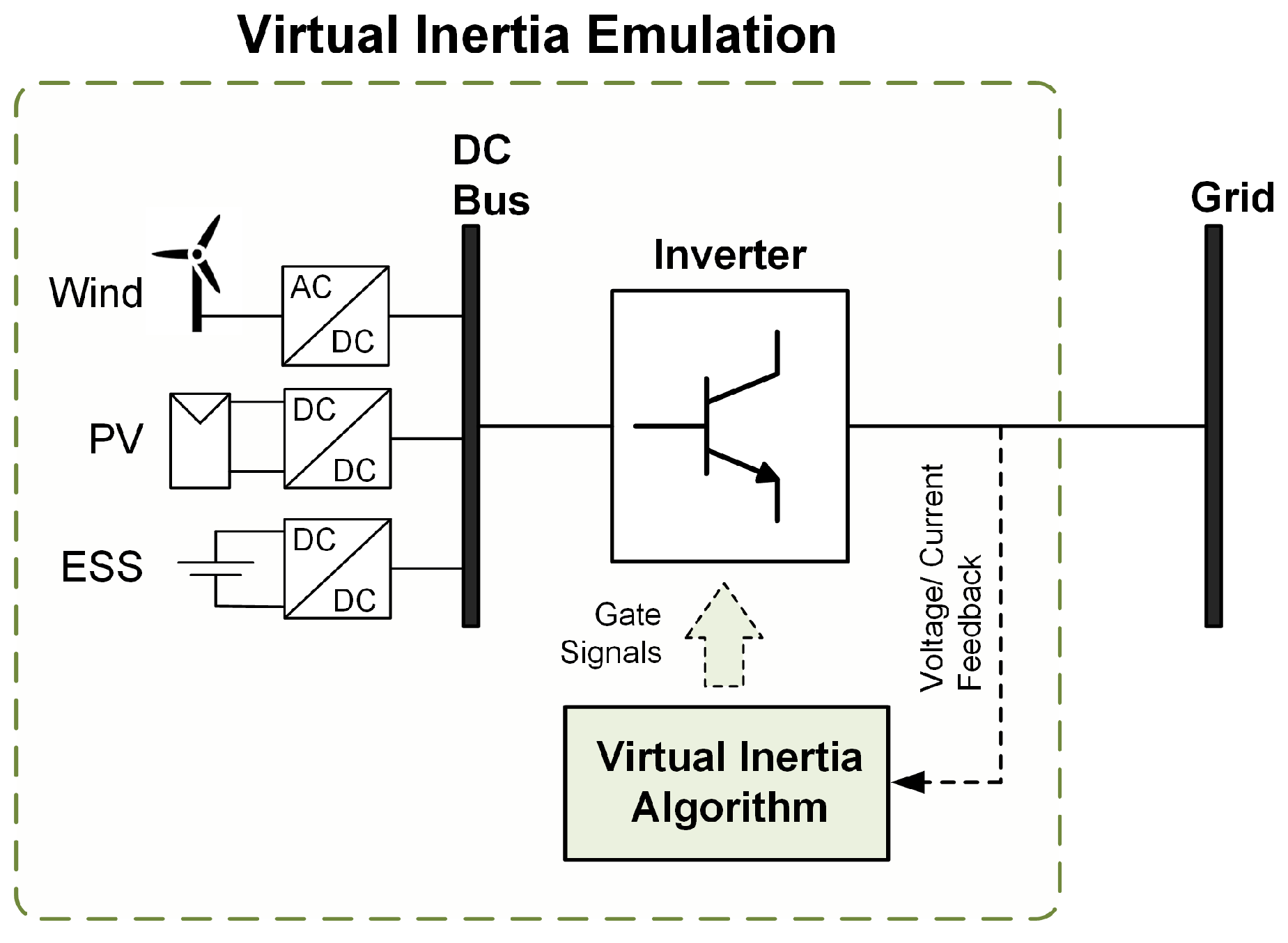
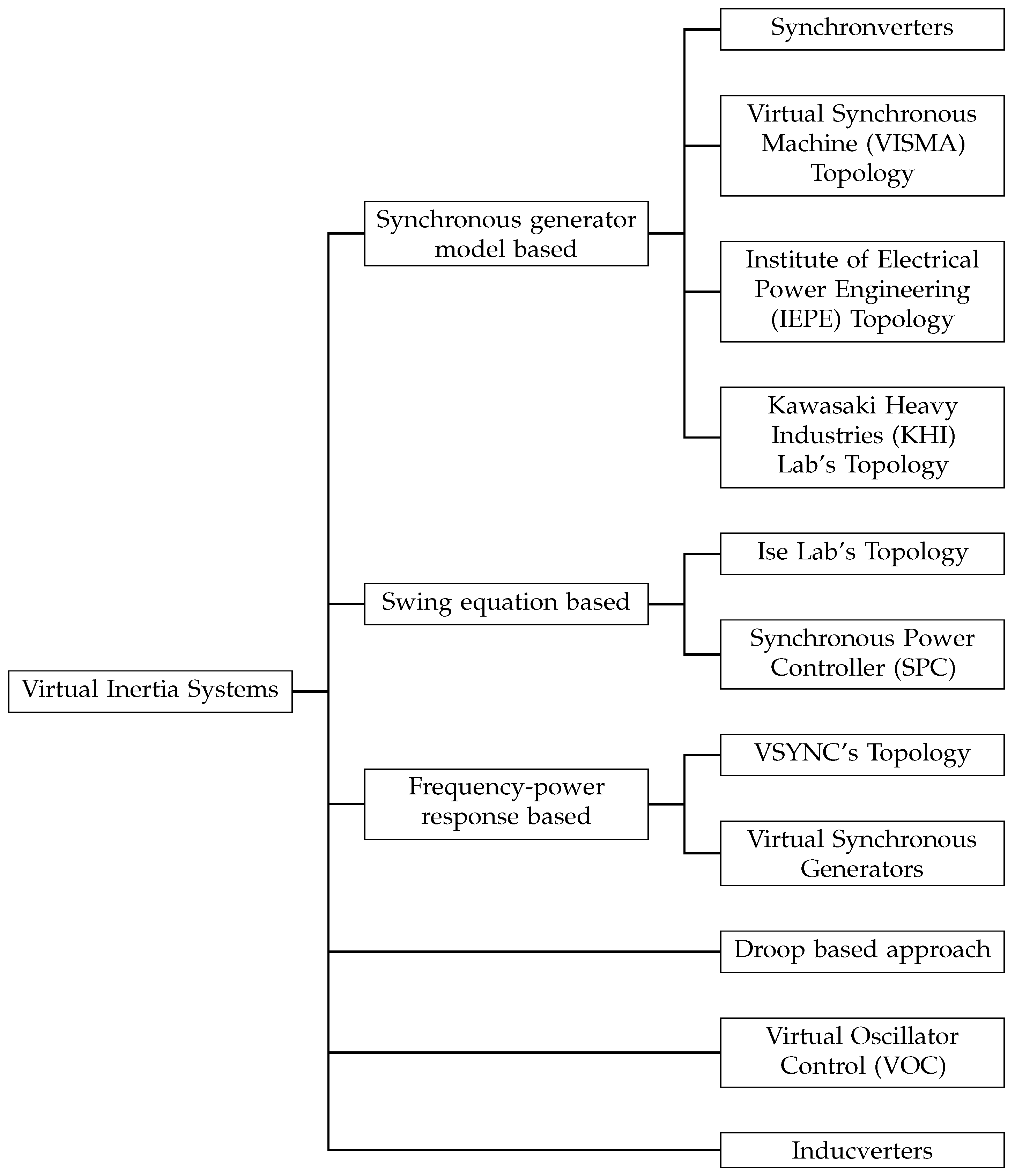
3.1. Concept and Classification of Virtual Inertia Topologies
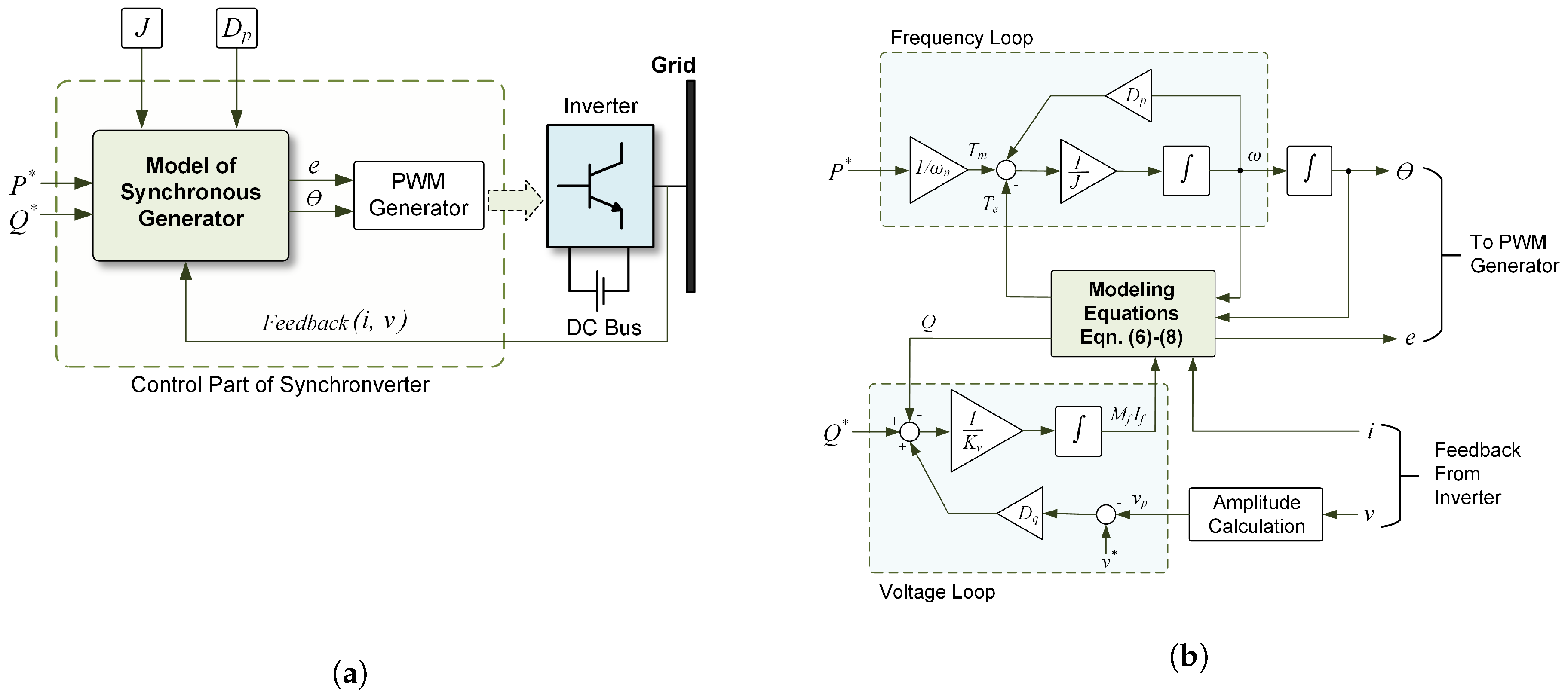
3.2. Synchronverters: A Synchronous Generator Model Based Topology
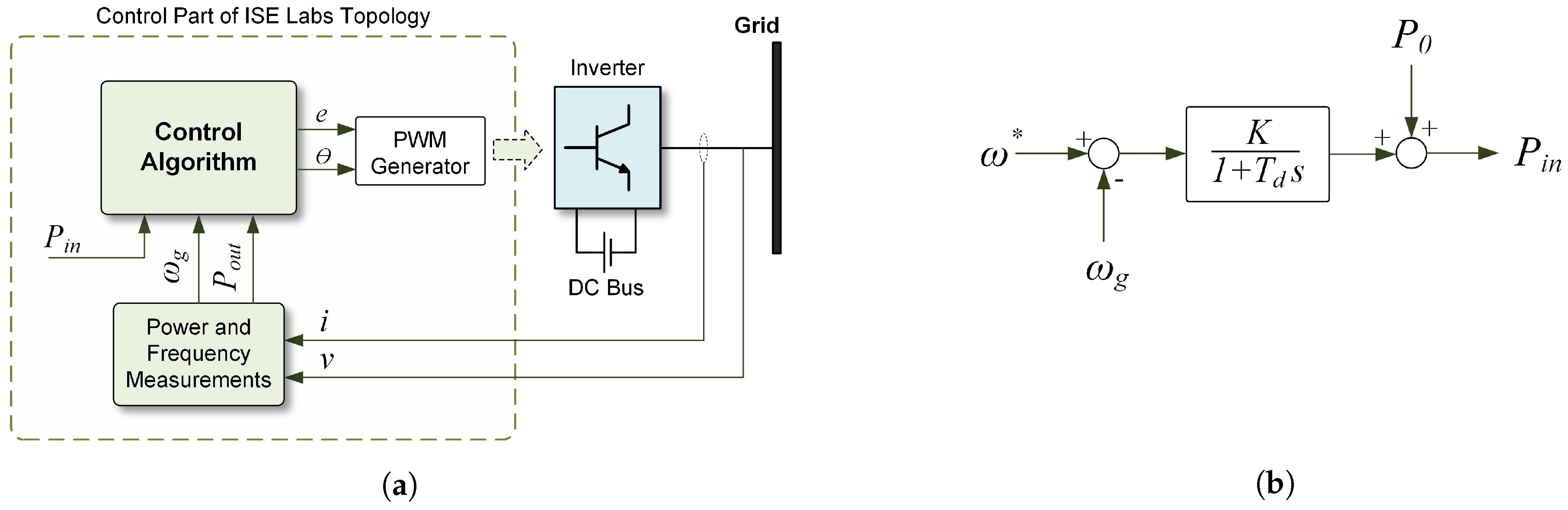
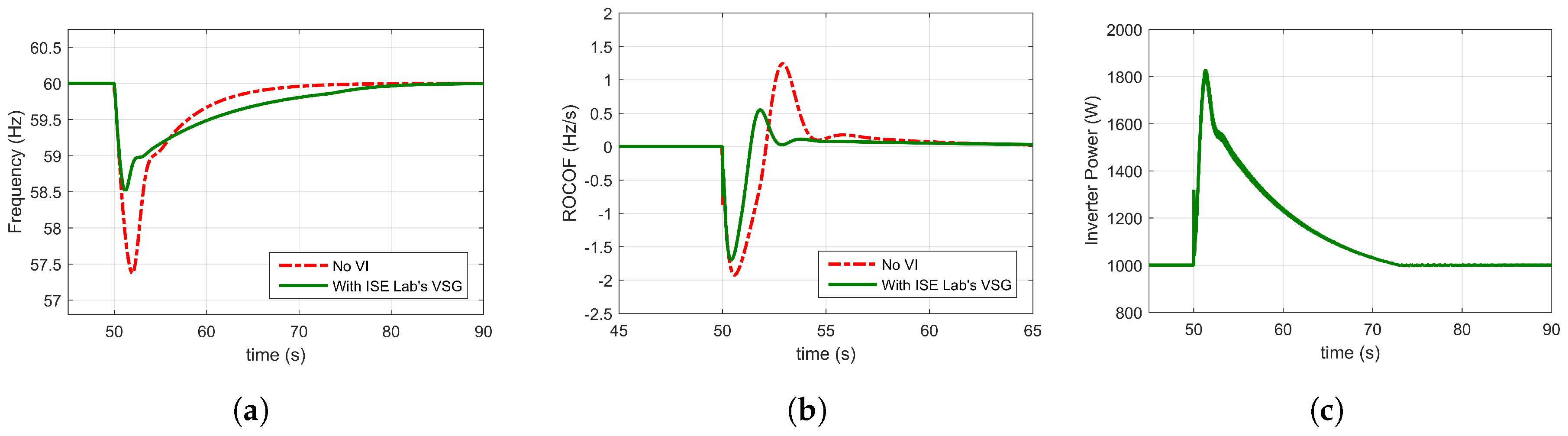
3.3. Ise Lab’s Topology: A Swing Equation Based Topology
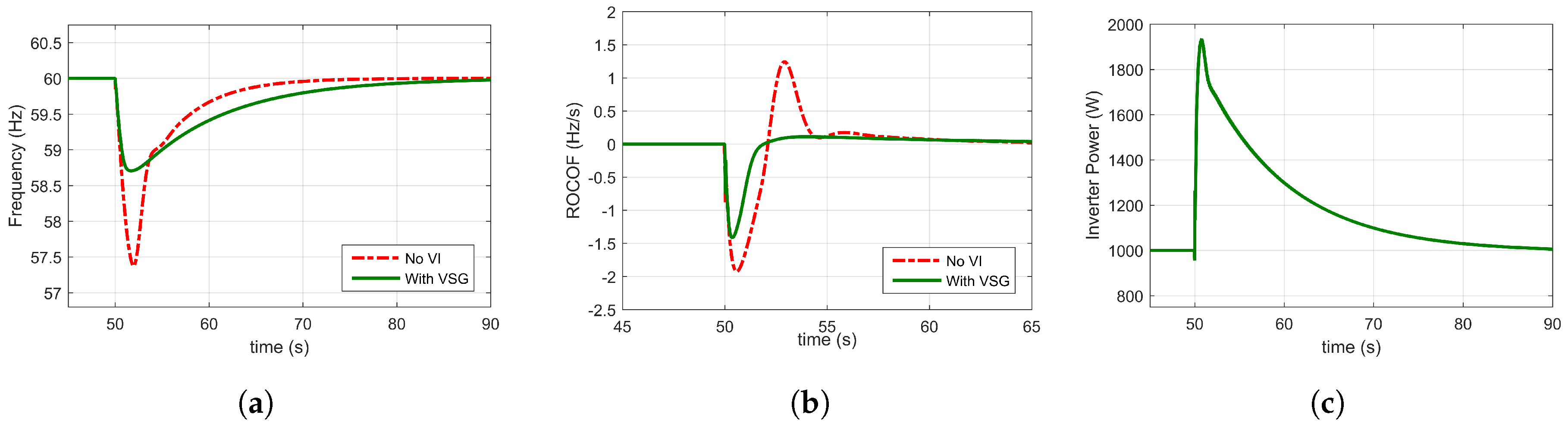
3.4. Virtual Synchronous Generators: A Frequency-Power Response Based Topology
3.5. Droop-Based Approaches
3.6. Other Topologies
3.7. Summary of Topologies
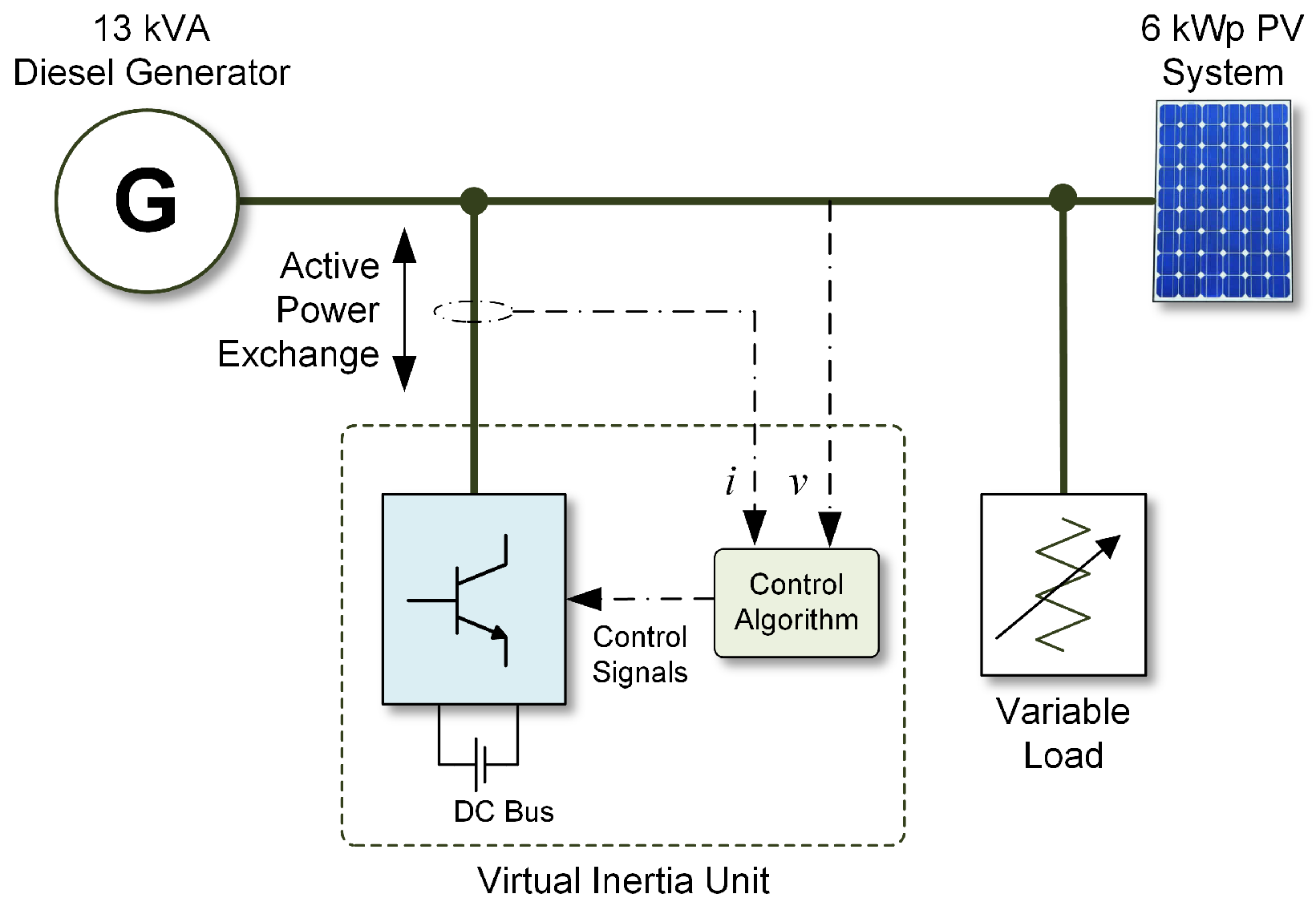
4. Design Procedures and Simulation Results
4.1. Design of Synchronverter Topology
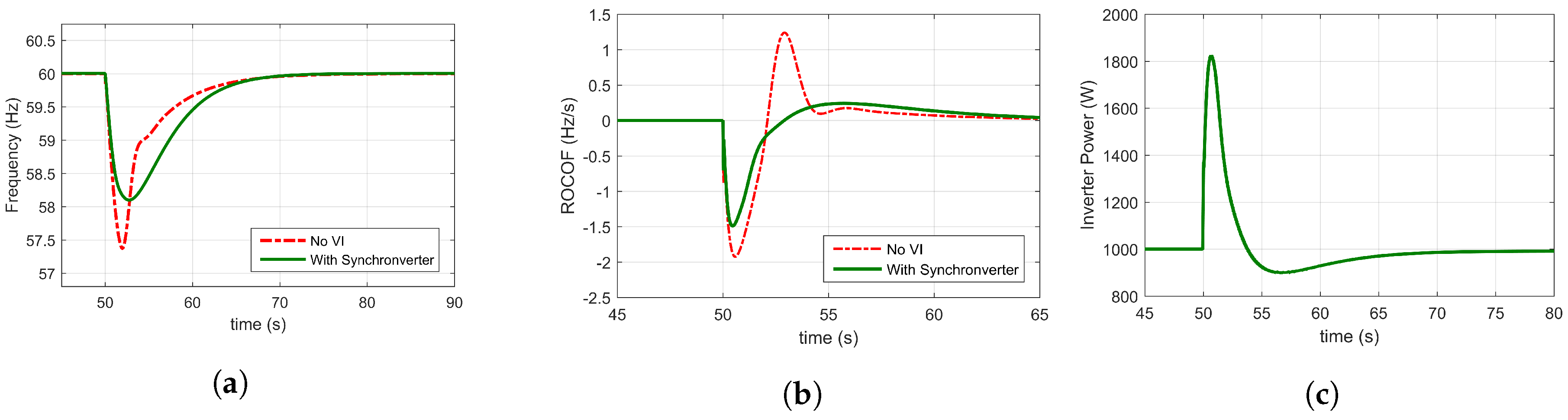
4.2. Design of Ise Lab’s Topology
4.3. Design of Virtual Synchronous Generator Topology
4.4. Summary of Simulations
5. Second Generation: Optimization of Virtual Inertia Systems
5.1. Second Generation of Synchronverters
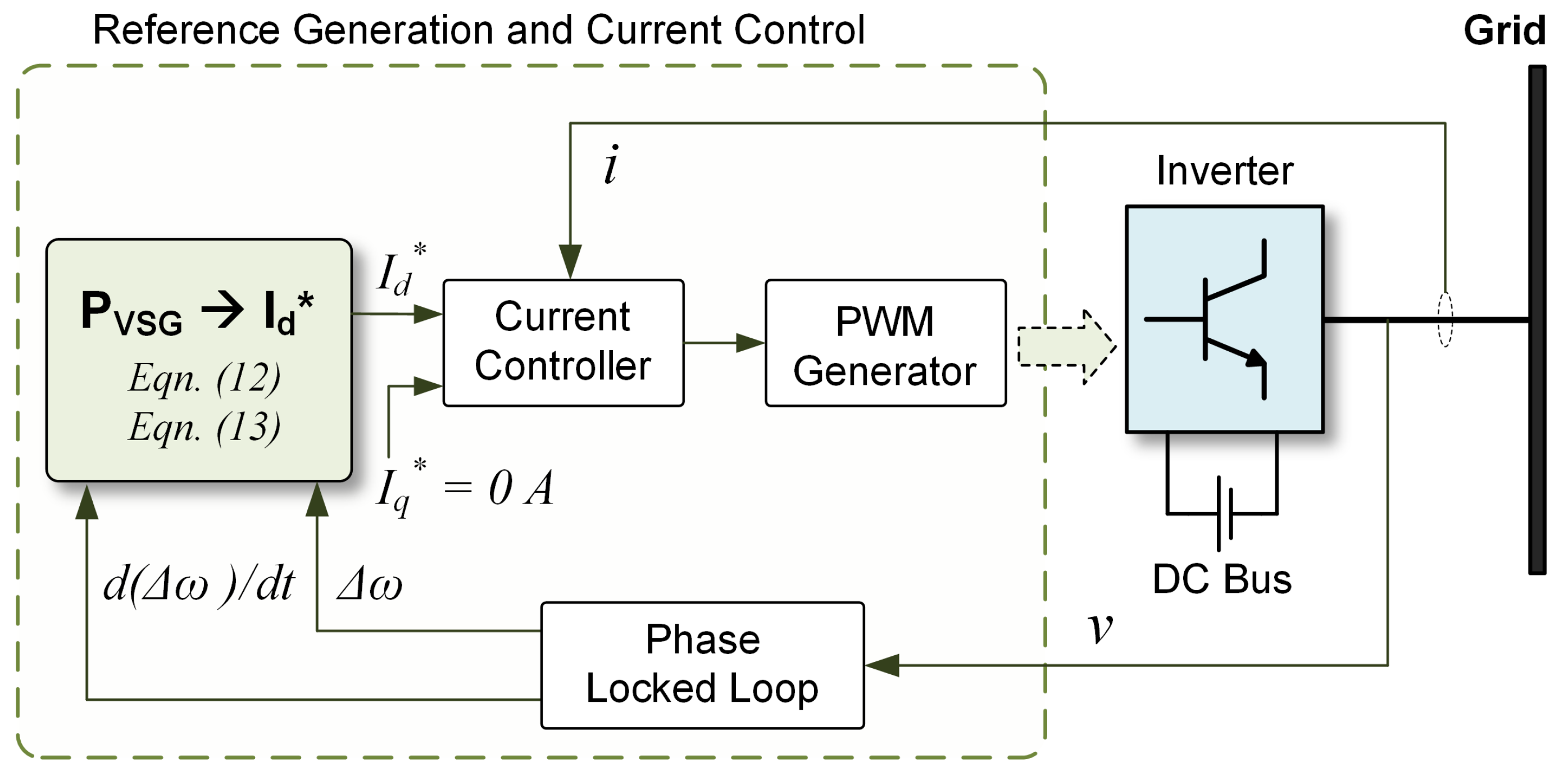
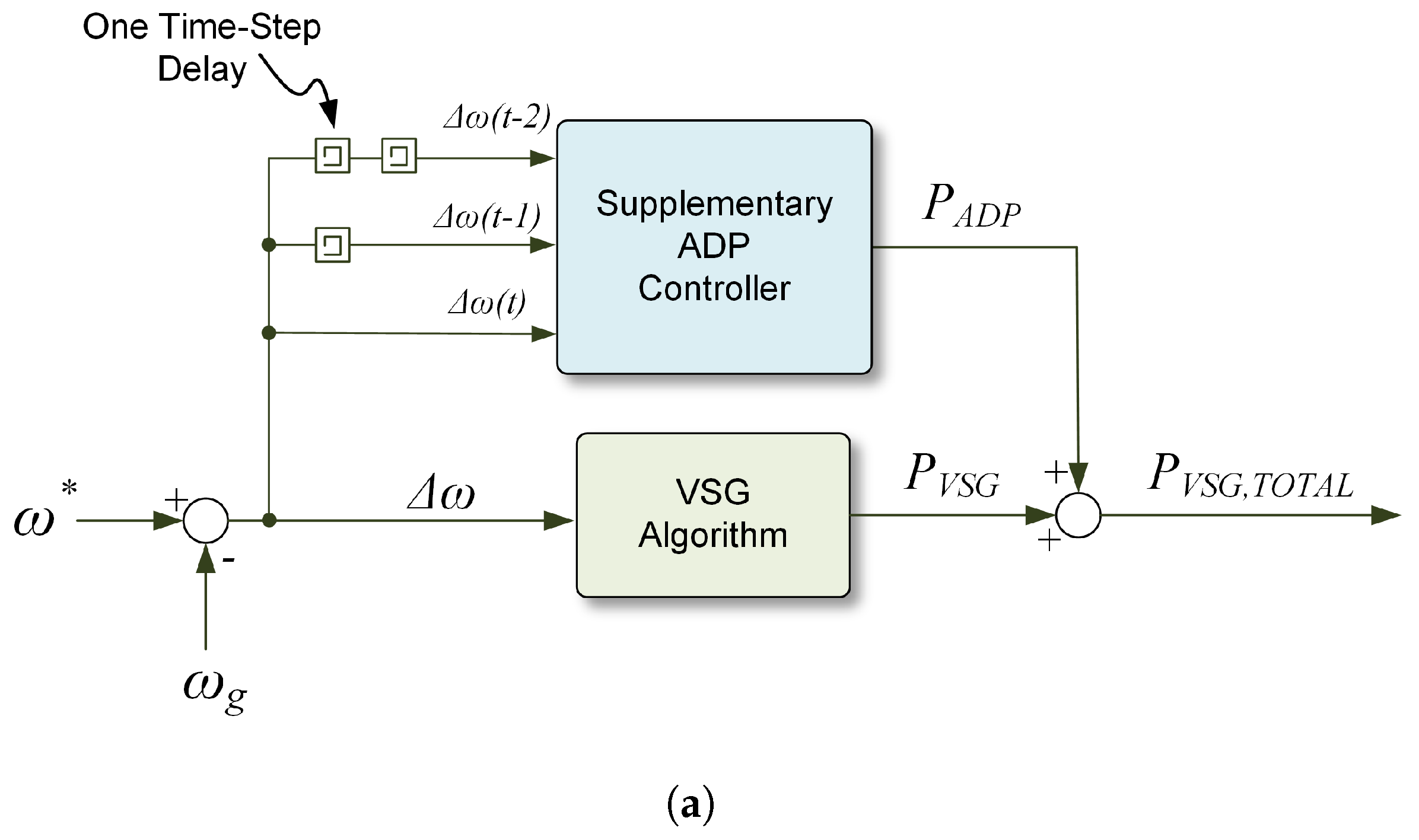
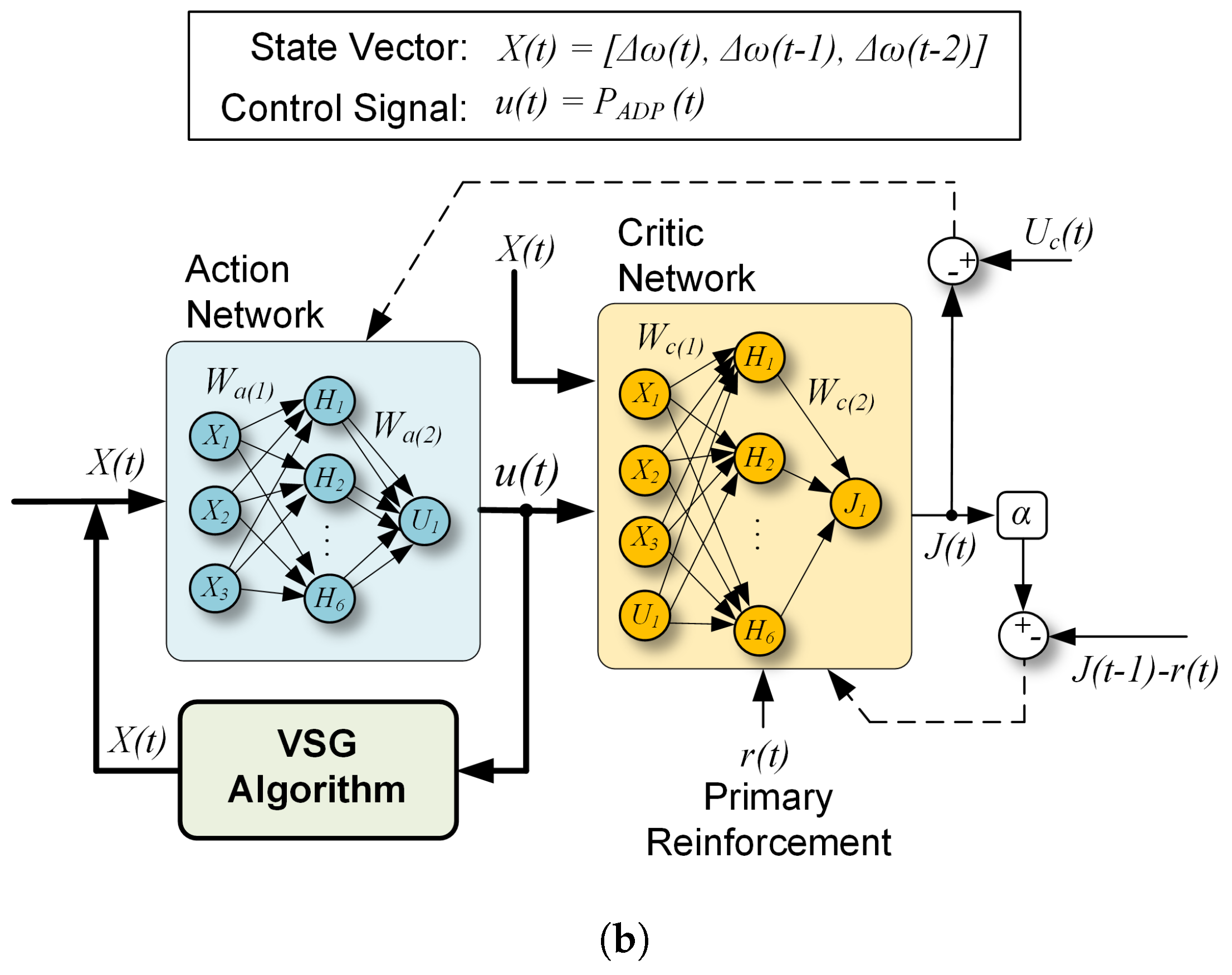
5.2. Second Generation of Ise Lab’s Topology
5.3. Second Generation of Virtual Synchronous Generators
6. Challenges and Future Research Directions
6.1. Virtual Inertia as an Ancillary Service
6.2. Inertia Estimation
6.3. Improved Modeling, Control and Aggregation of Virtual Inertia Systems
6.4. Market Structure for Virtual Inertia Systems
6.5. Energy Storage Resources for Virtual Inertia Systems
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ADP | Adaptive Dynamic Programming |
| DFIG | Double Fed Induction Generator |
| DG | Distributed Generation |
| ENTSO-E | European Network of Transmission System Operators for Electricity |
| ERCOT | Electricity Reliability Council of Texas |
| ESS | Energy Storage System |
| HVAC | Heating, Ventilation and Air Conditioning |
| IEEE | Institute of Electrical and Electronic Engineers |
| IEPE | Institute of Electrical Power Engineering |
| LQR | Linear Quadratic Regulator |
| KHI | Kawasaki Heavy Industries |
| MPP | Maximum Power Point |
| NERC | North American Electric Reliability Corporation |
| PI | Proportional-Integral |
| PLL | Phase Locked Loop |
| PWM | Pulse Width Modulation |
| QoS | Quality of Service |
| RES | Renewable Energy System |
| ROCOF | Rate of Change of Frequency |
| SG | Synchronous Generator |
| SPC | Synchronous Power Controller |
| STATCOM | Static Synchronous Compensator |
| VI | Virtual Inertia |
| VISMA | Virtual Synchronous Machine |
| VOC | Virtual Oscillator Controller |
| VSG | Virtual Synchronous Generator |
| UFLS | Under Frequency Load Shedding |
References
- U.S. Energy Information Administration. Annual Energy Outlook 2017; U.S. Department of Energy: Washington, DC, USA, 2017. Available online: https://www.eia.gov/outlooks/aeo/pdf/0383(2017).pdf (accessed on 21 June 2017).
- The Sunshot Initiative. Available online: http://www.webcitation.org/6pV7YpHo2 (accessed on 5 April 2017).
- IEA PVPS. Trends in 2016 in Photovoltaic Applications; T1-30:2016; IEA PVPS: Paris, France, 2016; Available online: http://iea-pvps.org/fileadmin/dam/public/report/national/Trends_2016_-_mr.pdf (accessed on 21 June 2017).
- Kroposki, B.; Johnson, B.; Zhang, Y.; Gevorgian, V.; Denholm, P.; Hodge, B.M.; Hannegan, B. Achieving a 100% Renewable Grid: Operating Electric Power Systems with Extremely High Levels of Variable Renewable Energy. IEEE Power Energy Mag. 2017, 15, 61–73. [Google Scholar] [CrossRef]
- Hussein, M.M.; Senjyu, T.; Orabi, M.; Wahab, M.A.; Hamada, M.M. Control of a stand-alone variable speed wind energy supply system. Appl. Sci. 2013, 3, 437–456. [Google Scholar] [CrossRef]
- Yan, R.; Saha, T.K.; Modi, N.; Masood, N.A.; Mosadeghy, M. The combined effects of high penetration of wind and PV on power system frequency response. Appl. Energy 2015, 145, 320–330. [Google Scholar] [CrossRef]
- Electricity Reliability Council of Texas (ERCOT). Future Ancillary Services in ERCOT; ERCOT: Taylor, TX, USA, 2013; Available online: http://www.ercot.com/content/news/presentations/2014/ERCOT_AS_Concept_Paper_Version_1.1_as_of_11-01-13_1445_black.pdf (accessed on 21 June 2017).
- Matevosyan, J.; Sharma, S.; Huang, S.H.; Woodfin, D.; Ragsdale, K.; Moorty, S.; Wattles, P.; Li, W. Proposed future Ancillary Services in Electric Reliability Council of Texas. In Proceedings of the IEEE PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–6. [Google Scholar]
- Poolla, B.K.; Bolognani, S.; Dorfler, F. Optimal placement of virtual inertia in power grids. In Proceedings of the American Control Conference, Boston, MA, USA, 6–8 July 2016. [Google Scholar]
- De Vyver, J.V.; Kooning, J.D.M.D.; Meersman, B.; Vandevelde, L.; Vandoorn, T.L. Droop Control as an Alternative Inertial Response Strategy for the Synthetic Inertia on Wind Turbines. IEEE Trans. Power Syst. 2016, 31, 1129–1138. [Google Scholar] [CrossRef]
- Thiesen, H.; Jauch, C.; Gloe, A. Design of a System Substituting Today’s Inherent Inertia in the European Continental Synchronous Area. Energies 2016, 9, 582. [Google Scholar] [CrossRef]
- Gurung, A.; Galipeau, D.; Tonkoski, R.; Tamrakar, I. Feasibility study of Photovoltaic-hydropower microgrids. In Proceedings of the 5th International Conference on Power and Energy Systems (ICPS), Kathmandu, Nepal, 28–30 October 2014; pp. 1–6. [Google Scholar]
- Tamrakar, U.; Galipeau, D.; Tonkoski, R.; Tamrakar, I. Improving transient stability of photovoltaic-hydro microgrids using virtual synchronous machines. In Proceedings of the IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–6. [Google Scholar]
- Guerrero, J.M.; de Vicuna, L.G.; Matas, J.; Castilla, M.; Miret, J. A wireless controller to enhance dynamic performance of parallel inverters in distributed generation systems. IEEE Trans. Power Electron. 2004, 19, 1205–1213. [Google Scholar] [CrossRef]
- Hatziargyriou, N.; Asano, H.; Iravani, R.; Marnay, C. Microgrids. IEEE Power Energy Mag. 2007, 5, 78–94. [Google Scholar] [CrossRef]
- Kim, J.; Guerrero, J.M.; Rodriguez, P.; Teodorescu, R.; Nam, K. Mode Adaptive Droop Control With Virtual Output Impedances for an Inverter-Based Flexible AC Microgrid. IEEE Trans. Power Electron. 2011, 26, 689–701. [Google Scholar] [CrossRef]
- Under Frequency Load Shedding. Available online: http://www.nerc.com/pa/RAPA/ri/Pages/UnderFrequencyLoadShedding.aspx (accessed on 25 May 2017).
- North American Electric Reliability Corporation (NERC). Frequency Response Initiative Report: The Reliability Role of Frequency Response; NERC: Atlanta, GA, USA, 2012; Available online: http://www.nerc.com/docs/pc/FRI_Report_10-30-12_Master_w-appendices.pdf (accessed on 21 June 2017).
- Voltage Characteristics of Electricity Supplied by Public Distribution Systems. Available online: http://www2.schneider-electric.com/library/SCHNEIDER_ELECTRIC/SE_LOCAL/APS/204836_1312/DraftStandard0026rev2-DraftEN501602005-05.pdf (accessed on 21 June 2017).
- ISO 8528-5:2005 Standard: Reciprocating Internal Combustion Engine Driven Alternating Current Generating Sets—Part 5: Generating Sets. 2005. Available online: https://www.iso.org/standard/39047.html (accessed on 21 June 2017).
- Torres, M.; Lopes, L.A. Virtual synchronous generator: A control strategy to improve dynamic frequency control in autonomous power systems. Energy Power Eng. 2013, 5, 2A:1–2A:7. Available online: http://file.scirp.org/Html/5-6201497_30602.htm (accessed on 29 April 2017). [CrossRef]
- Shrestha, D.; Tamrakar, U.; Ni, Z.; Tonkoski, R. Experimental Verification of Virtual Inertia in Diesel Generator based Microgrids. In Proceedings of the 18th Annual International Conference on Industrial Technology (ICIT), Toronto, ON, Canada, 22–25 March 2017; pp. 95–100. [Google Scholar]
- Rahmann, C.; Castillo, A. Fast Frequency Response Capability of Photovoltaic Power Plants: The Necessity of New Grid Requirements and Definitions. Energies 2014, 7, 6306–6322. [Google Scholar] [CrossRef]
- Chang-Chien, L.R.; Lin, W.T.; Yin, Y.C. Enhancing Frequency Response Control by DFIGs in the High Wind Penetrated Power Systems. IEEE Trans. Power Syst. 2011, 26, 710–718. [Google Scholar] [CrossRef]
- Tielens, P.; Hertem, D.V. The relevance of inertia in power systems. Renew. Sustain. Energy Rev. 2016, 55, 999–1009. [Google Scholar] [CrossRef]
- Beck, H.P.; Hesse, R. Virtual synchronous machine. In Proceedings of the 9th International Conference on Electrical Power Quality and Utilisation, Barcelona, Spain, 9–11 October 2007; pp. 1–6. [Google Scholar]
- Gonzalez-Longatt, F.; Chikuni, E.; Rashayi, E. Effects of the Synthetic Inertia from wind power on the total system inertia after a frequency disturbance. In Proceedings of the IEEE International Conference on Industrial Technology (ICIT), Cape Town, South Africa, 25–28 February 2013; pp. 826–832. [Google Scholar]
- Bevrani, H.; Ise, T.; Miura, Y. Virtual synchronous generators: A survey and new perspectives. Int. J. Electr. Power Energy Syst. 2014, 54, 244–254. [Google Scholar] [CrossRef]
- Zhong, Q.C.; Weiss, G. Synchronverters: Inverters That Mimic Synchronous Generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267. [Google Scholar] [CrossRef]
- Zhong, Q.C. Virtual Synchronous Machines: A unified interface for grid integration. IEEE Power Electron. Mag. 2016, 3, 18–27. [Google Scholar] [CrossRef]
- Kundur, P.; Balu, N.J.; Lauby, M.G. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Piya, P.; Karimi-Ghartemani, M. A stability analysis and efficiency improvement of synchronverter. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 3165–3171. [Google Scholar]
- Zhong, Q.C.; Hornik, T. Sinusoid-Locked Loops. In Control of Power Inverters in Renewable Energy and Smart Grid Integration; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2012; pp. 379–392. [Google Scholar]
- Ferreira, R.V.; Silva, S.M.; Brandao, D.I.; Antunes, H.M.A. Single-phase synchronverter for residential PV power systems. In Proceedings of the 17th International Conference on Harmonics and Quality of Power (ICHQP), Belo Horizonte, Brazil, 16–19 October 2016; pp. 861–866. [Google Scholar]
- Shinnaka, S. A Robust Single-Phase PLL System With Stable and Fast Tracking. IEEE Trans. Ind. Appl. 2008, 44, 624–633. [Google Scholar] [CrossRef]
- Zhang, L.; Harnefors, L.; Nee, H.P. Power-Synchronization Control of Grid-Connected Voltage-Source Converters. IEEE Trans. Power Syst. 2010, 25, 809–820. [Google Scholar] [CrossRef]
- Wang, S.; Hu, J.; Yuan, X. Virtual Synchronous Control for Grid-Connected DFIG-Based Wind Turbines. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 932–944. [Google Scholar] [CrossRef]
- Zhong, Q.C.; Nguyen, P.L.; Ma, Z.; Sheng, W. Self-Synchronized Synchronverters: Inverters Without a Dedicated Synchronization Unit. IEEE Trans. Power Electron. 2014, 29, 617–630. [Google Scholar] [CrossRef]
- Ma, Z.; Zhong, Q.C.; Yan, J.D. Synchronverter-based control strategies for three-phase PWM rectifiers. In Proceedings of the 7th IEEE Conference on Industrial Electronics and Applications (ICIEA), Singapore, 18–20 July 2012; pp. 225–230. [Google Scholar]
- Sakimoto, K.; Miura, Y.; Ise, T. Stabilization of a power system with a distributed generator by a Virtual Synchronous Generator function. In Proceedings of the 8th International Conference on Power Electronics (ECCE Asia), Jeju, Korea, 30 May–3 June 2011; pp. 1498–1505. [Google Scholar]
- Alipoor, J.; Miura, Y.; Ise, T. Power System Stabilization Using Virtual Synchronous Generator With Alternating Moment of Inertia. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 451–458. [Google Scholar] [CrossRef]
- Liu, J.; Miura, Y.; Ise, T. Dynamic characteristics and stability comparisons between virtual synchronous generator and droop control in inverter-based distributed generators. In Proceedings of the International Power Electronics Conference (IPEC-Hiroshima 2014-ECCE ASIA), Hiroshima, Japan, 18–21 May 2014; pp. 1536–1543. [Google Scholar]
- Sakimoto, K.; Miura, Y.; Ise, T. Characteristics of Parallel Operation of Inverter-Type Distributed Generators Operated by a Virtual Synchronous Generator. Electr. Eng. Jpn. 2015, 192, 9–19. [Google Scholar] [CrossRef]
- Torres, M.; Lopes, L.A.C. Virtual synchronous generator control in autonomous wind-diesel power systems. In Proceedings of the IEEE Electrical Power & Energy Conference (EPEC), Montreal, QC, Canada, 22–23 October 2009; pp. 1–6. [Google Scholar]
- Van Wesenbeeck, M.P.N.; de Haan, S.W.H.; Varela, P.; Visscher, K. Grid tied converter with virtual kinetic storage. In Proceedings of the IEEE Bucharest PowerTech, Bucharest, Romania, 28 June–2 July 2009; pp. 1–7. [Google Scholar]
- Van, T.V.; Visscher, K.; Diaz, J.; Karapanos, V.; Woyte, A.; Albu, M.; Bozelie, J.; Loix, T.; Federenciuc, D. Virtual synchronous generator: An element of future grids. In Proceedings of the IEEE Innovative Smart Grid Technologies Conference Europe (ISGT Europe), Gothenberg, Sweden, 11–13 October 2010; pp. 1–7. [Google Scholar]
- Wen, B.; Boroyevich, D.; Burgos, R.; Mattavelli, P.; Shen, Z. Small-Signal Stability Analysis of Three-Phase AC Systems in the Presence of Constant Power Loads Based on Measured d-q Frame Impedances. IEEE Trans. Power Electron. 2015, 30, 5952–5963. [Google Scholar] [CrossRef]
- Tamrakar, U.; Tonkoski, R.; Ni, Z.; Hansen, T.M.; Tamrakar, I. Current control techniques for applications in virtual synchronous machines. In Proceedings of the 6th IEEE International Conference on Power Systems (ICPS), New Delhi, India, 4–6 March 2016; pp. 1–6. [Google Scholar]
- Malesani, L.; Tomasin, P. PWM current control techniques of voltage source converters—A survey. In Proceedings of the International Conference on Industrial Electronics, Control, and Instrumentation (IECON ’93), Maui, HI, USA, 15–19 November 1993; pp. 670–675. [Google Scholar]
- Driesen, J.; Visscher, K. Virtual synchronous generators. In Proceedings of the 9th IEEE Power & Energy Society General Meeting, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–6. [Google Scholar]
- Karapanos, V.; de Haan, S.; Zwetsloot, K. Real time simulation of a power system with VSG hardware in the loop. In Proceedings of the 37th Annual Conference of the IEEE Industrial Electronics Society (IECON), Melbourne, Australia, 7–10 November 2011; pp. 3748–3754. [Google Scholar]
- Thong, V.V.; Woyte, A.; Albu, M.; Hest, M.V.; Bozelie, J.; Diaz, J.; Loix, T.; Stanculescu, D.; Visscher, K. Virtual synchronous generator: Laboratory scale results and field demonstration. In Proceedings of the IEEE Bucharest PowerTech, Bucharest, Romania, 28 June–2 July 2009; pp. 1–6. [Google Scholar]
- Morren, J.; Pierik, J.; de Haan, S.W. Inertial response of variable speed wind turbines. Electr. Power Syst. Res. 2006, 76, 980–987. [Google Scholar] [CrossRef]
- Arani, M.F.M.; El-Saadany, E.F. Implementing Virtual Inertia in DFIG-Based Wind Power Generation. IEEE Trans. Power Syst. 2013, 28, 1373–1384. [Google Scholar] [CrossRef]
- Zhang, W.; Cantarellas, A.M.; Rocabert, J.; Luna, A.; Rodriguez, P. Synchronous Power Controller With Flexible Droop Characteristics for Renewable Power Generation Systems. IEEE Trans. Sustain. Energy 2016, 7, 1572–1582. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of Control and Grid Synchronization for Distributed Power Generation Systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef]
- European Network of Transmission System Operators for Electricity (ENTSO-E). Need for Synthetic Inertia (SI) for Frequency Regulation; ENTSO-E: Brussels, Belgium, 2017; Available online: https://consultations.entsoe.eu/system-development/entso-e-connection-codes-implementation-guidance-d-3/user_uploads/igd-need-for-synthetic-inertia.pdf (accessed on 21 June 2017).
- Ashabani, M.; Freijedo, F.D.; Golestan, S.; Guerrero, J.M. Inducverters: PLL-Less Converters With Auto-Synchronization and Emulated Inertia Capability. IEEE Trans. Smart Grid 2016, 7, 1660–1674. [Google Scholar] [CrossRef]
- D’Arco, S.; Suul, J.A. Virtual synchronous machines- Classification of implementations and analysis of equivalence to droop controllers for microgrids. In Proceedings of the IEEE Grenoble Conference, Grenoble, France, 16–20 June 2013; pp. 1–7. [Google Scholar]
- Midtsund, T.; Suul, J.A.; Undeland, T. Evaluation of current controller performance and stability for voltage source converters connected to a weak grid. In Proceedings of the IEEE 2nd International Symposium on Power Electronics for Distributed Generation Systems, Hefei, China, 16–18 June 2010; pp. 382–388. [Google Scholar]
- Svensson, J. Synchronisation methods for grid-connected voltage source converters. IEE Proc. Gener. Transm. Distrib. 2001, 148, 229–235. [Google Scholar] [CrossRef]
- Katiraei, F.; Iravani, M.R. Power Management Strategies for a Microgrid With Multiple Distributed Generation Units. IEEE Trans. Power Syst. 2006, 21, 1821–1831. [Google Scholar] [CrossRef]
- Pogaku, N.; Prodanovic, M.; Green, T.C. Modeling, Analysis and Testing of Autonomous Operation of an Inverter-Based Microgrid. IEEE Trans. Power Electron. 2007, 22, 613–625. [Google Scholar] [CrossRef]
- D’Arco, S.; Suul, J.A. Equivalence of Virtual Synchronous Machines and Frequency-Droops for Converter-Based MicroGrids. IEEE Trans. Smart Grid 2014, 5, 394–395. [Google Scholar] [CrossRef]
- Li, C.; Burgos, R.; Cvetkovic, I.; Boroyevich, D.; Mili, L.; Rodriguez, P. Analysis and design of virtual synchronous machine based STATCOM controller. In Proceedings of the IEEE 15th Workshop on Control and Modeling for Power Electronics (COMPEL), Santander, Spain, 22–25 June 2014; pp. 1–6. [Google Scholar]
- Soni, N.; Doolla, S.; Chandorkar, M.C. Improvement of Transient Response in Microgrids Using Virtual Inertia. IEEE Trans. Power Deliv. 2013, 28, 1830–1838. [Google Scholar] [CrossRef]
- Hesse, R.; Turschner, D.; Beck, H.P. Micro grid stabilization using the Virtual Synchronous Machine (VISMA). In Proceedings of the International Conference on Renewable Energies and Power Quality, ICREPQ’09, Valencia, Spain, 15–17 April 2009; pp. 1–6. [Google Scholar]
- Virtual Synchronous Machine. Available online: https://fenix.tecnico.ulisboa.pt/downloadFile/395145918861/paper.pdf (accessed on 17 June 2017).
- Chen, Y.; Hesse, R.; Turschner, D.; Beck, H.P. Dynamic properties of the virtual synchronous machine (VISMA). In Proceedings of the International Conference on Renewable Energies and Power Quality, Las Palmas de Gran Canaria, Spain, 13–15 April 2011; pp. 1–5. [Google Scholar]
- Chen, Y.; Hesse, R.; Turschner, D.; Beck, H.P. Comparison of methods for implementing virtual synchronous machine on inverters. In Proceedings of the International Conference on Renewable Energies and Power Quality, Santiago de Compostela, Spain, 28–30 March 2012; pp. 1–6. [Google Scholar]
- Hirase, Y.; Abe, K.; Sugimoto, K.; Shindo, Y. A grid connected inverter with virtual synchronous generator model of algebraic type. IEEE Trans. Power Energy 2012, 132, 371–380. [Google Scholar] [CrossRef]
- Rodriguez, P.; Candela, I.; Luna, A. Control of PV generation systems using the synchronous power controller. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Denver, CO, USA, 15–19 September 2013; pp. 993–998. [Google Scholar]
- Rodriguez, C.; Candela, G.; Rocabert, D.; Teodorescu, R. Virtual Controller of Electromechanical Characteristics for Static Power Converters. U.S. Patent US20140067138 A1, 27 February 2012. [Google Scholar]
- Cortés, P.; Garcia, J.; Delgado, J.; Teodorescu, R. Virtual Admittance Controller Based on Static Power Converters. U.S. Patent US20140049233 A1, 20 February 2014. [Google Scholar]
- D’Arco, S.; Suul, J.A.; Fosso, O.B. Control system tuning and stability analysis of Virtual Synchronous Machines. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Denver, CO, USA, 15–19 September 2013; pp. 2664–2671. [Google Scholar]
- Zhang, W.; Remon, D.; Mir, A.; Luna, A.; Rocabert, J.; Candela, I.; Rodriguez, P. Comparison of different power loop controllers for synchronous power controlled grid-interactive converters. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 3780–3787. [Google Scholar]
- Behera, R.R.; Thakur, A.N. An overview of various grid synchronization techniques for single-phase grid integration of renewable distributed power generation systems. In Proceedings of the International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennai, India, 3–5 March 2016; pp. 2876–2880. [Google Scholar]
- Johnson, B.B.; Dhople, S.V.; Hamadeh, A.O.; Krein, P.T. Synchronization of Parallel Single-Phase Inverters With Virtual Oscillator Control. IEEE Trans. Power Electron. 2014, 29, 6124–6138. [Google Scholar] [CrossRef]
- Johnson, B.B.; Dhople, S.V.; Cale, J.L.; Hamadeh, A.O.; Krein, P.T. Oscillator-Based Inverter Control for Islanded Three-Phase Microgrids. IEEE J. Photovolt. 2014, 4, 387–395. [Google Scholar] [CrossRef]
- Dhople, S.V.; Johnson, B.B.; Hamadeh, A.O. Virtual Oscillator Control for voltage source inverters. In Proceedings of the 51st Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 2–4 October 2013; pp. 1359–1363. [Google Scholar]
- Zhang, C.H.; Zhong, Q.C.; Meng, J.S.; Chen, X.; Huang, Q.; Chen, S.H.; Lv, Z.P. An improved synchronverter model and its dynamic behaviour comparison with synchronous generator. In Proceedings of the 2nd IET Renewable Power Generation Conference (RPG), Beijing, China, 9–11 September 2013; pp. 1–4. [Google Scholar]
- Natarajan, V.; Weiss, G. Synchronverters with better stability due to virtual inductors, virtual capacitors and anti-windup. IEEE Trans. Ind. Electron. 2017, 64, 5994–6004. [Google Scholar] [CrossRef]
- Dong, S.; Chen, Y.C. Adjusting Synchronverter Dynamic Response Speed via Damping Correction Loop. IEEE Trans. Energy Convers. 2017, 32, 608–619. [Google Scholar] [CrossRef]
- Zhong, Q.C.; Konstantopoulos, G.C.; Ren, B.; Krstic, M. Improved Synchronverters with Bounded Frequency and Voltage for Smart Grid Integration. IEEE Trans. Smart Grid 2017. [Google Scholar] [CrossRef]
- Liu, J.; Miura, Y.; Bevrani, H.; Ise, T. Enhanced Virtual Synchronous Generator Control for Parallel Inverters in Microgrids. IEEE Trans. Smart Grid 2016. [Google Scholar] [CrossRef]
- Alipoor, J.; Miura, Y.; Ise, T. Stability Assessment and Optimization Methods for Microgrid with Multiple VSG Units. IEEE Trans. Smart Grid 2016. [Google Scholar] [CrossRef]
- Guo, W.; Liu, F.; Si, J.; Mei, S. Incorporating approximate dynamic programming-based parameter tuning into PD-type virtual inertia control of DFIGs. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Dallas, TX, USA, 4–9 August 2013; pp. 1–8. [Google Scholar]
- Torres, M.; Lopes, L.A. An optimal virtual inertia controller to support frequency regulation in autonomous diesel power systems with high penetration of renewables. In Proceedings of the International Conference on Renewable Energies and Power Quality (ICREPQ 11), la Palmas de Gran Canaria, Spain, 13–15 April 2011; pp. 1–6. [Google Scholar]
- Torres L., M.A.; Lopes, L.A.C.; Morán T., L.A.; Espinoza C., J.R. Self-Tuning Virtual Synchronous Machine: A Control Strategy for Energy Storage Systems to Support Dynamic Frequency Control. IEEE Trans. Energy Convers. 2014, 29, 833–840. [Google Scholar] [CrossRef]
- Shrestha, D.; Tamrakar, U.; Malla, N.; Ni, Z.; Tonkoski, R. Reduction of energy consumption of virtual synchronous machine using supplementary adaptive dynamic programming. In Proceedings of the IEEE International Conference on Electro Information Technology (EIT), Grand Forks, ND, USA, 19–21 May 2016; pp. 690–694. [Google Scholar]
- Shrestha, D. Virtual Inertia Emulation to Improve Dynamic Frequency Stability of Low Inertia Microgrids. Master of Science thesis, South Dakota State University, Brookings, SD, USA, 2016. [Google Scholar]
- Datta, M.; Ishikawa, H.; Naitoh, H.; Senjyu, T. Frequency control improvement in a PV-diesel hybrid power system with a virtual inertia controller. In Proceedings of the 7th IEEE Conference on Industrial Electronics and Applications (ICIEA), Singapore, 18–20 July 2012; pp. 1167–1172. [Google Scholar]
- Chen, D.; Xu, Y.; Huang, A.Q. Integration of DC Microgrids as Virtual Synchronous Machines into the AC Grid. IEEE Trans. Ind. Electron. 2017. [Google Scholar] [CrossRef]
- Bajracharya, L.; Awasthi, S.; Chalise, S.; Hansen, T.M.; Tonkoski, R. Economic analysis of a data center virtual power plant participating in demand response. In Proceedings of the IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Awasthi, S.R.; Chalise, S.; Tonkoski, R. Operation of datacenter as virtual power plant. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 3422–3429. [Google Scholar]
- Teng, F.; Strbac, G. Evaluation of synthetic inertia provision from wind plants. In Proceedings of the IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar]
- Bousseau, P.; Belhomme, R.; Monnot, E.; Laverdure, N.; Boëda, D.; Roye, D.; Bacha, S. Contribution of wind farms to ancillary services. Cigre 2006, 21, 1–11. [Google Scholar]
- Van Thong, V.; Driesen, J.; Belmans, R. Using Distributed Generation to Support and Provide Ancillary Services for the Power System. In Proceedings of the International Conference on Clean Electrical Power, Capri, Itlay, 21–23 May 2007; pp. 159–163. [Google Scholar]
- Teninge, A.; Jecu, C.; Roye, D.; Bacha, S.; Duval, J.; Belhomme, R. Contribution to frequency control through wind turbine inertial energy storage. IET Renew. Power Gen. 2009, 3, 358–370. [Google Scholar] [CrossRef]
- Yingcheng, X.; Nengling, T. Review of contribution to frequency control through variable speed wind turbine. Renew. Energy 2011, 36, 1671–1677. [Google Scholar] [CrossRef]
- Yan, R.; Saha, T.K. Frequency response estimation method for high wind penetration considering wind turbine frequency support functions. IET Renew. Power Gen. 2015, 9, 775–782. [Google Scholar] [CrossRef]
- Can Synthetic Inertia from Wind Power Stabilize Grids? Available online:. Available online: http://www.webcitation.org/6pscLoEBs (accessed on 20 April 2017).
- Kempton, W.; Tomić, J. Vehicle-to-grid power fundamentals: Calculating capacity and net revenue. J. Power Sources 2005, 144, 268–279. [Google Scholar] [CrossRef]
- Almeida, P.R.; Soares, F.; Lopes, J.P. Electric vehicles contribution for frequency control with inertial emulation. Electr. Power Syst. Res. 2015, 127, 141–150. [Google Scholar] [CrossRef]
- Meng, J.; Mu, Y.; Wu, J.; Jia, H.; Dai, Q.; Yu, X. Dynamic frequency response from electric vehicles in the Great Britain power system. J. Mod. Power Syst. Clean Energy 2015, 3, 203–211. [Google Scholar] [CrossRef]
- Inoue, T.; Taniguchi, H.; Ikeguchi, Y.; Yoshida, K. Estimation of power system inertia constant and capacity of spinning-reserve support generators using measured frequency transients. IEEE Trans. Power Syst. 1997, 12, 136–143. [Google Scholar] [CrossRef]
- Zhang, Y.; Bank, J.; Wan, Y.H.; Muljadi, E.; Corbus, D. Synchrophasor Measurement-Based Wind Plant Inertia Estimation. In Proceedings of the IEEE Green Technologies Conference (GreenTech), Denver, CO, USA, 4–5 April 2013; pp. 494–499. [Google Scholar]
- Ashton, P.M.; Saunders, C.S.; Taylor, G.A.; Carter, A.M.; Bradley, M.E. Inertia Estimation of the GB Power System Using Synchrophasor Measurements. IEEE Trans. Power Syst. 2015, 30, 701–709. [Google Scholar] [CrossRef]
- Lara-Jimenez, J.D.; Ramirez, J.M. Inertial frequency response estimation in a power system with high wind energy penetration. In Proceedings of the IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–6. [Google Scholar]
- Wall, P.; Regulski, P.; Rusidovic, Z.; Terzija, V. Inertia estimation using PMUs in a laboratory. In Proceedings of the IEEE Power & Energy Society Innovative Smart Grid Technologies (ISTG-Europe), Istanbul, Turkey, 12–15 October 2014; pp. 1–6. [Google Scholar]
- D’Arco, S.; Suul, J.A.; Fosso, O.B. Small-signal modeling and parametric sensitivity of a virtual synchronous machine in islanded operation. Int. J. Electr. Power Energy Syst. 2015, 72, 3–15. [Google Scholar] [CrossRef]
- Golpîra, H.; Seifi, H.; Messina, A.R.; Haghifam, M.R. Maximum Penetration Level of Micro-Grids in Large-Scale Power Systems: Frequency Stability Viewpoint. IEEE Trans. Power Syst. 2016, 31, 5163–5171. [Google Scholar] [CrossRef]
- Agranat, O.; MacGill, I.; Bruce, A. Fast Frequency Markets under High Penetrations of Renewable Energy in the Australian National Electricity Market. In Proceedings of the Asia-Pacific Solar Research Conference, Queensland, Australia, 8–10 December 2015. [Google Scholar]
- Gurung, A.; Chen, K.; Khan, R.; Abdulkarim, S.S.; Varnekar, G.; Pathak, R.; Naderi, R.; Qiao, Q. Highly Efficient Perovskite Solar Cell Photocharging of Lithium Ion Battery Using DC–DC Booster. Adv. Energy Mater. 2017. [Google Scholar] [CrossRef]
- Xu, T.; Jang, W.; Overbye, T. An Economic Evaluation Tool of Inertia Services for Systems with Integrated Wind Power and Fast-Acting Storage Resources. In Proceedings of the 49th Hawaii International Conference on System Sciences (HICSS), Hostelling International, Koloa, HI, USA, 5–8 January 2016; pp. 2456–2465. [Google Scholar]
- Garg, S.K.; Versteeg, S.; Buyya, R. A framework for ranking of cloud computing services. Future Gen. Comput. Syst. 2013, 29, 1012–1023. [Google Scholar] [CrossRef]
- Delille, G.; François, B.; Malarange, G. Dynamic frequency control support: A virtual inertia provided by distributed energy storage to isolated power systems. In Proceedings of the 2010 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT Europe), Gothenberg, Sweden, 18 November 2010; pp. 1–8. [Google Scholar]
- Baisden, A.C.; Emadi, A. ADVISOR-based model of a battery and an ultra-capacitor energy source for hybrid electric vehicles. IEEE Trans. Veh. Technol. 2004, 53, 199–205. [Google Scholar] [CrossRef]
- Pena-Alzola, R.; Campos-Gaona, D.; Ordonez, M. Control of flywheel energy storage systems as virtual synchronous machines for microgrids. In Proceedings of the IEEE 16th Workshop on Control and Modeling for Power Electronics (COMPEL), Vancouver, BC, Canada, 12–15 July 2015; pp. 1–7.
- Hao, H.; Lin, Y.; Kowli, A.S.; Barooah, P.; Meyn, S. Ancillary Service to the Grid Through Control of Fans in Commercial Building HVAC Systems. IEEE Trans. Smart Grid 2014, 5, 2066–2074. [Google Scholar] [CrossRef]
- Beil, I.; Hiskens, I.; Backhaus, S. Frequency Regulation From Commercial Building HVAC Demand Response. Proc. IEEE 2016, 104, 745–757. [Google Scholar] [CrossRef]
- Cao, Y.; Magerko, J.A.; Navidi, T.; Krein, P.T. Power Electronics Implementation of Dynamic Thermal Inertia to Offset Stochastic Solar Resources in Low-Energy Buildings. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1430–1441. [Google Scholar] [CrossRef]

| Control Technique | Key Features | Weaknesses |
|---|---|---|
| Synchronous generator (SG) model based |
|
|
| Swing equation based |
|
|
| Frequency-power response based |
|
|
| Droop-based approach |
|
|
| Parameter | No VI | Synchronverter | Ise Lab | VSG |
|---|---|---|---|---|
| Minimum Frequency | 57.3 Hz | 58.1 Hz | 58.6 Hz | 58.3 Hz |
| Maximum ROCOF | 1.9 Hz/s | 1.5 Hz/s | 1.6 Hz/s | 1.7 Hz/s |
| Settling time | 11.3 s | 13.2 s | 17.7 s | 17.9 s |
| Peak power delivered | 0 W | 1825 W | 1800 W | 1929 W |
| Energy exchanged | 0 Wh | 0.8 Wh | 3.8 Wh | 4.9 Wh |
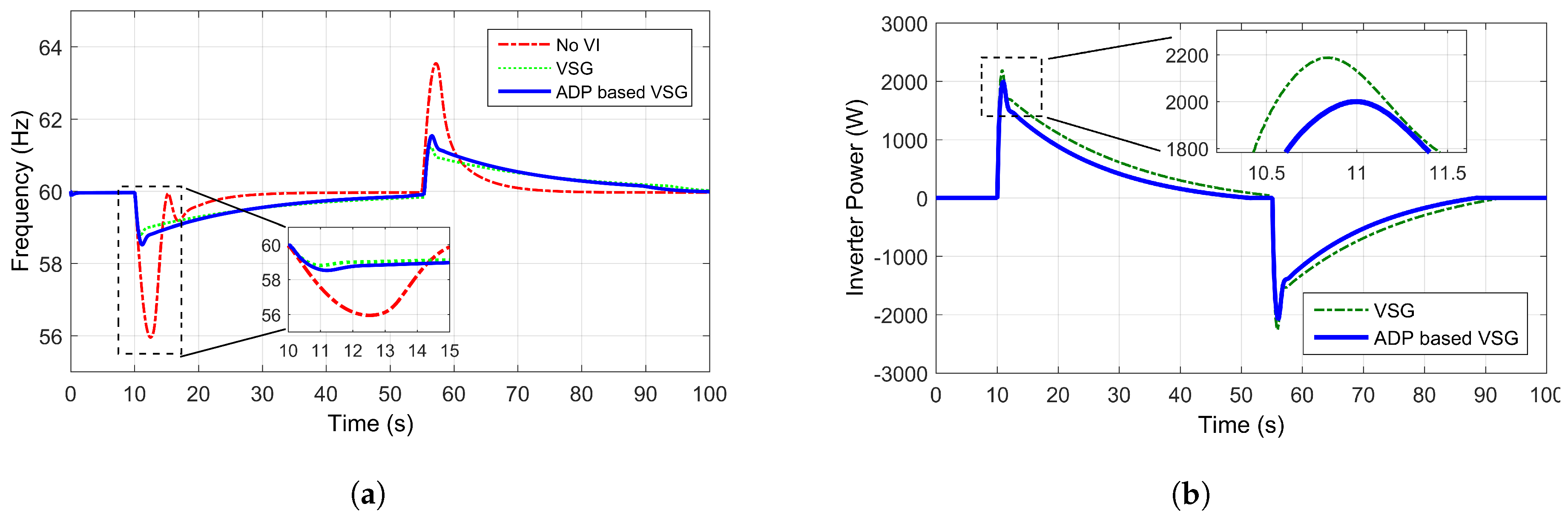
| Parameter | No VI | Simple VSG | ADP Based VSG |
|---|---|---|---|
| Peak Power for Event A | 0 W | 2184 W | 1979 W |
| Settling time for Event A | 12.6 s | 35.1 s | 31.3 s |
| Peak Power for Event B | 0 W | −2235 W | −2029 W |
| Settling time for Event B | 11.1 s | 29.1 s | 26.6 s |
| Energy delivered (Wh) | 0 Wh | 8.2 Wh | 6.2 Wh |
| Net energy exchanged (Wh) | 0 Wh | 1.6 Wh | 0.9 Wh |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tamrakar, U.; Shrestha, D.; Maharjan, M.; Bhattarai, B.P.; Hansen, T.M.; Tonkoski, R. Virtual Inertia: Current Trends and Future Directions. Appl. Sci. 2017, 7, 654. https://doi.org/10.3390/app7070654
Tamrakar U, Shrestha D, Maharjan M, Bhattarai BP, Hansen TM, Tonkoski R. Virtual Inertia: Current Trends and Future Directions. Applied Sciences. 2017; 7(7):654. https://doi.org/10.3390/app7070654
Chicago/Turabian StyleTamrakar, Ujjwol, Dipesh Shrestha, Manisha Maharjan, Bishnu P. Bhattarai, Timothy M. Hansen, and Reinaldo Tonkoski. 2017. "Virtual Inertia: Current Trends and Future Directions" Applied Sciences 7, no. 7: 654. https://doi.org/10.3390/app7070654
APA StyleTamrakar, U., Shrestha, D., Maharjan, M., Bhattarai, B. P., Hansen, T. M., & Tonkoski, R. (2017). Virtual Inertia: Current Trends and Future Directions. Applied Sciences, 7(7), 654. https://doi.org/10.3390/app7070654