Near-Field Coupling and Mode Competition in Multiple Anapole Systems
Abstract
:1. Introduction
2. Results
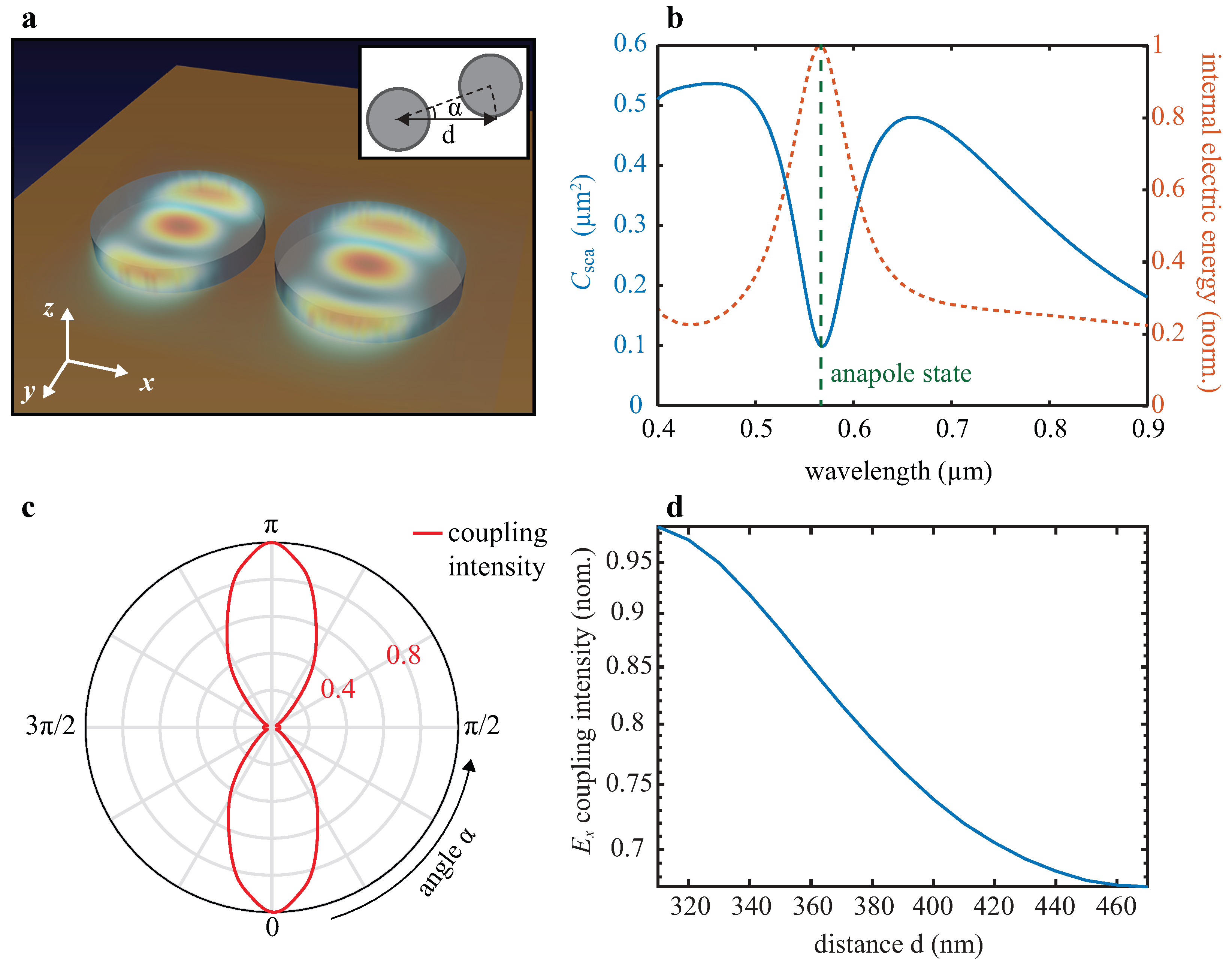
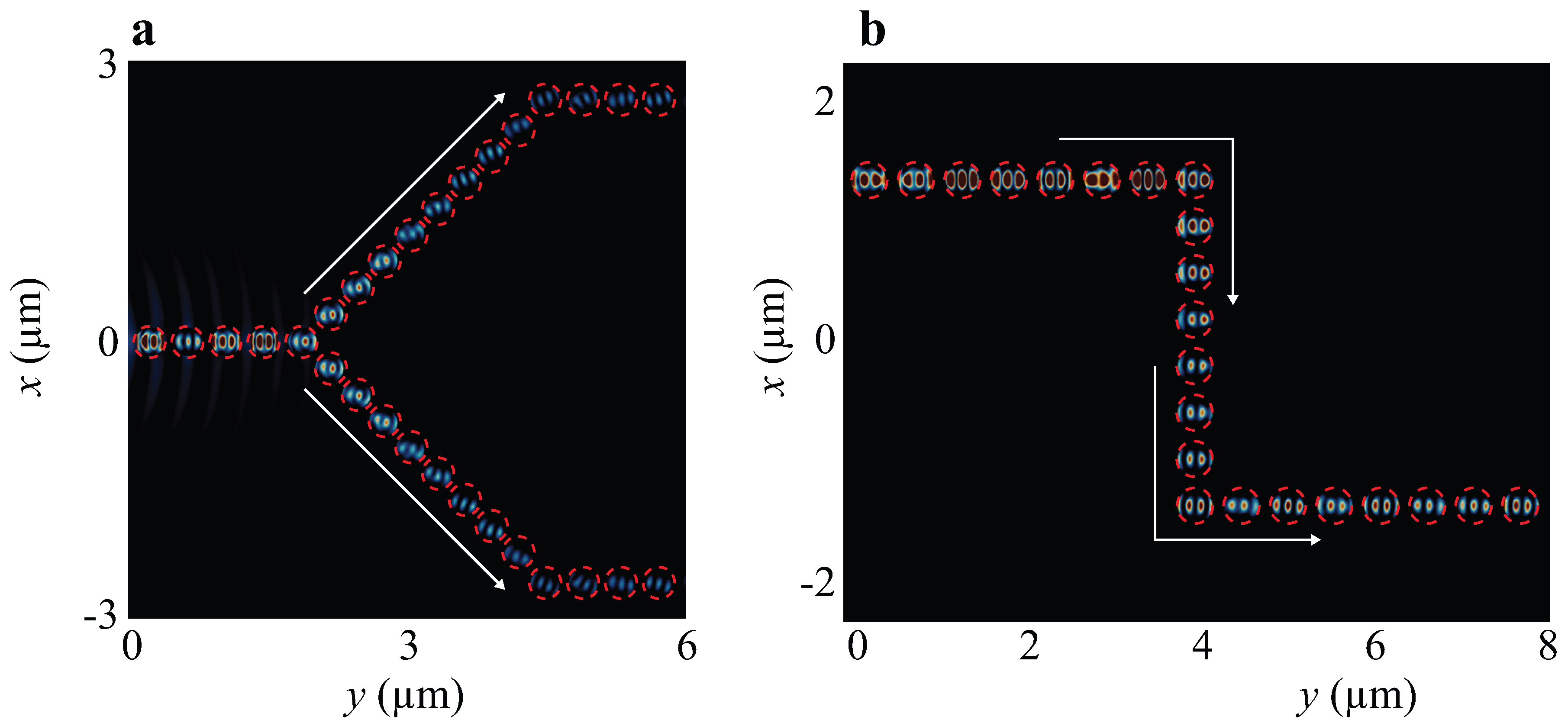
2.1. Ab-Initio Analysis of Multiple Anapole Systems
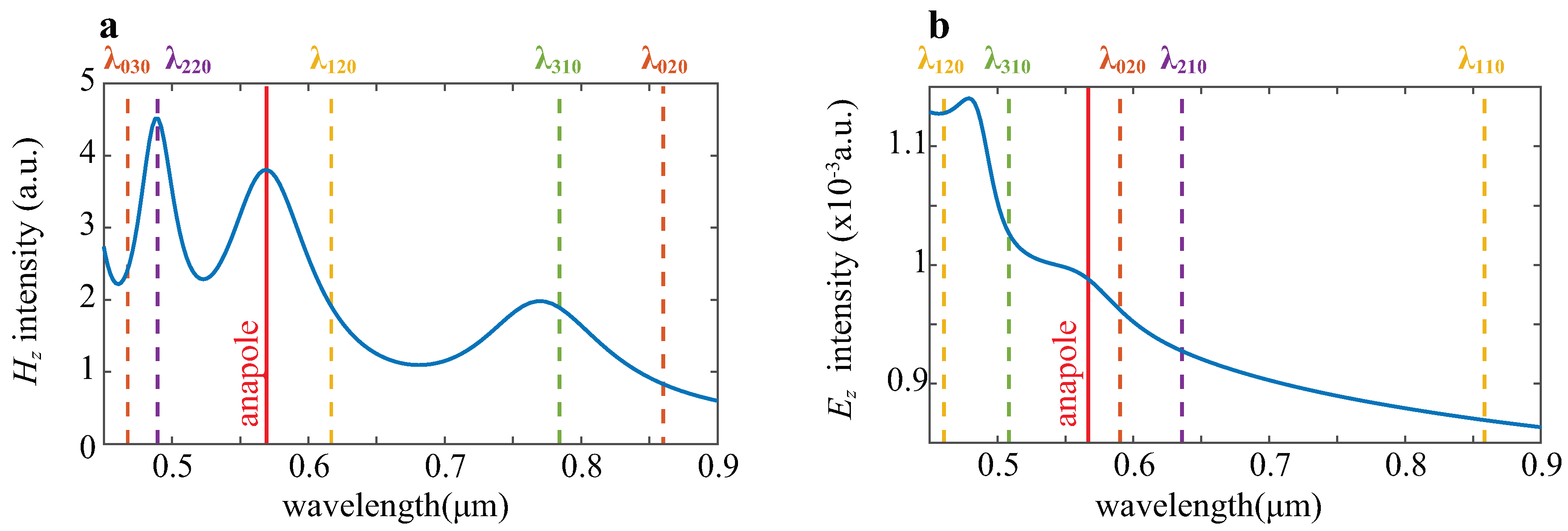
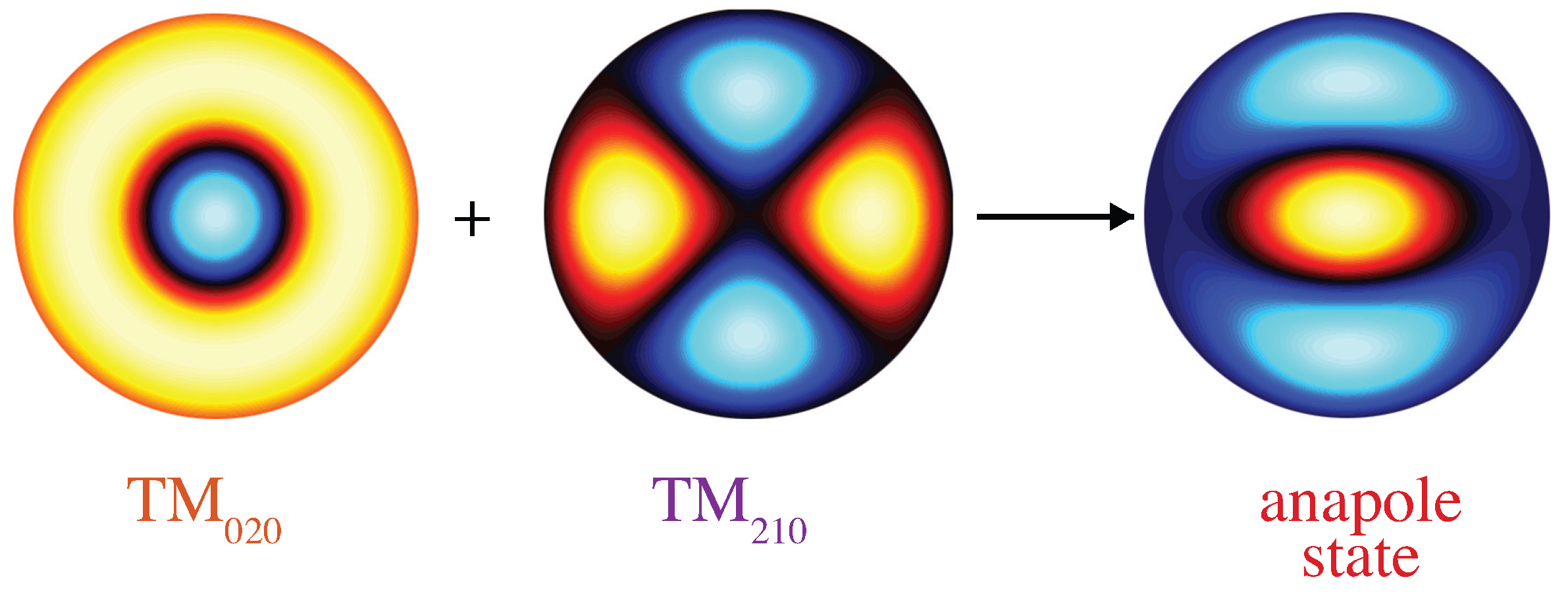
2.2. Fano–Feshbach Analysis of the Internal Modes
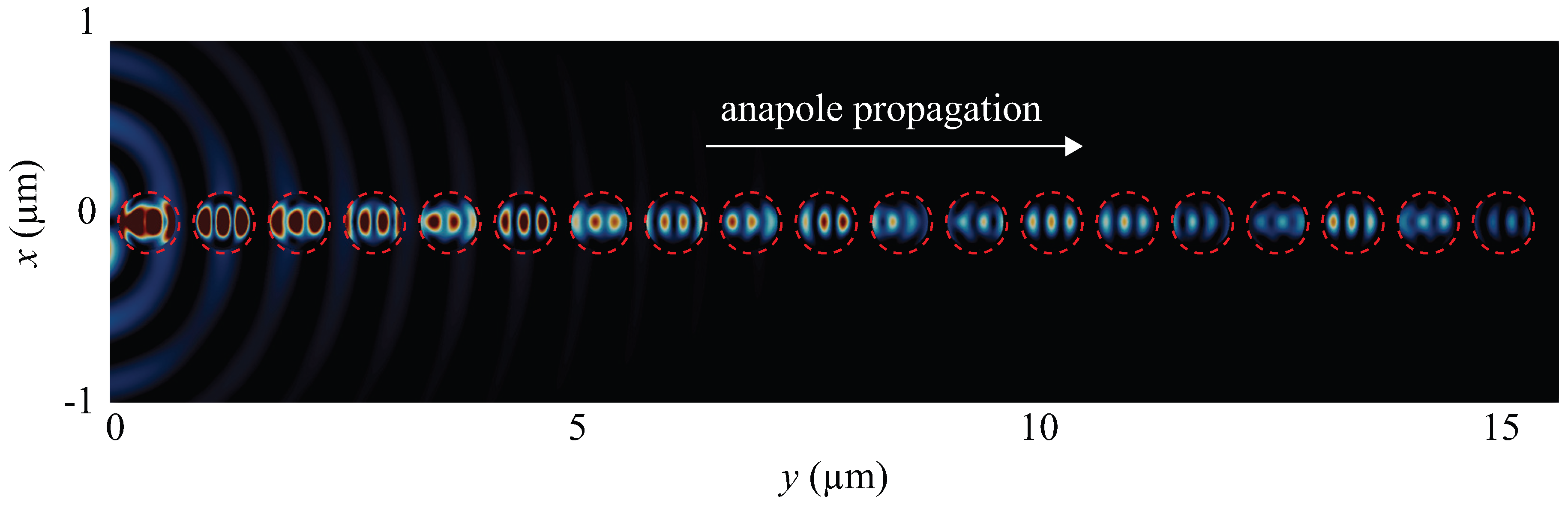
3. Discussion and Conclusions
4. Materials and Methods
4.1. FDTD Simulations
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| FDTD | Finite-Differences Time-Domain |
| DOS | Density Of States |
| UPML | Uniaxial Perfectly Matched Layer |
| TFSF | Total-Field Scattered-field |
| TM | Transverse Magnetic |
| TE | Transverse Electric |
| PEC | Perfect Electric Conductor |
| PMC | Perfect Magnetic Conductor |
| NSOM | Near-field scanning optical microscopy |
References
- Wang, K.X.; Yu, Z.; Sandhu, S.; Liu, V.; Fan, S. Condition for perfect antireflection by optical resonance at material interface. Optica 2014, 1, 388–395. [Google Scholar] [CrossRef]
- Liu, W.; Miroshnichenko, A.E.; Neshev, D.N.; Kivshar, Y.S. Broadband Unidirectional Scattering by Magneto-Electric Core-Shell Nanoparticles. ACS Nano 2012, 6, 5489–5497. [Google Scholar] [CrossRef] [PubMed]
- Miroshnichenko, A.E.; Evlyukhin, A.B.; Yu, Y.F.; Bakker, R.M.; Chipouline, A.; Kuznetsov, A.I.; Luk’yanchuk, B.; Chichkov, B.N.; Kivshar, Y.S. Nonradiating anapole modes in dielectric nanoparticles. Nat. Commun. 2015, 6, 8069. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Zhang, J.; Lei, B.; Hu, H.; Miroshnichenko, A.E. Invisible nanowires with interfering electric and toroidal dipoles. Optics Lett. 2015, 40, 2293–2296. [Google Scholar] [CrossRef] [PubMed]
- Luk’yanchuk, B.; Paniagua-Domínguez, R.; Kuznetsov, A.I.; Miroshnichenko, A.E.; Kivshar, Y.S. Suppression of scattering for small dielectric particles: anapole mode and invisibility. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2017, 375, 20160069. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.; Xi, Z.; Bhattacharya, N.; Urbach, H.P. Excitation of the radiationless anapole mode. Optica 2016, 3, 799–802. [Google Scholar] [CrossRef]
- Brongersma, M.L.; Hartman, J.W.; Atwater, H.A. Electromagnetic energy transfer and switching in nanoparticle chain arrays below the diffraction limit. Phys. Rev. B 2000, 62, R16356–R16359. [Google Scholar] [CrossRef]
- Totero Gongora, J.S.; Fratalocchi, A. Harnessing Disorder at the Nanoscale. In Encyclopedia of Nanotechnology; Bhushan, B., Ed.; Springer Netherlands: Heidelberg, Germany, 2015; pp. 1–13. [Google Scholar]
- Bakker, R.M.; Yu, Y.F.; Paniagua-Domínguez, R.; Luk’yanchuk, B.; Kuznetsov, A. Silicon Nanoparticles for Waveguiding. Frontiers in Optics; Optical Society of America: Washington, DC, USA, 2015; p. FM1B.2. [Google Scholar]
- Evlyukhin, A.B.; Reinhardt, C.; Seidel, A.; Luk’yanchuk, B.S.; Chichkov, B.N. Optical response features of Si-nanoparticle arrays. Phys. Rev. B 2010, 82, 045404. [Google Scholar] [CrossRef]
- Gongora, J.S.T.; Favraud, G.; Fratalocchi, A. Fundamental and high-order anapoles in all-dielectric metamaterials via Fano–Feshbach modes competition. Nanotechnology 2017, 28, 104001. [Google Scholar] [CrossRef] [PubMed]
- Grinblat, G.; Li, Y.; Nielsen, M.P.; Oulton, R.F.; Maier, S.A. Efficient Third Harmonic Generation and Nonlinear Subwavelength Imaging at a Higher-Order Anapole Mode in a Single Germanium Nanodisk. ACS Nano 2017, 11, 953–960. [Google Scholar] [CrossRef] [PubMed]
- Totero Gongora, J.S.; Miroshnichenko, A.E.; Kivshar, Y.S.; Fratalocchi, A. Anapole nanolasers for mode-locking and ultrafast pulse generation. Nat. Commun. 2017, in press. [Google Scholar]
- Taflove, A.; Oskooi, A.; Johnson, S.G. Advances in FDTD Computational Electrodynamics: Photonics and Nanotechnology; Artech House Antennas and Propagation Series; Artech House: Norwood, MA, USA, 2013. [Google Scholar]
- Yariv, A.; Yeh, P. Photonics: Optical Electronics in Modern Communications (The Oxford Series in Electrical and Computer Engineering); Oxford University Press, Inc.: New York, NY, USA, 2006. [Google Scholar]
- Türeci, H.E.; Ge, L.; Rotter, S.; Stone, A.D. Strong Interactions in Multimode Random Lasers. Science 2008, 320, 643–646. [Google Scholar] [CrossRef] [PubMed]
- Kristensen, P.T.; Hughes, S. Modes and Mode Volumes of Leaky Optical Cavities and Plasmonic Nanoresonators. ACS Photonics 2014, 1, 2–10. [Google Scholar] [CrossRef]
- Viviescas, C.; Hackenbroich, G. Field quantization for open optical cavities. Phys. Rev. A 2003, 67, 013805. [Google Scholar] [CrossRef]
- Jin, J.M. Theory and Computation of Electromagnetic Fields; John Wiley & Sons: Hoboken, NJ, USA, 2011; Google-Books-ID: D6SqmxJVV5wC. [Google Scholar]
- Viviescas, C.; Hackenbroich, G. Quantum theory of multimode fields: Applications to optical resonators. J. Opt. B Quantum Semiclass. Opt. 2004, 6, 211. [Google Scholar] [CrossRef]
- Van Bladel, J. Radiation in Free Space. In Electromagnetic Fields; Wiley-IEEE Press: Hoboken, NJ, USA, 2007; pp. 277–356. [Google Scholar]
- Tribelsky, M.I.; Miroshnichenko, A.E. Giant in-particle field concentration and Fano resonances at light scattering by high-refractive-index particles. Phys. Rev. A 2016, 93, 053837. [Google Scholar] [CrossRef]
- Cherchi, M.; Ylinen, S.; Harjanne, M.; Kapulainen, M.; Aalto, T. Dramatic size reduction of waveguide bends on a micron-scale silicon photonic platform. Opt. Express 2013, 21, 17814. [Google Scholar] [CrossRef] [PubMed]
- Gentilini, S.; Fratalocchi, A.; Angelani, L.; Ruocco, G.; Conti, C. Ultrashort pulse propagation and the Anderson localization. Opt. Lett. 2009, 34, 130–132. [Google Scholar] [CrossRef] [PubMed]
- Crosta, M.; Fratalocchi, A.; Trillo, S. Bistability and instability of dark-antidark solitons in the cubic-quintic nonlinear Schrödinger equation. Phys. Rev. A 2011, 84, 063809. [Google Scholar] [CrossRef]
- Huang, J.; Liu, C.; Zhu, Y.; Masala, S.; Alarousu, E.; Han, Y.; Fratalocchi, A. Harnessing structural darkness in the visible and infrared wavelengths for a new source of light. Nat. Nanotechnol. 2016, 11, 60–66. [Google Scholar] [CrossRef] [PubMed]
- Totero Gongora, J.S.; Miroshnichenko, A.E.; Kivshar, Y.S.; Fratalocchi, A. Energy equipartition and unidirectional emission in a spaser nanolaser. Laser Photonics Rev. 2016, 10, 432–440. [Google Scholar] [CrossRef]
- Labelle, A.J.; Bonifazi, M.; Tian, Y.; Wong, C.; Hoogland, S.; Favraud, G.; Walters, G.; Sutherland, B.; Liu, M.; Li, J.; et al. Broadband Epsilon-near-Zero Reflectors Enhance the Quantum Efficiency of Thin Solar Cells at Visible and Infrared Wavelengths. ACS Appl. Mater. Interfaces 2017, 9, 5556–5565. [Google Scholar] [CrossRef] [PubMed]
- Galinski, H.; Favraud, G.; Dong, H.; Totero Gongora, J.S.; Favaro, G.; Döbeli, M.; Spolenak, R.; Fratalocchi, A.; Capasso, F. Scalable, ultra-resistant structural colors based on network metamaterials. Light Sci. Appl. 2017, 6, e16233. [Google Scholar] [CrossRef]
- Berenger, J.P. A Perfectly Matched Layer for the Absorption of Electromagnetic-Waves. J. Comput. Phys. 1994, 114, 185–200. [Google Scholar] [CrossRef]
- Taflove, A.; Hagness, S.C. Computational Electrodynamics: The Finite-Difference Time-Domain Method, 3rd ed.; Artech House Antennas and Propagation Library, Artech House: Boston, MA, USA, 2005. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazzone, V.; Totero Gongora, J.S.; Fratalocchi, A. Near-Field Coupling and Mode Competition in Multiple Anapole Systems. Appl. Sci. 2017, 7, 542. https://doi.org/10.3390/app7060542
Mazzone V, Totero Gongora JS, Fratalocchi A. Near-Field Coupling and Mode Competition in Multiple Anapole Systems. Applied Sciences. 2017; 7(6):542. https://doi.org/10.3390/app7060542
Chicago/Turabian StyleMazzone, Valerio, Juan Sebastian Totero Gongora, and Andrea Fratalocchi. 2017. "Near-Field Coupling and Mode Competition in Multiple Anapole Systems" Applied Sciences 7, no. 6: 542. https://doi.org/10.3390/app7060542
APA StyleMazzone, V., Totero Gongora, J. S., & Fratalocchi, A. (2017). Near-Field Coupling and Mode Competition in Multiple Anapole Systems. Applied Sciences, 7(6), 542. https://doi.org/10.3390/app7060542






