Experimental Damage Identification of a Model Reticulated Shell
Abstract
:1. Introduction
2. Methodologies
2.1. The Auto-Regressive Time Series Model
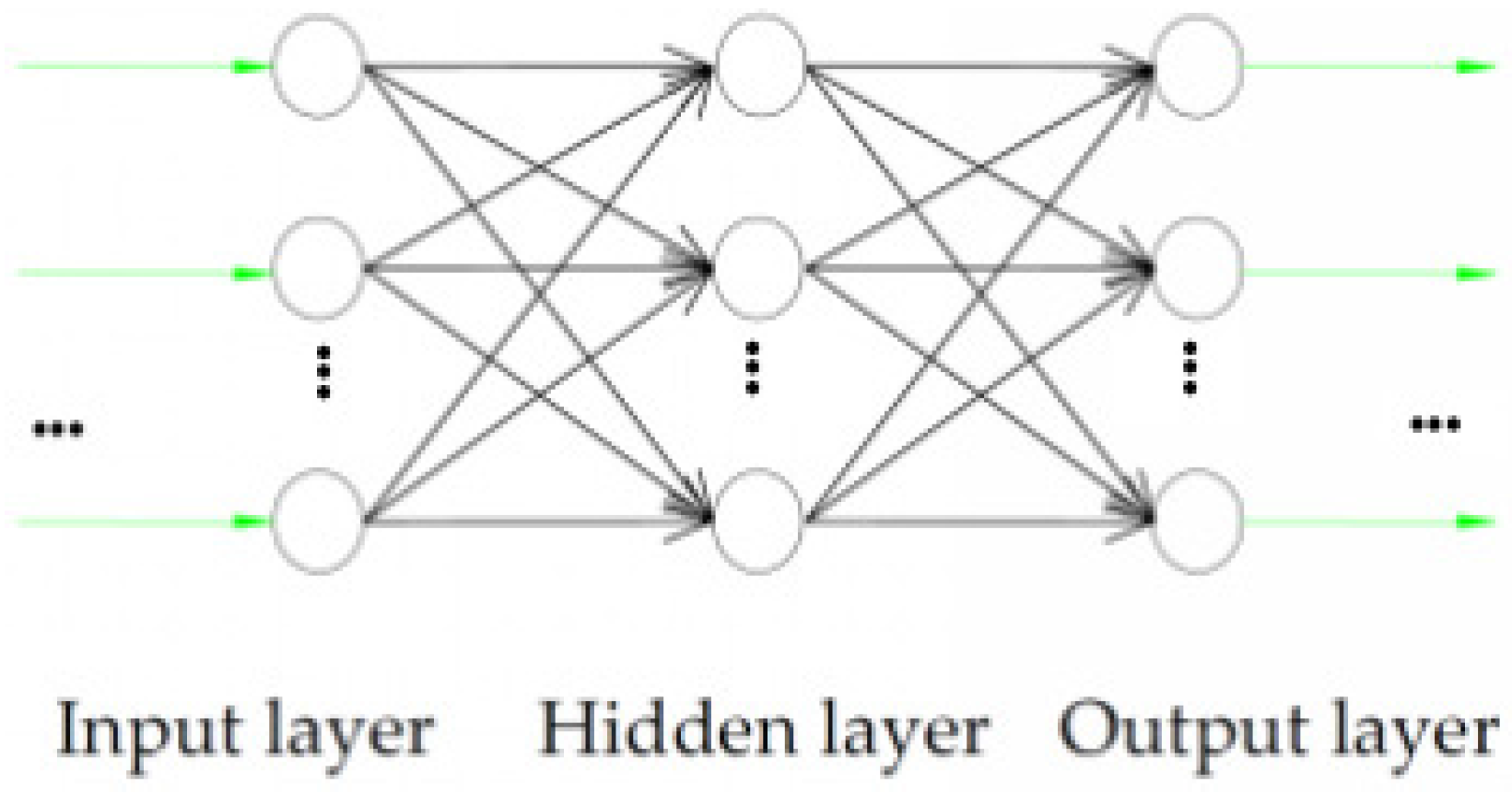
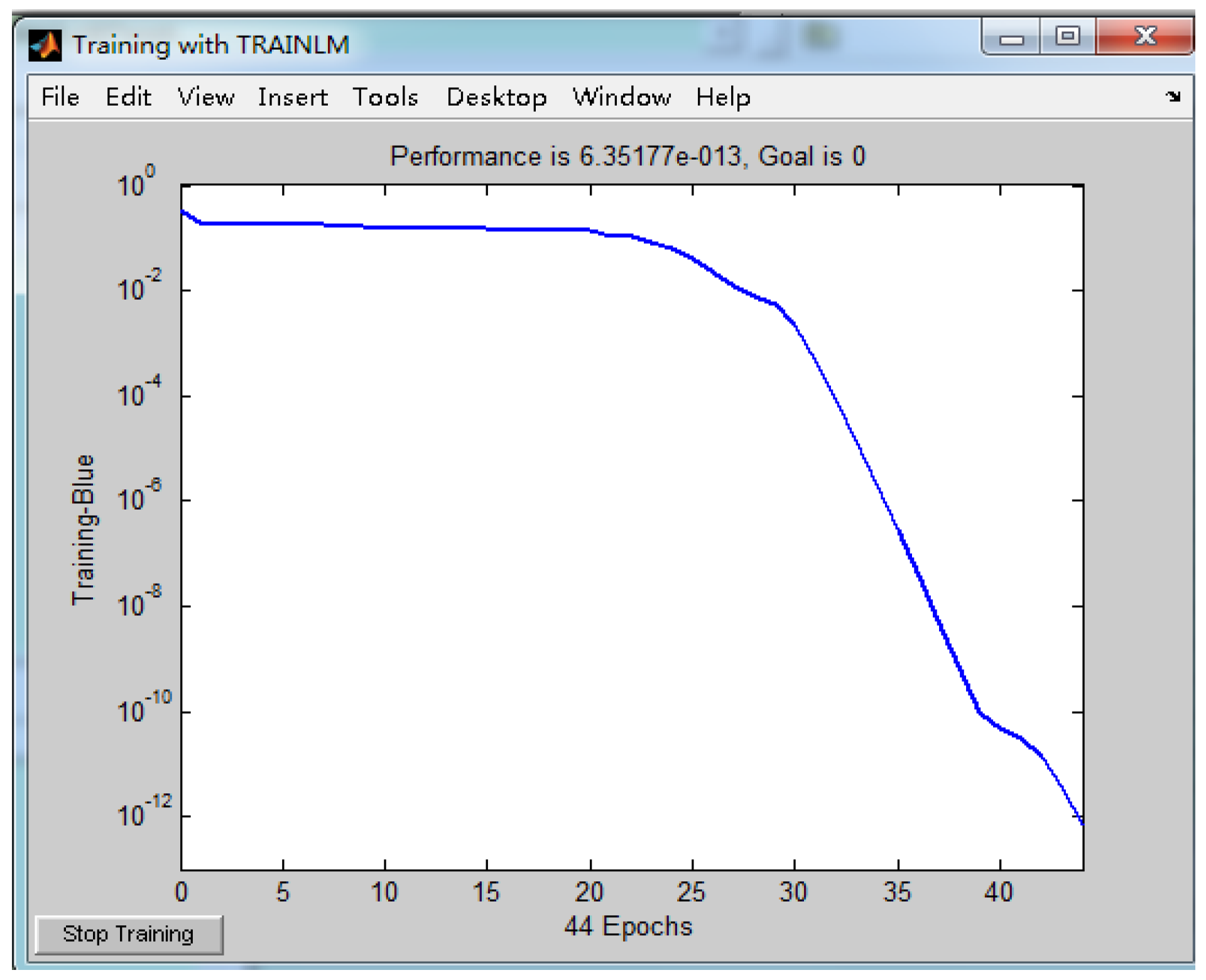
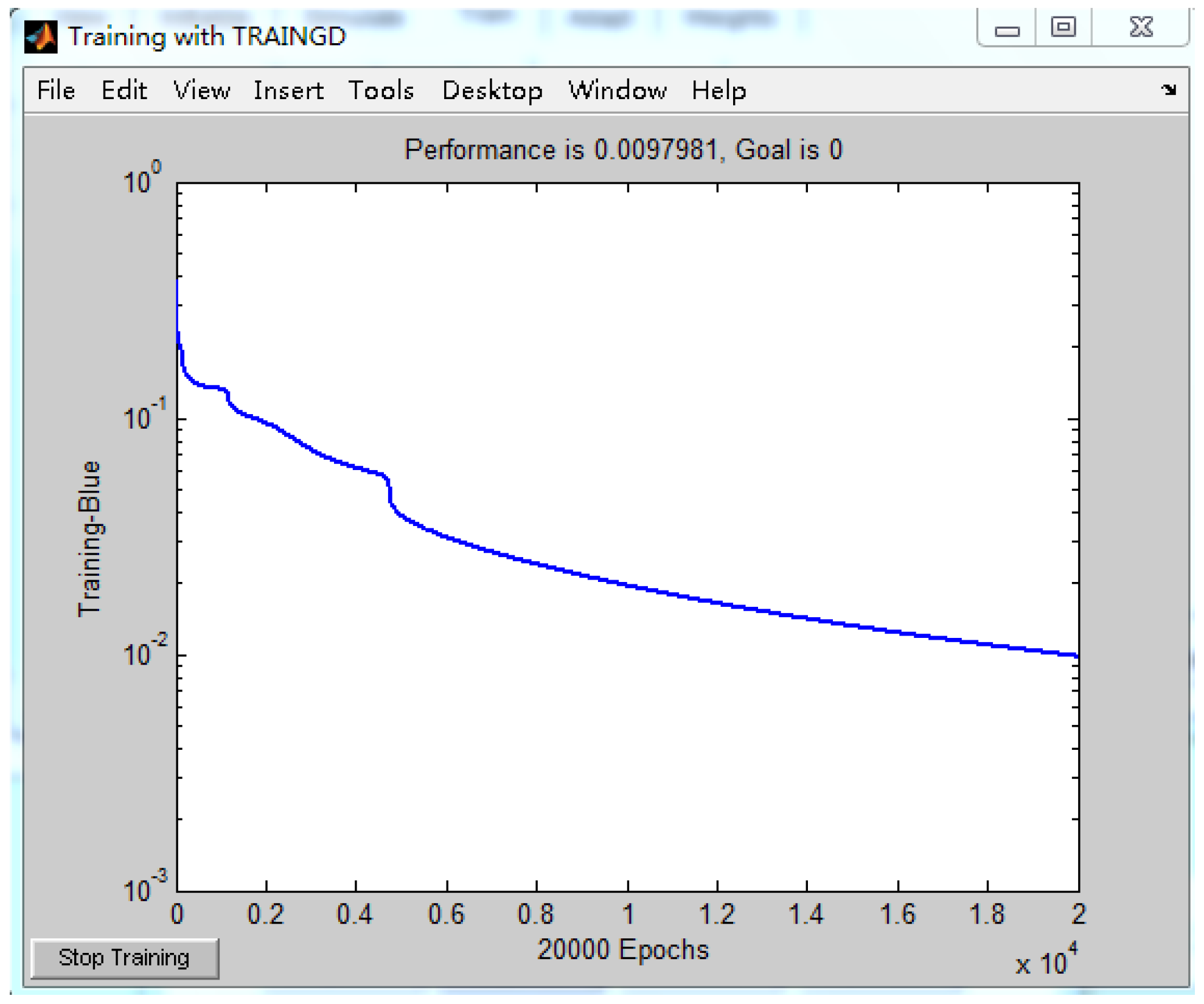
2.2. Back-Propagation Neural Network
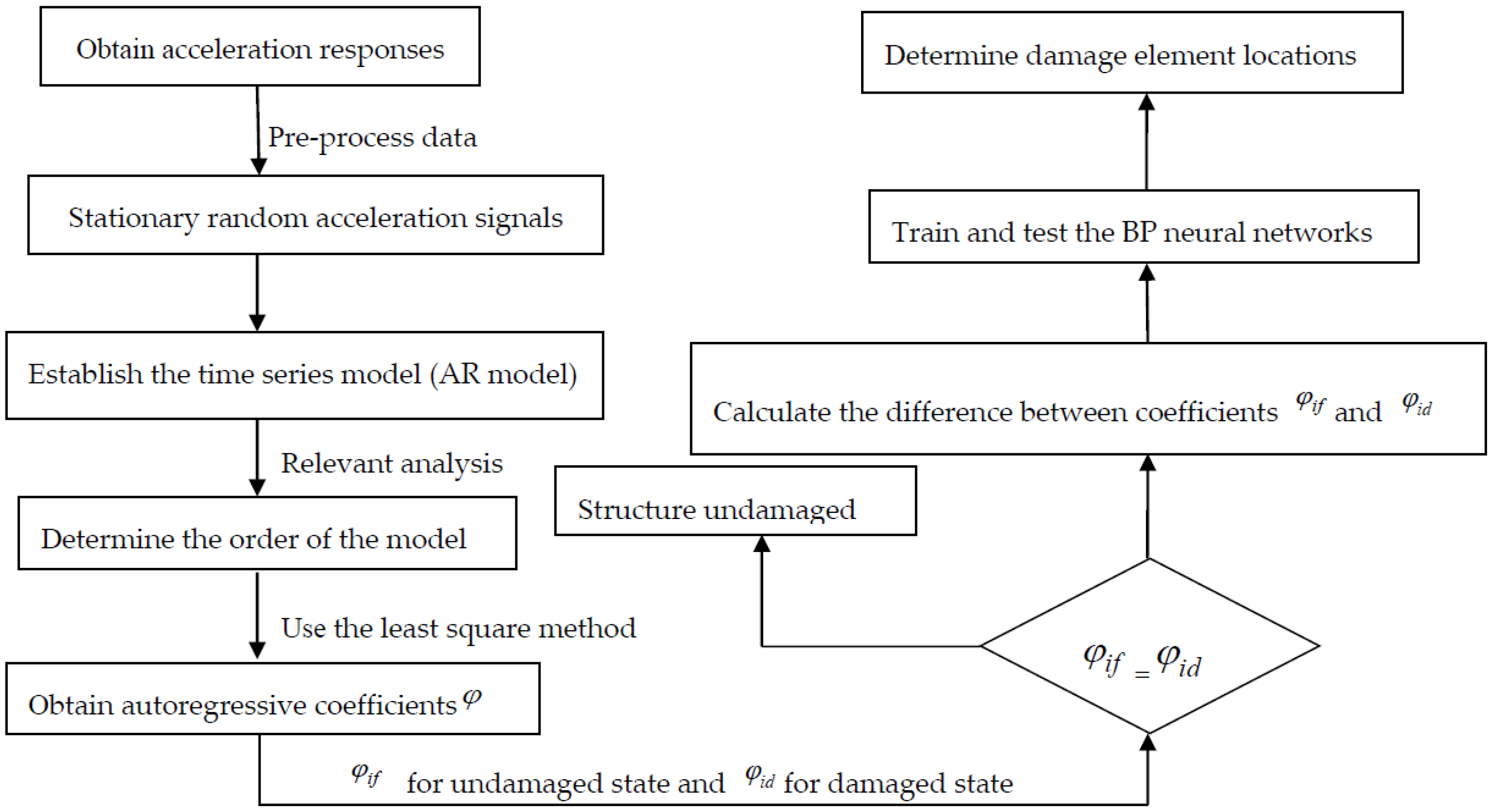
2.3. Damage Detection Flowchart
- (1)
- Measure the acceleration responses of the reticulated shell structure before and after damage under the excitation condition.
- (2)
- Obtain the stationary random acceleration signals by using the data pre-processed method introduced in Section 2.1.
- (3)
- Establish the auto-regressive time series model (AR model) by using the modeling method introduced in Section 2.1.
- (4)
- Detect the damage of the reticulated shell according to the changes in the coefficients of the AR model before and after damage.
- (5)
- Obtain the damage sensitive factors by using Equation (2).
- (6)
- Train the back-propagation neural networks (BPNNs) by using the method introduced in Section 2.2, with the damage sensitive factors as the inputs and the damage positions as the outputs.
- (7)
- Find the locations of the damages by testing the trained BPNNs.
3. Experimental Setup
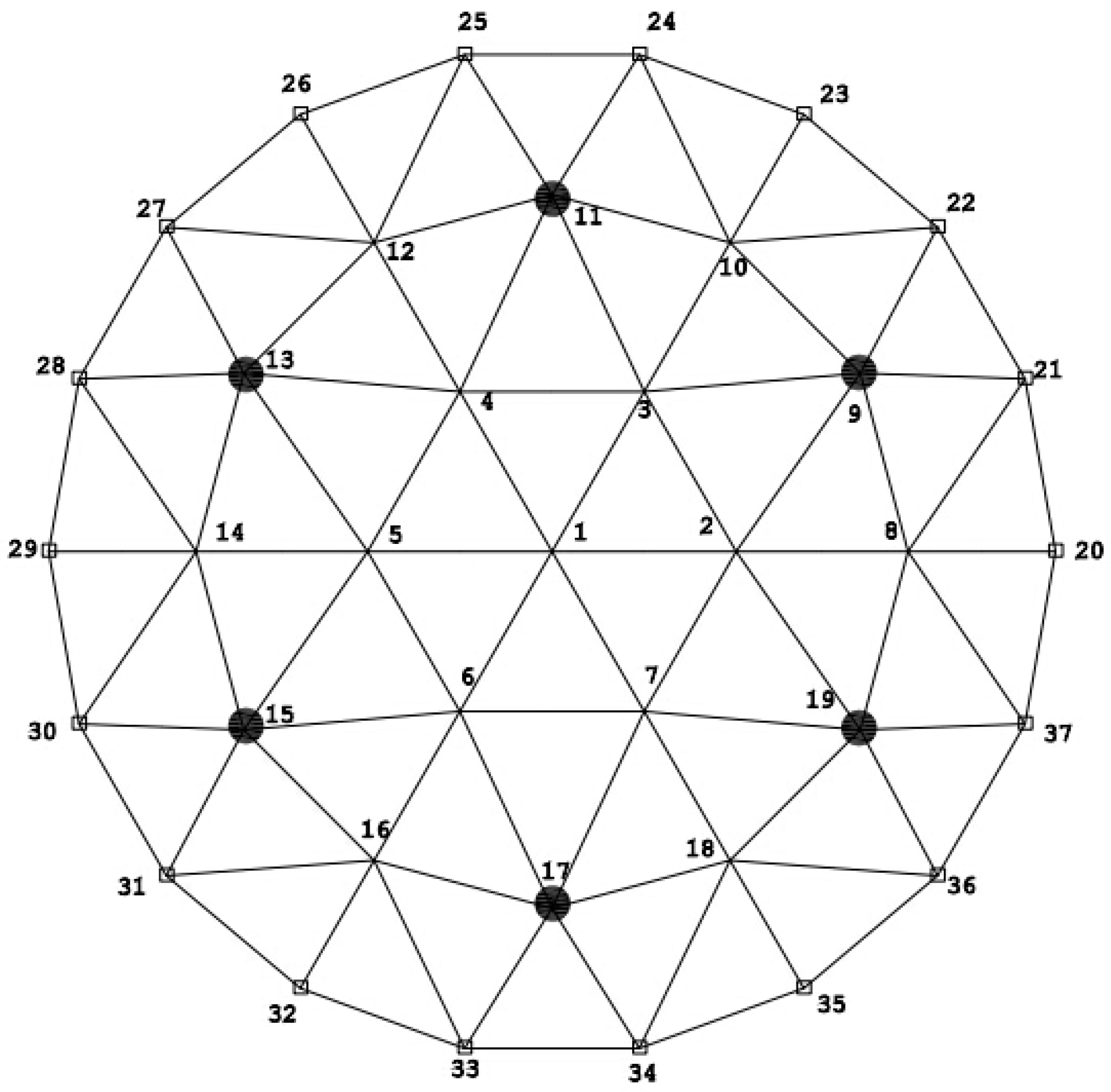
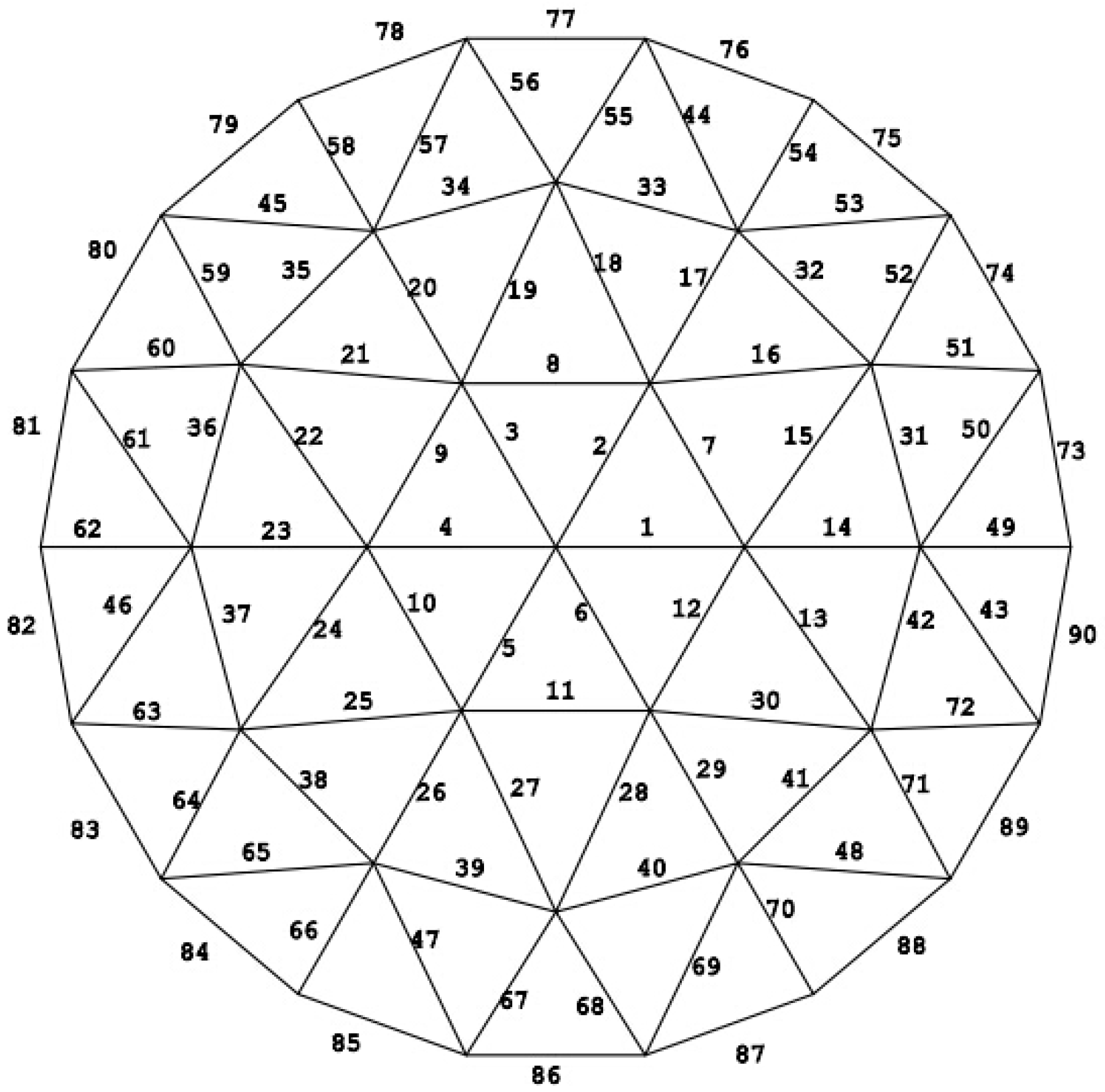
3.1. Experiment Model
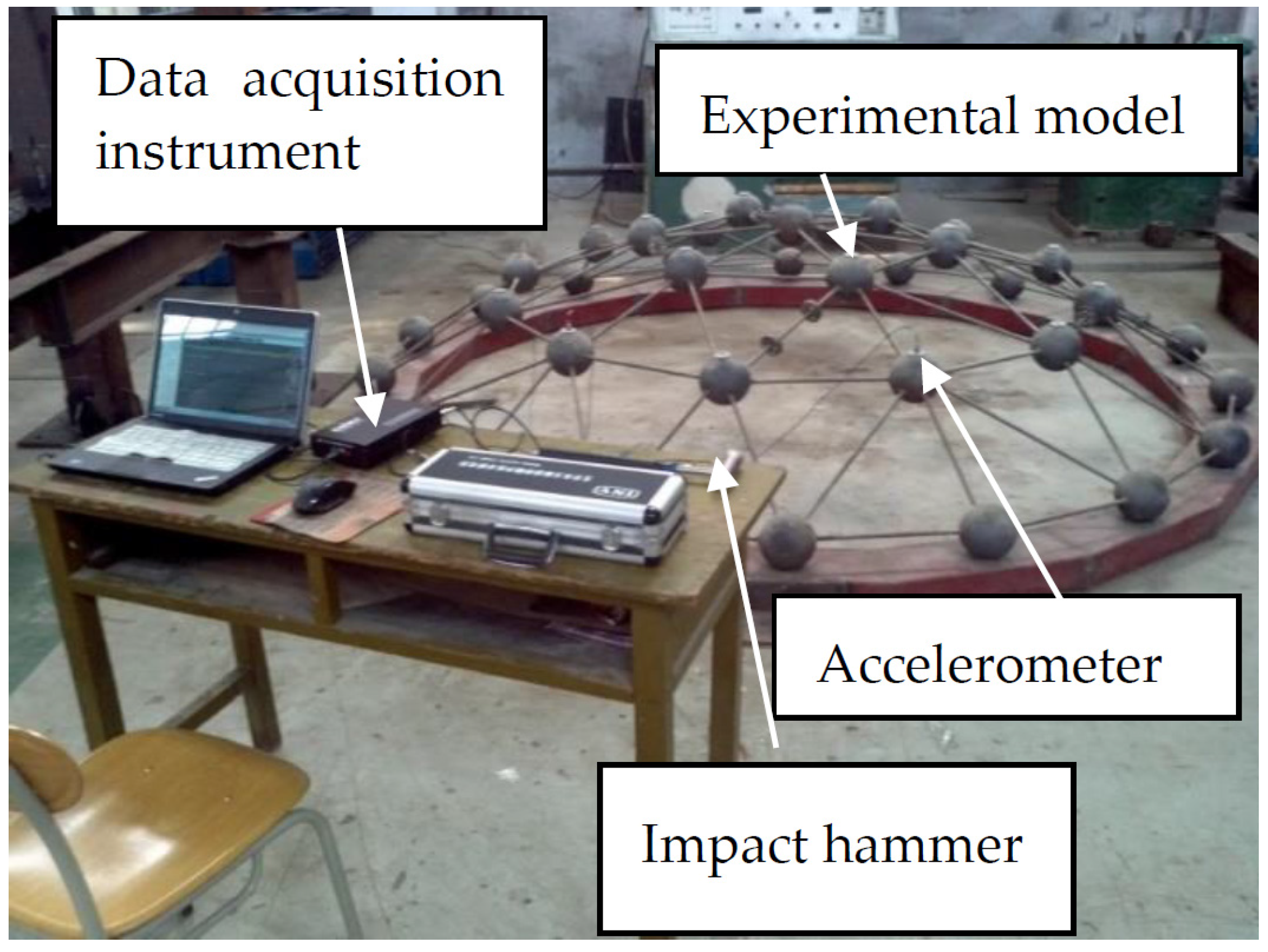
3.2. Experimental Scheme
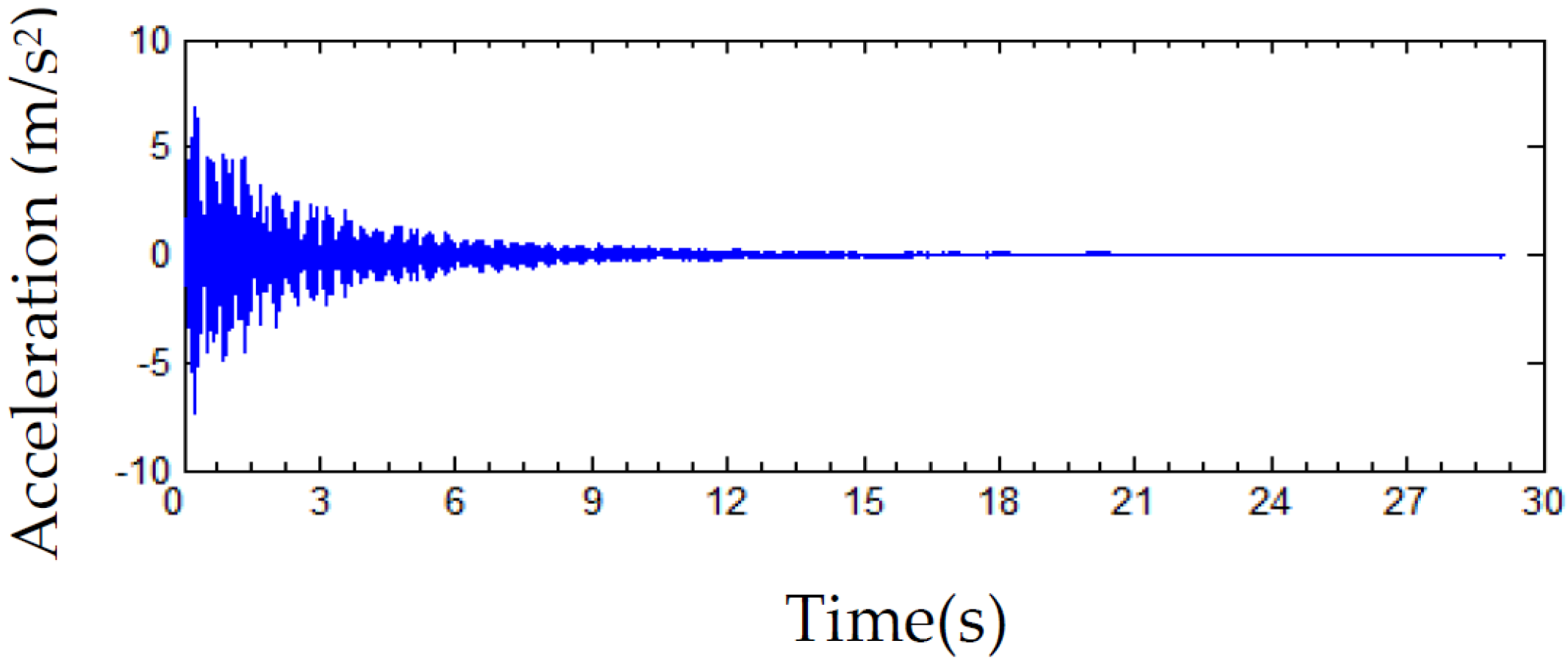
4. Experimental Results
5. Conclusions
- (1)
- The AR model was established based directly on the acceleration responses of the nodes. Using the coefficients of the AR model, the damage sensitive features were defined. Taking the damage sensitive features as the inputs and the damage locations as the outputs, an improved back-propagation neural network was established based on the L–M algorithm. The trained network can be used to detect the damage location of a reticulated shell. The proposed damage detection method does not require modal parameter identification and excitation information. It improves the accuracy of damage identification to some extent.
- (2)
- According to the principle of equivalent stiffness, we simulated the structural damage by replacing cross-sectional elements with smaller sized elements. The experiment scheme of single-point excitation and multi-point responses was adopted. Then, we conducted impact experiments on a K6 single-layer spherical shell with a scale of 1/10. The experimental results showed that the damage detection method based on the AR model and the L–M algorithm improved back-propagation neural network accurately identified the damage and the location of the damage that occurred in the reticulated shell.
- (3)
- Accuracy of the damage identification method is influenced by some factors, such as the sensor placement, neural network structure, and training algorithm of the neural network. In this paper, the sensor placement was optimized based on the particle swarm optimization algorithm.
- (4)
- The L–M algorithm was used to train the back-propagation neural network, which has the characteristics of faster training speed and better local searching ability. In addition, the accuracy of damage identification is effectively improved.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, H.-N. Safety assessment, health monitoring and damage diagnosis for structures in civil engineering. Earthq. Eng. Eng. Vib. 2002, 22, 82–90. [Google Scholar]
- Kong, Q.; Feng, Q.; Song, G. Water presence detection in a concrete crack using smart aggregates. Int. J. Smart Nano Mater. 2015, 6, 149–161. [Google Scholar] [CrossRef]
- Siu, S.; Ji, Q.; Wu, W.; Song, G.; Ding, Z. Stress wave communication in concrete: I. Characterization of a smart aggregate based concrete channel. Smart Mater. Struct. 2014, 23, 125030. [Google Scholar] [CrossRef]
- Kong, Q.; Hou, S.; Ji, Q.; Mo, Y.; Song, G. Very early age concrete hydration characterization monitoring using piezoceramic based smart aggregates. Smart Mater. Struct. 2013, 22, 085025. [Google Scholar] [CrossRef]
- Ho, S.C.M.; Ren, L.; Li, H.-N.; Song, G. A fiber bragg grating sensor for detection of liquid water in concrete structures. Smart Mater. Struct. 2013, 22, 055012. [Google Scholar] [CrossRef]
- Kong, Q.; Robert, R.H.; Silva, P.; Mo, Y. Cyclic crack monitoring of a reinforced concrete column under simulated pseudo-dynamic loading using piezoceramic-based smart aggregates. Appl. Sci. 2016, 6, 341. [Google Scholar] [CrossRef]
- Zhao, X.; Li, W.; Zhou, L.; Song, G.; Ba, Q.; Ho, S.C.M.; Ou, J. Application of support vector machine for pattern classification of active thermometry-based pipeline scour monitoring. Struct. Control Health Monit. 2015, 22, 903–918. [Google Scholar] [CrossRef]
- Hou, Q.; Jiao, W.; Ren, L.; Cao, H.; Song, G. Experimental study of leakage detection of natural gas pipeline using FBG based strain sensor and least square support vector machine. J. Loss Prev. Process Ind. 2014, 32, 144–151. [Google Scholar] [CrossRef]
- Feng, Q.; Kong, Q.; Huo, L.; Song, G. Crack detection and leakage monitoring on reinforced concrete pipe. Smart Mater. Struct. 2015, 24, 115020. [Google Scholar] [CrossRef]
- Jia, Z.G.; Ren, L.; Li, H.N.; Ho, S.C.; Song, G.B. Experimental study of pipeline leak detection based on hoop strain measurement. Struct. Control Health Monit. 2015, 22, 799–812. [Google Scholar] [CrossRef]
- Ren, L.; Jia, Z.-G.; Li, H.-N.; Song, G. Design and experimental study on FBG hoop-strain sensor in pipeline monitoring. Opt. Fiber Technol. 2014, 20, 15–23. [Google Scholar] [CrossRef]
- Du, G.; Kong, Q.; Lai, T.; Song, G. Feasibility study on crack detection of pipelines using piezoceramic transducers. Int. J. Distrib. Sens. Netw. 2013. [Google Scholar] [CrossRef]
- Yao, P.; Kong, Q.; Xu, K.; Jiang, T.; Huo, L.-S.; Song, G. Structural health monitoring of multi-spot welded joints using a lead zirconate titanate based active sensing approach. Smart Mater. Struct. 2015, 25, 015031. [Google Scholar] [CrossRef]
- Ruan, J.; Zhang, Z.; Wang, T.; Li, Y.; Song, G. An anti-noise real-time cross-correlation method for bolted joint monitoring using piezoceramic transducers. Smart Struct. Syst. 2015, 16, 281–294. [Google Scholar] [CrossRef]
- Yin, H.; Wang, T.; Yang, D.; Liu, S.; Shao, J.; Li, Y. A smart washer for bolt looseness monitoring based on piezoelectric active sensing method. Appl. Sci. 2016, 6, 320. [Google Scholar] [CrossRef]
- Shao, J.; Wang, T.; Yin, H.; Yang, D.; Li, Y. Bolt looseness detection based on piezoelectric impedance frequency shift. Appl. Sci. 2016, 6, 298. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M.Q. Vision-based multipoint displacement measurement for structural health monitoring. Struct. Control Health Monit. 2015. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M.Q. Experimental validation of cost-effective vision-based structural health monitoring. Mech. Syst. Signal Process. 2017, 88, 199–211. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M.Q. Output-only damage detection using vehicle-induced displacement response and mode shape curvature index. Struct. Control Health Monit. 2016. [Google Scholar] [CrossRef]
- Zagrai, A.; Doyle, D.; Arritt, B. Embedded nonlinear ultrasonics for structural health monitoring of satellite joints. In Proceedings of the 15th International Symposium on: Smart Structures and Materials & Nondestructive Evaluation and Health Monitoring, San Diego, CA, USA, 9 March 2008. [Google Scholar]
- Yi, C.; Lv, Y.; Dang, Z.; Xiao, H. A novel mechanical fault diagnosis scheme based on the convex 1-D second-order total variation denoising algorithm. Appl. Sci. 2016, 6, 403. [Google Scholar] [CrossRef]
- Mao, Z.; Todd, M. A structural transmissibility measurements-based approach for system damage detection. In Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, San Diego, CA, USA, 9 March 2010. [Google Scholar]
- Żak, A.; Krawczuk, M.; Ostachowicz, W. Vibration of a laminated composite plate with closing delamination. J. Intell. Mater. Syst. Struct. 2001, 12, 545–551. [Google Scholar] [CrossRef]
- Mroz, Z.; Lekszycki, T. Identification of damage in structures using parameter dependent modal response. In Proceedings of the International Seminar on Modal Analysis, Leuven, Belgium, 10–12 September 1998; pp. 121–126. [Google Scholar]
- Todd, M.; Johnson, G.; Vohra, S. Progress towards deployment of bragg grating-based fiber optic systems in structural monitoring applications. In Proceedings of the European COST F3 Conference on System Identification and Structural Health Monitoring, Madrid, Spain, 6–9 June 2000; pp. 521–530. [Google Scholar]
- Natke, H.; Cempel, C. Model-aided diagnosis based on symptoms. In Proceedings of the DAMAS, Sheffield, UK, 30 June–2 July 1997; pp. 363–375. [Google Scholar]
- Strubbs, N.; Sikorsky, C.; Park, S.; Bolton, R. Verification of a Methodology to Nondestructively Evaluate the Structural Properties of Bridges; Structural Health Monitoring Workshop, Stanford Univ.: Palo Alto, CA, USA, 1999; pp. 440–449. [Google Scholar]
- Maeck, J.; Wahab, M.A.; Peeters, B.; De Roeck, G.; De Visscher, J.; De Wilde, W.; Ndambi, J.-M.; Vantomme, J. Damage identification in reinforced concrete structures by dynamic stiffness determination. Eng. Struct. 2000, 22, 1339–1349. [Google Scholar] [CrossRef]
- Wang, M.L.; Xu, F.L.; Lloyd, G.M. Systematic numerical analysis of the damage index method used for bridge diagnostics. In Proceedings of the SPIE’s 7th Annual International Symposium on Smart Structures and Materials, Newport Beach, CA, USA, 6 March 2000; pp. 154–164. [Google Scholar]
- Zhang, L.; Quiong, W.; Link, M. A structural damage identification approach based on element modal strain energy. In Proceedings of the ISMA23, Noise and Vibration Engineering, Leuven, Belgium, 16–18 September 1998. [Google Scholar]
- Worden, K.; Manson, G.; Fieller, N.R. Damage detection using outlier analysis. J. Sound Vib. 2000, 229, 647–667. [Google Scholar] [CrossRef]
- Carrasco, C.J.; Osegueda, R.A.; Ferregut, C.M.; Grygier, M. Localization and quantification of damage in a space truss model using modal strain energy. In Proceedings of the Smart Structures and Materials 1997, San Diego, CA, USA, 23 May 1997; pp. 181–192. [Google Scholar]
- Zhuo, W. Validity analysis on curvature modal method for damage localization to reticulated shell structures. Sichuan Build. Sci. 2012, 3, 024. [Google Scholar]
- Liu, F.-L.; Yan, W.-M.; He, H.-X.; Wang, Z. Mode shape characterization and damage detection in latticed shell structures based on zernike moments. Eng. Mech. 2013, 8, 003. [Google Scholar]
- Lu, W.; Teng, J.; Xu, Y.; Su, Z. Identification of damage in dome-like structures using hybrid sensor measurements and artificial neural networks. Smart Mater. Struct. 2013, 22, 105014. [Google Scholar] [CrossRef]
- Wang, M.H.; Ji, C.M.; Luo, S.S. Research on structural damage identification of reticulated shell based on change rate of modal strain energy and wavelet analysis. Appl. Mech. Mater. 2014, 578–579, 296–300. [Google Scholar] [CrossRef]
- Wang, M.; Dong, S.; Ji, C.; Yang, X. Research on damage identification of grid structures based on frequency response function, energy, environment and green building materials. In Proceedings of the 2014 International Conference on Energy, Environment and Green Building Materials (EEGBM 2014), Guilin, China, 28–30 November 2014; CRC Press: Guilin, China, 2015; p. 399. [Google Scholar]
- Nair, K.K.; Kiremidjian, A.S.; Law, K.H. Time series-based damage detection and localization algorithm with application to the asce benchmark structure. J. Sound Vib. 2006, 291, 349–368. [Google Scholar] [CrossRef]
- Krishnan Nair, K.; Kiremidjian, A.S. Time series based structural damage detection algorithm using gaussian mixtures modeling. J. Dyn. Syst. Meas. Control 2007, 129, 285–293. [Google Scholar] [CrossRef]
- Noh, H.Y.; Nair, K.K.; Kiremidjian, A.S.; Loh, C. Application of time series based damage detection algorithms to the benchmark experiment at the national center for research on earthquake engineering (NCREE) in taipei, taiwan. Smart Struct. Syst. 2009, 5, 95–117. [Google Scholar] [CrossRef]
- Carnimeo, L.; Foti, D.; Ivorra, S. On modeling an innovative monitoring network for protecting and managing cultural heritage from risk events. Key Eng. Mater. 2014, 628, 243–249. [Google Scholar] [CrossRef]
- Carnimeo, L.; Nitti, R. A NN-based approach for monitoring early warnings of risk in historic buildings via image novelty detection. Key Eng. Mater. 2014, 628, 212–217. [Google Scholar] [CrossRef]
- Carnimeo, L.; Foti, D.; Vacca, V. On damage monitoring in historical buildings via neural networks. In Proceedings of the Environmental, Energy and Structural Monitoring Systems (EESMS), Trento, Italy, 9–10 July 2015; IEEE Workshop: Trento, Italy; pp. 157–161. [Google Scholar]
- Ivorra, S.; Brotóns, V.; Foti, D.; Diaferio, M. A preliminary approach of dynamic identification of slender buildings by neuronal networks. Int. J. Non-Linear Mech. 2016, 80, 183–189. [Google Scholar] [CrossRef]
- Chang, C.; Chang, T.; Xu, Y.; Wang, M. Structural damage detection using an iterative neural network. J. Intell. Mater. Syst. Struct. 2000, 11, 32–42. [Google Scholar] [CrossRef]
- Kennedy, J. Particle swarm optimization. In Encyclopedia of Machine Learning; Springer: New York, NY, USA, 2011; pp. 760–766. [Google Scholar]
- Kulkarni, R.V.; Venayagamoorthy, G.K. Particle swarm optimization in wireless-sensor networks: A brief survey. IEEE Trans. Syst. Man Cybern. C (Appl. Rev.) 2011, 41, 262–267. [Google Scholar] [CrossRef]
- Xu, J.; Li, Z.; Diao, Y.-S. Optimal placement of strain sensors for monitoring systems on reticulated shells using particle swarm optimization. Progress Steel Build. Struct. 2013, 1, 017. [Google Scholar]
- Lv, J.; Ren, H.; Gao, K. Artificial neural network-based constitutive relationship of inconel 718 superalloy construction and its application in accuracy improvement of numerical simulation. Appl. Sci. 2017, 7, 124. [Google Scholar] [CrossRef]


| Grade of Steel | Elastic Modulus E (N/m2) | Steel Density (kg/m3) | Poisson’s Ratio |
|---|---|---|---|
| Q235 | 2.07 × 1011 | 7800 | 0.3 |
| Main Rib Elements | First Ring Elements | Second Radial Elements | Second Ring Elements | Third Radial Elements-1 | Third Radial Elements-2 | Third Ring Elements |
|---|---|---|---|---|---|---|
| 35.2 | 532.1 | 659.4 | 538.3 | 577.8 | 688.9 | 520.9 |
| Damaged Degree | 0 | 40% | 50% | 60% | 70% | 80% |
|---|---|---|---|---|---|---|
| Cross-section | Φ13 × 2 | Φ10 × 3 | Φ10 × 2 | Φ9 × 2 | Φ8 × 2 | Φ7 × 2 |
| Condition | Damage Element Number and Damage Degree | Specifications of Replacements | |
|---|---|---|---|
| Undamaged condition | GK1 | No damage | Φ13 × 2 (undamaged) |
| Double component damage training condition | GK2 | No. 8 and 38: 50% damage | Φ10 × 2 |
| GK3 | No. 8 and 67: 50% damage | Φ10 × 2 | |
| GK4 | No. 22 and 38: 50% damage | Φ10 × 2 | |
| GK5 | No. 22 and 67: 50% damage | Φ10 × 2 | |
| GK6 | No. 38 and 67: 50% damage | Φ10 × 2 | |
| Double component damage experiment condition | GK7 | No. 8 and 67: 40% damage | Φ10 × 3 |
| GK8 | No. 22 and 38: 60% damage | Φ9 × 2 | |
| GK9 | No. 22 and 67: 70% damage | Φ8 × 2 | |
| GK10 | No. 38 and 67: 80% damage | Φ7 × 2 | |
| Number of the Nodes | Undamaged Condition | Damaged Condition | |||||
|---|---|---|---|---|---|---|---|
| GK1 | GK7 | GK8 | GK9 | GK10 | |||
| Node 9 | −3.08 | −3.165 | −3.496 | −3.708 | −3.209 | ||
| 5.627 | 5.403 | 6.802 | 7.637 | 5.378 | |||
| −9.294 | −7.658 | −11.09 | −13.14 | −7.433 | |||
| 13.99 | 10.25 | 16.61 | 20.9 | 9.613 | |||
| Node 11 | −3.074 | −3.403 | −3.174 | −3.21 | −3.391 | ||
| 5.509 | 6.362 | 5.772 | 6.006 | 6.323 | |||
| −8.796 | −9.887 | −9.19 | −9.806 | −9.857 | |||
| 13.18 | 14.35 | 13.78 | 15.15 | 14.45 | |||
| Node 13 | −3.191 | −3.627 | −3.168 | −3.456 | −3.038 | ||
| 6.135 | 7.446 | 5.186 | 6.485 | 4.658 | |||
| −10.76 | −12.9 | −7.004 | −10.11 | −6.053 | |||
| 17.28 | 20.78 | 9.16 | 14.99 | 8.029 | |||
| Node 15 | −3.05 | −3.384 | −2.986 | −2.927 | −2.992 | ||
| 5.534 | 6.198 | 4.536 | 4.618 | 4.745 | |||
| −8.938 | −9.564 | −5.832 | −6.559 | −6.477 | |||
| 13.35 | 13.87 | 7.439 | 9.219 | 8.446 | |||
| Node 17 | −3.37 | −3.296 | −3.077 | −2.928 | −3.154 | ||
| 6.882 | 6 | 5.252 | 5.029 | 5.507 | |||
| −11.91 | −9.375 | −7.925 | −7.84 | −8.37 | |||
| 18.52 | 13.65 | 11.41 | 11.29 | 11.99 | |||
| Node 19 | −2.939 | −3.336 | −3.517 | −3.587 | −2.883 | ||
| 5.223 | 6.047 | 7.164 | 7.271 | 4.454 | |||
| −8.489 | −9.355 | −12.67 | −12.58 | −6.095 | |||
| 12.83 | 13.64 | 20.85 | 20.3 | 8.032 | |||
| Element Number | GK7 | GK8 | GK9 | GK10 |
|---|---|---|---|---|
| No. 8 and 38 | 6.51 × 10−15 (0) | 1.93 × 10−7 (0) | 3.54 × 10−8 (0) | 6.67 × 10−10 (0) |
| No. 8 and 67 | 1(1) | 2.25 × 10−8 (0) | 4.04 × 10−8 (0) | 3.54 × 10−8 (0) |
| No. 22 and 38 | 3.4 × 10−9 (0) | 1(1) | 2.96 × 10−4 (0) | 8.55 × 10−4 (0) |
| No. 22 and 67 | 2.45 × 10−6 (0) | 2.64 × 10−7 (0) | 1(1) | 1.1 × 10−7 (0) |
| No. 38 and 67 | 7.21 × 10−8 (0) | 1.59 × 10−7 (0) | 4.77 × 10−8 (0) | 1(1) |
| results | true | true | true | true |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Hao, J.; Li, H.; Luo, M.; Guo, W.; Li, W. Experimental Damage Identification of a Model Reticulated Shell. Appl. Sci. 2017, 7, 362. https://doi.org/10.3390/app7040362
Xu J, Hao J, Li H, Luo M, Guo W, Li W. Experimental Damage Identification of a Model Reticulated Shell. Applied Sciences. 2017; 7(4):362. https://doi.org/10.3390/app7040362
Chicago/Turabian StyleXu, Jing, Jiajia Hao, Hongnan Li, Minzhang Luo, Wen Guo, and Weijie Li. 2017. "Experimental Damage Identification of a Model Reticulated Shell" Applied Sciences 7, no. 4: 362. https://doi.org/10.3390/app7040362
APA StyleXu, J., Hao, J., Li, H., Luo, M., Guo, W., & Li, W. (2017). Experimental Damage Identification of a Model Reticulated Shell. Applied Sciences, 7(4), 362. https://doi.org/10.3390/app7040362







