Investigation on Unsteady Flow Characteristics of a SCO2 Centrifugal Compressor
Abstract
:1. Introduction
2. Design of a Centrifugal Compressor
2.1. 1D Calculations and Analyses
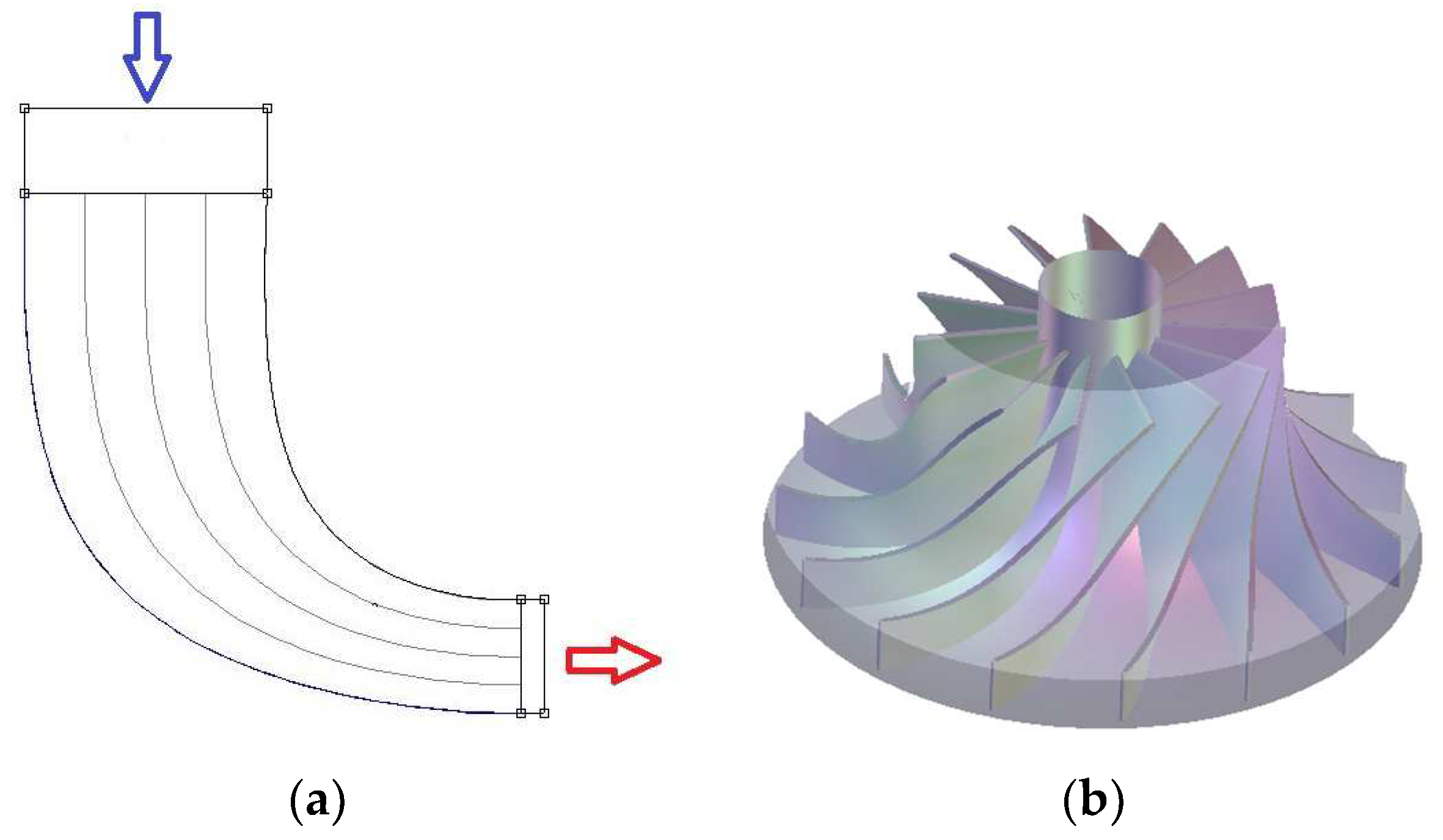
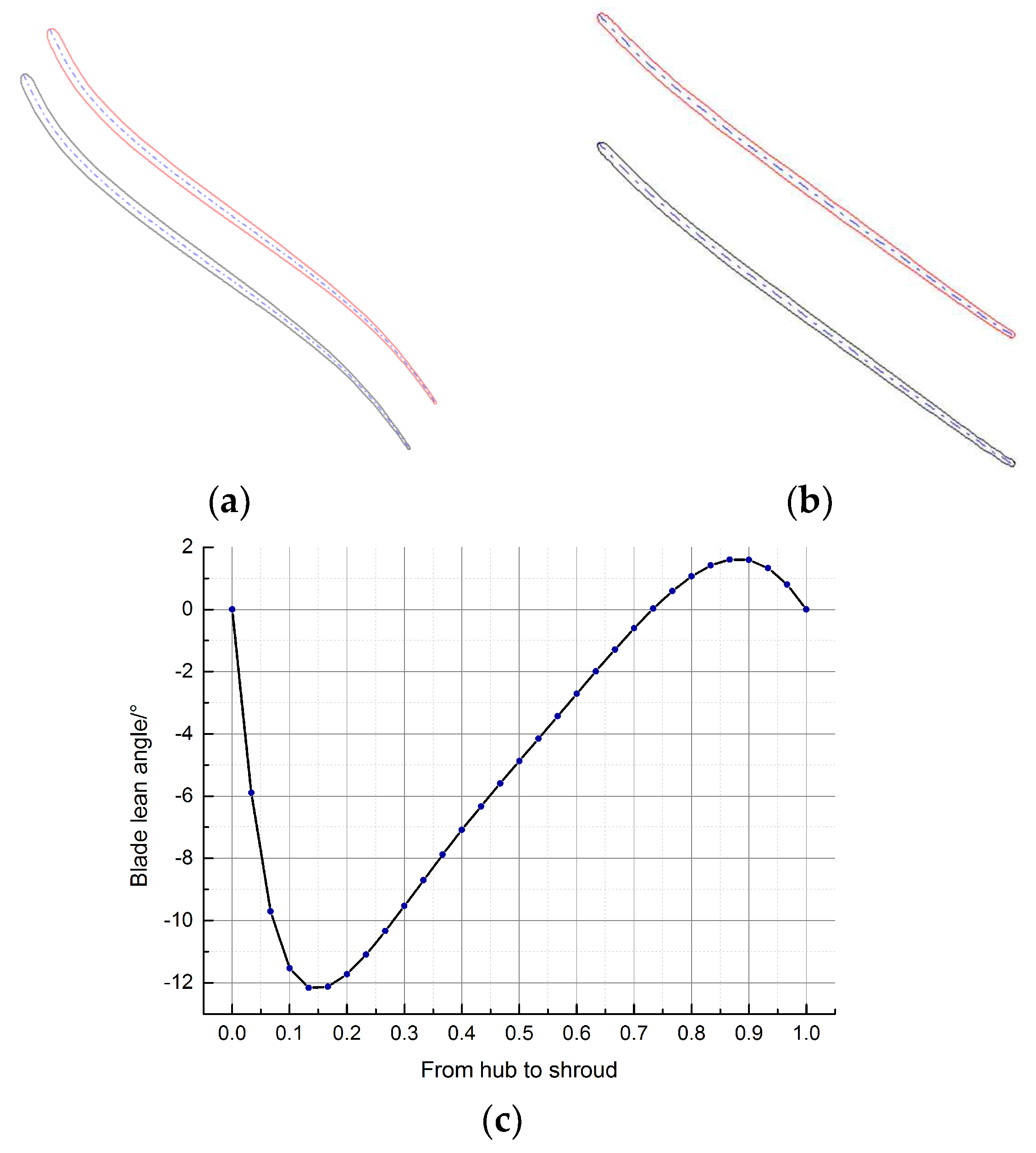
2.2. Geometry of Impeller
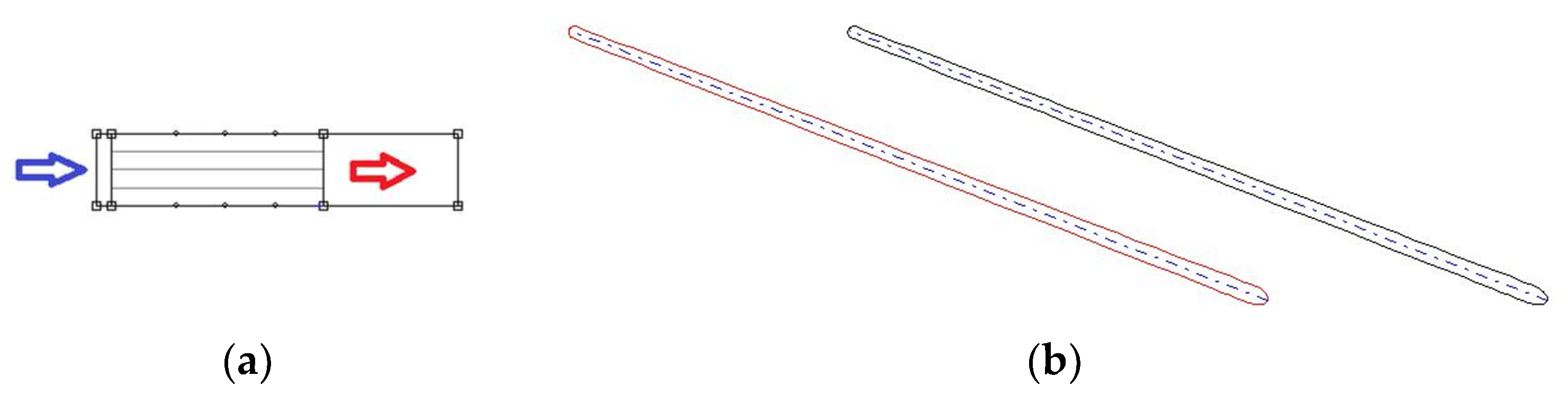
2.3. Geometry of Diffuser
3. Computational Method
3.1. Governing Equations
3.2. Discretization Method and Boundary Conditions
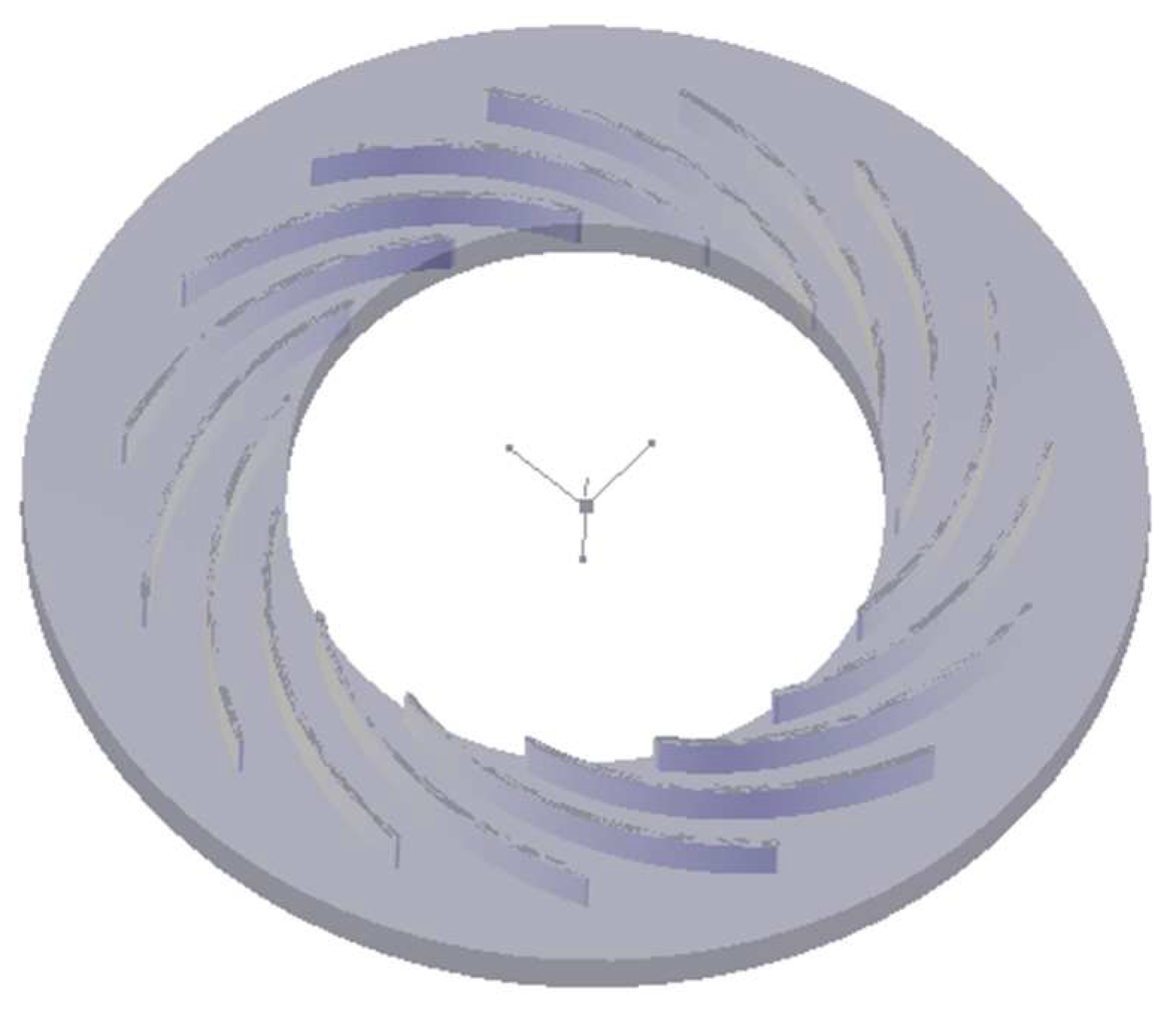
3.3. Generation of Mesh
4. Results and Discussion
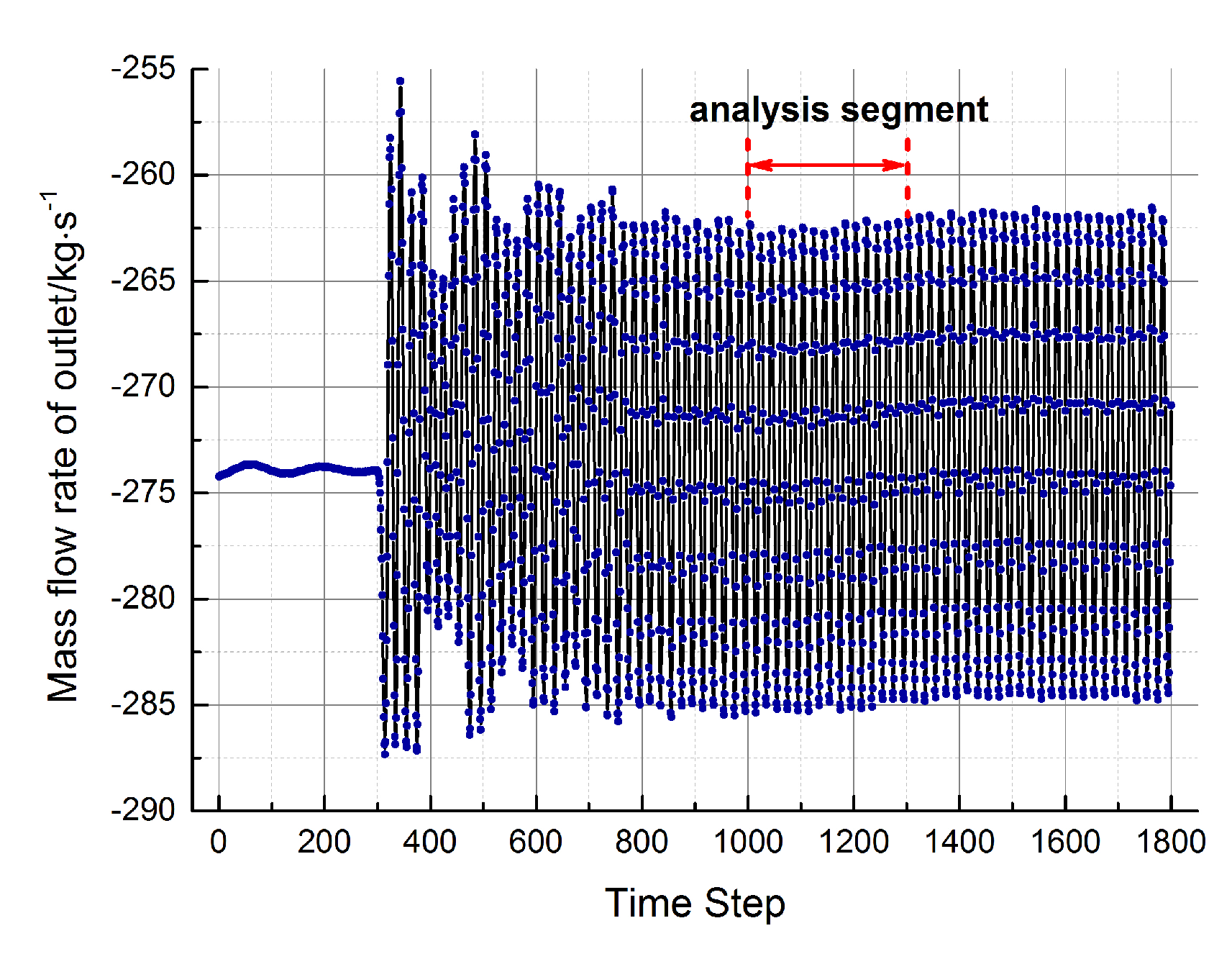
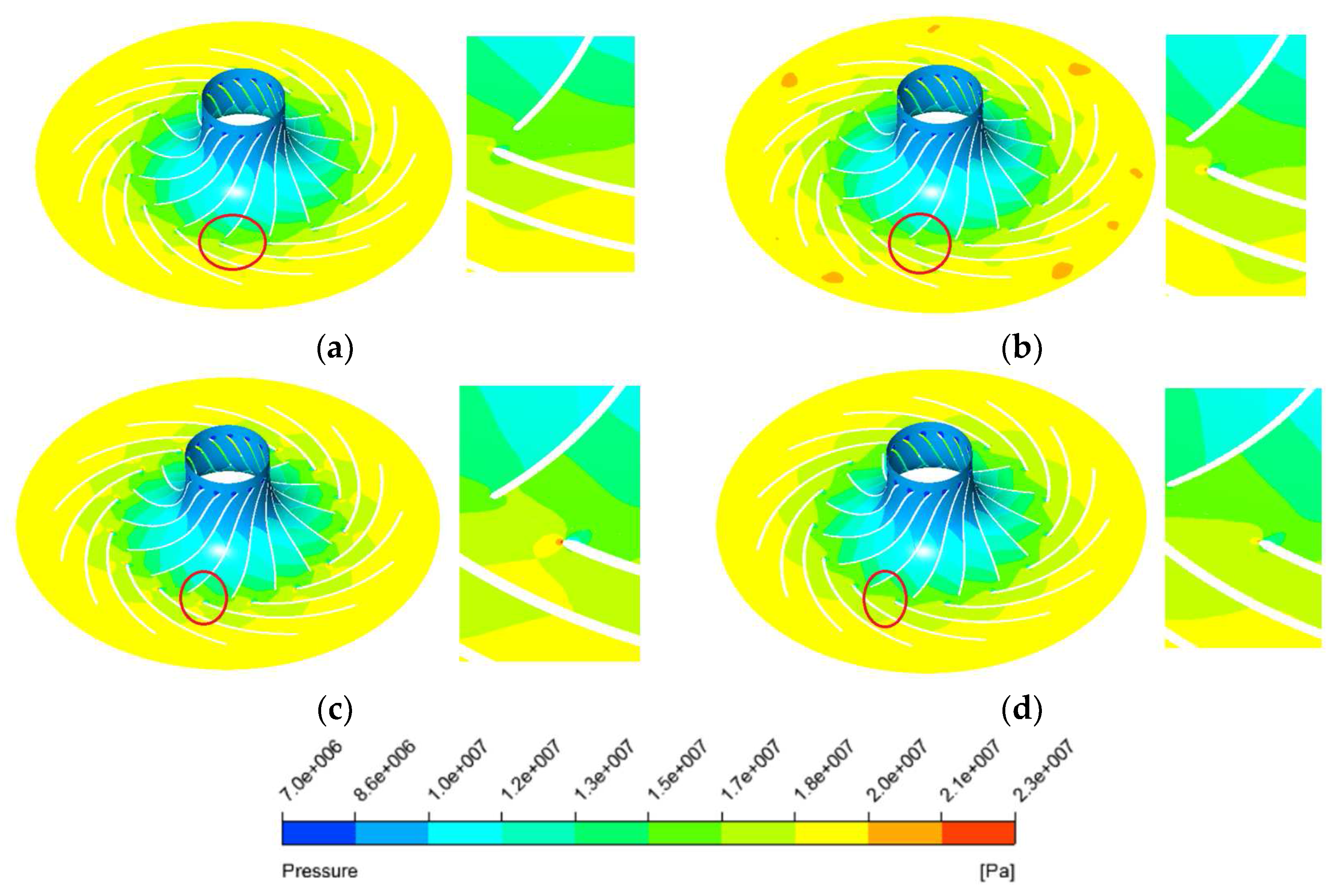
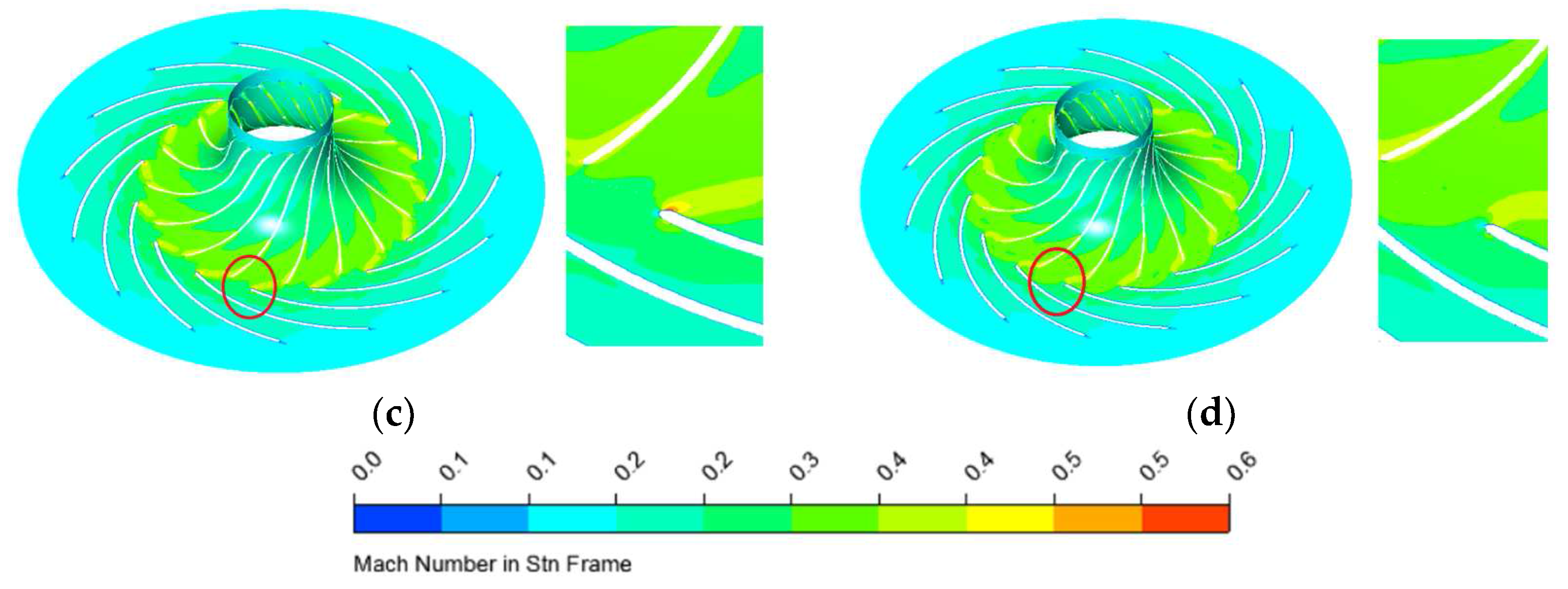
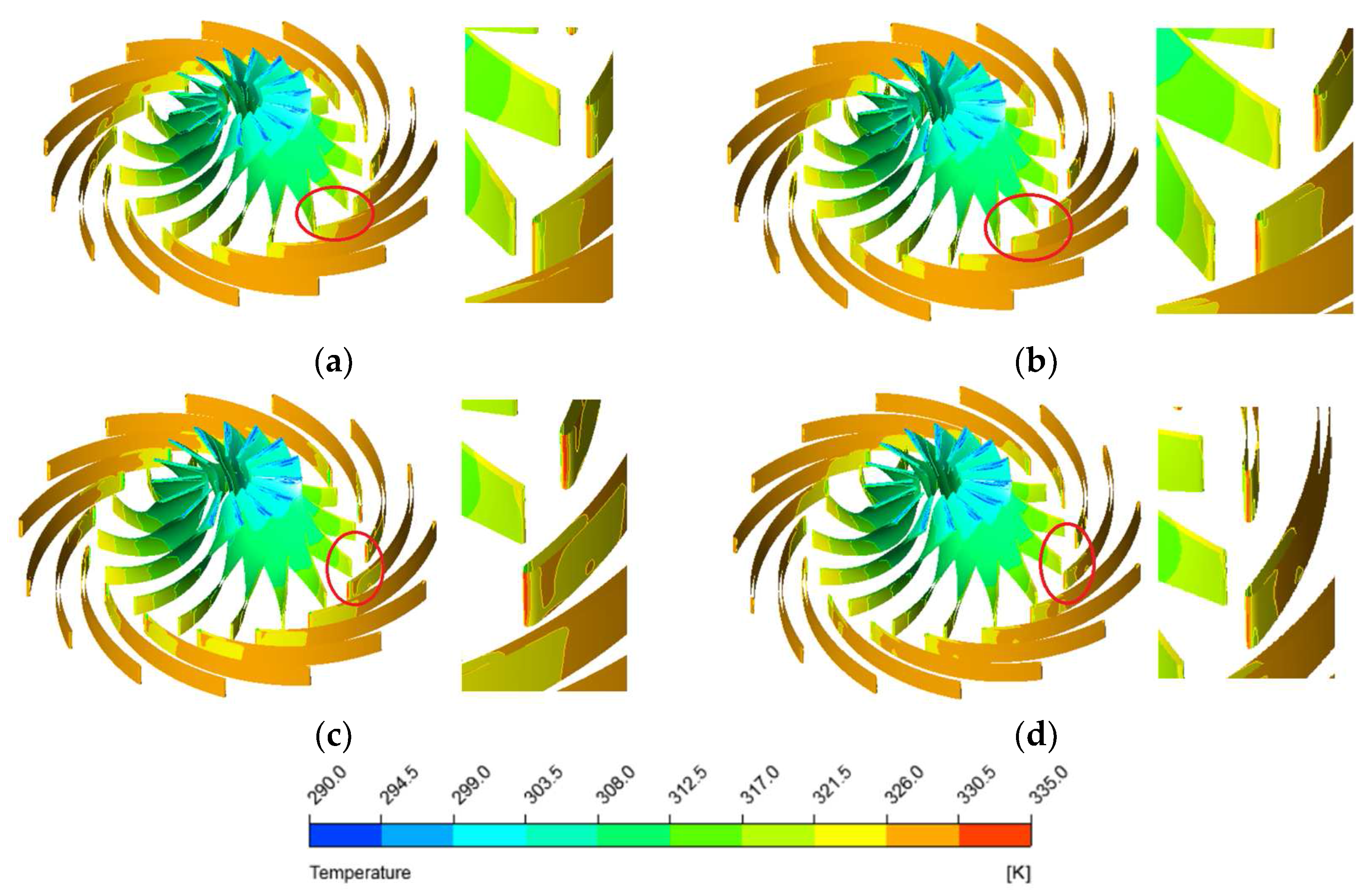
4.1. Unsteady Flow Phenomenon in the Centrifugal Compressor
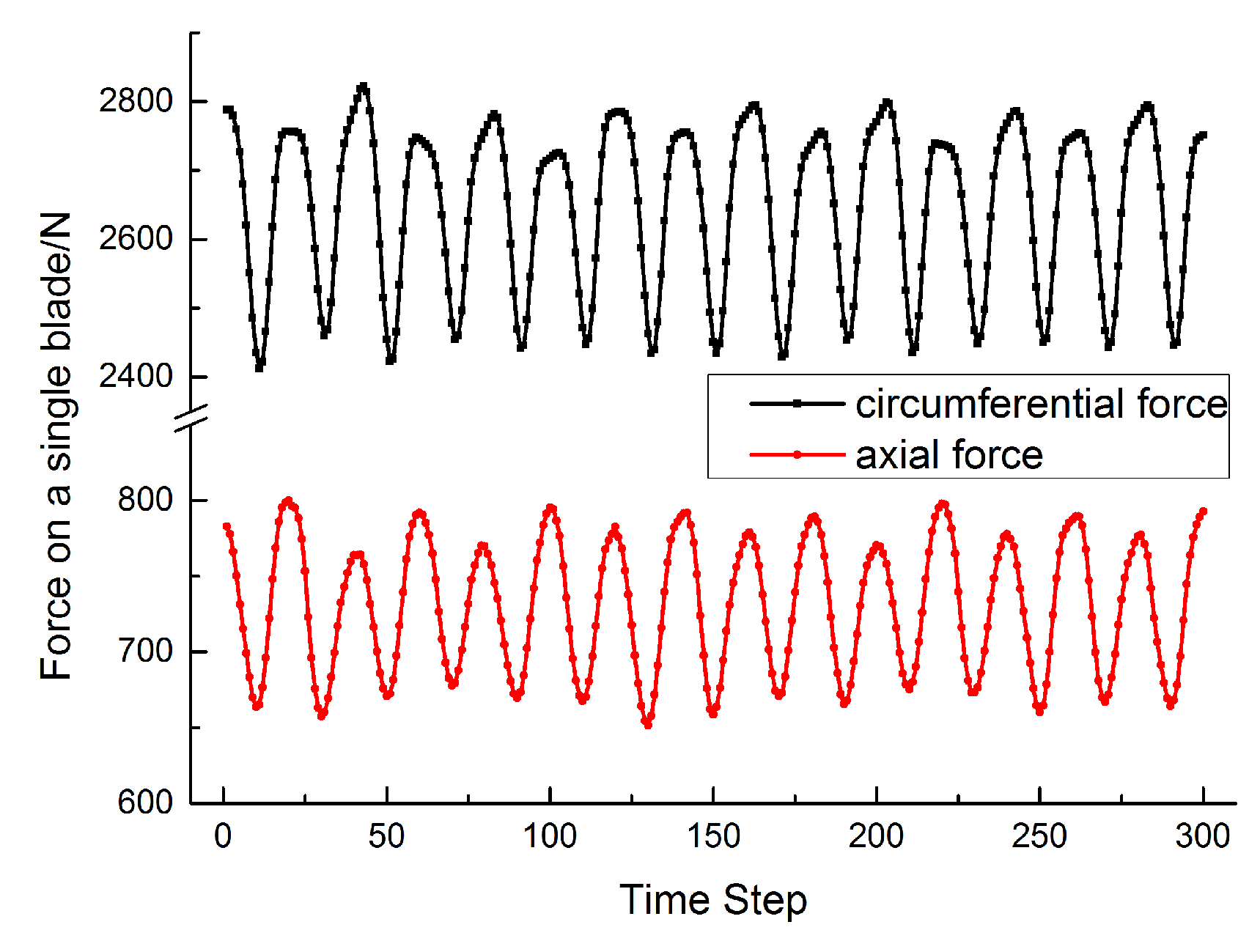
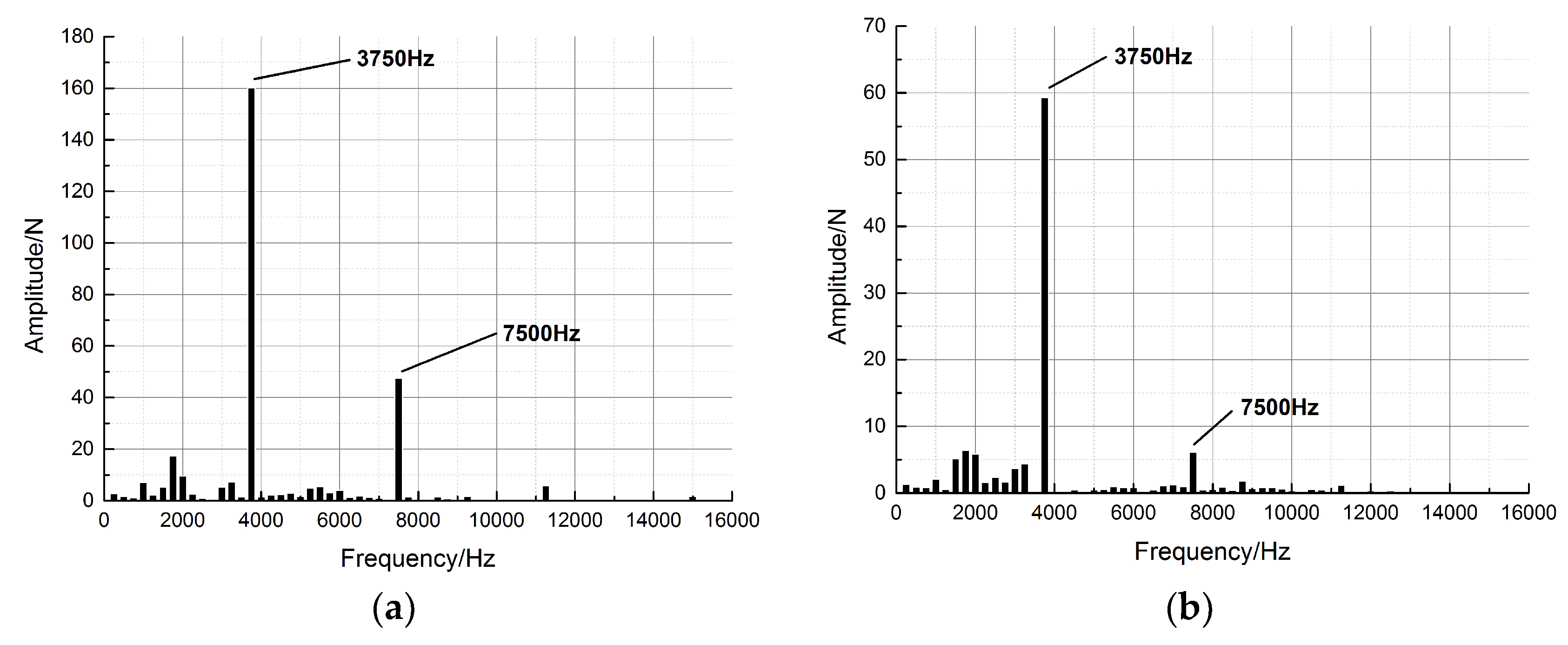
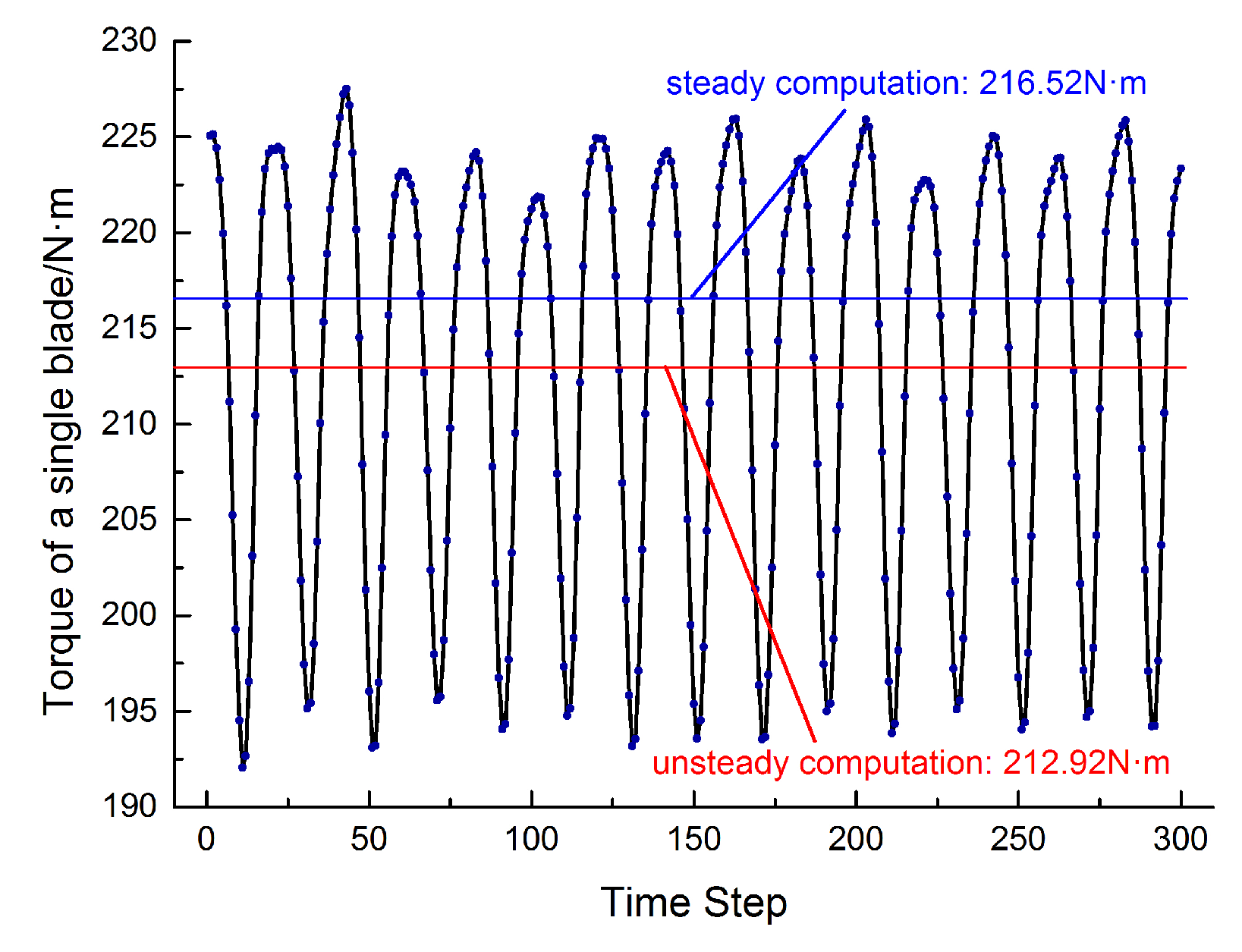
4.2. Unsteady Forces on a Rotor Blade
4.3. Power and Efficiency of the Designed Turbine
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Gil, L.; Otin, S.F.; Embid, J.M.; Gallardo, M.A.; Blanco, S.; Artal, M.; Velasco, I. Experimental setup to measure critical properties of pure and binary mixtures and their densities at different pressures and temperatures determination of the precision and uncertainty in the results. J. Supercrit. Fluids 2008, 44, 123–138. [Google Scholar] [CrossRef]
- Dostal, V.; Hejzlar, P.; Driscoll, M.J. High-performance supercritical carbon dioxide cycle for next-generation nuclear reactors. Nucl. Technol. 2006, 154, 265–282. [Google Scholar] [CrossRef]
- Tanaka, H.; Nishiwaki, N.; Hirata, M.; Tsuge, A. Forced convection heat transfer to fluid near critical point flowing in circular tube. Int. J. Heat Mass Transf. 1971, 14, 739–750. [Google Scholar]
- Mecheri, M.; Le Moullec, Y. Supercritical CO2 brayton cycles for coal-fired power plants. Energy 2016, 103, 758–771. [Google Scholar] [CrossRef]
- Garg, P.; Kumar, P.; Srinivasan, K. Supercritical carbon dioxide brayton cycle for concentrated solar power. J. Supercrit. Fluids 2013, 76, 54–60. [Google Scholar] [CrossRef]
- Ahn, Y.; Bae, S.J.; Kim, M.; Cho, S.K.; Baik, S.; Lee, J.I.; Cha, J.E. Review of supercritical CO2 power cycle technology and current status of research and development. Nucl. Eng. Technol. 2015, 47, 647–661. [Google Scholar] [CrossRef]
- Chen, M.-F.; Yamaguchi, H.; Zhang, X.-W.; Niu, X.-D. Performance analyses of a particularly designed turbine for a supercritical CO2-based solar rankine cycle system. Int. J. Energy Res. 2015, 39, 1819–1827. [Google Scholar] [CrossRef]
- Osorio, J.D.; Hovsapian, R.; Ordonez, J.C. Dynamic analysis of concentrated solar supercritical CO2-based power generation closed-loop cycle. Appl. Therm. Eng. 2016, 93, 920–934. [Google Scholar] [CrossRef]
- Chacartegui, R.; de Escalona, J.M.M.; Sanchez, D.; Monje, B.; Sanchez, T. Alternative cycles based on carbon dioxide for central receiver solar power plants. Appl. Therm. Eng. 2011, 31, 872–879. [Google Scholar] [CrossRef]
- Monje, B.; Sanchez, D.; Savill, M.; Pilidis, P.; Sanchez, T. A Design Strategy for Supercritical CO2 Compressors; American Society of Mechanical Engineers: New York, NY, USA, 2014. [Google Scholar]
- Lopez, A.; Monje, B.; Sanchez, D.; Chacartegul, R.; Sanchez, T. Effect of Turbulence and Flow Distortion on the Performance of Conical Diffusers Operating on Supercritical Carbon Dioxide; American Society of Mechanical Engineers: New York, NY, USA, 2013. [Google Scholar]
- Valdes, M.; Abbas, R.; Rovira, A.; Martin-Aragon, J. Thermal efficiency of direct, inverse and sco(2) gas turbine cycles intended for small power plants. Energy 2016, 100, 66–72. [Google Scholar] [CrossRef]
- Zhang, H.Z.; Zhao, H.; Deng, Q.H.; Feng, Z.P. Aerothermodynamic Design and Numerical Investigation of Supercritical Carbon Dioxide Turbine; American Society of Mechanical Engineers: New York, NY, USA, 2015. [Google Scholar]
- Monje, B.; Sanchez, D.; Chacartegui, R.; Sanchez, T.; Savill, M.; Pilidis, P. Aerodynamic analysis of conical diffusers operating with air and supercritical carbon dioxide. Int. J. Heat Fluid Flow 2013, 44, 542–553. [Google Scholar] [CrossRef]
- Budinis, S.; Thornhill, N.F. Supercritical fluid recycle for surge control of CO2 centrifugal compressors. Comput. Chem. Eng. 2016, 91, 329–342. [Google Scholar] [CrossRef]
- Utamura, M.; Fukuda, T.; Aritomi, M. Aerodynamic characteristics of a centrifugal compressor working in supercritical carbon dioxide. Energy Procedia 2012, 14, 1149–1155. [Google Scholar] [CrossRef]
- Rinaldi, E.; Pecnik, R.; Colonna, P. Steady State Cfd Investigation of a Radial Compressor Operating with Supercritical CO2; American Society of Mechanical Engineers: New York, NY, USA, 2013. [Google Scholar]
- Rinaldi, E.; Pecnik, R.; Colonna, P. Computational fluid dynamic simulation of a supercritical CO2 compressor performance map. J. Eng. Gas Turbines Power Trans. ASME 2015, 137. [Google Scholar] [CrossRef]
- Ghidoni, A.; Colombo, A.; Rebay, S.; Bassi, F. Simulation of the transitional flow in a low pressure gas turbine cascade with a high-order discontinuous galerkin method. J. Fluids Eng. Trans. ASME 2013, 135. [Google Scholar] [CrossRef]
- Schobeiri, M.T.; Abdelfattah, S.; Chibli, H. Investigating the cause of computational fluid dynamics deficiencies in accurately predicting the efficiency and performance of high pressure turbines: A combined experimental and numerical study. J. Fluids Eng. Trans. ASME 2012, 134. [Google Scholar] [CrossRef]
- Stel, H.; Amaral, G.D.L.; Negrao, C.O.R.; Chiva, S.; Estevam, V.; Morales, R.E.M. Numerical analysis of the fluid flow in the first stage of a two-stage centrifugal pump with a vaned diffuser. J. Fluids Eng. Trans. ASME 2013, 135. [Google Scholar] [CrossRef]
- Fu, Y.X.; Yuan, J.P.; Yuan, S.Q.; Pace, G.; d’Agostino, L.; Huang, P.; Li, X.J. Numerical and experimental analysis of flow phenomena in a centrifugal pump operating under low flow rates. J. Fluids Eng. Trans. ASME 2015, 137. [Google Scholar] [CrossRef]
- Zhao, H.; Deng, Q.; Huang, W.; Zheng, K.; Feng, Z. Numerical investigation on the blade tip two-phase flow characteristics of a supercritical CO2 centrifugal compressor. J. Eng. Thermophys. 2015, 36, 1433–1436. [Google Scholar]
- Behafarid, F.; Podowski, M.Z. Modeling and computer simulation of centrifugal CO2 compressors at supercritical pressures. J. Fluids Eng. Trans. ASME 2016, 138. [Google Scholar] [CrossRef]
- Kim, S.G.; Lee, J.; Ahn, Y.; Lee, J.I.; Addad, Y.; Ko, B. Cfd investigation of a centrifugal compressor derived from pump technology for supercritical carbon dioxide as a working fluid. J. Supercrit. Fluids 2014, 86, 160–171. [Google Scholar] [CrossRef]
- Kimball, K.J.; Clementoni, E.M. Supercritical Carbon Dioxide Brayton Power Cycle Development Overview; American Society of Mechanical Engineers: New York, NY, USA, 2012; pp. 931–940. [Google Scholar]
- Ahn, Y.; Lee, J.; Kim, S.G.; Lee, J.I.; Cha, J.E.; Lee, S.W. Design consideration of supercritical CO2 power cycle integral experiment loop. Energy 2015, 86, 115–127. [Google Scholar] [CrossRef]
- Li, P.Y.; Gu, C.W.; Song, Y. A new optimization method for centrifugal compressors based on 1d calculations and analyses. Energies 2015, 8, 4317–4334. [Google Scholar] [CrossRef]
- Wang, F. Anlysis of Computational Fluid Dynamics; Tsinghua University Press: Beijing, China, 2004; pp. 124–125. [Google Scholar]
- Hu, S.; Su, M. Comparison of different turbulence models for numerical simulation of internal flow of centrifugal compressor. Fluid Mach. 2010, 38, 22–26. [Google Scholar]
- Smith, L.M.; Woodruff, S.L. Renormalization-group analysis of turbulence. Annu. Rev. Fluid Mech. 1998, 30, 275–310. [Google Scholar] [CrossRef]
- Jameson, A. Time dependent calculations using multigrid, with applications to unsteady flows past airfoils and wings. In Proceedings of the Computational Fluid Dynamics Conference, Honolulu, HI, USA, 24–26 June 1991. [Google Scholar]
- Redlich, O.; Kwong, J.N.S. On the thermodynamics of solutions. 5. An equation of state—Fugacities of gaseous solutions. Chem. Rev. 1949, 44, 233–244. [Google Scholar] [CrossRef] [PubMed]
- Nasri, Z.; Binous, H. Applications of the soave-redlich-kwong equation of state using mathematica (r). J. Chem. Eng. Jpn. 2007, 40, 534–538. [Google Scholar] [CrossRef]
- Peneloux, A.; Rauzy, E.; Freze, R. A consistent correction for redlich-kwong-soave volumes. Fluid Phase Equilib. 1982, 8, 7–23. [Google Scholar] [CrossRef]
- Valderrama, J.O.; Silva, A. Modified soave-redlich-kwong equations of state applied to mixtures containing supercritical carbon dioxide. Korean J. Chem. Eng. 2003, 20, 709–715. [Google Scholar] [CrossRef]
- Munkejord, S.T.; Jakobsen, J.P.; Austegard, A.; Molnvik, M.J. Thermo- and fluid-dynamical modeling of two-phase multi-component carbon dioxide mixtures. In Greenhouse Gas Control Technologies 9; Gale, J., Herzog, H., Braitsch, J., Eds.; Elsevier Science Bv: Amsterdam, The Netherlands, 2009; Volume 1, pp. 1649–1656. [Google Scholar]
- Liu, Y.W.; Liu, B.J.; Lu, L.P. Study of modeling unsteady blade row interaction in a transonic compressor stage part 1: Code development and deterministic correlation analysis. Acta Mech. Sin. 2012, 28, 281–290. [Google Scholar] [CrossRef]
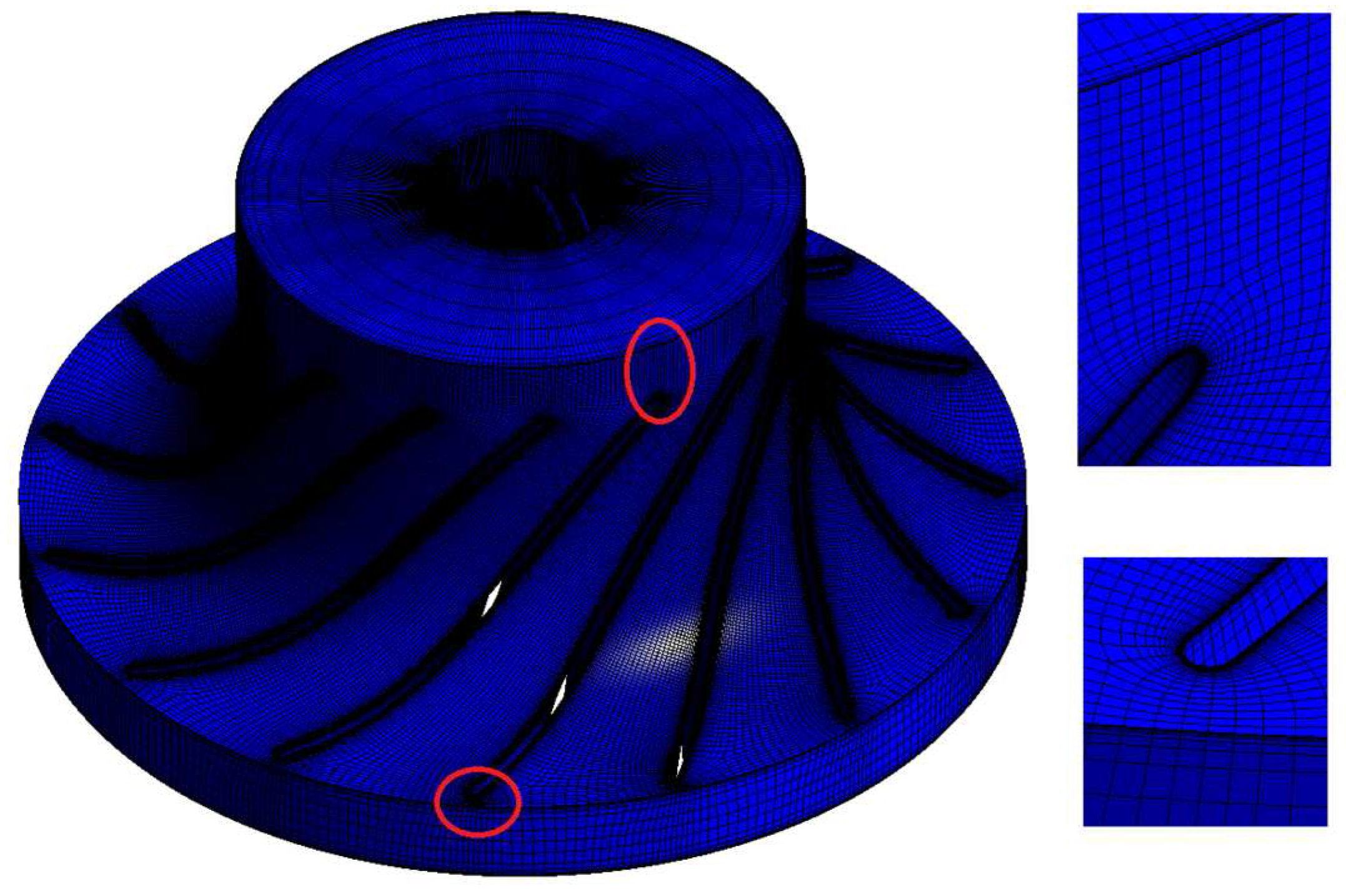
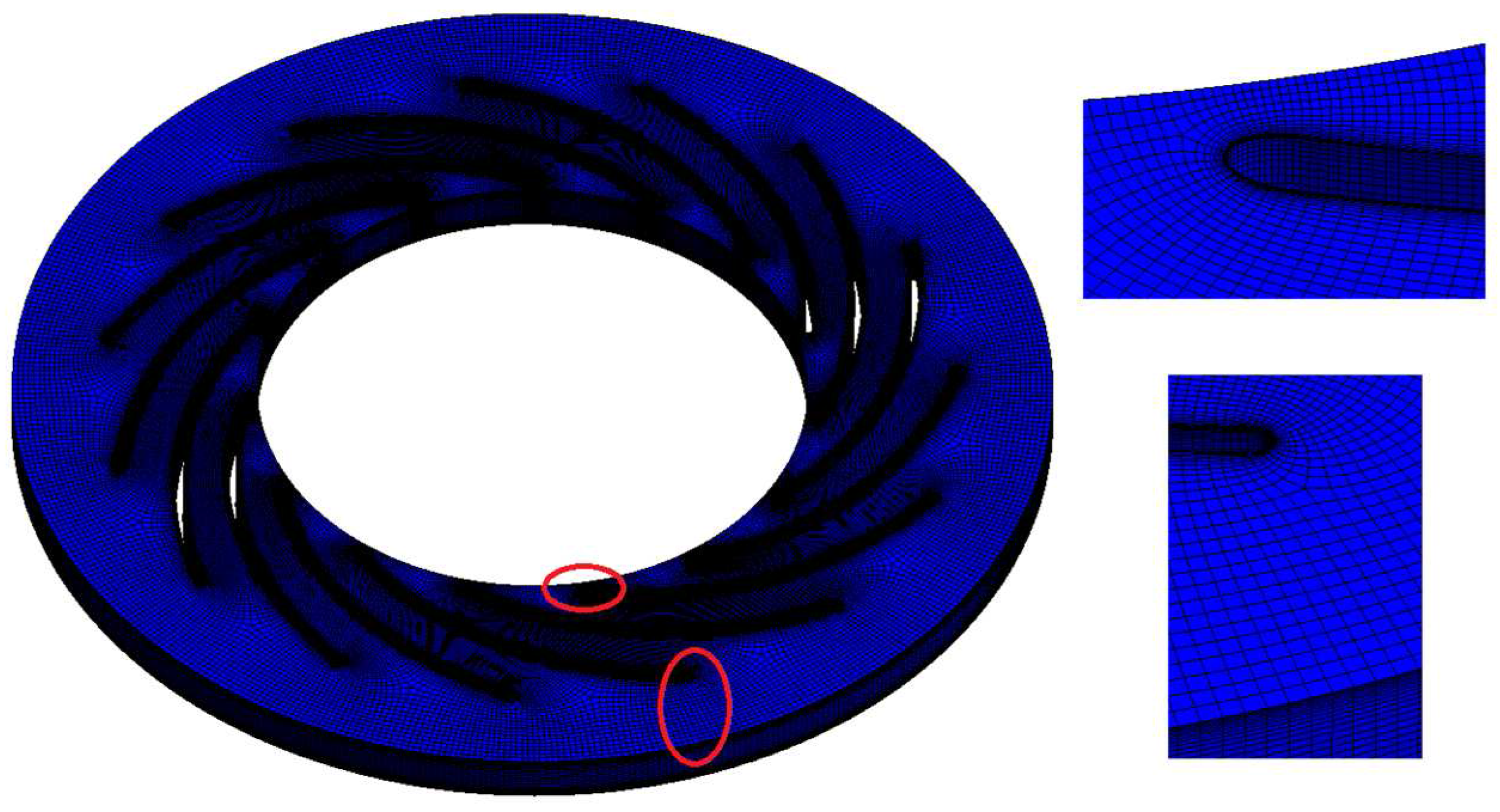

| Type | Parameter | Value |
|---|---|---|
| performance estimates | input power (MW) | 5 |
| mass flow rate (kg∙s−1) | 273.1 | |
| rotational speed (rpm) | 15,000 | |
| isentropic efficiency (%) | 76.3 | |
| state parameters | temperature of inlet (K) | 306.7 |
| pressure of inlet (MPa) | 8.8 | |
| temperature of outlet (K) | 327.5 | |
| pressure of outlet (MPa) | 18.9 |
| Location | Parameter | Value |
|---|---|---|
| meridian plane | inner diameter of inlet (mm) | 40 |
| external diameter of inlet (mm) | 120 | |
| diameter of outlet (mm) | 204 | |
| axial length (mm) | 86 | |
| blades | blade number | 15 |
| blade height at outlet (mm) | 19 | |
| cord length at hub (mm) | 145.5 | |
| cord length at shroud (mm) | 116.9 | |
| thickness (mm) | 2 |
| Location | Parameter | Value |
|---|---|---|
| meridian plane | diameter at inlet (mm) | 220 |
| diameter at outlet (mm) | 330 | |
| diameter of channel outlet (mm) | 400 | |
| blades | blade number | 15 |
| blade height (mm) | 18.8 | |
| cord length (mm) | 152.3 | |
| thickness (mm) | 3 |
| Sequence Number | Element Number (104) | Single Blade Torque (N∙m) | Relative Error (%) |
|---|---|---|---|
| 1 | 150.1 | 227.9 | / |
| 2 | 301.5 | 223.6 | 1.92 |
| 3 | 450.7 | 216.2 | 3.42 |
| 4 | 599.6 | 216.5 | 0.14 |
| 5 | 748.8 | 216.3 | 0.09 |
| Parameter | Design | Steady CFD Result | Unsteady CFD Result |
|---|---|---|---|
| pressure of inlet (MPa) | 8.80 | 8.72 | 8.74 |
| pressure ratio | 2.15 | 2.17 | 2.16 |
| input power (MW) | 5.00 | 5.10 | 5.06 |
| isentropic efficiency (%) | 76.30 | 75.70 | 75.54 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Shi, D.; Zhang, D.; Xie, Y. Investigation on Unsteady Flow Characteristics of a SCO2 Centrifugal Compressor. Appl. Sci. 2017, 7, 310. https://doi.org/10.3390/app7040310
Wang Y, Shi D, Zhang D, Xie Y. Investigation on Unsteady Flow Characteristics of a SCO2 Centrifugal Compressor. Applied Sciences. 2017; 7(4):310. https://doi.org/10.3390/app7040310
Chicago/Turabian StyleWang, Yuqi, Dongbo Shi, Di Zhang, and Yonghui Xie. 2017. "Investigation on Unsteady Flow Characteristics of a SCO2 Centrifugal Compressor" Applied Sciences 7, no. 4: 310. https://doi.org/10.3390/app7040310
APA StyleWang, Y., Shi, D., Zhang, D., & Xie, Y. (2017). Investigation on Unsteady Flow Characteristics of a SCO2 Centrifugal Compressor. Applied Sciences, 7(4), 310. https://doi.org/10.3390/app7040310





