Full-Field Optical Coherence Tomography as a Diagnosis Tool: Recent Progress with Multimodal Imaging
Abstract
:1. Introduction
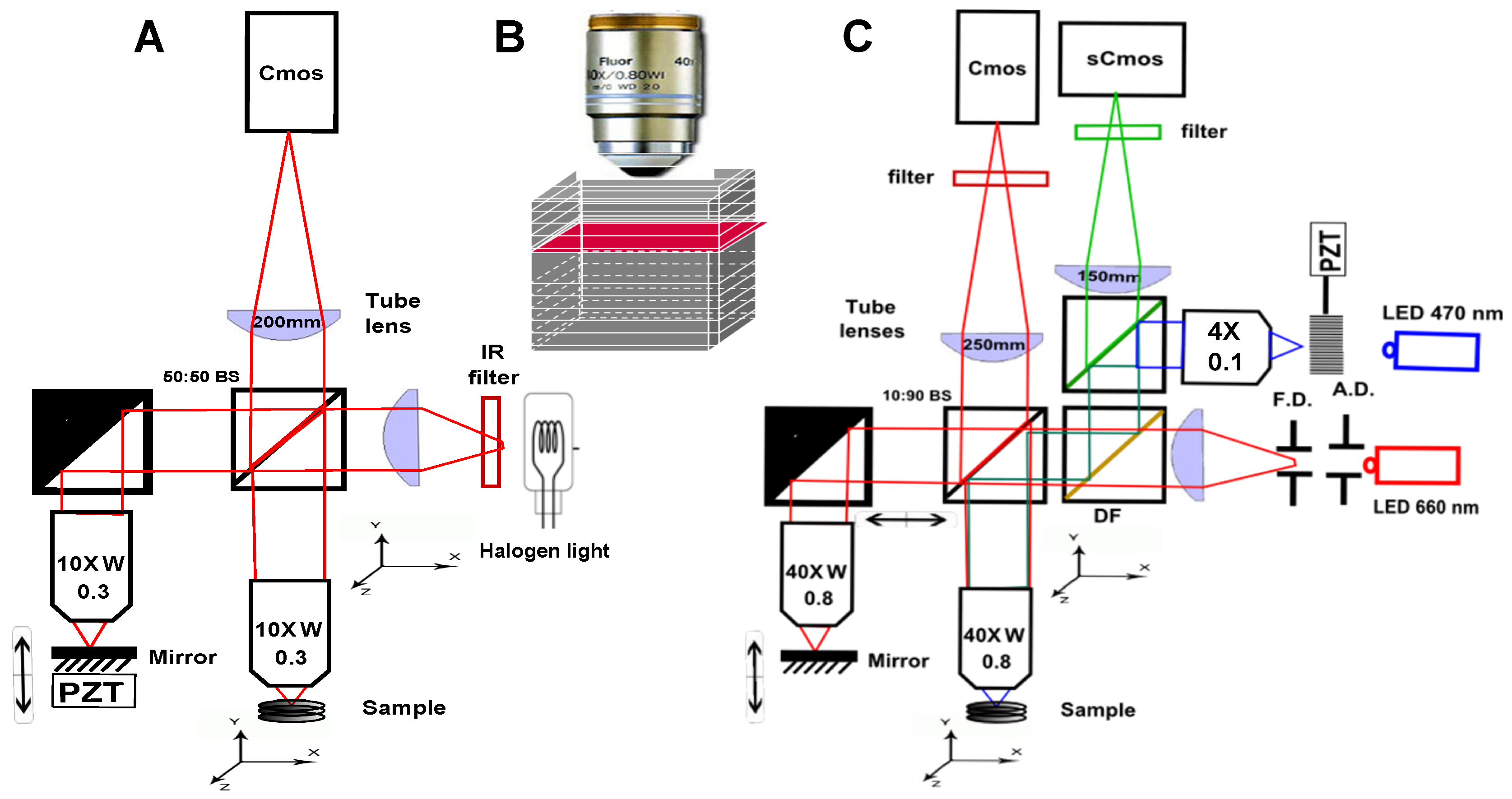
2. Scanning OCT versus Full-Field OCT and Technological Description of the Setups Description
- Because it looks at a single depth at a time, FF-OCT can be performed with a small depth of field, and therefore with high numerical aperture (NA) objectives. This enables high transverse resolution to be obtained, below 1 m for visible light. Other elegant OCT systems have greatly increased their transverse resolution [1,29,30,31,32], however these techniques remain more complex and often have to sacrifice their temporal resolution.
- Moreover, scanning in two directions imposes a trade-off between exposure time and the field of view. In scanning OCT, each pixel is only illuminated for a few microseconds, while in FF-OCT, the entire field of view is usually evenly illuminated during a few milliseconds. It can make a difference in the light dose delivered to the sample, and the most rapid speckle fluctuations are often averaged out [33].
- The time required to get information from the sample is much longer in FF-OCT, since it is limited by the camera frame rate, which is hardly below 1 ms, while some scanning OCT systems can now acquire lines at more than 100,000 lines per second [34]. The consequence is that FF-OCT is much more sensitive to sample motion, and is difficult to perform in vivo, other than on anesthetized animal or by pressing the sample against an imaging window [35].
- A last important difference when looking at en face images either performed in scanning OCT or FF-OCT is that all the pixels have been acquired at different times in OCT, while they are acquired at the same time in FF-OCT (if the camera is operated in global shutter mode), which can introduce some artifacts when looking at moving objects. On the other hand, all axial pixels are acquired simultaneously in OCT, while they are largely separated in time for FF-OCT. An important consequence is that the optical phase can be directly retrieved in OCT by subtracting two adjacent axial pixels [36] while FF-OCT requires multiple phase-shifted measurements to retrieve the optical phase.
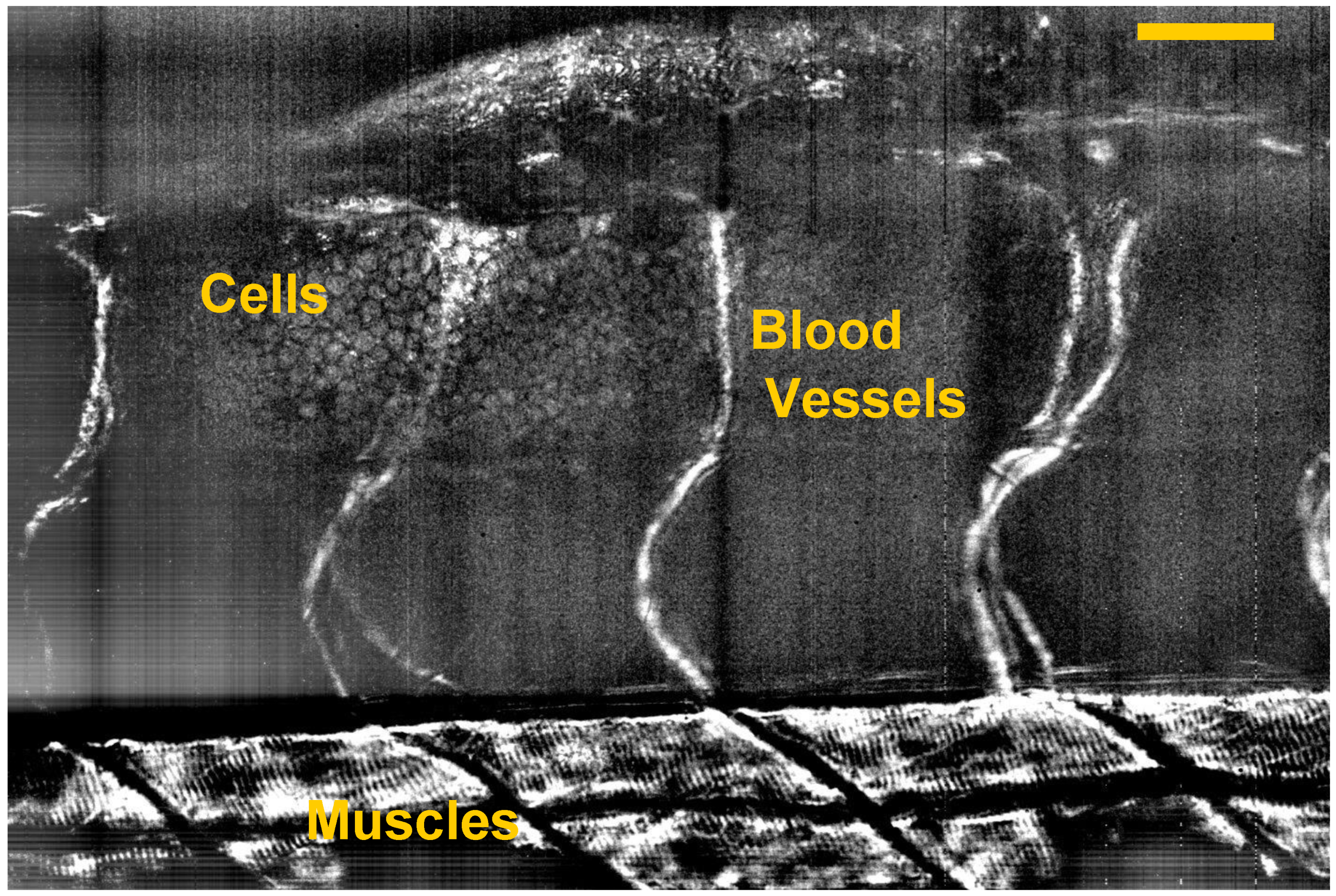
3. FF-OCT and Histology Contrasts
4. FF-OCT and Biomechanics
4.1. Description of the Different Mechanical Parameters and Approximations
4.2. Static Elastography Based on Digital Volume Correlation (DVC)
- Strain magnitudeIn order to quantify the strain magnitude, we chose to use an equivalent Von Mises strain defined as:This parameter is independent of the base in which the strain tensor is expressed and allows quantification of the strain amplitude in the case of incompressible media such as biological samples. To illustrate this, we present strain amplitude maps calculated for a human breast tissue in Figure 3A,B, which highlight mechanical differences.
- Strain anisotropyThe full 3D strain tensor also allows calculation of eigenvalues and eigenvectors of the strain tensor that gives access to information on the mechanical anisotropy of the sample. One should keep in mind that, since the compression of the sample is generally performed along the optical axis, the local stress field is inherently anisotropic. In order to display and to quantify strain anisotropy, we mainly use two parameters. The first parameter is the principal strain direction. For each pixel, the eigenvector corresponding to the largest eigenvalue of the strain tensor is calculated. This vector gives the principal strain direction. For example, Figure 3C is a cross-sectional slice from the volumetric FF-OCT image of a rat heart. In the FF-OCT image, it is difficult to evaluate the fiber direction, and the two different fiber orientations are not visible. However, if the projection angle of the principal strain direction vector on the plane perpendicular to the compression (see Figure 3D) is plotted, it is clear that there are two different fiber orientations.Another parameter used to quantify the strain anisotropy is the fractional anisotropy . In a similar manner to classical diffusion tensor imaging (DTI) in MRI [93,94] or ultrasound [95], we define the fractional anisotropy as:where , and are the strain tensor eigenvalues and is the mean of the absolute value of the strain tensor eigenvalues.Using this parameter, it is possible to differentiate isotropic from anisotropic strain. In Figure 3E,G, we show that computing the fractional anisotropy in isotropic and anisotropic polyvinyl alcohol (PVA) polymer gels [96] enables discrimination of the two samples, in a case where FF-OCT fails to detect a difference.
4.3. Transient Elastography Based on Shear Wave Imaging
5. Dynamic FF-OCT
6. Full-Field OCT and Fluorescence
7. Comparison with Other Popular Novel Microscopies
8. Conclusions and Perspectives
Acknowledgments
Conflicts of Interest
References
- Drexler, W.; Fujimoto, J.G. Optical Coherence Tomography: Technology and Applications, 2nd ed.; Springer: Gewerbestrasse, Switzerland, 2015. [Google Scholar]
- Zaitsev, V.Y.; Vitkin, I.A.; Matveev, L.A.; Gelikonov, V.M.; Matveyev, A.L.; Gelikonov, G.V. Recent Trends in Multimodal Optical Coherence Tomography. II. The Correlation-Stability Approach in OCT Elastography and Methods for Visualization of Microcirculation. Radiophys. Quant. Electron. 2014, 57, 210–225. [Google Scholar] [CrossRef]
- Zaitsev, V.Y.; Gelikonov, V.M.; Matveev, L.A.; Gelikonov, G.V.; Matveyev, A.L.; Shilyagin, P.A.; Vitkin, I.A. Recent trends in multimodal optical coherence tomography. I. Polarization-sensitive oct and conventional approaches to OCT elastography. Radiophys. Quant. Electron. 2014, 57, 52–66. [Google Scholar] [CrossRef]
- Oldenburg, A.L.; Chhetri, R.K.; Cooper, J.M.; Wu, W.C.; Troester, M.A.; Tracy, J.B. Motility-, autocorrelation-, and polarization-sensitive optical coherence tomography discriminates cells and gold nanorods within 3D tissue cultures. Opt. Lett. 2013, 38, 2923–2926. [Google Scholar] [CrossRef] [PubMed]
- Beaurepaire, E.; Moreaux, L.; Amblard, F.; Mertz, J. Combined scanning optical coherence and two-photon-excited fluorescence microscopy. Opt. Lett. 1999, 24, 969–971. [Google Scholar] [CrossRef] [PubMed]
- Beaurepaire, E.; Boccara, A.C.; Lebec, M.; Blanchot, L.; Saint-Jalmes, H. Full-field optical coherence microscopy. Opt. Lett. 1998, 23, 244–246. [Google Scholar] [CrossRef] [PubMed]
- Dubois, A.; Vabre, L.; Boccara, A.C.; Beaurepaire, E. High-resolution full-field optical coherence tomography with a Linnik microscope. Appl. Opt. 2002, 41, 805–812. [Google Scholar] [CrossRef] [PubMed]
- Jain, M.; Shukla, N.; Manzoor, M.; Nadolny, S.; Mukherjee, S. Modified full-field optical coherence tomography: A novel tool for rapid histology of tissues. J. Pathol. Inf. 2011, 2, 28. [Google Scholar]
- Grieve, K.; Mouslim, K.; Assayag, O.; Dalimier, E.; Harms, F.; Bruhat, A.; Boccara, C.; Antoine, M. Assessment of Sentinel Node Biopsies With Full-Field Optical Coherence Tomography. Technol. Cancer Res. Treat. 2016, 15, 266–274. [Google Scholar] [CrossRef] [PubMed]
- De Leeuw, F.; Casiraghi, O.; Lakhdar, A.B.; Abbaci, M.; Laplace-Builhé, C. Full-field OCT for fast diagnostic of head and neck cancer. In Proceedings of the SPIE BiOS, San Francisco, CA, USA, 7–12 February 2015; p. 93031Z.
- Yang, C.; Ricco, R.; Sisk, A.; Duc, A.; Sibony, M.; Beuvon, F.; Dalimier, E.; Delongchamps, N.B. High efficiency for prostate biopsy qualification with full-field OCT after training. In Proceedings of the SPIE BiOS, San Francisco, CA, USA, 13–18 February 2016; p. 96891J.
- Grieve, K.; Georgeon, C.; Andreiuolo, F.; Borderie, M.; Ghoubay, D.; Rault, J.; Borderie, V.M. Imaging Microscopic Features of Keratoconic Corneal Morphology. Cornea 2016, 35, 1621. [Google Scholar] [CrossRef] [PubMed]
- Assayag, O.; Grieve, K.; Devaux, B.; Harms, F.; Pallud, J.; Chretien, F.; Boccara, C.; Varlet, P. Imaging of non-tumorous and tumorous human brain tissues with full-field optical coherence tomography. NeuroImage Clin. 2013, 2, 549–557. [Google Scholar] [CrossRef] [PubMed]
- Assayag, O.; Antoine, M.; Sigal-Zafrani, B.; Riben, M.; Harms, F.; Burcheri, A.; Grieve, K.; Dalimier, E.; de Poly, B.L.C.; Boccara, C. Large field, high resolution full-field optical coherence tomography: A pre-clinical study of human breast tissue and cancer assessment. Technol. Cancer Res. Treat. 2014, 13, 455–468. [Google Scholar] [CrossRef] [PubMed]
- Peters, I.T.A.; Stegehuis, P.L.; Peek, R.; Boer, F.L.; Zwet, E.W.V.; Eggermont, J.; Westphal, J.R.; Kuppen, P.J.K.; Trimbos, J.B.M.Z.; Hilders, C.G.J.M.; et al. Non-invasive detection of metastases and follicle density in ovarian tissue using full-field optical coherence tomography. Clin. Cancer Res. 2016. [Google Scholar] [CrossRef] [PubMed]
- Handbook of Full-Field Optical Coherence Microscopy: Technology and Applications; Pan Stanford Publishing Pte. Ltd.: Singapore, 2016.
- Jain, M.; Robinson, B.D.; Salamoon, B.; Thouvenin, O.; Boccara, C.; Mukherjee, S. Rapid evaluation of fresh ex vivo kidney tissue with full-field optical coherence tomography. J. Pathol. Inf. 2015, 6. [Google Scholar] [CrossRef] [PubMed]
- Auksorius, E.; Bromberg, Y.; Motiejūnaitė, R.; Pieretti, A.; Liu, L.; Coron, E.; Aranda, J.; Goldstein, A.M.; Bouma, B.E.; Kazlauskas, A.; et al. Dual-modality fluorescence and full-field optical coherence microscopy for biomedical imaging applications. Biomed. Opt. Express 2012, 3, 661–666. [Google Scholar] [CrossRef] [PubMed]
- Nahas, A.; Varna, M.; Fort, E.; Boccara, A.C. Detection of plasmonic nanoparticles with full field-OCT: Optical and photothermal detection. Biomed. Opt. Express 2014, 5, 3541–3546. [Google Scholar] [CrossRef] [PubMed]
- Nahas, A.; Bauer, M.; Roux, S.; Boccara, A.C. 3D static elastography at the micrometer scale using Full Field OCT. Biomed. Opt. Express 2013, 4, 2138–2149. [Google Scholar] [CrossRef] [PubMed]
- Moneron, G.; Boccara, A.C.; Dubois, A. Polarization-sensitive full-field optical coherence tomography. Opt. Lett. 2007, 32, 2058–2060. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Kim, M. Full-color three-dimensional microscopy by wide-field optical coherence tomography. Opt. Express 2004, 12, 6632–6641. [Google Scholar] [CrossRef] [PubMed]
- Federici, A.; Dubois, A. Three-band, 1.9-μm axial resolution full-field optical coherence microscopy over a 530–1700 nm wavelength range using a single camera. Opt. Lett. 2014, 39, 1374–1377. [Google Scholar] [CrossRef] [PubMed]
- Dubois, A.; Moreau, J.; Boccara, C. Spectroscopic ultrahigh-resolution full-field optical coherence microscopy. Opt. Express 2008, 16, 17082–17091. [Google Scholar] [CrossRef] [PubMed]
- Huang, D.; Swanson, E.A.; Lin, C.P.; Schuman, J.S.; Stinson, W.G.; Chang, W.; Hee, M.R.; Flotte, T.; Gregory, K.; Puliafito, C.A.; et al. Optical coherence tomography. Science 1991, 254, 1178. [Google Scholar] [CrossRef] [PubMed]
- Izatt, J.A.; Swanson, E.A.; Fujimoto, J.G.; Hee, M.R.; Owen, G.M. Optical coherence microscopy in scattering media. Opt. Lett. 1994, 19, 590–592. [Google Scholar] [CrossRef] [PubMed]
- Fercher, A.F.; Hitzenberger, C.K.; Kamp, G.; El-Zaiat, S.Y. Measurement of intraocular distances by backscattering spectral interferometry. Opt. Commun. 1995, 117, 43–48. [Google Scholar] [CrossRef]
- De Boer, J.F.; Cense, B.; Park, B.H.; Pierce, M.C.; Tearney, G.J.; Bouma, B.E. Improved signal-to-noise ratio in spectral-domain compared with time-domain optical coherence tomography. Opt. Lett. 2003, 28, 2067–2069. [Google Scholar] [CrossRef] [PubMed]
- Pircher, M.; Götzinger, E.; Hitzenberger, C.K. Dynamic focus in optical coherence tomography for retinal imaging. J. Biomed. Opt. 2006, 11, 054013. [Google Scholar] [CrossRef] [PubMed]
- Holmes, J.; Hattersley, S.; Stone, N.; Bazant-Hegemark, F.; Barr, H. Multi-channel Fourier domain OCT system with superior lateral resolution for biomedical applications. In Proceedings of the Biomedical Optics (BiOS), San Jose, CA, USA, 19–24 January 2008; p. 68470O.
- Ding, Z.; Ren, H.; Zhao, Y.; Nelson, J.S.; Chen, Z. High-resolution optical coherence tomography over a large depth range with an axicon lens. Opt. Lett. 2002, 27, 243–245. [Google Scholar] [CrossRef] [PubMed]
- Ralston, T.S.; Marks, D.L.; Carney, P.S.; Boppart, S.A. Interferometric synthetic aperture microscopy. Nat. Phys. 2007, 3, 129–134. [Google Scholar] [CrossRef] [PubMed]
- Kazmi, S.S.; Wu, R.K.; Dunn, A.K. Evaluating multi-exposure speckle imaging estimates of absolute autocorrelation times. Opt. Lett. 2015, 40, 3643–3646. [Google Scholar] [CrossRef] [PubMed]
- Potsaid, B.; Gorczynska, I.; Srinivasan, V.J.; Chen, Y.; Jiang, J.; Cable, A.; Fujimoto, J.G. Ultrahigh speed spectral/Fourier domain OCT ophthalmic imaging at 70,000 to 312,500 axial scans per second. Opt. Express 2008, 16, 15149–15169. [Google Scholar] [CrossRef] [PubMed]
- Grieve, K.; Dubois, A.; Simonutti, M.; Paques, M.; Sahel, J.; Le Gargasson, J.F.; Boccara, C. In vivo anterior segment imaging in the rat eye with high speed white light full-field optical coherence tomography. Opt. Express 2005, 13, 6286–6295. [Google Scholar] [CrossRef] [PubMed]
- Song, S.; Huang, Z.; Nguyen, T.M.; Wong, E.Y.; Arnal, B.; O’Donnell, M.; Wang, R.K. Shear modulus imaging by direct visualization of propagating shear waves with phase-sensitive optical coherence tomography. J. Biomed. Opt. 2013, 18, 121509. [Google Scholar] [CrossRef] [PubMed]
- Commercial System LLTech. Avaiable online: http://www.lltechimaging.com/products-applications/products/ (accessed on 20 January 2017).
- Nahas, A.; Tanter, M.; Nguyen, T.M.; Chassot, J.M.; Fink, M.; Boccara, A.C. From supersonic shear wave imaging to full-field optical coherence shear wave elastography. J. Biomed. Opt. 2013, 18, 121514. [Google Scholar] [CrossRef] [PubMed]
- Apelian, C.; Harms, F.; Thouvenin, O.; Boccara, A.C. Dynamic full field optical coherence tomography: Subcellular metabolic contrast revealed in tissues by temporal analysis of interferometric signals. arXiv, 2016; arXiv:1601.01208. [Google Scholar] [CrossRef] [PubMed]
- Leroux, C.E.; Bertillot, F.; Thouvenin, O.; Boccara, A.C. Intracellular dynamics measurements with full field optical coherence tomography suggest hindering effect of actomyosin contractility on organelle transport. Biomed. Opt. Express 2016, 7, 4501–4513. [Google Scholar] [CrossRef] [PubMed]
- Thouvenin, O.; Fink, M.; Boccara, C. Dynamic multimodal full-field optical coherence tomography and fluorescence structured illumination microscopy. J. Biomed. Opt. 2017, 22, 026004. [Google Scholar] [CrossRef] [PubMed]
- Makhlouf, H.; Perronet, K.; Dupuis, G.; Lévêque-Fort, S.; Dubois, A. Simultaneous optically sectioned fluorescence and optical coherence microscopy with full-field illumination. Opt. Lett. 2012, 37, 1613–1615. [Google Scholar] [CrossRef] [PubMed]
- Abdulhalim, I. Spatial and temporal coherence effects in interference microscopy and full-field optical coherence tomography. Ann. Phys. 2012, 524, 787–804. [Google Scholar] [CrossRef]
- Dubois, A.; Selb, J.; Vabre, L.; Boccara, A.C. Phase measurements with wide-aperture interferometers. Appl. Opt. 2000, 39, 2326–2331. [Google Scholar] [CrossRef] [PubMed]
- Karamata, B.; Lambelet, P.; Laubscher, M.; Salathé, R.; Lasser, T. Spatially incoherent illumination as a mechanism for cross-talk suppression in wide-field optical coherence tomography. Opt. Lett. 2004, 29, 736–738. [Google Scholar] [CrossRef] [PubMed]
- Xiao, P.; Fink, M.; Boccara, A.C. Full-field spatially incoherent illumination interferometry: A spatial resolution almost insensitive to aberrations. Opt. Lett. 2016, 41, 3920–3923. [Google Scholar] [CrossRef] [PubMed]
- CMOSIS New Camera by Adimec. Avaiable online: http://info.adimec.com/blogposts/careioca-project-results-in-several-new-products-including-cmosis-csi2100-adimec-q-2a750-and-lltech-ffoct-microscope-and-endoscope (accessed on 20 January 2017).
- Mandrioli, P.; Ariatti, A. Marcello Malpighi, a pioneer of the experimental research in biology. Aerobiologia 1991, 7, 3–9. [Google Scholar] [CrossRef]
- Reverón, R.R. Marcello Malpighi (1628–1694), founder of microanatomy. Int. J. Morphol. 2011, 29, 399–402. [Google Scholar] [CrossRef]
- Cohen, A.L.; Hayat, M.A. Principles and Techniques of Scanning Electron Microscopy. Biological Applications. Volume 1; Van Nostrand Reinhold Company: Cincinatti, OH, USA, 1974. [Google Scholar]
- Digital Microscope. Avaiable online: http://www.histology.be/digital_microscope_histology_.html (accessed on 20 January 2017).
- Histology Guide: Virtual Histology Lab. Avaiable online: http://histologyguide.org/index.html (accessed on 20 January 2017).
- Amunts, K.; Lepage, C.; Borgeat, L.; Mohlberg, H.; Dickscheid, T.; Rousseau, M.É.; Bludau, S.; Bazin, P.L.; Lewis, L.B.; Oros-Peusquens, A.M.; et al. BigBrain: An ultrahigh-resolution 3D human brain model. Science 2013, 340, 1472–1475. [Google Scholar] [CrossRef] [PubMed]
- Leslie, P.; Gartner, L.P. Color Atlas and Text of Histology, 6th ed.; Lippincott Williams and Wilkins: Philadelphia, PA, USA, 2013. [Google Scholar]
- Auth, A.C. A Text-Book of Histology. Descriptive and Practical. For the Use of Students; John Wright and Co.: Bristol, UK, 1986. [Google Scholar]
- Spitalnik, P.F. Histology Lab Manual; Columbia University: New York, NY, USA, 2015. [Google Scholar]
- Clinical Atlas LLTech. Avaiable online: http://www.lltechimaging.com/image-gallery/atlas-of-images/ (accessed on 20 January 2017).
- Magnain, C.; Augustinack, J.C.; Konukoglu, E.; Frosch, M.P.; Sakadžić, S.; Varjabedian, A.; Garcia, N.; Wedeen, V.J.; Boas, D.A.; Fischl, B. Optical coherence tomography visualizes neurons in human entorhinal cortex. Neurophotonics 2015, 2, 015004. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Zhu, J.; Akkin, T. Serial optical coherence scanner for large-scale brain imaging at microscopic resolution. Neuroimage 2014, 84, 1007–1017. [Google Scholar] [CrossRef] [PubMed]
- Quinten, M. Optical Properties of Nanoparticle Systems: Mie and Beyond; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Arous, J.B.; Binding, J.; Léger, J.F.; Casado, M.; Topilko, P.; Gigan, S.; Boccara, A.C.; Bourdieu, L. Single myelin fiber imaging in living rodents without labeling by deep optical coherence microscopy. J. Biomed. Opt. 2011, 16, 116012. [Google Scholar] [CrossRef] [PubMed]
- Grieve, K.; Thouvenin, O.; Sengupta, A.; Borderie, V.M.; Paques, M. Appearance of the Retina With Full-Field Optical Coherence Tomography. Investig. Opthalmol. Vis. Sci. 2016, 57, OCT96. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Liu, C.H.; Zakharov, V.P.; Lazar, A.J.; Pollock, R.E.; Larin, K.V. Three-dimensional computational analysis of optical coherence tomography images for the detection of soft tissue sarcomas. J. Biomed. Opt. 2014, 19, 0211022. [Google Scholar] [CrossRef] [PubMed]
- Boppart, S.A.; Luo, W.; Marks, D.L.; Singletary, K.W. Optical coherence tomography: Feasibility for basic research and image-guided surgery of breast cancer. Breast Cancer Res. Treat. 2004, 84, 85–97. [Google Scholar] [CrossRef] [PubMed]
- McLaughlin, R.A.; Scolaro, L.; Robbins, P.; Hamza, S.; Saunders, C.; Sampson, D.D. Imaging of human lymph nodes using optical coherence tomography: Potential for staging cancer. Cancer Res. 2010, 70, 2579–2584. [Google Scholar] [CrossRef] [PubMed]
- Vakoc, B.J.; Fukumura, D.; Jain, R.K.; Bouma, B.E. Cancer imaging by optical coherence tomography: Preclinical progress and clinical potential. Nat. Rev. Cancer 2012, 12, 363–368. [Google Scholar] [CrossRef] [PubMed]
- Sharma, M.; Verma, Y.; Rao, K.; Nair, R.; Gupta, P. Imaging growth dynamics of tumour spheroids using optical coherence tomography. Biotechnol. Lett. 2007, 29, 273–278. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Wang, T.; Biswal, N.C.; Wang, X.; Sanders, M.; Brewer, M.; Zhu, Q. Optical scattering coefficient estimated by optical coherence tomography correlates with collagen content in ovarian tissue. J. Biomed. Opt. 2011, 16, 090504. [Google Scholar] [CrossRef] [PubMed]
- Vakoc, B.J.; Lanning, R.M.; Tyrrell, J.A.; Padera, T.P.; Bartlett, L.A.; Stylianopoulos, T.; Munn, L.L.; Tearney, G.J.; Fukumura, D.; Jain, R.K.; et al. Three-dimensional microscopy of the tumor microenvironment in vivo using optical frequency domain imaging. Nat. Med. 2009, 15, 1219–1223. [Google Scholar] [CrossRef] [PubMed]
- Sullivan, A.C.; Hunt, J.P.; Oldenburg, A.L. Fractal analysis for classification of breast carcinoma in optical coherence tomography. J. Biomed. Opt. 2011, 16, 066010. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Zhu, Y. Fractal analysis of en face tomographic images obtained with full field optical coherence tomography. Ann. Phys. 2016, 93. [Google Scholar] [CrossRef]
- Nicolson, M. The art of diagnosis: Medicine and the five senses. In Companion Encyclopedia of the History of Medicine, Volume 2; Bynum, W., Porter, R., Eds.; Routledge: London, UK, 1997; pp. 801–825. [Google Scholar]
- Medical Diagnosis in Egyptian World. Available online: http://www.arabworldbooks.com/articles8.htm (accessed on 20 January 2017).
- Sarvazyan, A. Shear acoustic properties of soft biological tissues in medical diagnostics. J. Acoust. Soc. Am. 1993, 93, 2329–2330. [Google Scholar] [CrossRef]
- Bataller, R.; Brenner, D.A. Liver fibrosis. J. Clin. Investig. 2005, 115, 209–218. [Google Scholar] [CrossRef] [PubMed]
- Mueller, S.; Sandrin, L. Liver stiffness: A novel parameter for the diagnosis of liver disease. Hepat. Med. 2010, 2, 49–67. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Weaver, V.M. Mechanics, malignancy, and metastasis: The force journey of a tumor cell. Cancer Metastasis Rev. 2009, 28, 113–127. [Google Scholar] [CrossRef] [PubMed]
- Mouw, J.K.; Yui, Y.; Damiano, L.; Bainer, R.O.; Lakins, J.N.; Acerbi, I.; Ou, G.; Wijekoon, A.C.; Levental, K.R.; Gilbert, P.M.; et al. Tissue mechanics modulate microRNA-dependent PTEN expression to regulate malignant progression. Nat. Med. 2014, 20, 360. [Google Scholar] [CrossRef] [PubMed]
- Ophir, J.; Cespedes, I.; Ponnekanti, H.; Yazdi, Y.; Li, X. Elastography: A quantitative method for imaging the elasticity of biological tissues. Ultrason. Imaging 1991, 13, 111–134. [Google Scholar] [CrossRef] [PubMed]
- Muthupillai, R.; Lomas, D.; Rossman, P.; Greenleaf, J.F.; Manduca, A.; Ehman, R.L. Magnetic resonance elastography by direct visualization of propagating acoustic strain waves. Science 1995, 269, 1854. [Google Scholar] [CrossRef] [PubMed]
- Mariappan, Y.K.; Glaser, K.J.; Ehman, R.L. Magnetic resonance elastography: A review. Clin. Anat. 2010, 23, 497–511. [Google Scholar] [CrossRef] [PubMed]
- Tanter, M.; Bercoff, J.; Athanasiou, A.; Deffieux, T.; Gennisson, J.L.; Montaldo, G.; Muller, M.; Tardivon, A.; Fink, M. Quantitative assessment of breast lesion viscoelasticity: Initial clinical results using supersonic shear imaging. Ultras. Med. Biol. 2008, 34, 1373–1386. [Google Scholar] [CrossRef] [PubMed]
- Gayrard, C.; Borghi, N. FRET-based molecular tension microscopy. Methods 2016, 94, 33–42. [Google Scholar] [CrossRef] [PubMed]
- Schmitt, J.M. OCT elastography: Imaging microscopic deformation and strain of tissue. Opt. Express 1998, 3, 199–211. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.K.; Ma, Z.; Kirkpatrick, S.J. Tissue Doppler optical coherence elastography for real time strain rate and strain mapping of soft tissue. Appl. Phys. Lett. 2006, 89, 144103. [Google Scholar] [CrossRef]
- Kennedy, B.F.; Kennedy, K.M.; Sampson, D.D. A review of optical coherence elastography: Fundamentals, techniques and prospects. IEEE J. Sel. Top. Quant. Electron. 2014, 20, 272–288. [Google Scholar] [CrossRef]
- Wang, S.; Larin, K.V. Optical coherence elastography for tissue characterization: A review. J. Biophoton. 2015, 8, 279–302. [Google Scholar] [CrossRef] [PubMed]
- Mulligan, J.A.; Untracht, G.R.; Chandrasekaran, S.N.; Brown, C.N.; Adie, S.G. Emerging Approaches for High-Resolution Imaging of Tissue Biomechanics With Optical Coherence Elastography. IEEE J. Sel. Top. Quant. Electron. 2016, 22, 1–20. [Google Scholar] [CrossRef]
- Royer, D.; Dieulesaint, E. Elastic Waves in Solids I: Free and Guided Propagation; Morgan, D.P., Translator; Springer: New York, NY, USA, 2000. [Google Scholar]
- Sarvazyan, A.P.; Rudenko, O.V.; Swanson, S.D.; Fowlkes, J.B.; Emelianov, S.Y. Shear wave elasticity imaging: A new ultrasonic technology of medical diagnostics. Ultras. Med. Boil. 1998, 24, 1419–1435. [Google Scholar] [CrossRef]
- Roux, S.; Hild, F.; Viot, P.; Bernard, D. Three-dimensional image correlation from X-ray computed tomography of solid foam. Compos. A Appl. Sci. Manuf. 2008, 39, 1253–1265. [Google Scholar] [CrossRef]
- Leclerc, H.; Périé, J.N.; Hild, F.; Roux, S. Digital volume correlation: What are the limits to the spatial resolution? Mech. Ind. 2012, 13, 361–371. [Google Scholar] [CrossRef]
- Basser, P.J.; Mattiello, J.; LeBihan, D. MR diffusion tensor spectroscopy and imaging. Biophys. J. 1994, 66, 259. [Google Scholar] [CrossRef]
- Le Bihan, D.; Mangin, J.F.; Poupon, C.; Clark, C.A.; Pappata, S.; Molko, N.; Chabriat, H. Diffusion tensor imaging: Concepts and applications. J. Magn. Reson. Imaging 2001, 13, 534–546. [Google Scholar] [CrossRef] [PubMed]
- Papadacci, C.; Tanter, M.; Pernot, M.; Fink, M. Ultrasound backscatter tensor imaging (BTI): Analysis of the spatial coherence of ultrasonic speckle in anisotropic soft tissues. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 986–996. [Google Scholar] [CrossRef] [PubMed]
- Chatelin, S.; Bernal, M.; Deffieux, T.; Papadacci, C.; Flaud, P.; Nahas, A.; Boccara, C.; Gennisson, J.L.; Tanter, M.; Pernot, M. Anisotropic polyvinyl alcohol hydrogel phantom for shear wave elastography in fibrous biological soft tissue: A multimodality characterization. Phys. Med. Biol. 2014, 59, 6923. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, K.M.; Es’haghian, S.; Chin, L.; McLaughlin, R.A.; Sampson, D.D.; Kennedy, B.F. Optical palpation: Optical coherence tomography-based tactile imaging using a compliant sensor. Opt. Lett. 2014, 39, 3014–3017. [Google Scholar] [CrossRef] [PubMed]
- Wellman, P.S.; Howe, R.D.; Dewagan, N.; Cundari, M.A.; Dalton, E.; Kern, K.A. Tactile imaging: A method for documenting breast masses. In Proceedings of the First Joint IEEE Engineering in Medicine and Biology, 21st Annual Conference and the 1999 Annual Fall Meetring of the Biomedical Engineering Society, Atlanta, GA, USA, 13–16 October 1999; Volume 2, p. 1131.
- Razani, M.; Mariampillai, A.; Sun, C.; Luk, T.W.; Yang, V.X.; Kolios, M.C. Feasibility of optical coherence elastography measurements of shear wave propagation in homogeneous tissue equivalent phantoms. Biomed. Opt. Express 2012, 3, 972–980. [Google Scholar] [CrossRef] [PubMed]
- Catheline, S.; Thomas, J.L.; Wu, F.; Fink, M.A. Diffraction field of a low frequency vibrator in soft tissues using transient elastography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1999, 46, 1013–1019. [Google Scholar] [CrossRef] [PubMed]
- Sandrin, L.; Catheline, S.; Tanter, M.; Hennequin, X.; Fink, M. Time-resolved pulsed elastography with ultrafast ultrasonic imaging. Ultrason. Imaging 1999, 21, 259–272. [Google Scholar] [CrossRef] [PubMed]
- Bercoff, J.; Tanter, M.; Fink, M. Supersonic shear imaging: A new technique for soft tissue elasticity mapping. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2004, 51, 396–409. [Google Scholar] [CrossRef] [PubMed]
- Chatelin, S.; Constantinesco, A.; Willinger, R. Fifty years of brain tissue mechanical testing: From in vitro to in vivo investigations. Biorheology 2010, 47, 255–276. [Google Scholar] [PubMed]
- Macé, E.; Cohen, I.; Montaldo, G.; Miles, R.; Fink, M.; Tanter, M. In vivo mapping of brain elasticity in small animals using shear wave imaging. IEEE Trans. Med. Imaging 2011, 30, 550–558. [Google Scholar] [CrossRef] [PubMed]
- Catheline, S.; Souchon, R.; Rupin, M.; Brum, J.; Dinh, A.; Chapelon, J.Y. Tomography from diffuse waves: Passive shear wave imaging using low frame rate scanners. Appl. Phys. Lett. 2013, 103, 014101. [Google Scholar] [CrossRef]
- Zorgani, A.; Souchon, R.; Dinh, A.H.; Chapelon, J.Y.; Ménager, J.M.; Lounis, S.; Rouvière, O.; Catheline, S. Brain palpation from physiological vibrations using MRI. Proc. Natl. Acad. Sci. USA 2015, 112, 12917–12921. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.M.; Zorgani, A.; Lescanne, M.; Boccara, C.; Fink, M.; Catheline, S. Diffuse shear wave imaging: Toward passive elastography using low-frame rate spectral-domain optical coherence tomography. J. Biomed. Opt. 2016, 21, 126013. [Google Scholar] [CrossRef] [PubMed]
- Pecora, R. Dynamic Light Scattering: Applications of Photon Correlation Spectroscopy; Springer Science & Business Media: Heidelberg, Germany, 2013. [Google Scholar]
- Suissa, M.; Place, C.; Goillot, E.; Berge, B.; Freyssingeas, E. Dynamic light scattering as an investigating tool to study the global internal dynamics of a living cell nucleus. EPL Europhys. Lett. 2007, 78, 38005. [Google Scholar] [CrossRef]
- Suissa, M.; Place, C.; Goillot, E.; Freyssingeas, E. Internal dynamics of a living cell nucleus investigated by dynamic light scattering. Eur. Phys. J. E 2008, 26, 435–448. [Google Scholar] [CrossRef] [PubMed]
- Jeong, K.; Turek, J.J. Volumetric motility-contrast imaging of tissue response to cytoskeletal anti-cancer drugs. Opt. Express 2007, 15, 14057–14064. [Google Scholar] [CrossRef] [PubMed]
- Nolte, D.D.; An, R.; Turek, J.; Jeong, K. Tissue dynamics spectroscopy for phenotypic profiling of drug effects in three-dimensional culture. Biomed. Opt. Express 2012, 3, 2825–2841. [Google Scholar] [CrossRef] [PubMed]
- An, R.; Wang, C.; Turek, J.; Machaty, Z.; Nolte, D.D. Biodynamic imaging of live porcine oocytes, zygotes and blastocysts for viability assessment in assisted reproductive technologies. Biomed. Opt. Express 2015, 6, 963–976. [Google Scholar] [CrossRef] [PubMed]
- Tan, W.; Oldenburg, A.L.; Norman, J.J.; Desai, T.A.; Boppart, S.A. Optical coherence tomography of cell dynamics in three-dimensional tissue models. Opt. Express 2006, 14, 7159–7171. [Google Scholar] [CrossRef] [PubMed]
- Oldenburg, A.L.; Yu, X.; Gilliss, T.; Alabi, O.; Taylor, R.M.; Troester, M.A. Inverse-power-law behavior of cellular motility reveals stromal–epithelial cell interactions in 3D co-culture by OCT fluctuation spectroscopy. Optica 2015, 2, 877. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Wu, W.; Jiang, J.Y.; Zhu, B.; Boas, D.A. Dynamic light scattering optical coherence tomography. Opt. Express 2012, 20, 22262–22277. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Farkas, E.R.; Webb, W.W. In vivo applications of fluorescence correlation spectroscopy. Methods Cell Biol. 2008, 89, 3–35. [Google Scholar] [PubMed]
- Tishler, R.B.; Carlson, F.D. A study of the dynamic properties of the human red blood cell membrane using quasi-elastic light-scattering spectroscopy. Biophys. J. 1993, 65, 2586. [Google Scholar] [CrossRef]
- Miller, M.J.; Wei, S.H.; Parker, I.; Cahalan, M.D. Two-photon imaging of lymphocyte motility and antigen response in intact lymph node. Science 2002, 296, 1869–1873. [Google Scholar] [CrossRef] [PubMed]
- Ammari, H.; Romero, F.; Shi, C. A signal separation technique for sub-cellular imaging using dynamic optical coherence tomography. arXiv, 2016; arXiv:1608.04382. [Google Scholar]
- Demené, C.; Deffieux, T.; Pernot, M.; Osmanski, B.F.; Biran, V.; Gennisson, J.L.; Sieu, L.A.; Bergel, A.; Franqui, S.; Correas, J.M.; et al. Spatiotemporal clutter filtering of ultrafast ultrasound data highly increases Doppler and fUltrasound sensitivity. IEEE Trans. Med. Imaging 2015, 34, 2271–2285. [Google Scholar] [CrossRef] [PubMed]
- Zink, D.; Fischer, A.H.; Nickerson, J.A. Nuclear structure in cancer cells. Nat. Rev. Cancer 2004, 4, 677–687. [Google Scholar] [CrossRef] [PubMed]
- Slater, D.; Rice, S.; Stewart, R.; Melling, S.; Hewer, E.; Smith, J. Proposed Sheffield quantitative criteria in cervical cytology to assist the grading of squamous cell dyskaryosis, as the British Society for Clinical Cytology definitions require amendment. Cytopathology 2005, 16, 179–192. [Google Scholar] [CrossRef] [PubMed]
- Popescu, G.; Park, Y.; Choi, W.; Dasari, R.R.; Feld, M.S.; Badizadegan, K. Imaging red blood cell dynamics by quantitative phase microscopy. Blood Cells Mol. Dis. 2008, 41, 10–16. [Google Scholar] [CrossRef] [PubMed]
- Sato, E.; Olson, S.H.; Ahn, J.; Bundy, B.; Nishikawa, H.; Qian, F.; Jungbluth, A.A.; Frosina, D.; Gnjatic, S.; Ambrosone, C.; et al. Intraepithelial CD8+ tumor-infiltrating lymphocytes and a high CD8+/regulatory T cell ratio are associated with favorable prognosis in ovarian cancer. Proc. Natl. Acad. Sci. USA 2005, 102, 18538–18543. [Google Scholar] [CrossRef] [PubMed]
- Mahmoud, S.M.; Paish, E.C.; Powe, D.G.; Macmillan, R.D.; Grainge, M.J.; Lee, A.H.; Ellis, I.O.; Green, A.R. Tumor-infiltrating CD8+ lymphocytes predict clinical outcome in breast cancer. J. Clin. Oncol. 2011, 29, 1949–1955. [Google Scholar] [CrossRef] [PubMed]
- Weidner, N.; Carroll, P.; Flax, J.; Blumenfeld, W.; Folkman, J. Tumor angiogenesis correlates with metastasis in invasive prostate carcinoma. Am. J. Pathol. 1993, 143, 401. [Google Scholar] [PubMed]
- Weidner, N. Current pathologic methods for measuring intratumoral microvessel density within breast carcinoma and other solid tumors. Breast Cancer Res. Treat. 1995, 36, 169–180. [Google Scholar] [CrossRef] [PubMed]
- Maier, J.G.; Schamber, D.T. The role of lymphangiography in the diagnosis and treatment of malignant testicular tumors. Am. J. Roentgenol. 1972, 114, 482–491. [Google Scholar] [CrossRef]
- Shaked, N.T.; Rinehart, M.T.; Wax, A. Quantitative phase microscopy of biological cell dynamics by wide-field digital interferometry. In Coherent Light Microscopy; Springer: Heidelberg, Germany, 2011; pp. 169–198. [Google Scholar]
- Ma, L.; Rajshekhar, G.; Wang, R.; Bhaduri, B.; Sridharan, S.; Mir, M.; Chakraborty, A.; Iyer, R.; Prasanth, S.; Millet, L.; et al. Phase correlation imaging of unlabeled cell dynamics. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
- Berclaz, C.; Szlag, D.; Nguyen, D.; Extermann, J.; Bouwens, A.; Marchand, P.J.; Nilsson, J.; Schmidt-Christensen, A.; Holmberg, D.; Grapin-Botton, A.; et al. Label-free fast 3D coherent imaging reveals pancreatic islet micro-vascularization and dynamic blood flow. Biomed. Opt. Express 2016, 7, 4569–4580. [Google Scholar] [CrossRef] [PubMed]
- Bouwens, A.; Szlag, D.; Szkulmowski, M.; Bolmont, T.; Wojtkowski, M.; Lasser, T. Quantitative lateral and axial flow imaging with optical coherence microscopy and tomography. Opt. Express 2013, 21, 17711–17729. [Google Scholar] [CrossRef] [PubMed]
- Leitgeb, R.A.; Werkmeister, R.M.; Blatter, C.; Schmetterer, L. Doppler optical coherence tomography. Progr. Retin. Eye Res. 2014, 41, 26–43. [Google Scholar] [CrossRef] [PubMed]
- Bouwens, A.; Bolmont, T.; Szlag, D.; Berclaz, C.; Lasser, T. Quantitative cerebral blood flow imaging with extended-focus optical coherence microscopy. Opt. Lett. 2014, 39, 37–40. [Google Scholar] [CrossRef] [PubMed]
- Hicks, J.; Matthaei, E. Fluorescence in histology. J. Pathol. Bacteriol. 1955, 70, 1–12. [Google Scholar] [CrossRef] [PubMed]
- John, D.; Bancroft, M.G. Theory and Practice Of Histological Techniques, 5th ed.; Churchill Livingstone: London, UK, 2002. [Google Scholar]
- Volpi, E.V.; Bridger, J.M. FISH glossary: An overview of the fluorescence in situ hybridization technique. Biotechniques 2008, 45, 385–386. [Google Scholar] [CrossRef] [PubMed]
- Roulston, J.E.; Bartlett, J.M. Molecular Diagnosis Of Cancer: Methods and Protocols; Springer Science & Business Media: New York, NY, USA, 2004; Volume 97. [Google Scholar]
- Transidico, P.; Bianchi, M.; Capra, M.; Pelicci, P.G.; Faretta, M. From cells to tissues: Fluorescence confocal microscopy in the study of histological samples. Microsc. Res. Tech. 2004, 64, 89–95. [Google Scholar] [CrossRef] [PubMed]
- Yuste, R. Fluorescence microscopy today. Nat. Methods 2005, 2, 902–904. [Google Scholar] [CrossRef] [PubMed]
- Jung, J.C.; Mehta, A.D.; Aksay, E.; Stepnoski, R.; Schnitzer, M.J. In vivo mammalian brain imaging using one-and two-photon fluorescence microendoscopy. J. Neurophysiol. 2004, 92, 3121–3133. [Google Scholar] [CrossRef] [PubMed]
- Flusberg, B.A.; Cocker, E.D.; Piyawattanametha, W.; Jung, J.C.; Cheung, E.L.; Schnitzer, M.J. Fiber-optic fluorescence imaging. Nat. Methods 2005, 2, 941–950. [Google Scholar] [CrossRef] [PubMed]
- Tuchin, V.V. Optical clearing of tissues and blood using the immersion method. J. Phys. D Appl. Phys. 2005, 38, 2497. [Google Scholar] [CrossRef]
- Chung, K.; Deisseroth, K. CLARITY for mapping the nervous system. Nat. Methods 2013, 10, 508–513. [Google Scholar] [CrossRef] [PubMed]
- Larin, K.V.; Ghosn, M.G.; Bashkatov, A.N.; Genina, E.A.; Trunina, N.A.; Tuchin, V.V. Optical clearing for OCT image enhancement and in-depth monitoring of molecular diffusion. IEEE J. Sel. Top. Quant. Electron. 2012, 18, 1244–1259. [Google Scholar] [CrossRef]
- Yuan, S.; Roney, C.A.; Wierwille, J.; Chen, C.W.; Xu, B.; Griffiths, G.; Jiang, J.; Ma, H.; Cable, A.; Summers, R.M.; Chen, Y. Co-registered optical coherence tomography and fluorescence molecular imaging for simultaneous morphological and molecular imaging. Phys. Med. Biol. 2010, 55, 191–206. [Google Scholar] [CrossRef] [PubMed]
- Harms, F.; Dalimier, E.; Vermeulen, P.; Fragola, A.; Boccara, A. Multimodal Full-Field Optical Coherence Tomography on biological tissue: Toward all optical digital pathology. In Prcoeedings of the SPIE BiOS, San Francisco, CA, USA, 21–26 January 2012; p. 821609.
- Coron, E.; Auksorius, E.; Pieretti, A.; Mahé, M.; Liu, L.; Steiger, C.; Bromberg, Y.; Bouma, B.; Tearney, G.; Neunlist, M.; et al. Full-field optical coherence microscopy is a novel technique for imaging enteric ganglia in the gastrointestinal tract. Neurogastroenterol. Motil. 2012, 24, e611–e621. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.W.; Wardill, T.J.; Sun, Y.; Pulver, S.R.; Renninger, S.L.; Baohan, A.; Schreiter, E.R.; Kerr, R.A.; Orger, M.B.; Jayaraman, V.; et al. Ultrasensitive fluorescent proteins for imaging neuronal activity. Nature 2013, 499, 295–300. [Google Scholar] [CrossRef] [PubMed]
- Gee, K.; Brown, K.; Chen, W.N.; Bishop-Stewart, J.; Gray, D.; Johnson, I. Chemical and physiological characterization of fluo-4 Ca2+-indicator dyes. Cell Calcium 2000, 27, 97–106. [Google Scholar] [CrossRef] [PubMed]
- Siegel, M.S.; Isacoff, E.Y. A genetically encoded optical probe of membrane voltage. Neuron 1997, 19, 735–741. [Google Scholar] [CrossRef]
- Imamura, H.; Nhat, K.P.H.; Togawa, H.; Saito, K.; Iino, R.; Kato-Yamada, Y.; Nagai, T.; Noji, H. Visualization of ATP levels inside single living cells with fluorescence resonance energy transfer-based genetically encoded indicators. Proc. Natl. Acad. Sci. USA 2009, 106, 15651–15656. [Google Scholar] [CrossRef] [PubMed]
- Kit for Apoptosis Detection from ThermoFisher Scientific. Available online: https://www.thermofisher.com/order/catalog/product/C10617 (accessed on 20 January 2017).
- Farhat, G.; Mariampillai, A.; Yang, V.X.; Czarnota, G.J.; Kolios, M.C. Detecting apoptosis using dynamic light scattering with optical coherence tomography. J. Biomed. Opt. 2011, 16, 0705055. [Google Scholar] [CrossRef] [PubMed]
- Rappaz, B.; Marquet, P.; Cuche, E.; Emery, Y.; Depeursinge, C.; Magistretti, P. Measurement of the integral refractive index and dynamic cell morphometry of living cells with digital holographic microscopy. Opt. Express 2005, 13, 9361–9373. [Google Scholar] [CrossRef] [PubMed]
- Brown, E.; McKee, T.; diTomaso, E.; Pluen, A.; Seed, B.; Boucher, Y.; Jain, R.K. Dynamic imaging of collagen and its modulation in tumors in vivo using second-harmonic generation. Nat. Med. 2003, 9, 796–800. [Google Scholar] [CrossRef] [PubMed]
- Débarre, D.; Supatto, W.; Pena, A.M.; Fabre, A.; Tordjmann, T.; Combettes, L.; Schanne-Klein, M.C.; Beaurepaire, E. Imaging lipid bodies in cells and tissues using third-harmonic generation microscopy. Nat. Methods 2006, 3, 47–53. [Google Scholar] [CrossRef] [PubMed]
- Aptel, F.; Olivier, N.; Deniset-Besseau, A.; Legeais, J.M.; Plamann, K.; Schanne-Klein, M.C.; Beaurepaire, E. Multimodal nonlinear imaging of the human cornea. Investig. Ophthalmol. Vis. Sci. 2010, 51, 2459–2465. [Google Scholar] [CrossRef] [PubMed]
- Olivier, N.; Luengo-Oroz, M.A.; Duloquin, L.; Faure, E.; Savy, T.; Veilleux, I.; Solinas, X.; Débarre, D.; Bourgine, P.; Santos, A.; et al. Cell lineage reconstruction of early zebrafish embryos using label-free nonlinear microscopy. Science 2010, 329, 967–971. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.G.; König, K.; Halbhuber, K.J. Two-photon microscopy of deep intravital tissues and its merits in clinical research. J. Microsc. 2010, 238, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Chang, S.; Tai, D.C.; Tan, N.; Xiao, G.; Tang, H.; Yu, H. Nonlinear optical microscopy: Use of second harmonic generation and two-photon microscopy for automated quantitative liver fibrosis studies. J. Biomed. Opt. 2008, 13, 064010. [Google Scholar] [CrossRef] [PubMed]
- Commercial Multiphoton Platform for Histology. Available online: http://www.histoindex.com/Genesis-200 (accessed on 20 January 2017).
- Evans, C.L.; Xie, X.S. Coherent anti-Stokes Raman scattering microscopy: Chemical imaging for biology and medicine. Annu. Rev. Anal. Chem. 2008, 1, 883–909. [Google Scholar] [CrossRef] [PubMed]
- Bégin, S.; Burgoyne, B.; Mercier, V.; Villeneuve, A.; Vallée, R.; Côté, D. Coherent anti-Stokes Raman scattering hyperspectral tissue imaging with a wavelength-swept system. Biomed. Opt. Express 2011, 2, 1296–1306. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.Y.; Suhalim, J.L.; Nien, C.L.; MiljkoviÄ, M.D.; Diem, M.; Jester, J.V.; Potma, E.O. Picosecond spectral coherent anti-Stokes Raman scattering imaging with principal component analysis of meibomian glands. J. Biomed. Opt. 2011, 16, 021104. [Google Scholar] [CrossRef] [PubMed]
- Mahou, P.; Olivier, N.; Labroille, G.; Duloquin, L.; Sintes, J.M.; Peyriéras, N.; Legouis, R.; Débarre, D.; Beaurepaire, E. Combined third-harmonic generation and four-wave mixing microscopy of tissues and embryos. Biomed. Opt. Express 2011, 2, 2837–2849. [Google Scholar] [CrossRef] [PubMed]
- Michels, S.; Pircher, M.; Geitzenauer, W.; Simader, C.; Götzinger, E.; Findl, O.; Schmidt-Erfurth, U.; Hitzenberger, C. Value of polarisation-sensitive optical coherence tomography in diseases affecting the retinal pigment epithelium. Br. J. Ophthalmol. 2008, 92, 204–209. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Léger, J.F.; Binding, J.; Boccara, A.C.; Gigan, S.; Bourdieu, L. Measuring aberrations in the rat brain by coherence-gated wavefront sensing using a Linnik interferometer. Biomed. Opt. Express 2012, 3, 2510–2525. [Google Scholar] [CrossRef] [PubMed]
- Xiao, P.; Fink, M.; Boccara, A.C. Adaptive optics full-field optical coherence tomography. J. Biomed. Opt. 2016, 21, 121505. [Google Scholar] [CrossRef] [PubMed]
- Auksorius, E.; Boccara, A.C. Dark-field full-field optical coherence tomography. Opt. Lett. 2015, 40, 3272–3275. [Google Scholar] [CrossRef] [PubMed]
- Badon, A.; Li, D.; Lerosey, G.; Boccara, A.C.; Fink, M.; Aubry, A. Smart optical coherence tomography for ultra-deep imaging through highly scattering media. arXiv, 2015; arXiv:1510.08613. [Google Scholar] [CrossRef] [PubMed]
- Srinivasan, V.J.; Sakadžić, S.; Gorczynska, I.; Ruvinskaya, S.; Wu, W.; Fujimoto, J.G.; Boas, D.A. Quantitative cerebral blood flow with optical coherence tomography. Opt. Express 2010, 18, 2477–2494. [Google Scholar] [CrossRef] [PubMed]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thouvenin, O.; Apelian, C.; Nahas, A.; Fink, M.; Boccara, C. Full-Field Optical Coherence Tomography as a Diagnosis Tool: Recent Progress with Multimodal Imaging. Appl. Sci. 2017, 7, 236. https://doi.org/10.3390/app7030236
Thouvenin O, Apelian C, Nahas A, Fink M, Boccara C. Full-Field Optical Coherence Tomography as a Diagnosis Tool: Recent Progress with Multimodal Imaging. Applied Sciences. 2017; 7(3):236. https://doi.org/10.3390/app7030236
Chicago/Turabian StyleThouvenin, Olivier, Clement Apelian, Amir Nahas, Mathias Fink, and Claude Boccara. 2017. "Full-Field Optical Coherence Tomography as a Diagnosis Tool: Recent Progress with Multimodal Imaging" Applied Sciences 7, no. 3: 236. https://doi.org/10.3390/app7030236
APA StyleThouvenin, O., Apelian, C., Nahas, A., Fink, M., & Boccara, C. (2017). Full-Field Optical Coherence Tomography as a Diagnosis Tool: Recent Progress with Multimodal Imaging. Applied Sciences, 7(3), 236. https://doi.org/10.3390/app7030236




