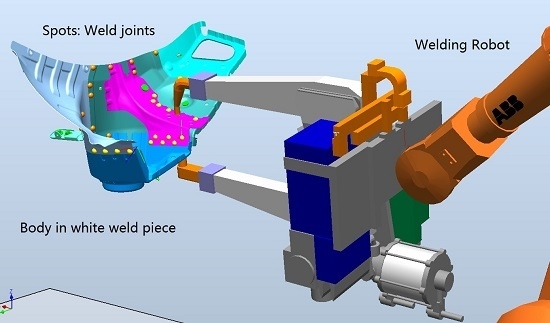
Welding Robot Collision-Free Path Optimization
Abstract
:1. Introduction
2. Model Description of Welding Robot Path Planning with Obstacle Avoidance
3. 3D Environment Modeling
- (1)
- (2)
- Set up grid matrix. The whole space is divided into small cubes, and the centers of the cubes are set as the welding torch’s footholds (Figure 4). Because the diameter of the welding electrode is 4.48 mm, each side length of the cubes is set to 5 mm. Then, all centers of the cubes are mapped on the triangles. If the projected point is located in the triangle and the vertical length is less than 5 mm, the triangle is the obstacle for the center; otherwise, the triangle is not the obstacle for the center.
- (3)
- If there are no obstacle triangles for a center, the center is a free point. Otherwise, the center is an obstacle point, which means that the welding torch cannot be located in the point.
- (4)
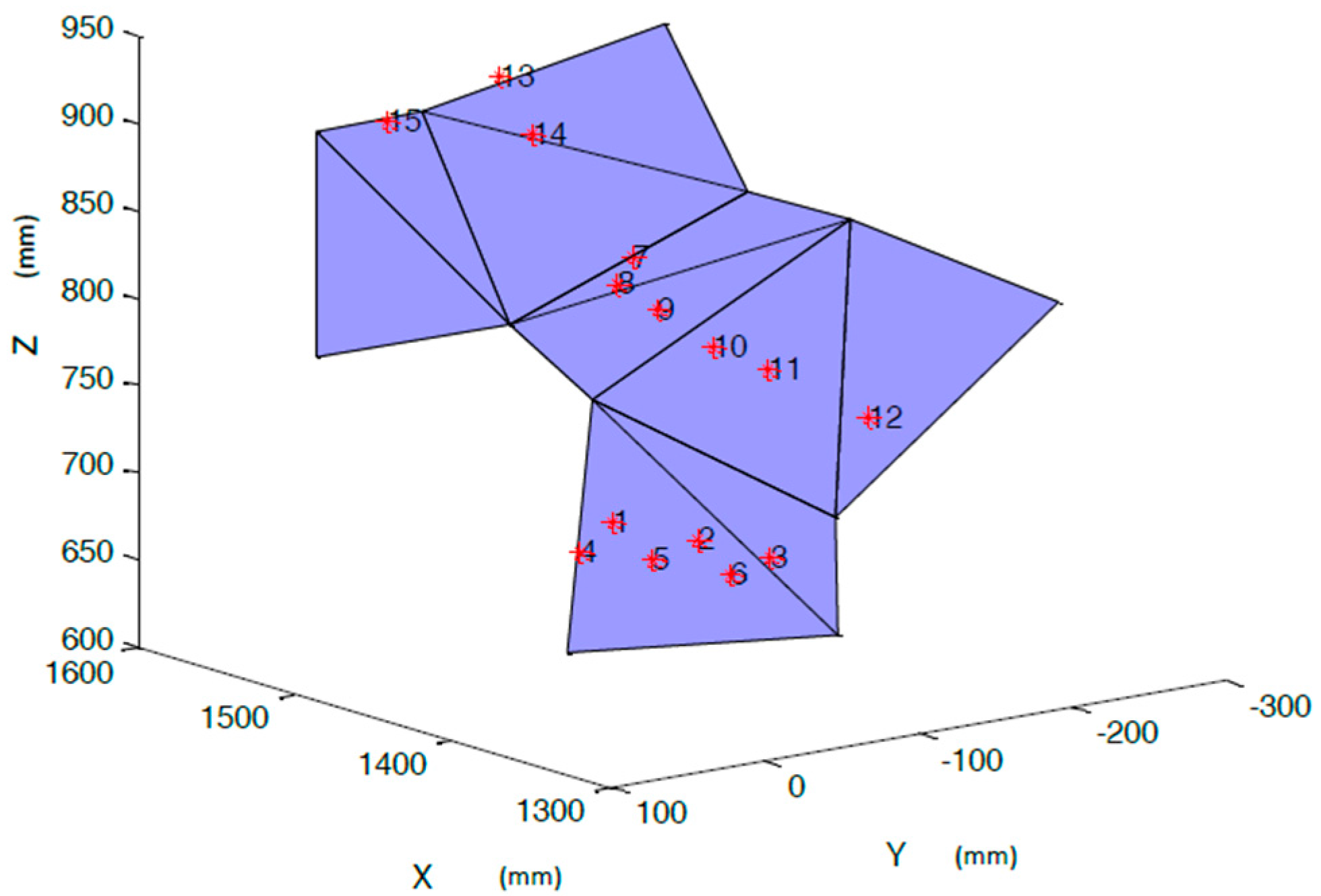
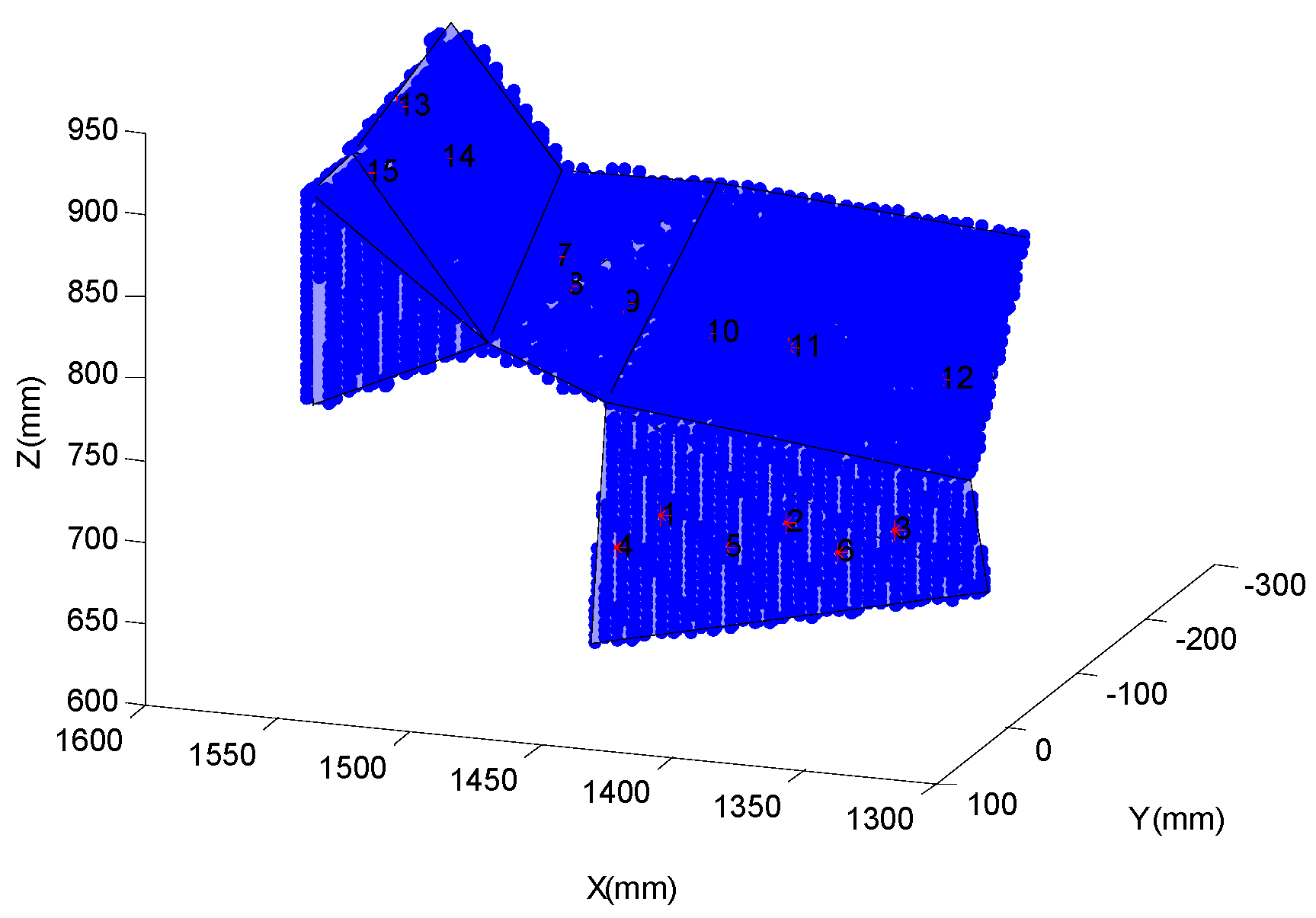
- Because the actual weld joints are located on the surface of the weldment, the weld joints cannot be located in the free points. However, in the process of path planning, the welding torch can only move among the free points. To solve this problem, a nearest free point is defined as a virtual weld joint for the weld joint. Because the distance between actual weld joints and virtual weld joints is invariable and is small in terms of the whole path length, the distance is ignored in the optimization process. The path planning mentioned below only considers the path between the virtual weld joints.
4. Collision Free Path Optimization
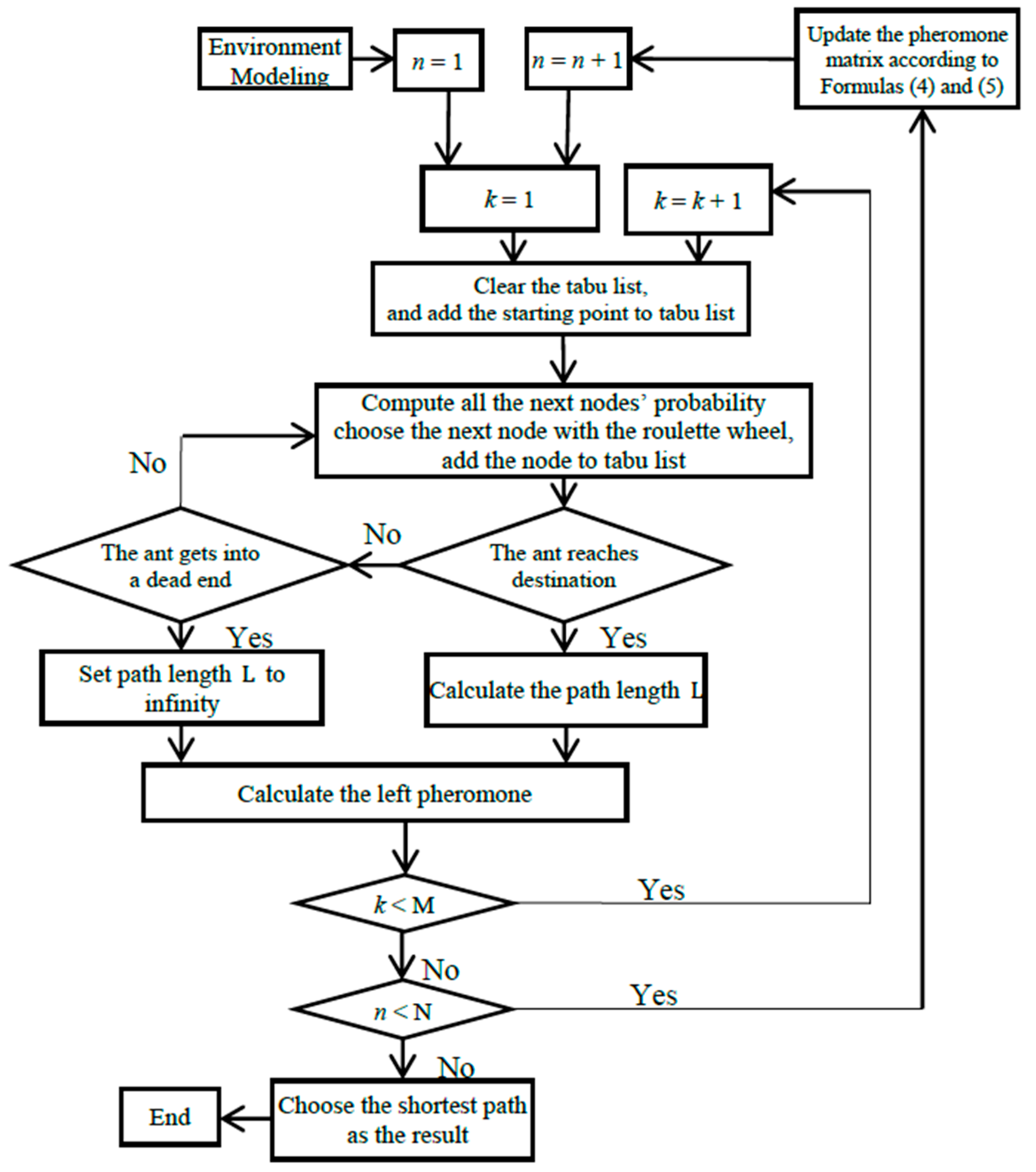
4.1. Ant Colony Optimization Algorithm (ACO)
4.2. Collision Free Path Optimization Based on ACO
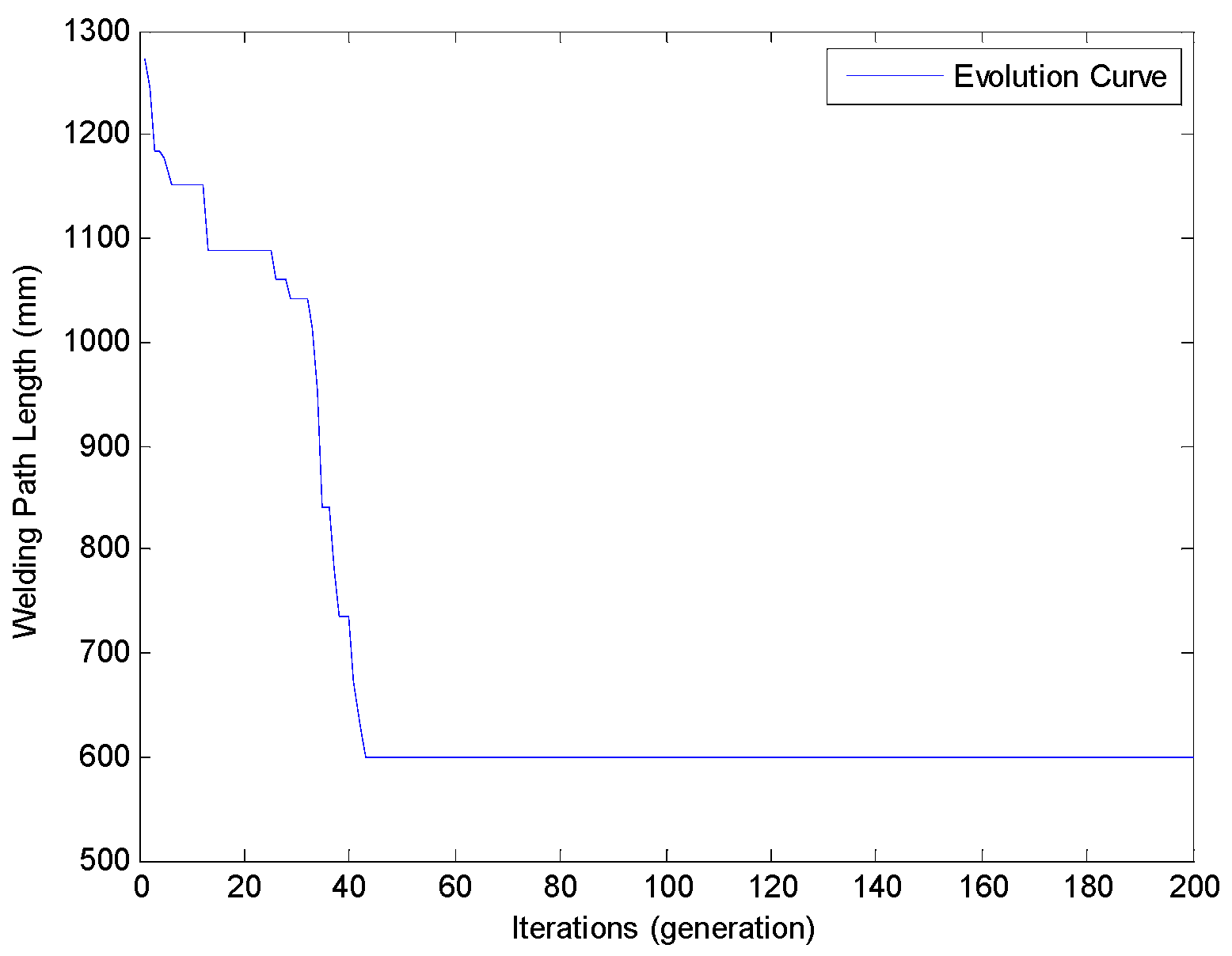
4.3. The Secondary Optimization of ACO (SO-ACO)
5. Global Welding Robot Path Planning
5.1. Particle Swarm Optimization Algorithm
5.2. Global Path Planning Based on PSO
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, X.; Shi, Y.; Ding, D.; Gu, X. Double global optimum genetic algorithm-particle swarm optimization-based welding robot path planning. Eng. Optim. 2016, 48, 299–316. [Google Scholar] [CrossRef]
- Ramer, C.; Reitelshofer, S.; Franke, J. A robot motion planner for 6-DOF industrial robots based on the cell decomposition of the workspace. In Proceedings of the 2013 44th International Symposium on Robotics (ISR), Seoul, Korea, 24–26 October 2013; IEEE: New York, NY, USA, 2013; pp. 1–4. [Google Scholar]
- Yang, H.; Shao, H. Distortion-oriented welding path optimization based on elastic net method and genetic algorithm. J. Mater. Process. Technol. 2009, 209, 407–412. [Google Scholar] [CrossRef]
- Willms, A.R.; Yang, S.X. Real-time robot path planning via a distance-propagating dynamic system with obstacle clearance. IEEE Trans. Syst. Man Cybern. B Cybern. 2008, 38, 884–893. [Google Scholar] [CrossRef] [PubMed]
- Yu, N.; Wang, Z. Collision avoidance planning of manipulator based on C-space layered search arithmetic. In Proceedings of the 2011 International Conference on Electronic and Mechanical Engineering and Information Technology (EMEIT), Harbin, China, 12–14 August 2011; IEEE: New York, NY, USA, 2011; Volume 6, pp. 3258–3262. [Google Scholar]
- Masehian, E.; Amin Naseri, M.R. A voronoi diagram-visibility graph-potential field compound algorithm for robot path planning. J. Robot. Syst. 2004, 21, 275–300. [Google Scholar] [CrossRef]
- Teschner, M.; Kimmerle, S.; Heidelberger, B.; Zachmann, G.; Raghupathi, L.; Fuhrmann, A.; Cani, M.-P.; Faure, F.; Magnenat-Thalmann, N.; Strasser, W.; et al. Collision detection for deformable objects. In Computer Graphics Forum; Blackwell Publishing Ltd.: Oxford, UK, 2005; Volume 24, pp. 61–81. [Google Scholar]
- Duan, H.; Huang, L. Imperialist competitive algorithm optimized artificial neural networks for UCAV global path planning. Neurocomputing 2014, 125, 166–171. [Google Scholar] [CrossRef]
- Mo, H.; Xu, L. Research of biogeography particle swarm optimization for robot path planning. Neuro Comput. 2015, 148, 91–99. [Google Scholar] [CrossRef]
- Li, G.; Tong, S.; Cong, F.; Yamashita, A.; Asama, H. Improved artificial potential field-based simultaneous forward search method for robot path planning in complex environment. In Proceedings of the 2015 IEEE/SICE International Symposium on System Integration (SII), Nagoya, Japan, 11–13 December 2015; IEEE: New York, NY, USA, 2015; pp. 760–765. [Google Scholar]
- Cao, J. Robot Global Path Planning Based on an Improved Ant Colony Algorithm. J. Comput. Commun. 2016, 4, 11–19. [Google Scholar] [CrossRef]
- Lei, L.; Shiru, Q. Path planning for unmanned air vehicles using an improved artificial bee colony algorithm. In Proceedings of the 2012 31st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2012; IEEE: New York, NY, USA, 2012; pp. 2486–2491. [Google Scholar]
- Wang, Y.; Mulvaney, D.; Sillitoe, I. Genetic-based mobile robot path planning using vertex heuristics. In Proceedings of the 2006 IEEE Conference on Cybernetics and Intelligent Systems, Bangkok, Thailand, 7–9 June 2006; IEEE: New York, NY, USA, 2006; pp. 1–6. [Google Scholar]
- Colorni, A.; Dorigo, M.; Maniezzo, V. Distributed optimization by ant colonies. In Proceedings of the First European Conference on Artificial Life, Paris, France, 13 December 1991; Volume 142, pp. 134–142.
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; IEEE: New York, NY, USA, 1995; pp. 1942–1948. [Google Scholar]
- Clerc, M. Discrete particle swarm optimization, illustrated by the traveling salesman problem. In New Optimization Techniques in Engineering; Springer: Berlin/Heidelberg, Germany, 2004; pp. 219–239. [Google Scholar]


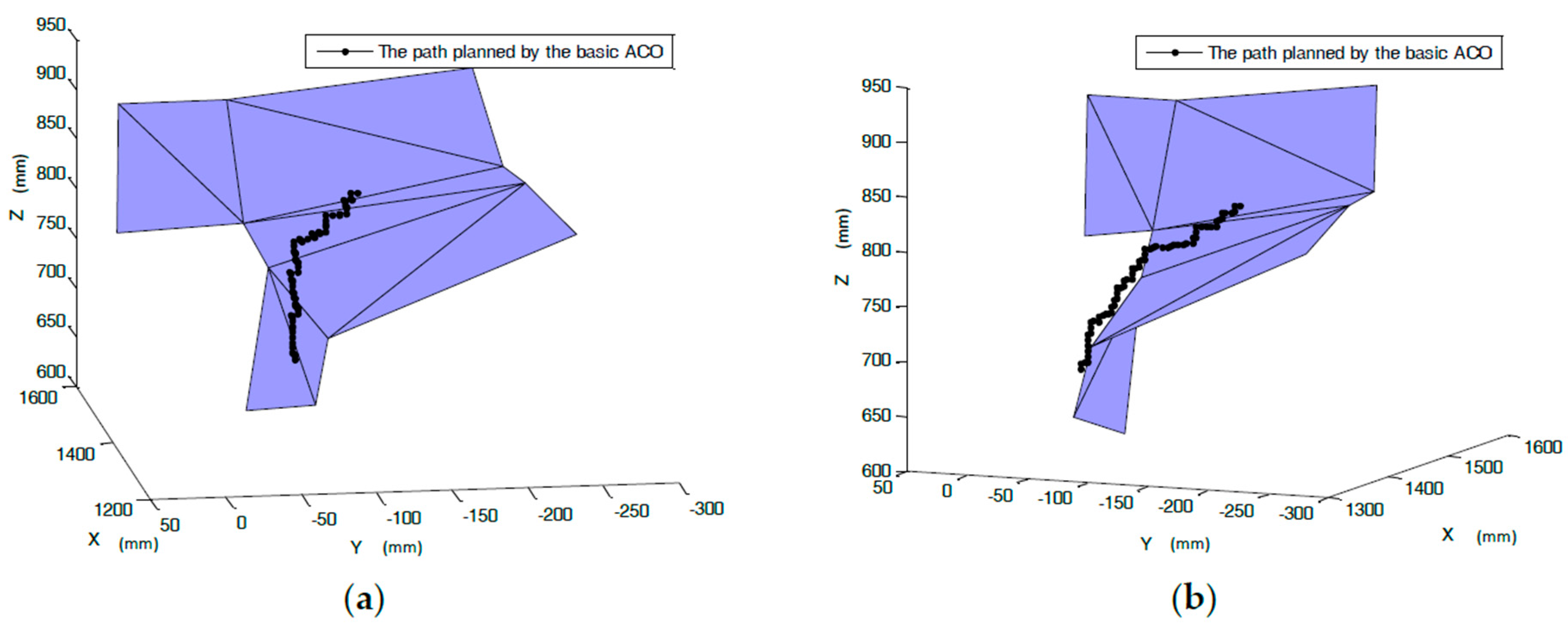
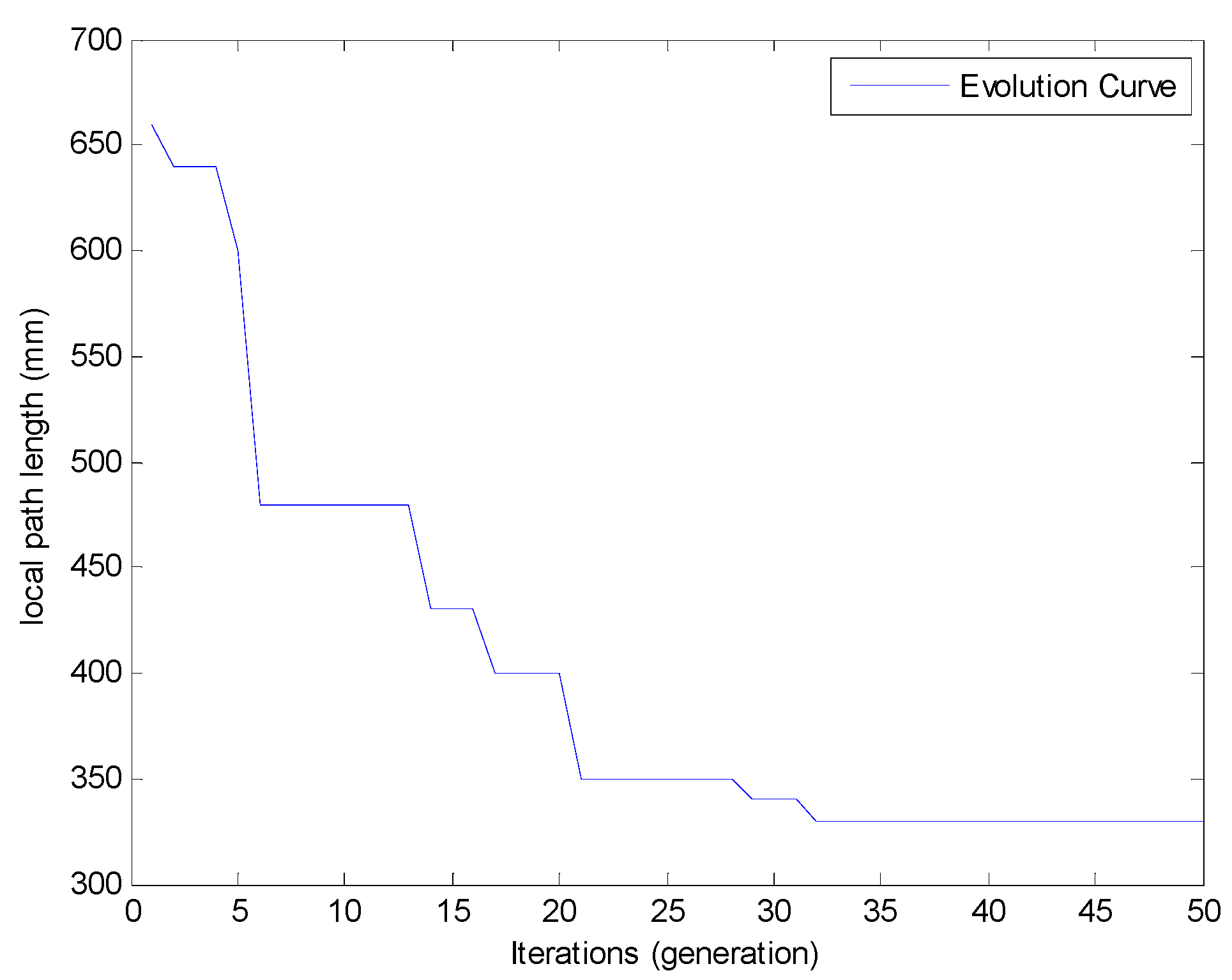
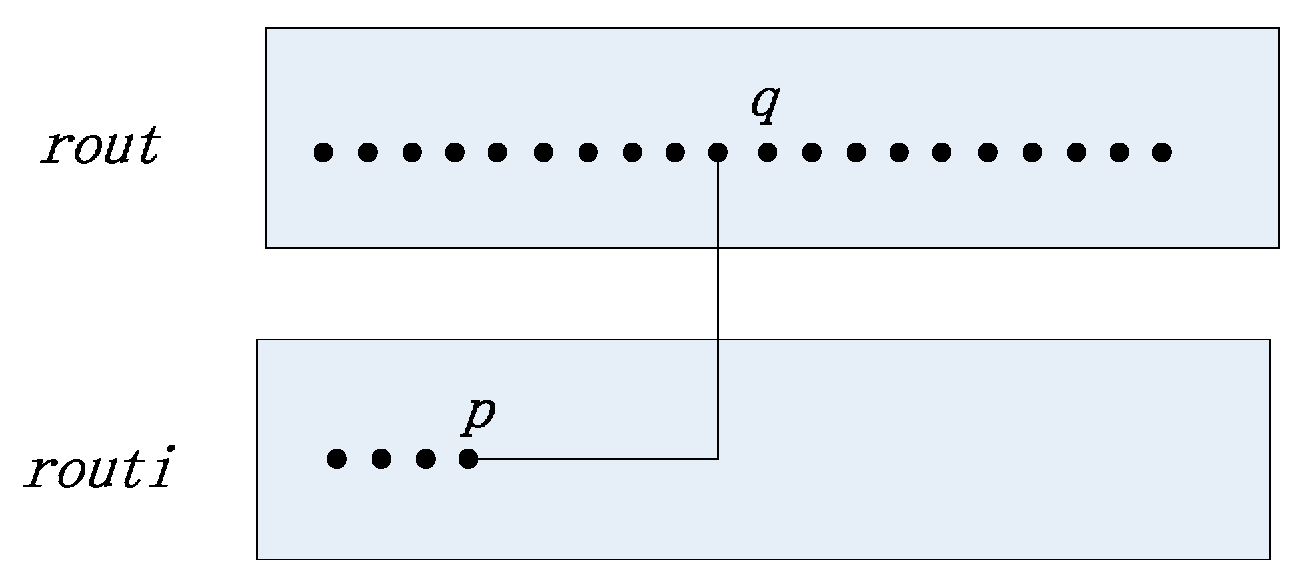
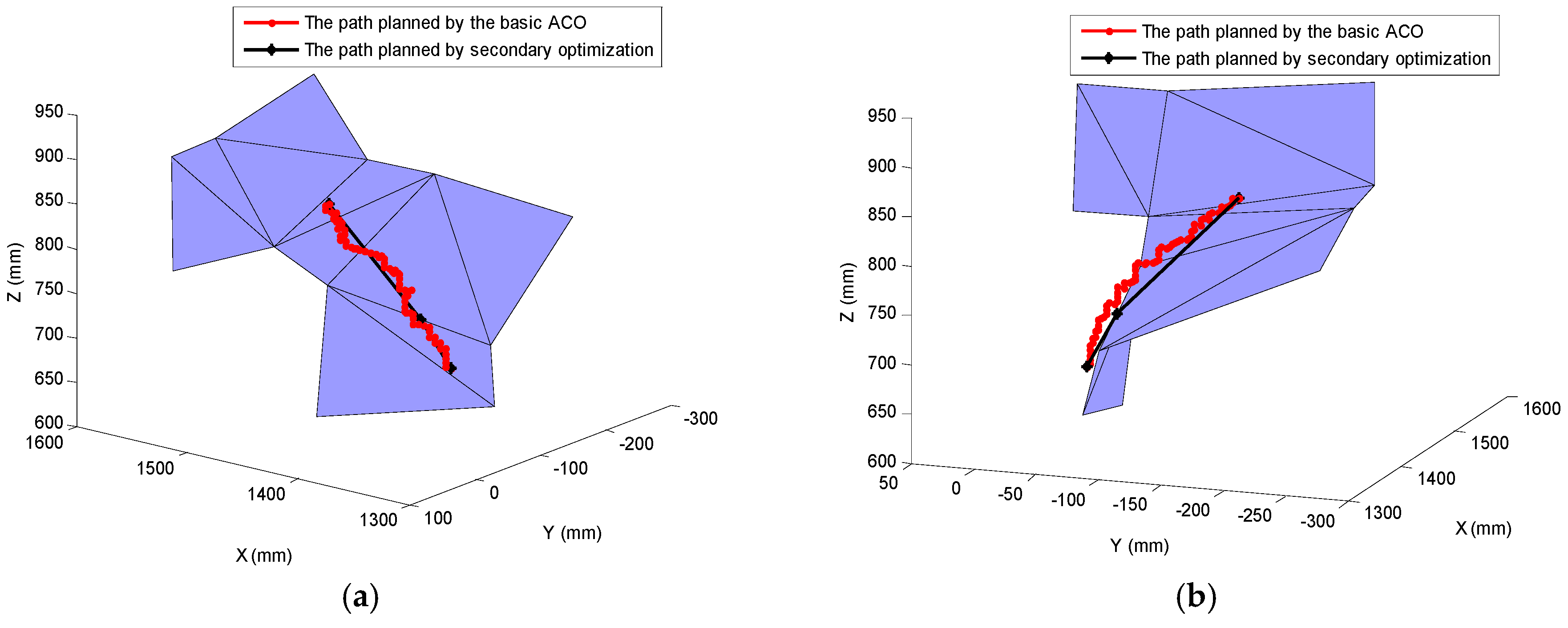
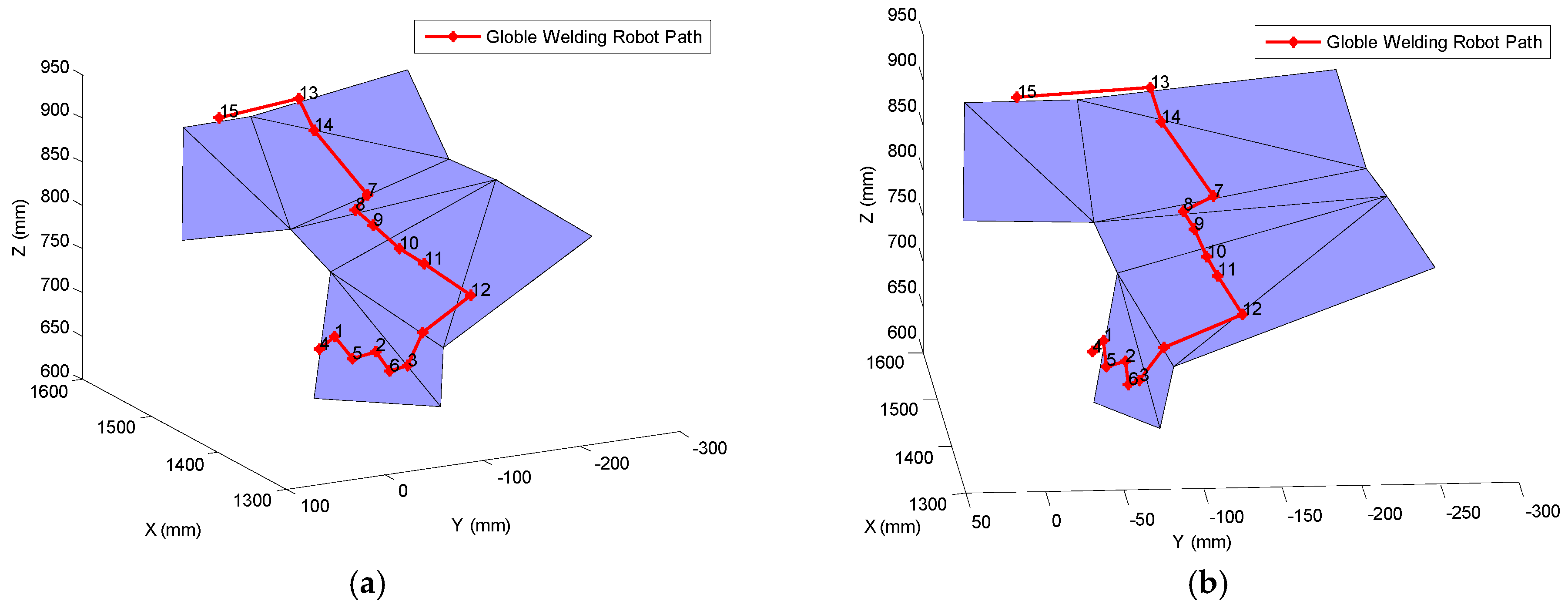
| NO. | X (mm) | Y (mm) | Z (mm) | NO. | X (mm) | Y (mm) | Z (mm) |
|---|---|---|---|---|---|---|---|
| 1 | 1443.60 | −53.20 | 686.00 | 9 | 1474.16 | −111.25 | 791.00 |
| 2 | 1399.56 | −60.05 | 688.49 | 10 | 1442.88 | −117.47 | 779.19 |
| 3 | 1356.00 | −66.67 | 689.57 | 11 | 1414.82 | −122.26 | 771.35 |
| 4 | 1456.36 | −48.49 | 669.34 | 12 | 1356.71 | −132.48 | 759.65 |
| 5 | 1417.70 | −54.51 | 671.94 | 13 | 1554.17 | −94.37 | 909.95 |
| 6 | 1379.31 | −60.57 | 674.61 | 14 | 1539.25 | −99.03 | 879.83 |
| 7 | 1504.91 | −126.99 | 813.51 | 15 | 1549.76 | −8.79 | 903.34 |
| 8 | 1493.74 | −109.17 | 801.14 | - | - | - | - |
| Q | N | M | Initial Pheromone | |||
|---|---|---|---|---|---|---|
| 1 | 11 | 0.9 | 5 | 50 | 50 | 0.5 |
| N | M | Method | Path Length L (mm) | Time t (s) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Min | Max | Mean | SD | Min | Max | |||
| 5 | 5 | ACO | 681.000 | 97.002 | 560.000 | 910.000 | 1.094 | 0.105 | 0.909 | 1.294 |
| SO-ACO | 206.326 | 8.760 | 202.507 | 242.524 | 1.242 | 0.102 | 1.066 | 1.403 | ||
| 10 | 10 | ACO | 579.500 | 55.864 | 490.000 | 670.000 | 4.234 | 0.286 | 3.739 | 4.950 |
| SO-ACO | 203.085 | 0.617 | 202.390 | 204.582 | 4.369 | 0.303 | 3.844 | 5.098 | ||
| 20 | 20 | ACO | 460.500 | 33.162 | 400.000 | 530.000 | 13.391 | 0.440 | 12.672 | 14.584 |
| SO-ACO | 203.219 | 0.931 | 202.390 | 206.187 | 13.511 | 0.436 | 12.783 | 14.676 | ||
| 30 | 30 | ACO | 361.000 | 12.937 | 340.000 | 390.000 | 25.038 | 0.901 | 23.776 | 28.028 |
| SO | 203.039 | 0.770 | 202.507 | 205.451 | 25.152 | 0.893 | 23.901 | 28.122 | ||
| 40 | 40 | ACO | 330.500 | 2.236 | 330.000 | 340.000 | 43.199 | 2.118 | 38.954 | 47.122 |
| SO-ACO | 202.930 | 0.357 | 202.370 | 203.426 | 43.332 | 2.125 | 39.063 | 47.263 | ||
| 50 | 50 | ACO | 330.000 | 0.000 | 330.000 | 330.000 | 56.213 | 3.892 | 50.827 | 68.322 |
| SO-ACO | 203.120 | 1.069 | 202.390 | 206.187 | 56.340 | 3.901 | 50.930 | 68.468 | ||
| 60 | 60 | ACO | 330.000 | 0.000 | 330.000 | 330.000 | 76.361 | 6.807 | 65.979 | 89.289 |
| SO-ACO | 202.800 | 0.477 | 202.390 | 204.443 | 76.492 | 6.814 | 66.093 | 89.455 | ||
| Iterations | Population Size | Weight | Initial Positions | Initial Velocities | ||
|---|---|---|---|---|---|---|
| 100 | 50 | 1.0 | 1.0 | 0.4 | random | random |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Xue, L.; Yan, Y.; Gu, X. Welding Robot Collision-Free Path Optimization. Appl. Sci. 2017, 7, 89. https://doi.org/10.3390/app7020089
Wang X, Xue L, Yan Y, Gu X. Welding Robot Collision-Free Path Optimization. Applied Sciences. 2017; 7(2):89. https://doi.org/10.3390/app7020089
Chicago/Turabian StyleWang, Xuewu, Lika Xue, Yixin Yan, and Xingsheng Gu. 2017. "Welding Robot Collision-Free Path Optimization" Applied Sciences 7, no. 2: 89. https://doi.org/10.3390/app7020089
APA StyleWang, X., Xue, L., Yan, Y., & Gu, X. (2017). Welding Robot Collision-Free Path Optimization. Applied Sciences, 7(2), 89. https://doi.org/10.3390/app7020089