A GTA Welding Cooling Rate Analysis on Stainless Steel and Aluminum Using Inverse Problems
Abstract
:1. Introduction
2. Materials and Methods
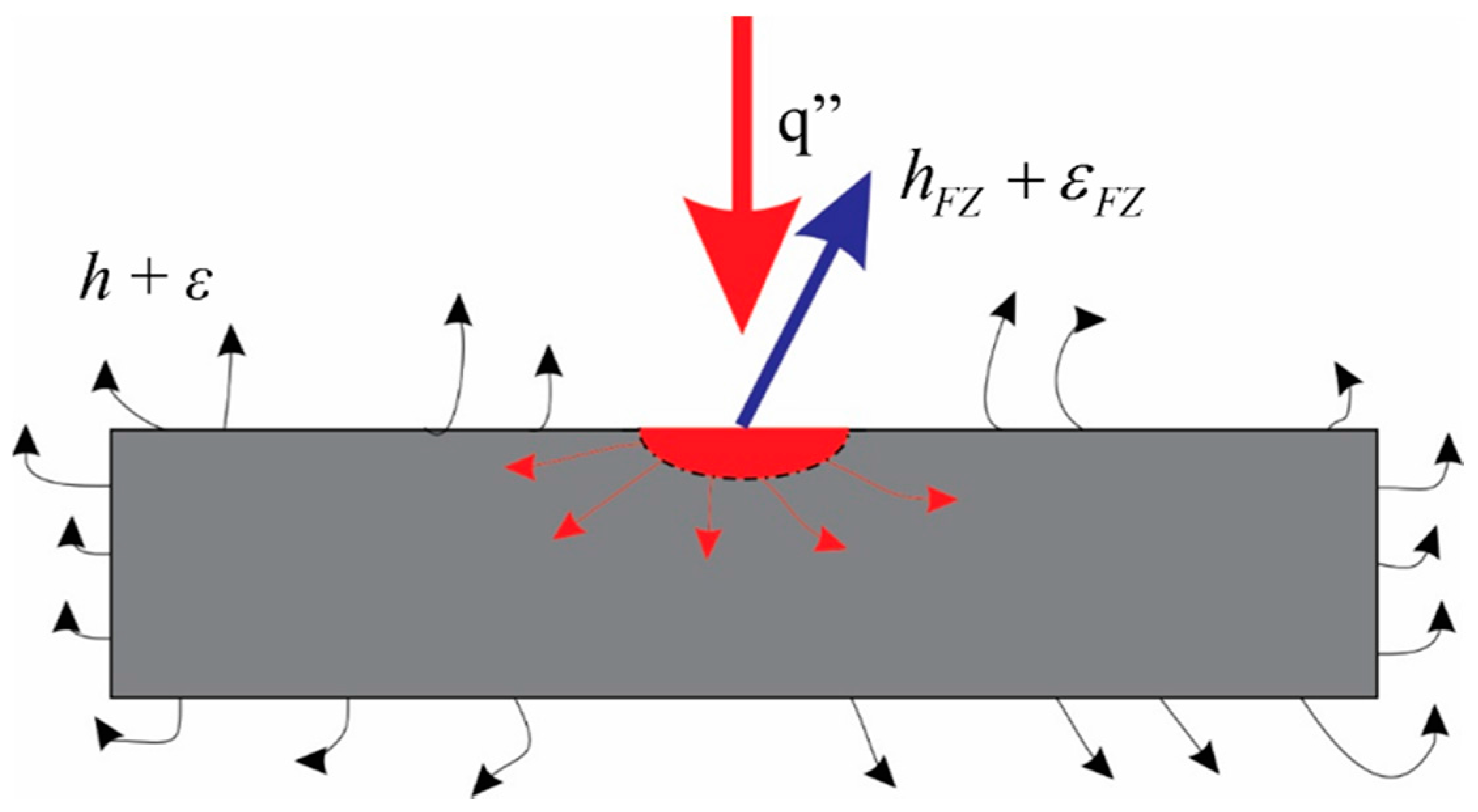
2.1. Thermal Model
2.2. Aluminum 6065-T5
2.3. Stainless Steel AISI 304L
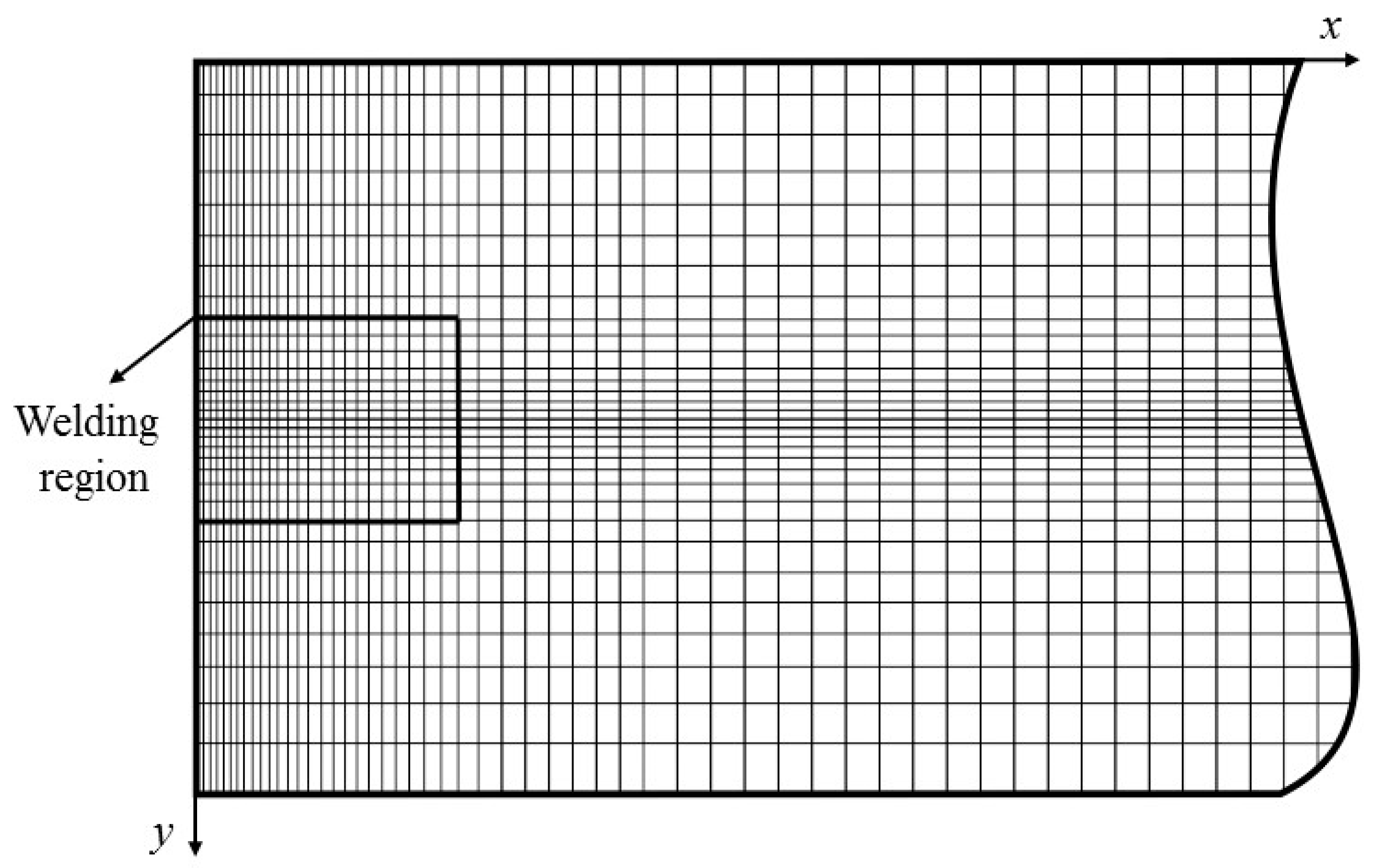
2.4. Numerical Analysis
3. Results and Discussion
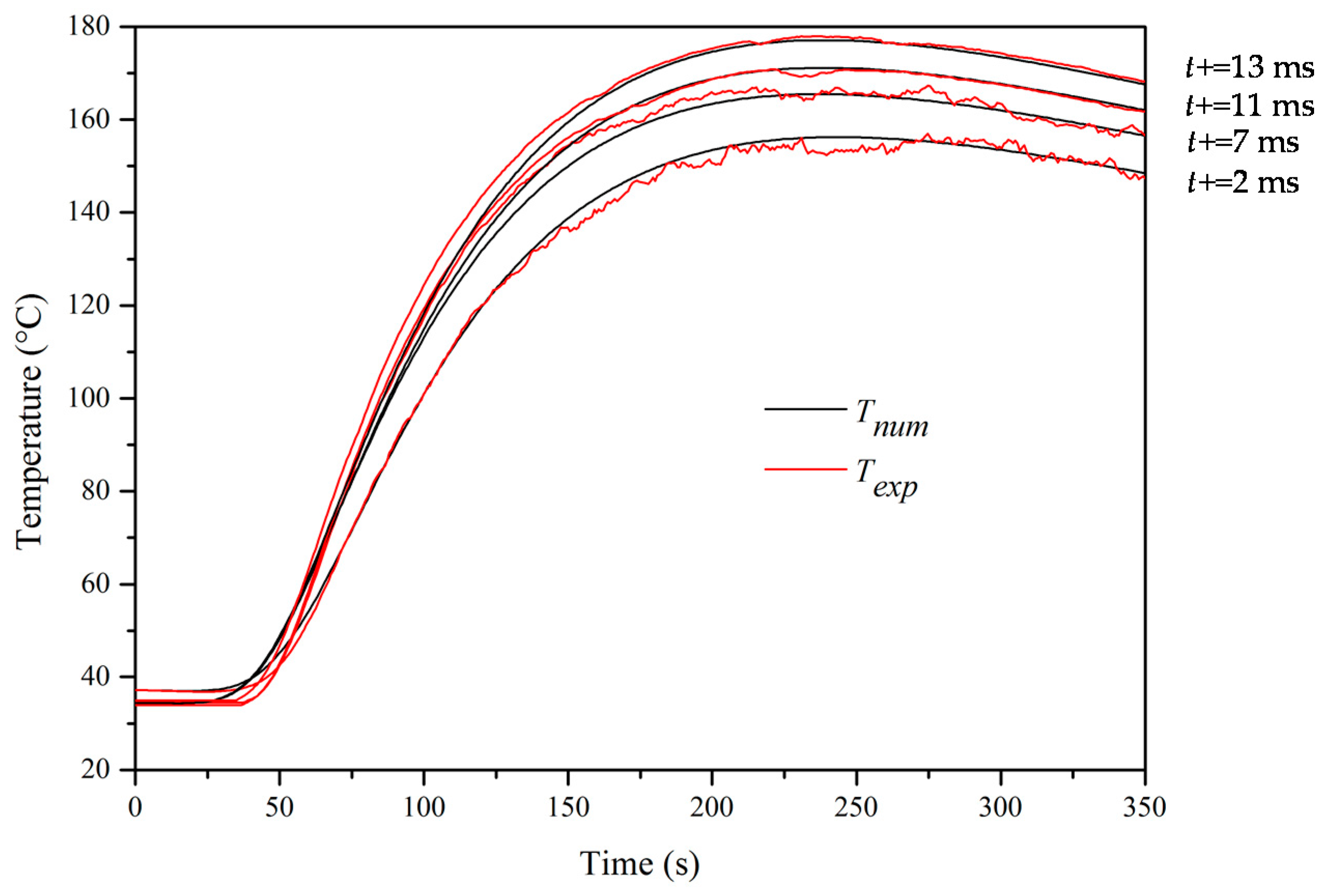
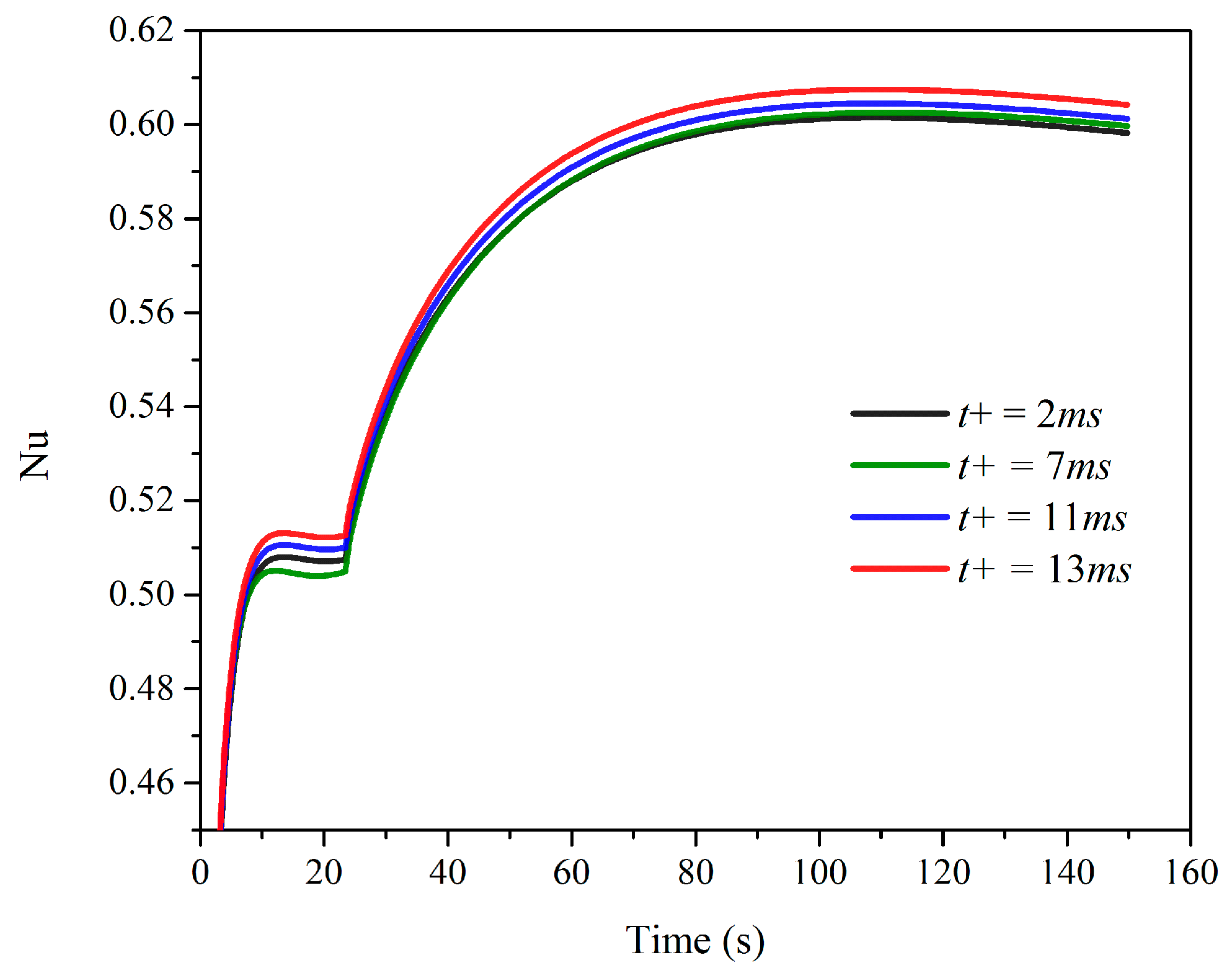
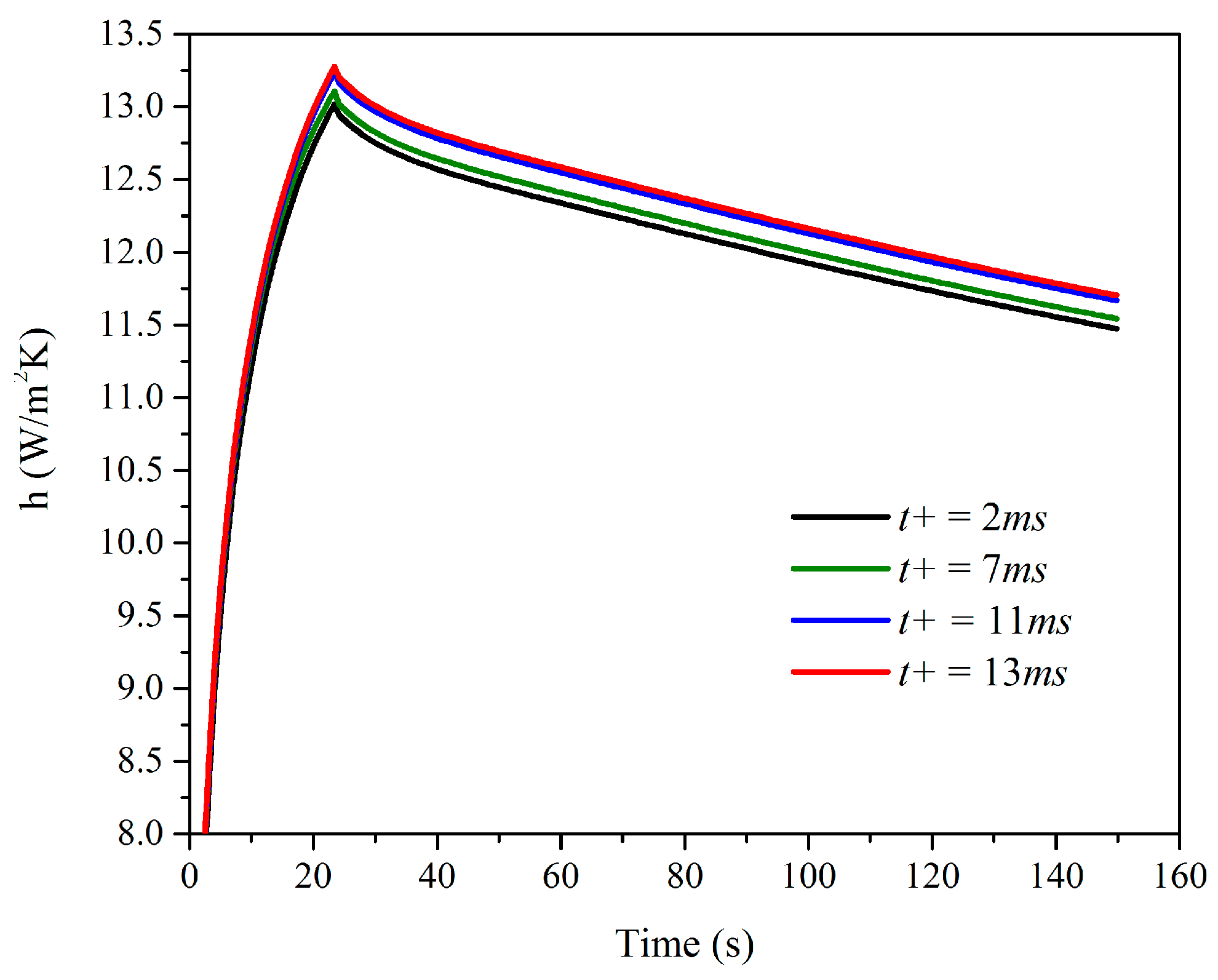
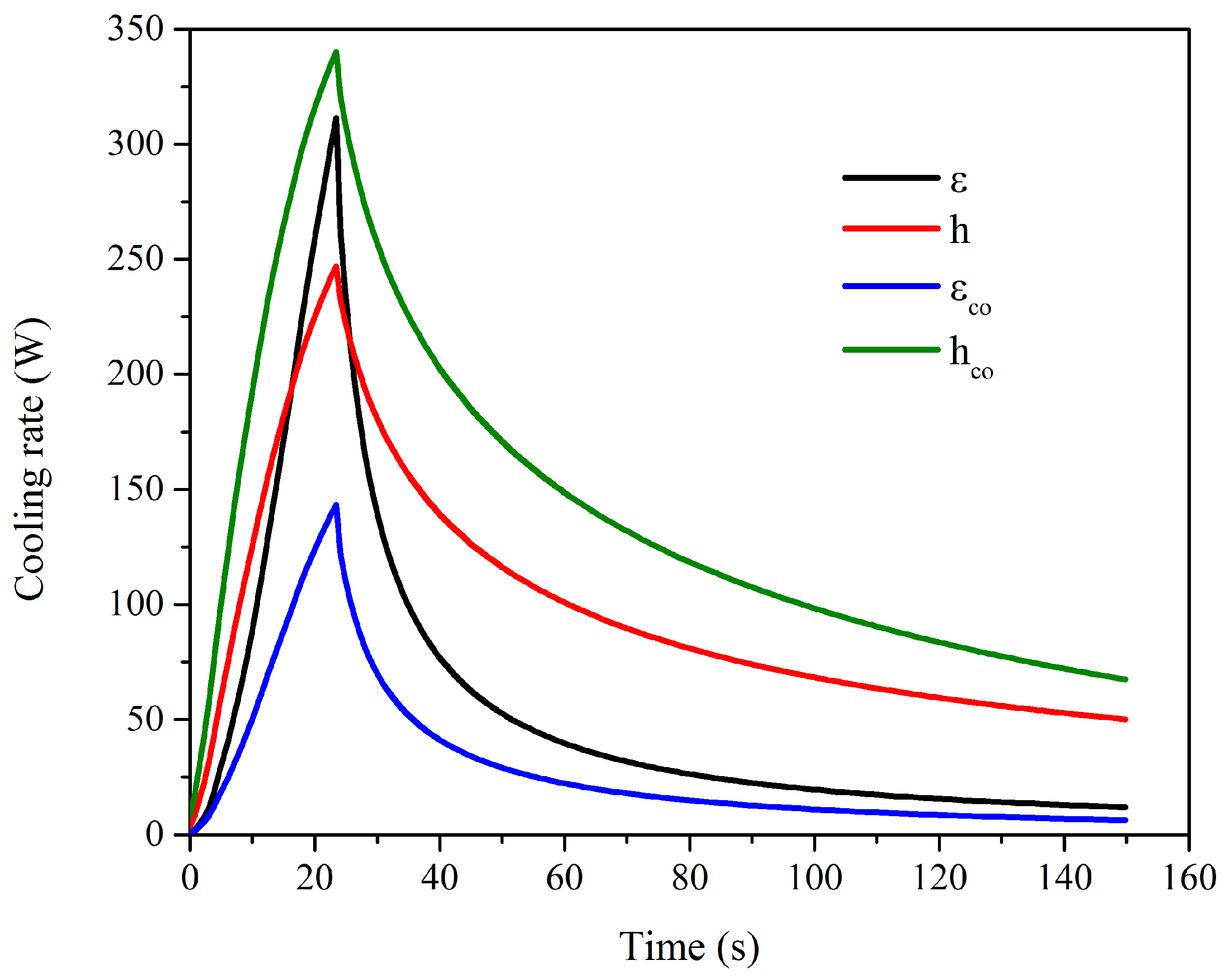
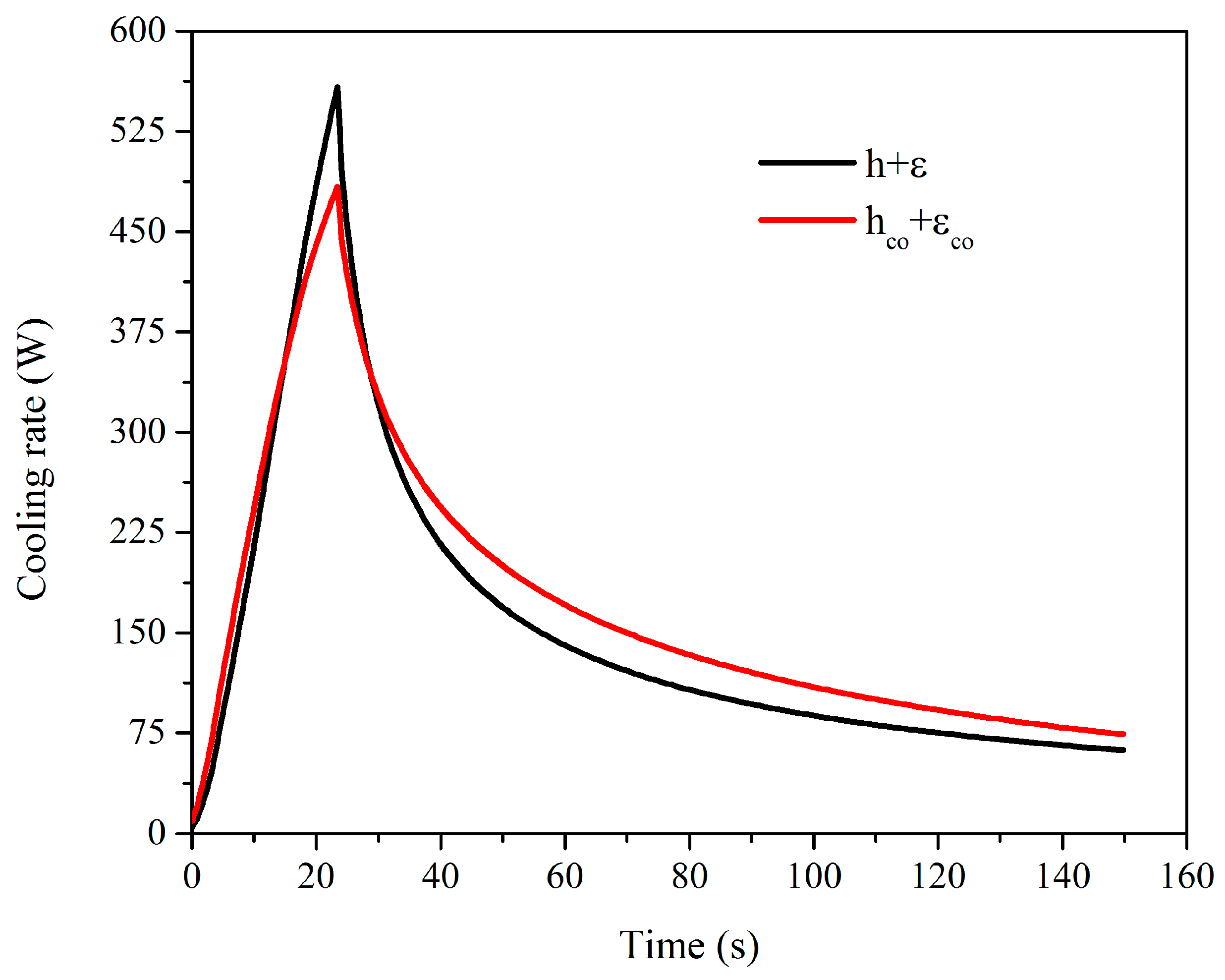
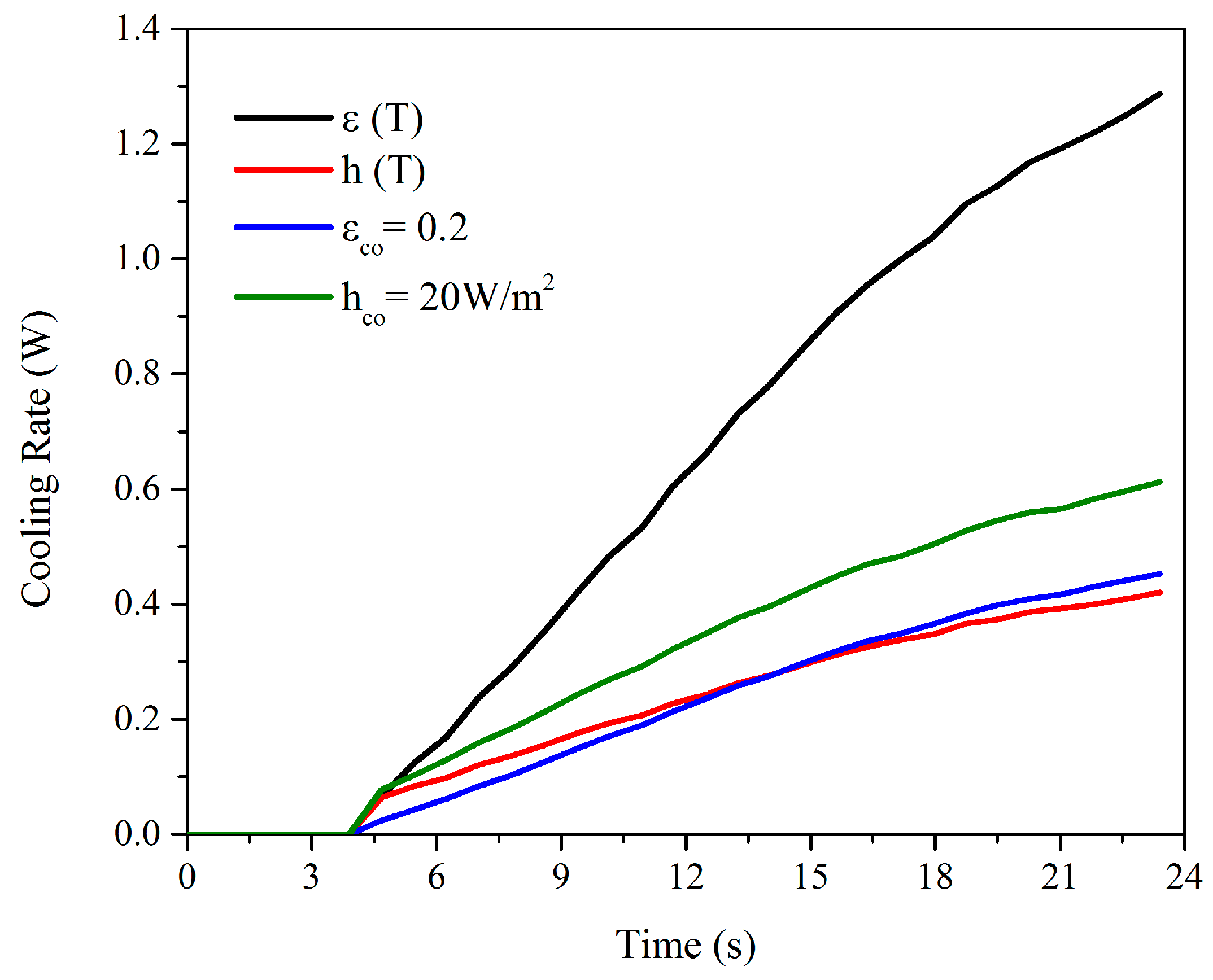
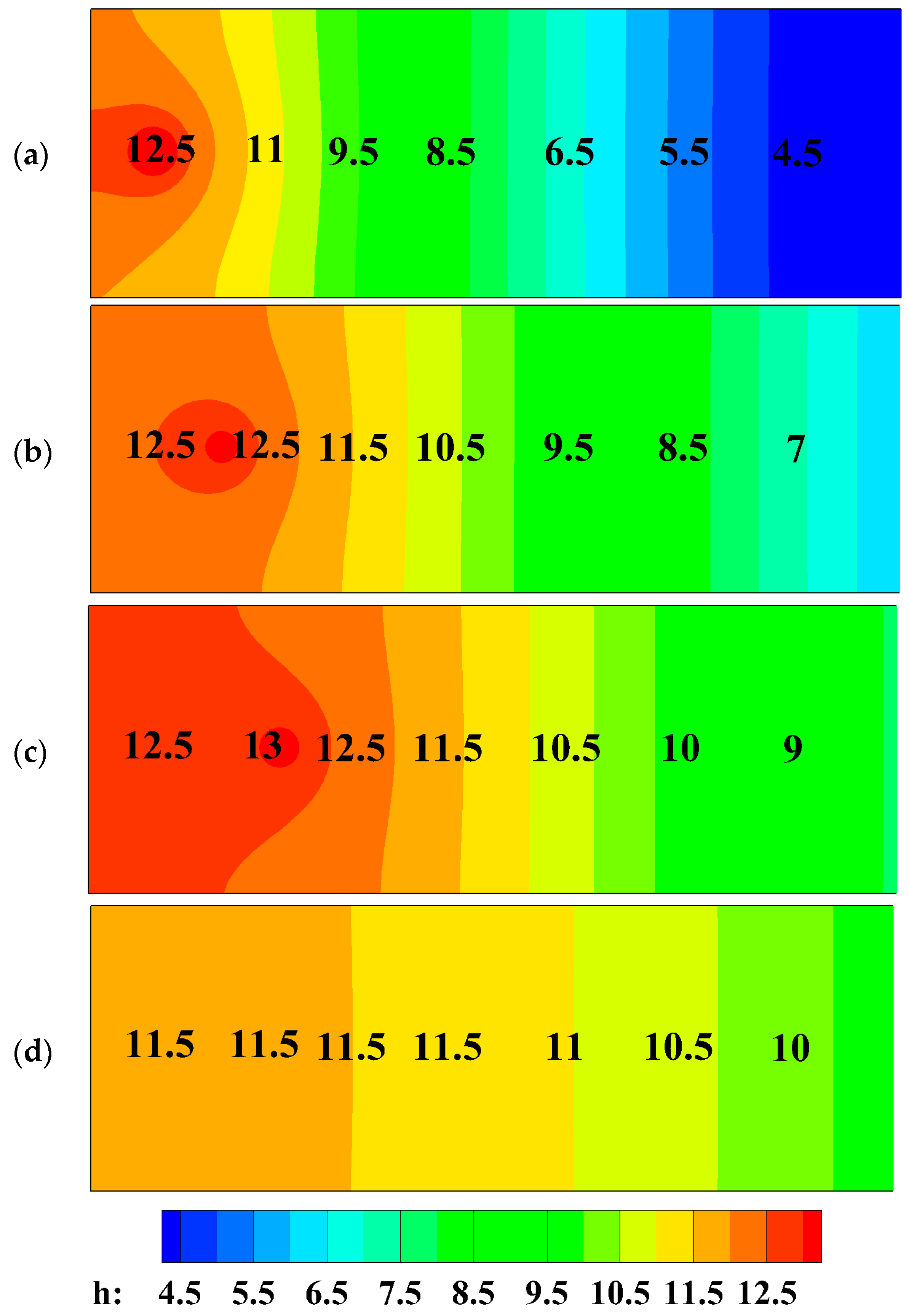
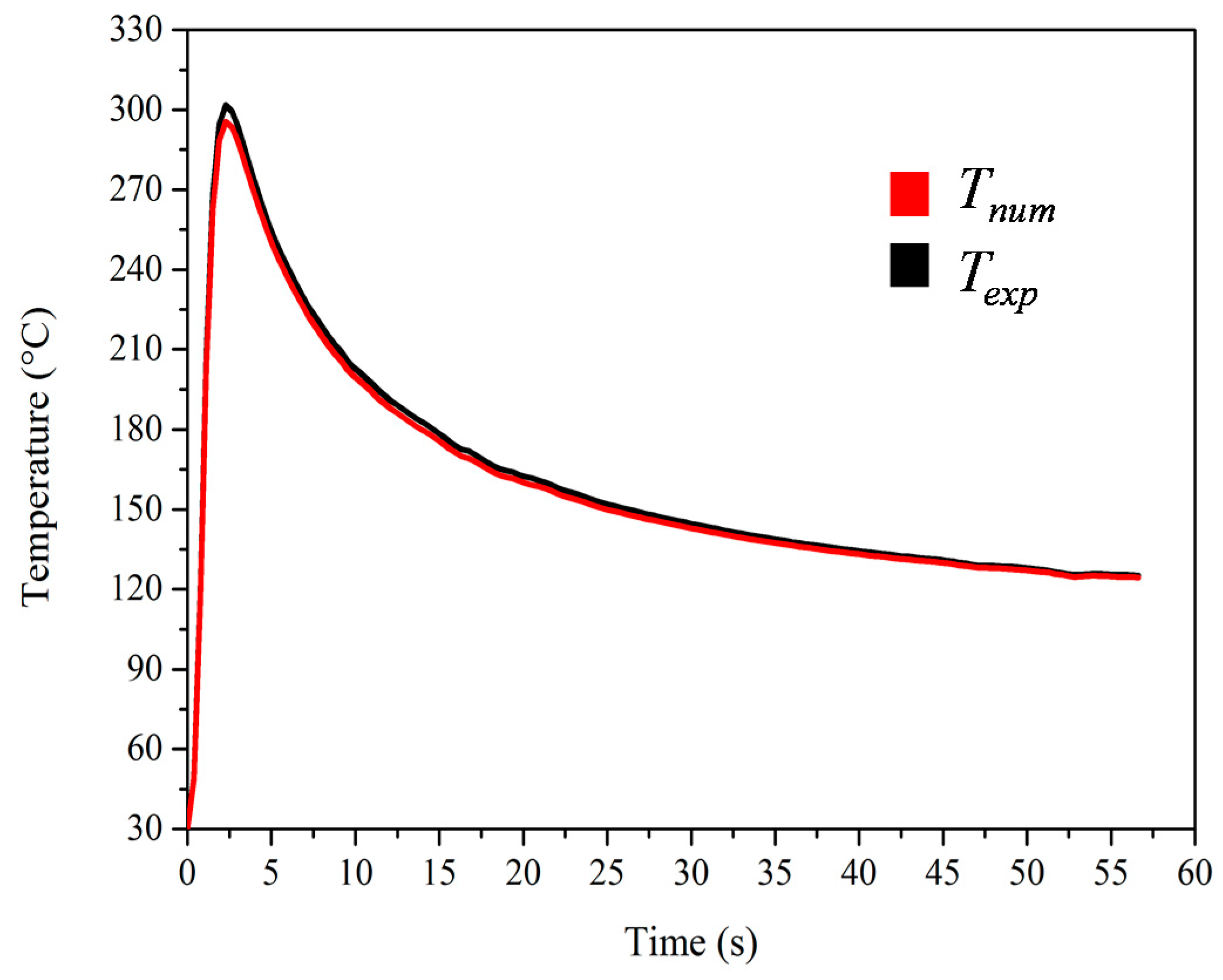
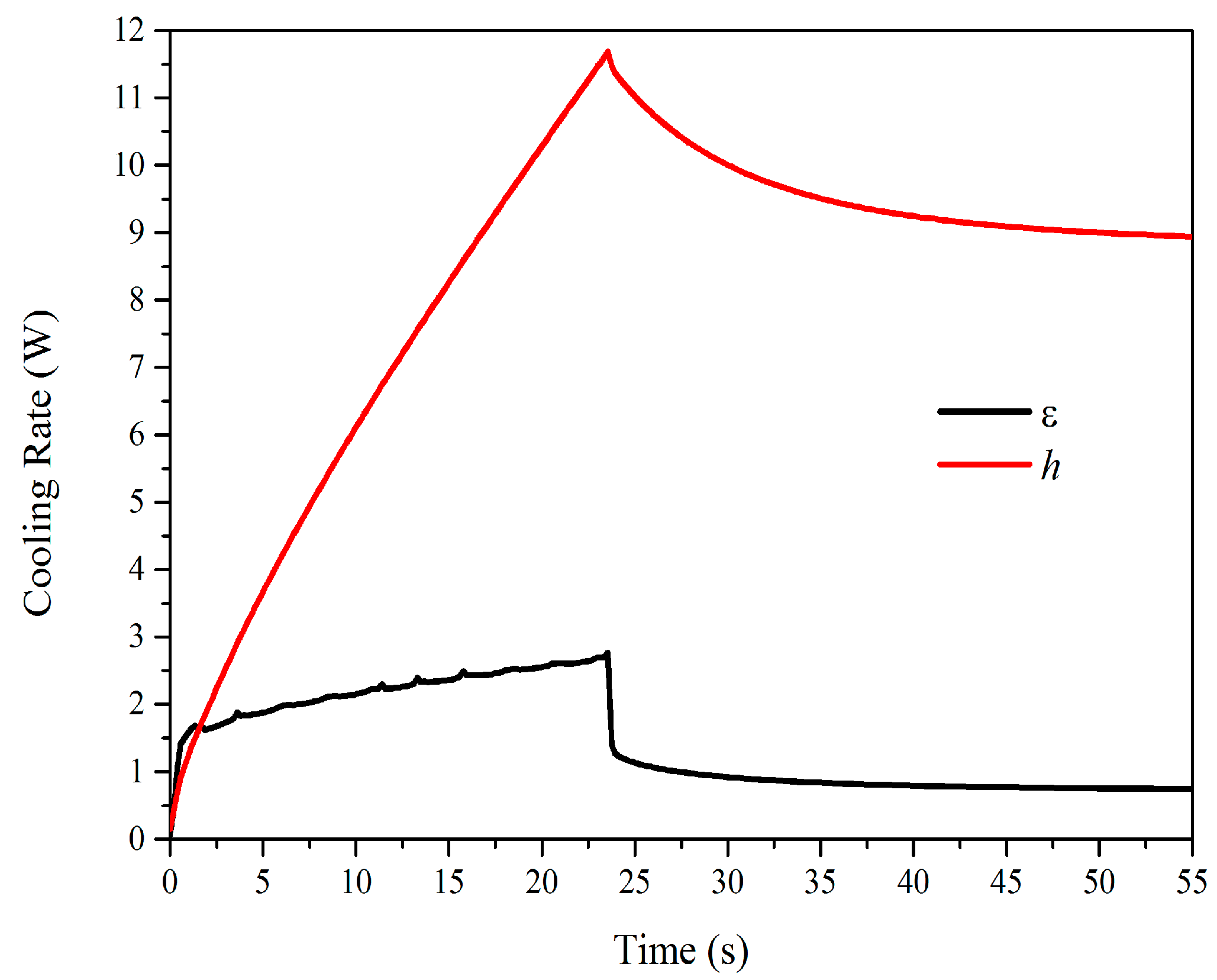
3.1. Aluminum 6065 T5
3.2. Stainless Steel
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dong, W.; Lu, S.; Li, D.; Li, Y. GTAW liquid pool convections and the weld shape variations under helium gas shielding. Int. J. Heat Mass Transf. 2011, 54, 1420–1431. [Google Scholar] [CrossRef]
- Goldak, J.A.; Akhlaghi, M. Computational Welding Mechanics; Springer: New York, NY, USA, 2005. [Google Scholar]
- Li, D.; Lu, S.; Dong, W.; Li, D.; Li, Y. Study of the law between the weld pool shape variations with the welding parameters under two TIG processes. J. Mater. Process. Technol. 2012, 212, 128–136. [Google Scholar] [CrossRef]
- Yadaiah, N.; Bag, S. Effect of Heat Source Parameters in Thermal and Mechanical Analysis of Linear GTA Welding Process. ISIJ Int. 2012, 52, 2069–2075. [Google Scholar] [CrossRef]
- Zareie Rajani, H.R.; Torkamani, H.; Sharbati, M.; Raygan, S. Corrosion resistance improvement in Gas Tungsten Arc Welded 316L stainless steel joints through controlled preheat treatment. Mater. Des. 2012, 34, 51–57. [Google Scholar] [CrossRef]
- Radzievskii, V.N.; Rymar, V.I.; Besednyi, V.A.; Chernov, V.Y. Use of high-temperature vaccum welding in fabrication of the parts of centrifugal compressors. Chem. Pet. Eng. 1975, 11, 925–927. [Google Scholar] [CrossRef]
- Gonçalves, C.V.; Carvalho, S.R.; Guimarães, G. Application of optimization techniques and the enthalpy method to solve a 3D-inverse problem during a TIG welding process. Appl. Therm. Eng. 2010, 30, 2396–2402. [Google Scholar] [CrossRef]
- Aissani, M.; Guessasma, S.; Zitouni, A.; Hamzaoui, R.; Bassir, D.; Benkedda, Y. Three-dimensional simulation of 304L steel TIG welding process: Contribution of the thermal flux. Appl. Therm. Eng. 2015, 89, 822–832. [Google Scholar] [CrossRef]
- Magalhães, E.D.S.; de Carvalho, S.R.; de Lima E Silva, A.L.F.; Lima E Silva, S.M.M. The use of non-linear inverse problem and enthalpy method in GTAW process of aluminum. Int. Commun. Heat Mass Transf. 2015, 66, 114–121. [Google Scholar] [CrossRef]
- Schneider, G.E.; Zedan, M. A Modified Strongly Implicit Procedure for the Numerical Solution of Field problems. Numer. Heat Transf. Part B Fundam. 1981, 4, 1–19. [Google Scholar] [CrossRef]
- Vanderplaats, G.N. Numerical Optimization Techniques for Engineering Design, 4th ed.; Vanderplaats Research and Development Inc.: Colorado Springs, CO, USA, 2005. [Google Scholar]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; DeWitt, D.P. Fundamentals of Heat and Mass Transfer; Wiley: New York, NY, USA, 2011. [Google Scholar]
- Toten, E.; Macknzie, D. Handbook of Aluminum—Physical Metallurgy and Process; Marcel Dekker Inc.: New York, NY, 2003. [Google Scholar]
- Jensen, J.E.; Tuttle, W.A.; Stwart, R.B.; Brechna, H.; Prodell, A.G. Selected Cryogenic Data Notebook; Brookhaven National Laboratory: Upton, NY, USA, 1980; Vol. 2.
- Lima e Silva, S.M.M.; Vilarinho, L.; Scotti, A.; Ong, T.; Guimaraes, G. Heat flux determination in gas-tungsten-arc welding process by using a three–dimensional model in inverse heat conduction problem. High Temp. Press. 2003, 35/36, 117–126. [Google Scholar] [CrossRef]
- International, A. ASM Ready Reference: Thermal Properties of Metals; ASM International: Materials Park, OH, USA, 2002. [Google Scholar]
- Touloukian, Y.S.; Kirby, R.K.; Taylor, R.E.; Desai, P.D. Volume 1: Thermal conductivity—Metallic elements and alloys. In Thermophysical Properties of Matter—The TPRC Data Series; Defense Technical Information Center: Fort Belvoir, VA, USA, 1975; p. 1595. [Google Scholar]
- Roger, C.R.; Yen, S.H.; Ramanathan, K.G. Temperature variation of total hemispherical emissivity of stainless steel AISI 304. J. Opt. Soc. Am. 1979, 69, 1384–1390. [Google Scholar] [CrossRef]
- Mehrtash, M.; Tari, I. A correlation for natural convection heat transfer from inclined plate-finned heat sinks. Appl. Therm. Eng. 2013, 51, 1067–1075. [Google Scholar] [CrossRef]



© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magalhaes, E.D.S.; Lima e Silva, A.L.F.d.; Lima e Silva, S.M.M. A GTA Welding Cooling Rate Analysis on Stainless Steel and Aluminum Using Inverse Problems. Appl. Sci. 2017, 7, 122. https://doi.org/10.3390/app7020122
Magalhaes EDS, Lima e Silva ALFd, Lima e Silva SMM. A GTA Welding Cooling Rate Analysis on Stainless Steel and Aluminum Using Inverse Problems. Applied Sciences. 2017; 7(2):122. https://doi.org/10.3390/app7020122
Chicago/Turabian StyleMagalhaes, Elisan Dos Santos, Ana Lúcia Fernandes de Lima e Silva, and Sandro Metrevelle Marcondes Lima e Silva. 2017. "A GTA Welding Cooling Rate Analysis on Stainless Steel and Aluminum Using Inverse Problems" Applied Sciences 7, no. 2: 122. https://doi.org/10.3390/app7020122
APA StyleMagalhaes, E. D. S., Lima e Silva, A. L. F. d., & Lima e Silva, S. M. M. (2017). A GTA Welding Cooling Rate Analysis on Stainless Steel and Aluminum Using Inverse Problems. Applied Sciences, 7(2), 122. https://doi.org/10.3390/app7020122





