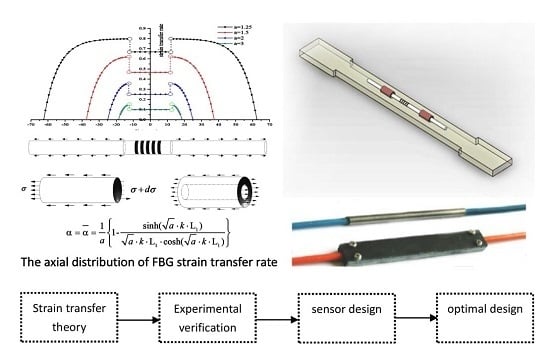
Strain Transfer Analysis of a Clamped Fiber Bragg Grating Sensor
Abstract
:1. Introduction
2. Basic Theory
3. Theoretical Strain Transfer Analysis
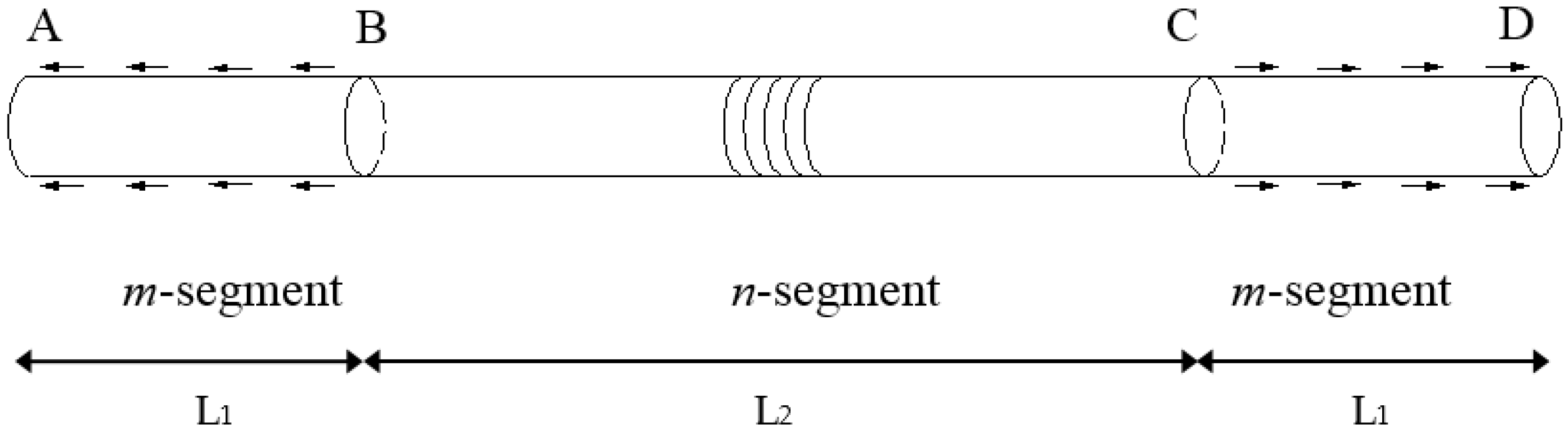
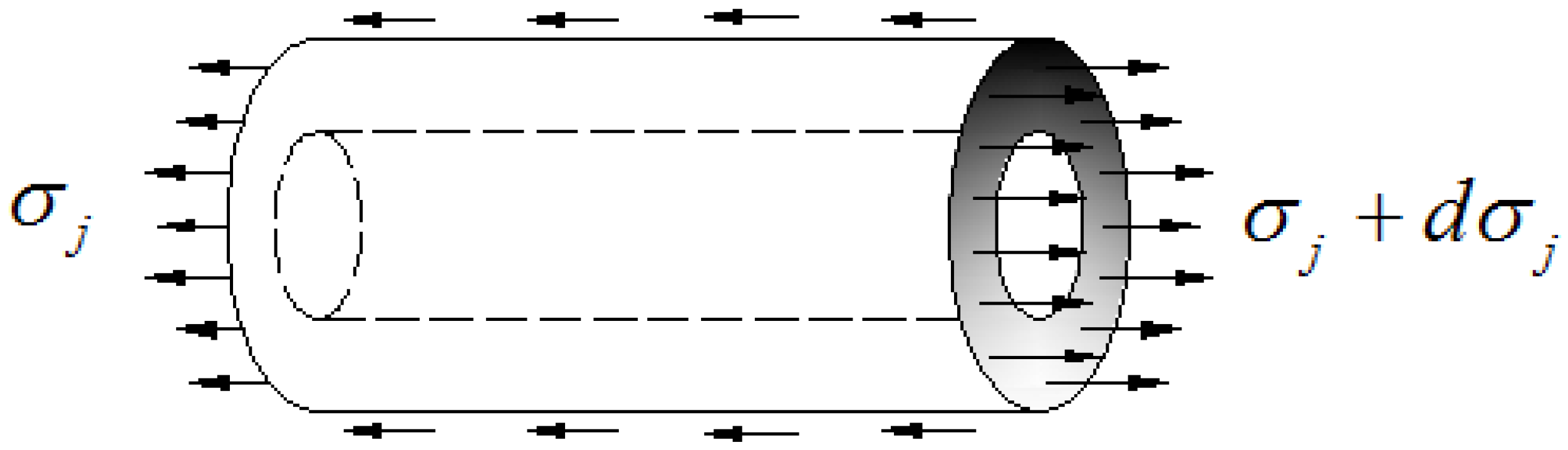
- The optical fiber is linearly elastic with its m-segment and n-segment having the same mechanical properties. The mechanical properties of optical fiber are impacted by taking advantage of phase masks and ultraviolet irradiation methods when processing FBG writing. The FBG sensor does not carry the external force directly, and the axial strain is supposed to transfer from the host material to the optical fiber by the interlayer shear deformation.
- The interlayer is a hollow cylinder, which is homogeneously coated on the fiber surface to undergo the shear deformation, regardless of its axial deformation.
- There is no relative slip between the FBG sensor and the interlayer.
3.1. Strain Transfer Rate Distribution of the m-Segment of the Optical Fiber
3.2. Strain Transfer Rate Distribution of the n-Segment of the Optical Fiber
4. Theoretical Analysis Results
4.1. Strain Transfer Rate of a Clamped FBG Sensor
4.2. Main Factors Affecting the Strain Transfer Rate
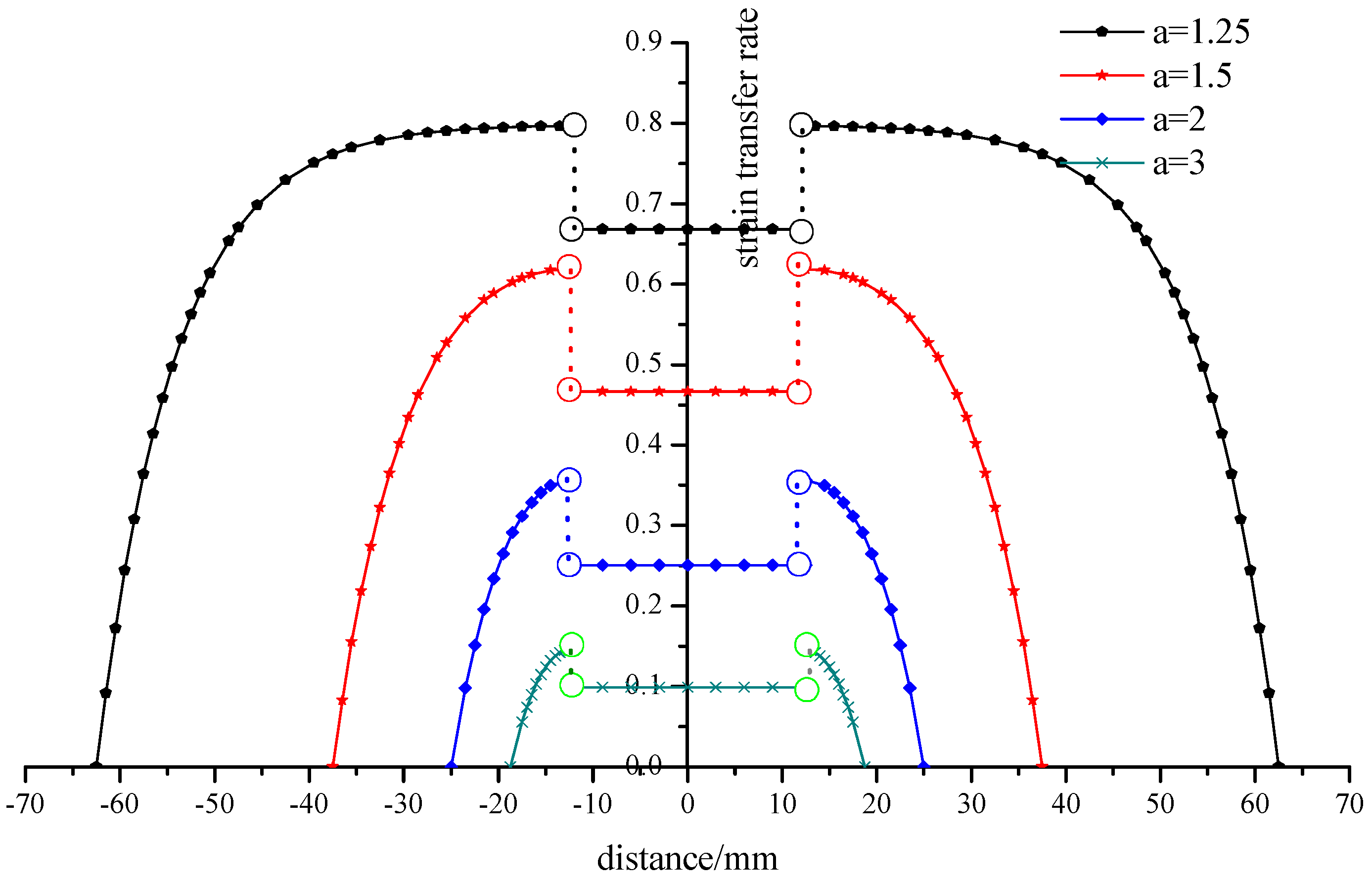
4.2.1. Effect of the Gauge Ratio
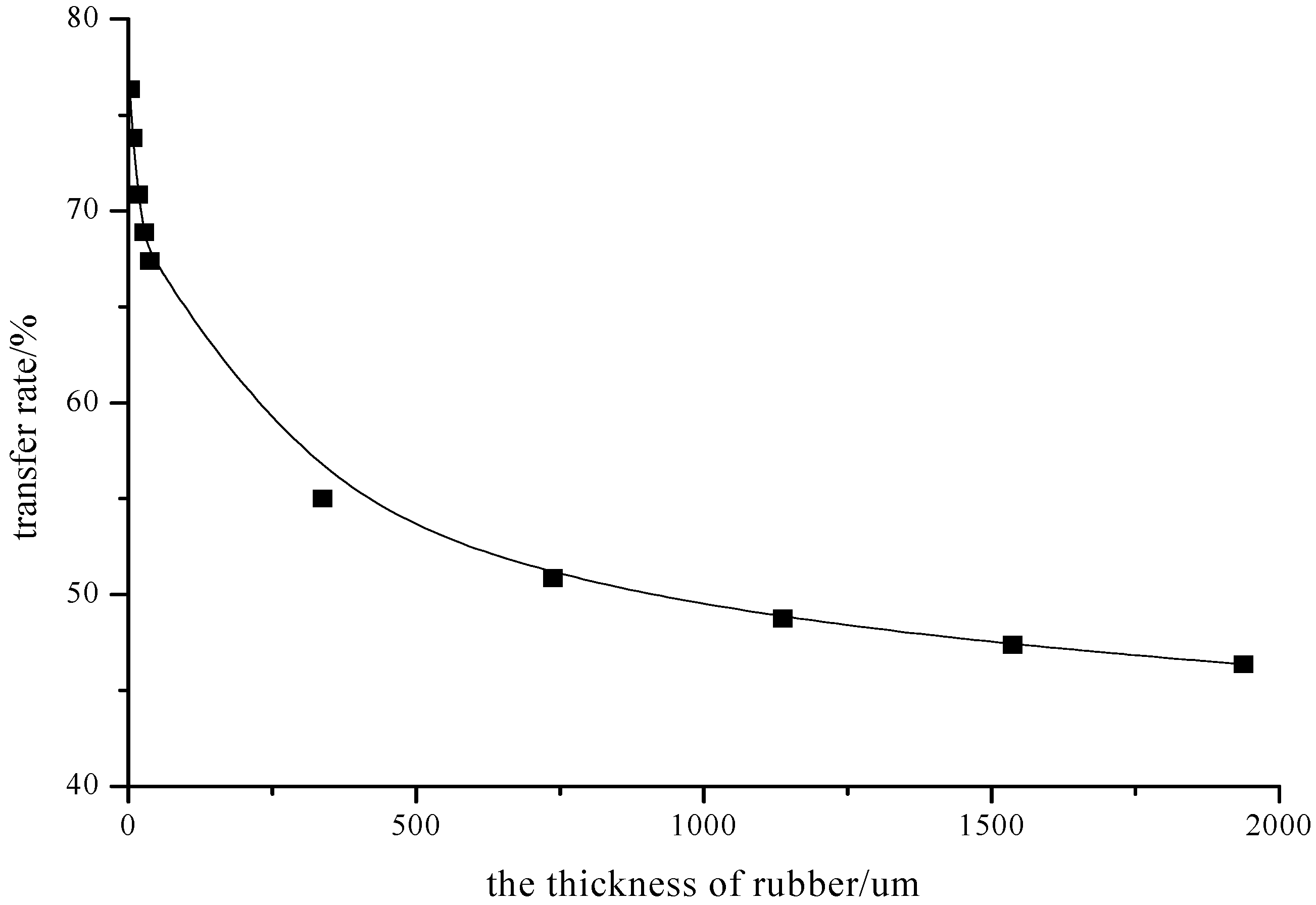
4.2.2. Effect of the Interlayer Thickness
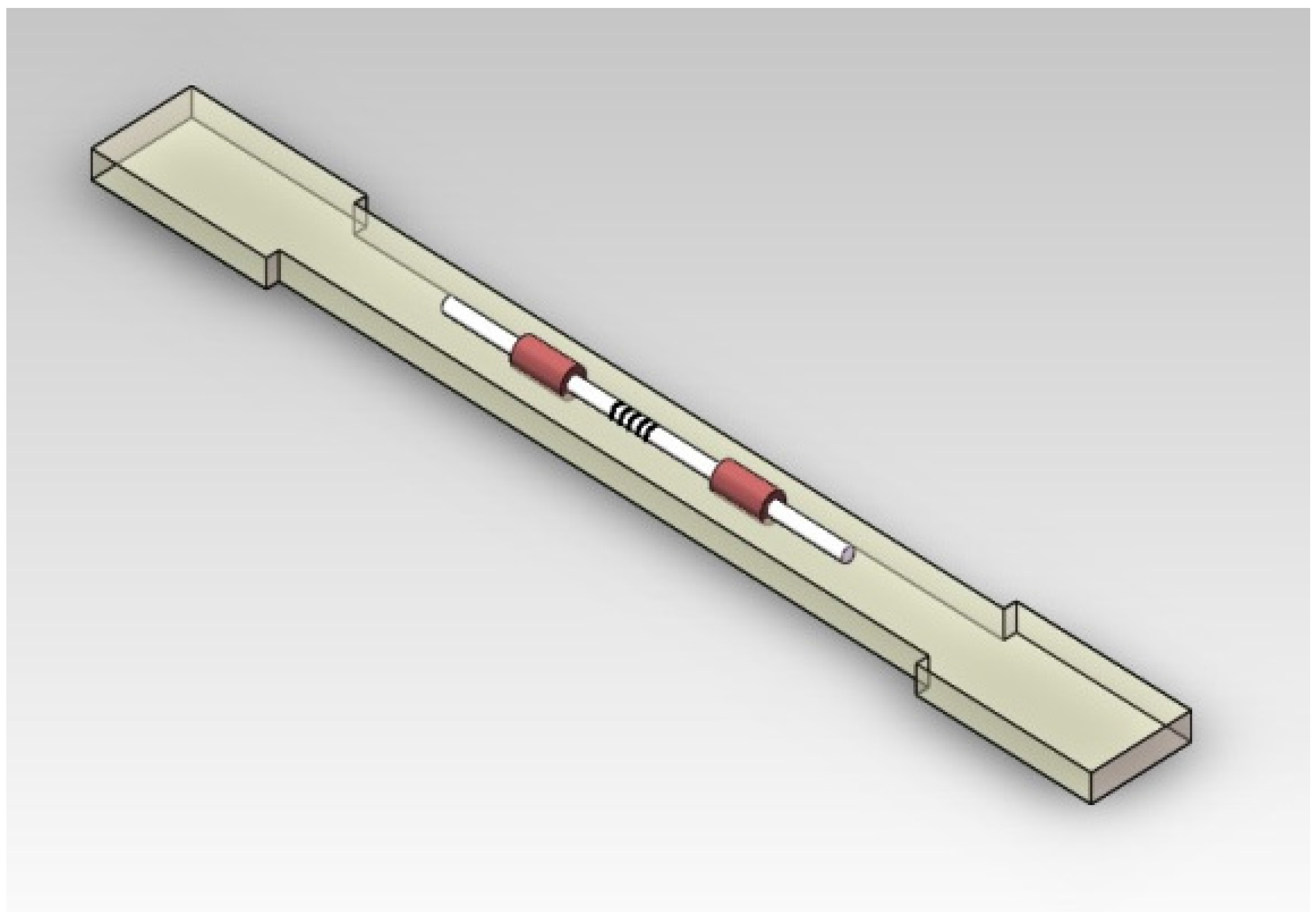
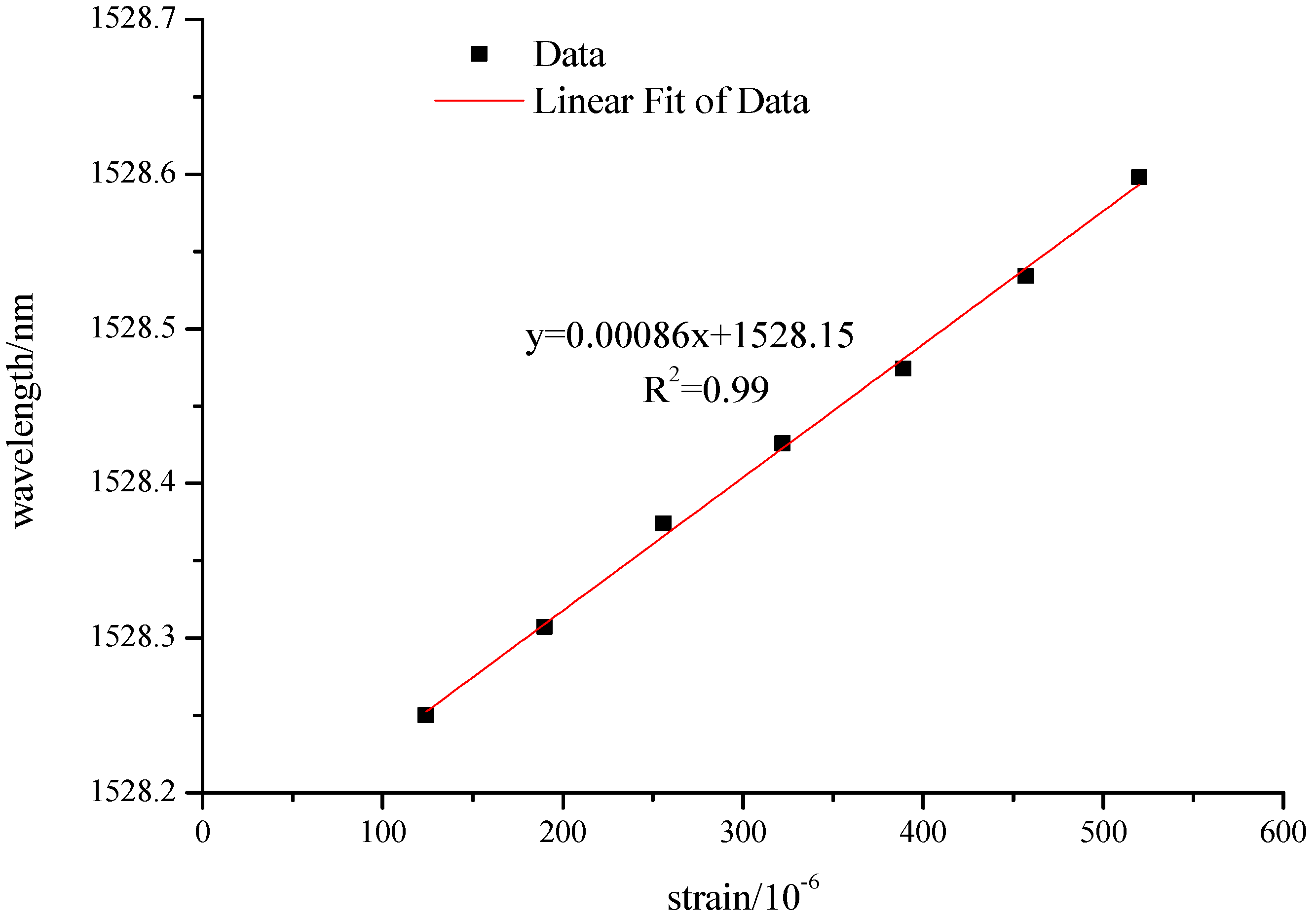
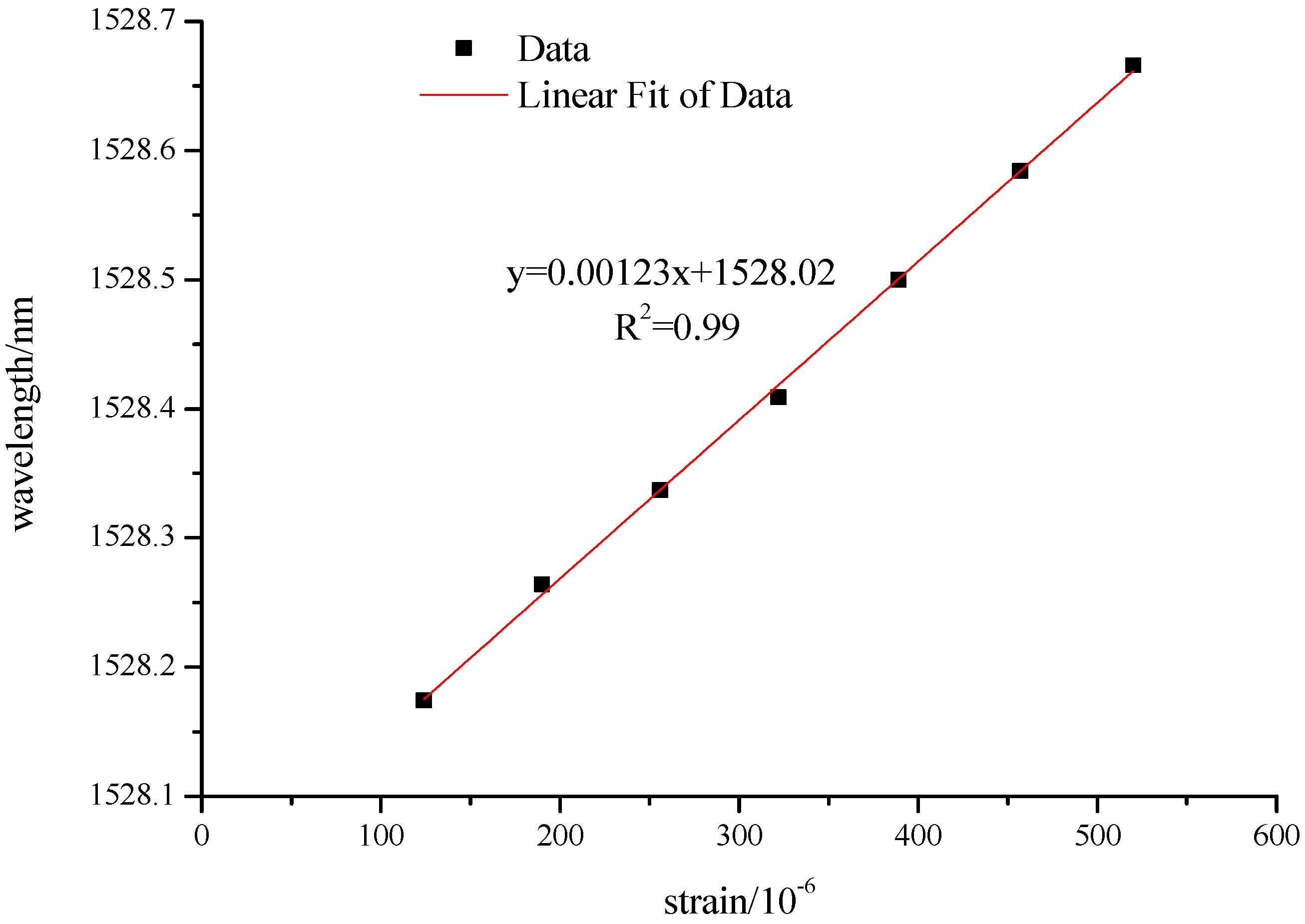
5. Experimental Verification
- (1).
- Specimen is clamped by supports on the testing machine. The pre-loading applied to the specimen is 30 kN, and the step loading is 5 kN every ten seconds until the total loading of 60 kN.
- (2).
- In ten seconds pause time, the resistances of the strain sensor and FBG demodulators are acquired as the immediate data.
- (1)
- Parameter error: The strain transfer rate of the theoretical model involves the elastic modulus of the optical fiber, shear modulus of the interlayer, Poisson ratio, etc. This may generate errors because of the difference between the used and actual values in testing conditions.
- (2)
- Model error: Some assumptions of the theoretical model lead to model errors. For example, the defect of the n-segment optical fiber appears in the writing process, which could alter the mechanical properties.
- (3)
- Test error: This is one important error source including sensor zero drift, asynchronous acquisition and the artificial reading error.
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sun, L.; Chen, C.; Sun, Q. Experimental and finite element analyses on the corrosion of underground pipelines. Sci. China Technol. Sci. 2015, 58, 1015–1020. [Google Scholar] [CrossRef]
- Nanni, A.; Yang, C.C.; Pan, K.; Wang, J.S.; Michael, R.R. Fiber-optic sensors for concrete strain/stress measurement. ACI Mater. J. 1991, 88, 257–264. [Google Scholar]
- Pak, Y.E. Longitudinal shear transfer in fiber optic sensors. Smart Mater. Struct. 1992, 1, 57–62. [Google Scholar] [CrossRef]
- Ansari, F.; Libo, Y. Mechanics of bond and interface shear transfer in optical fiber sensors. J. Eng. Mech. 1998, 124, 385–394. [Google Scholar] [CrossRef]
- Li, D.; Li, H.N. Strain transferring analysis of embedded fiber Bragg grating sensors. Acta Mech. Sin. Chin. Ed. 2005, 37, 435–441. [Google Scholar]
- Zhou, G.; Li, H.; Ren, L.; Li, D. Influencing parameters analysis of strain transfer in optic fiber Bragg grating sensors. SPIE Proc. 2006, 6179. [Google Scholar] [CrossRef]
- Sun, L.; Hao, H.; Zhang, B.; Ren, X.; Li, J. Strain Transfer Analysis of Embedded Fiber Bragg Grating Strain Sensor. J. Test. Eval. 2016, 44. [Google Scholar] [CrossRef]
- Yuan, L.; Zhou, L. Sensitivity coefficient evaluation of an embedded fiber-optic strain sensor. Sens. Actuators A 1998, 69, 5–11. [Google Scholar] [CrossRef]
- Zhang, G.; Jing, C.; Li, X.; Mi, X.; Li, Y.; Hao, L. Research on strain transfer of surface fiber grating sensor. Laser Optoelectron. Prog. 2014, 1, 52–57. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, J.L.; Ou, J.P. Interface strain transfer mechanism and error modification of embedded FBG strain sensors. J. Harbin Inst. Technol. 2006, 1, 49–55. [Google Scholar]
- Zhou, Z.; Wang, Q.; Hao, X. Strain transfer analysis of the FBG sensor considering the creep of the concrete host. China Meas. Test 2016, 42, 1–32. [Google Scholar]
- Chen, H.; Guo, Y. Strain transfer analysis and experimental research of substrate package fiber grating sensor. Transducer Microsyst. Technol. 2016, 35, 38–41. [Google Scholar]
- LI, T.; Tan, Y. Strain transfer factors of pasted FBG on bending part surface. Opt. Precis. Eng. 2015, 23, 1254–1264. [Google Scholar]
- Wan, K.T.; Leung, C.K.Y.; Olson, N.G. Investigation of the strain transfer for surface-attached optical fiber strain sensors. Smart Mater. Struct. 2008, 17, 035037. [Google Scholar] [CrossRef]
- Ho, S.C.M.; Ren, L.; Li, H.; Song, G. Dynamic fiber Bragg grating sensing method. Smart Mater. Struct. 2016, 25, 025028. [Google Scholar] [CrossRef]
- Rodriguez-Cobo, L.; Cobo, A.; Lopez-Higuera, J.M. Embedded compaction pressure sensor based on Fiber Bragg Gratings. Measurement 2015, 68, 257–261. [Google Scholar] [CrossRef]
- Tang, C.; Wang, T.X.; Huang, W.M.; Sun, L.; Gao, X.Y. Temperature sensors based on the temperature memory effect inshape memory alloys to check minor over-heating. Sens. Actuators 2016, 238, 337–343. [Google Scholar] [CrossRef]
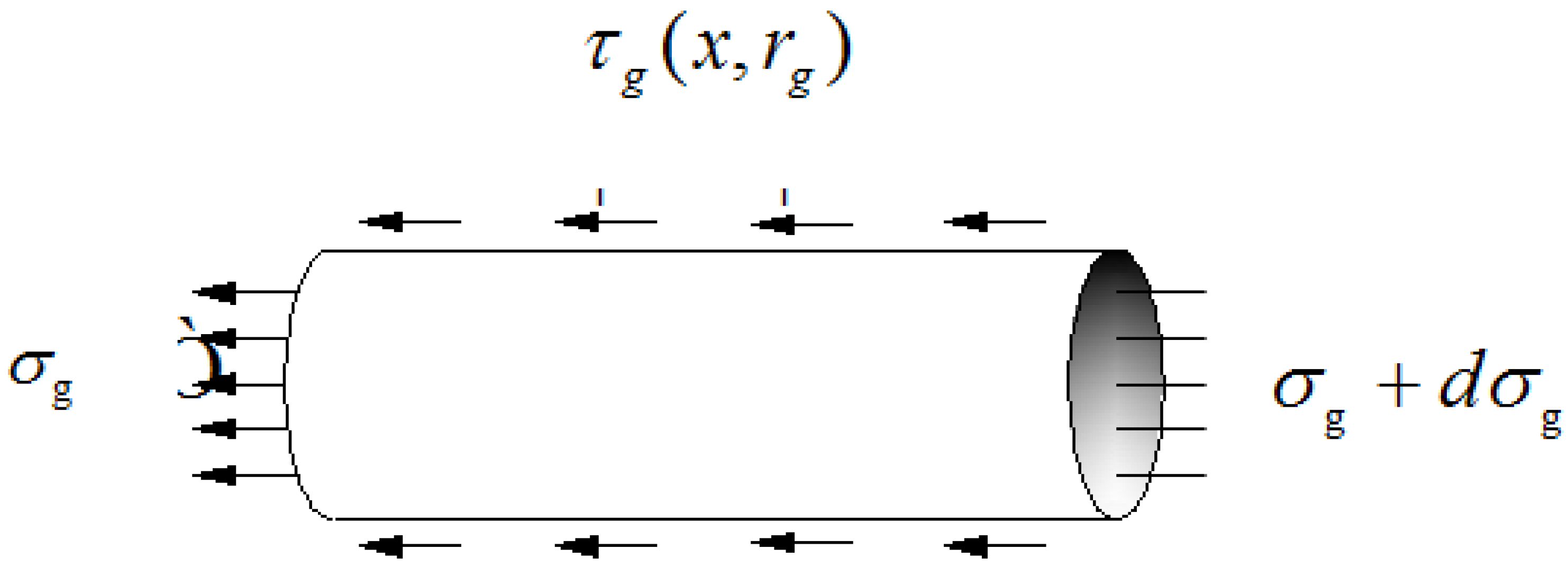


| Parameter/Unit | Symbol | Value |
|---|---|---|
| Elastic modulus of optical fiber/MPa | Eg | 72,000 |
| Elastic modulus of interlayer/MPa | Ej | 30 |
| Poisson ratio | µ | 0.48 |
| Radius of optical fiber/μm | rg | 62.5 |
| Interlayer thickness/μm | h | 440 |
| Gauge ratio parameter | A | 1.25 |
| Interlayer length/mm | L1 | 25 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, L.; Li, C.; Li, J.; Zhang, C.; Ding, X. Strain Transfer Analysis of a Clamped Fiber Bragg Grating Sensor. Appl. Sci. 2017, 7, 188. https://doi.org/10.3390/app7020188
Sun L, Li C, Li J, Zhang C, Ding X. Strain Transfer Analysis of a Clamped Fiber Bragg Grating Sensor. Applied Sciences. 2017; 7(2):188. https://doi.org/10.3390/app7020188
Chicago/Turabian StyleSun, Li, Chuang Li, Jun Li, Chunwei Zhang, and Xiaosu Ding. 2017. "Strain Transfer Analysis of a Clamped Fiber Bragg Grating Sensor" Applied Sciences 7, no. 2: 188. https://doi.org/10.3390/app7020188
APA StyleSun, L., Li, C., Li, J., Zhang, C., & Ding, X. (2017). Strain Transfer Analysis of a Clamped Fiber Bragg Grating Sensor. Applied Sciences, 7(2), 188. https://doi.org/10.3390/app7020188