Steady-State Creep of Asphalt Concrete

Abstract

This paper reports the experimental investigation of the steady-state creep process for fine-grained asphalt concrete at a temperature of 20 ± 2 °С and under stress from 0.055 to 0.311 MPa under direct tension and was found to occur at a constant rate. The experimental results also determined the start, the end point, and the duration of the steady-state creep process. The dependence of these factors, in addition to the steady-state creep rate and viscosity of the asphalt concrete on stress is satisfactorily described by a power function. Furthermore, it showed that stress has a great impact on the specific characteristics of asphalt concrete: stress variation by one order causes their variation by 3–4.5 orders. The described relations are formulated for the steady-state of asphalt concrete in a complex stressed condition. The dependence is determined between stress intensity and strain rate intensity.

1. Introduction

Asphalt concrete is one of the main materials used for highway pavements. Mechanical properties of an asphalt concrete are highly dependent on temperature and time of loading [1,2,3]. Therefore, the determination of the mechanical behavior of an asphalt concrete, taking into account the variation of the above-mentioned factors, has important practical value.

It is known that the basic methods for evaluating the mechanical behavior of viscoelastic materials are tests on creep and relaxation [4,5,6]. Technically, creep test investigations are easy to conduct, and their results make it possible to construct creep and long-term strength curves. Relaxation curves can be obtained from the creep curves by using known methods [6,7]. The long-term strength curves enable us to determine the service life of an asphalt concrete pavement.

The work in Reference [8] analyzes experimentally the process of uniaxial and triaxial creep for two asphalt concrete types (dense bitumen macadam and hot rolled asphalt) at a temperature range of 10 to 40 °C. It was determined that the creep curve of asphalt concretes has three characteristic stages, the second of which (steady-state creep stage) has a constant strain rate. The viscosity of asphalt concretes for this stage of creep curve depends nonlinearly on the stress.

As the result of experimental tests for four asphalt concrete types, Hassan [9] approximated the first and the second stages of the creep curve by power function. However, an attempt to establish a linear correlation relationship between an exponent of power function and an exponent of Paris law was not successful.

Soleimanbeigi et al. [10] obtained results experimentally that demonstrated the creep strain rate of recycled asphalt shingles with bottom ash (RAS-BA) increased the most with the increase of applied stress value. The relationship of creep strain rate with stress is described by the power function and showed that the strain and the strain rate of creep increased with a temperature increase.

The asphalt concrete test for uniaxial creep at four different temperatures and three levels of stress, with the purpose of permanent strain evaluation was performed by Mahan [11]. Test results showed that both stress and temperature impact greatly on creep strain and permanent strain. Having tested the cylindrical specimens of two asphalt concrete types for uniaxial creep during compression at the temperatures of 25, 40, and 60 °C and three levels of stress, Zhigang et al. [12] also determined that the creep curve of asphalt concrete had three stages, where the second stage had a constant strain rate. The authors defined creep strain as a viscous flow deformation, and also called the gradual reduction of deformation on the first stage and maintenance of strain rate as a constant on the second stage as the “consolidation effect”. Either temperature or stress greatly impacts creep strain. The greater the temperature, the less the asphalt concrete resists strain. The greater the stress at a similar temperature, the faster the damage occurs. The time period for the test was 5000 s. A simple model of creep with five parameters was determined from a generalized model of Kelvin, and was proposed for the same maximum duration of deformation.

The work in Reference [13] used the test results of asphalt concretes based on the three point bending test at different temperatures and levels of stress to develop master curves of stiffness modulus.

In this paper, test results of hot fine-grained asphalt concrete samples on creep are presented. Creep tests were carried out by a direct tensile scheme until complete fracture of the asphalt concrete samples was obtained. The test temperature was 20 ± 2 °C. The applied stress was changed from 0.055 to 0.311 MPa. Creep curves under different loads of the asphalt concrete were constructed. Three characteristic stages of creep curves—the unsteady-state, the steady-state, and the accelerating creep stages—are shown. The first creep curve stage of asphalt concrete was satisfactorily approximated by Rabotnov’s fractional exponential function [14]. A description of the third creep curve stage should be carried out on the basis of continuum damage mechanics approach [15,16], which is currently work in progress. Therefore, the second stage of the asphalt concrete creep curve is described.

2. Materials and Methods

2.1. Bitumen

Bitumen of grade 100–130, which met the requirements of the Kazakhstan standard [17], was used in this study. The bitumen grade on Superpave is PG (Performance Grade) 64–40 [18]. Basic standard indicators of the bitumen are shown in

Table 1. Basic standard indicators of the bitumen, ST RK: Standard of the Republic of Kazakhstan.

Indicator	Measurement Unit	Requirements of ST RK 1373	Value
Penetration, 25 °С, 100 gr, 5 s	0.1 mm	101–130	104
Penetration Index PI	-	−1.0, … ,+1.0	−0.34
Tensility at temperature:	cm	-	-
25 °С	-	≥90	140
0 °С	-	≥4.0	5.7
Softening point	°С	≥43	46.0
Fraas point	°С	≤−22	−25.9
Dynamic viscosity, 60 °С	Pa·s	≥120	175.0
Kinematic viscosity	mm2/s	≥180	398.0

. Bitumen is produced by the Pavlodar processing plant from the crude oil of Western Siberia (Oil processing plant, Omsk, Russia) by the direct oxidation method.

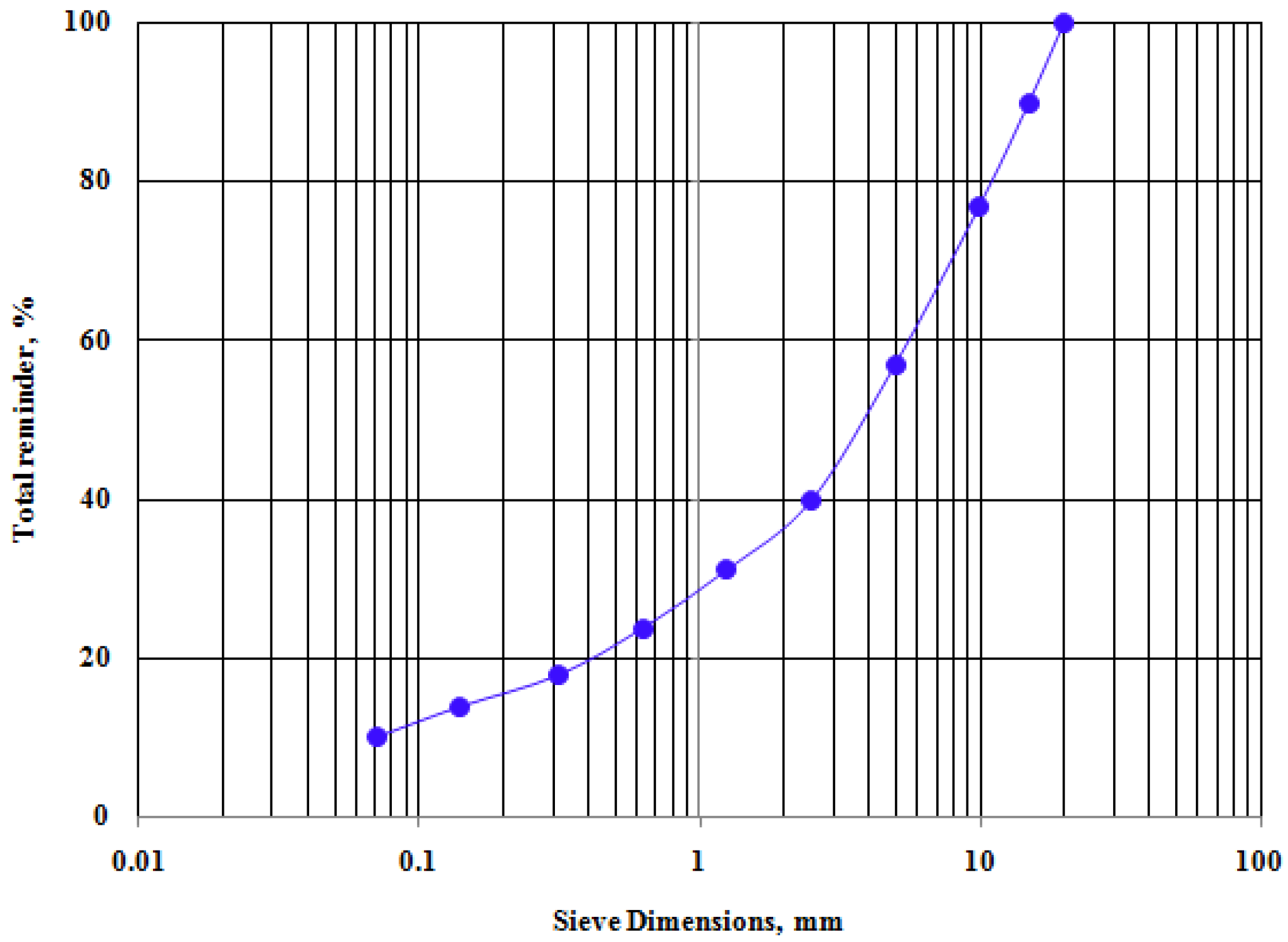
2.2. Asphalt Concrete

Hot dense asphalt concrete of type B that met the requirements of the Kazakhstan standard [19] was prepared with the use of aggregate fractions of 5–10 mm (20%); 10–15 mm (13%); and 15–20 mm (10%) from the Novo-Alekseevsk rock pit (Almaty region, Kazakhstan); sand of fraction 0–5 mm (50%) from the plant “Asphaltconcrete-1” (Almaty city, Kazakhstan); and activated mineral powder (7%) from the Kordai rock pit (Zhambyl region, Kazakhstan).

The bitumen content of grade 100–130 in the asphalt concrete was 4.8% by weight of dry mineral material. Basic standard indicators of the aggregate and the asphalt concrete are shown in

Table 2. Basic standard indicators of the crushed stone.

Indicator	Measurement Unit	Requirements of ST RK 1284 [20]	Value
			Fraction 5–10 mm	Fraction 10–20 mm
Average density	g/cm3	-	2.55	2.62
Elongated particle content	%	≤25	13	9
Clay particle content	%	≤1.0	0.3	0.2
Bitumen adhesion	-	-	satisf.	satisf.
Water absorption	%	-	1.93	0.90

and

Table 3. Basic standard indicators of the asphalt concrete.

Indicator	Measurement Unit	Requirements of ST RK 1225	Value
Average density	g/cm3	-	2.39
Water saturation	%	1.5–4.0	2.3
Voids in mineral aggregate	%	≤19	14
Air void content in asphalt concrete	%	2.5–5.0	3.8
Compression strength at temperature	MPa	-	-
0 °С	-	≤13.0	7.0
20 °С	-	-	3.4
50 °С	-	≥1.3	1.4

, respectively. A granulometric composition curve for the mineral part of asphalt concrete is shown in Figure 1.

2.3. Sample Preparation

Samples of the hot asphalt concrete in the form of a rectangular prism with dimensions 15,050 × 50 mm (Figure 2) were manufactured as follows. First, the asphalt concrete samples were prepared in the form of a square slab (Figure 3) using a Cooper compactor (model CRT-RC2S, Cooper, Nottingham, UK) (Figure 4) according to the standard in [21]. The samples were then cut from the asphalt concrete slabs in the form of a prism. Deviations in sizes of the beams did not exceed two millimeters.

2.4. Test

Tests on creep were carried out on hot asphalt concrete samples in the form of a rectangular prism, according to the direct tensile scheme until complete failure was reached. The test temperature was equal to 20 ± 2 °C, stress was variable from 0.055 to 0.311 MPa. The tests were carried out in a specially assembled installation (Figure 5). The sample strain was measured by means of two clock type indicators while data were recorded on a video camera.

3. Results and Discussion

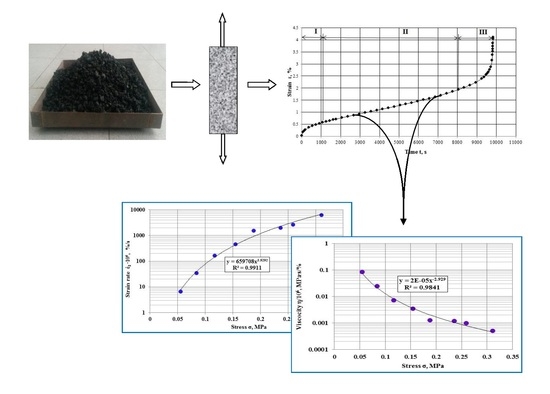
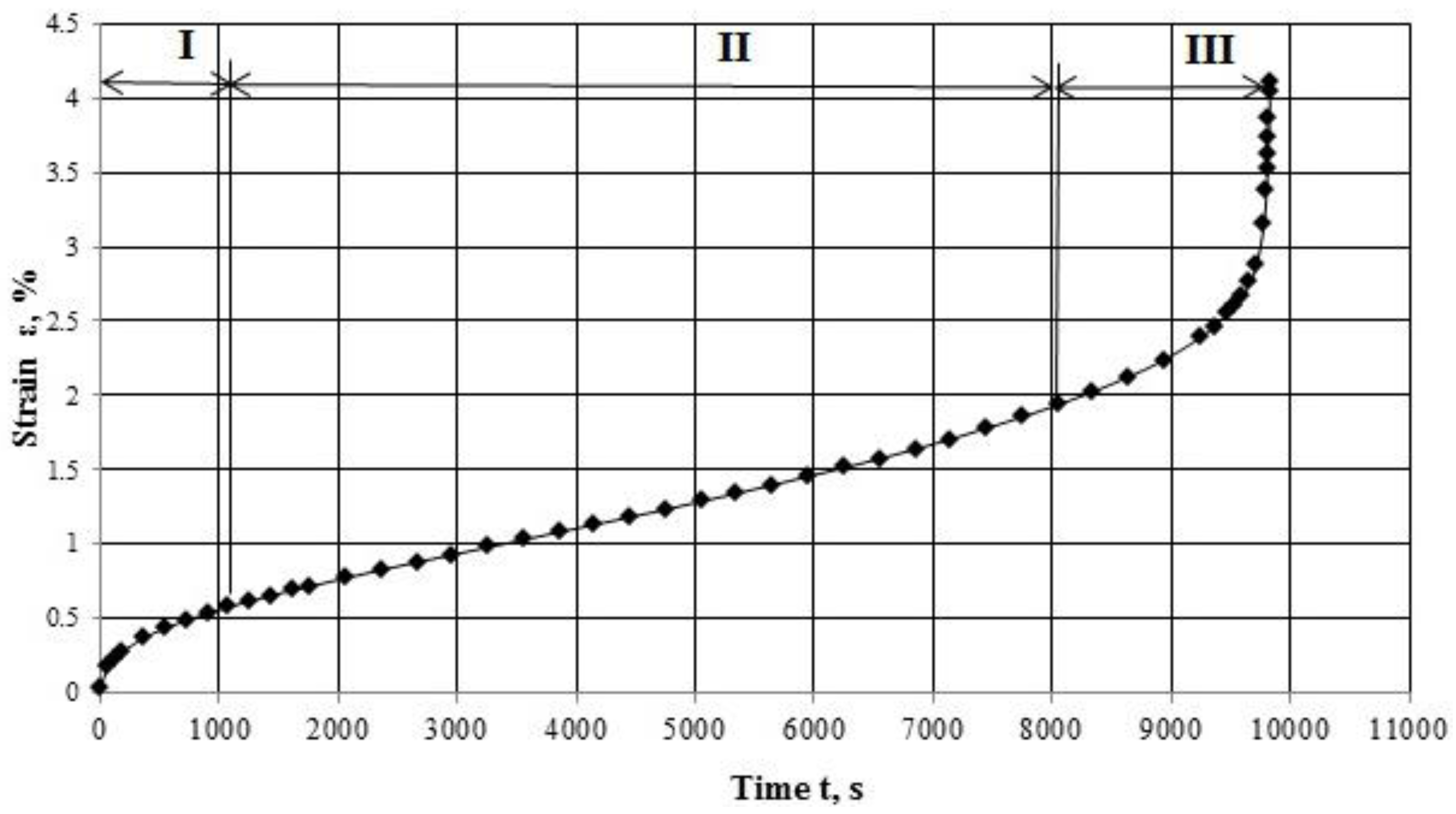
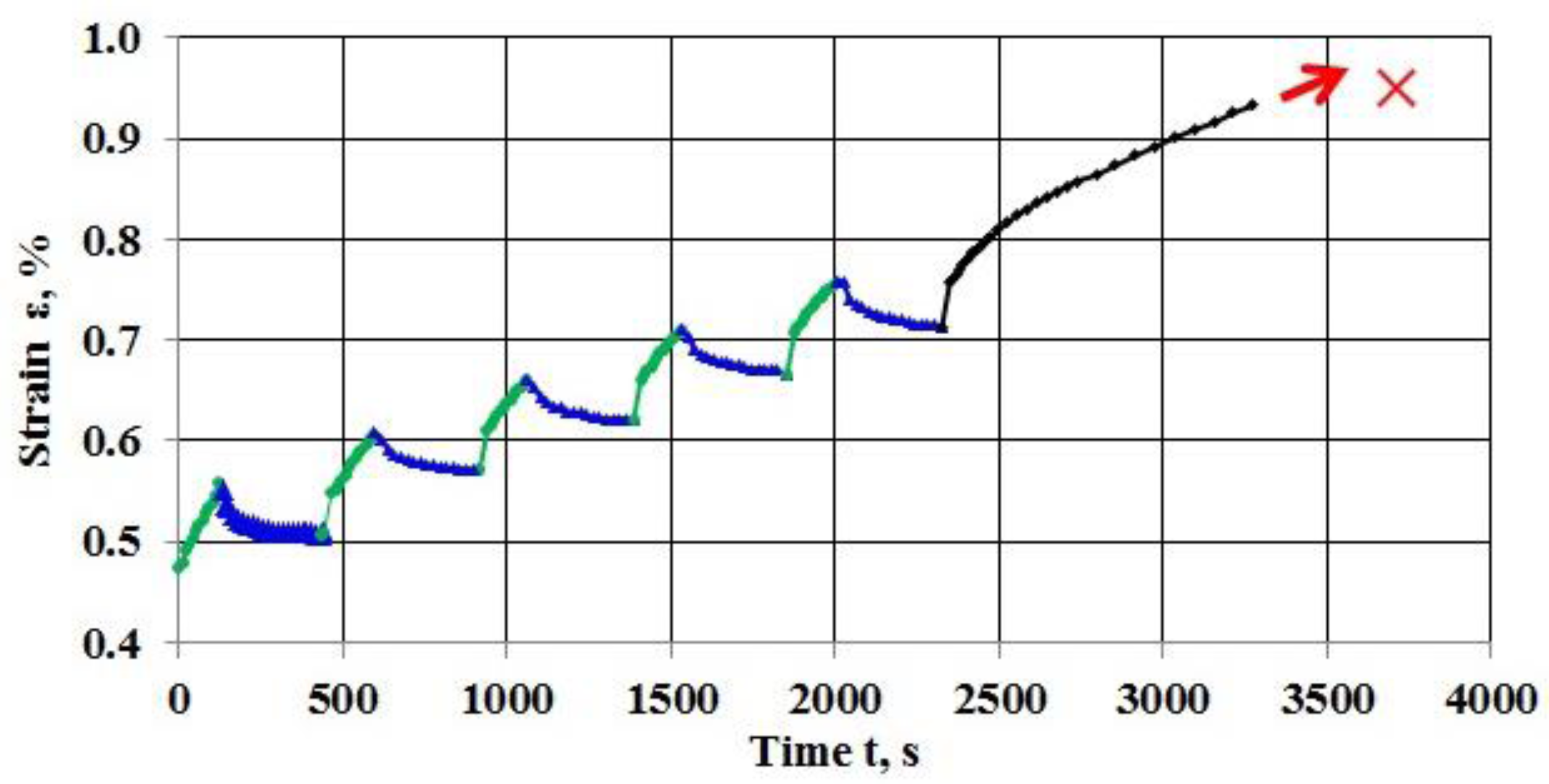
3.1. Creep Curve

Previous works [14,22,23] showed that an asphalt concrete creep curve—as with most viscoelastic materials—had three characteristic stages: stage I of unsteady-state creep with decreasing rate; stage II of steady-state creep with a constant (minimum) rate; and stage III of accelerating creep with increasing rate which precedes failure. The above studies presented test results of asphalt concrete for creep with relatively narrow ranges of stress variation. This work includes test results for seven values of stress from 0.055 MPa to 0.311 MPa. Practically, five samples of asphalt concrete were tested for each value of stress.

Figure 6 shows the creep curve for asphalt concrete at stress 0.117 MPa. It is clearly seen that the creep curve contains all three stages. It is important to underline that since the beginning of loading to the failure moment, the asphalt concrete passes three stages of deformation.

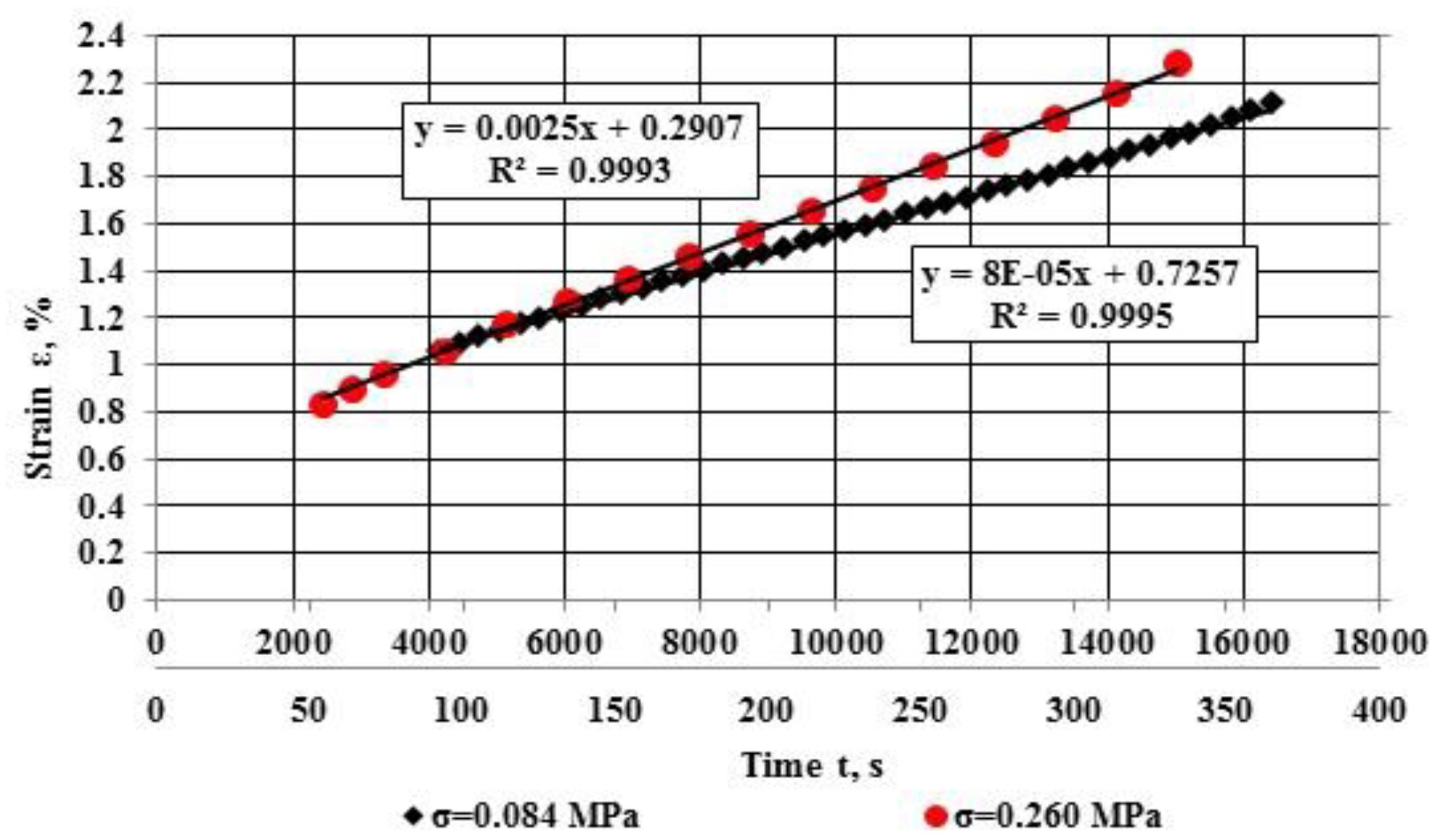
3.2. Steady-State Creep

To solve practical problems, it is important to describe a creep curve obtained experimentally. Usually the third stage of the creep curve for the material is not considered in engineering calculations, as within its range the intensive accumulation of damage occurs, which results in a short life [16]. Therefore, the first and second stages of the creep curve are of main interest for mathematical description. The first stage of the creep curve for asphalt concrete was described with the use of Rabotnov’s fractional exponential function [16] and was reported previously by the authors of Reference [14].

Analyzing the results for the creep experiment, we can represent the second stage of the creep curve as a straight line under all applied stresses with high accuracy, i.e., the deformation of asphalt concrete under constant stress occurs at a constant rate ${\stackrel{•}{\mathsf{\epsilon }}}_2$ (Figure 7). Figure 8 shows that the strain rate depends on the stress, and its dependence is satisfactorily described by a power function. It should be emphasized that stress impacts greatly on strain rate: the increase of the stress by one order causes the increase of strain rate approximately by four orders.

It is very important to know when steady-state creep starts and finishes, and the length of duration. As Figure 9, Figure 10 and Figure 11 show, the specific time characteristics of asphalt concrete depend on stress and are satisfactorily approximated by a power function. It was found that the stress also impacts greatly on start point, end point, and steady-state creep duration, where the increase of stress for one order increases these time characteristics for 4.3–4.5 orders.

To show the full strain reached by the start of stage II of the creep curve through ${\mathsf{\epsilon }}_1$, then the strain of creep for this stage at any time t ,is calculated as:

$${\mathsf{\epsilon }}_2(t)={\mathsf{\epsilon }}_1+{\stackrel{•}{\mathsf{\epsilon }}}_2\cdot t,(t_1<t\le t_2),$$

(1)

where ${\mathsf{\epsilon }}_2(t)$ is strain of creep at time moment t, %; ${\mathsf{\epsilon }}_1$ is the strain at the start of stage II for creep curve, %; $\stackrel{•}{{\mathsf{\epsilon }}_2}$ is the steady-state creep rate, %/s; t is time, s.

As a result of processing by the least square method, the following dependence was obtained between the steady-state creep rate of asphalt concrete and stress (Figure 8):

$$\stackrel{•}{{\mathsf{\epsilon }}_2}=0,6597\cdot {\mathsf{\sigma }}^{3,9292},$$

(2)

where σ is stress, MPa.

Having substituted the dependence in Equation (2) into Equation (1), we have:

$${\mathsf{\epsilon }}_2(t)={\mathsf{\epsilon }}_1+0,6597\cdot {\mathsf{\sigma }}^{3,9292}\cdot t,(t_1<t\le t_2).$$

(3)

As mentioned above, the dependences of start point $t_1$ and end point $t_2$ of steady-state creep on stress are approximated by power functions, and in particular by the following ones (Figure 9 and Figure 10):

$$t_1=0,1889\cdot {\mathsf{\sigma }}^{-4,465},$$

(4)

$$t_2=0,7996\cdot {\mathsf{\sigma }}^{-4,370}.$$

(5)

The strain ${\epsilon }_1$ can be calculated by the methods described in [14]. Equations (3)–(5) allow the determination of the creep strain of asphalt concrete for the stage of steady-state creep (stage II) at the time moment t (t₁ < t ≤ t₂).

Similar to Newton’s law for ideal viscous liquid, in our case for each creep curve, we can write [24]:

$$\mathsf{\sigma }=\mathsf{\eta }\times \stackrel{•}{{\mathsf{\epsilon }}_2},$$

(6)

where $\mathsf{\sigma }$ is stress; $\stackrel{•}{{\mathsf{\epsilon }}_2}$ is steady-state creep (flow) rate; $\mathsf{\eta }$ is viscosity of steady-state flow.

Additionally, for all considered stress variation limit, we can write the Equation (6) in the following form:

$$\mathsf{\sigma }=\mathsf{\eta }(\mathsf{\sigma })\cdot \stackrel{•}{{\mathsf{\epsilon }}_2}(\mathsf{\sigma }).$$

(7)

From Equation (7), we obtain viscosity:

$$\mathsf{\eta }(\mathsf{\sigma })=\frac{\mathsf{\sigma }}{\stackrel{•}{{\mathsf{\epsilon }}_2}(\mathsf{\sigma })}.$$

(8)

The dependence of viscosity of asphalt concrete on stress, constructed under the Equation (8) with the use of experimental results, is shown in Figure 12, which is satisfactorily approximated by a power function. The stress impacts greatly on the viscosity of asphalt concrete, the increase of stress by one order reduces the viscosity by three orders.

3.3. Defining Relations for Steady-State Creep of Asphalt Concrete at Complex Stressed Condition

In the reality of pavement structure, the points of asphalt concrete pavement during the loading impact of vehicle wheels are in a complex stressed and strained condition [3,25]. Experimental tests for determining the mechanical characteristics of asphalt concrete, as a rule, are carried out under simple loading and strain schemes (uniaxial tension, uniaxial compression, three-point bending, four-point bending) [2]. Therefore, the integration of these experimental results, which are carried out under simple loading and strain schemes for cases of complex stress and strained condition, is of significant importance for use in practice [24].

By assuming that (x, y, z) is a Cartesian coordinate system, the stressed condition in point of asphalt concrete pavement is described by stress tensor [26]:

$$\left(\begin{array}{ccc}{\mathsf{\sigma }}_{xx}& {\mathsf{\sigma }}_{xy}& {\mathsf{\sigma }}_{xz}\\ {\mathsf{\sigma }}_{yx}& {\mathsf{\sigma }}_{yy}& {\mathsf{\sigma }}_{yz}\\ {\mathsf{\sigma }}_{zx}& {\mathsf{\sigma }}_{zy}& {\mathsf{\sigma }}_{zz}\end{array}\right)=\left(\begin{array}{ccc}{\mathsf{\sigma }}_0& 0& 0\\ 0& {\mathsf{\sigma }}_0& 0\\ 0& 0& {\mathsf{\sigma }}_0\end{array}\right)+\left(\begin{array}{ccc}{\mathsf{\sigma }}_{xx}-{\mathsf{\sigma }}_0& {\mathsf{\sigma }}_{xy}& {\mathsf{\sigma }}_{xz}\\ {\mathsf{\sigma }}_{yx}& {\mathsf{\sigma }}_{yy}-{\mathsf{\sigma }}_0& {\mathsf{\sigma }}_{yz}\\ {\mathsf{\sigma }}_{zx}& {\mathsf{\sigma }}_{zy}& {\mathsf{\sigma }}_{zz}-{\mathsf{\sigma }}_0\end{array}\right),$$

(9)

where $\left(\begin{array}{ccc}{\mathsf{\sigma }}_{xx}-{\mathsf{\sigma }}_0& {\mathsf{\sigma }}_{xy}& {\mathsf{\sigma }}_{xz}\\ {\mathsf{\sigma }}_{yx}& {\mathsf{\sigma }}_{yy}-{\mathsf{\sigma }}_0& {\mathsf{\sigma }}_{yz}\\ {\mathsf{\sigma }}_{zx}& {\mathsf{\sigma }}_{zy}& {\mathsf{\sigma }}_{zz}-{\mathsf{\sigma }}_0\end{array}\right)$ is the deviator of stress; and ${\mathsf{\sigma }}_0=\frac{1}{3}({\mathsf{\sigma }}_{xx}+{\mathsf{\sigma }}_{yy}+{\mathsf{\sigma }}_{zz})$ is the mean stress.

Strained condition in the point is determined by strain rate tensor:

$$\left(\begin{array}{ccc}{\stackrel{•}{\mathsf{\epsilon }}}_{xx}& {\stackrel{•}{\mathsf{\epsilon }}}_{xy}& {\stackrel{•}{\mathsf{\epsilon }}}_{xz}\\ {\stackrel{•}{\mathsf{\epsilon }}}_{yx}& {\stackrel{•}{\mathsf{\epsilon }}}_{yy}& {\stackrel{•}{\mathsf{\epsilon }}}_{yz}\\ {\stackrel{•}{\mathsf{\epsilon }}}_{zx}& {\stackrel{•}{\mathsf{\epsilon }}}_{zy}& {\stackrel{•}{\mathsf{\epsilon }}}_{zz}\end{array}\right)=\left(\begin{array}{ccc}{\stackrel{•}{\mathsf{\epsilon }}}_0& 0& 0\\ 0& {\stackrel{•}{\mathsf{\epsilon }}}_0& 0\\ 0& 0& {\stackrel{•}{\mathsf{\epsilon }}}_0\end{array}\right)+\left(\begin{array}{ccc}{\stackrel{•}{\mathsf{\epsilon }}}_{xx}-{\stackrel{•}{\mathsf{\epsilon }}}_0& {\stackrel{•}{\mathsf{\epsilon }}}_{xy}& {\stackrel{•}{\mathsf{\epsilon }}}_{xz}\\ {\stackrel{•}{\mathsf{\epsilon }}}_{yx}& {\stackrel{•}{\mathsf{\epsilon }}}_{yy}-{\stackrel{•}{\mathsf{\epsilon }}}_0& {\stackrel{•}{\mathsf{\epsilon }}}_{yz}\\ {\stackrel{•}{\mathsf{\epsilon }}}_{zx}& {\stackrel{•}{\mathsf{\epsilon }}}_{zy}& {\stackrel{•}{\mathsf{\epsilon }}}_{zz}-{\stackrel{•}{\mathsf{\epsilon }}}_0\end{array}\right),$$

(10)

where $\left(\begin{array}{ccc}{\stackrel{•}{\mathsf{\epsilon }}}_{xx}-{\stackrel{•}{\mathsf{\epsilon }}}_0& {\stackrel{•}{\mathsf{\epsilon }}}_{xy}& {\stackrel{•}{\mathsf{\epsilon }}}_{xz}\\ {\stackrel{•}{\mathsf{\epsilon }}}_{yx}& {\stackrel{•}{\mathsf{\epsilon }}}_{yy}-{\stackrel{•}{\mathsf{\epsilon }}}_0& {\stackrel{•}{\mathsf{\epsilon }}}_{yz}\\ {\stackrel{•}{\mathsf{\epsilon }}}_{zx}& {\stackrel{•}{\mathsf{\epsilon }}}_{zy}& {\stackrel{•}{\mathsf{\epsilon }}}_{zz}-{\stackrel{•}{\mathsf{\epsilon }}}_0\end{array}\right)$ is the deviator of strain rates; and ${\stackrel{•}{\mathsf{\epsilon }}}_0=\frac{1}{3}({\stackrel{•}{\mathsf{\epsilon }}}_{xx}+{\stackrel{•}{\mathsf{\epsilon }}}_{yy}+{\stackrel{•}{\mathsf{\epsilon }}}_{zz})$ is the mean strain.

As seen in Figure 13, the strain of asphalt concrete at the start ${\mathsf{\epsilon }}_1$ and final ${\mathsf{\epsilon }}_2$ of the steady-state creep depends on the stress and at a minimum stress of 0.055 MPa, does not exceed 1.2% and 1.9% respectively, i.e., they are very small.

To describe the steady-state creep of asphalt concrete, we assumed the following three hypotheses:

(1) Material is uncompressible, i.e., the incompressibility condition is true [24]:

$${\stackrel{•}{\mathsf{\epsilon }}}_{xx}+{\stackrel{•}{\mathsf{\epsilon }}}_{yy}+{\stackrel{•}{\mathsf{\epsilon }}}_{zz}=0.$$

(11)

(2) The deviator of stresses is proportional to deviator of strain rates [24]:

$$\begin{array}{c}{\mathsf{\sigma }}_{xx}-{\mathsf{\sigma }}_0=\mathsf{\psi }{\stackrel{•}{\mathsf{\epsilon }}}_{xx},{\mathsf{\sigma }}_{xy}=\mathsf{\psi }{\stackrel{•}{\mathsf{\epsilon }}}_{xy},\\ {\mathsf{\sigma }}_{yy}-{\mathsf{\sigma }}_0=\mathsf{\psi }{\stackrel{•}{\mathsf{\epsilon }}}_{yy},{\mathsf{\sigma }}_{yz}=\mathsf{\psi }{\stackrel{•}{\mathsf{\epsilon }}}_{yz},\\ {\mathsf{\sigma }}_{zz}-{\mathsf{\sigma }}_0=\mathsf{\psi }{\stackrel{•}{\mathsf{\epsilon }}}_{zz},{\mathsf{\sigma }}_{zx}=\mathsf{\psi }{\stackrel{•}{\mathsf{\epsilon }}}_{zx},\end{array}$$

(12)

where ψ is the parameter of proportionality depending on stress and strain rates.

Stress intensity:

$${\mathsf{\sigma }}_i=\frac{1}{\sqrt{2}}\sqrt{{({\mathsf{\sigma }}_{xx}-{\mathsf{\sigma }}_{yy})}^2+{({\mathsf{\sigma }}_{yy}-{\mathsf{\sigma }}_{zz})}^2+{({\mathsf{\sigma }}_{zz}-{\mathsf{\sigma }}_{xx})}^2+6({{\mathsf{\sigma }}_{xy}}^2+{{\mathsf{\sigma }}_{yz}}^2+{{\mathsf{\sigma }}_{zx}}^2).}$$

(13)

Strain rate intensity:

$${\stackrel{•}{\mathsf{\epsilon }}}_i=\frac{\sqrt{2}}{3}\sqrt{{({\stackrel{•}{\mathsf{\epsilon }}}_{xx}-{\stackrel{•}{\mathsf{\epsilon }}}_{yy})}^2+{({\stackrel{•}{\mathsf{\epsilon }}}_{yy}-{\stackrel{•}{\mathsf{\epsilon }}}_{zz})}^2+{({\stackrel{•}{\mathsf{\epsilon }}}_{zz}-{\stackrel{•}{\mathsf{\epsilon }}}_{xx})}^2+6({\stackrel{•}{\mathsf{\epsilon }}}_{xy}^2+{\stackrel{•}{\mathsf{\epsilon }}}_{yz}^2+{\stackrel{•}{\mathsf{\epsilon }}}_{zx}^2).}$$

(14)

Having substituted the Equation (12) into Equation (13), we have

$${\mathsf{\sigma }}_i=\frac{1}{\sqrt{2}}\sqrt{{\mathsf{\psi }}^2\left[{({\stackrel{•}{\mathsf{\epsilon }}}_{xx}-{\stackrel{•}{\mathsf{\epsilon }}}_{yy})}^2+{({\stackrel{•}{\mathsf{\epsilon }}}_{yy}-{\stackrel{•}{\mathsf{\epsilon }}}_{zz})}^2+{({\stackrel{•}{\mathsf{\epsilon }}}_{zz}-{\stackrel{•}{\mathsf{\epsilon }}}_{xx})}^2+6({\stackrel{•}{\mathsf{\epsilon }}}_{xy}^2+{\stackrel{•}{\mathsf{\epsilon }}}_{yz}^2+{\stackrel{•}{\mathsf{\epsilon }}}_{zx}^2)\right]}.$$

(15)

Comparison of Equation (15) with Equation (14) shows that

$${\mathsf{\sigma }}_i=\frac{3}{2}\mathsf{\psi }{\stackrel{•}{\mathsf{\epsilon }}}_i.$$

(16)

From Equation (16), we obtained

$$\mathsf{\psi }=\frac{2}{3}\frac{{\mathsf{\sigma }}_i}{{\stackrel{•}{\mathsf{\epsilon }}}_i}.$$

(17)

Then, we write Equation (12) again considering Equation (17):

$$\begin{array}{l}{\mathsf{\sigma }}_{xx}-{\mathsf{\sigma }}_0=\frac{2}{3}\frac{{\mathsf{\sigma }}_i}{{\stackrel{•}{\mathsf{\epsilon }}}_i}{\stackrel{•}{\mathsf{\epsilon }}}_{xx},{\mathsf{\sigma }}_{xy}=\frac{2}{3}\frac{{\mathsf{\sigma }}_i}{{\stackrel{•}{\mathsf{\epsilon }}}_i}{\stackrel{•}{\mathsf{\epsilon }}}_{xy,}\\ {\mathsf{\sigma }}_{yy}-{\mathsf{\sigma }}_0=\frac{2}{3}\frac{{\mathsf{\sigma }}_i}{{\stackrel{•}{\mathsf{\epsilon }}}_i}{\stackrel{•}{\mathsf{\epsilon }}}_{yy},{\mathsf{\sigma }}_{yz}=\frac{2}{3}\frac{{\mathsf{\sigma }}_i}{{\stackrel{•}{\mathsf{\epsilon }}}_i}{\stackrel{•}{\mathsf{\epsilon }}}_{yz,}\\ {\mathsf{\sigma }}_{zz}-{\mathsf{\sigma }}_0=\frac{2}{3}\frac{{\mathsf{\sigma }}_i}{{\stackrel{•}{\mathsf{\epsilon }}}_i}{\stackrel{•}{\mathsf{\epsilon }}}_{zz},{\mathsf{\sigma }}_{zx}=\frac{2}{3}\frac{{\mathsf{\sigma }}_i}{{\stackrel{•}{\mathsf{\epsilon }}}_i}{\stackrel{•}{\mathsf{\epsilon }}}_{zx}.\end{array}$$

(18)

(3) There is a functional dependence between stress intensity and strain rate intensity, which does not depend on the type of stressed condition:

$${\stackrel{•}{\mathsf{\epsilon }}}_i=f({\mathsf{\sigma }}_i).$$

(19)

For uniaxial tension σ_хх > 0, σ_yy = σ_zz = σ_хy = σ_yz = σ_zx = 0. Therefore, from Equation (13), we have

$${\mathsf{\sigma }}_i={\mathsf{\sigma }}_{xx}$$

(20)

Considering the condition of incompressibility for the material from Equation (11) for uniaxial tension is also true, ${\stackrel{•}{\mathsf{\epsilon }}}_{xx}>0,{\stackrel{•}{\mathsf{\epsilon }}}_{xy}={\stackrel{•}{\mathsf{\epsilon }}}_{yz}={\stackrel{•}{\mathsf{\epsilon }}}_{zx}=0,{\stackrel{•}{\mathsf{\epsilon }}}_{yy}={\stackrel{•}{\mathsf{\epsilon }}}_{zz}=-\frac{1}{2}{\stackrel{•}{\mathsf{\epsilon }}}_{xx.}$

Then, from Equation (14), we have

$${\stackrel{•}{\mathsf{\epsilon }}}_i={\stackrel{•}{\mathsf{\epsilon }}}_{xx.}$$

(21)

Taking into account Equations (19)–(21) for the considered asphalt concrete, the relation between strain rate intensity and stress intensity will have the following form:

$${\stackrel{•}{\mathsf{\epsilon }}}_i=0.6597\cdot {{\mathsf{\sigma }}_i}^{3.9292},$$

(22)

where ${\stackrel{•}{\mathsf{\epsilon }}}_i$ is strain rate intensity, %/s; ${\mathsf{\sigma }}_i$ is stress intensity, MPa.

Comparing Equations (19) and (22), we have

$$f({\mathsf{\sigma }}_i)=0.6597\cdot {\mathsf{\sigma }}^{3.9292}.$$

(23)

The previous paper in Reference [22] showed that asphalt concrete is deformed as a plastic material at 20 °С during cyclic loading under scheme “loading—deforming under constant load—rest”. Thus, keeping the applied stress equal to 0.138 MPa constant for 120 s and keeping the asphalt concrete sample without load for the following 300 s in each cycle showed that even after four to five cycles the elastic (recovered) strain was only 5%–6% (Figure 14), i.e., asphalt concrete was deformed plastically.

The above data emphasized the importance of defining relations for the steady-state creep of asphalt concrete as seen in Equations (18) and (22); and should also be considered as defining relations for steady-state plastic flow. By using them we can set the problems and solve them for the modeling of rutting in asphalt concrete layers of highways (Figure 15).

4. Conclusions

The results of the experimental investigation into fine-grained asphalt concrete at static loading at a temperature of 20 ± 2 °С and at stress between 0.055 and 0.311 MPa showed the following:

-

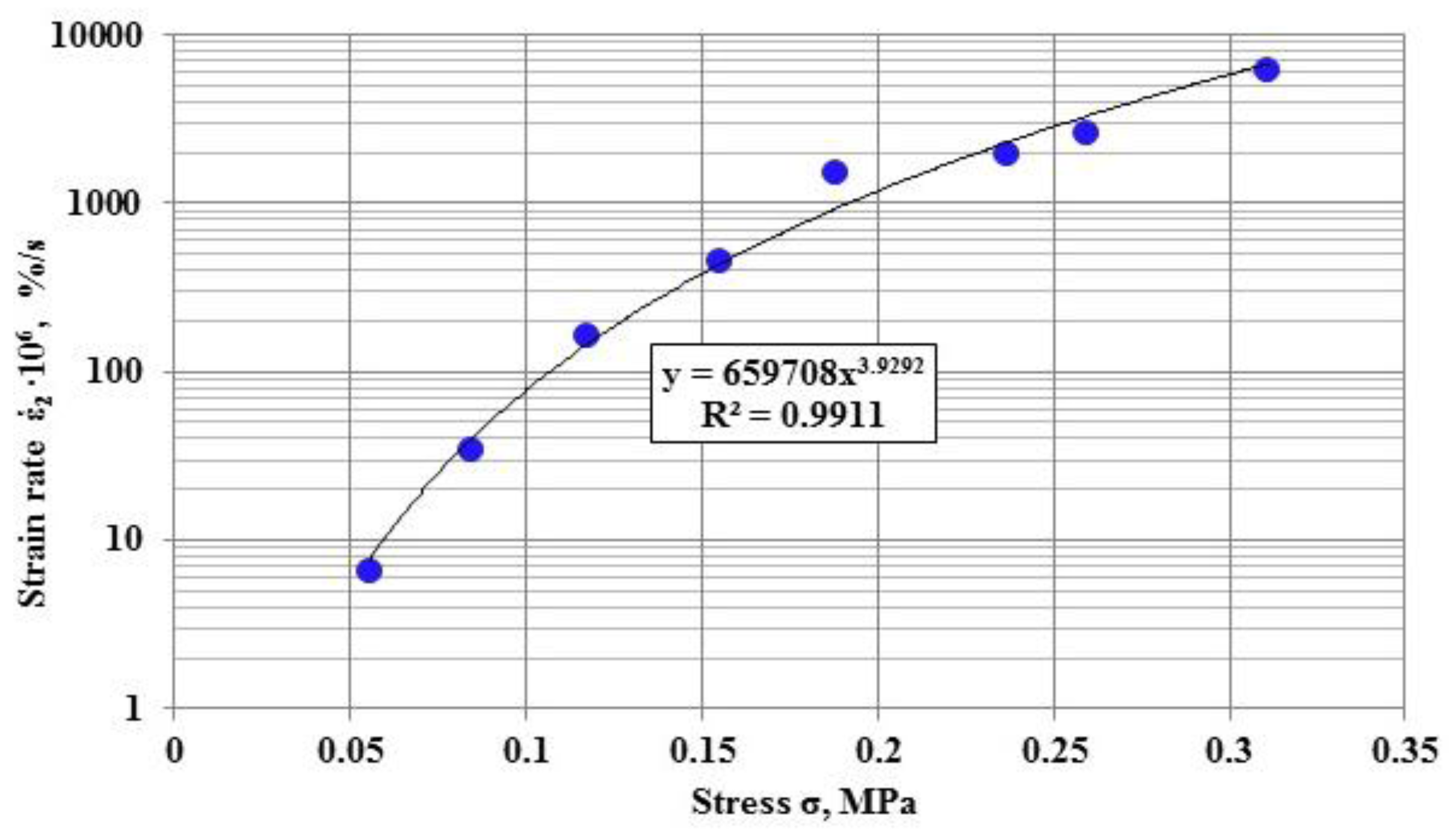
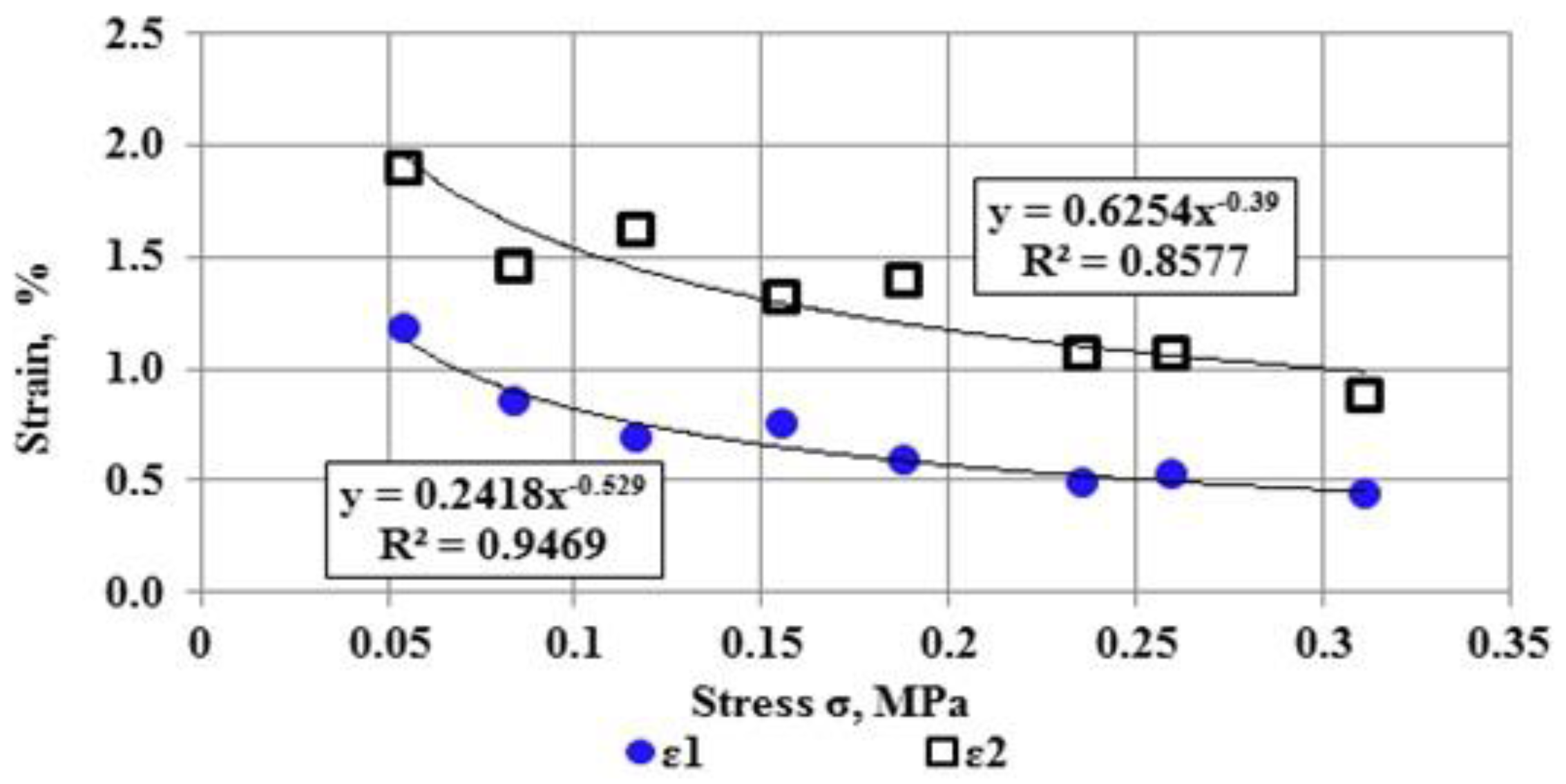
For creep curve stage II, the asphalt concrete deformation occurred at a constant rate. The strain rate for this stage is dependent on the stress, and this dependence is satisfactorily described by a power function. The stress has a great influence on the strain rate where the increase of stress by one order increases the strain rate approximately by four orders;

-

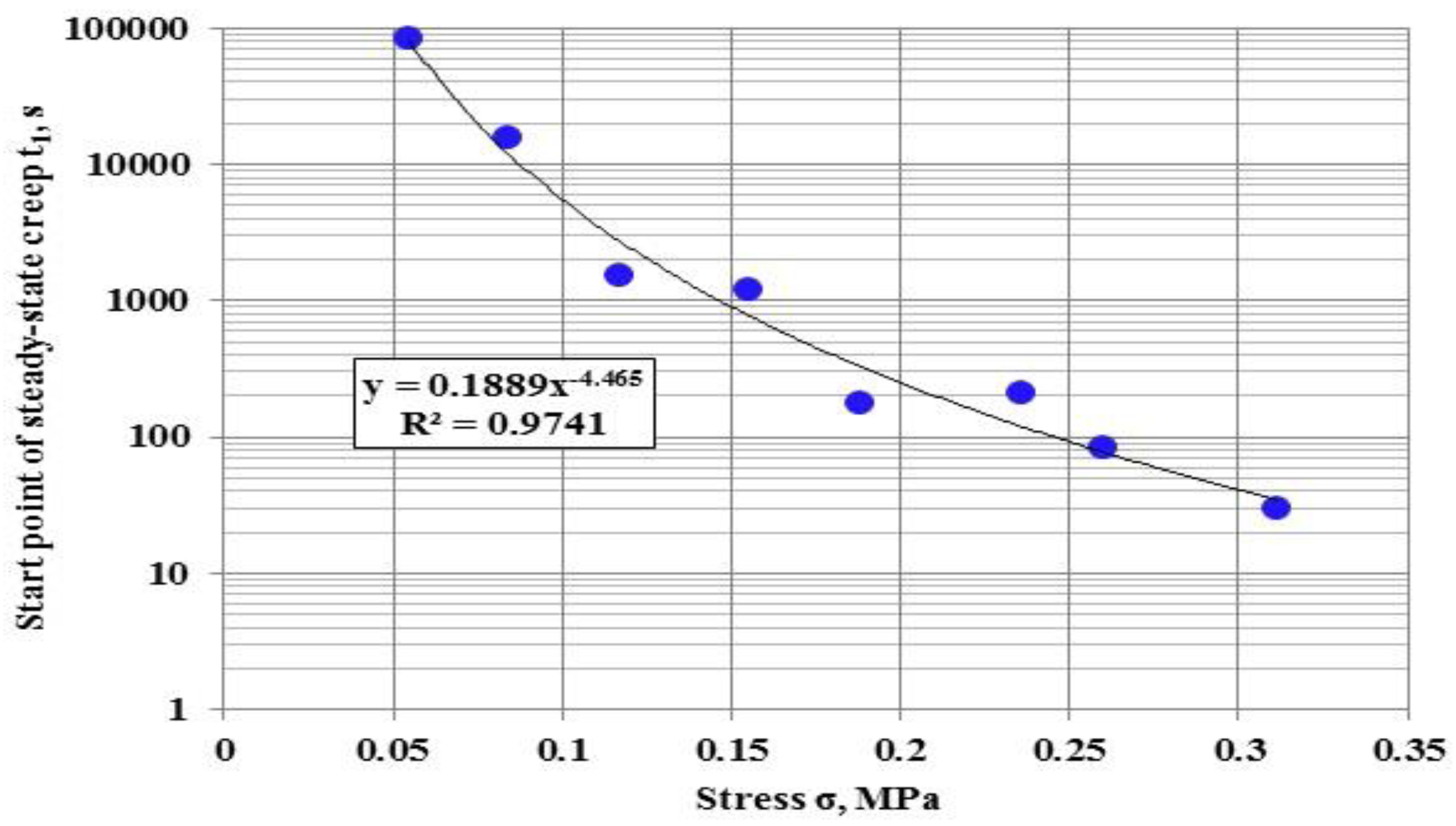
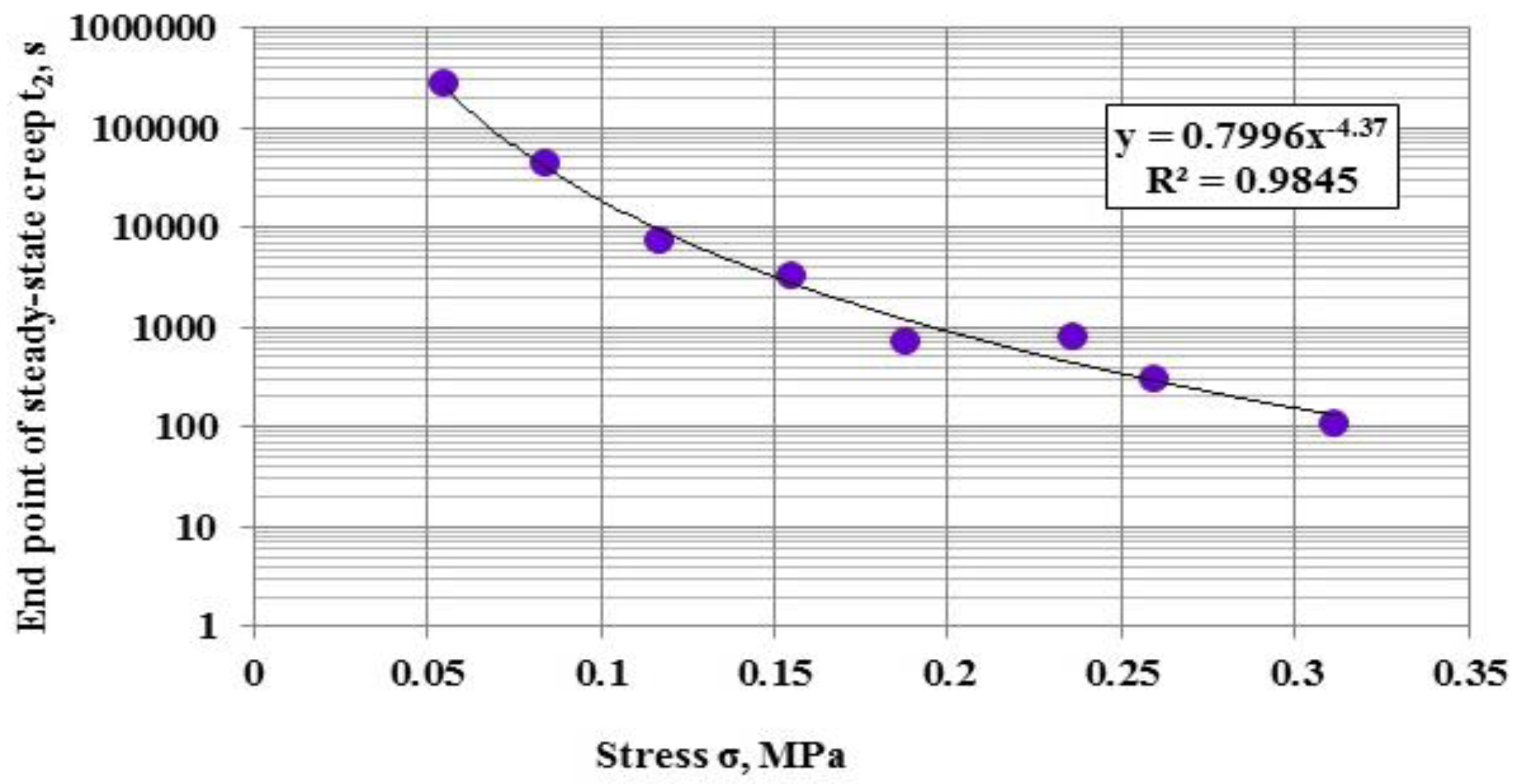
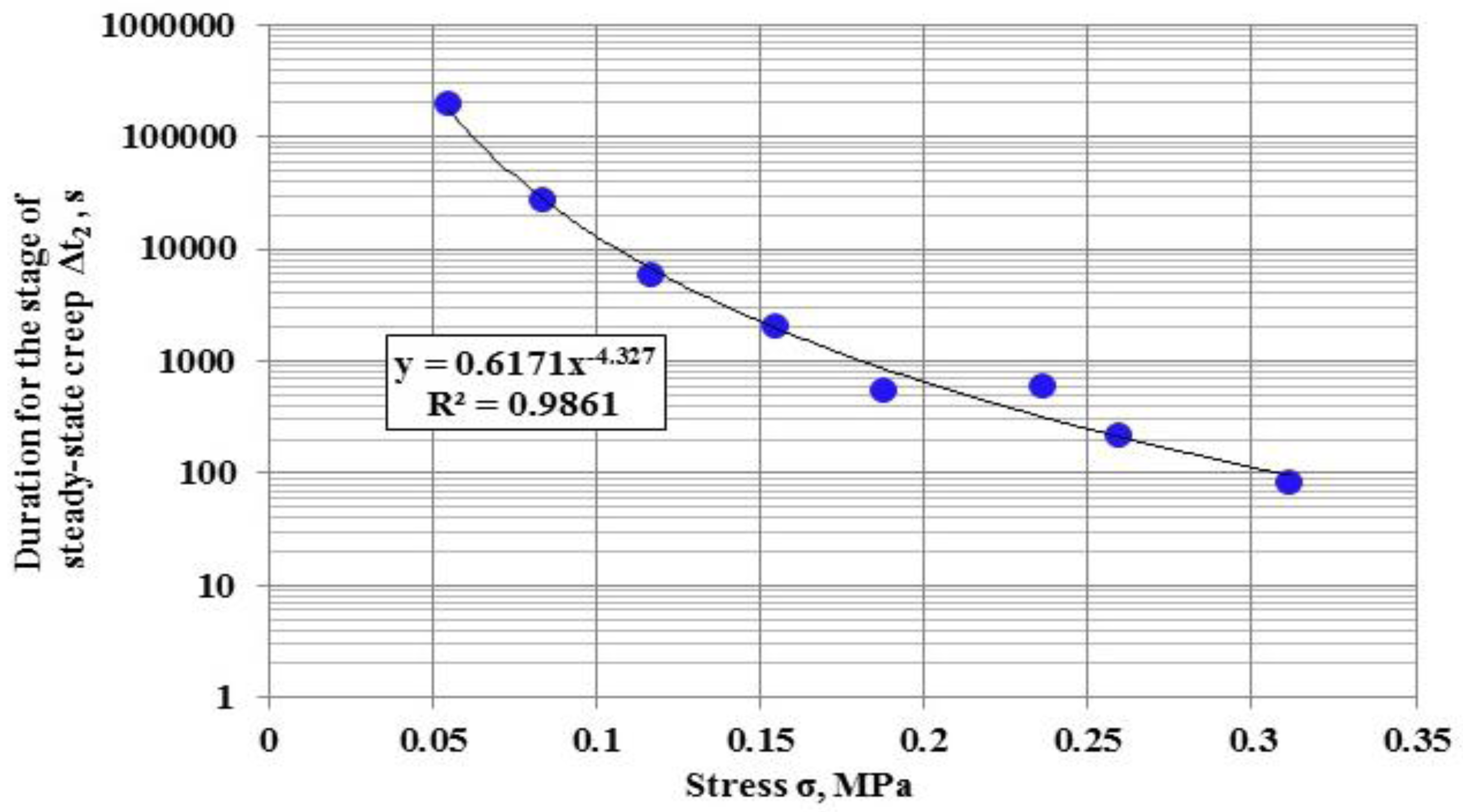
The dependences were constructed for the start point, end point, and the duration of the stage of steady-state creep on the stress. The stress also impacts greatly on the specified time characteristics, where the increase of stress by one order increases these characteristics for 4.3–4.5 orders;

-

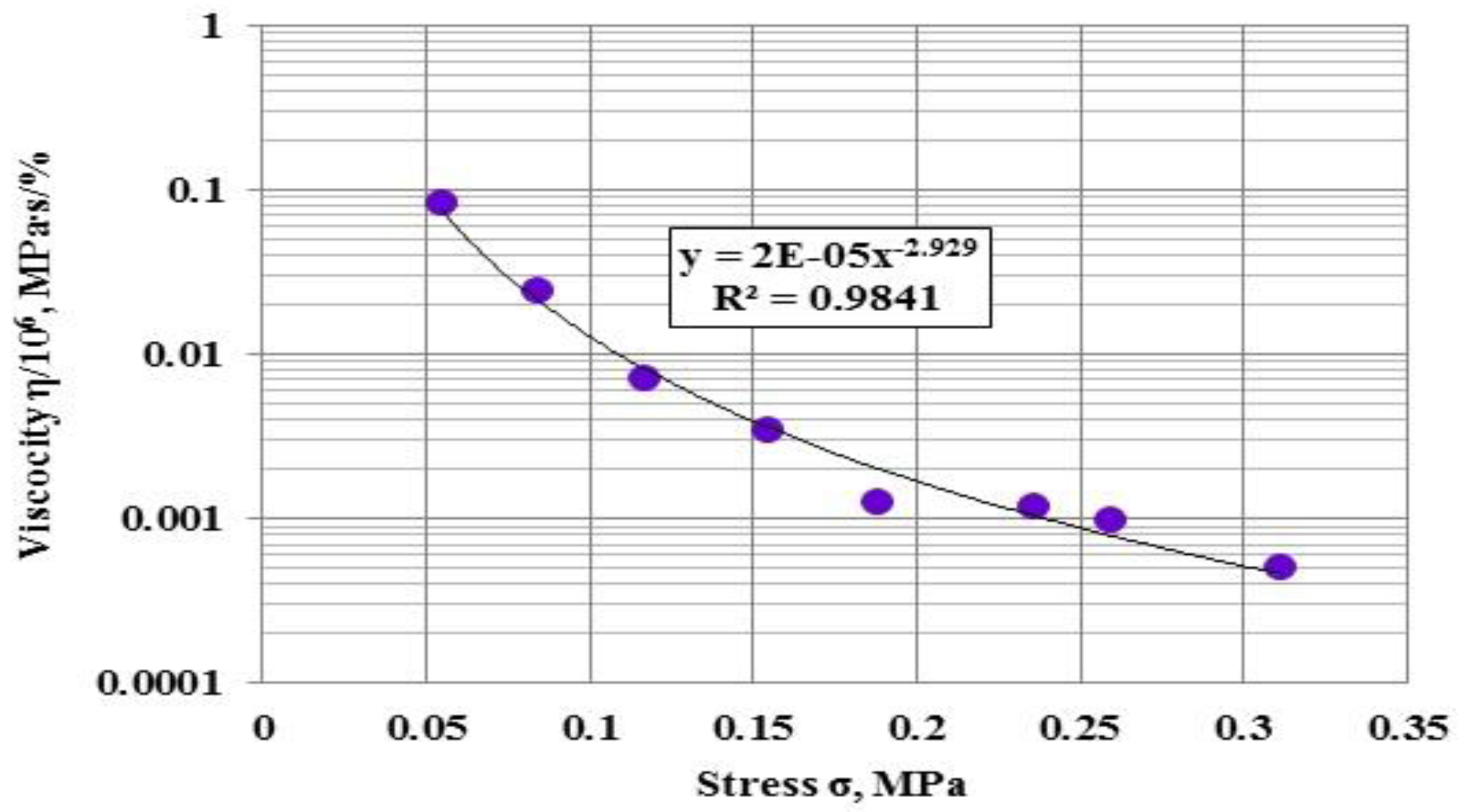
The values of viscosity for asphalt concrete were determined at various stresses. The dependence was defined for viscosity on the stress and can also be satisfactorily described by a power function. In particular, the increase of stress by one order reduces the viscosity by three orders;

-

Assuming that asphalt concrete is an incompressible material, then the stress deviator is proportional to the strain rate deviator. Hence, there is a functional relationship between the stress intensity and the strain rate intensity, which does not depend on the type of stress condition. The defining relations were formulated for the steady-state creep of asphalt concrete under complex stressed conditions.