Plasmon Modulation Spectroscopy of Noble Metals to Reveal the Distribution of the Fermi Surface Electrons in the Conduction Band

Abstract

To directly access the dynamics of electron distribution near the Fermi-surface after plasmon excitation, pump-probe spectroscopy was performed by pumping plasmons on noble-metal films and probing the interband transition. Spectral change in the interband transitions is sensitive to the electron distribution near the Fermi-surface, because it involves the d valence-band to the conduction band transitions and should reflect the k-space distribution dynamics of electrons. For the continuous-wave pump and probe experiment, the plasmon modulation spectra are found to differ from both the current modulation and temperature difference spectra, possibly reflecting signatures of the plasmon wave function. For the femtosecond-pulse pump and probe experiment, the transient spectra agree well with the known spectra upon the excitation of the respective electrons resulting from plasmon relaxation, probably because the lifetime of plasmons is shorter than the pulse duration.

1. Introduction

Recent years have witnessed a dramatic increase in the research on plasmons. From an application point of view, studies that utilize various attractive features of surface plasmons including optical field enhancement [1], surface sensitivity [2], focusing below diffraction limit [3,4], nonlinear optical effects [5,6], plasmonic energy conversion [7], etc., are being actively pursued. Further, fundamental research on the properties of plasmons including quantum effects [8] and real space imaging [9] have also attracted attention. However, due to the short lifetime of surface plasmons, the energy distribution of electrons in the momentum space at the time of surface plasmon excitation has not yet been elucidated [10,11]. The purpose of this research is to obtain information about the electron distribution in the conduction band of metals associated with the surface plasmon excitation.

To shed light on the energy distribution of electrons in the momentum space in the conduction band of the metal in the presence of surface plasmon excitation, plasmon modulation spectra in the Kretschmann geometry are measured: plasmons are excited with a continuous wave (CW) laser at the surface plasmon resonance, and the interband transition band edge is probed with a CW white light. This is motivated by the expectation that the k-space distribution dynamics of electrons should be reflected on the spectral change in the interband transition edge (the d band to the Fermi-surface transition), which is sensitive to the Fermi-surface distribution of electrons. As the signal due to CW laser excitation is unavoidably affected by the temperature increase in the sample, electric current modulation and temperature difference spectra are also measured for independently evaluating the contribution from temperature.

Further, to probe the plasmon relaxation dynamics before temperature rise (before thermalization with the lattice sub-system), femtosecond pump-probe spectroscopy experiments are performed by pumping plasmons and probing the interband transition. Figure 1 schematically shows the relaxation process of the surface plasmon. Phase relaxation of plasmons takes place within 10–30 fs, as estimated from the surface plasmon polariton (SPP) resonance width. After about 500 fs, the electron system is equilibrated at some electronic temperature, and thereafter, thermal equilibrium with the lattice system is established several ps later. Although fast dynamics of non-equilibrium electrons excited by femtosecond laser pulses has been studied intensively [12,13,14,15], our interest is the dynamics of plasmons before the phase relaxation into individual particles. In order to obtain information before the equilibration of the electron system, the signal on the order of 100 femtoseconds after SPP excitation should be traced. Therefore, pump-probe spectroscopy with a femtosecond pulsed laser is carried out. The spectrum of the probe pulse laser needs to be wide enough to cover the surface plasmon resonance and the interband absorption edge. In view of this requirement, gold is selected as a suitable material to be studied using the femtosecond Ti: sapphire laser. To achieve a longer phase relaxation time, silver is more suitable because the plasmon resonance width is narrower, but the interband transition wavelength is too short (about 325 nm) for the wavelength of the Ti:sapphire laser.

2. Experiment

All experiments were carried out at room temperature. In this study, the Kretschmann arrangement was used for the surface plasmon excitation [16]. The surface plasmon is excited at the silver-(gold-)air interface by illuminating light from the prism side into the hypotenuse surface deposited with silver (gold) of ~50-nm thick.

2.1. Sample Preparation and Evaluation of Plasmon Resonance and Interband Transition

Noble metal films were deposited by vacuum evaporation (resistive heating) onto the hypotenuse surface of UV fused quartz right-angle prisms (20 mm × 28 mm) or a glass slide (for temperature difference spectra) at room temperature. The evaporations were performed in a diffusion pumped vacuum deposition system (VPC-260, ULVAC) for gold and silver films using 99.95% pure Au and 99.99% pure Ag wires on a tungsten boat at pressures of 8 × 10⁻⁵ Torr and a deposition rate of about 10 µÅ/s. The approximate thickness of the film was evaluated using a reflection interference microscope. Plasmon resonance spectra (incident from the prism side) in the Kretschmann configuration and reflection spectra in the interband transition energy region (from air or prism side) were measured with a spectrophotometer (SolidSpec-3700 DUV, Shimadzu, Kyoto, Japan) or with a spectrometer with a cooled CCD. The experimental protocols for sample preparation and measurement to evaluate the plasmon resonance spectra of noble metals are described in detail in [17].

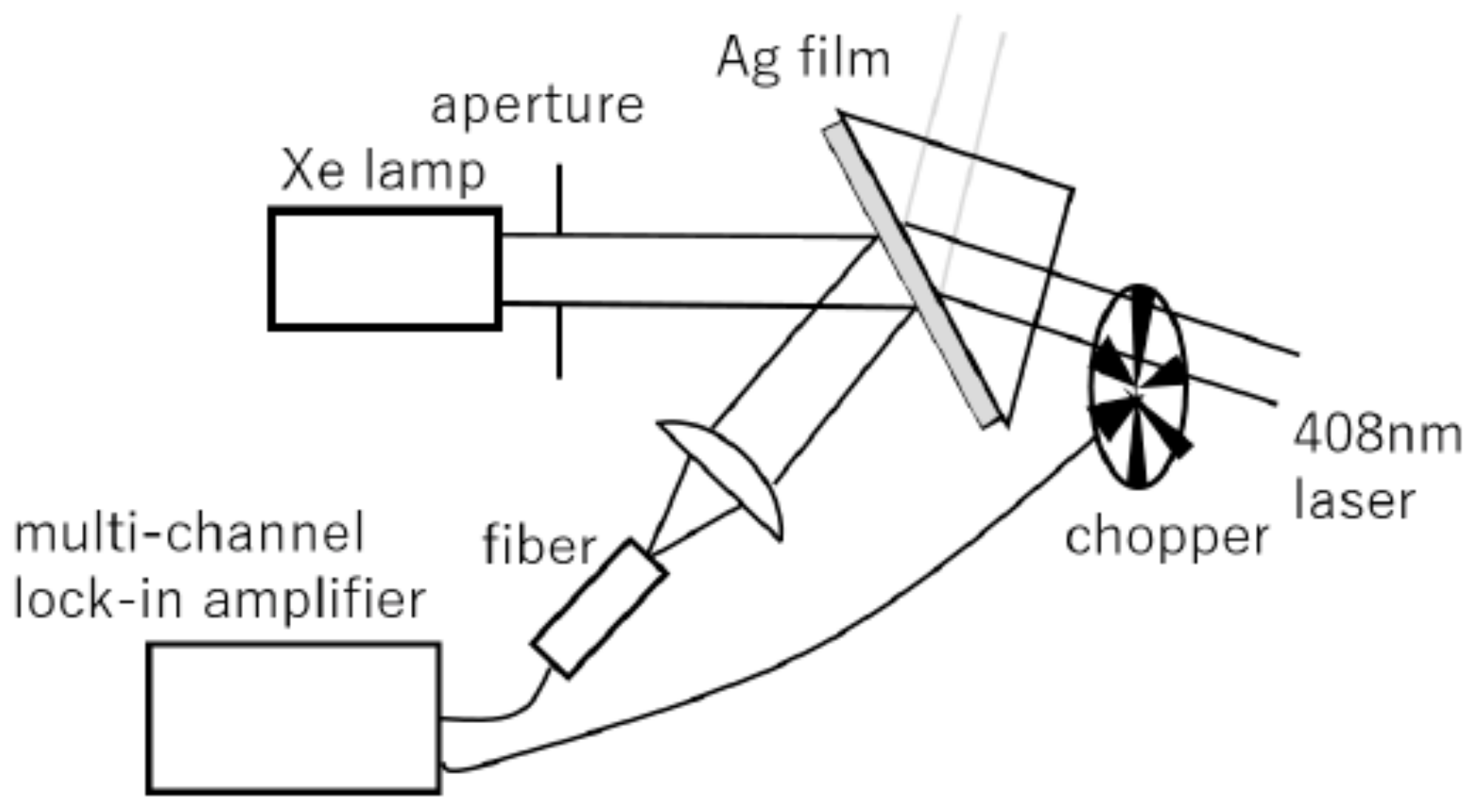
2.2. CW Experiment

2.2.1. Plasmon Modulation (Reflectance Change in the Interband Transition Due to Surface Plasmon Excitation)

In this experiment, the surface plasmon was resonantly excited from the prism side by the CW pump from a laser diode at 408 nm, and the p-polarized probe white light from a laser-driven light source (LDLS, ENERGETIQ EQ-99) was incident from the air side at an incidence angle of 55°. The experimental setup is shown schematically in Figure 2. The pump light with a power of 100 mW was intensity-modulated at f = 221 Hz with a chopper, and the change in the reflectance synchronized with f was measured at 128 wavelengths simultaneously with a spectrometer combined with a 128-channel lock-in amplifier [18,19]. The pump light was irradiated on the Ag film without focusing, and the probe light was collimated to be irradiated on the Ag surface through an aperture so that the beam diameter was about the same as the diameter of the pump beam (5 mm) at the surface.

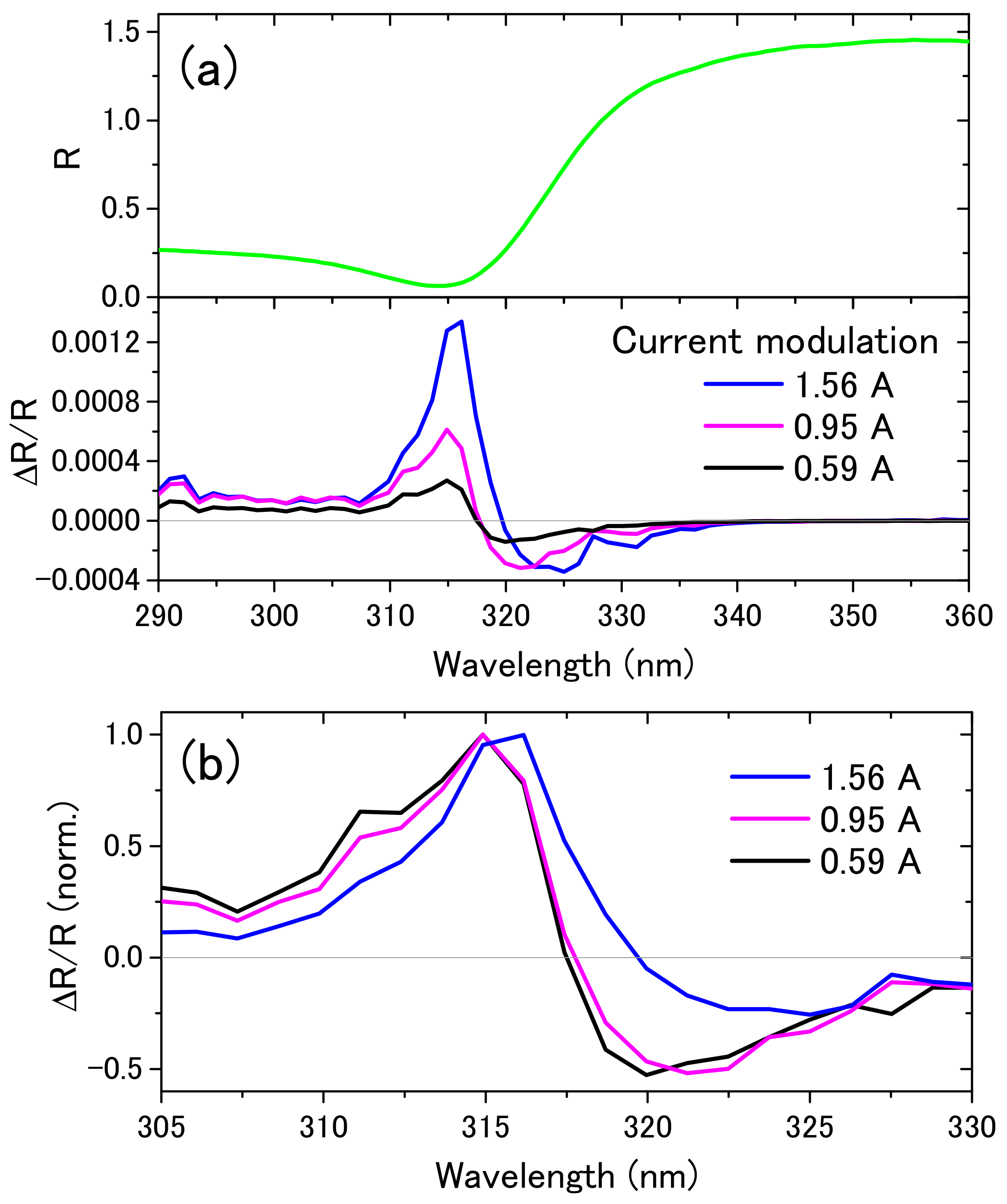
2.2.2. Current Modulation (Current Modulation Spectroscopy of Interband Transition)

The experimental setup is similar to that in Figure 2 except that the light modulation is replaced by the current modulation. In addition, to measure a change in the reflection spectrum both at the interband transition edge and at the plasmon resonance (not shown in the present paper), the p-polarized white-light probe was incident from the prism side. To measure the current direction dependence, a conductive wire was brought into contact with four sides of a rectangular silver surface on the prism in a cross shape. A silver paste was spread to the portion where the conductive wire and silver thin film were in contact, and the conductive wire was further bonded to the prism with an adhesive tape. We found that there was no significant dependence on the current direction with respect to the probe polarization, and hence, no specification is given on the current direction below. The incident angle and reflection angle were measured by fixing a protractor to the prism with a double-sided adhesive tape. The frequency f of the alternating current is 101 Hz, and the magnitude of the current is 0.25–1.56 A. The small change synchronized with 2f in the p-polarized reflection spectrum at an incidence angle of 55 degree in the prism was measured with the multi-lock in amplifier.

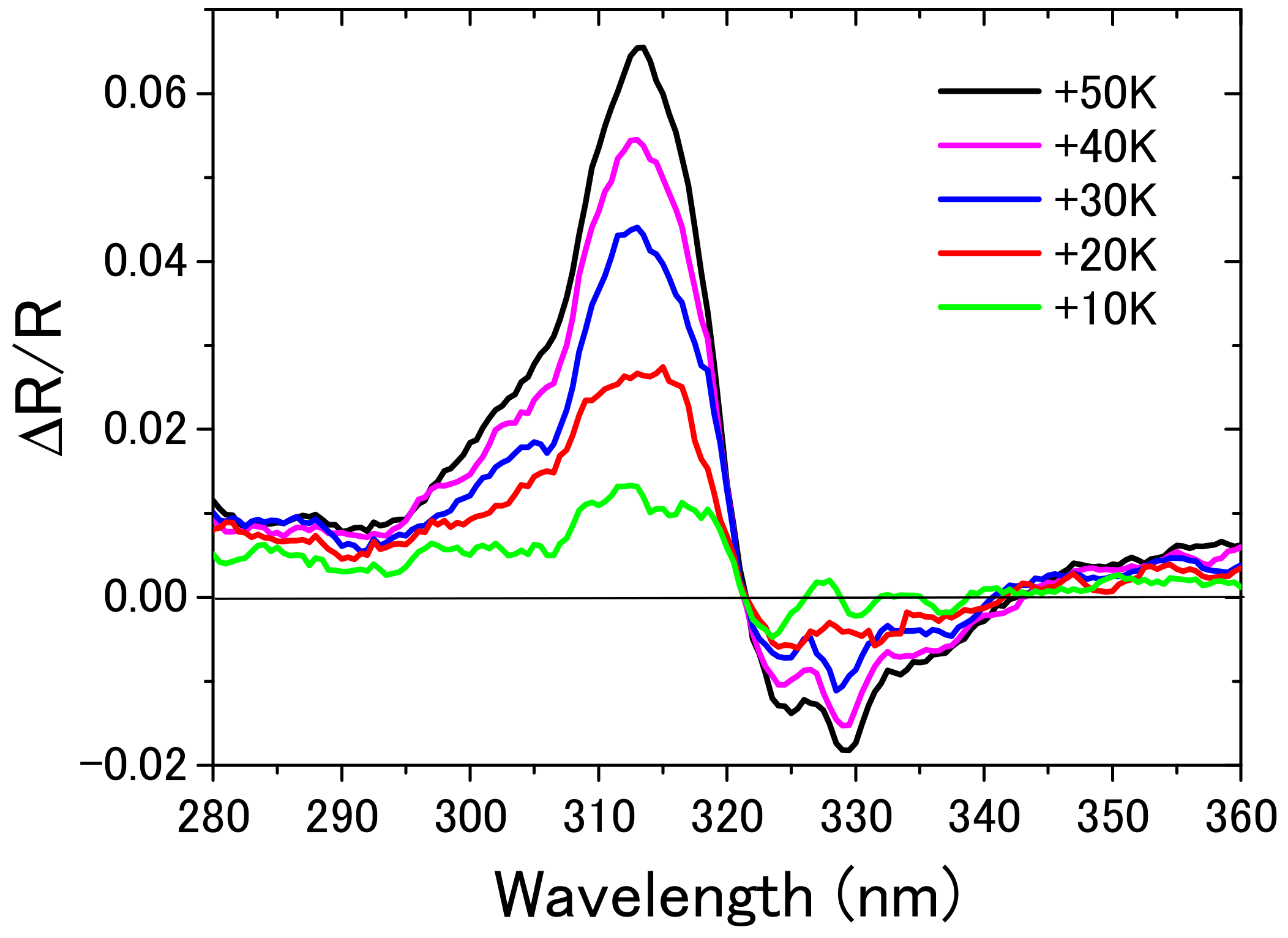
2.2.3. Temperature Difference Spectrum

By bringing a heater into contact with the back of the glass substrate (glass slide) on which a silver thin film of about 50 nm in thickness was deposited, the temperature of the sample was raised from room temperature. Temperature was measured by inserting a thermocouple sensor between the glass substrate and the heater. The non-polarized reflection spectrum relative to that of an aluminum mirror without protective coating was measured at an incident angle of 5°, and a temperature difference spectrum was deduced.

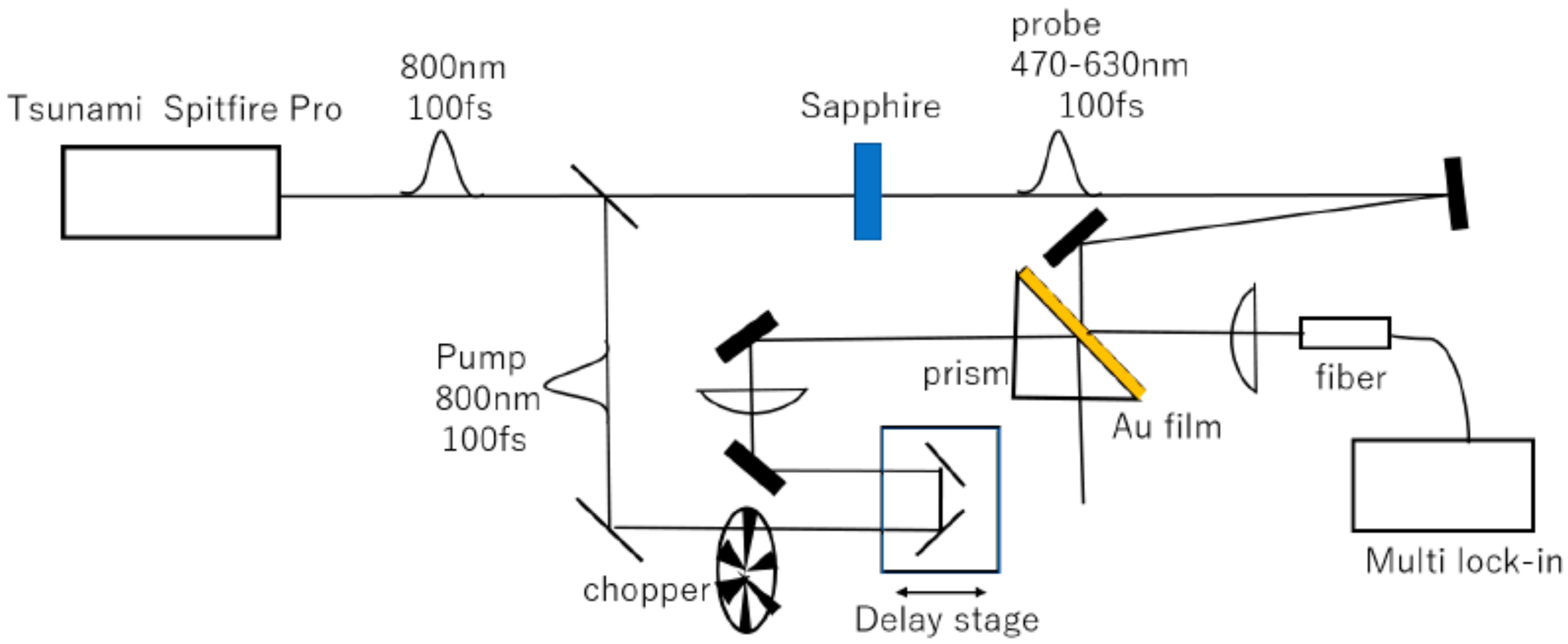
2.3. Time-Resolved Experiment (Femtosecond Pump-Probe Spectroscopy)

The optical system is shown in Figure 3. After exciting the surface plasmons of gold at the air-metal interface by the pump light incident from the prism side, the adjustably delayed probe light was applied to the same position from the air side, and the change in the reflectance was detected with the multichannel lock-in amplifier. By sweeping the delay time of the probe light with respect to the pump light, time evolution of the reflection spectral change can be obtained. For the experiment on gold, the output light from the femtosecond laser (Tsunami Spitfire Pro, center wavelength of 800 nm, pulse duration of 100 fs and pulse repletion rate of 5 kHz) was divided by a beam splitter into two, one for the pump and the other for the probe. The latter was focused into a sapphire plate to generate white-light continuum ranging from 470–630 nm with temporal duration of 100 fs to be used for broad-band monitoring. The incidence angle of the pump from the prism side was 45 degrees so that the pump energy was resonant with the plasmon in gold [17], and that of the probe from air was also 45 degrees. The wavelength resolution of time-resolved spectra was about 1.5 nm.

3. Results and Discussion

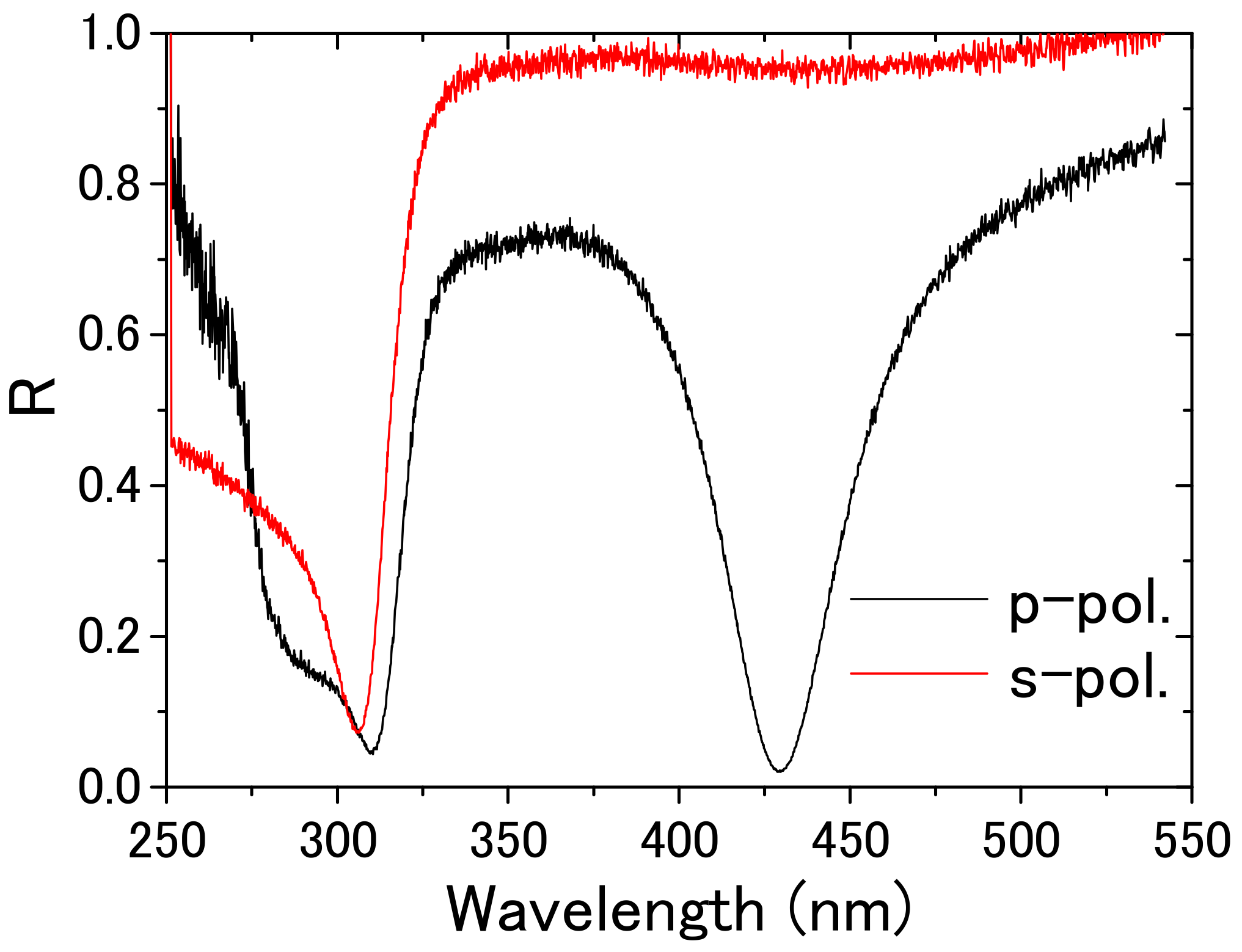
3.1. Observation of Surface Plasmon Resonance and Interband Transition Spectra

Figure 4 shows the plasmon resonance reflection spectra of a silver film of about 50 nm in thickness deposited on a quartz prism at an incidence angle of more than 45 degrees within the quartz. The data shown are the reflection spectra from the prism with Ag (total internal reflection) divided by that without Ag for each polarization measured with the spectrometer with a CCD. Surface plasmon resonance is seen in the vicinity of 430 nm for p-polarized light, while the surface plasmon is not excited by s-polarized light. The dip near 310 nm, which is also seen in s-polarized light, is due to interband absorption.

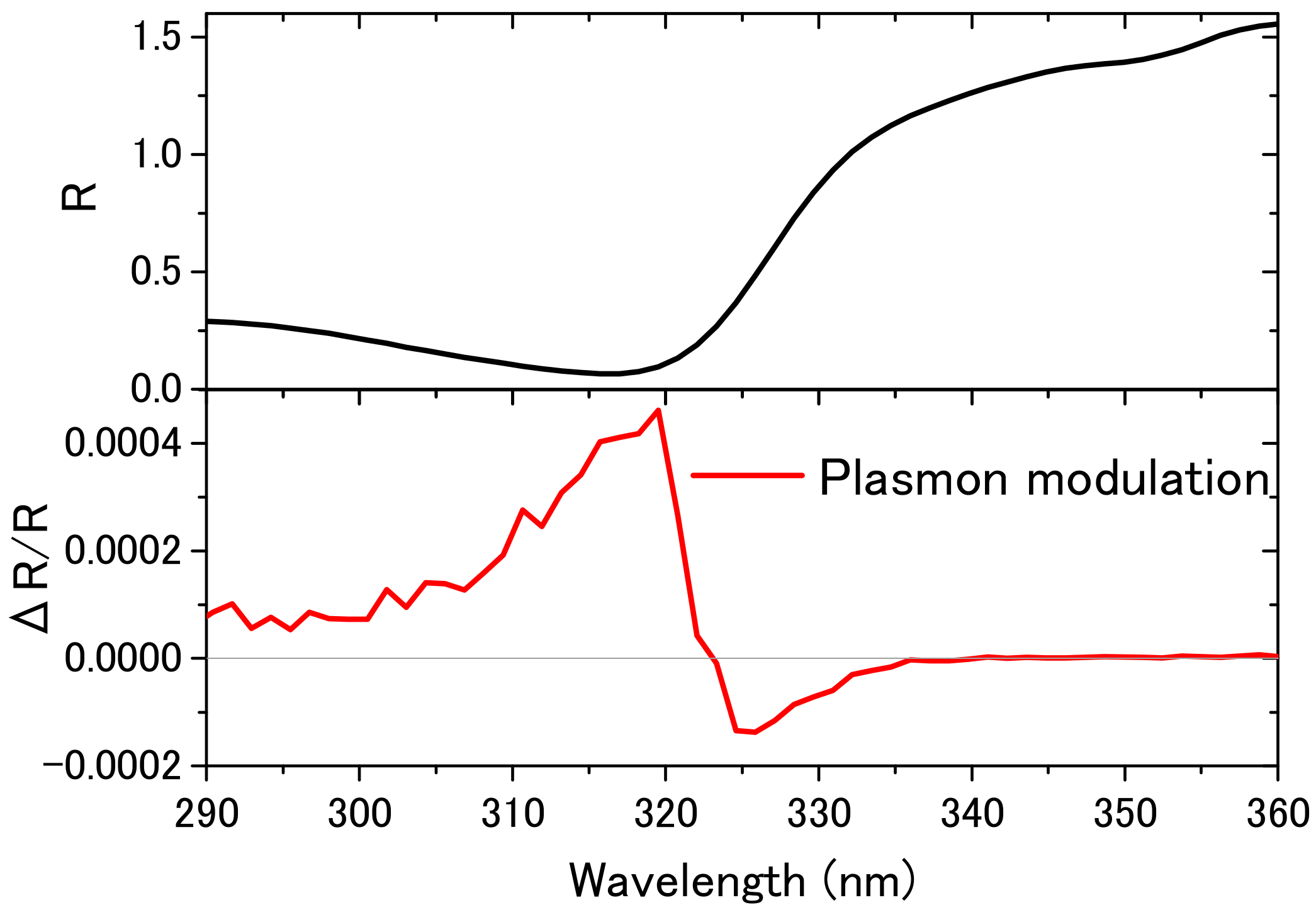
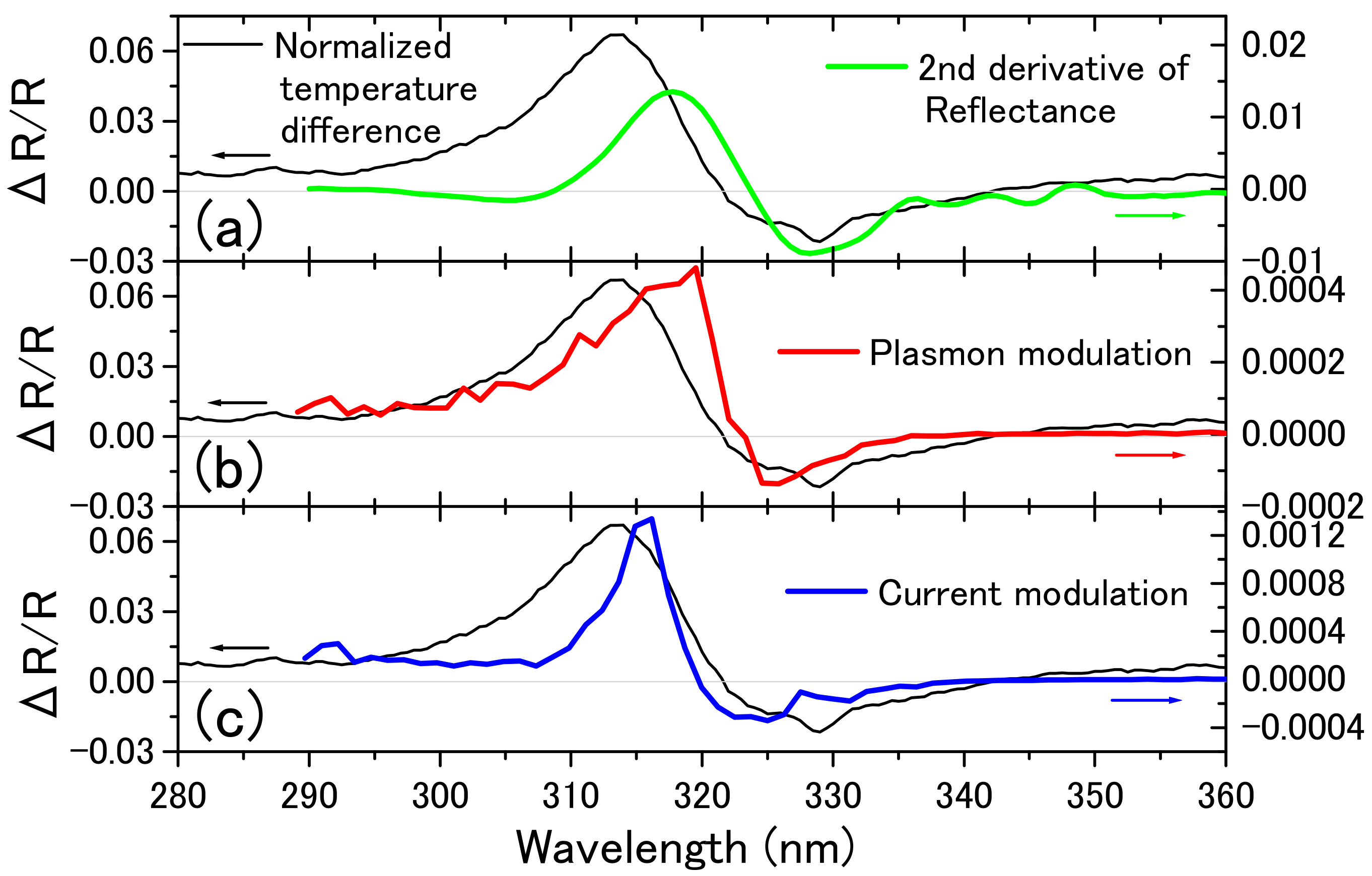
3.2. Plasmon Modulation Spectrum

The difference reflection spectrum near the interband transition edge of silver at the time of plasmon excitation is shown in Figure 5, together with the stationary reflection spectrum. The incident angle of white light is 55°; the chopper frequency is 221 Hz; the laser power is 100 mW; and the laser spot diameter is 5 mm. The dip of the reflection spectrum seen on the shorter than 325 nm wavelength side is due to the interband transition. The spectral shape of the change in the reflection spectrum induced by plasmon excitation indicates a broadening of the interband transition edge.

3.3. Current Modulation and Temperature Difference Spectra

Figure 6 shows the current modulation spectra near the interband transition edge of silver, together with the reflection spectrum. Similar to the plasmon modulation spectrum, the current modulated reflection spectra show such a change that corresponds to the interband transition edge becoming broader. As the current is increased, the reflectance change increases accompanied by a slight change in the spectral shape such that the zero-crossing point is red-shifted with increasing magnitude of the current. Figure 7 shows the normalized temperature difference spectra. In marked contrast with the current modulation spectra, the zero-crossing point is fixed throughout the change in temperature from +10 K–+50 K, indicating that any change in the spectral shape with temperature is negligibly small.

3.4. CW Modulation Spectra

Figure 8 shows a comparison of the difference reflection spectrum in the interband transition energy region caused by plasmon modulation and by current modulation (current = 1.56 A) with the temperature difference spectrum (ΔT = 50 K). The contribution due to temperature rise is comparable for both modulation spectra since the laser intensity was 4.0 × 10⁻¹ W/cm² and the amount of heat generated per unit time and unit area by a current of 1.56 A is 3.1 × 10⁻¹ W/cm². The plasmon and the current modulation spectra qualitatively agree with the second derivative of the reflectance as expected for a modulation of the joint-electron distribution function of the valence band and the conduction band. However, the plasmon modulation spectrum is distinctly different from the current modulation spectrum and differs from the temperature difference spectrum, as well.

The current modulation spectra of metals were previously studied by Rosei and Lynch [20]. They used the electric current as a method of Joule heating to obtain thermo-reflection spectra of Al, Au and Cu. The observed spectral shapes for all the metals have a characteristic feature of the second derivative of the stationary reflection spectra. They argued that this is caused by broadening of the Fermi distribution by temperature increase. However, they did not study the dependence on the magnitude of the current, so that the shift in the zero-crossing was not reported previously.

Although the incidence angle is different between the plasmon/current modulation and temperature difference spectra, the reflection spectra are nearly the same, so that the difference in the incidence angle is irrelevant to the discrepancy noted above. Currently, there is no theoretical explanation for this observation, and this signal may contain some signature of the k-space wave function of the plasmon.

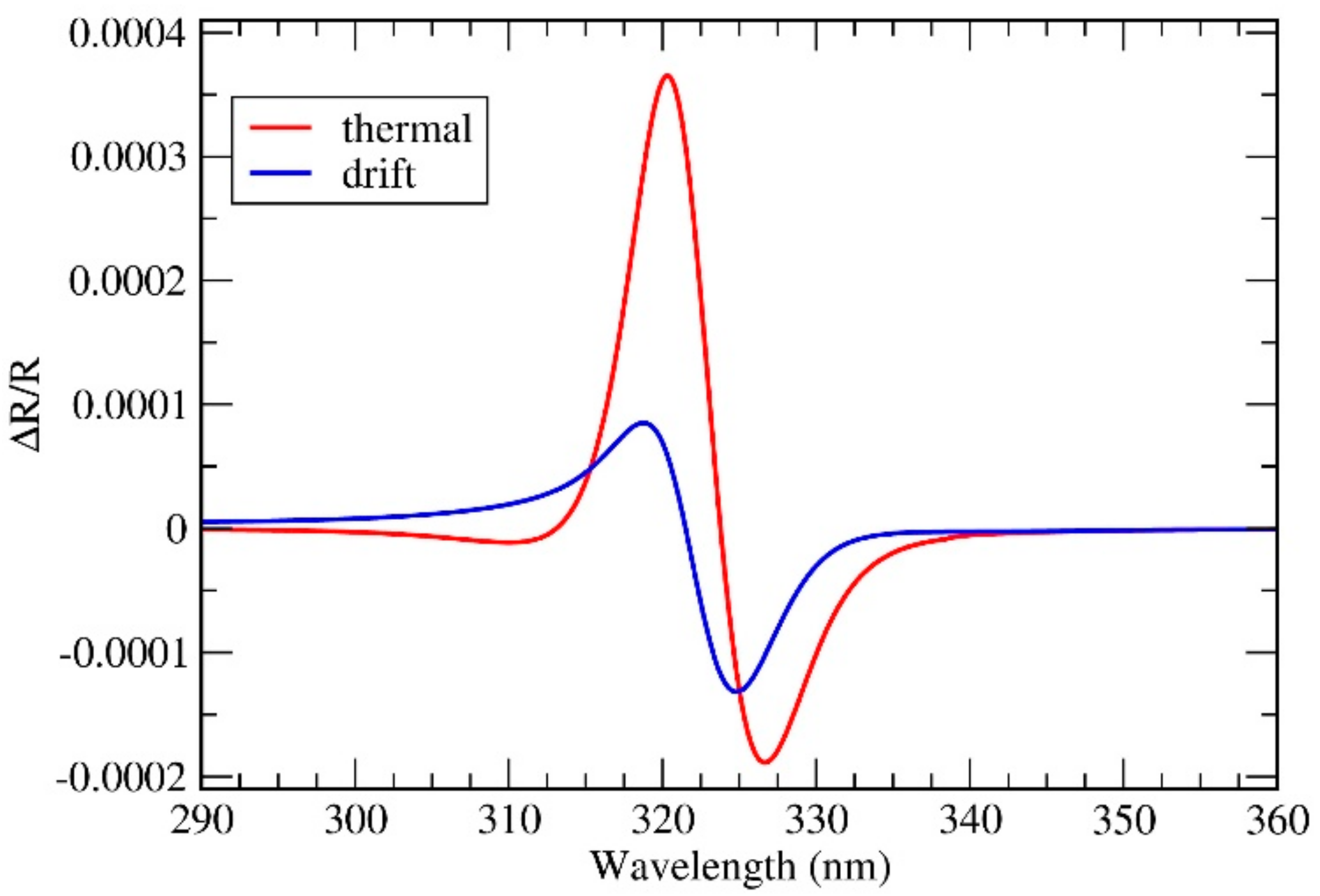
3.5. Calculation of Reflectivity Modulation

We calculated the change in the dielectric constant and the resulting modulation of reflectivity due to perturbation of the electron distribution using a model previously applied to gold by Rosei et al. [20]. In this model, the onset of inter-band absorption is assumed to be the d-p transition near the L-point as supported by band structure calculations [21]. Within a constant matrix element approximation [21], the imaginary part of the dielectric constant close to this inter-band transition at frequency $\omega$ is given by:

$${ϵ}_2\left(\omega \right)\propto \frac{1}{{\omega }^2}{{\displaystyle \int }}^{\text{}}\left(1-f\left(k, T_e\right)\right) \delta \left(E_p\left(k\right)-E_d\left(k\right)-\hslash \omega \right) d^{3}k$$

(1)

where $f$ is the electron distribution function in the conduction band at electron temperature $T_e$ and $E_p\left(k\right)$, $E_d\left(k\right)$ are the band dispersions assumed to be parabolic with:

$$E_p\left(k\right) = E_{pL} -\frac{{\hslash }^2{k}^2{}_{\parallel }}{2m_{p\parallel }} + \frac{{\hslash }^2{k}^2{}_{\perp }}{2m_{p\perp }}$$

$$E_d\left(k\right)= E_{dL} -\frac{{\hslash }^2{k}^2{}_{\parallel }}{2m_{d\parallel }} - \frac{{\hslash }^2{k}^2{}_{\perp }}{2m_{d\perp }}$$

Here, $k_{\parallel }$ and $k_{\perp }$ denote the components of k along and perpendicular to the [111] direction, taking the L-point as the origin. For silver, we use $m_{p\parallel }=0.32$,$m_{p\perp }=0.17$, $m_{d\parallel }=2.08$, $m_{d\perp }=2.58,E_{pL}=-0.155\mathrm{eV}$ and $E_{dL}=-3.818\mathrm{eV}$ [13]. The constant of proportionality in Equation (1) is determined by fitting the result to the experimentally-measured dielectric constant of silver [22].

The change in the imaginary part $\Delta {ϵ}_2$ due to a change $\Delta f$ of the electron distribution is given by replacing ($1-f$) by $-\Delta f$ in Equation (1). We consider two kinds of perturbations, (i) a temperature change of the electrons by $\Delta T_e$, referred to as thermal and (ii) a rigid shift of the Fermi-sphere by $\Delta \mathrm{k}$ with the shift direction isotropically averaged, referred to as drift. The corresponding change in the real part ($\Delta {ϵ}_1$) is obtained by Kramers–Kronig transformation of $\Delta {ϵ}_2$. For the unperturbed dielectric constant, we use the experimental values from [22]. The change in reflectivity is then readily obtained by applying the Fresnel formula to the thin-film geometry. The results are shown in Figure 9.

The calculated reflectivity spectrum for a thermal distribution with $\Delta T_e=0.16$K (red line in Figure 9) agrees with the gross features of the experimental results for plasmon and current modulations shown in Figure 5 and Figure 6. Although the drift perturbation gives a spectrum that is weaker and more spread out than the thermal case for the same energy content, the spectral shape is not remarkably different from the latter. Further, the predicted width of the spectrum is mainly determined by the dispersions of the bands and is not strongly dependent on the strength of the perturbation. These facts combined with the uncertainties in band structure parameters makes it difficult to clearly isolate any non-thermal components in the observed spectrum based on calculations alone.

We conclude that, in order to unambiguously identify non-thermal electron populations, it is necessary to probe the system in a regime where such contributions dominate, viz., in short time scales immediately following the plasmon excitation.

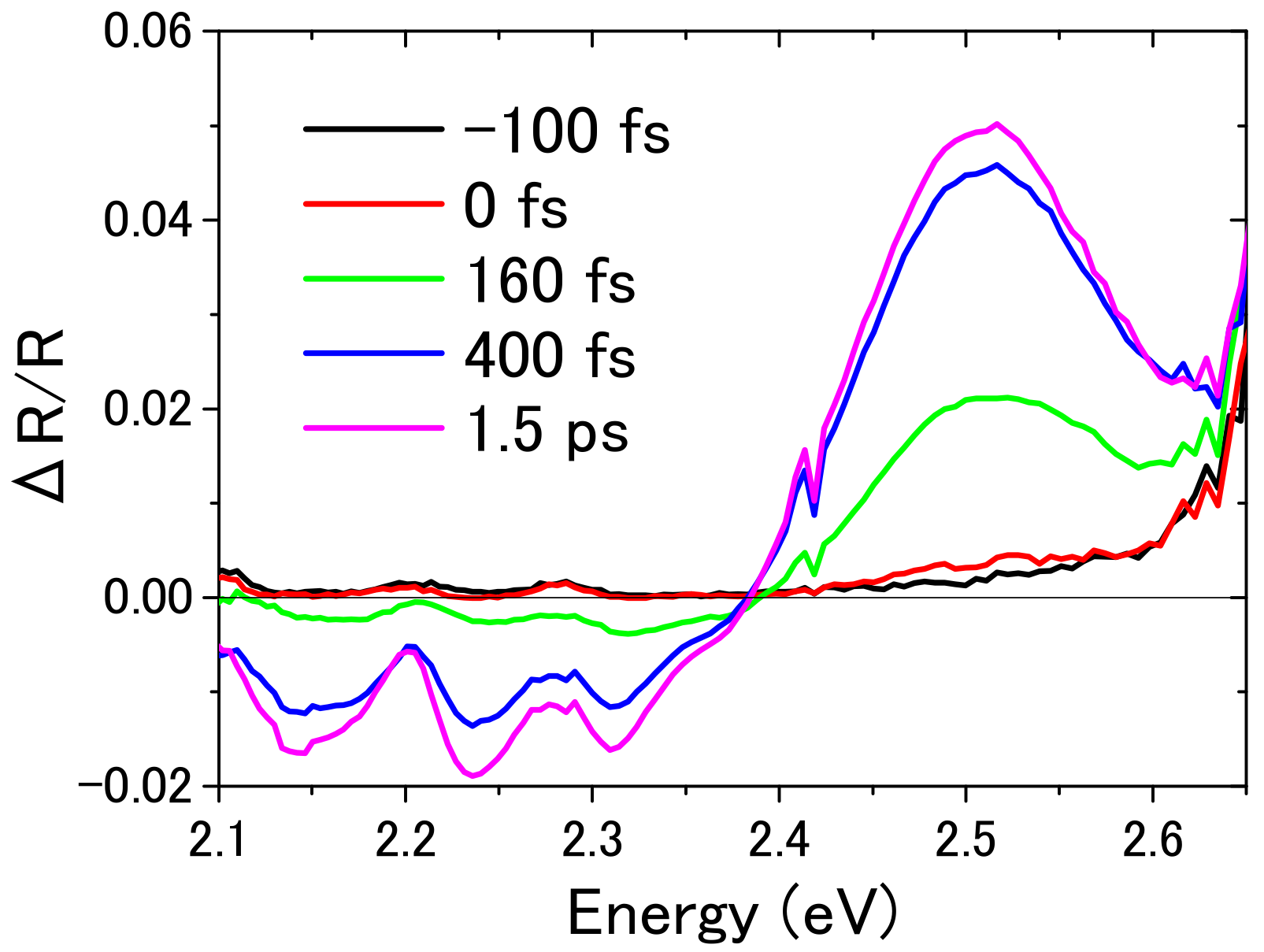
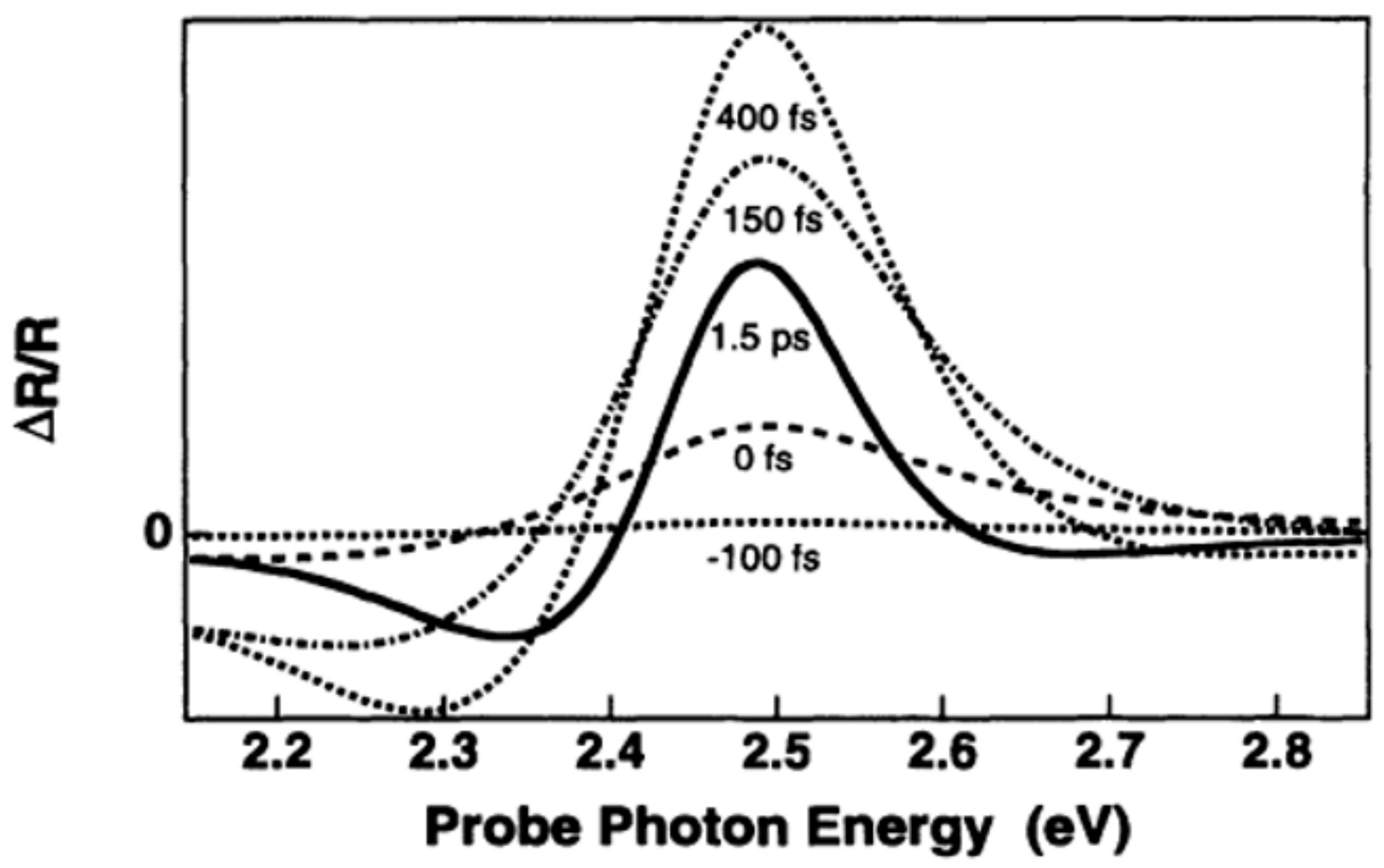
3.6. Femtosecond Time-Resolved Spectra

From the experiments results presented above using CW light, it is found that the electron distribution changes near the Fermi surface due to plasmon, current and temperature modulation are mutually different (temperature difference spectra are equivalent to temperature modulation spectra). To understand the remarkable difference observed among these spectra, it is desirable to obtain temporally-resolved information of the spectral change before thermal relaxation and thus to isolate any direct contribution due to plasmon from that of the temperature rise.

The result of the femtosecond pump-probe experiment is shown in Figure 10, where the reflection change spectra near the interband transition edge at different delay times are overlaid on each other. The change in the reflection spectrum rises for times over about 500 fs.

Figure 11 shows the calculated reflectance change near the interband transition region after single particle excitation performed by Sun et al. [14]. Our measured relative difference reflectance (ΔR/R) spectra following plasmon excitation show a very similar variation with the maximum change around 500 fs as that predicted for single-particle excitation. From this comparison, the dynamic signal observed is attributed to the process in which the plasmon relaxes to individual (independent or uncoupled) electronic excitations, which evolve into the thermal equilibrium state of the electron system.

4. Conclusions and Prospects

To access information of the plasmon wavefunction in the conduction band of metals, we have successfully obtained difference reflection spectra in the interband transition band edge due to CW plasmon, current, and temperature modulations in silver. Surprisingly, these spectra are mutually different, indicating that the effect of plasmon oscillations and current flow are not merely expressed by a broadening of the Fermi distribution of electrons, which should determine the temperature modulation spectra. In addition to temperature modulation due to Joule heating, current flow also introduces an anisotropic change in the momentum distribution function of electrons. However, we find that the corresponding change in the interband transitions is too small to explain the observed results. In case of plasmon modulation, existing theories only account for the hot electrons generated by plasmon relaxation and their subsequent thermalization. Further theoretical studies that take into account the collective nature of the plasmons may be required to explain the specific spectral features observed in the experiments.

In order to separate the effect of temperature rise, a time-resolved experiment was performed to excite plasmons and probe the interband transition in gold. Because of the limitation of the time resolution, no inherent feature of the plasmon wavefunction was observed, but relaxation dynamics of the respective particles were observed in agreement with known results. In the present femtosecond pump-probe experiment, fundamental 100-fs pulses at 800 nm from the Ti:sapphire amplifier were used as the pump for surface plasmons in gold, and supercontinuum pulses were used for the probe to extend the wavelength range to cover the interband transition edge of gold, which is about 500 nm. This selection is mainly due to the requirement of the wavelength coverage over the plasmon resonance and interband transitions of gold sacrificing the time resolution. To meet the requirement of higher time resolution, sub-5-fs pulses from a noncollinear optical parametric amplifier (NOPA) system are the most suitable, which are the shortest visible pulses presently available [23]. However, it is difficult for NOPA pulses to cover wavelengths shorter than 500 nm, so that silver and gold are not suitable samples, while copper matches best with the specifications of NOPA pulses. Although there is a limited number of studies on plasmons in copper, recently copper films of high quality have been fabricated, and recipes for sample preparation and detailed studies of copper plasmons have been reported [17,24,25]. We are presently preparing for pump-probe measurements in copper.