A Psychoacoustic-Based Multiple Audio Object Coding Approach via Intra-Object Sparsity

Abstract

Rendering spatial sound scenes via audio objects has become popular in recent years, since it can provide more flexibility for different auditory scenarios, such as 3D movies, spatial audio communication and virtual classrooms. To facilitate high-quality bitrate-efficient distribution for spatial audio objects, an encoding scheme based on intra-object sparsity (approximate k-sparsity of the audio object itself) is proposed in this paper. The statistical analysis is presented to validate the notion that the audio object has a stronger sparseness in the Modified Discrete Cosine Transform (MDCT) domain than in the Short Time Fourier Transform (STFT) domain. By exploiting intra-object sparsity in the MDCT domain, multiple simultaneously occurring audio objects are compressed into a mono downmix signal with side information. To ensure a balanced perception quality of audio objects, a Psychoacoustic-based time-frequency instants sorting algorithm and an energy equalized Number of Preserved Time-Frequency Bins (NPTF) allocation strategy are proposed, which are employed in the underlying compression framework. The downmix signal can be further encoded via Scalar Quantized Vector Huffman Coding (SQVH) technique at a desirable bitrate, and the side information is transmitted in a lossless manner. Both objective and subjective evaluations show that the proposed encoding scheme outperforms the Sparsity Analysis (SPA) approach and Spatial Audio Object Coding (SAOC) in cases where eight objects were jointly encoded.

1. Introduction

With the development of multimedia video/audio signal processing, multi-channel 3D audio has been widely employed for applications, such as cinemas and home theatre systems, since it can provide excellent spatial realism of the original sound field, as compared to the traditional mono/stereo audio format.

There are multiple formats for rendering 3D audio, which contain channel-based, object-based and HOA-based audio formats. In traditional spatial sound rendering approach, the channel-based format is adopted in the early stage. For example, the 5.1 surround audio format [1] provides a horizontal soundfield and it has been widely employed for applications, such as the cinema and home theater. Furthermore, typical ‘3D’ formats include a varying number of height channels, such as 7.1 audio format (with two height channels). As the channel number increases, the audio data will raise dramatically. Due to the bandwidth constrained usage scenarios, the spatial audio coding technique has become an ongoing research topic in recent decades. In 1997, ISO /MPEG (Moving Picture Experts Group) designed the first commercially-used multi-channel audio coder MPEG-2 Advanced Audio Coding (MPEG-2 AAC) [2]. It could compress multi-channel audio by adding a number of advanced coding tools to MPEG-1 audio codecs, delivering European Broadcasting Union (EBU) broadcast quality at a bitrate of 320 kbps for a 5.1 signal. In 2006, MPEG Surround (MPS) [3,4] was created for highly transmission of multi-channel sound by downmixing the multi-channel signals into mono/stereo signal and extracting Interaural Level Differences (ILD), ITD (Interaural Time Differences) and IC (Interaural Coherence) as side information. Spatially Squeezed Surround Audio Coding (S³AC) [5,6,7], as a new method instead of original “downmix plus spatial parameters” model, exploited spatial direction of virtual sound source and mapping the soundfield from 360° into 60°. At the receiver, the decoded signals can be achieved by inverse mapping the 60° stereo soundfield into 360°.

However, such channel-based audio format has its limitation on flexibility, i.e., each channel is designated to feed a loudspeaker in a known prescribed position and cannot be adjusted for different reproduction needs by the users. Alternatively, a spatial sound scene can be described by a number of sound objects, each positioned at a certain target object position in space, which can be totally independent from the locations of available loudspeakers [8]. In order to fulfill the demand of interactive audio elements, object-based (a.k.a. object-oriented) audio format enables users to control audio content or sense of direction in application scenarios where the number of sound sources varies, sources move are commonly encountered. Hence, object signals generally need to be rendered to their target positions by appropriate rendering algorithms, e.g., Vector Base Amplitude Panning (VBAP) [9]. Therefore, object-based audio format can personalize customer’s listening experience and make surround sound more realistic. By now, object-based audio has been commercialized in many acoustic field, e.g., Dolby ATMOS for cinemas [10].

To facilitate high-quality bitrate-efficient distribution of audio objects, several methods have been developed, one of these techniques is MPEG Spatial Audio Object Coding (SAOC) [11,12]. SAOC encodes audio objects into a mono/stereo downmix signal plus side information via Quadrature Mirror Filter (QMF) and extract the parameters that stand for the energy relationship between different audio objects. Additionally, Directional Audio Coding (DirAC) [13,14] compress a spatial scene by calculating a direction vector representing spatial location information of the virtual sources. At the decoder side, the virtual sources are created from the downmixed signal at positions given by the direction vectors and they are panned by combining different loudspeakers through VBAP. The latest MPEG-H 3D audio coding standard incorporates the existing MPEG technology components to provide universal means for carriage of channel-based, object-based and Higher Order Ambisonics (HOA) based inputs [15]. Both MPEG-Surround (MPEG-S) and SAOC are included in MPEG-H 3D audio standard.

Recently, a Psychoacoustic-based Analysis-By-Synthesis (PABS) method [16,17] was proposed for encoding multiple speech objects, which could compress four simultaneously occurring speech sources in two downmix signals relied on inter-object sparsity [18]. However, with the number of objects increases, the inter-object sparsity becomes weakened, which leads to quality loss of decoded signal. In our previous work [19,20,21], a multiple audio objects encoding approach was proposed based on intra-object sparsity. Unlike the inter-object sparsity employed in PABS framework, this encoding scheme exploited the sparseness of object itself. That is, in a certain domain, an object signal can be represented by a small number of time-frequency instants. The evaluation results validated that this intra-object based approach achieved a better performance than PABS algorithm and retain the superior perceptual quality of the decoded signals. However, the aforementioned technique still has some restrictions which leads to a sub-optimum solution for object compression. Firstly, Short Time Fourier Transform (STFT) is chosen as the linear time-frequency transform to analyze audio objects. Yet the energy compaction capability of STFT is not optimal. Secondly, the above object encoding scheme concentrated on the features of object signal itself without considering the psychoacoustic, thus it is not an optimal quantization means for Human Auditory System (HAS).

This paper expands on the contributions in [19]. Based on intra-object sparsity, we propose a novel encoding scheme for multiple audio objects to further optimize our previous proposed approach and minimize the quality loss caused by compression. Firstly, by exploiting intra-object sparsity in the Modified Discrete Cosine Transform (MDCT) domain, multiple simultaneously occurring audio objects are compressed into a mono downmix signal with side information. Secondly, psychoacoustic model is utilized in the proposed codec to accomplish an optimal quantization for HAS. Hence, a Psychoacoustic-based Time-Frequency (TF) instants sorting algorithm is proposed for extracting the dominant TF instants in the MDCT domain. Furthermore, by utilizing these extracted TF instants, we propose a fast algorithm of Number of Preserved Time-Frequency Bins (NPTF, defined in Appendix A) allocation strategy to ensure a balanced perception quality for all object signals. Finally, the downmix signal can be further encoded via SQVH technique at desirable bitrate and the side information is transmitted in a lossless manner. In addition, a comparative study of intra-object sparsity of audio signal in the STFT domain and MDCT domain is presented via statistical analysis. The results show that audio objects have sparsity-promoting property in the MDCT domain, which means that a greater data compression ratio can be achieved.

The remainder of the paper is structured as follows: Section 2 introduces the architecture of the encoding framework in detail. Experimental results are presented and discussed in Section 3, while the conclusion is given in Section 4. Appendix A investigates the sparsity of audio objects in the STFT and MDCT domain, respectively.

2. Proposed Compression Framework

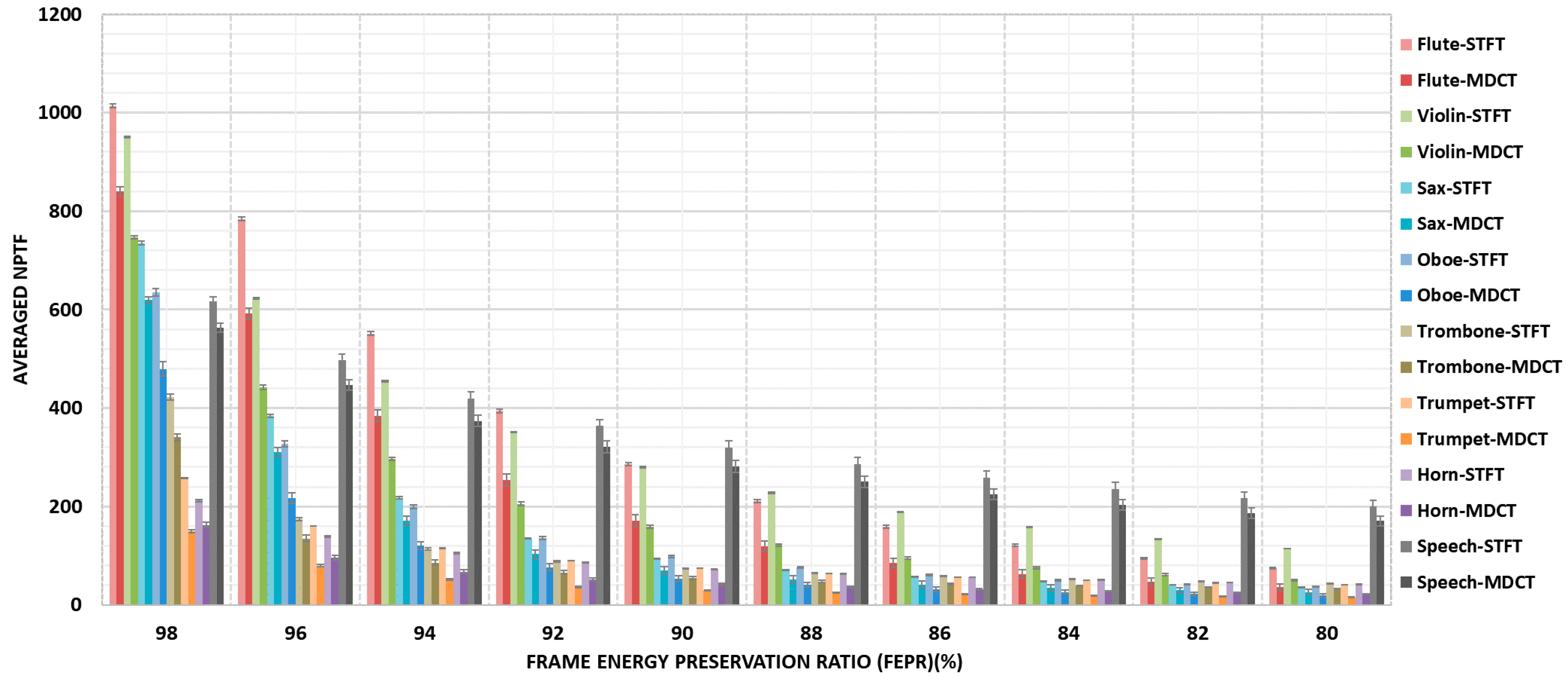
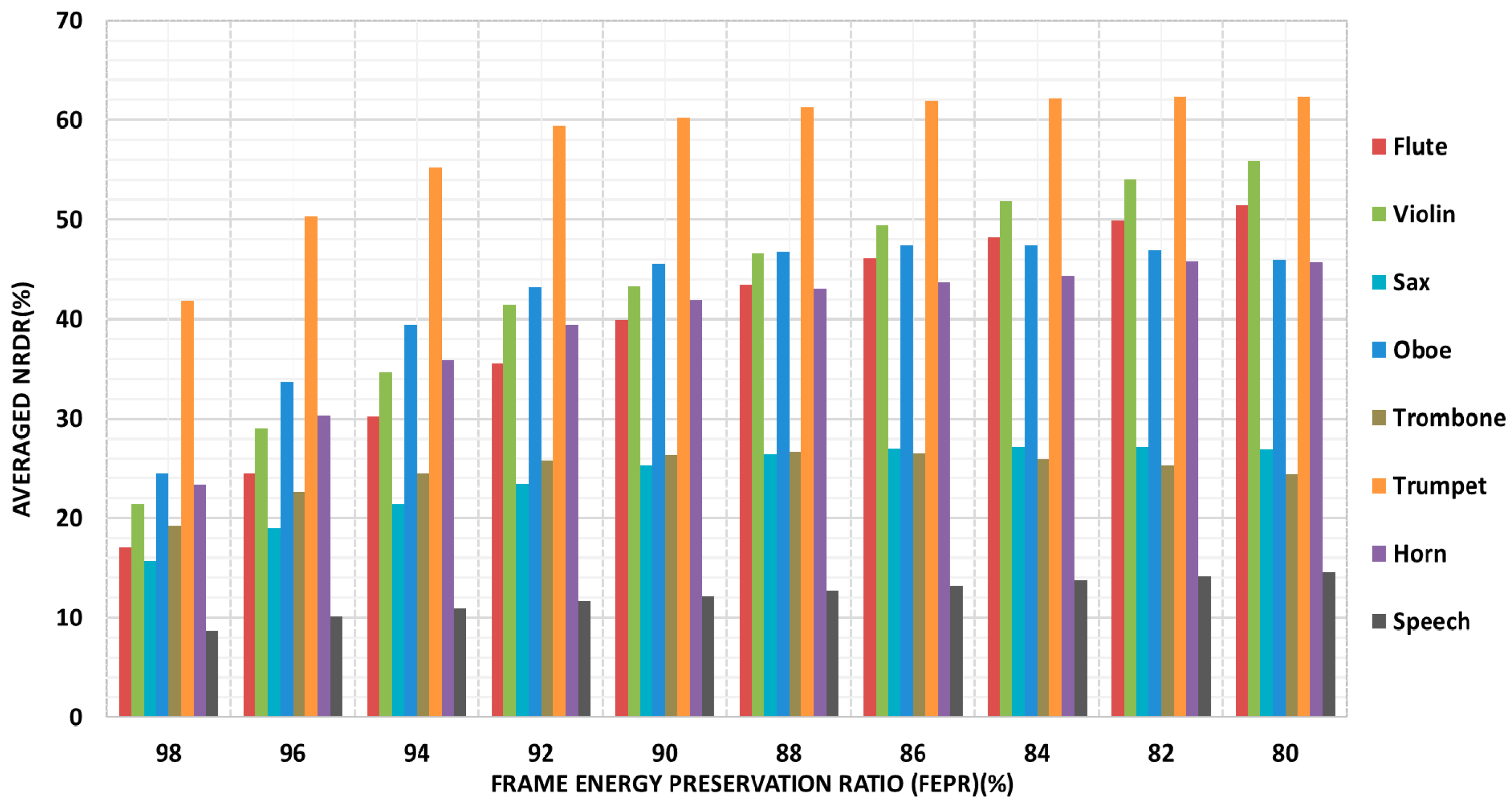
In the previous work, we adopted STFT as time-frequency transform to analyze the sparsity of audio signal and designed a codec based on the intra-object sparsity. From the statistical results of sparsity presented in Appendix A, we know that audio signals satisfy the approximate k-sparsity both in the STFT and MDCT domain, i.e., the energy of audio signal is almost concentrated in k time-frequency instants. In other words, audio signals have sparsity-promoting property in the MDCT domain in contrast to STFT, that is, $k{\left(r_{FEPR}\right)}_{\mathrm{MDCT}}<k{\left(r_{FEPR}\right)}_{\mathrm{STFT}}$. By using this advantage of MDCT, a multiple audio objects compression framework is proposed in this section based on intra-object sparsity. The proposed encoding scheme consists of five modules: time-frequency transform, active object detection, psychoacoustic-based TF instants sorting, NPTF allocation strategy and Scalar Quantized Vector Huffman Coding (SQVH).

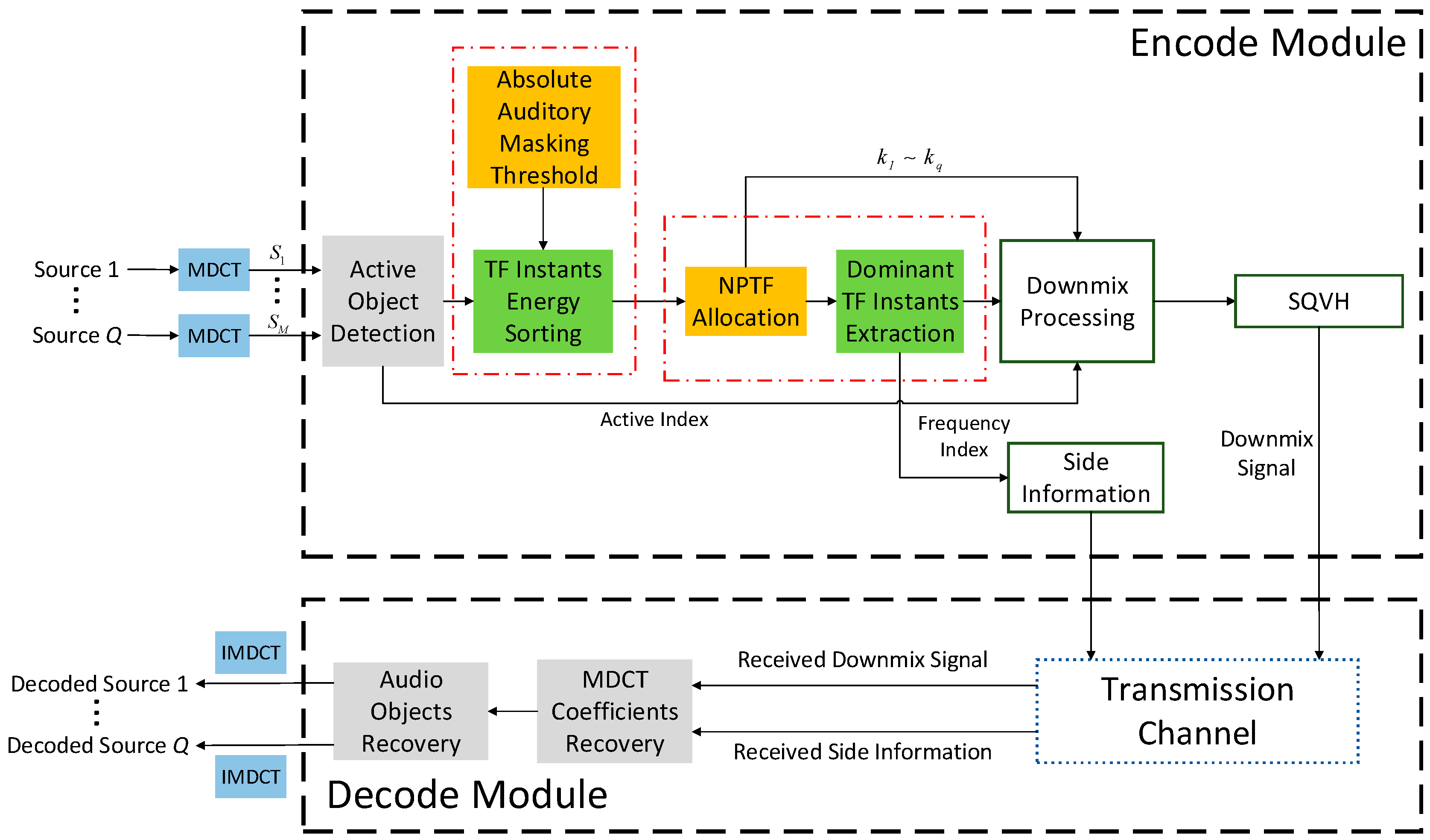
The following process is operated in a frame-wise fashion. As is shown in Figure 1, all input audio objects (Source 1 to Source Q) are converted into time-frequency domain using MDCT. After active object detection, the TF instants of all active objects will be sorted according to Psychoacoustic model in order to extract the most perceptually important time-frequency instants. Then, a NPTF allocation strategy among all audio objects is proposed to counterpoise the energy of all preserved TF instants of each object. Thereafter, the extracted time-frequency instants are downmixed into a mono mixture stream plus side information via downmix processing operation. Particularly attention is that the downmix signal can be further compressed by existing audio coding methods. In this proposed method, SQVH technique is employed after de-mixing all TF instants, because it can compress audio signal at desirable bitrate. At the receiving end, Source 1 to Source Q can be decoded by exploiting the received downmix signal and the side information. The detailed contents are described below.

2.1. MDCT and Active Object Detection

In n^th frame, an input audio object s_n = [s_n(1), s_n(2), …, s_n(M)] is transformed into the MDCT domain, denoted by S(n, l), where n (1 ≤ n ≤ N) and l (1 ≤ l ≤ L) are frame number and frequency index, respectively. M = 1024 is the frame length. Here, a 2048-points MDCT is applied with 50% overlapped [22]. By this overlap, discontinuity at block boundary is smoothed out without increasing the number of transform coefficients. Afterwards, MDCT of an original signal s_n can be formulated as:

$$S\left(n,l\right)=2\left[{\mathit{s}}_n\cdot {\left({\mathit{\varphi }}_l^1\right)}^T+{\mathit{s}}_{n+1}\cdot {\left({\mathit{\varphi }}_l^2\right)}^T\right]$$

(1)

where L = 1024, ${\mathit{\varphi }}_l^1\triangleq \left\{{\varphi }_l^1(1),{\varphi }_l^1(2),\cdots ,{\varphi }_l^1(M)\right\}$, ${\mathit{\varphi }}_l^2\triangleq \left\{{\varphi }_l^2(1),{\varphi }_l^2(2),\cdots ,{\varphi }_l^2(M)\right\}$ are the basis functions corresponding to n^th frame and (n + 1)^th frame. ${\varphi }_l^1(m)=\omega (m)\cdot \cos \left[\frac{\pi }{M}\cdot \left(m+\frac{M+1}{2}\right)\cdot \left(l-\frac{1}{2}\right)\right]$, ${\varphi }_l^2(m)=\omega \left(m+M\right)\cdot \cos \left[\frac{\pi }{M}\cdot \left(m+\frac{3M+1}{2}\right)\cdot \left(l-\frac{1}{2}\right)\right]$ and ^T is the transpose operation. In addition, a Kaiser–Bessel derived (KBD) short-time window slid along the time axis with 50% overlapping between frames is used as window function ω(m).

In order to ensure the encoding scheme only encodes active frames without processing the silence frames, an Active Object Detection technique is applied to check the active audio objects in the current frame. Hence, Voice Activity Detection (VAD) [23] is utilized in this work, which is based on the short-time energy of audio in the current frame and comparison with the estimated background noise level. Each source uses a flag to indicate whether it is active in current frame. i.e.,

$$flag=\{\begin{array}{cc}1,& \mathrm{if}\mathrm{the}\mathrm{current}\mathrm{object}\mathrm{is}\mathrm{active}\\ 0,& \mathrm{otherwise}\end{array}$$

(2)

Afterwards, only the frames which are detected as active will be sent into the next module. In contrast, the mute frames will be ignored in the proposed codec. This procedure ensures that silence frames cannot be selected.

2.2. Psychoacoustic-Based TF Instants Sorting

In Appendix A, it is proved that the majority of the frame energy concentrates in finite k time-frequency instants for each audio object. For this reason, we can extract these k dominant TF instants for compression. In our previous work [19,20,21], TF instants are sorted and extracted by natural ordering via the magnitude of the normalized energy. However, this approach does not take into account HAS. It is well-known that HAS is not equally sensitive to all frequencies within the audible band since it has a non-flat frequency response. This simply means that we can hear some tones better than others. Thus, tones played at the same volume (intensity) at different frequencies are perceived as if they are being played at different volumes. For the purpose of enhance perceptual quality, we design a novel method through absolute auditory masking threshold to extract the dominant TF instants.

The absolute threshold of hearing characterizes the amount of energy needed in a pure tone such that it can be detected by a listener in a noiseless environment and it is expressed in terms of dB Sound Pressure Level (SPL) [24]. The quiet threshold is well approximated by the continuous nonlinear function, which is based on a number of listeners that were generated in a National Institutes of Health (NIH) study of typical American hearing acuity [25]:

$$T(f)=3.64\times {(f/1000)}^{-0.8}-6.5\times {e^{-0.6(f/1000-3.3)}}^2+{10}^{-3}\times {(f/1000)}^4$$

(3)

where T(f) reflects the auditory properties for human ear in the STFT domain. Hence, the T(f) should be discretized and converted into the MDCT domain. The whole processing procedure includes two steps: inverse time-frequency transform and MDCT [26]. After these operations, absolute auditory masking threshold in the MDCT domain is denoted as T_mdct (l) (dB expression), where l = 1, 2, …, L. Then, an L-dimensional Absolute Auditory Masking Threshold (AAMT) vector T ≡ [T_mdct(1), T_mdct(2), …, T_mdct(L)] is generated for subsequent computing. From psychoacoustic theory, it is clear that if there exists a TF bin (n₀, l₀) that the difference between S_dB(n₀, l₀) (dB expression of S(n₀, l₀)) and T_mdct(l₀) is larger than other TF bins, which means that S(n₀, l₀) can be perceived more easily than other TF components, but not vice versa. Specifically, any signals below this threshold curve (i.e., S_dB(n₀, l₀) − T_mdct(l₀) < 0) is imperceptible (because T_mdct (l) is the lowest limit of HAS). Rely on this phenomenon, the AAMT vector T is used for extracting the perceptual dominant TF instants efficiently.

For q^th (1 ≤ q ≤ Q) audio object S_q(n, l), whose dB expression is written as S_{q_dB}(n, l). An aggregated vector can be attained by converging each S_{q_dB}(n, l) denoted as S_{q_dB}≡ [S_{q_dB}(n, 1), S_{q_dB}(n, 2), …, S_{q_dB}(n, L)]. Subsequently, a perceptual detection vector is designed as:

$${\mathit{P}}_q=S_{q\_dB}–\mathit{T}\equiv \left[P_q(n,1),P_q(n,2),\cdots ,P_q(n,L)\right]$$

(4)

where P_q(n,l) = S_{q_dB}(n,l) − T_mdct(l). To sort each element in P_q according to the magnitude in descending order, mathematically, a new vector can be attained as:

$${\mathit{P}}_q^{\prime }\equiv \left[P_q(n,l_1^q),\cdots ,P_q(n,l_L^q)\right]$$

(5)

the elements in ${\mathit{P}}_q^{\prime }$ satisfy:

$$P_q(n,l_i^q)\ge P_q(n,l_j^q),\forall i<j,i,j\in \{1，2，\cdots ,L\}$$

(6)

where $l_1^q,\cdots ,l_L^q$ is the reorder frequency index which represent the perceptual significantly TF instants in order of importance for HAS. In other words, $S_q(n,l_1^q)$ is the most considerable component with respect to HAS. In contrast, $S_q(n,l_L^q)$ is almost the least significant TF instant for HAS.

2.3. NPTF Allocation Strategy

Allocating the NPTF for each active object signal can be actualized with various manners according to realistic application scenarios. As a most common used means called simplified average distribution method, all active objects share the same NPTF has been employed in [19,21]. This allocation method balances a tradeoff between computational complexity and perceptual quality. Therefore, it is a simple and efficient way. Nonetheless, this allocation strategy cannot guarantee all decoded objects with similar perceptual quality. Especially, the uneven quality can be emerged if there exists big difference of intra-object sparseness amongst objects. To conquer the above-mentioned issue, an Analysis-by-Synthesis (ABS) framework was proposed to balance the perceptual quality for all objects through solving a minimax problem via the iterative processing [20]. The test results show that this technique yields the approximate evenly distributed Frame Energy Preservation Ratio (FEPR, defined in Appendix A) for all objects. Despite the harmonious perceptual quality can be maintained, the attendant problem which is the sharp increase in computational complexity cannot be neglected. Accordingly, relied on the TF sorting result obtained in Section 2.2, an NPTF allocation strategy for obtaining a balanced perceptual quality of all inputs is proposed in this work.

In the n^th frame, we assume that the q^th object will be distributed k_q NPTF, i.e., k_q TF instants will be extracted for coding. An Individual Object Energy Retention ratio (IOER) function for the q^th object is defined by:

$$f_{IOER}\left(k,q\right)=\frac{{\displaystyle \sum _{i=1}^k{S}_q\left(n,l_i^q\right)}}{{\displaystyle \sum _{l=1}^L{S}_q\left(n,l\right)}}$$

(7)

where $l_i^q$ is the reorder frequency index obtained in the previous section. IOER function represents the energy of the k perceptual significant elements against the original signal S_q(n, l). Thus, k_q will be allocated for each object with approximate IOER. Under the criterion of minimum mean-square error, for all $q\in \{1,2,\dots ,Q\}$ the k_q can be attained via a constrained optimization equation as follow:

$$\begin{array}{c}\underset{k_1,k_2,\cdots ,k_Q}{\min }{\displaystyle \sum _{q=1}^Q{\Vert f_{IOER}(k_q,q)-\overline{f}\Vert }^2}\\ \mathrm{s}.\mathrm{t}.{\displaystyle \sum _{q=1}^Q{k}_q}=L\end{array}$$

(8)

where $\overline{f}=\frac{1}{Q}{\displaystyle \sum _{q=1}^Q{f}_{IOER}\left(k,q\right)}$ represents the average energy of all objects. The optimal solution k₁, k₂, …, k_Q for each object are the desired NPTF₁, NPTF₂, …, NPTF_Q, which can be searched by our proposed method elaborated in Algorithm 1.

Algorithm 1: NPTF allocation strategy based on bisection method
Input: Q	►number of audio objects
Input: ${\left\{S_q\left(n,l\right)\right\}}_{q=1}^Q$	►MDCT coefficients of each audio object
Input: ${\left\{l_i^q\right\}}_{i=1}^L$	►reordered frequency index by psychoacoustic model
Input: BPA	►lower limit used in dichotomy part
Input: BPB	►upper limit used in dichotomy part
Input: BPM	►median used in dichotomy part
Output: K	►desired NPTF allocation result
1. Set K = Ø
2. for q = 1 to Q do
3.  for k = 1 to L do
4.  Calculate IOER function fIOER(k, q) using ${\left\{S_q\left(n,l\right)\right\}}_{q=1}^Q$ and ${\left\{l_i^q\right\}}_{i=1}^L$ in Formula (12).
5.  end for
6. end for
7. Initialize BPA = 0, BPB = 1, BPM = 0.5·(BPA + BPB), STOP = 0.01 chosen based on a series of informal experimental results.
8. while (BPB–BPA > STOP) do
9.  Find the index value corresponding to BPM value in IOER function (i.e., fIOER(kq, q) ≈ BPM), denoted by kq.
10.   if ${\displaystyle \sum _{q=1}^Q{k}_q}>L$ then
11.    BPB = BPM,
12.    BPM = [0.5·(BPA + BPB)].
13.   else
14.    BPA = BPM,
15.    BPM = [0.5·(BPA + BPB)].
16.   end if
17.  end while
18. $\mathit{K}={\left\{k_q\right\}}_{q=1}^Q$
19. return K

The proposed NPTF allocation strategy allows different reserved TF instants (i.e., MDCT coefficients) for each object among a certain group of multi-track audio objects without iterative processing, therefore, the computational complexity decrease rapidly through the dynamic TF instants distribution algorithm. In addition, a sub-equal perception quality for each object can be maintained via our proposed NPTF allocation strategy rather than pursuit the quality of a particular object.

Thereafter, vector ${\mathit{P}}_q^{\prime }$ needs to be extract the NPTF_q(k_q) elements to forming a new vector ${\tilde{\mathit{p}}}_q\equiv [P_q(n,l_1^q),\cdots ,p_q(n,l_{NPT{F}_q}^q)].$. It should be note that $l_1^q,l_2^q,\dots ,l_{NPT{F}_q}^q$ indicate the origin of $S_q\left(n,l_1^q\right),S_q\left(n,l_2^q\right),\dots ,S_q\left(n,l_{NPT{F}_q}^q\right)$, respectively. We group $l_1^q,l_2^q,\dots ,l_{NPT{F}_q}^q$ into a vector ${\mathit{I}}_q\equiv \left[l_1^q,l_2^q,\dots ,l_{NPT{F}_q}^q\right]$, in the meantime, a new vector containing all extracted TF instants ${\widehat{\mathit{S}}}_q\equiv \left[S_q\left(n,l_1^q\right),S_q\left(n,l_2^q\right),\dots ,S_q\left(n,l_{NPT{F}_q}^q\right)\right]$ is generated. Finally, both I_q and ${\widehat{\mathit{S}}}_q$ should be stored locally and sent into the Downmix Processing module.

2.4. Downmix Processing

After extracting the dominant TF instants ${\widehat{\mathit{S}}}_q$, source 1 to source Q only contains the perception significantly MDCT coefficients of all active audio objects. However, each source include a number of zero entries, hence, the downmix processing must be exploited which aims to redistributing the nonzero entries of the extracted TF instants from 1 to L in the frequency axis to generate the mono downmix signal.

For each active source q, a k-sparse (k = NPTF_q) approximation signal of S_q(n, l) can be attained by rearrange ${\widehat{\mathit{S}}}_q$ in the original position, expressed as:

$${\tilde{S}}_q(n,l)=\{\begin{array}{cc}{S}_q(n,l),& \mathrm{if}l\in {\mathit{I}}_q\\ 0,& \mathrm{otherwise}\end{array}$$

(9)

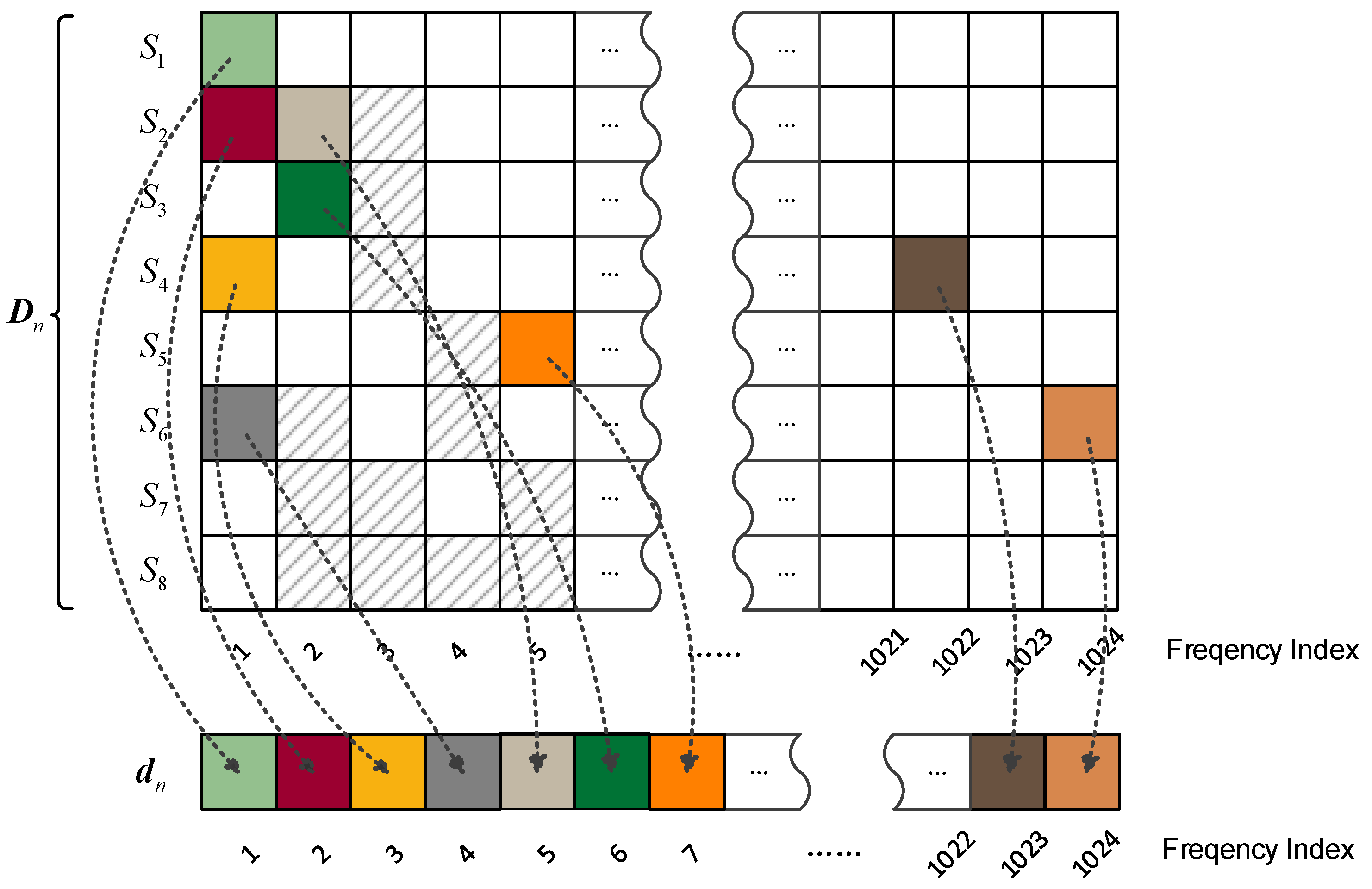
The downmix matrix is denoted as ${\mathit{D}}_n\equiv {\left[{\tilde{\mathit{S}}}_1,{\tilde{\mathit{S}}}_2,\cdots ,{\tilde{\mathit{S}}}_Q\right]}^{\mathrm{T}}$, where ${\tilde{\mathit{S}}}_q\equiv \left[{\tilde{S}}_q\left(n,1\right),{\tilde{S}}_q\left(n,2\right),\dots ,{\tilde{S}}_q\left(n,L\right)\right]$ and ^T is the transpose operation. This matrix is sparse matrix containing M × L entries. Through a column-wise scanning of D_n and sequencing the nonzero entries onto the frequency axis according to the scanning order, the mono downmix signal and side information can be obtained via Algorithm 2.

Figure 2 indicates the demixing procedure in accordance with an example of eight simultaneously occurring audio objects. Each square represents a time-frequency instant. The preserved TF components for each sound source (a total of 8 audio objects in this example) are represented by various color-block and shading.

Furthermore, the above-presented downmix processing guarantees the redistributed TF components locating in the nearby frequency position as their original position, which is prerequisite for subsequent Scalar Quantized Vector Huffman Coding (SQVH). Consequently, the downmix signal d_n can be further encoded by SQVH technique. Meanwhile, the side information compressed via the Run Length Coding (RLC) and the Golomb-Rice coding [19] at about 90 kbps.

2.5. Downmix Signal Compressing by SQVH

SQVH is a kind of efficient transform coding method which is used in fixed bitrate codec [26,27,28]. In this section, SQVH with variable bitrate for encoding downmix signal is designed and described as follows.

For the n^th frame, the downmix signal d_n attained in Algorithm 2 can be expressed as:

$${\mathit{d}}_n\equiv \left[d_n(1),d_n(2),\cdots ,d_n(L)\right]$$

(10)

d_n need to be divided into 51 sub-bands, each sub-band contains 20 TF instants, respectively (without considering the last 4 instants). The sub-band power (spectrum energy) is determined for each of the 51 regions and it is defined as root-mean-square (rms) value of coterminous 20 MDCT coefficients computed as:

$$R_{rms}(r)=\sqrt{\frac{1}{20}{\displaystyle \sum _{l=1}^{20}{d}_n^2\left(20(r-1)+l\right)}}$$

(11)

where r is region index, r = 0, 1, …, 50. The region power is then quantized with a logarithmic quantizer, 2^(i/2+1) are set to be quantization values, where i is an integer in the range [−8, 31]. R_rms(0) is the lowest frequency region, which is quantized with 5 bits and transmitted directly in transmission channel. The quantization indices of the remaining 50 regions, which are differentially coded against the last highest-numbered region and then Huffman coded with variable bitrates. In each sub-band, the Quantized Index (QI) value can be given by:

$$Q{I}_r(l)=\min \left\{\begin{array}{cc}\lfloor \frac{\left|d_n\left(20\cdot \left(r-1\right)+l\right)\right|}{R_{rms}(r)\times q_{stepsize}}+b\rfloor ,& MAX\end{array}\right\}$$

(12)

where q_stepsize is quantization steps, b is an offset value according to different categories, $\lfloor \rfloor$ denotes a round-up operation, MAX is maximum of MDCT coefficients corresponding to that category and l represents the l^th vector in the region r. There are several categories designed in SQVH coding. The category assigned to a region defines the quantization and coding parameters such as quantization step size, offset, vector dimension v_d and an expected total number of bits. The coding parameters for different category is given in

Table 1. The coding parameters for different category.

Categories	qstepsize	b	MAX	vd	Bit Count
0	2−1.5	0.3	13	2	52
1	2−1.0	0.33	9	2	47
2	2−0.5	0.36	6	2	43
3	20.0	0.39	4	4	37

.

Algorithm 2: Downmix processing compression algorithm
Input: Q	►number of audio objects
Input: L	►frequency index
Input: λ	►downmix signal index
Input: ${\tilde{\mathit{S}}}_q$	►k-sparse approximation signal of Sq
Output: SIn	►side information matrix
Output: dn	►downmix signal
1. Initialize λ= 1.
2. Set SIn = 0, dn = 0.
3. for l = 1 to L do
4.  for q = 1 to Q do
5.   if ${\tilde{S}}_q(n,l)$ ≠ 0 then
6.    ${\mathrm{d}}_n(\lambda )={\tilde{S}}_q(n,l)$.
7.    SIn(q, l) = 1.
8.    Increment λ.
9.   end if
10.  end for
11. end for
12. return dn and SIn

As is depicted in Table 1, four categories are selected in this work. Category 0 has the smallest quantization step size and uses the most bits, but not vice-versa. The set of scalar values, QI_r(l), correspond to a unique vector is identified by an index as follows:

$$v_{index}(i)={\displaystyle \sum _{j=0}^{v_d-1}Q{I}_r(i\times v_d+j){(MAX+1)}^{[v_d-(j+1)]}}$$

(13)

where i represents the i^th vector in region r and j is the index to the j^th value of QI_r(l) in a given vector. Then, all vector indices are Huffman coded with variable bit-length code for that region. Three types of bit-stream distributions are given in the proposed method, whose performance is evaluated in next section.

2.6. Decoding Process

In decoding stage, MDCT coefficients recovery is an inverse operation of de-mixing procedure, thus it needs the received downmix signal and the side information as auxiliary information. The downmix signal is decoded by the same standard audio codec as used in the encoder and the side information is decoded by the lossless codec. Thereafter, all recovered TF instants are assigned to the corresponding audio object. Finally, all audio object signals are obtained by transforming back to the time domain using the IMDCT.

3. Performance Evaluation

In this section, a series of objective and subjective tests are presented, which aim to examine the performance of the proposed encoding framework.

3.1. Test Conditions

The QUASI audio database [29] is employed as the test database in our evaluation work, which offers a vast variety categories of audio object signals (e.g., piano, vocal, drums, vocal, etc.) sampled at 44.1 kHz. All the test audio data are selected from this database. Four test files are used for evaluate the encoding quality when multiple audio objects are active simultaneously. Each test file consists of eight audio segments which is created with the length of 15 s. In other words, eight audio segments representing eight different types of audio objects are grouped together to form a multi-track test audio file, where the notes are also different among the eight tracks. The MUltiple Stimuli with Hidden Reference and Anchor (MUSRHA) methodology [30] and Perceptual Evaluation of Audio Quality (PEAQ) are employed in subjective and objective evaluation, respectively. Moreover, there are 15 listeners who took part in each subjective listening test. A 2048-points MDCT is utilized with 50% overlapping while adopting KBD window as window function.

3.2. Objective Evaluations

The first experiment is performed in the lossless transmission case, it means that both the downmix signal and the side information are compressed using lossless techniques. The Sparsity Analysis (SPA) multiple audio objects compression technique proposed in our previous work is served as reference approach [19] (named “SPA-STFT”) because of its superior performance. Meanwhile, the intermediate step given by SPA that uses the MDCT (named ‘SPA-MDCT’) is also compared in this test. The Objective Difference Grade (ODG) score calculated by the PEAQ of ITU-R BS.1387 is chosen as the evaluation criterion, which reflect the perceptual difference between the compressed signal and the original one. The ODG values vary from 0 to −4 with 0 being imperceptible loss in quality and −4 being a very annoying degradation in quality. What needs to be emphasized is that ODG scores cannot be treated as an absolute criterion because it only provide a relative reference value of the perceptual quality. Condition ‘Pro’ represents the objects encoded by our proposed encoding framework while condition ‘SPA-STFT’ and ‘SPA-MDCT’ are the reference approaches. Note that ‘SPA-STFT’ encoding approach exploits a 2048-points Short Time Fourier Transform (STFT) with 50% overlapping.

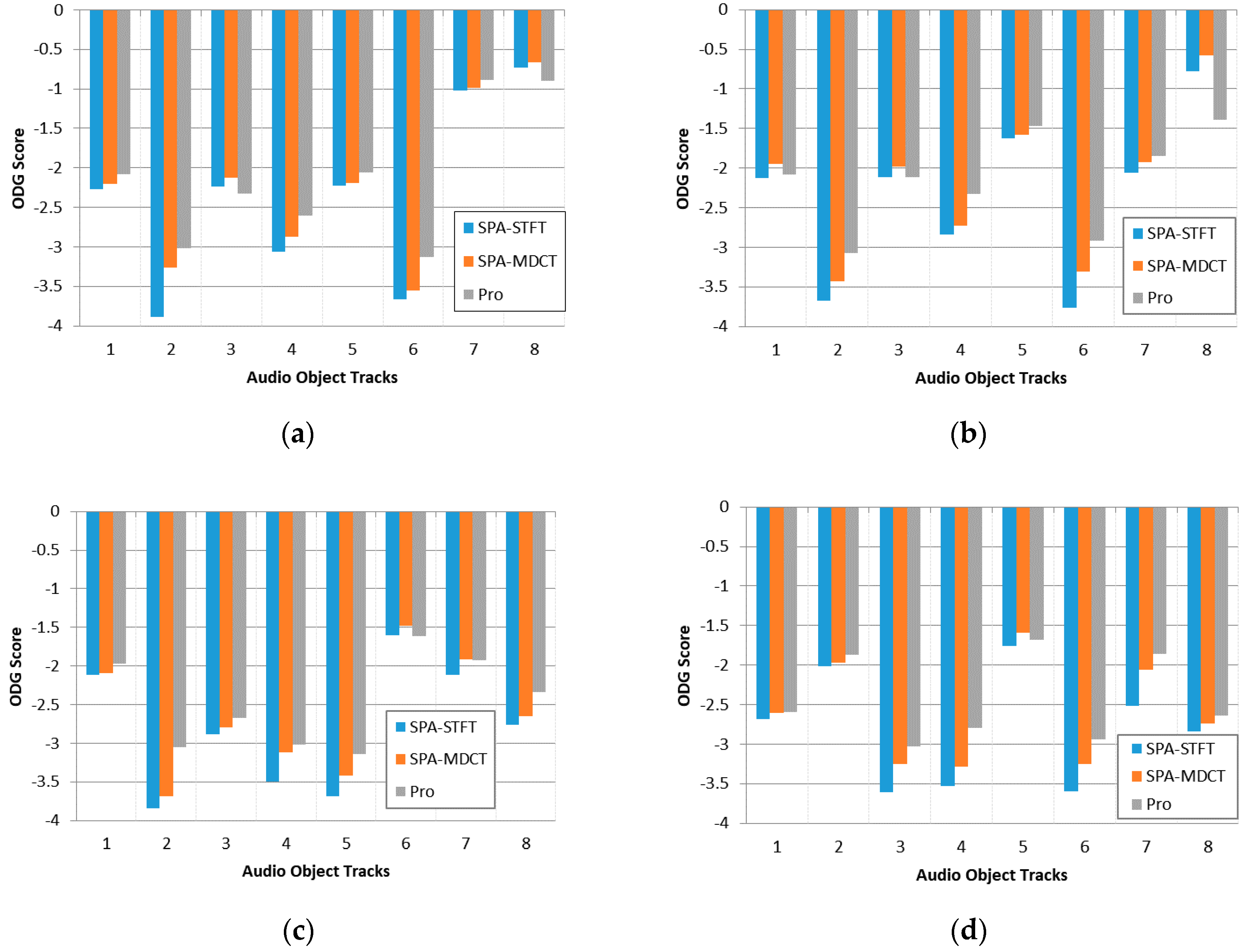
Statistical results are shown in Figure 3 where each subfigure corresponds to an eight-track audio file. From each subfigure, it can be observed that the decoded signals through our proposed encoding framework has the highest ODG score compared to both the SPA and the MDCT-based SPA approach, which indicates that the proposed framework can cause less damage to audio quality compared to these two reference approaches.

In addition, the performance of the MDCT-based SPA approach is better than the SPA, which prove that the selection of MDCT as time-frequency transform is efficient. Furthermore, in order to observe the quality differences of decoded objects, the standard deviation of each file is given as follow:

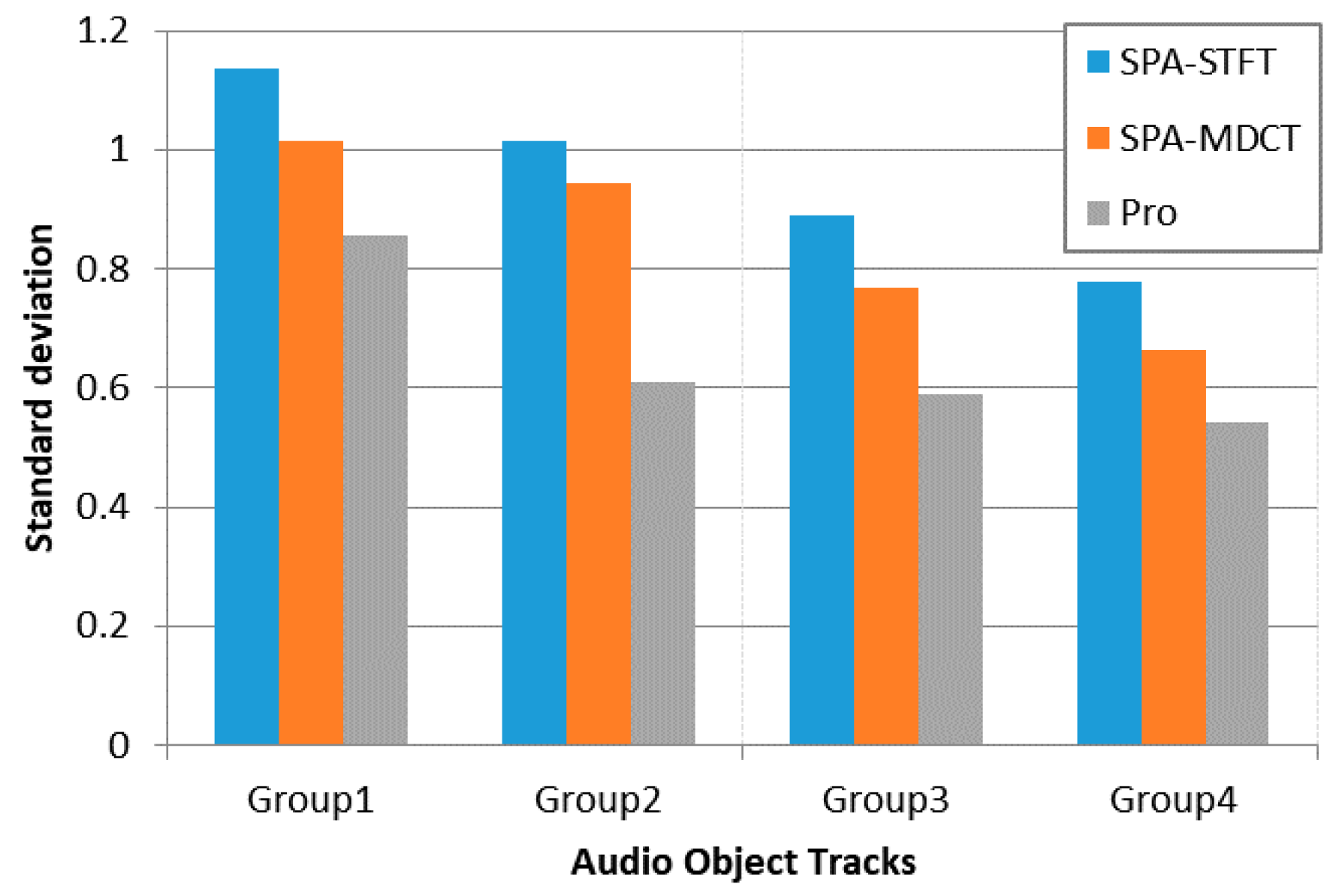
As illustrated in Figure 4, our proposed encoding framework has a lower standard deviation than the reference algorithms for each multi-track audio file. Hence, it proves that a more balanced quality of decoded objects can be maintained compared to the reference approaches. In general, this test validates that the proposed approach is robust to different kinds of audio objects.

In the lossy transmission case, the downmix signal which generated by encoder is further compressed using the SQVH at 105.14 kbps, 112.53 kbps and 120.7 kbps, respectively. Each sub-band corresponds to a group of certain q_stepsize, whose allocation for three types of bitrates can be calculated as shown in

Table 2. The q_stepsize allocation for three types of bitrates.

The Index of the Bitrate Sub-Band	r
	1~13	14~26	27~39	40~51
105.14 kbps	2−1.5	2−1.0	2−0.5	20.0
112.53 kbps	2−1.5	2−1.0	2−1.0	2−1.0
120.7 kbps	2−1.5	2−1.5	2−1.5	2−1.5

.

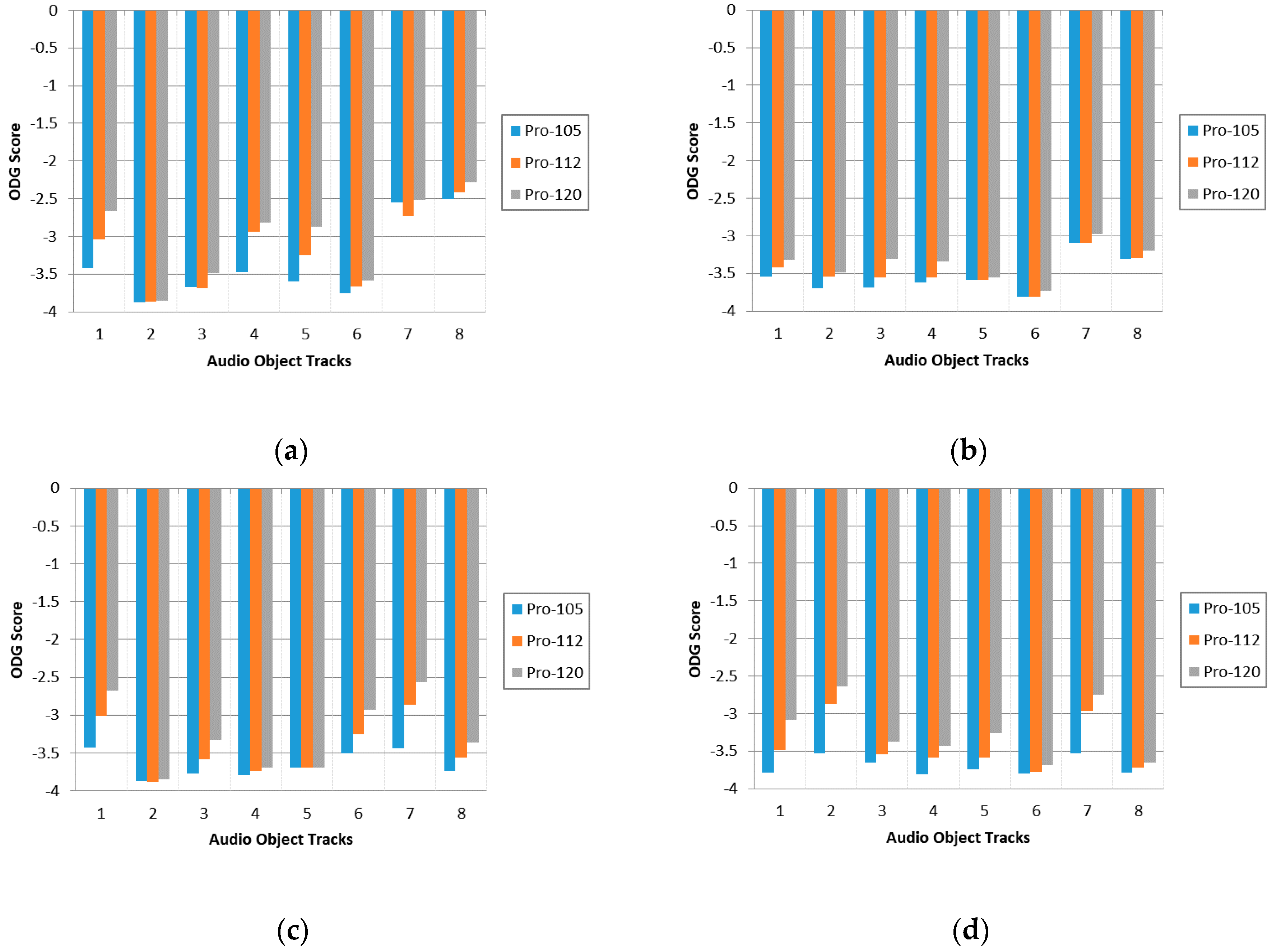
The ODG score in three types of bitrates are presented in Figure 5. Condition ‘Pro-105’, ‘Pro-112’, ‘Pro-120’ correspond to compress downmix signal at 105.14 kbps, 112.53 kbps and 120.7 kbps, respectively. It can be observed that the higher quantization precision leads to the better quality of decoded objects but the total bitrates increase as well. Therefore, we cannot pursuit a single factor such as high audio quality or low bitrate for transmission [25]. In consequence, we need to make a trade-off between audio quality and total bitrates in practical application scenarios.

3.3. Subjective Evaluation

The subjective evaluation is further utilized to measure the perceptual quality of decoded object signals, which consists of four MUltiple Stimuli with Hidden Reference and Anchor (MUSHRA) listening tests. Sennheiser HD600 headphone is used for playback. Note that for the first three tests, each decoded object generated by the corresponding approach is played independently without spatialization.

The first test is the lossless transmission case, aims to make a comparison between our proposed encoding framework and the SPA algorithm. Four group multi-track audio files used in previous experiments are also treated as test data in this section. Condition ‘SPA’ means the reference approach (the same as condition ‘SPA-STFT’ in Section 3.2) and condition ‘Pro’ means the proposed framework. The original object signal is served as the Hidden Reference (condition ’Ref’) and condition ‘Anchor’ is 3.5 kHz low-pass filtered anchor signal. A total of 15 listeners participated in the test.

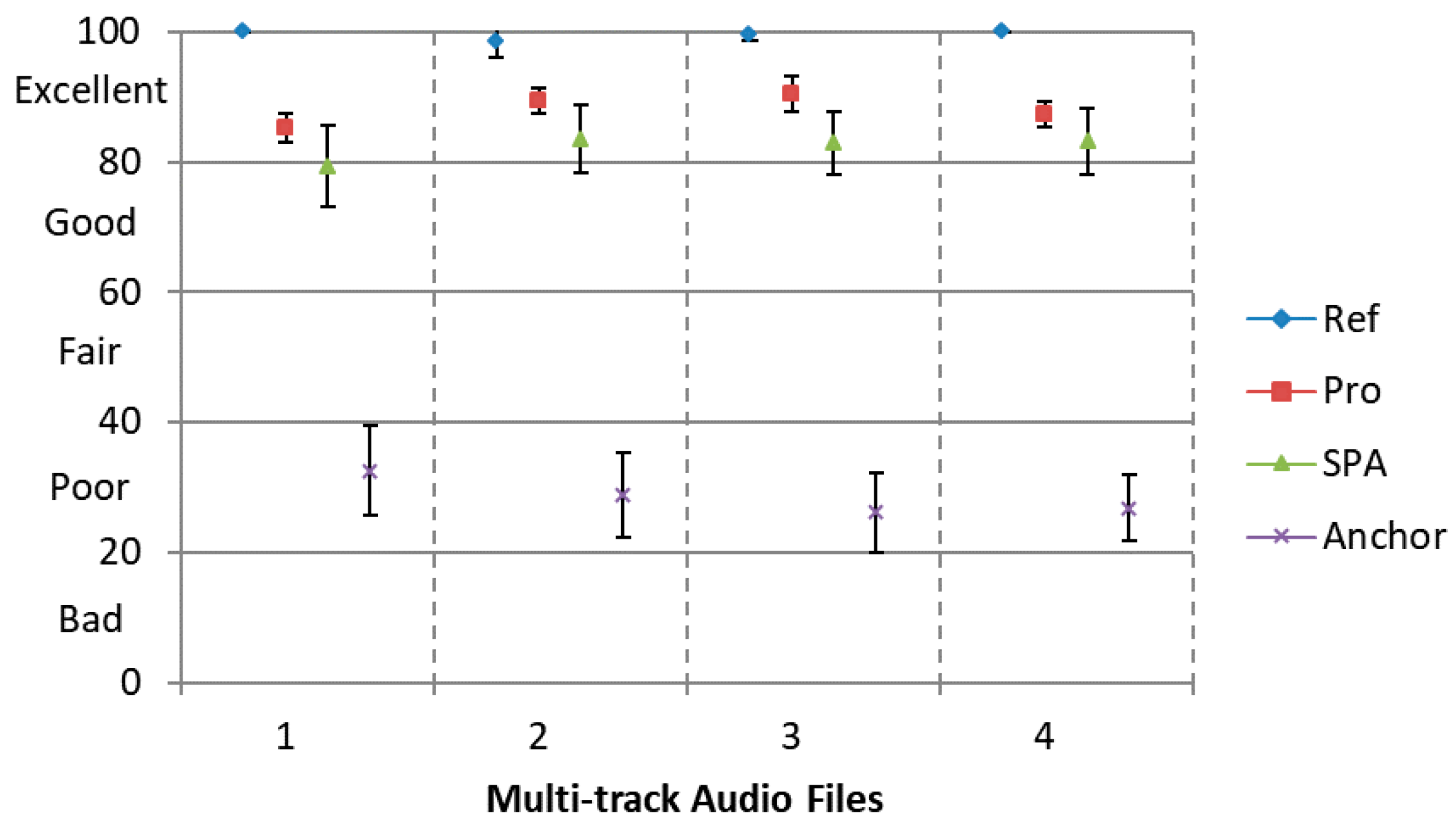
Results are shown in Figure 6 with 95% confidence intervals. It can be observed that the proposed encoding framework achieves a higher score than the SPA approach with clear statistical significant differences. Moreover, the MUSHRA scores for the proposed framework achieve over 80 indicating ’Excellent’ subjective quality compared to the Hidden Reference, which proves that the better perceptual quality can be attained compared to the reference approach.

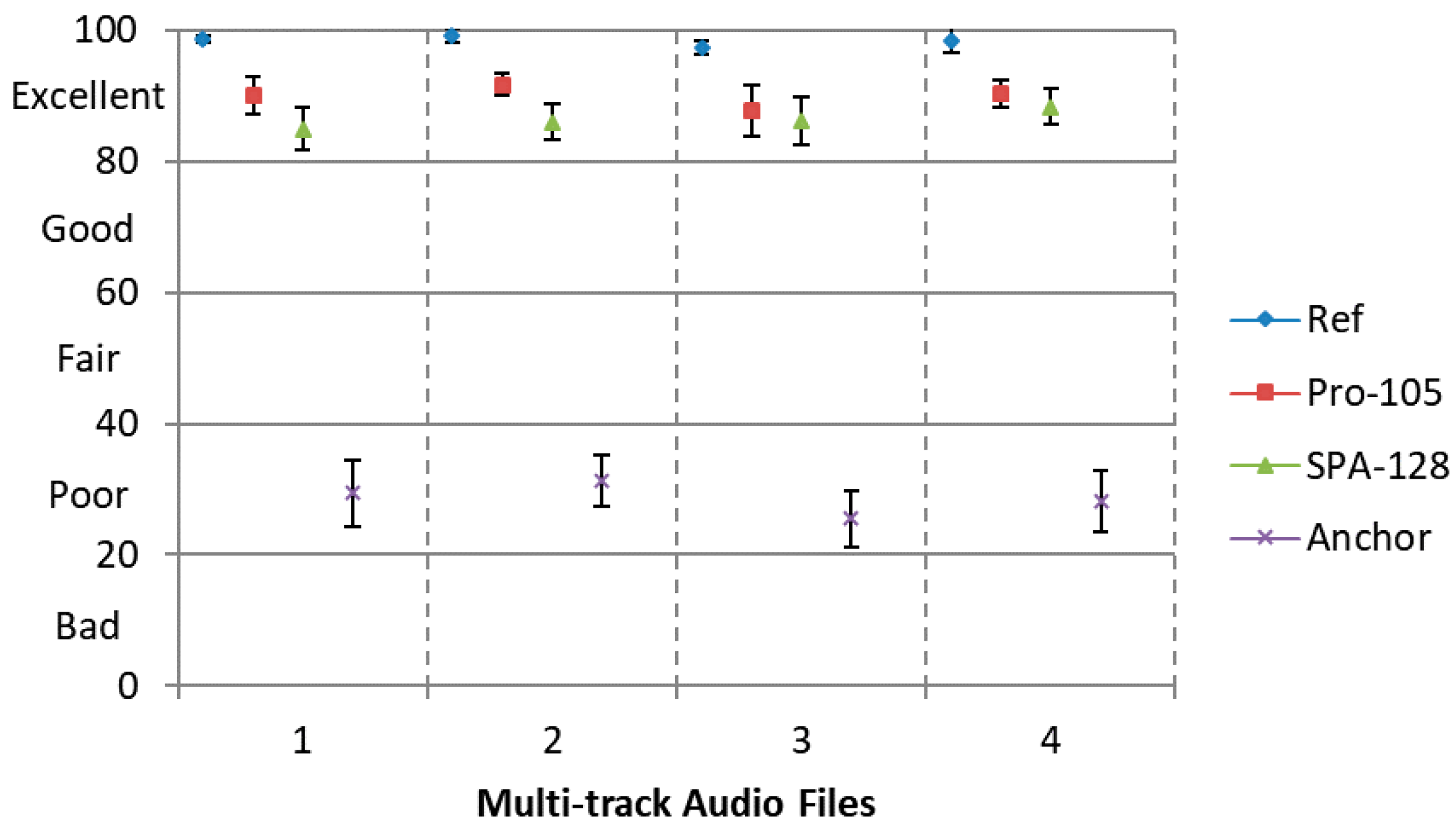
For lossy transmission case, the downmix signal encoded at 105 kbps via SQVH corresponds to ‘Pro-105’. Condition ‘SPA-128’ means the reference approach whose downmix signal compressed at the bitrate of 128 kbps using the MPEG-2 AAC codec.

Results are presented in Figure 7 with 95% confidence intervals. Obviously, our proposed encoding scheme has a better perceptual quality and a lower bitrate compared to the SPA approach. That is, when a similar perceptual quality is desired, the proposed method requires less total bitrate than the SPA approach.

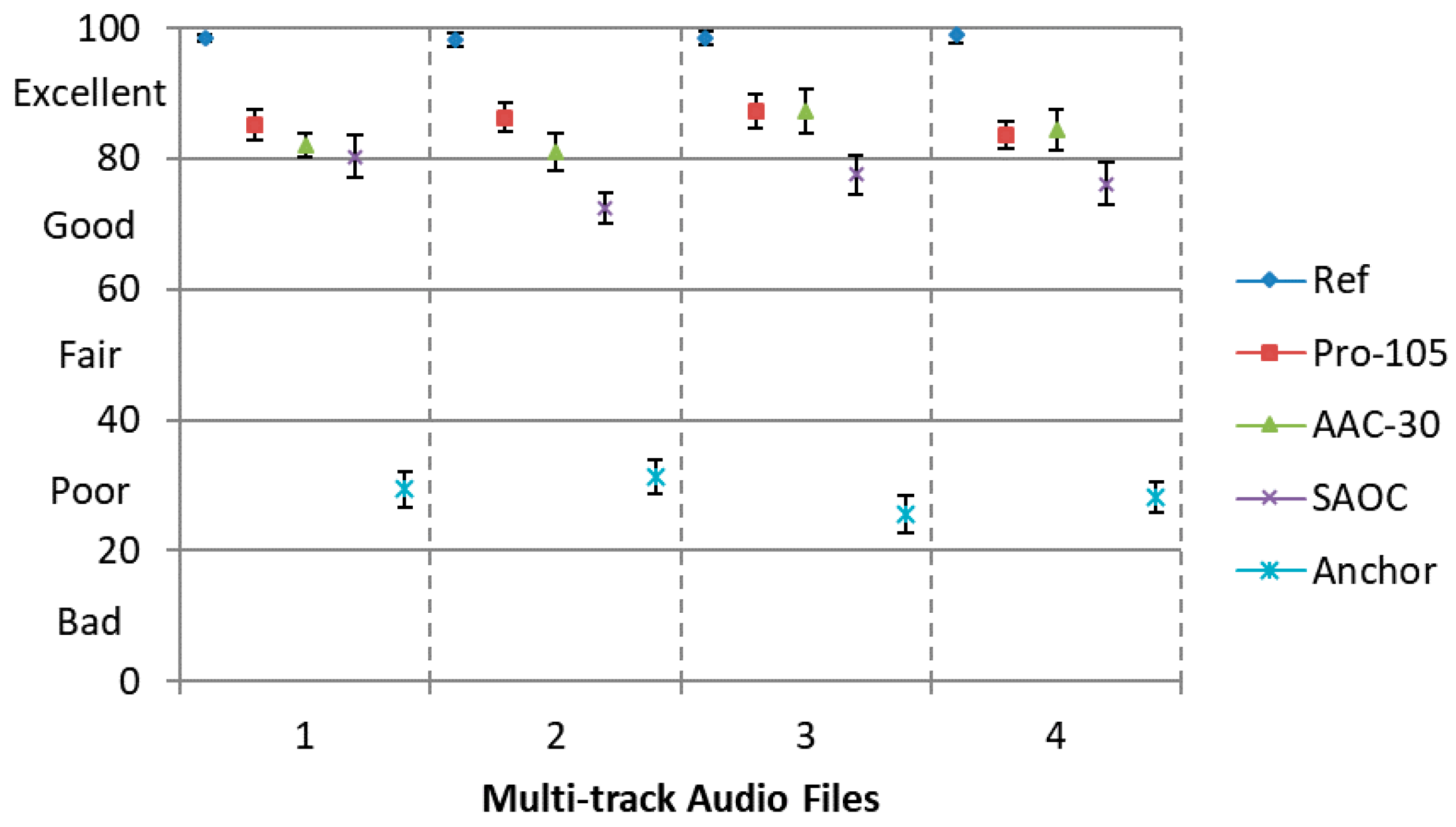
Furthermore, we evaluate the perceptual quality of the decoded audio objects using our proposed approach, using MPEG-2 AAC to encode each object independently and using Spatial Audio Object Coding (SAOC). The MUSHRA listening test is employed with five conditions, namely, Ref, Pro-105, AAC-30, SAOC and Anchor. The downmix signal in condition ‘Pro-105’ is further compressed using SQVH at 105.14 kbps. Meanwhile, the side information can be compressed at about 90 kbps [19]. Condition ‘AAC-30’ is the separate encoding of each original audio object using the MPEG-2 AAC codec at 30 kbps, the total bitrate is almost the same as ‘Pro-120’ (30 kbps/channel × 8 channels = 240 kbps). Condition ‘SAOC’ represents the objects are encoded by SAOC. The total SAOC side information rate of input objects is about 40 kbps (5 kbps per object), while the downmix signal generated by SAOC is compressed by the standard audio codec MPEG-2 AAC at the bitrate of 128 kbps.

It is demonstrated in Figure 8 that our proposed approach at 105 kbps possess the similar perceptual quality as separate encoding approach using MPEG-2 AAC. Yet the complexity of separate encoding is much higher than our proposed approach. Furthermore, both our proposed method and separate encoding approach attained a better performance compared with SAOC.

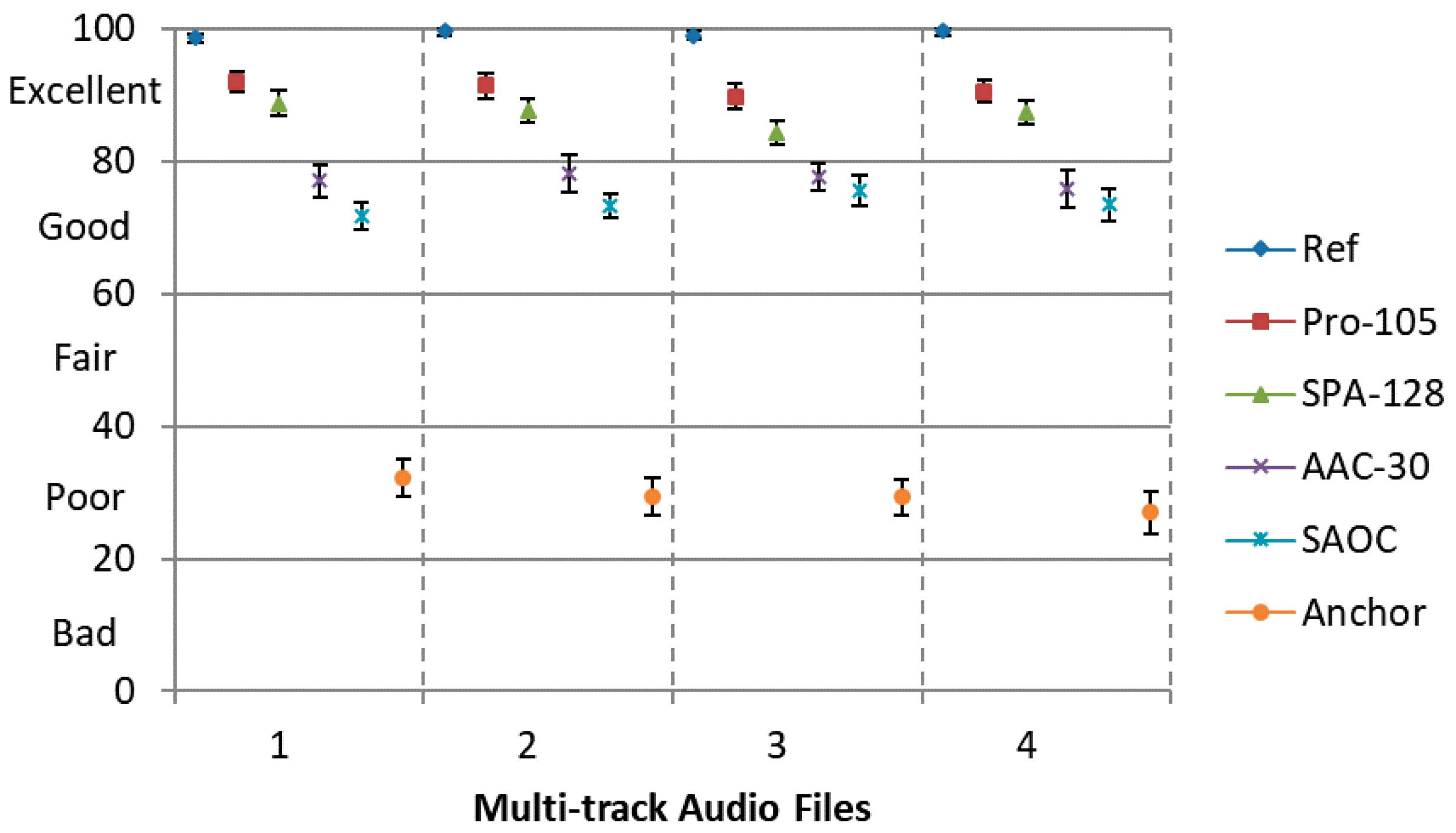
The last test devotes to evaluate the quality of the spatial soundfield generated by positioning the decoded audio objects in different spatial locations, which stands for the real application scenario. Specifically, for each eight-track audio, which are positioned uniformly in a circumference with a center at the listener, i.e., the locations are 0°, ±45°, ±90°, ±135°, ±180°, respectively. A binaural signal (test audio data) is created by convoluting each independent decoded audio object signal with the corresponding Head-Related Impulse Responses (HRIR) [31]. The MUSHRA listening test is employed with 6 conditions, namely, Ref, Pro-105, SPA-128, AAC-30, SAOC and Anchor, which are the same as previous tests. Here, Sennheiser HD600 headphone is used for playing the synthesized binaural signal.

It can be observed from Figure 9 that our proposed method can achieve a higher scores compared to all the rest encoding approaches. The results (Figure 8 and Figure 9) also show that the proposed approach achieves a significant improvement over separate encoding method using MPEG-2 AAC for binaural rendering but not in the independently playback scenario. This is due to the spatial hearing theory, which reveals that in each frequency only a few audio objects located at different positions can be perceived by the human ear (i.e., not all audio objects are sensitive at same frequency). In our proposed codec, only the most perceptually important time-frequency instants (not all time-frequency instants) of each audio object are coded with a higher quantization precision, while these frequency components are important for HAS. The coding error produced by our codec can be masked by spatial masking effect to a great extant from the last experiment. However, MPEG-2 AAC encodes all time-frequency instants with a relatively lower quantization precision at 30 kbps. When multiple audio objects were encoded separately by MPEG-2 AAC, there are some coding error that cannot be reduced by spatial masking effect. Hence, the proposed approach shows significant improvements over condition ‘AAC-30’ for binaural rendering.

From a series of objective and subjective listening test, we prove that the proposed approach can adapt to various bitrates conditions and it is suitable for encoding multiple audio objects in real application scenarios.

4. Conclusions

In this paper, an efficiently encoding approach for multiple audio objects based on intra-object sparsity was presented. Unlike the existing STFT-based compression framework, statistical analysis validated that for the case of tonal solo instruments audio objects possess better energy concentration property in the MDCT domain so that MDCT is selected as basic transform in our encoding scheme. In order to achieve a balanced perceptual quality for all object signals, both psychoacoustic-based and energy balanced NPTF allocation strategy algorithm is proposed for obtaining the optimal MDCT coefficients of each object. Moreover, SQVH is utilized to further encode downmix signal at variable bitrates. Objective and subjective evaluations shows that the proposed approach outperforms the existing intra-object based approach and achieves a more balanced perceptual quality when eight simultaneously occurring audio objects were encoded jointly. The results also confirmed that the proposed framework attained higher perceptual quality compared to SAOC. Further research could include the investigation of relative auditory masking threshold, in order to acquire a better perceptual quality amongst all objects.