Abstract
Rendering spatial sound scenes via audio objects has become popular in recent years, since it can provide more flexibility for different auditory scenarios, such as 3D movies, spatial audio communication and virtual classrooms. To facilitate high-quality bitrate-efficient distribution for spatial audio objects, an encoding scheme based on intra-object sparsity (approximate k-sparsity of the audio object itself) is proposed in this paper. The statistical analysis is presented to validate the notion that the audio object has a stronger sparseness in the Modified Discrete Cosine Transform (MDCT) domain than in the Short Time Fourier Transform (STFT) domain. By exploiting intra-object sparsity in the MDCT domain, multiple simultaneously occurring audio objects are compressed into a mono downmix signal with side information. To ensure a balanced perception quality of audio objects, a Psychoacoustic-based time-frequency instants sorting algorithm and an energy equalized Number of Preserved Time-Frequency Bins (NPTF) allocation strategy are proposed, which are employed in the underlying compression framework. The downmix signal can be further encoded via Scalar Quantized Vector Huffman Coding (SQVH) technique at a desirable bitrate, and the side information is transmitted in a lossless manner. Both objective and subjective evaluations show that the proposed encoding scheme outperforms the Sparsity Analysis (SPA) approach and Spatial Audio Object Coding (SAOC) in cases where eight objects were jointly encoded.
1. Introduction
With the development of multimedia video/audio signal processing, multi-channel 3D audio has been widely employed for applications, such as cinemas and home theatre systems, since it can provide excellent spatial realism of the original sound field, as compared to the traditional mono/stereo audio format.
There are multiple formats for rendering 3D audio, which contain channel-based, object-based and HOA-based audio formats. In traditional spatial sound rendering approach, the channel-based format is adopted in the early stage. For example, the 5.1 surround audio format [1] provides a horizontal soundfield and it has been widely employed for applications, such as the cinema and home theater. Furthermore, typical ‘3D’ formats include a varying number of height channels, such as 7.1 audio format (with two height channels). As the channel number increases, the audio data will raise dramatically. Due to the bandwidth constrained usage scenarios, the spatial audio coding technique has become an ongoing research topic in recent decades. In 1997, ISO /MPEG (Moving Picture Experts Group) designed the first commercially-used multi-channel audio coder MPEG-2 Advanced Audio Coding (MPEG-2 AAC) [2]. It could compress multi-channel audio by adding a number of advanced coding tools to MPEG-1 audio codecs, delivering European Broadcasting Union (EBU) broadcast quality at a bitrate of 320 kbps for a 5.1 signal. In 2006, MPEG Surround (MPS) [3,4] was created for highly transmission of multi-channel sound by downmixing the multi-channel signals into mono/stereo signal and extracting Interaural Level Differences (ILD), ITD (Interaural Time Differences) and IC (Interaural Coherence) as side information. Spatially Squeezed Surround Audio Coding (S3AC) [5,6,7], as a new method instead of original “downmix plus spatial parameters” model, exploited spatial direction of virtual sound source and mapping the soundfield from 360° into 60°. At the receiver, the decoded signals can be achieved by inverse mapping the 60° stereo soundfield into 360°.
However, such channel-based audio format has its limitation on flexibility, i.e., each channel is designated to feed a loudspeaker in a known prescribed position and cannot be adjusted for different reproduction needs by the users. Alternatively, a spatial sound scene can be described by a number of sound objects, each positioned at a certain target object position in space, which can be totally independent from the locations of available loudspeakers [8]. In order to fulfill the demand of interactive audio elements, object-based (a.k.a. object-oriented) audio format enables users to control audio content or sense of direction in application scenarios where the number of sound sources varies, sources move are commonly encountered. Hence, object signals generally need to be rendered to their target positions by appropriate rendering algorithms, e.g., Vector Base Amplitude Panning (VBAP) [9]. Therefore, object-based audio format can personalize customer’s listening experience and make surround sound more realistic. By now, object-based audio has been commercialized in many acoustic field, e.g., Dolby ATMOS for cinemas [10].
To facilitate high-quality bitrate-efficient distribution of audio objects, several methods have been developed, one of these techniques is MPEG Spatial Audio Object Coding (SAOC) [11,12]. SAOC encodes audio objects into a mono/stereo downmix signal plus side information via Quadrature Mirror Filter (QMF) and extract the parameters that stand for the energy relationship between different audio objects. Additionally, Directional Audio Coding (DirAC) [13,14] compress a spatial scene by calculating a direction vector representing spatial location information of the virtual sources. At the decoder side, the virtual sources are created from the downmixed signal at positions given by the direction vectors and they are panned by combining different loudspeakers through VBAP. The latest MPEG-H 3D audio coding standard incorporates the existing MPEG technology components to provide universal means for carriage of channel-based, object-based and Higher Order Ambisonics (HOA) based inputs [15]. Both MPEG-Surround (MPEG-S) and SAOC are included in MPEG-H 3D audio standard.
Recently, a Psychoacoustic-based Analysis-By-Synthesis (PABS) method [16,17] was proposed for encoding multiple speech objects, which could compress four simultaneously occurring speech sources in two downmix signals relied on inter-object sparsity [18]. However, with the number of objects increases, the inter-object sparsity becomes weakened, which leads to quality loss of decoded signal. In our previous work [19,20,21], a multiple audio objects encoding approach was proposed based on intra-object sparsity. Unlike the inter-object sparsity employed in PABS framework, this encoding scheme exploited the sparseness of object itself. That is, in a certain domain, an object signal can be represented by a small number of time-frequency instants. The evaluation results validated that this intra-object based approach achieved a better performance than PABS algorithm and retain the superior perceptual quality of the decoded signals. However, the aforementioned technique still has some restrictions which leads to a sub-optimum solution for object compression. Firstly, Short Time Fourier Transform (STFT) is chosen as the linear time-frequency transform to analyze audio objects. Yet the energy compaction capability of STFT is not optimal. Secondly, the above object encoding scheme concentrated on the features of object signal itself without considering the psychoacoustic, thus it is not an optimal quantization means for Human Auditory System (HAS).
This paper expands on the contributions in [19]. Based on intra-object sparsity, we propose a novel encoding scheme for multiple audio objects to further optimize our previous proposed approach and minimize the quality loss caused by compression. Firstly, by exploiting intra-object sparsity in the Modified Discrete Cosine Transform (MDCT) domain, multiple simultaneously occurring audio objects are compressed into a mono downmix signal with side information. Secondly, psychoacoustic model is utilized in the proposed codec to accomplish an optimal quantization for HAS. Hence, a Psychoacoustic-based Time-Frequency (TF) instants sorting algorithm is proposed for extracting the dominant TF instants in the MDCT domain. Furthermore, by utilizing these extracted TF instants, we propose a fast algorithm of Number of Preserved Time-Frequency Bins (NPTF, defined in Appendix A) allocation strategy to ensure a balanced perception quality for all object signals. Finally, the downmix signal can be further encoded via SQVH technique at desirable bitrate and the side information is transmitted in a lossless manner. In addition, a comparative study of intra-object sparsity of audio signal in the STFT domain and MDCT domain is presented via statistical analysis. The results show that audio objects have sparsity-promoting property in the MDCT domain, which means that a greater data compression ratio can be achieved.
The remainder of the paper is structured as follows: Section 2 introduces the architecture of the encoding framework in detail. Experimental results are presented and discussed in Section 3, while the conclusion is given in Section 4. Appendix A investigates the sparsity of audio objects in the STFT and MDCT domain, respectively.
2. Proposed Compression Framework
In the previous work, we adopted STFT as time-frequency transform to analyze the sparsity of audio signal and designed a codec based on the intra-object sparsity. From the statistical results of sparsity presented in Appendix A, we know that audio signals satisfy the approximate k-sparsity both in the STFT and MDCT domain, i.e., the energy of audio signal is almost concentrated in k time-frequency instants. In other words, audio signals have sparsity-promoting property in the MDCT domain in contrast to STFT, that is, . By using this advantage of MDCT, a multiple audio objects compression framework is proposed in this section based on intra-object sparsity. The proposed encoding scheme consists of five modules: time-frequency transform, active object detection, psychoacoustic-based TF instants sorting, NPTF allocation strategy and Scalar Quantized Vector Huffman Coding (SQVH).
The following process is operated in a frame-wise fashion. As is shown in Figure 1, all input audio objects (Source 1 to Source Q) are converted into time-frequency domain using MDCT. After active object detection, the TF instants of all active objects will be sorted according to Psychoacoustic model in order to extract the most perceptually important time-frequency instants. Then, a NPTF allocation strategy among all audio objects is proposed to counterpoise the energy of all preserved TF instants of each object. Thereafter, the extracted time-frequency instants are downmixed into a mono mixture stream plus side information via downmix processing operation. Particularly attention is that the downmix signal can be further compressed by existing audio coding methods. In this proposed method, SQVH technique is employed after de-mixing all TF instants, because it can compress audio signal at desirable bitrate. At the receiving end, Source 1 to Source Q can be decoded by exploiting the received downmix signal and the side information. The detailed contents are described below.
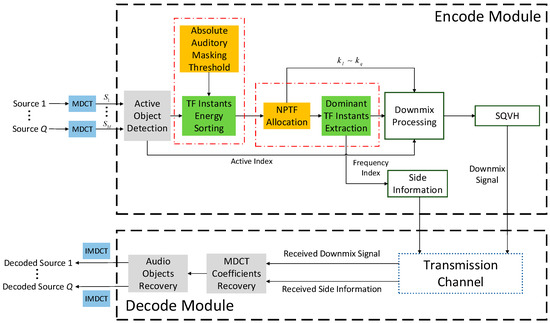
Figure 1.
The block diagram for the proposed compression framework. (MDCT, Modified Discrete Cosine Transform; IMDCT, Inverse Modified Discrete Cosine Transform; NPTF, Number of Preserved Time-Frequency Bins; SQVH, Scalar Quantized Vector Huffman Coding; TF, Time-Frequency).
2.1. MDCT and Active Object Detection
In nth frame, an input audio object sn = [sn(1), sn(2), …, sn(M)] is transformed into the MDCT domain, denoted by S(n, l), where n (1 ≤ n ≤ N) and l (1 ≤ l ≤ L) are frame number and frequency index, respectively. M = 1024 is the frame length. Here, a 2048-points MDCT is applied with 50% overlapped [22]. By this overlap, discontinuity at block boundary is smoothed out without increasing the number of transform coefficients. Afterwards, MDCT of an original signal sn can be formulated as:
where L = 1024, , are the basis functions corresponding to nth frame and (n + 1)th frame. , and T is the transpose operation. In addition, a Kaiser–Bessel derived (KBD) short-time window slid along the time axis with 50% overlapping between frames is used as window function ω(m).
In order to ensure the encoding scheme only encodes active frames without processing the silence frames, an Active Object Detection technique is applied to check the active audio objects in the current frame. Hence, Voice Activity Detection (VAD) [23] is utilized in this work, which is based on the short-time energy of audio in the current frame and comparison with the estimated background noise level. Each source uses a flag to indicate whether it is active in current frame. i.e.,
Afterwards, only the frames which are detected as active will be sent into the next module. In contrast, the mute frames will be ignored in the proposed codec. This procedure ensures that silence frames cannot be selected.
2.2. Psychoacoustic-Based TF Instants Sorting
In Appendix A, it is proved that the majority of the frame energy concentrates in finite k time-frequency instants for each audio object. For this reason, we can extract these k dominant TF instants for compression. In our previous work [19,20,21], TF instants are sorted and extracted by natural ordering via the magnitude of the normalized energy. However, this approach does not take into account HAS. It is well-known that HAS is not equally sensitive to all frequencies within the audible band since it has a non-flat frequency response. This simply means that we can hear some tones better than others. Thus, tones played at the same volume (intensity) at different frequencies are perceived as if they are being played at different volumes. For the purpose of enhance perceptual quality, we design a novel method through absolute auditory masking threshold to extract the dominant TF instants.
The absolute threshold of hearing characterizes the amount of energy needed in a pure tone such that it can be detected by a listener in a noiseless environment and it is expressed in terms of dB Sound Pressure Level (SPL) [24]. The quiet threshold is well approximated by the continuous nonlinear function, which is based on a number of listeners that were generated in a National Institutes of Health (NIH) study of typical American hearing acuity [25]:
where T(f) reflects the auditory properties for human ear in the STFT domain. Hence, the T(f) should be discretized and converted into the MDCT domain. The whole processing procedure includes two steps: inverse time-frequency transform and MDCT [26]. After these operations, absolute auditory masking threshold in the MDCT domain is denoted as Tmdct (l) (dB expression), where l = 1, 2, …, L. Then, an L-dimensional Absolute Auditory Masking Threshold (AAMT) vector T ≡ [Tmdct(1), Tmdct(2), …, Tmdct(L)] is generated for subsequent computing. From psychoacoustic theory, it is clear that if there exists a TF bin (n0, l0) that the difference between SdB(n0, l0) (dB expression of S(n0, l0)) and Tmdct(l0) is larger than other TF bins, which means that S(n0, l0) can be perceived more easily than other TF components, but not vice versa. Specifically, any signals below this threshold curve (i.e., SdB(n0, l0) − Tmdct(l0) < 0) is imperceptible (because Tmdct (l) is the lowest limit of HAS). Rely on this phenomenon, the AAMT vector T is used for extracting the perceptual dominant TF instants efficiently.
For qth (1 ≤ q ≤ Q) audio object Sq(n, l), whose dB expression is written as Sq_dB(n, l). An aggregated vector can be attained by converging each Sq_dB(n, l) denoted as Sq_dB≡ [Sq_dB(n, 1), Sq_dB(n, 2), …, Sq_dB(n, L)]. Subsequently, a perceptual detection vector is designed as:
where Pq(n,l) = Sq_dB(n,l) − Tmdct(l). To sort each element in Pq according to the magnitude in descending order, mathematically, a new vector can be attained as:
the elements in
satisfy:
where is the reorder frequency index which represent the perceptual significantly TF instants in order of importance for HAS. In other words, is the most considerable component with respect to HAS. In contrast, is almost the least significant TF instant for HAS.
2.3. NPTF Allocation Strategy
Allocating the NPTF for each active object signal can be actualized with various manners according to realistic application scenarios. As a most common used means called simplified average distribution method, all active objects share the same NPTF has been employed in [19,21]. This allocation method balances a tradeoff between computational complexity and perceptual quality. Therefore, it is a simple and efficient way. Nonetheless, this allocation strategy cannot guarantee all decoded objects with similar perceptual quality. Especially, the uneven quality can be emerged if there exists big difference of intra-object sparseness amongst objects. To conquer the above-mentioned issue, an Analysis-by-Synthesis (ABS) framework was proposed to balance the perceptual quality for all objects through solving a minimax problem via the iterative processing [20]. The test results show that this technique yields the approximate evenly distributed Frame Energy Preservation Ratio (FEPR, defined in Appendix A) for all objects. Despite the harmonious perceptual quality can be maintained, the attendant problem which is the sharp increase in computational complexity cannot be neglected. Accordingly, relied on the TF sorting result obtained in Section 2.2, an NPTF allocation strategy for obtaining a balanced perceptual quality of all inputs is proposed in this work.
In the nth frame, we assume that the qth object will be distributed kq NPTF, i.e., kq TF instants will be extracted for coding. An Individual Object Energy Retention ratio (IOER) function for the qth object is defined by:
where is the reorder frequency index obtained in the previous section. IOER function represents the energy of the k perceptual significant elements against the original signal Sq(n, l). Thus, kq will be allocated for each object with approximate IOER. Under the criterion of minimum mean-square error, for all the kq can be attained via a constrained optimization equation as follow:
where represents the average energy of all objects. The optimal solution k1, k2, …, kQ for each object are the desired NPTF1, NPTF2, …, NPTFQ, which can be searched by our proposed method elaborated in Algorithm 1.
| Algorithm 1: NPTF allocation strategy based on bisection method | |
| Input: Q | ►number of audio objects |
| Input: | ►MDCT coefficients of each audio object |
| Input: | ►reordered frequency index by psychoacoustic model |
| Input: BPA | ►lower limit used in dichotomy part |
| Input: BPB | ►upper limit used in dichotomy part |
| Input: BPM | ►median used in dichotomy part |
| Output: K | ►desired NPTF allocation result |
| 1. Set K = Ø | |
| 2. for q = 1 to Q do | |
| 3. for k = 1 to L do | |
| 4. Calculate IOER function fIOER(k, q) using and in Formula (12). | |
| 5. end for | |
| 6. end for | |
| 7. Initialize BPA = 0, BPB = 1, BPM = 0.5·(BPA + BPB), STOP = 0.01 chosen based on a series of informal experimental results. | |
| 8. while (BPB–BPA > STOP) do | |
| 9. Find the index value corresponding to BPM value in IOER function (i.e., fIOER(kq, q) ≈ BPM), denoted by kq. | |
| 10. if then | |
| 11. BPB = BPM, | |
| 12. BPM = [0.5·(BPA + BPB)]. | |
| 13. else | |
| 14. BPA = BPM, | |
| 15. BPM = [0.5·(BPA + BPB)]. | |
| 16. end if | |
| 17. end while | |
| 18. | |
| 19. return K | |
The proposed NPTF allocation strategy allows different reserved TF instants (i.e., MDCT coefficients) for each object among a certain group of multi-track audio objects without iterative processing, therefore, the computational complexity decrease rapidly through the dynamic TF instants distribution algorithm. In addition, a sub-equal perception quality for each object can be maintained via our proposed NPTF allocation strategy rather than pursuit the quality of a particular object.
Thereafter, vector needs to be extract the NPTFq(kq) elements to forming a new vector . It should be note that indicate the origin of , respectively. We group into a vector , in the meantime, a new vector containing all extracted TF instants is generated. Finally, both Iq and should be stored locally and sent into the Downmix Processing module.
2.4. Downmix Processing
After extracting the dominant TF instants , source 1 to source Q only contains the perception significantly MDCT coefficients of all active audio objects. However, each source include a number of zero entries, hence, the downmix processing must be exploited which aims to redistributing the nonzero entries of the extracted TF instants from 1 to L in the frequency axis to generate the mono downmix signal.
For each active source q, a k-sparse (k = NPTFq) approximation signal of Sq(n, l) can be attained by rearrange in the original position, expressed as:
The downmix matrix is denoted as , where and T is the transpose operation. This matrix is sparse matrix containing M × L entries. Through a column-wise scanning of Dn and sequencing the nonzero entries onto the frequency axis according to the scanning order, the mono downmix signal and side information can be obtained via Algorithm 2.
Figure 2 indicates the demixing procedure in accordance with an example of eight simultaneously occurring audio objects. Each square represents a time-frequency instant. The preserved TF components for each sound source (a total of 8 audio objects in this example) are represented by various color-block and shading.
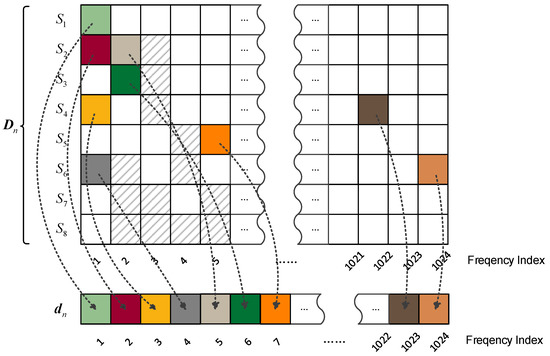
Figure 2.
Example of TF (Time-Frequency) instants extraction and de-mixing procedure with eight unique simultaneously occurring sources.
Furthermore, the above-presented downmix processing guarantees the redistributed TF components locating in the nearby frequency position as their original position, which is prerequisite for subsequent Scalar Quantized Vector Huffman Coding (SQVH). Consequently, the downmix signal dn can be further encoded by SQVH technique. Meanwhile, the side information compressed via the Run Length Coding (RLC) and the Golomb-Rice coding [19] at about 90 kbps.
2.5. Downmix Signal Compressing by SQVH
SQVH is a kind of efficient transform coding method which is used in fixed bitrate codec [26,27,28]. In this section, SQVH with variable bitrate for encoding downmix signal is designed and described as follows.
For the nth frame, the downmix signal dn attained in Algorithm 2 can be expressed as:
dn need to be divided into 51 sub-bands, each sub-band contains 20 TF instants, respectively (without considering the last 4 instants). The sub-band power (spectrum energy) is determined for each of the 51 regions and it is defined as root-mean-square (rms) value of coterminous 20 MDCT coefficients computed as:
where r is region index, r = 0, 1, …, 50. The region power is then quantized with a logarithmic quantizer, 2(i/2+1) are set to be quantization values, where i is an integer in the range [−8, 31]. Rrms(0) is the lowest frequency region, which is quantized with 5 bits and transmitted directly in transmission channel. The quantization indices of the remaining 50 regions, which are differentially coded against the last highest-numbered region and then Huffman coded with variable bitrates. In each sub-band, the Quantized Index (QI) value can be given by:
where qstepsize is quantization steps, b is an offset value according to different categories, denotes a round-up operation, MAX is maximum of MDCT coefficients corresponding to that category and l represents the lth vector in the region r. There are several categories designed in SQVH coding. The category assigned to a region defines the quantization and coding parameters such as quantization step size, offset, vector dimension vd and an expected total number of bits. The coding parameters for different category is given in Table 1.
| Algorithm 2: Downmix processing compression algorithm | |
| Input: Q | ►number of audio objects |
| Input: L | ►frequency index |
| Input: λ | ►downmix signal index |
| Input: | ►k-sparse approximation signal of Sq |
| Output: SIn | ►side information matrix |
| Output: dn | ►downmix signal |
| 1. Initialize λ= 1. | |
| 2. Set SIn = 0, dn = 0. | |
| 3. for l = 1 to L do | |
| 4. for q = 1 to Q do | |
| 5. if ≠ 0 then | |
| 6. . | |
| 7. SIn(q, l) = 1. | |
| 8. Increment λ. | |
| 9. end if | |
| 10. end for | |
| 11. end for | |
| 12. return dn and SIn | |

Table 1.
The coding parameters for different category.
As is depicted in Table 1, four categories are selected in this work. Category 0 has the smallest quantization step size and uses the most bits, but not vice-versa. The set of scalar values, QIr(l), correspond to a unique vector is identified by an index as follows:
where i represents the ith vector in region r and j is the index to the jth value of QIr(l) in a given vector. Then, all vector indices are Huffman coded with variable bit-length code for that region. Three types of bit-stream distributions are given in the proposed method, whose performance is evaluated in next section.
2.6. Decoding Process
In decoding stage, MDCT coefficients recovery is an inverse operation of de-mixing procedure, thus it needs the received downmix signal and the side information as auxiliary information. The downmix signal is decoded by the same standard audio codec as used in the encoder and the side information is decoded by the lossless codec. Thereafter, all recovered TF instants are assigned to the corresponding audio object. Finally, all audio object signals are obtained by transforming back to the time domain using the IMDCT.
3. Performance Evaluation
In this section, a series of objective and subjective tests are presented, which aim to examine the performance of the proposed encoding framework.
3.1. Test Conditions
The QUASI audio database [29] is employed as the test database in our evaluation work, which offers a vast variety categories of audio object signals (e.g., piano, vocal, drums, vocal, etc.) sampled at 44.1 kHz. All the test audio data are selected from this database. Four test files are used for evaluate the encoding quality when multiple audio objects are active simultaneously. Each test file consists of eight audio segments which is created with the length of 15 s. In other words, eight audio segments representing eight different types of audio objects are grouped together to form a multi-track test audio file, where the notes are also different among the eight tracks. The MUltiple Stimuli with Hidden Reference and Anchor (MUSRHA) methodology [30] and Perceptual Evaluation of Audio Quality (PEAQ) are employed in subjective and objective evaluation, respectively. Moreover, there are 15 listeners who took part in each subjective listening test. A 2048-points MDCT is utilized with 50% overlapping while adopting KBD window as window function.
3.2. Objective Evaluations
The first experiment is performed in the lossless transmission case, it means that both the downmix signal and the side information are compressed using lossless techniques. The Sparsity Analysis (SPA) multiple audio objects compression technique proposed in our previous work is served as reference approach [19] (named “SPA-STFT”) because of its superior performance. Meanwhile, the intermediate step given by SPA that uses the MDCT (named ‘SPA-MDCT’) is also compared in this test. The Objective Difference Grade (ODG) score calculated by the PEAQ of ITU-R BS.1387 is chosen as the evaluation criterion, which reflect the perceptual difference between the compressed signal and the original one. The ODG values vary from 0 to −4 with 0 being imperceptible loss in quality and −4 being a very annoying degradation in quality. What needs to be emphasized is that ODG scores cannot be treated as an absolute criterion because it only provide a relative reference value of the perceptual quality. Condition ‘Pro’ represents the objects encoded by our proposed encoding framework while condition ‘SPA-STFT’ and ‘SPA-MDCT’ are the reference approaches. Note that ‘SPA-STFT’ encoding approach exploits a 2048-points Short Time Fourier Transform (STFT) with 50% overlapping.
Statistical results are shown in Figure 3 where each subfigure corresponds to an eight-track audio file. From each subfigure, it can be observed that the decoded signals through our proposed encoding framework has the highest ODG score compared to both the SPA and the MDCT-based SPA approach, which indicates that the proposed framework can cause less damage to audio quality compared to these two reference approaches.
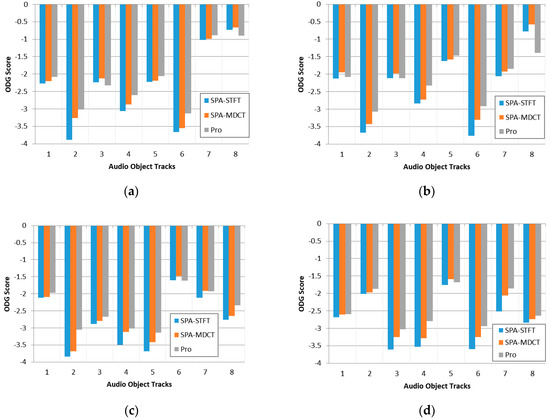
Figure 3.
ODG (Objective Difference Grade) Score for the proposed audio object encoding approach and the SPA (Sparsity Analysis) framework (both in the STFT (Short Time Fourier Transform) and MDCT domain). (a–d) represent the results for 4 multi-track audio files.
In addition, the performance of the MDCT-based SPA approach is better than the SPA, which prove that the selection of MDCT as time-frequency transform is efficient. Furthermore, in order to observe the quality differences of decoded objects, the standard deviation of each file is given as follow:
As illustrated in Figure 4, our proposed encoding framework has a lower standard deviation than the reference algorithms for each multi-track audio file. Hence, it proves that a more balanced quality of decoded objects can be maintained compared to the reference approaches. In general, this test validates that the proposed approach is robust to different kinds of audio objects.
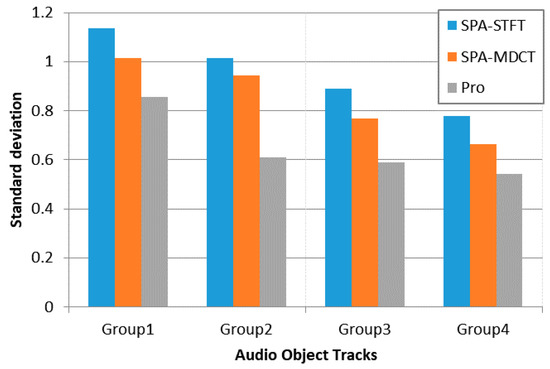
Figure 4.
The standard deviation of ODG score of four multi-track audio files.
In the lossy transmission case, the downmix signal which generated by encoder is further compressed using the SQVH at 105.14 kbps, 112.53 kbps and 120.7 kbps, respectively. Each sub-band corresponds to a group of certain qstepsize, whose allocation for three types of bitrates can be calculated as shown in Table 2.

Table 2.
The qstepsize allocation for three types of bitrates.
The ODG score in three types of bitrates are presented in Figure 5. Condition ‘Pro-105’, ‘Pro-112’, ‘Pro-120’ correspond to compress downmix signal at 105.14 kbps, 112.53 kbps and 120.7 kbps, respectively. It can be observed that the higher quantization precision leads to the better quality of decoded objects but the total bitrates increase as well. Therefore, we cannot pursuit a single factor such as high audio quality or low bitrate for transmission [25]. In consequence, we need to make a trade-off between audio quality and total bitrates in practical application scenarios.
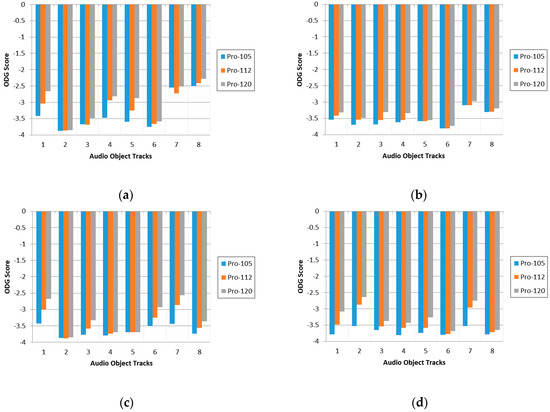
Figure 5.
The ODG score of four multi-track audio files, where each file correspond to three types of bitrates. (a–d) represent the results for 4 multi-track audio files.
3.3. Subjective Evaluation
The subjective evaluation is further utilized to measure the perceptual quality of decoded object signals, which consists of four MUltiple Stimuli with Hidden Reference and Anchor (MUSHRA) listening tests. Sennheiser HD600 headphone is used for playback. Note that for the first three tests, each decoded object generated by the corresponding approach is played independently without spatialization.
The first test is the lossless transmission case, aims to make a comparison between our proposed encoding framework and the SPA algorithm. Four group multi-track audio files used in previous experiments are also treated as test data in this section. Condition ‘SPA’ means the reference approach (the same as condition ‘SPA-STFT’ in Section 3.2) and condition ‘Pro’ means the proposed framework. The original object signal is served as the Hidden Reference (condition ’Ref’) and condition ‘Anchor’ is 3.5 kHz low-pass filtered anchor signal. A total of 15 listeners participated in the test.
Results are shown in Figure 6 with 95% confidence intervals. It can be observed that the proposed encoding framework achieves a higher score than the SPA approach with clear statistical significant differences. Moreover, the MUSHRA scores for the proposed framework achieve over 80 indicating ’Excellent’ subjective quality compared to the Hidden Reference, which proves that the better perceptual quality can be attained compared to the reference approach.
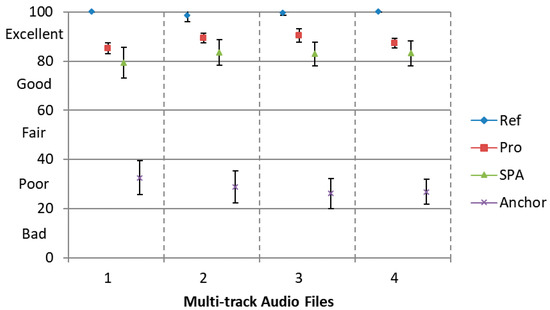
Figure 6.
MUltiple Stimuli with Hidden Reference and Anchor (MUSHRA) test results for the SPA framework and the proposed framework with 95% confidence intervals.
For lossy transmission case, the downmix signal encoded at 105 kbps via SQVH corresponds to ‘Pro-105’. Condition ‘SPA-128’ means the reference approach whose downmix signal compressed at the bitrate of 128 kbps using the MPEG-2 AAC codec.
Results are presented in Figure 7 with 95% confidence intervals. Obviously, our proposed encoding scheme has a better perceptual quality and a lower bitrate compared to the SPA approach. That is, when a similar perceptual quality is desired, the proposed method requires less total bitrate than the SPA approach.
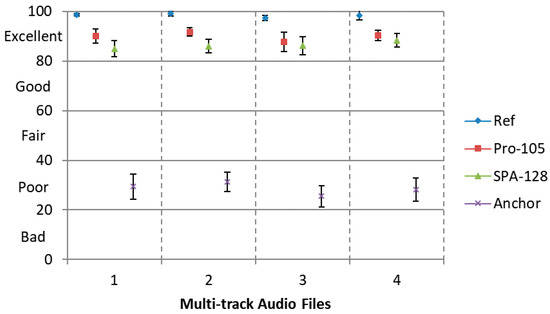
Figure 7.
MUSHRA test results for the SPA method encoding at 128 kbps and the proposed approach at 105.14 kbps with 95% confidence intervals.
Furthermore, we evaluate the perceptual quality of the decoded audio objects using our proposed approach, using MPEG-2 AAC to encode each object independently and using Spatial Audio Object Coding (SAOC). The MUSHRA listening test is employed with five conditions, namely, Ref, Pro-105, AAC-30, SAOC and Anchor. The downmix signal in condition ‘Pro-105’ is further compressed using SQVH at 105.14 kbps. Meanwhile, the side information can be compressed at about 90 kbps [19]. Condition ‘AAC-30’ is the separate encoding of each original audio object using the MPEG-2 AAC codec at 30 kbps, the total bitrate is almost the same as ‘Pro-120’ (30 kbps/channel × 8 channels = 240 kbps). Condition ‘SAOC’ represents the objects are encoded by SAOC. The total SAOC side information rate of input objects is about 40 kbps (5 kbps per object), while the downmix signal generated by SAOC is compressed by the standard audio codec MPEG-2 AAC at the bitrate of 128 kbps.
It is demonstrated in Figure 8 that our proposed approach at 105 kbps possess the similar perceptual quality as separate encoding approach using MPEG-2 AAC. Yet the complexity of separate encoding is much higher than our proposed approach. Furthermore, both our proposed method and separate encoding approach attained a better performance compared with SAOC.
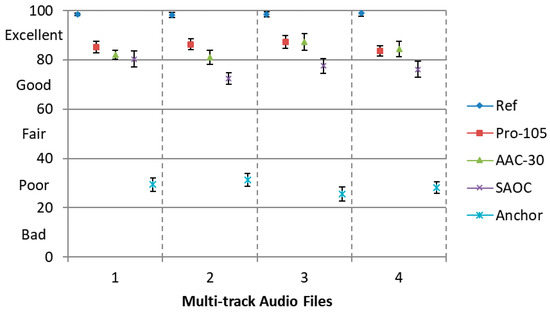
Figure 8.
MUSHRA test results for separate AAC (Advanced Audio Coding) encoding at 30 kbps, SAOC (Spatial Audio Object Coding) and our proposed approach at 105 kbps with 95% confidence intervals.
The last test devotes to evaluate the quality of the spatial soundfield generated by positioning the decoded audio objects in different spatial locations, which stands for the real application scenario. Specifically, for each eight-track audio, which are positioned uniformly in a circumference with a center at the listener, i.e., the locations are 0°, ±45°, ±90°, ±135°, ±180°, respectively. A binaural signal (test audio data) is created by convoluting each independent decoded audio object signal with the corresponding Head-Related Impulse Responses (HRIR) [31]. The MUSHRA listening test is employed with 6 conditions, namely, Ref, Pro-105, SPA-128, AAC-30, SAOC and Anchor, which are the same as previous tests. Here, Sennheiser HD600 headphone is used for playing the synthesized binaural signal.
It can be observed from Figure 9 that our proposed method can achieve a higher scores compared to all the rest encoding approaches. The results (Figure 8 and Figure 9) also show that the proposed approach achieves a significant improvement over separate encoding method using MPEG-2 AAC for binaural rendering but not in the independently playback scenario. This is due to the spatial hearing theory, which reveals that in each frequency only a few audio objects located at different positions can be perceived by the human ear (i.e., not all audio objects are sensitive at same frequency). In our proposed codec, only the most perceptually important time-frequency instants (not all time-frequency instants) of each audio object are coded with a higher quantization precision, while these frequency components are important for HAS. The coding error produced by our codec can be masked by spatial masking effect to a great extant from the last experiment. However, MPEG-2 AAC encodes all time-frequency instants with a relatively lower quantization precision at 30 kbps. When multiple audio objects were encoded separately by MPEG-2 AAC, there are some coding error that cannot be reduced by spatial masking effect. Hence, the proposed approach shows significant improvements over condition ‘AAC-30’ for binaural rendering.
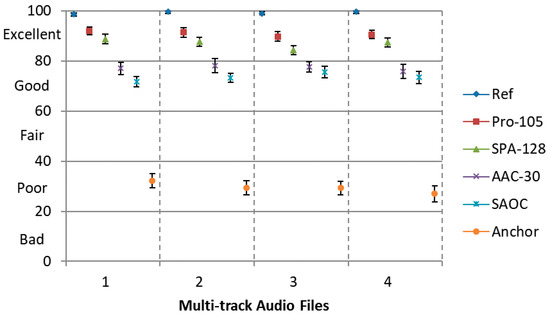
Figure 9.
MUSHRA test results with 95% confidence intervals for the soundfield rendering using separate AAC encoding at 30 kbps, SAOC, SPA and our proposed approach at 105 kbps.
From a series of objective and subjective listening test, we prove that the proposed approach can adapt to various bitrates conditions and it is suitable for encoding multiple audio objects in real application scenarios.
4. Conclusions
In this paper, an efficiently encoding approach for multiple audio objects based on intra-object sparsity was presented. Unlike the existing STFT-based compression framework, statistical analysis validated that for the case of tonal solo instruments audio objects possess better energy concentration property in the MDCT domain so that MDCT is selected as basic transform in our encoding scheme. In order to achieve a balanced perceptual quality for all object signals, both psychoacoustic-based and energy balanced NPTF allocation strategy algorithm is proposed for obtaining the optimal MDCT coefficients of each object. Moreover, SQVH is utilized to further encode downmix signal at variable bitrates. Objective and subjective evaluations shows that the proposed approach outperforms the existing intra-object based approach and achieves a more balanced perceptual quality when eight simultaneously occurring audio objects were encoded jointly. The results also confirmed that the proposed framework attained higher perceptual quality compared to SAOC. Further research could include the investigation of relative auditory masking threshold, in order to acquire a better perceptual quality amongst all objects.
Acknowledgments
The authors would like to thank the reviewers for their helpful comments. This work has been supported by China Postdoctoral Science Foundation funded project (No. 2017M610731), the Project supported by Beijing Postdoctoral Research Foundation, “Ri xin” Training Programme Foundation for the Talents by Beijing University of Technology.
Author Contributions
Maoshen Jia and Jiaming Zhang contributed equally in conceiving the whole proposed codec architecture, designing and performing the experiments, collecting and analyzing the data, and writing the paper. Changchun Bao corrected some syntax mistake. Xiguang Zheng critically reviewed and implemented final revisions. Maoshen Jia supervised all aspects of this research.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Sparsity Analysis of Audio Signal in the MDCT Domain
Considering that the MDCT is a commonly used time-frequency transform in signal processing, the intra-object sparsity of audio signal in the MDCT domain should be investigated. Thus, a quantitative analysis for sparsity of audio signals both in the MDCT and STFT domain is given in this appendix.
According to the k-sparsity theory interpreted in compressed sensing [32,33], a signal/sequence is regarded as (strict) k-sparse when it contains k nonzero entries with k « K, where K is the length of the signal or sequence. In addition, a sequence can be considered as an approximate k-sparse if k entries of the sequence occupy the majority of the total amount in magnitude, while the magnitude of other entries are remarkable small. In our previous work [19], we validated that an audio signal is not sparse in time domain, but its STFT coefficients in frequency domain fulfills the approximate k-sparsity. For this reason, STFT is selected as basic transform in our preceding designed object encoding system. The perceptual quality of the decoded signal can achieve a satisfactory level. However, STFT is not an optimum sparseness time-frequency transform. In consideration of the energy compaction property (i.e., a small number of TF instants capture the majority of the energy) of MDCT, therefore, approximate k-sparsity of audio signal in the MDCT domain will be investigated compared to that in the STFT domain by statistical analysis.
Appendix A.1. Measuring the Sparsity of Audio Signal
A time-frequency representations of an audio signal can be obtained by a linear transform. Specifically, for a general dictionary of atoms , the linear representation of an audio signal sn(m) in nth frame can be defined by:
where n, m and l represent frame number, time index and frequency index, respectively. M is the length of each frame. Short-time Fourier Transform (STFT) basis functions and Discrete Cosine Transform (DCT) basis functions are ordinarily used as time-frequency atoms in speech and audio signal compression. DCT is widely used in audio coding mainly because of its energy compaction feature. Nevertheless, due to the blocking effect caused by the different quantitative level between frames, the processed signal cannot be perfectly reconstructed by IDCT. Evolved from DCT, MDCT has emerged as an efficaciously tool in high quality audio coding over the last decade because it helps to mitigate the blocking artifacts that deteriorate the reconstruction of transform audio coders with non-overlapped transforms [34]. It should be noted that MDCT can be taken as a filterbank with 50% overlapped window, hence, Time Domain Aliasing Cancellation (TDAC) must be exploited in the practical processing. Meanwhile, the chosen window function must satisfy the TDAC requirement. In this work, a Kaiser-Bessel derived (KBD) window [35] is chosen to meet the computing needs of TDAC and overlap-add algorithms. Particularly, for a finite-length audio signal whose MDCT coefficients are densely concentrated at low indices than the STFT (Short Time Fourier Transform) does, which is called “energy compaction” property [36]. With this prerequisite, a detailed comparative study and analyses of energy compaction feature (a.k.a. sparsity) of different audio objects in the STFT domain and MDCT domain is implemented.
To measure and explore sparsity of audio signal in the time-frequency domain, a measurement addressed as Frame Energy Preservation Ratio (FEPR) and the Number of Preserved TF bins (NPTF) was proposed in [19]. Specifically, the sparse approximation signal of S(n, l), referred as S’(n, l), contains the maximum K* TF instants by preserving the portion of TF instants according to their amplitude of S(n, l) while setting the other TF instants to zero, which can be expressed by:
where , is the set of K* frequency indices corresponding to the maximum K* time-frequency instants. Thus, S’(n, l) is a K*-sparse signal.
Suppose is the L-dimensional vector denotes the TF representation of the audio object signal in nth frame, is sparse approximation vector of . Then, the Frame Energy Preservation Ratio (FEPR) can be given by:
where denotes the lp-norm.
Afterwards, for arbitrary given , if there exists a series of subset , i = 1, 2, …, such that the corresponding sparse signal vector . The Number of Preserved TF instants (NPTF), written as k, is defined as a function of :
where inf{·} represents the infimum. describes the least achievable preserved TF bins for arbitrary . Especially, a lower with a certain means stronger sparsity for an audio signal.
Appendix A.2. Statistical Analysis Results
To reveal the superior properties of MDCT, in each frame, 315 mono audio recordings selected from University of Iowa Music Instrument Samples (Iowa-MIS) audio database [37] sampled at 44.1 kHz and 100 mono speech recordings selected from Nippon Telegraph & Telephone (NTT) database are chosen as the test data. The selected audio recordings contain 7 types of tonal solo instruments. In this statistics work, a 2048-point STFT and MDCT basis with 50% overlapping is applied to form the time-frequency instants. Meanwhile, a KBD window with the size of 2048 points is used as the window function to meet the demand of overlap-add. A statistical analysis of NPTF is taken with the FEPR ranged from 98% to 80%. Results are shown in Figure A1 with 95% confidence intervals. Note that STFT-domain descriptions corresponding to instruments or speech are respectively denoted by ‘Flute-STFT’, ‘Violin-STFT’, ‘Sax-STFT’, ‘Oboe-STFT’, ‘Trombone-STFT’, ‘Trumpet-STFT’, ‘Horn-STFT’ and ‘Speech-STFT’. In contrast, MDCT-domain representations are respectively regarded as ‘Flute-MDCT’, ‘Violin-MDCT’, ‘Sax-MDCT’, ‘Oboe-MDCT’, ‘Trombone-MDCT’, ‘Trumpet-MDCT’, ‘Horn-MDCT’ and ‘Speech-MDCT’.
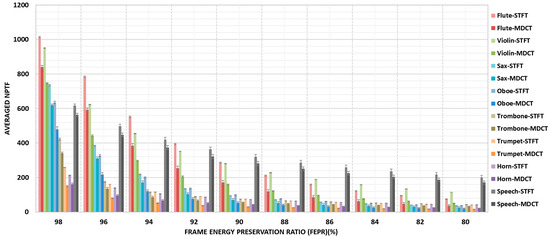
Figure A1.
NPTF (Number of Preserved Time-Frequency Bins) results calculated from eight types of audio signals in various FEPR (Frame Energy Preservation Ratio).
Figure A1 indicates that by decreasing FEPR, the averaged NPTF degrades as well. More precisely, NPTF is a convex function as FEPR decreases uniformly in terms of all test instruments and speech, that is, audio object or speech signal are sparse both in STFT and MDCT domain. Furthermore, it shows that there exists a noticeable difference between adjacent light color and dark color bars, in other words, the averaged NPTF in the MDCT domain is much lower than that in the STFT domain for each instrument and speech with a certain FEPR.
While the energy compaction property of MDCT is fairly intuitive, it becomes agnostic as the FEPR changes. To measure the disparity between the averaged NPTF for MDCT coefficients and STFT coefficients of audio signal with a known FEPR, a Normalized Relative Difference Ratio (NRDR) is defined as (k is NPTF and rFEPR is FEPR):
where k(rFEPR)STFT and k(rFEPR)MDCT are the averaged NPTF for an audio signal in the STFT and MDCT domain with a certain FEPR, respectively. NRDR is the difference between them. The larger the NRDR is, means that the less NPTF needed in the MDCT domain. Then, a statistical bar graph is presented which reflects the relationship between NRDR and FEPR.
Results are shown in Figure A2 with different NRDR at rFEPR = 98~80%. It can be observe that the NRDR of all tested audio signals are non-negative, which means that the averaged NPTF in the MDCT domain is higher than that in the STFT domain. This result testifies that the performance of MDCT is absolutely dominant for all of the tested 8 items.
Interestingly, we find that NRDR is gradually increasing as rFEPR uniformly decrease from 98% to 88%. When 80% ≤ rFEPR ≤ 88%, the NRDR maintains at the same level or slightly grow. Videlicet, with the decrement of FEPR, the superiority of MDCT is becoming increasingly obvious.
The next phenomenon needs to be noted is that the sparsity of violin and trumpet is particularly evident in the MDCT domain, because their NRDR can reach up to 60% when rFEPR = 80% whilst other instruments can only achieve roughly 45%~55%. Besides, the sparseness of selected speech signals is weaker than all instruments in the MDCT domain but maintain consistency as far as the global regularity.
Hence, the results in Figure A2 confirm that, for all tested signals, MDCT has a better energy compaction capability than STFT to the great extent. It means that audio or speech signal is more sparse in the MDCT domain than in the STFT domain.
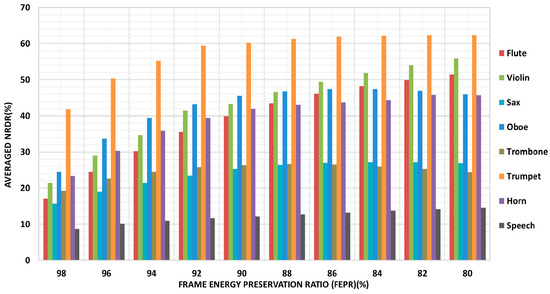
Figure A2.
NRDR (Normalized Relative Difference Ratio) of eight types of audio signals under STFT (Short Time Fourier Transform) and MDCT (Modified Discrete Cosine Transform) in various FEPR.
References
- International Telecommunication Union. BS.775: Multichannel Stereophonic Sound System with and without Accompanying Picture; International Telecommunications Union: Geneva, Switzerland, 2006. [Google Scholar]
- Bosi, M.; Brandenburg, K.; Quackenbush, S.; Fielder, L.; Akagiri, K.; Fuchs, H.; Dietz, M. ISO/IEC MPEG-2 advanced audio coding. J. Audio Eng. Soc. 1997, 45, 789–814. [Google Scholar]
- Breebaart, J.; Disch, S.; Faller, C.; Herre, J.; Hotho, G.; Kjörling, K.; Myburg, F.; Neusinger, M.; Oomen, W.; Purnhagen, H.; et al. MPEG spatial audio coding/MPEG surround: Overview and current status. In Proceedings of the Audio Engineering Society Convention 119, New York, NY, USA, 7–10 October 2005. [Google Scholar]
- Quackenbush, S.; Herre, J. MPEG surround. IEEE MultiMedia 2005, 12, 18–23. [Google Scholar] [CrossRef]
- Cheng, B.; Ritz, C.; Burnett, I. Principles and analysis of the squeezing approach to low bit rate spatial audio coding. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Honolulu, HI, USA, 16–20 April 2007; pp. I-13–I-16. [Google Scholar]
- Cheng, B.; Ritz, C.; Burnett, I. A spatial squeezing approach to ambisonic audio compression. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Las Vegas, NV, USA, 31 March–4 April 2008; pp. 369–372. [Google Scholar]
- Cheng, B.; Ritz, C.; Burnett, I.; Zheng, X. A general compression approach to multi-channel three-dimensional audio. IEEE Trans. Audio Speech Lang. Process. 2013, 21, 1676–1688. [Google Scholar] [CrossRef]
- Bleidt, R.; Borsum, A.; Fuchs, H.; Weiss, S.M. Object-based audio: Opportunities for improved listening experience and increased listener involvement. In Proceedings of the SMPTE 2014 Annual Technical Conference & Exhibition, Hollywood, CA, USA, 20–23 October 2014. [Google Scholar]
- Pulkki, V. Virtual sound source positioning using vector base amplitude panning. J. Audio Eng. Soc. 1997, 45, 456–466. [Google Scholar]
- Dolby Laboratories, “Dolby ATMOS Cinema Specifications”. 2014. Available online: http://www.dolby.com/us/en/technologies/dolbyatmos/dolby-atmos-specifications.pdf (accessed on 25 October 2017).
- Breebaart, J.; Engdegard, J.; Falch, C.; Hellmuth, O.; Hilpert, J.; Holzer, A.; Koppens, J.; Oomen, W.; Resch, B.; Schuijers, E.; et al. Spatial Audio Object Coding (SAOC)—The upcoming MPEG standard on parametric object based audio coding. In Proceedings of the Audio Engineering Society Convention 124, Amsterdam, The Netherlands, 17–20 May 2008. [Google Scholar]
- Herre, J.; Purnhagen, H.; Koppens, J.; Hellmuth, O.; Engdegard, J.; Hilper, J.; Villemoes, L.; Terentiv, L.; Falch, C.; Holzer, A.; et al. MPEG Spatial Audio Object Coding—The ISO/MPEG standard for efficient coding of interactive audio scenes. J. Audio Eng. Soc. 2012, 60, 655–673. [Google Scholar]
- Pulkki, V. Directional audio coding in spatial sound reproduction and stereo upmixing. In Proceedings of the Audio Engineering Society Conference: 28th International Conference: The Future of Audio Technology—Surround and Beyond, Piteå, Sweden, 30 June–2 July 2006. [Google Scholar]
- Faller, C.; Pulkki, V. Directional audio coding: Filterbank and STFT-based design. In Proceedings of the Audio Engineering Society Convention 120, Paris, France, 20–23 May 2006. [Google Scholar]
- Herre, J.; Hilpert, J.; Kuntz, A.; Plogsties, J. MPEG-H 3D audio—The new standard for coding of immersive spatial audio. IEEE J. Sel. Top. Signal Process. 2015, 9, 770–779. [Google Scholar] [CrossRef]
- Zheng, X.; Ritz, C.; Xi, J. Encoding navigable speech sources: An analysis by synthesis approach. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 405–408. [Google Scholar]
- Zheng, X.; Ritz, C.; Xi, J. Encoding navigable speech sources: A psychoacoustic-based analysis-by-synthesis approach. IEEE Trans. Audio Speech Lang. Process. 2013, 21, 29–38. [Google Scholar] [CrossRef]
- Yilmaz, O.; Rickard, S. Blind separation of speech mixtures via time-frequency masking. IEEE Trans. Audio Speech Lang. Process. 2004, 52, 1830–1847. [Google Scholar] [CrossRef]
- Jia, M.; Yang, Z.; Bao, C.; Zheng, X.; Ritz, C. Encoding multiple audio objects using intra-object sparsity. IEEE Trans. Audio Speech Lang. Process. 2015, 23, 1082–1095. [Google Scholar]
- Yang, Z.; Jia, M.; Bao, C.; Wang, W. An analysis-by-synthesis encoding approach for multiple audio objects. In Proceedings of the IEEE Signal and Information Processing Association Annual Summit and Conference (APSIPA), Hong Kong, China, 16–19 December 2015; pp. 59–62. [Google Scholar]
- Yang, Z.; Jia, M.; Wang, W.; Zhang, J. Multi-Stage Encoding Scheme for Multiple Audio Objects Using Compressed Sensing. Cybern. Inf. Technol. 2015, 15, 135–146. [Google Scholar]
- Wang, Y.; Vilermo, M. Modified discrete cosine transform: Its implications for audio coding and error concealment. J. Audio Eng. Soc. 2003, 51, 52–61. [Google Scholar]
- Enqing, D.; Guizhong, L.; Yatong, Z.; Yu, C. Voice activity detection based on short-time energy and noise spectrum adaptation. In Proceedings of the IEEE International Conference on Signal Processing (ICSP), Beijing, China, 26–30 August 2002; pp. 464–467. [Google Scholar]
- Painter, T.; Spanias, A. Perceptual coding of digital audio. Proc. IEEE 2000, 88, 451–515. [Google Scholar] [CrossRef]
- Spanias, A.; Painter, T.; Atti, V. Audio Signal Processing and Coding; John Wiley & Sons: Hoboken, NJ, USA, 2006; pp. 114 & 274. ISBN 9780470041970. [Google Scholar]
- Jia, M.; Bao, C.; Liu, X. An embedded speech and audio coding method based on bit-plane coding and SQVH. In Proceedings of the IEEE International Symposium on Signal Processing and Information Technology (ISSPIT), Ajman, UAE, 11–16 December 2009; pp. 43–48. [Google Scholar]
- Xie, M.; Lindbergh, D.; Chu, P. ITU-T G.722.1 Annex C: A new low-complexity 14 kHz audio coding standard. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toulouse, France, 14–19 May 2006; pp. 173–176. [Google Scholar]
- Xie, M.; Lindbergh, D.; Chu, P. From ITU-T G.722.1 to ITU-T G.722.1 Annex C: A New Low-Complexity 14kHz Bandwidth Audio Coding Standard. J. Multimed. 2007, 2, 65–76. [Google Scholar] [CrossRef]
- QUASI Database—A Musical Audio Signal Database for Source Separation. Available online: http://www.tsi.telecomparistech.fr/aao/en/2012/03/12/quasi/ (accessed on 25 October 2017).
- International Telecommunication Union. BS.1534: Method for the Subjective Assessment of Intermediate Quality Levels of Coding Systems; International Telecommunication Union: Geneva, Switzerland, 1997. [Google Scholar]
- Gardner, B.; Martin, K. HRTF Measurements of a KEMAR Dummy-Head Microphone. Available online: http://sound.media.mit.edu/resources/KEMAR.html (accessed on 25 October 2017).
- Candes, E.J.; Wakin, M.B. An introduction to compressive sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Candes, E.J.; Romberg, J.K.; Tao, T. Stable signal recovery from incomplete and inaccurate measurements. Commun. Pure Appl. Math. 2006, 59, 1207–1223. [Google Scholar] [CrossRef]
- Dhas, M.D.K.; Sheeba, P.M. Analysis of audio signal using integer MDCT with Kaiser Bessel Derived window. In Proceedings of the IEEE International Conference on Advanced Computing and Communication Systems (ICACCS), Coimbatore, India, 6–7 January 2017; pp. 1–6. [Google Scholar]
- Bosi, M.; Goldberg, R.E. Introduction to Digital Audio Coding and Standards; Springer: Berlin, Germany, 2003. [Google Scholar]
- Oppenheim, A.V.; Schafer, R.W. Discrete-Time Signal Processing, 3rd ed.; Publishing House of Electronics Industry: Beijing, China, 2011; pp. 673–683. ISBN 9787121122026. [Google Scholar]
- University of Iowa Music Instrument Samples. Available online: http://theremin.music.uiowa.edu/MIS.html (accessed on 25 October 2017).
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).