A New Compact Octagonal Shape Perfect Metamaterial Absorber for Microwave Applications
Abstract
:1. Introduction
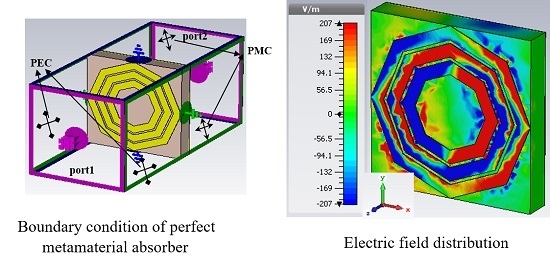
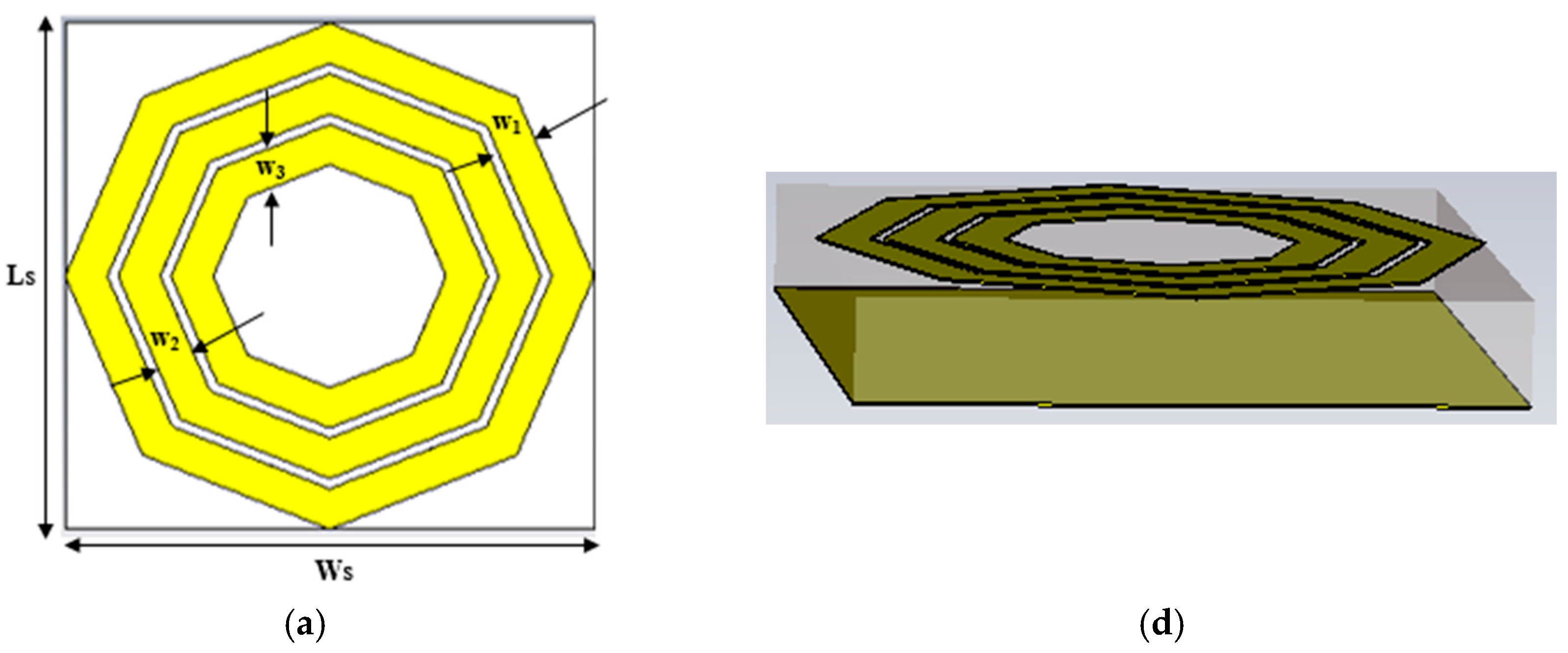
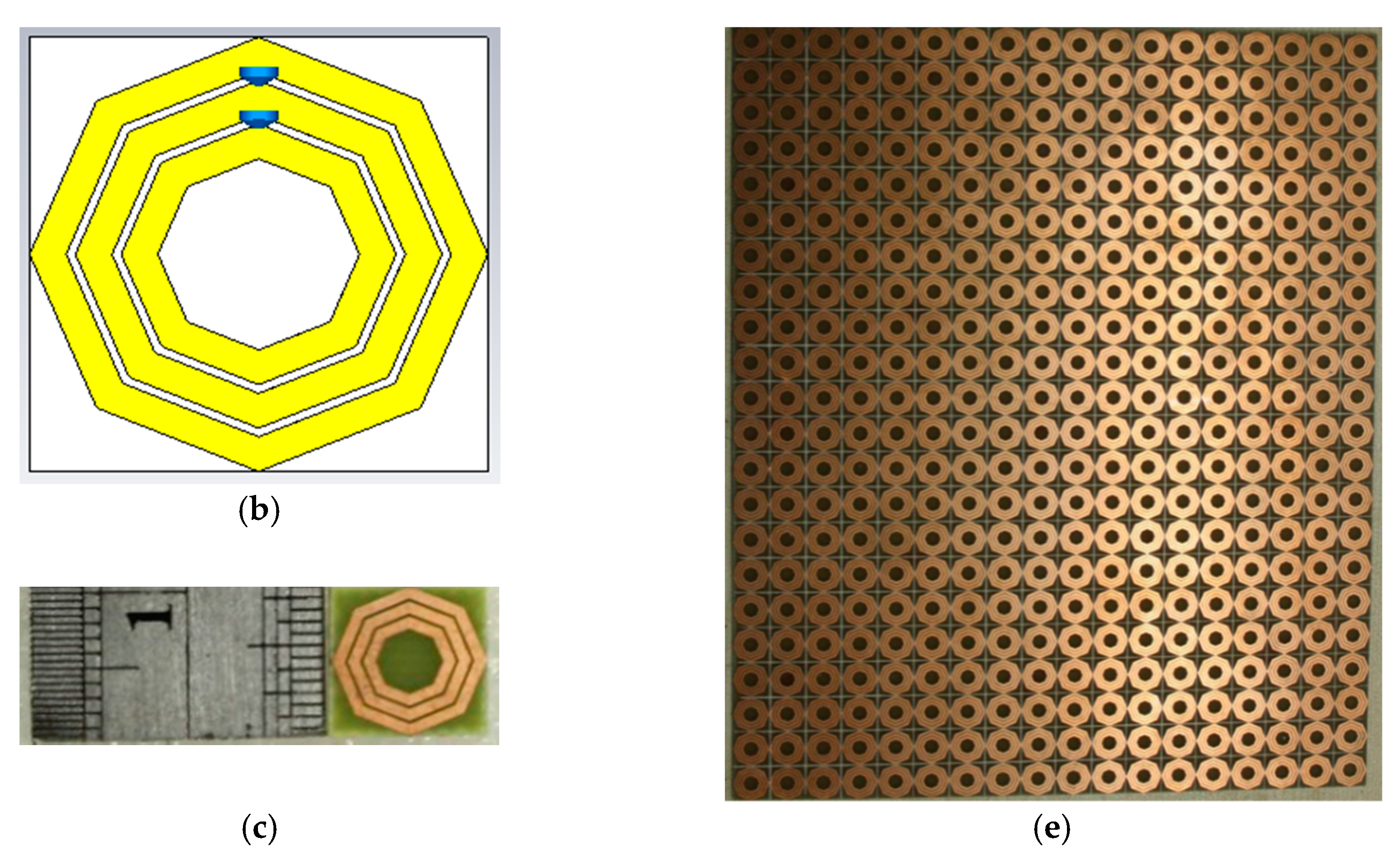
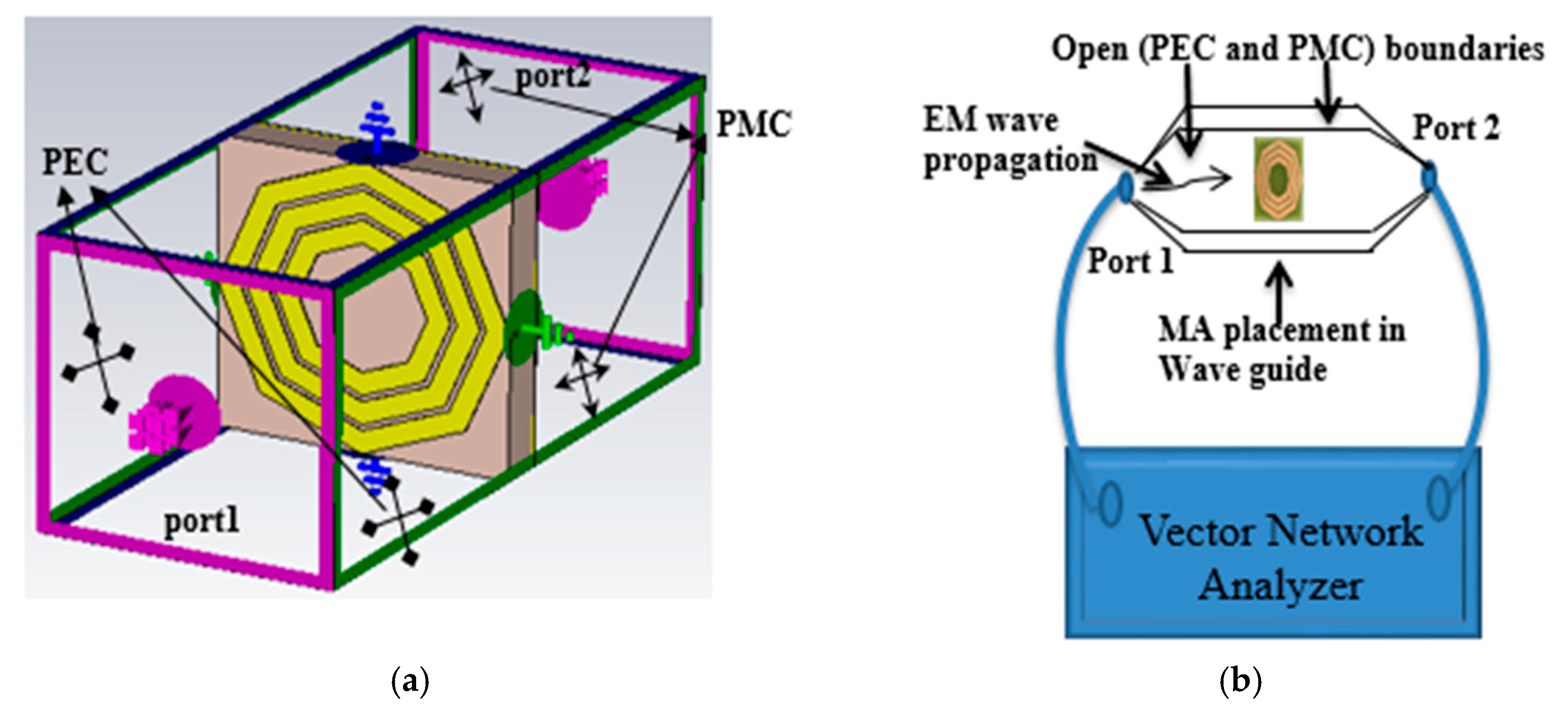
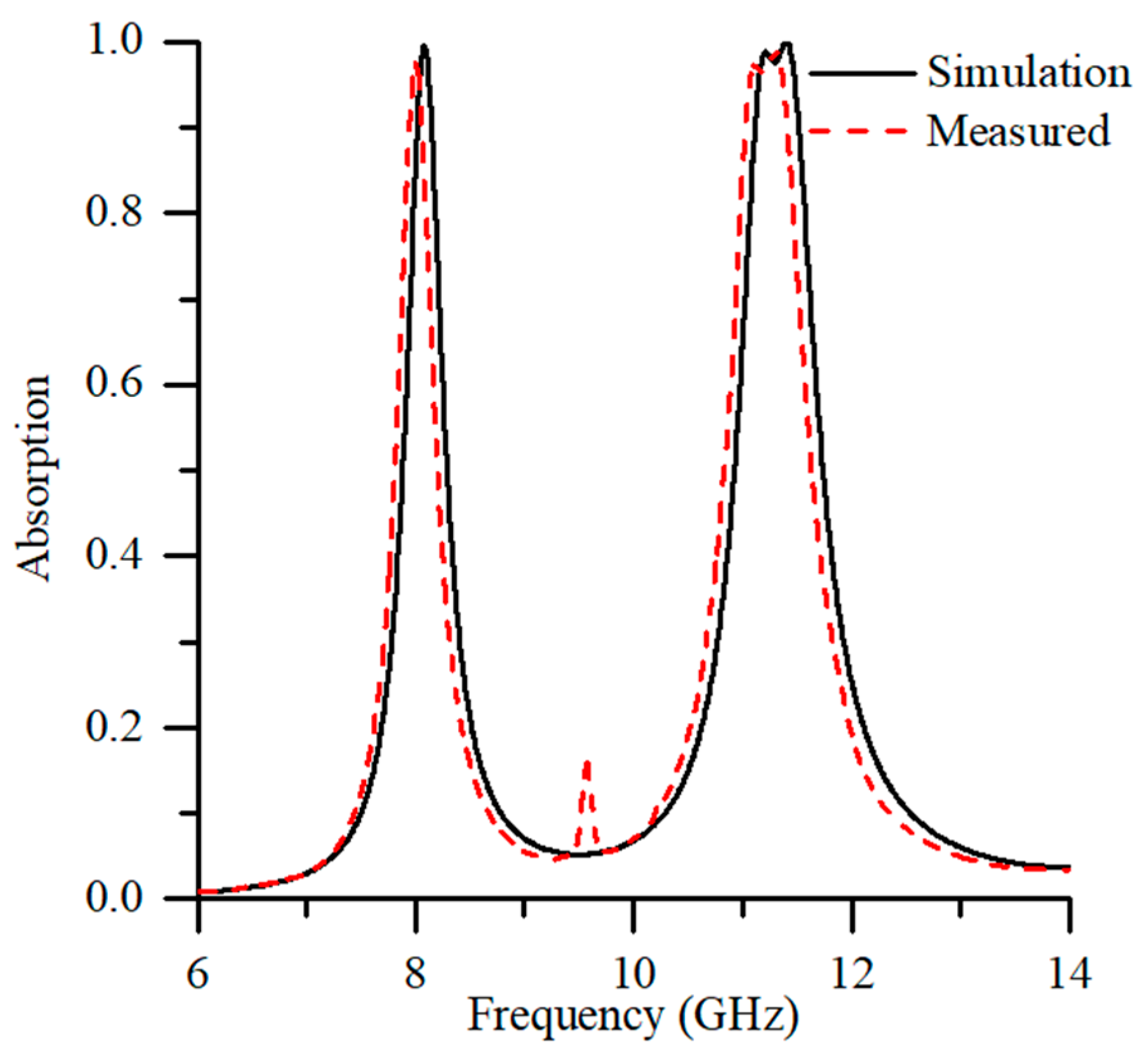
2. Design, Numerical Simulation, and Experiment
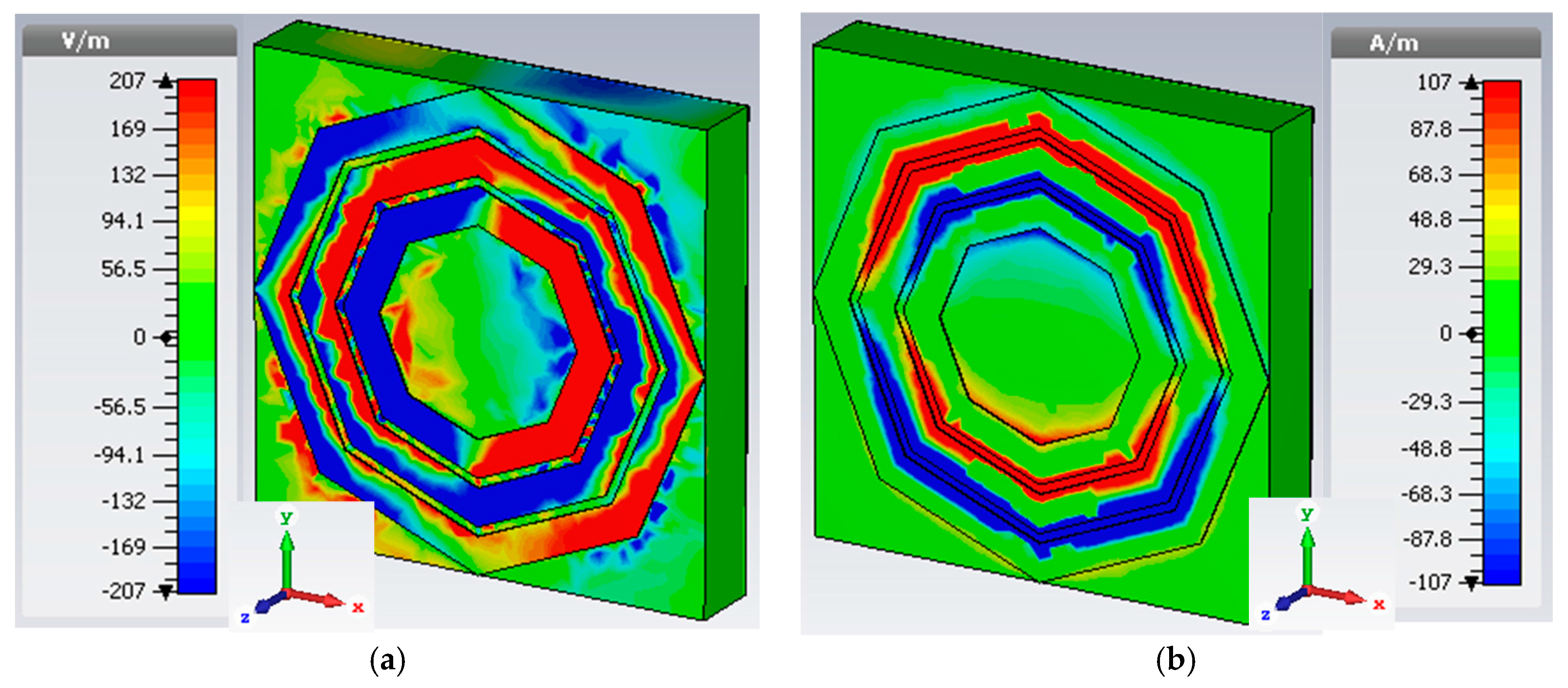
3. Results and Discussions
3.1. Analysis of Design Structure with Polarization Angle
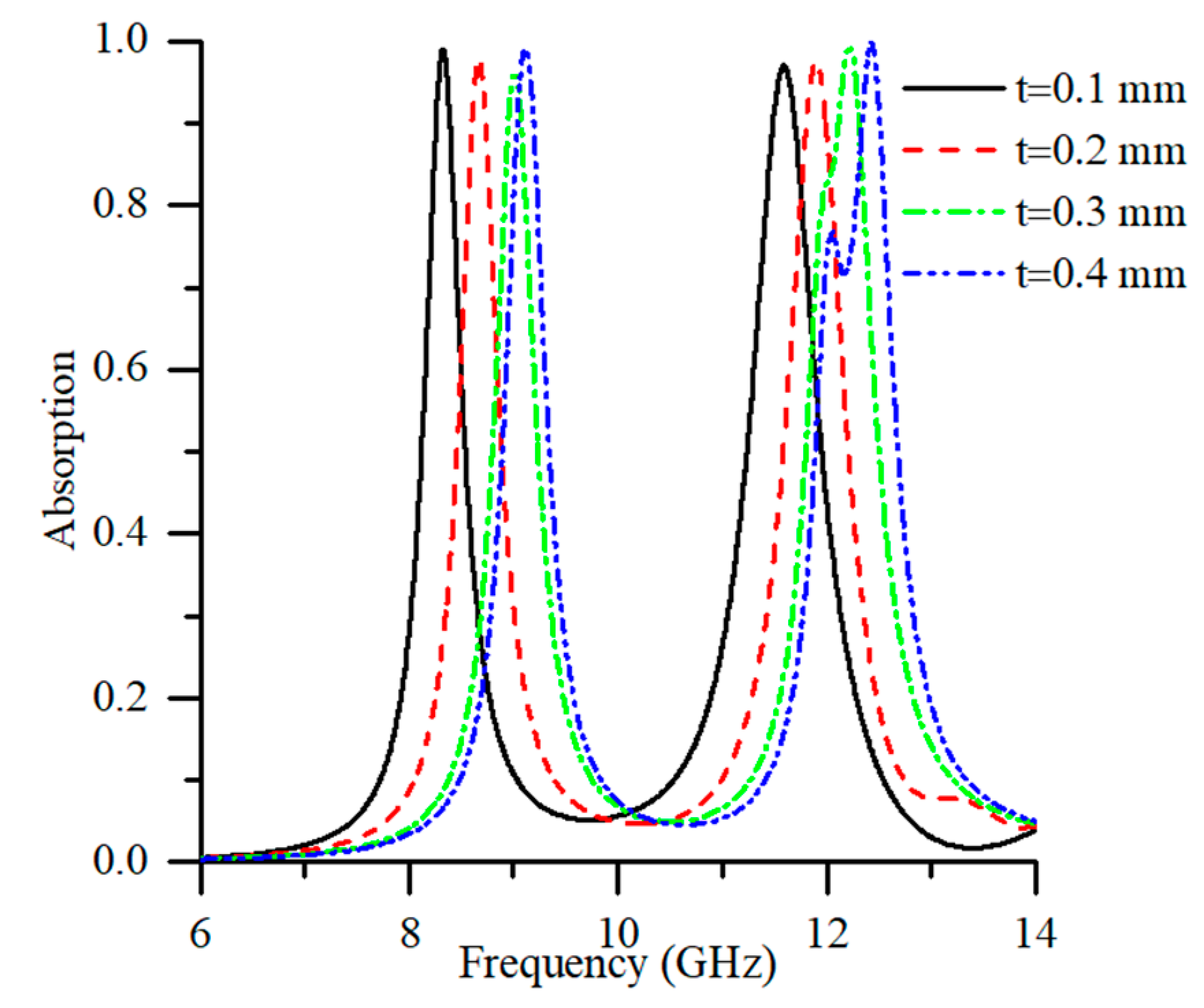
3.2. Analysis of Design Structure with Different Thickness of FR4 Substrate Materials
3.3. Analysis of Design Structure with Different Thickness of Metallic Materials
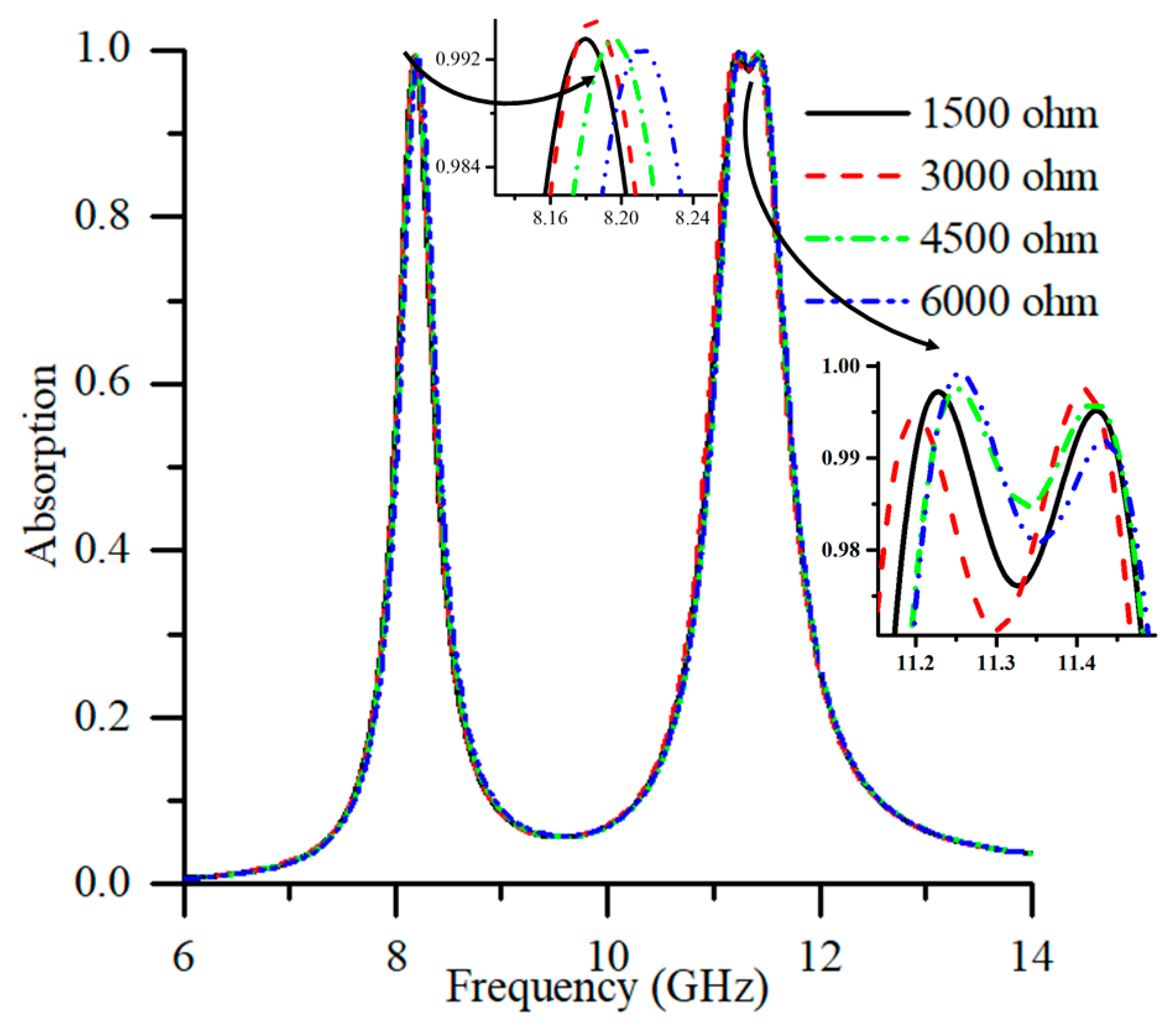
3.4. Analysis of Design Structure with Resistive Load
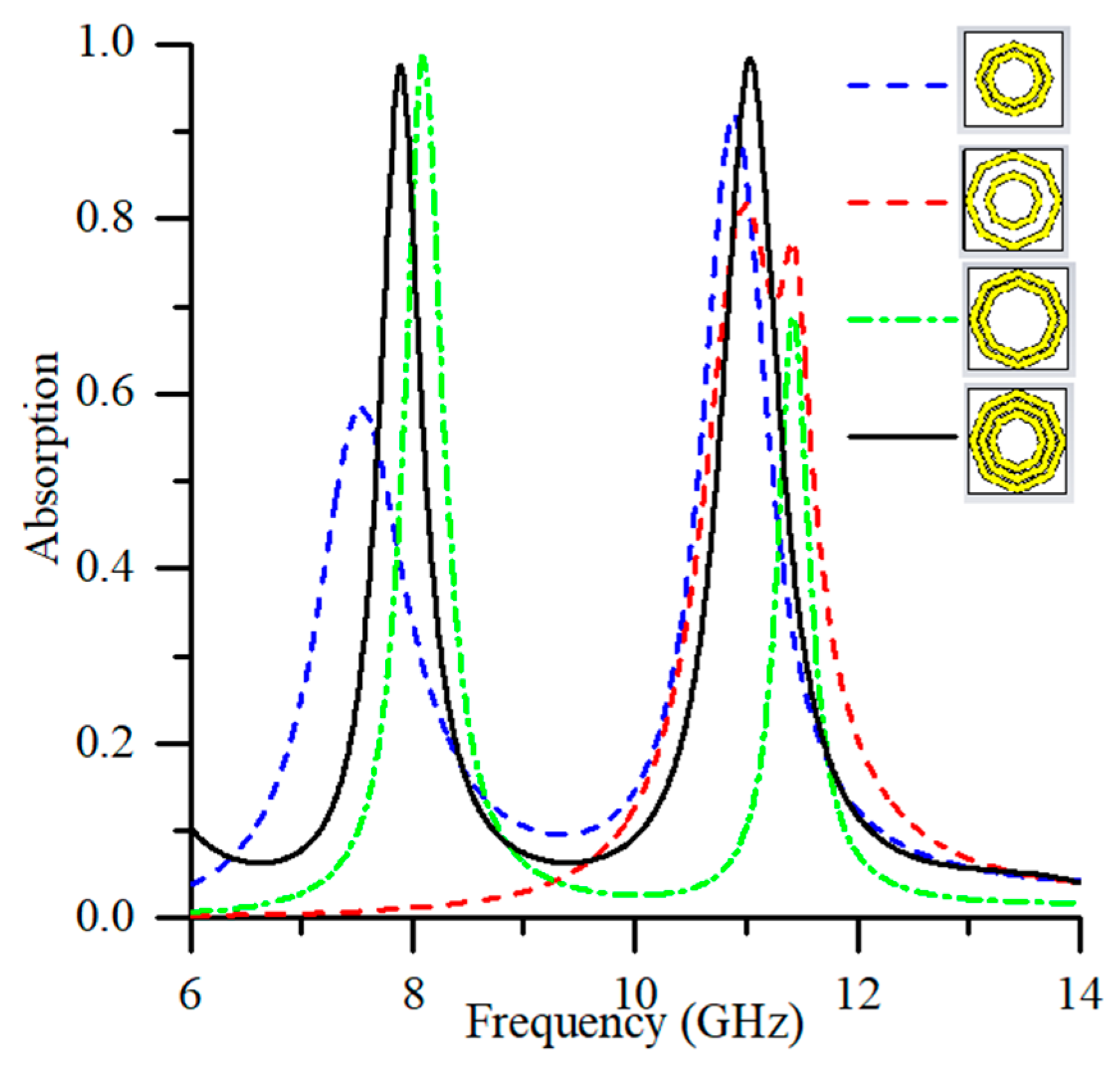
3.5. Analysis of Design Structure with Resonator’s Number
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Smith, D.R.; Pendry, J.B.; Wiltshire, M.C. Metamaterials and negative refractive index. Science 2004, 305, 788–792. [Google Scholar] [CrossRef] [PubMed]
- Soukoulis, C.M.; Linden, S.; Wegener, M. Negative refractive index at optical wavelengths. Science 2007, 315, 47–49. [Google Scholar] [CrossRef] [PubMed]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.; Smith, D.; Padilla, W. Perfect metamaterial absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef] [PubMed]
- Singh, P.; Ameri, S.K.; Chao, L.; Afsar, M.N.; Sonkusale, S. Broadband millimeterwave metamaterial absorber based on embedding of dual resonators. Prog. Electromagn. Res. 2013, 142, 625–638. [Google Scholar] [CrossRef]
- Huang, X.; Yang, H.; Yu, S.; Wang, J.; Li, M.; Ye, Q. Triple-band polarization-insensitive wide-angle ultra-thin planar spiral metamaterial absorber. J. Appl. Phys. 2013, 113, 213516. [Google Scholar] [CrossRef]
- Xu, Y.Q.; Zhou, P.H.; Zhang, H.B.; Chen, L.; Deng, L.J. A wide-angle planar metamaterial absorber based on split ring resonator coupling. J. Appl. Phys. 2011, 110, 044102. [Google Scholar]
- Shrekenhamer, D.; Xu, W.; Venkatesh, S.; Schurig, D.; Sonkusale, S.; Padilla, W.J. Experimental realization of a metamaterial detector focal plane array. Phys. Rev. Lett. 2012, 109, 177401. [Google Scholar] [CrossRef] [PubMed]
- Shrekenhamer, D.; Watts, C.M.; Montoya, J.; Krishna, S.; Padilla, W.J. Metamaterial-based imaging for potential security applications. SPIE OPTO 2013, 8632, 863221. [Google Scholar]
- Xiong, H.; Hong, J.-S.; Luo, C.-M.; Zhong, L.-L. An ultrathin and broadband metamaterial absorber using multi-layer structures. J. Appl. Phys. 2013, 114, 064109. [Google Scholar] [CrossRef]
- Hunt, J.; Driscoll, T.; Mrozack, A.; Lipworth, G.; Reynolds, M.; Brady, D.; Smith, D.R. Metamaterial apertures for computational imaging. Science 2013, 339, 310–313. [Google Scholar] [CrossRef] [PubMed]
- Pfeiffer, C.; Grbic, A. Metamaterial Huygens’ surfaces: Tailoring wave fronts with reflectionless sheets. Phys. Rev. Lett. 2013, 110, 197401. [Google Scholar] [CrossRef] [PubMed]
- Naser-Moghadasi, M.; Nia, A.Z.; Toolabi, M.; Heydari, S. Microwave metamaterial Absorber based on Jerusalem Cross with meandered load for bandwidth enhancement. Opt. Int. J. Light Electron Opt. 2017, 140, 515–522. [Google Scholar] [CrossRef]
- Lin, B.; Zhao, S.; Da, X.; Fang, Y.; Ma, J.; Li, W.; Zhu, Z. Triple-band low frequency ultra-compact metamaterial absorber. J. Appl. Phys. 2015, 117, 184503. [Google Scholar] [CrossRef]
- Zhao, J.; Cheng, Y. Ultrabroadband microwave metamaterial absorber based on electric SRR loaded with lumped resistors. J. Electron. Mater. 2016, 45, 5033–5039. [Google Scholar] [CrossRef]
- Dincer, F.; Karaaslan, M.; Sabah, C. Design and analysis of perfect metamaterial absorber in GHz and THz frequencies. J. Electromagn. Waves Appl. 2015, 29, 2492–2500. [Google Scholar] [CrossRef]
- Hossain, M.J.; Faruque, M.R.I.; Islam, M.T. Design and analysis of a new composite double negative metamaterial for multi-band communication. Curr. Appl. Phys. 2017, 17, 931–939. [Google Scholar] [CrossRef]
- Islam, S.S.; Faruque, M.R.I.; Islam, M.T. Design and absorption analysis of a new multiband split-S-shaped metamaterial. Sci. Eng. Compos. Mater. 2017, 24, 139–148. [Google Scholar] [CrossRef]
- Kim, Y.; Yoo, Y.; Hwang, J.; Lee, Y. Ultra-broadband microwave metamaterial absorber based on resistive sheets. J. Opt. 2016, 19, 015103. [Google Scholar] [CrossRef]
- Wen, Q.-Y.; Zhang, H.-W.; Xie, Y.-S.; Yang, Q.-H.; Liu, Y.-L. Dual band terahertz metamaterial absorber: Design, fabrication, and characterization. Appl. Phys. Lett. 2009, 95, 241111. [Google Scholar] [CrossRef]
- Tao, H.; Bingham, C.; Pilon, D.; Fan, K.; Strikwerda, A.; Shrekenhamer, D.; Padilla, W.J.; Zhang, X.; Averitt, R.D. A dual band terahertz metamaterial absorber. J. Phys. D Appl. Phys. 2010, 43, 225102. [Google Scholar] [CrossRef]
- Kollatou, T.M.; Dimitriadis, A.I.; Assimonis, S.; Kantartzis, N.V.; Antonopoulos, C.S. A family of ultra-thin, polarization-insensitive, multi-band, highly absorbing metamaterial structures. Prog. Electromagn. Res. 2013, 136, 579–594. [Google Scholar] [CrossRef]
- Rana, C.R.; Inamdar, K.; Lalluwadia, A. Study, Design and Analysis of U-Shaped Metamaterial Absorber for X-Band Application. IUP J. Telecommun. 2016, 8, 23. [Google Scholar]
- Borah, D.; Bhattacharyya, N.S. Design and Development of Expanded Graphite-Based Non-metallic and Flexible Metamaterial Absorber for X-band Applications. J. Electron. Mater. 2017, 46, 226–232. [Google Scholar] [CrossRef]
- Mahmood, A.; Yetkin, G.Ö.; Sabah, C. Design and Fabrication of a Novel Wideband DNG Metamaterial with the Absorber Application in Microwave X-Band. Adv. Condens. Matter Phys. 2017, 2017, 1279849. [Google Scholar] [CrossRef]
- Sen, G.; Islam, S.N.; Banerjee, A.; Das, S. Broadband Perfect Metamaterial Absorber on Thin Substrate for X-Band and Ku-Band Applications. Prog. Electromagn. Res. C 2017, 73, 9–16. [Google Scholar] [CrossRef]



| Author Name | Design Structure | Size (mm2) | Proposed Band | Absorption Rate (%) | Year of Published |
|---|---|---|---|---|---|
| Kollatou et al. [21] | Modified Square | 8 × 8 | X-band | 95.81 | 2013 |
| Rana et al. [22] | U-shape | 15 × 15 | X-band | 98.00 | 2016 |
| Borah et al. [23] | O-shape | 12 × 12 | X-band | 98.90 | 2016 |
| Islam et al. [17] | S-shape | 20 × 20 | S-, X-, Ku-band | 55.00 | 2017 |
| Sen et al. [25] | L-shape | 9 × 9 | X-, Ku-band | 95.00 | 2017 |
| Mahmood et al. [24] | Modified S-shape | 16 × 16 | X-band | 90.00 | 2017 |
| Proposed PMA | Octagonal shape | 10 × 10 | X-band | 98.97 | - |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hossain, M.J.; Faruque, M.R.I.; Islam, M.T.; Mat, K.B. A New Compact Octagonal Shape Perfect Metamaterial Absorber for Microwave Applications. Appl. Sci. 2017, 7, 1263. https://doi.org/10.3390/app7121263
Hossain MJ, Faruque MRI, Islam MT, Mat KB. A New Compact Octagonal Shape Perfect Metamaterial Absorber for Microwave Applications. Applied Sciences. 2017; 7(12):1263. https://doi.org/10.3390/app7121263
Chicago/Turabian StyleHossain, Mohammad Jakir, Mohammad Rashed Iqbal Faruque, Mohammad Tariqul Islam, and Kamarulzaman Bin Mat. 2017. "A New Compact Octagonal Shape Perfect Metamaterial Absorber for Microwave Applications" Applied Sciences 7, no. 12: 1263. https://doi.org/10.3390/app7121263
APA StyleHossain, M. J., Faruque, M. R. I., Islam, M. T., & Mat, K. B. (2017). A New Compact Octagonal Shape Perfect Metamaterial Absorber for Microwave Applications. Applied Sciences, 7(12), 1263. https://doi.org/10.3390/app7121263