Time-Domain Functional Diffuse Optical Tomography System Based on Fiber-Free Silicon Photomultipliers
Abstract
1. Introduction
2. Materials and Methods
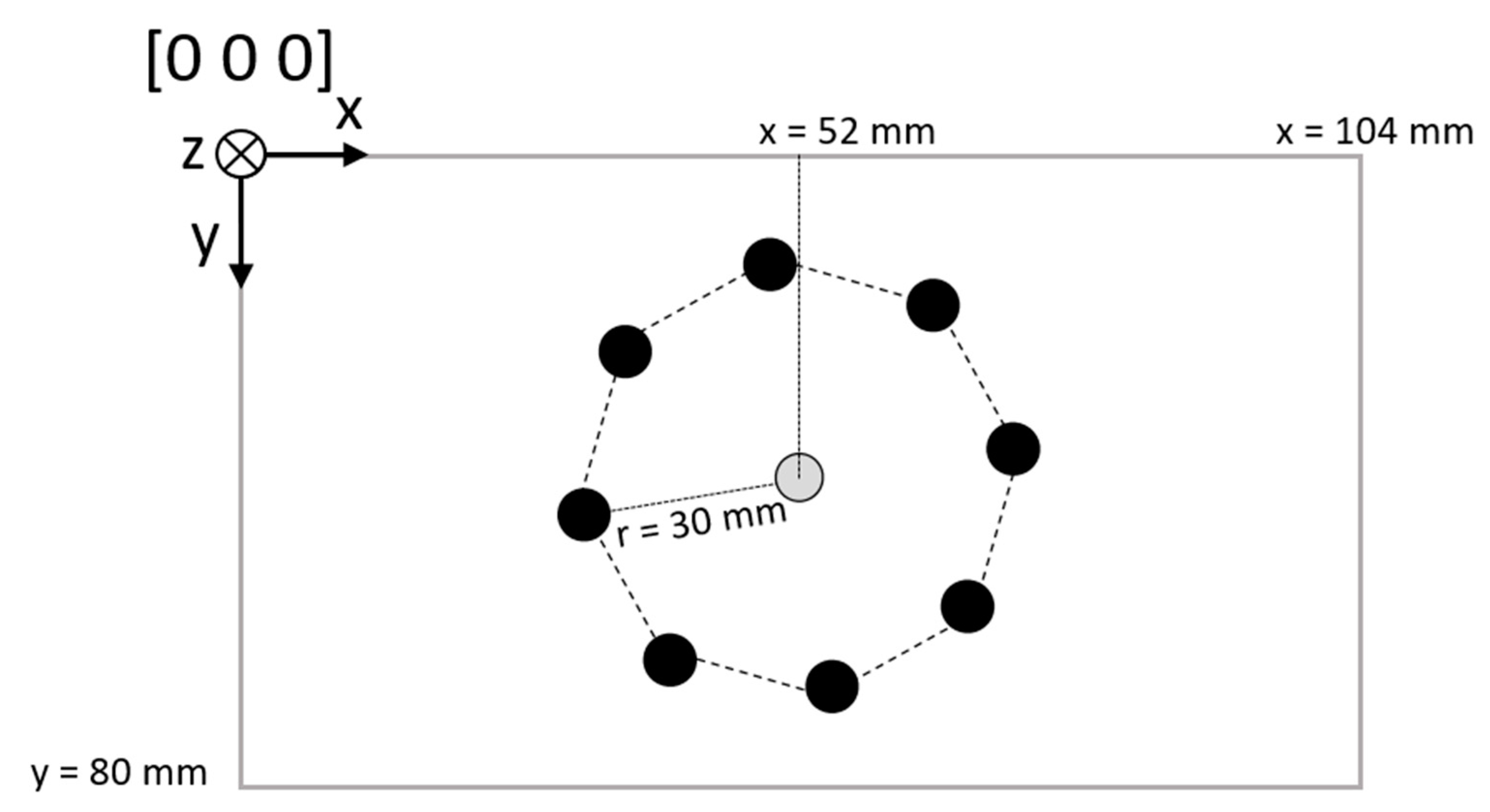
2.1. Setup
2.2. Tomographic Reconstruction
2.3. Simulation Approach
2.4. Phantom Test
2.5. In Vivo Measurements
3. Results and Discussion
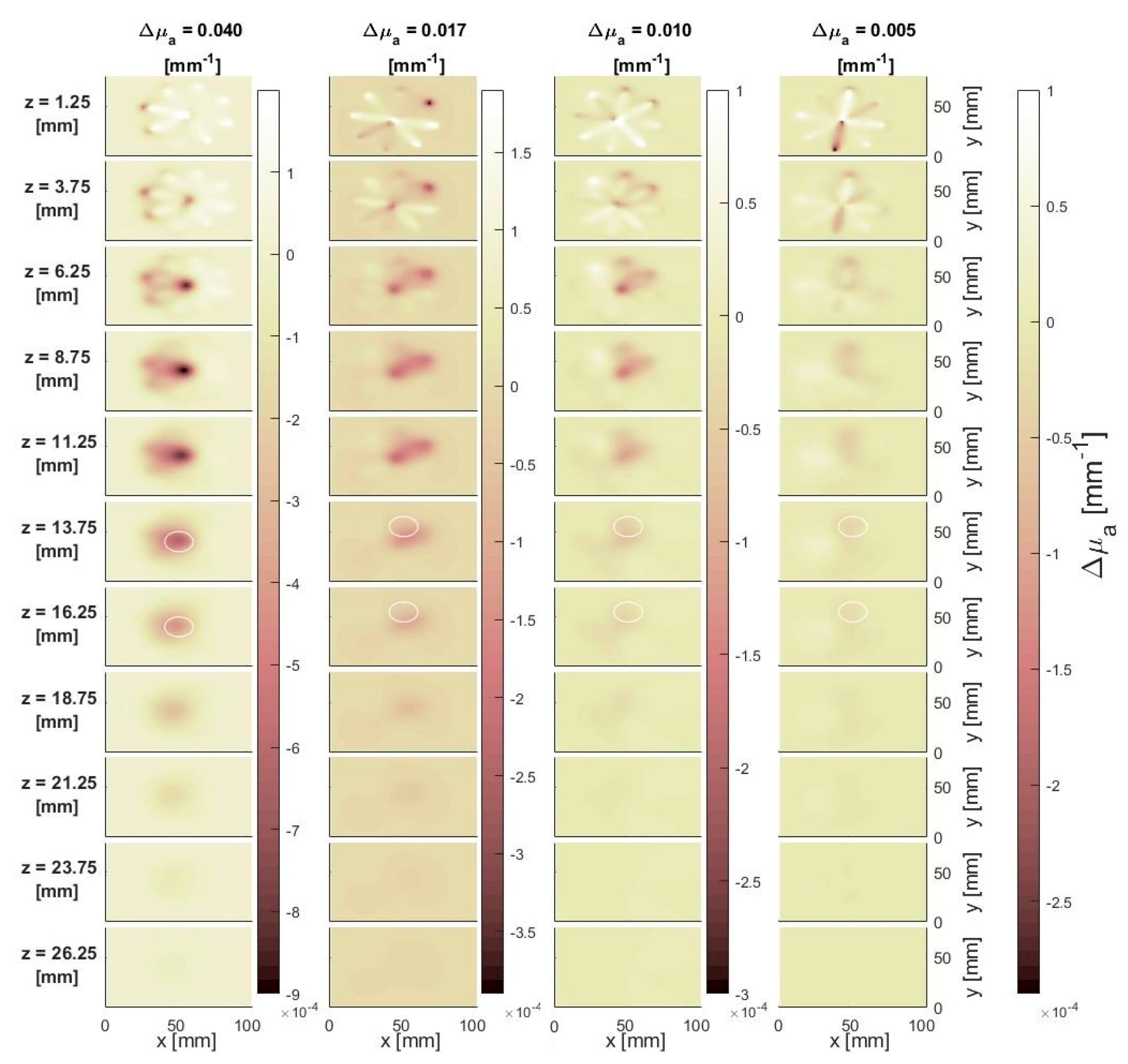
3.1. Simulations
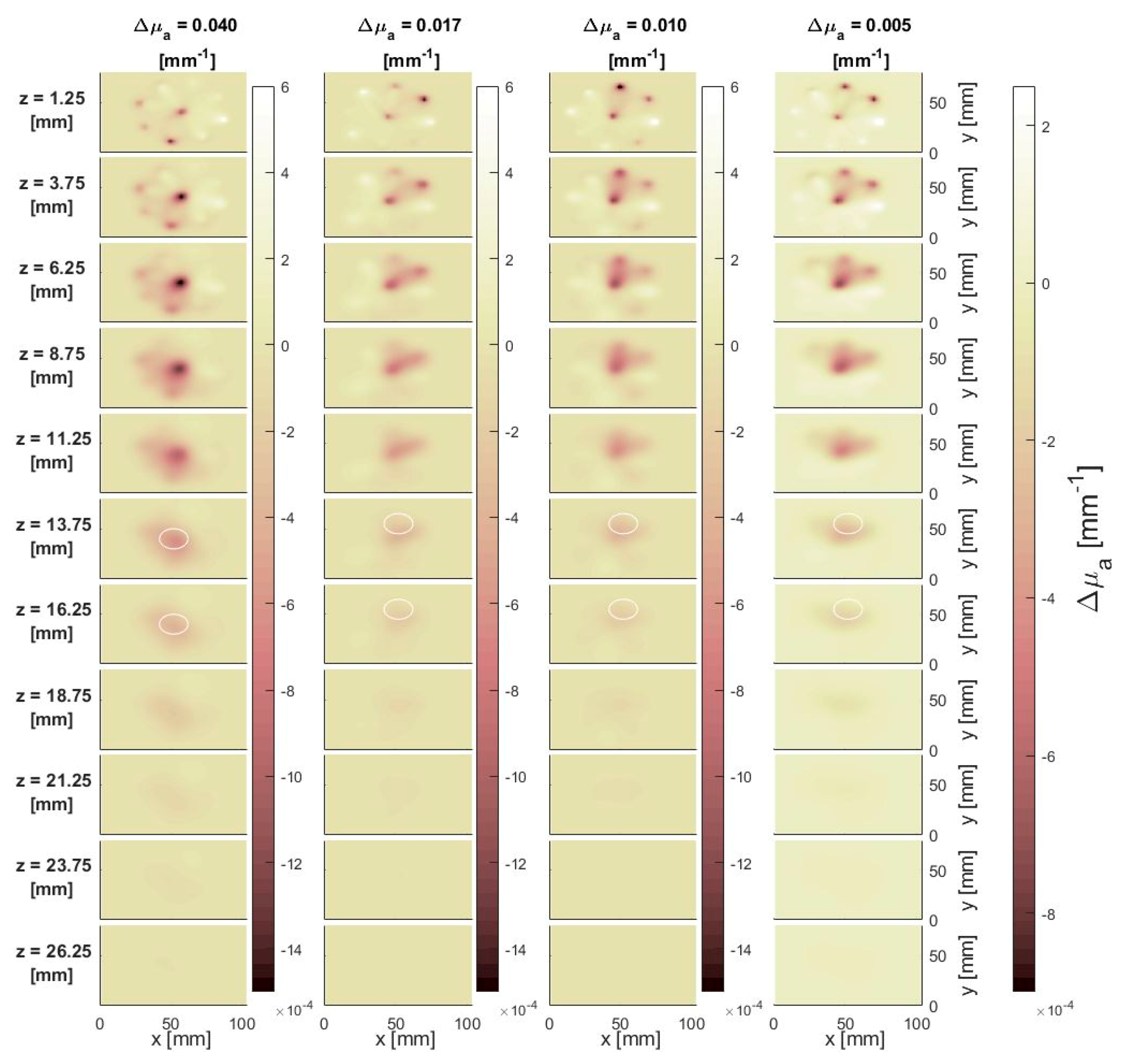
3.1.1. Effect of the Perturbation
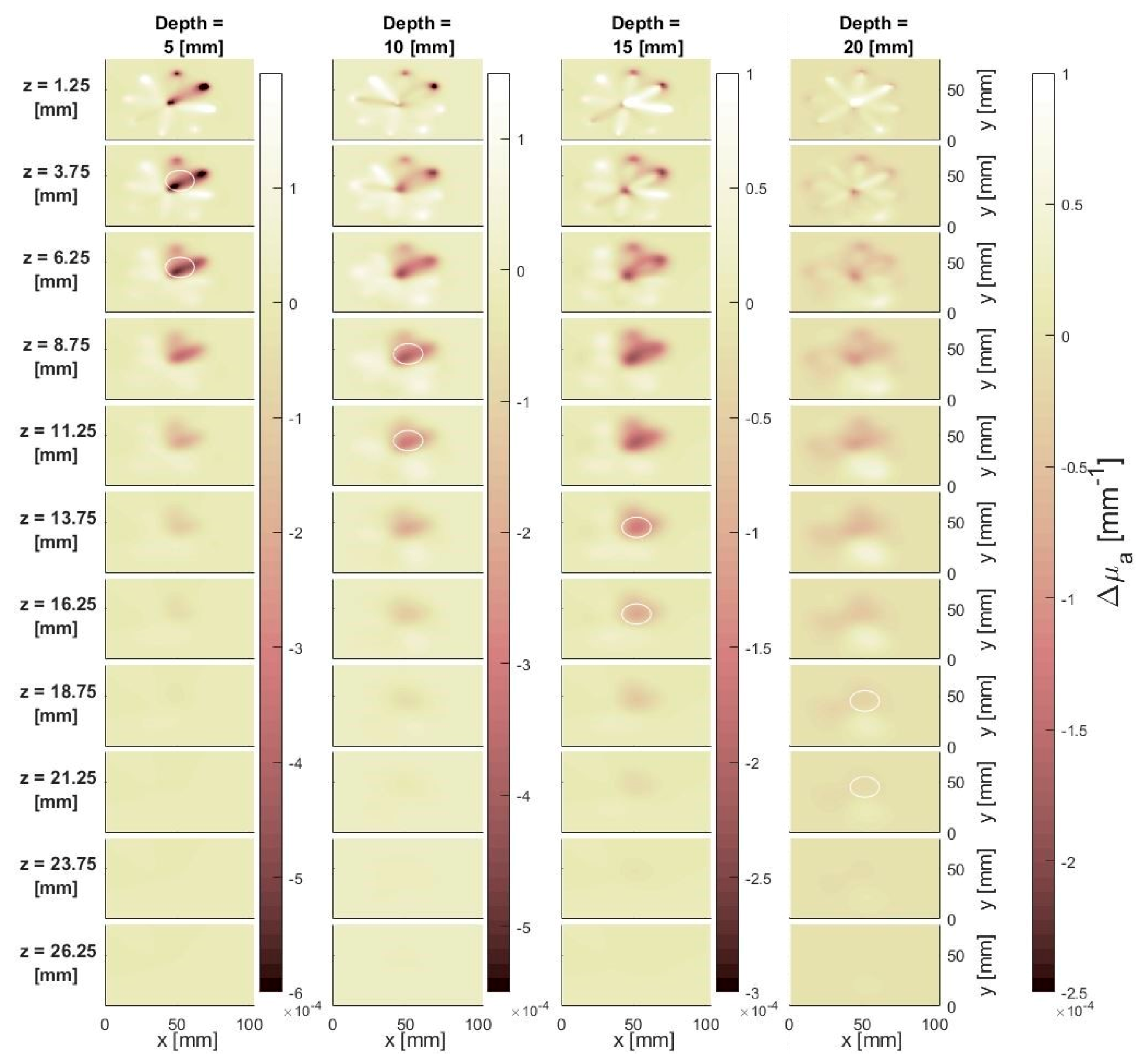
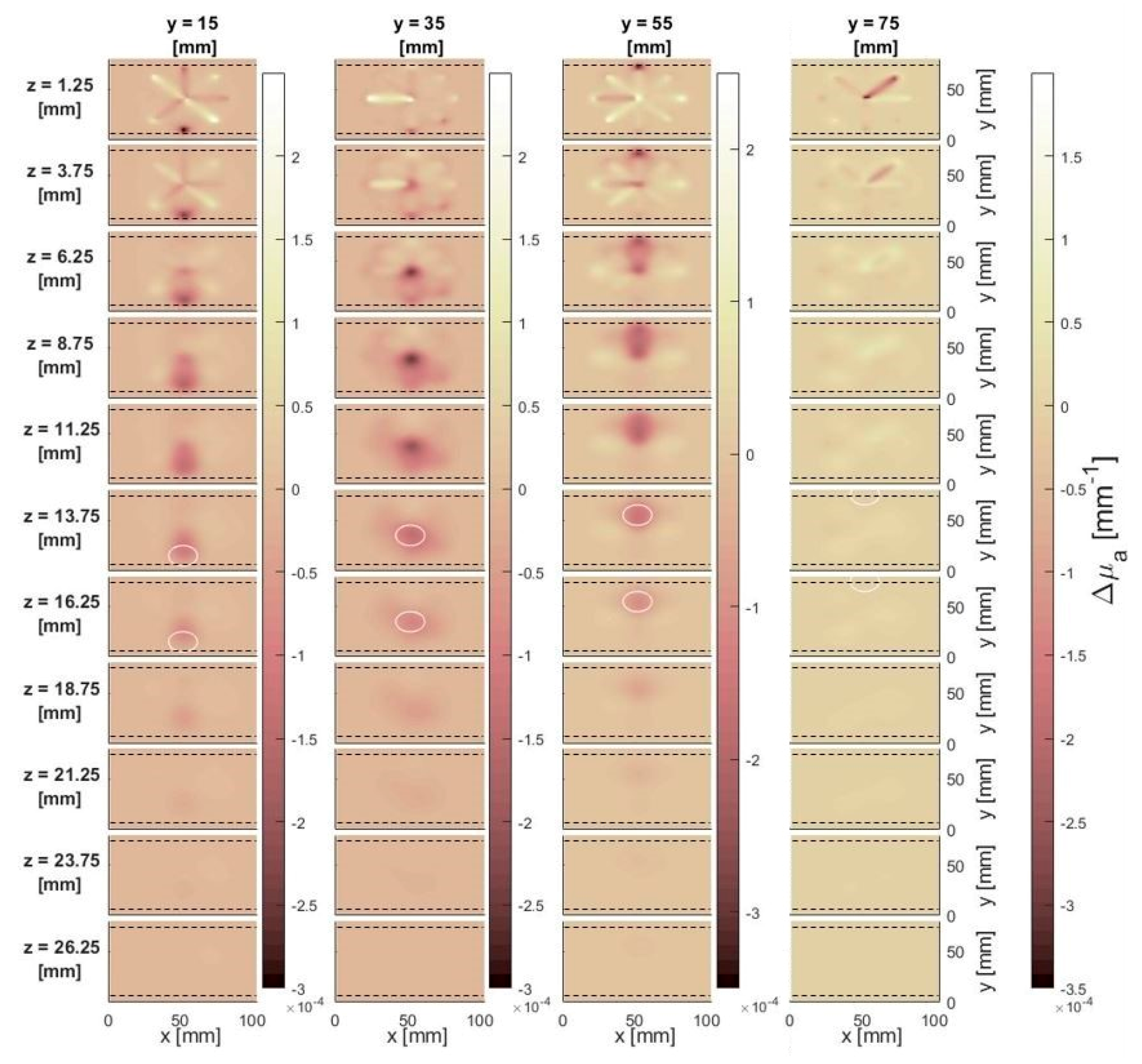
3.1.2. Effect of Depth
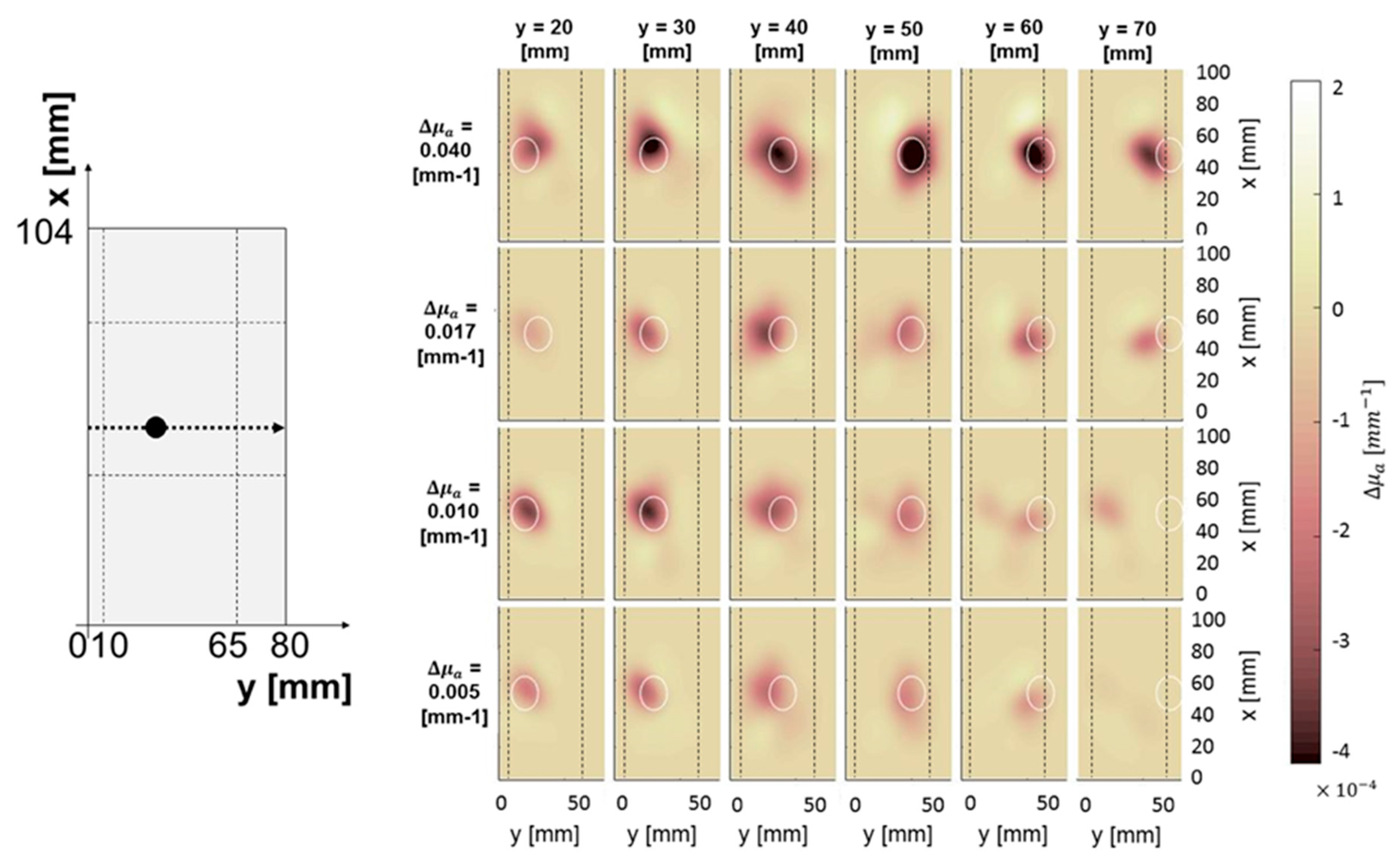
3.1.3. Effect of Lateral Distance
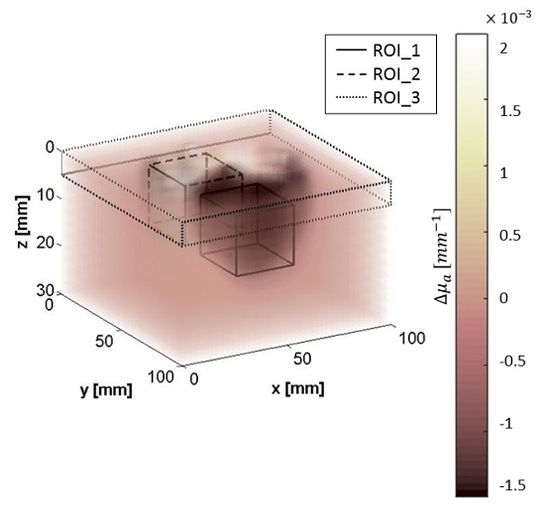
3.2. Test on Phantoms
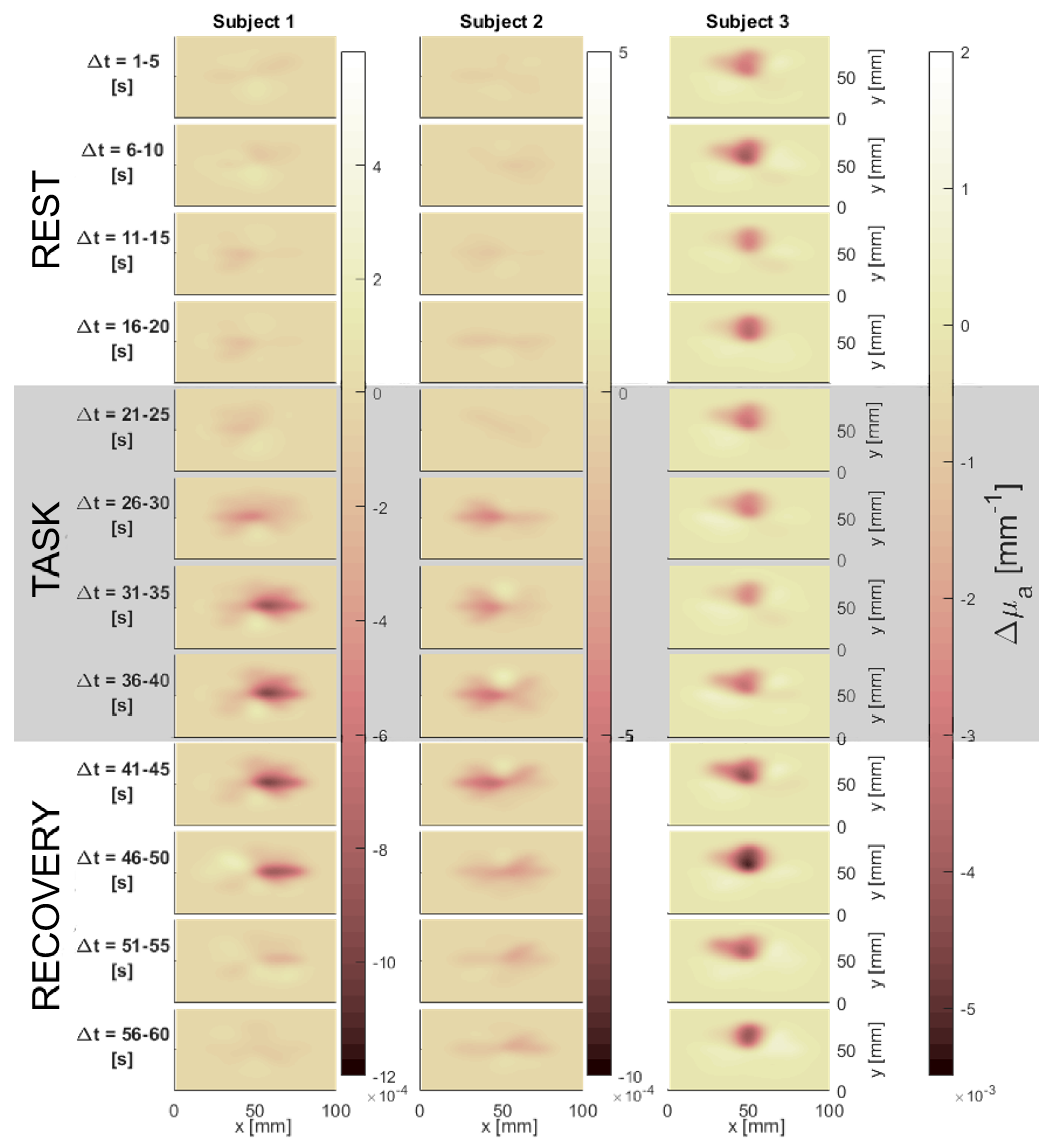
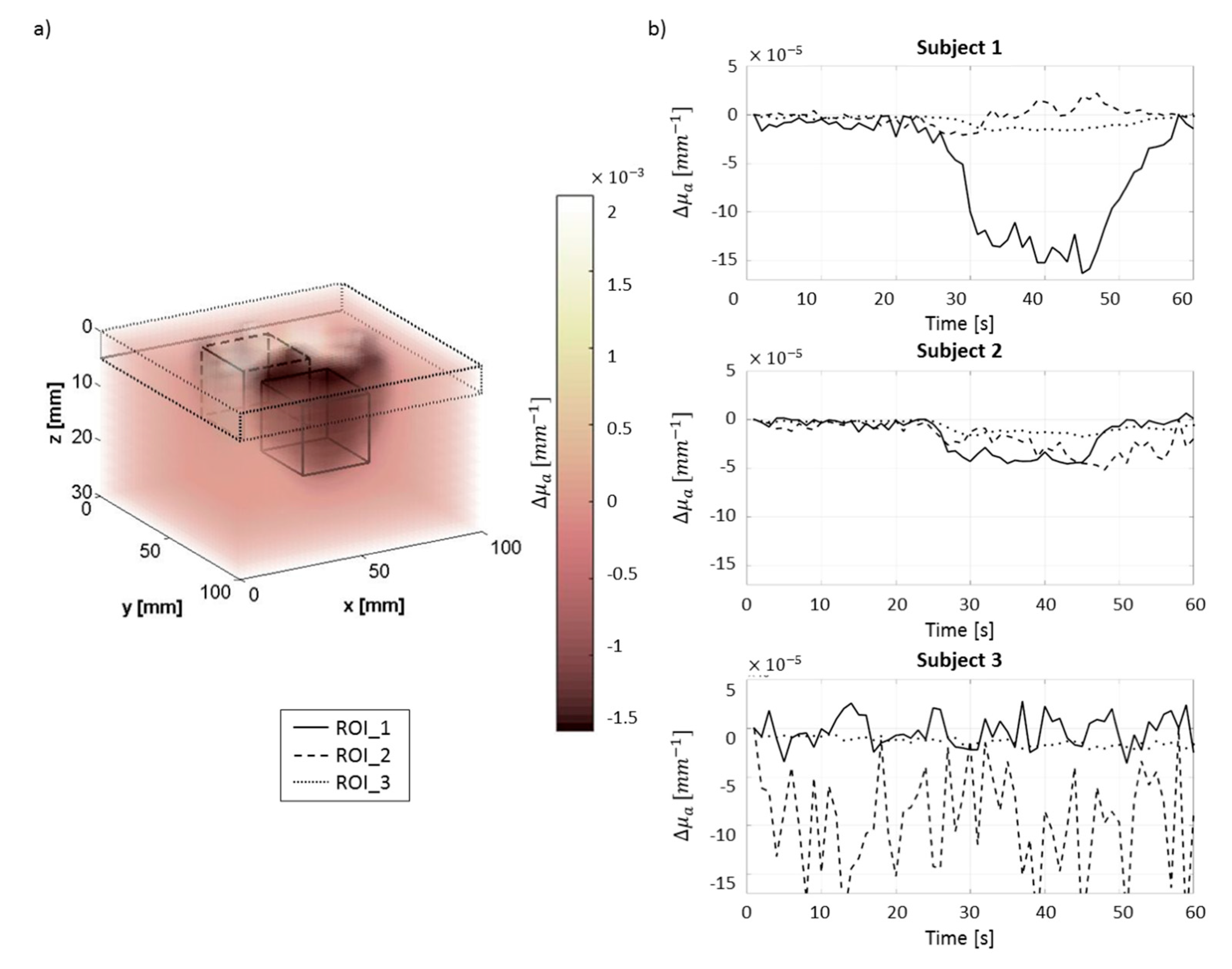
3.3. In Vivo Test
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Culver, J.P.; Choe, R.; Holboke, M.J.; Zubkov, L.; Durduran, T.; Slemp, A.; Ntziachristos, V.; Chance, B.; Yodh, A.G. Three-dimensional diffuse optical tomography in the parallel plane transmission geometry: Evaluation of a hybrid frequency domain/continuous wave clinical system for breast imaging. Med. Phys. 2003, 30, 235–247. [Google Scholar] [CrossRef] [PubMed]
- Deng, B.; Brooks, D.H.; Boas, D.A.; Lundqvist, M.; Fang, Q. Characterization of structural-prior guided optical tomography using realistic breast models derived from dual-energy X-ray mammography. Biomed. Opt. Express 2015, 6, 2366. [Google Scholar] [CrossRef] [PubMed]
- Singh, B.; Fang, Q.; Deng, B.; Zimmermann, B.; Boas, D.A.; Cormier, J.; Moore, R.; Kopans, D.; Saksena, M.; Carp, S. Integrated Near-infrared Diffuse Optical Imaging and Digital Breast Tomography for monitoring compression induced hemodynamics in breast cancer patients. In Biomedical Optics 2016; Optical Society of America: Washington, DC, USA, 2016. [Google Scholar] [CrossRef]
- Chen, L.; Pan, M.; Pan, M. Flexible near-infrared diffuse optical tomography with varied weighting functions of edge-preserving regularization. Appl. Opt. 2013, 52, 1173–1182. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.Y.; Pan, M.C.; Pan, M.C. Visualized numerical assessment for near infrared diffuse optical tomography with contrast-and-size detail analysis. Opt. Rev. 2013, 20, 19–25. [Google Scholar] [CrossRef]
- Eggebrecht, A.T.; Ferradal, S.L.; Robichaux-Viehoever, A.; Hassanpour, M.S.; Dehghani, H.; Snyder, A.Z.; Hershey, T.; Culver, J.P. Mapping distributed brain function and networks with diffuse optical tomography. Nat. Photonics 2014, 8, 448–454. [Google Scholar] [CrossRef] [PubMed]
- Culver, J.P.; Durduran, T.; Furuya, D.; Cheung, C.; Greenberg, J.H.; Yodh, A.G. Diffuse optical tomography of cerebral blood flow, oxygenation, and metabolism in rat during focal ischemia. J. Cereb. Blood Flow Metab. 2003, 23, 911–924. [Google Scholar] [CrossRef] [PubMed]
- Ntziachristos, V. Fluorescence molecular imaging. Annu. Rev. Biomed. Eng. 2006, 8, 1–33. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Huang, Y.; Lu, R. Innovative hyperspectral imaging-based techniques for quality evaluation of fruits and vegetables: A review. Appl. Sci. 2017, 7, 189. [Google Scholar] [CrossRef]
- Qin, J.; Kim, M.S.; Chao, K.; Chan, D.E.; Delwiche, S.R.; Cho, B.-K. Line-scan hyperspectral imaging techniques for food safety and quality applications. Appl. Sci. 2017, 7, 125. [Google Scholar] [CrossRef]
- Arridge, S.R. Optical tomography in medical imaging. Inverse Probl. 1999, 15, R41–R93. [Google Scholar] [CrossRef]
- Durduran, T.; Choe, R.; Baker, W.B.; Yodh, A.G. Diffuse optics for tissue monitoring and tomography. Rep. Prog. Phys. 2010, 73, 76701. [Google Scholar] [CrossRef] [PubMed]
- Ntziachristos, V.; Yodh, A.G.; Schnall, M.; Chance, B. Concurrent MRI and diffuse optical tomography of breast after indocyanine green enhancement. Proc. Natl. Acad. Sci. USA 2000, 97, 2767–2772. [Google Scholar] [CrossRef] [PubMed]
- Choe, R.; Konecky, S.D.; Corlu, A.; Lee, K.; Durduran, T.; Busch, D.R.; Pathak, S.; Czerniecki, B.J.; Tchou, J.; Fraker, D.L.; et al. Differentiation of benign and malignant breast tumors by in-vivo three-dimensional parallel-plate diffuse optical tomography. J. Biomed. Opt. 2009, 14, 24020. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Z.; Zhang, Q.; Sobel, E.S.; Jiang, H. Tomographic X-ray–guided three-dimensional diffuse optical tomography of osteoarthritis in the finger joints. J. Biomed. Opt. 2008, 13, 44006. [Google Scholar] [CrossRef] [PubMed]
- Khalil, M.A.; Kim, H.K.; Kim, I.-K.; Flexman, M.; Dayal, R.; Shrikhande, G.; Hielscher, A.H. Dynamic diffuse optical tomography imaging of peripheral arterial disease. Biomed. Opt. Express 2012, 3, 2288–2298. [Google Scholar] [PubMed]
- Gagnon, L.; Yücel, M.A.; Boas, D.A.; Cooper, R.J. Further improvement in reducing superficial contamination in NIRS using double short separation measurements. Neuroimage 2014, 85, 127–135. [Google Scholar] [CrossRef] [PubMed]
- Caldwell, M.; Scholkmann, F.; Wolf, U.; Wolf, M.; Elwell, C.; Tachtsidis, I. Modelling confounding effects from extracerebral contamination and systemic factors on functional near-infrared spectroscopy. Neuroimage 2016, 143, 91–105. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Cooper, R.J. Review of recent progress toward a fiberless, whole-scalp diffuse optical tomography system. Neurophotonics 2017, 5, 11012. [Google Scholar] [CrossRef] [PubMed]
- Quaresima, V.; Ferrari, M. Functional Near-Infrared Spectroscopy (fNIRS) for assessing cerebral cortex function during human behavior in natural/social situations: A concise review. Organ. Res. Methods 2016. [Google Scholar] [CrossRef]
- Dalla Mora, A.; Contini, D.; Arridge, S.; Martelli, F.; Tosi, A.; Boso, G.; Farina, A.; Durduran, T.; Martinenghi, E.; Torricelli, A.; et al. Towards next-generation time-domain diffuse optics for extreme depth penetration and sensitivity. Biomed. Opt. Express 2015, 6, 1749–1760. [Google Scholar] [CrossRef] [PubMed]
- Cooper, R.J.; Magee, E.; Everdell, N.; Magazov, S.; Varela, M.; Airantzis, D.; Gibson, A.P.; Hebden, J.C. MONSTIR II: A 32-channel, multispectral, time-resolved optical tomography system for neonatal brain imaging. Rev. Sci. Instrum. 2014, 85, 53105. [Google Scholar] [CrossRef] [PubMed]
- Lapointe, E.; Pichette, J.; Bérubé-Lauzière, Y. A multi-view time-domain non-contact diffuse optical tomography scanner with dual wavelength detection for intrinsic and fluorescence small animal imaging. Rev. Sci. Instrum. 2012, 83, 63703. [Google Scholar] [CrossRef] [PubMed]
- Eda, H.; Oda, I.; Ito, Y.; Wada, Y.; Oikawa, Y.; Tsunazawa, Y.; Takada, M.; Tsuchiya, Y.; Yamashita, Y.; Oda, M.; et al. Multichannel time-resolved optical tomographic imaging system. Rev. Sci. Instrum. 1999, 70, 3595. [Google Scholar] [CrossRef]
- Dolgoshein, B.; Balagura, V.; Buzhan, P.; Danilov, M.; Filatov, L.; Garutti, E.; Groll, M.; Ilyin, A.; Kantserov, V.; Kaplin, V.; et al. Status report on silicon photomultiplier development and its applications. Nucl. Instrum. Methods Phys. Res. Sect. A 2006, 563, 368–376. [Google Scholar] [CrossRef]
- Zimmermann, R.; Braun, F.; Achtnich, T.; Lambercy, O.; Gassert, R.; Wolf, M. Silicon photomultipliers for improved detection of low light levels in miniature near-infrared spectroscopy instruments. Biomed. Opt. Express 2013, 4, 659–666. [Google Scholar] [CrossRef] [PubMed]
- Sanfilippo, D.; Valvo, G.; Mazzillo, M.; Piana, A.; Carbone, B.; Renna, L.; Fallica, P.G.; Agrò, D.; Morsellino, G.; Pinto, M.; et al. Design and development of a fNIRS system prototype based on SiPM detectors. In Proceedings of the SPIE Photonics West 2014-OPTO: Optoelectronic Devices and Materials, San Francisco, CA, USA, 8 March 2014; Volume 8990, p. 899016. [Google Scholar]
- Pifferi, A.; Contini, D.; Dalla Mora, A.; Farina, A.; Spinelli, L.; Torricelli, A. New frontiers in time-domain diffuse optics, a review. J. Biomed. Opt. 2016, 21, 91310. [Google Scholar] [CrossRef] [PubMed]
- Alayed, M.; Deen, M.J. Time-resolved diffuse optical spectroscopy and imaging using solid-state detectors: characteristics, present status, and research challenges. Sensors 2017, 17. [Google Scholar] [CrossRef] [PubMed]
- Martinenghi, E.; Dalla Mora, A.; Contini, D.; Farina, A.; Villa, F.; Torricelli, A.; Pifferi, A. Spectrally-resolved single-photon timing of silicon photomultipliers for time-domain diffuse optics. Photonics J. IEEE 2015, 7. [Google Scholar] [CrossRef]
- Re, R.; Martinenghi, E.; Dalla Mora, A.; Contini, D.; Pifferi, A.; Torricelli, A. Probe-hosted silicon photomultipliers for time-domain functional near-infrared spectroscopy: Phantom and in vivo tests. Neurophotonics 2016, 3, 45004. [Google Scholar] [CrossRef] [PubMed]
- Di Sieno, L.; Dalla Mora, A.; Boso, G.; Tosi, A.; Pifferi, A.; Cubeddu, R.; Contini, D. Diffuse optics using a dual window fast-gated counter. Appl. Opt. 2014, 53, 7394–7401. [Google Scholar] [CrossRef] [PubMed]
- Kalisz, J. Review of methods for time interval measurements with picosecond resolution. Metrologia 2004, 41, 17–32. [Google Scholar] [CrossRef]
- Nissinen, J.; Kostamovaara, J. A high repetition rate CMOS driver for high-energy Sub-ns laser pulse generation in SPAD-based time-of-flight range finding. IEEE Sens. J. 2016, 16, 1628–1633. [Google Scholar] [CrossRef]
- Di Sieno, L.; Nissinen, J.; Hallman, L.; Martinenghi, E.; Contini, D.; Pifferi, A.; Kostamovaara, J.; Dalla Mora, A. Miniaturized pulsed laser source for time-domain diffuse optics routes to wearable devices. J. Biomed. Opt. 2017, 22, 85004. [Google Scholar] [CrossRef] [PubMed]
- Di Sieno, L.; Zouaoui, J.; Hervé, L.; Pifferi, A.; Farina, A.; Martinenghi, E.; Derouard, J.; Dinten, J.-M.; Dalla Mora, A. Time-domain diffuse optical tomography using silicon photomultipliers: A feasibility study. J. Biomed. Opt. 2016, 21, 116002. [Google Scholar] [CrossRef] [PubMed]
- Martinenghi, E.; Di Sieno, L.; Contini, D.; Sanzaro, M.; Pifferi, A.; Dalla Mora, A. Time-resolved single-photon detection module based on silicon photomultiplier: A novel building block for time-correlated measurement systems. Rev. Sci. Instrum. 2016, 87, 73101. [Google Scholar] [CrossRef] [PubMed]
- Hamamatsu Photonics K.K. Available online: http://www.hamamatsu.com (accessed on 5 June 2017).
- Pifferi, A.; Torricelli, A.; Bassi, A.; Taroni, P.; Cubeddu, R.; Wabnitz, H.; Grosenick, D.; Möller, M.; Macdonald, R.; Swartling, J.; et al. Performance assessment of photon migration instruments: The MEDPHOT protocol. Appl. Opt. 2005, 44, 2104–2114. [Google Scholar] [CrossRef] [PubMed]
- Wabnitz, H.; Taubert, D.R.; Mazurenka, M.; Steinkellner, O.; Jelzow, A.; Macdonald, R.; Milej, D.; Sawosz, P.; Kacprzak, M.; Liebert, A.; et al. Performance assessment of time-domain optical brain imagers, part 1: Basic instrumental performance protocol. J. Biomed. Opt. 2014, 19, 86010. [Google Scholar] [CrossRef] [PubMed]
- Martelli, F.; Del Bianco, S.; Ismaelli, A.; Zaccanti, G. Light Propagation through Biological Tissue and Other Diffusive Media: Theory, Solutions, and Software; SPIE: Washington, DC, USA, 2009; ISBN 9780819476586. [Google Scholar]
- Contini, D.; Martelli, F.; Zaccanti, G. Photon migration through a turbid slab described by a model based on diffusion approximation. I. Theory. Appl. Opt. 1997, 36, 4587–4599. [Google Scholar] [CrossRef] [PubMed]
- Martelli, F.; Pifferi, A.; Contini, D.; Spinelli, L.; Torricelli, A.; Wabnitz, H.; Macdonald, R.; Sassaroli, A.; Zaccanti, G. Phantoms for diffuse optical imaging based on totally absorbing objects, part 1: Basic concepts. J. Biomed. Opt. 2013, 18, 66014. [Google Scholar] [CrossRef] [PubMed]
- Pifferi, A.; Torricelli, A.; Cubeddu, R.; Quarto, G.; Re, R.; Konugolu Venkata Sekar, S.; Spinelli, L.; Farina, A.; Martelli, F.; Wabnitz, H. Mechanically switchable solid inhomogeneous phantom for performance tests in diffuse imaging and spectroscopy. J. Biomed. Opt. 2015, 20, 121304. [Google Scholar] [CrossRef] [PubMed]
- Dehghani, H.; White, B.R.; Zeff, B.W.; Tizzard, A.; Culver, J.P. Depth sensitivity and image reconstruction analysis of dense imaging arrays for mapping brain function with diffuse optical tomography. Appl. Opt. 2009, 48, D137–D143. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.-K.; Sun, C.-W.; Lee, P.-L.; Lee, H.-C.; Yang, C.; Jiang, C.-P.; Tong, Y.-P.; Yeh, T.-C.; Hsieh, J.-C. Study of photon migration with various source-detector separations in near-infrared spectroscopic brain imaging based on three-dimensional Monte Carlo modeling. Opt. Express 2005, 13, 8339–8348. [Google Scholar] [CrossRef] [PubMed]
- Picoquant GmbH Datasheet TimeHarp 260. Available online: https://www.picoquant.com/products/category/tcspc-and-time-tagging-modules/timeharp-260-tcspc-and-mcs-board-with-pcie-interface#specification (accessed on 5 June 2017).
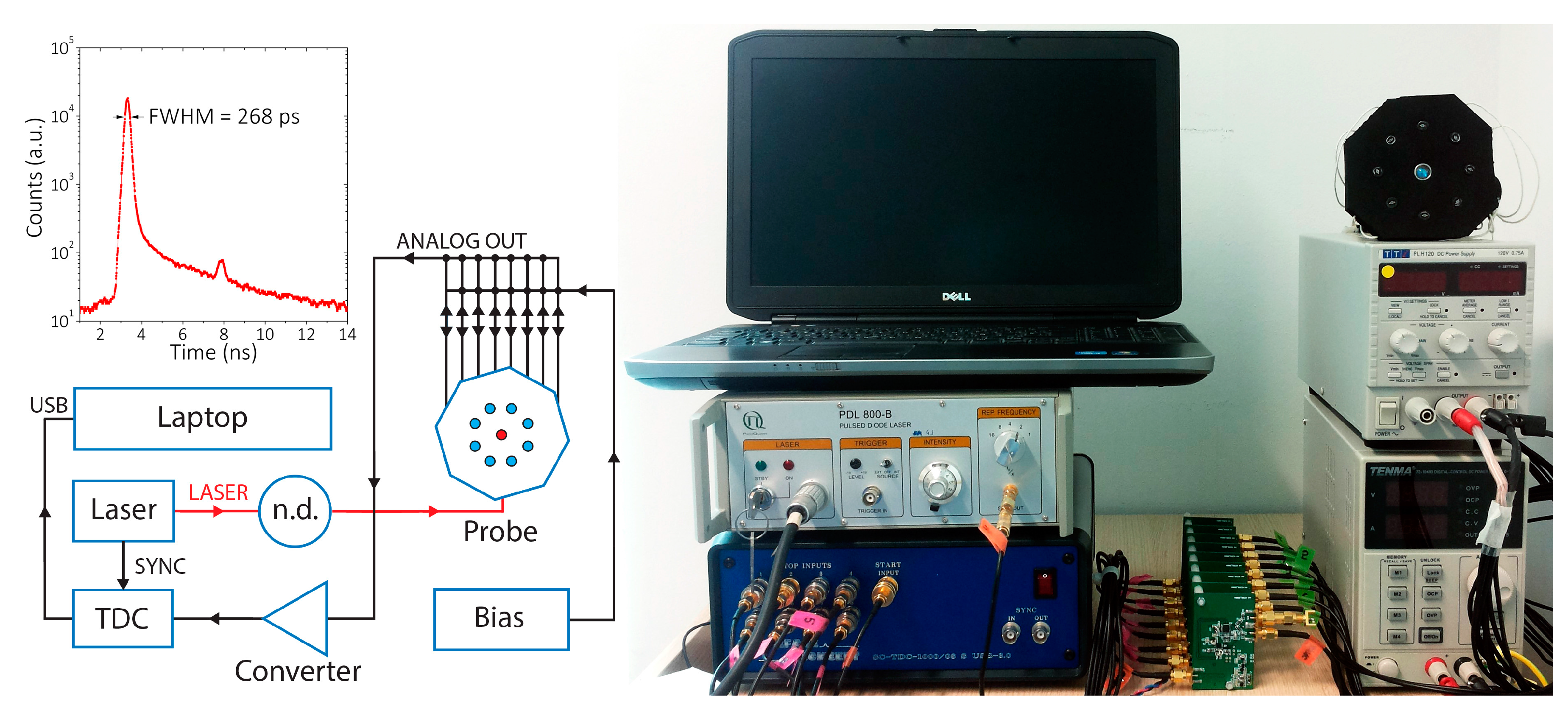
| Building Block | Dimension (mm) |
|---|---|
| Time-to-Digital Converter (TDC) | 237 × 310 × 97 |
| Stack of 9 signal-translation boards | 170 × 65 × 40 |
| Photosensitive chip area | 1.3 × 1.3 |
| SiPM channel | Length = 40 mm; diameter = 6 mm |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farina, A.; Tagliabue, S.; Di Sieno, L.; Martinenghi, E.; Durduran, T.; Arridge, S.; Martelli, F.; Torricelli, A.; Pifferi, A.; Dalla Mora, A. Time-Domain Functional Diffuse Optical Tomography System Based on Fiber-Free Silicon Photomultipliers. Appl. Sci. 2017, 7, 1235. https://doi.org/10.3390/app7121235
Farina A, Tagliabue S, Di Sieno L, Martinenghi E, Durduran T, Arridge S, Martelli F, Torricelli A, Pifferi A, Dalla Mora A. Time-Domain Functional Diffuse Optical Tomography System Based on Fiber-Free Silicon Photomultipliers. Applied Sciences. 2017; 7(12):1235. https://doi.org/10.3390/app7121235
Chicago/Turabian StyleFarina, Andrea, Susanna Tagliabue, Laura Di Sieno, Edoardo Martinenghi, Turgut Durduran, Simon Arridge, Fabrizio Martelli, Alessandro Torricelli, Antonio Pifferi, and Alberto Dalla Mora. 2017. "Time-Domain Functional Diffuse Optical Tomography System Based on Fiber-Free Silicon Photomultipliers" Applied Sciences 7, no. 12: 1235. https://doi.org/10.3390/app7121235
APA StyleFarina, A., Tagliabue, S., Di Sieno, L., Martinenghi, E., Durduran, T., Arridge, S., Martelli, F., Torricelli, A., Pifferi, A., & Dalla Mora, A. (2017). Time-Domain Functional Diffuse Optical Tomography System Based on Fiber-Free Silicon Photomultipliers. Applied Sciences, 7(12), 1235. https://doi.org/10.3390/app7121235