Thermal Buckling of Nanocomposite Stiffened Cylindrical Shells Reinforced by Functionally Graded Wavy Carbon Nanotubes with Temperature-Dependent Properties
Abstract
:1. Introduction
2. Material Properties in FG-CNTRC Cylinders
3. Fundamental Equations
4. Numerical Study of the Buckling Behaviour
- (1)
- The buckling analysis is carried out for material properties at ambient temperature of (i.e., ), and the critical temperature is determined at the first step;
- (2)
- The material properties are updated at the increased temperature of . The buckling analysis is carried out with these new properties, and a new value of critical temperature is determined;
- (3)
- Step 2 is repeated systematically until and the solution converges to the critical temperature with TD material properties.
5. Numerical Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chang, J.S.; Chiu, W.C. Thermal buckling analysis of antisymmetric laminated cylindrical-shell panels. Int. J. Solids Struct. 1991, 27, 1295–1309. [Google Scholar]
- Shariyat, M. Thermal buckling analysis of rectangular composite plates with temperature-dependent properties based on a layerwise theory. Thin-Walled Struct. 2007, 45, 439–452. [Google Scholar] [CrossRef]
- Dai, H.L.; Zheng, H.Y. Buckling and post-buckling analyses for an axially compressed laminated cylindrical shell of FGM with PFRC in thermal environments. Eur. J. Mech. A/Soild 2011, 30, 913–923. [Google Scholar] [CrossRef]
- Ghannadpour, S.A.M.; Ovesy, H.R.; Nassirnia, M. Buckling analysis of functionally graded plates under thermal loadings using the finite strip method. Comput. Struct. 2012, 108, 93–99. [Google Scholar] [CrossRef]
- Jinqiang, L.; Yoshihiro, N.; Zhihua, W. The effects of non-uniform temperature distribution and locally distributed anisotropic properties on thermal buckling of laminated panels. Compos. Struct. 2015, 119, 610–619. [Google Scholar]
- Bhagat, V.S.; Pitchaimani, J.; Murigendrappa, S.M. Buckling and dynamic characteristics of a laminated cylindrical panel under non-uniform thermal load. Steel Compos. Struct. 2016, 22, 1359–1389. [Google Scholar] [CrossRef]
- Katariya, P.V.; Panda, S.K. Thermal buckling and vibration analysis of laminated composite curved shell panel. Aircr. Eng. Aerosp. Technol. 2016, 88, 97–107. [Google Scholar] [CrossRef]
- Tauchert, T.R. Thermal buckling of antisymmetric angle-ply laminates. J. Therm. Stress. 1987, 10, 113–124. [Google Scholar] [CrossRef]
- Avci, A.; Sahin, O.S.; Ataberk, N. Thermal buckling behavior of cross-ply hybrid composite laminates with inclined crack. Compos. Sci. Technol. 2006, 66, 2965–2970. [Google Scholar] [CrossRef]
- Lee, J. Thermally induced buckling of laminated composites by a layerwise theory. Comput. Struct. 1997, 65, 917–922. [Google Scholar] [CrossRef]
- Matsunaga, H. Thermal buckling of angle-ply laminated composite and sandwich panels according to a global higher-order deformation theory. Compos. Struct. 2006, 72, 177–192. [Google Scholar] [CrossRef]
- Baruta, A.; Madencia, E.; Tesslerb, A. Nonlinear thermoelastic analysis of composite panels under non-uniform temperature distribution. Int. J. Solids Struct. 2000, 37, 3681–3713. [Google Scholar] [CrossRef]
- Ghomshei, M.M.M.; Mahmoudi, A. Thermal buckling analysis of cross-ply laminated rectangular panels under nonuniform temperature distribution: A differential quadrature approach. J. Mech. Sci. Technol. 2010, 24, 2519–2527. [Google Scholar] [CrossRef]
- Spallino, R.; Thierauf, G. Thermal buckling optimization of composite laminates by evolution strategies. Comput. Struct. 2000, 78, 691–697. [Google Scholar] [CrossRef]
- Topal, U.; Uzman, U. Thermal buckling load optimization of laminated composite panels. Thin-Walled Struct. 2008, 46, 667–675. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Vosoughi, A.; Sadeghpour, M.; Vosoughi, H. Thermal buckling optimization of temperature-dependent laminated composite skew panels. J. Aerosp. Eng. 2014, 27, 64–75. [Google Scholar] [CrossRef]
- Setoodeh, S.; Abdalla, M.M.; Ijsselmuiden, S.T.; Gürdal, Z. Design of variable-stiffness composite panels for maximum buckling load. Compos. Struct. 2009, 87, 109–117. [Google Scholar] [CrossRef]
- Duong, H.M.; Gong, F.; Liu, P.; Tran, T.Q. Advanced fabrication and properties of aligned carbon nanotube composites: Experiments and modeling. In Carbon Nanotubes—Current Progress of Their Polymer Composites 2016; Berber, M.R., Hafez, I.H., Eds.; InTech: London, UK, 2016; ISBN 978-953-51-2470-2. [Google Scholar]
- Natarajan, B.; Lachman, N.; Lam, T.; Jacobs, D.; Long, C.; Zhao, M.; Wardle, B.L.; Sharma, R.; Liddle, J.A. The evolution of carbon nanotube network structure in unidirectional nanocomposites resolved by quantitative electron tomography. ACS Nano 2015, 9, 6050–6058. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.S. Nonlinear bending of functionally graded carbon nanotube reinforced composite plates in thermal environments. Compos. Struct. 2009, 91, 9–19. [Google Scholar] [CrossRef]
- Shi, D.L.; Feng, X.Q.; Huang, Y.Y.; Hwang, K.C.; Gao, H. The Effect of Nanotube Waviness and Agglomeration on the Elastic Property of Carbon Nanotube-Reinforced Composites. J. Eng. Mater. Technol. ASME 2010, 126, 250–257. [Google Scholar] [CrossRef]
- Sobhaniaragh, B.; Barati, A.H.N.; Hedayati, H. Eshelbye-Mori-Tanaka approach for vibrational behavior of continuously graded carbon nanotube-reinforced cylindrical panels. Compos. Part B Eng. 2012, 43, 1943–1954. [Google Scholar] [CrossRef]
- Mirzaei, M.; Kiani, Y. Thermal buckling of temperature dependent FG-CNT reinforced composite plates. Meccanica 2016, 51, 2185–2201. [Google Scholar] [CrossRef]
- Reddy, J.N. A refined nonlinear theory of plates with transverse shear deformation. Int. J. Solids Struct. 1984, 20, 881–896. [Google Scholar] [CrossRef]
- Nejati, M.; Eslampanah, A.H.; Najafizadeh, M.M. Buckling and Vibration Analysis of Functionally Graded Carbon Nanotube-Reinforced Beam under Axial Load. Int. J. Appl. Mech. 2016, 8. [Google Scholar] [CrossRef]
- Mohammadzadeh, R.; Najafizadeh, M.M.; Nejati, M. Buckling of 2D-FGCylindrical Shells under Combined External Pressure and Axial Compression. Adv. Appl. Math. Mech. 2013, 5, 391–406. [Google Scholar] [CrossRef]
- Suresh, S.; Mortensen, A. Fundamentals of Functionally Graded Materials; The Institute of Materials: London, UK, 1998; LMM-CHAPTER-1998-001. [Google Scholar]
- Nejati, M.; Malekzadehfard, K.; Eslampanah, A.H. Effects of fiber orientation and temperature on natural frequencies of a functionally graded beam reinforced with fiber. J. Mech. Sci. Technol. 2015, 29, 33–63. [Google Scholar] [CrossRef]
- Yas, M.H.; Nejati, M.; Asanjarani, A. Free Vibration Analysis of Continuously Graded Fiber Reinforced Truncated Conical Shell via Third-Order Shear Deformation Theory. J. Solid Mech. 2016, 8, 212–231. [Google Scholar]
- Nejati, M.; Asanjarani, A.; Dimitri, R.; Tornabene, F. Static and Free Vibration Analysis of Functionally Graded Conical Shells Reinforced by Carbon Nanotubes. Int. J. Mech. Sci. 2017, 130, 383–398. [Google Scholar] [CrossRef]
- Nejati, M.; Malekzadehfard, K.; Eslampanah, A.H.; Jafari, S.S. Free Vibration Analysis of Reinforced Composite Functionally Graded Plates with Steady State Thermal Conditions. Lat. Am. J. Solids Struct. 2017, 14, 886–905. [Google Scholar] [CrossRef]
- Kandasamy, R.; Dimitri, R.; Tornabene, F. Numerical study on the free vibration and thermal buckling behavior of moderately thick functionally graded structures in thermal environments. Compos. Struct. 2016, 157, 207–221. [Google Scholar] [CrossRef]
- Kamarian, S.; Salim, M.; Dimitri, R.; Tornabene, F. Free vibration analysis conical shells reinforced with agglomerated Carbon Nanotubes. Int. J. Mech. Sci. 2016, 108–109, 157–165. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Tornabene, F.; Bacciocchi, M.; Dimitri, R. Free vibration of arbitrarily shaped Functionally Graded Carbon Nanotube-reinforced plates. Compos. Part B Eng. 2017, 115, 384–408. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Dimitri, R. Free vibrations of composite oval and elliptic cylinders by the generalized differential quadrature method. Thin-Walled Struct. 2015, 97, 114–129. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Effect of Agglomeration on the natural frequencies of functionally graded carbon nanotube-reinforced laminated composite doubly-curved shells. Compos. Part B Eng. 2016, 89, 187–218. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Higher-order theories for the free vibration of doubly-curved laminated panels with curvilinear reinforcing fibers by means of a local version of the GDQ method. Compos. Part B Eng. 2015, 81, 196–230. [Google Scholar] [CrossRef]
- Liu, G.R.; Wu, T.Y. In-plane vibration analyses of circular arches by the generalized differential quadrature rule. Int. J. Mech. Sci. 2001, 43, 2597–2611. [Google Scholar] [CrossRef]
- Kang, K.; Bert, C.W.; Striz, A.G. Vibration analysis of shear deformable circular arches by the differential quadrature method. J. Sound Vib. 1995, 181, 353–360. [Google Scholar] [CrossRef]
- Karami, G.; Malekzadeh, P. In-plane free vibration analysis of circular arches with varying cross-sections using differential quadrature method. J. Sound Vib. 2004, 274, 777–799. [Google Scholar] [CrossRef]
- De Rosa, M.A.; Franciosi, C. Exact and approximate dynamic analysis of circular arches using DQM. Int. J. Solids Struct. 2000, 37, 1103–1117. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Karami, G. Out-of-plane static analysis of circular arches by DQM. Int. J. Solids Struct. 2003, 40, 6527–6545. [Google Scholar] [CrossRef]
- Viola, E.; Tornabene, F. Vibration analysis of damaged circular arches with varying cross-section. Struct. Integr. Durab. 2005, 1, 155–169. [Google Scholar]
- Tomasiello, S. Differential quadrature method: Application to initial-boundary-value problems. J. Sound Vib. 1998, 218, 573–585. [Google Scholar] [CrossRef]
- Maleki, S.; Tahani, M.; Andakhshideh, A. Transient response of laminated plates with arbitrary laminations and boundary conditions under general dynamic loadings. Arch. Appl. Mech. 2011, 82, 615–630. [Google Scholar] [CrossRef]
- Hong, C.C. Transient responses of magnetostrictive plates by using the GDQ method. Eur. J. Mech. A/Solid 2010, 29, 1015–1021. [Google Scholar] [CrossRef]
- Kurtaran, H. Geometrically nonlinear transient analysis of moderately thick laminated composite shallow shells with generalized differential quadrature method. Compos. Struct. 2015, 125, 605–614. [Google Scholar] [CrossRef]
- Tornabene, F.; Dimitri, R.; Viola, E. Transient dynamic response of generally-shaped arches based on a GDQ-time-stepping method. Int. J. Mech. Sci. 2016, 114, 277–314. [Google Scholar] [CrossRef]
- Tomasiello, S. Stability and accuracy of the iterative differential quadrature method. Int. J. Numer. Methods Eng. 2003, 58, 1277–1296. [Google Scholar] [CrossRef]
- Tomasiello, S. Simulating non-linear coupled oscillators by an iterative differential quadrature method. J. Sound Vib. 2003, 265, 507–525. [Google Scholar] [CrossRef]
- Martone, A.; Faiella, G.; Antonucci, V.; Giordano, M.; Zarrelli, M. The effect of the aspect ratio of carbon nanotubes on their effective reinforcement modulus in an epoxy matrix. Compos. Sci. Technol. 2011, 71, 1117–1123. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminate Composite Plates and Shell. Theory and Analysis; CRC Press LLC: Boca Raton, FL, USA, 2004. [Google Scholar]
- Zhang, L.; Li, X. Buckling and vibration analysis of functionally graded magneto-electro-thermo-elastic circular cylindrical shells. Appl. Math. Model. 2013, 37, 2279–2292. [Google Scholar]
- Wang, Z.X.; Shen, H.S. Nonlinear vibration of nanotube-reinforced composite plates in thermal environments. Comput. Mater. Sci. 2011, 50, 2319–2330. [Google Scholar] [CrossRef]
- Dung, V.D.; Hoa, K.L. Research on nonlinear torsional buckling and post-buckling of eccentrically stiffened functionally graded thin circular cylindrical shells. Compos. Part B Eng. 2013, 51, 300–309. [Google Scholar] [CrossRef]
- Dung, V.D.; Chan, D.Q. Analytical investigation on mechanical buckling of FGM truncated conical shells reinforced by orthogonal stiffeners based on FSDT. Compos. Struct. 2017, 159, 827–841. [Google Scholar] [CrossRef]
- Duc, N.D.; Cong, P.H. Nonlinear postbuckling of an eccentrically stiffened thin FGM plate resting on elastic foundations in thermal environments. Thin-Walled Struct. 2014, 75, 103–112. [Google Scholar]
- Duc, N.D.; Cong, P.H. Nonlinear thermal stability of eccentrically stiffened functionally graded truncated conical shells surrounded on elastic foundations. Eur. J. Mech. A/Solid 2015, 50, 120–131. [Google Scholar] [CrossRef]
- Ventsel, E.; Krauthammer, T. Thin Plates and Shells: Theory: Analysis and Application; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Brush, D.O.; Almorth, B.O. Buckling of Bars, Plates and Shells; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Bagherizadeh, E.; Kiani, Y.; Eslami, M.R. Mechanical buckling of functionally graded material cylindrical shells surrounded by Pasternak elastic foundation. Compos. Struct. 2011, 93, 3063–3071. [Google Scholar] [CrossRef]
- Shu, C. Differential Quadrature and Its Application in Engineering; Springer Science & Business Media: London, UK, 2012. [Google Scholar]
- Nejati, M.; Yas, M.H.; Eslampanah, A.H.; Bagheriasl, M. Extended three-dimensional generalized differential quadrature method: The basic equations and thermal vibration analysis of functionally graded fiber orientation rectangular plates. Mech. Adv. Mater. Struct. 2017, 24, 854–870. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Ubertini, F.; Viola, E. Strong formulation finite element method based on differential quadrature: A survey. Appl. Mech. Rev. 2015, 67, 020801. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Strong and Weak Formulations Based on Differential and Integral Quadrature Methods for the Free Vibration Analysis of Composite Plates and Shells: Convergence and Accuracy. Eng. Anal. Bound. Elem. 2017, in press. [Google Scholar] [CrossRef]
- Shu, C.; Richards, B.E. Parallel simulation of incompressible viscous flows by generalized differential quadrature. Comput. Syst. Eng. 1992, 3, 271–281. [Google Scholar] [CrossRef]
- Shu, C.; Richards, B.E. Application of generalized differential quadrature to solve two-dimensional incompressible Navier-Stokes equations. Int. J. Numer. Methods Fluids 1992, 15, 791–798. [Google Scholar] [CrossRef]
- Quan, J.R.; Chang, C.T. New insights in solving distributed system equations by the quadrature method—I. Analysis. Comput. Chem. Eng. 1989, 13, 779–788. [Google Scholar] [CrossRef]
- Bert, C.; Malik, M. Differential quadrature method in computational mechanics. Appl. Mech. Rev. 1996, 49, 1–27. [Google Scholar] [CrossRef]
- Shu, C.; Chen, W.; Xue, H.; Du, H. Numerical study of grid distribution effect on accuracy of DQ analysis of beams and plates by error estimation of derivative approximation. Int. J. Numer. Methods Eng. 2001, 51, 159–179. [Google Scholar] [CrossRef]
- Mirzavand, B.; Eslami, M.R. Thermal Buckling of Imperfect Functionally Graded Cylindrical Shells Based on the Wan–Donnell Model. J. Therm. Stress. 2006, 29, 37–55. [Google Scholar] [CrossRef]
- Shen, H.S. Functionally Graded Materials: Nonlinear Analysis of Plates and Shells; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Shen, H.S. Thermal postbuckling behavior of functionally graded cylindrical shells with temperature-dependent properties. Int. J. Solids Struct. 2004, 41, 1961–1974. [Google Scholar] [CrossRef]
- Sun, J.; Xu, X.; Lim, C.W. Accurate symplectic space solutions for thermal buckling of functionally graded cylindrical shells. Compos. Part B Eng. 2013, 55, 208–214. [Google Scholar] [CrossRef]
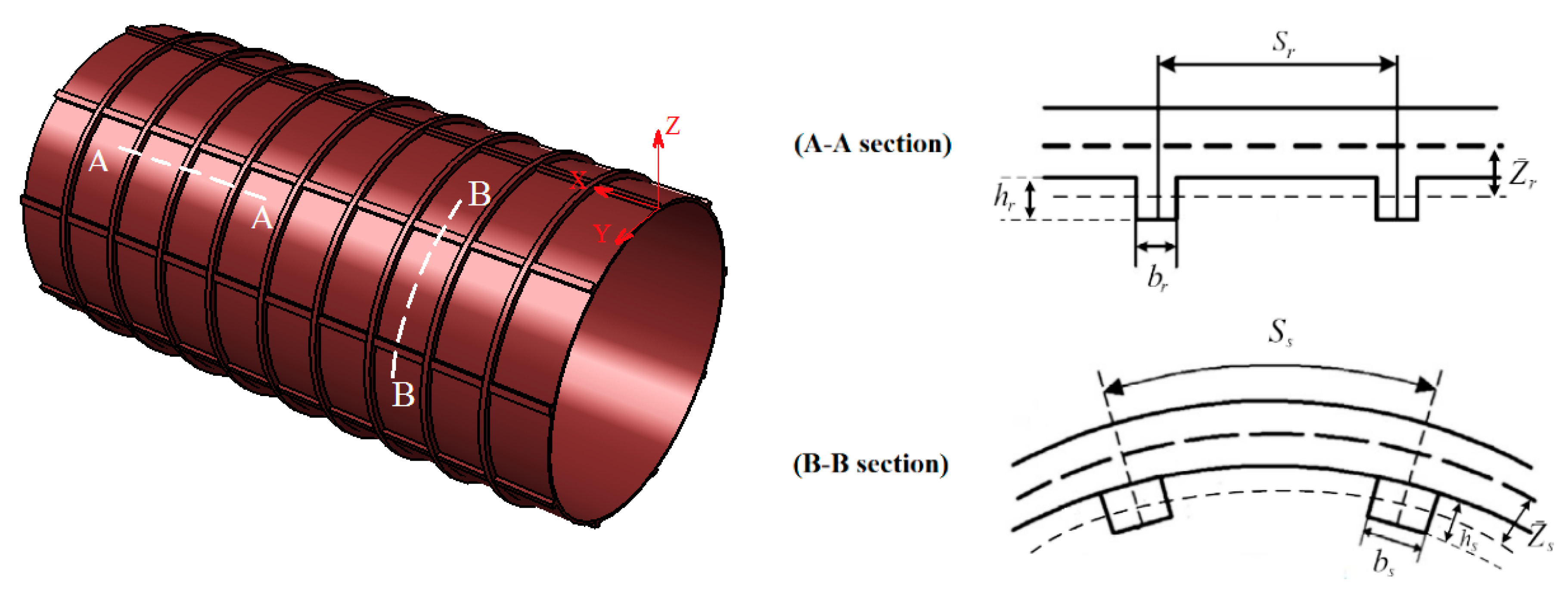
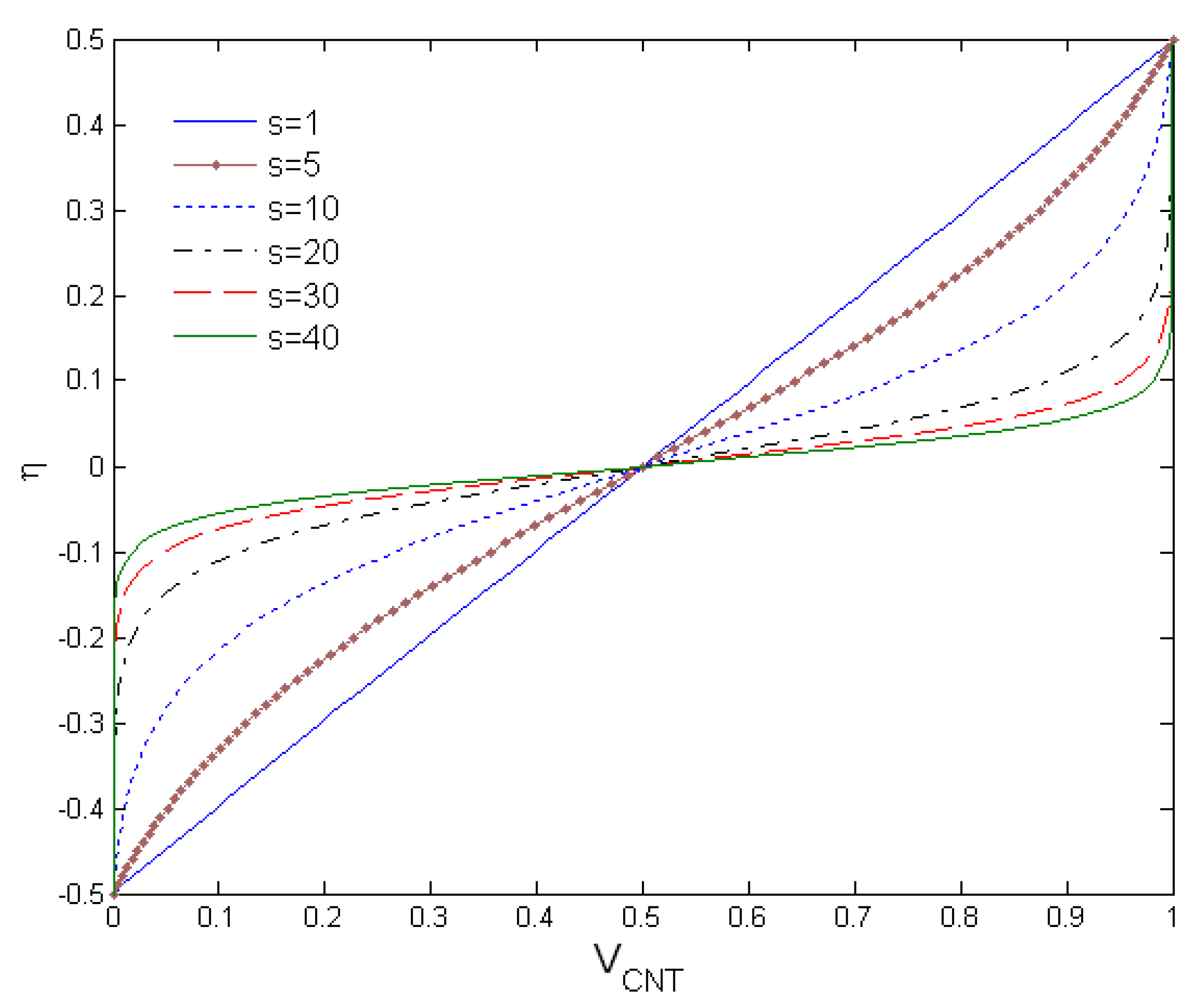
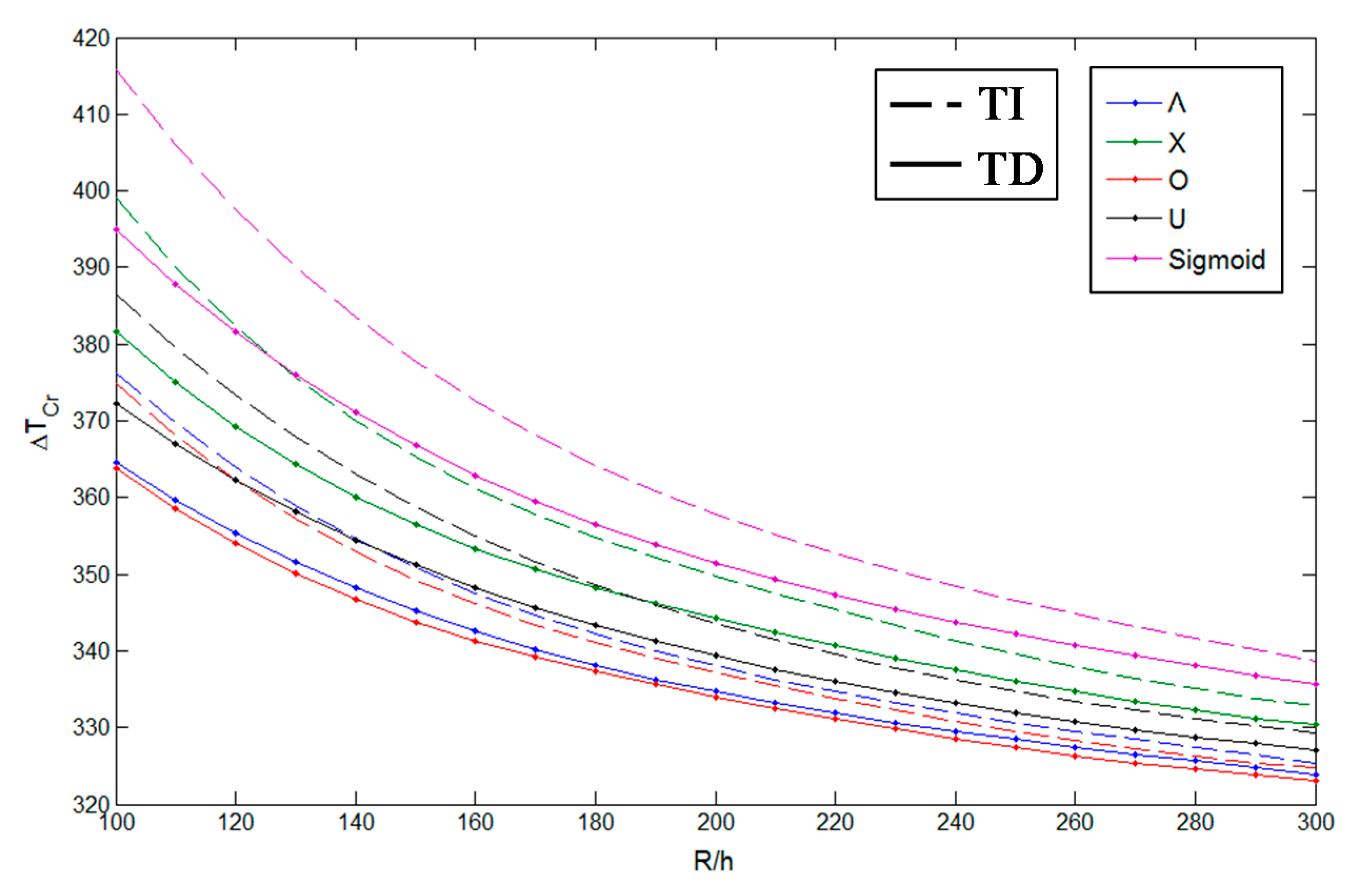
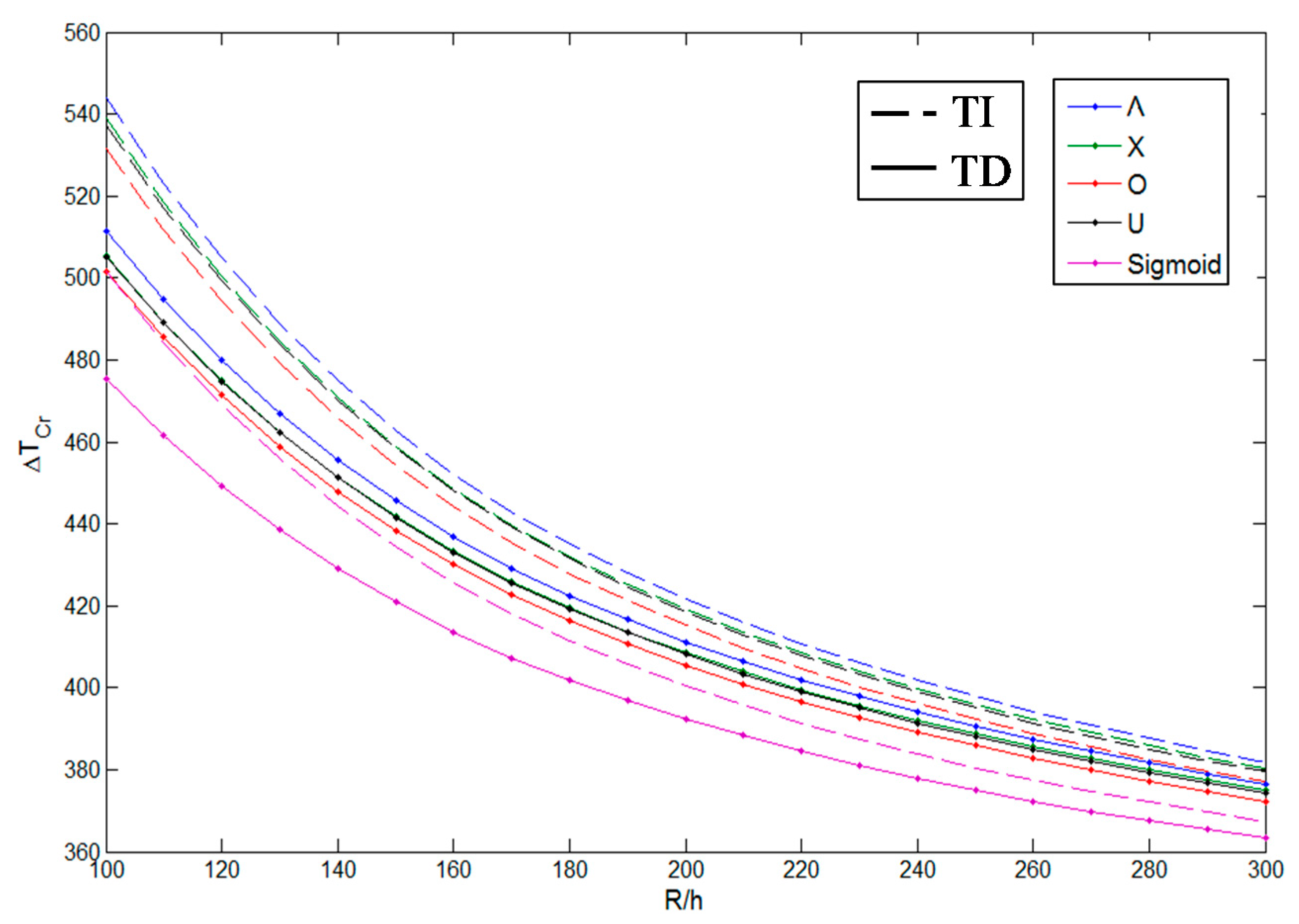
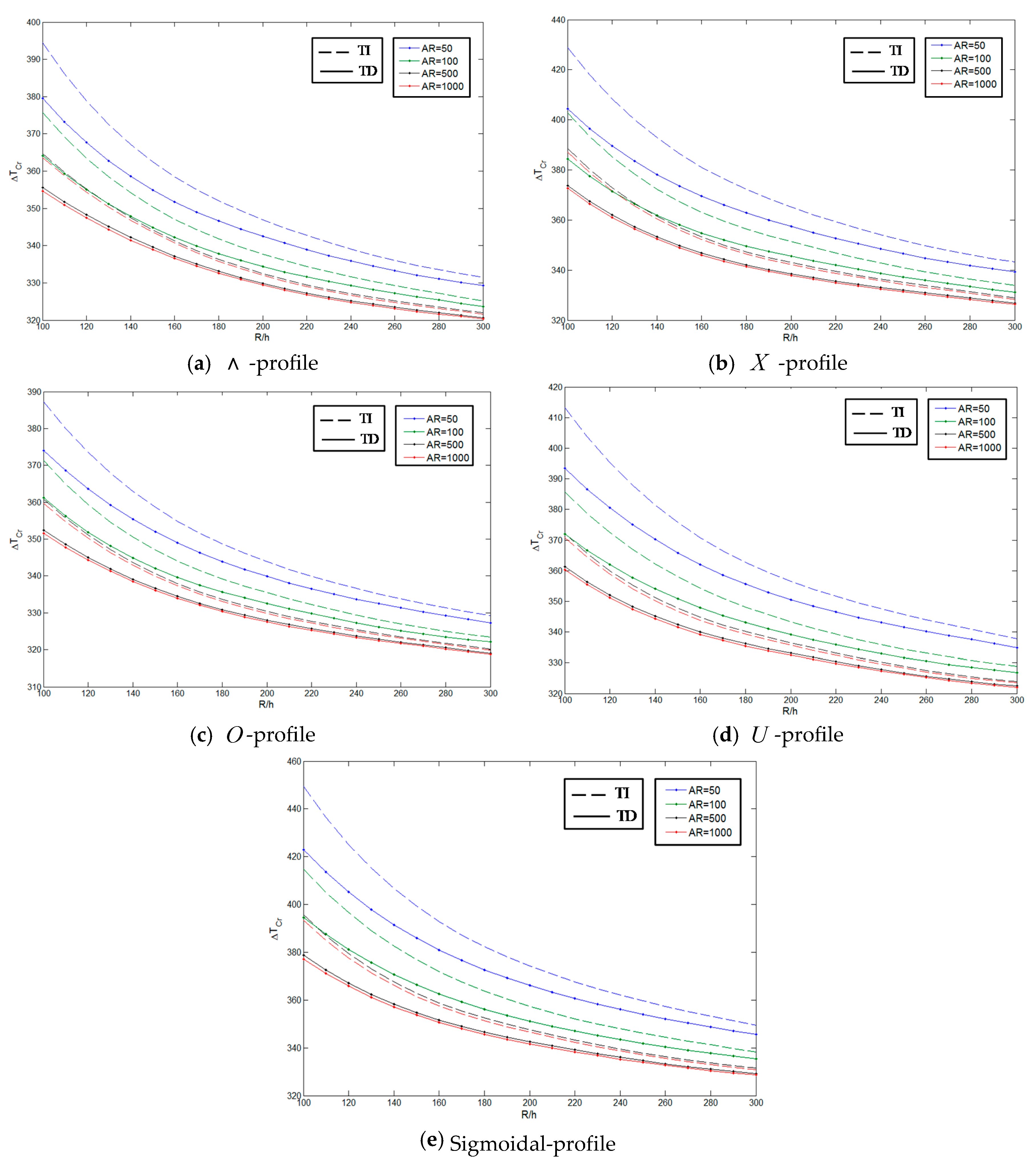
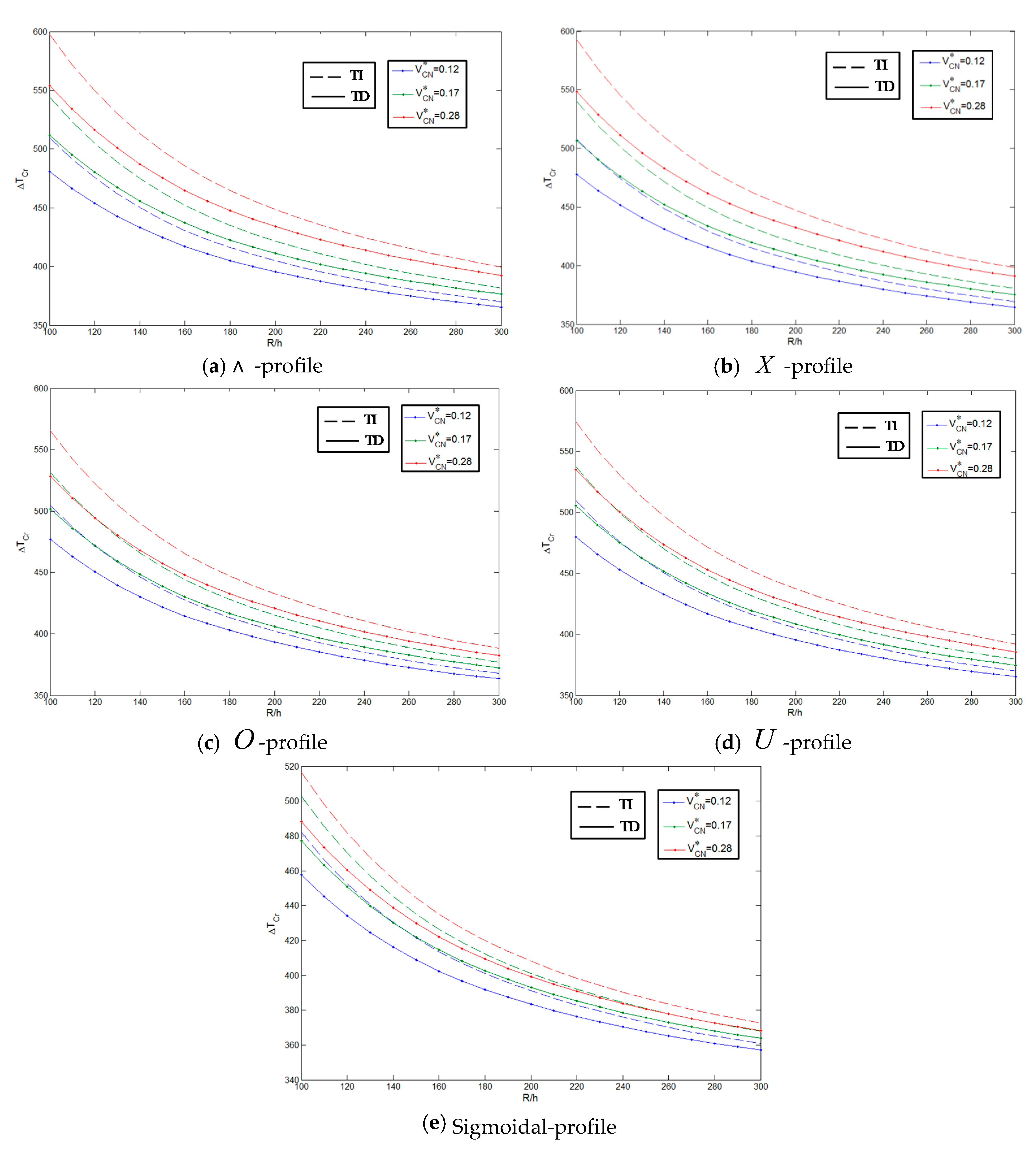
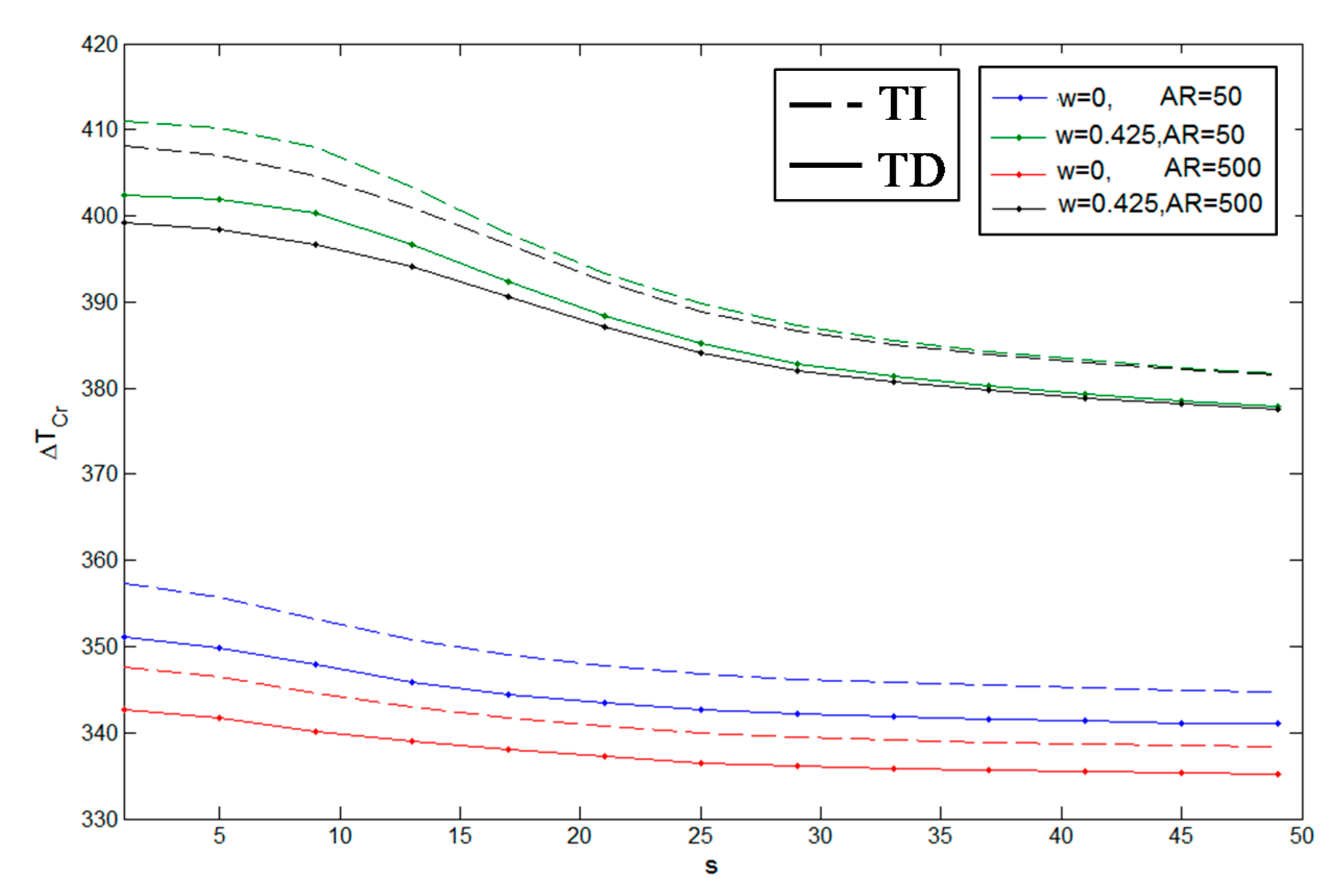
| Method | Pure Metal (Aluminum) | Pure Ceramic (Alumina) | |
|---|---|---|---|
| 0.003 | Present | 55.1114 | 171.2921 |
| [71] | 52.1867 | 181.375 | |
| 0.005 | Present | 91.7741 | 285.2439 |
| [71] | 90.8012 | 289.537 | |
| 0.007 | Present | 128.4551 | 399.2525 |
| [71] | 124.447 | 402.683 | |
| 0.01 | Present | 182.6926 | 567.8284 |
| [71] | 187.33 | 597.253 | |
| 0.012 | Present | 219.6345 | 682.6477 |
| [71] | 216.007 | 688.039 | |
| 0.015 | Present | 273.1372 | 848.9400 |
| [71] | 268.953 | 862.72 |
| p | Method | TD | TI |
|---|---|---|---|
| 0.2 | Present | 354.5263 | 363.8471 |
| [73] | 365.0509 | 378.5620 | |
| [74] | 353.7 | - | |
| 0.5 | Present | 360.8525 | 371.0475 |
| [73] | 372.6016 | 387.4075 | |
| [74] | 360.119 | - | |
| 1 | Present | 369.8812 | 380.9365 |
| [73] | 383.4589 | 399.5912 | |
| [74] | 368.785 | - | |
| 2 | Present | 384.4789 | 395.7673 |
| [73] | 401.2534 | 417.9189 | |
| [74] | 383.244 | - | |
| 3 | Present | 395.9562 | 406.1519 |
| [73] | 415.4941 | 430.7708 | |
| [74] | 394.319 | - | |
| 5 | Present | 413.3029 | 419.3226 |
| [73] | 437.9041 | 447.0620 | |
| [74] | 411.669 | - |
| Profiles | |||||
|---|---|---|---|---|---|
| -profile | = 50 | 355.6195 | 409.7686 | 346.9656 | 446.356 |
| = 100 | 342.6400 | 407.8564 | 338.9678 | 447.5867 | |
| = 500 | 336.1531 | 404.8622 | 334.6581 | 448.6354 | |
| = 1000 | 335.5539 | 404.3232 | 333.9651 | 448.7409 | |
| -profile | = 50 | 375.9555 | 413.1924 | 366.8814 | 450.1936 |
| = 100 | 356.2644 | 409.7816 | 351.3718 | 449.1031 | |
| = 500 | 344.5911 | 404.1034 | 343.0042 | 446.3097 | |
| = 1000 | 343.5005 | 403.1505 | 342.1739 | 445.7818 | |
| -profile | = 50 | 356.0734 | 406.7710 | 343.8665 | 431.8363 |
| = 100 | 341.6468 | 404.8307 | 335.4600 | 432.9287 | |
| = 500 | 334.4003 | 402.2474 | 331.3018 | 432.8269 | |
| = 1000 | 333.7368 | 401.8458 | 330.8940 | 432.7693 | |
| -profile | = 50 | 367.6717 | 410.8309 | 358.5940 | 437.8143 |
| = 100 | 352.3555 | 408.3589 | 344.8158 | 437.9515 | |
| = 500 | 341.3101 | 405.0617 | 336.4925 | 437.7304 | |
| = 1000 | 340.1902 | 404.5425 | 335.6926 | 437.6768 | |
| Sigmoidal-profile | = 50 | 384.5763 | 401.4333 | 375.2713 | 412.1084 |
| = 100 | 366.8624 | 397.5881 | 357.3245 | 411.5575 | |
| = 500 | 354.0331 | 391.1778 | 347.7359 | 408.1837 | |
| = 1000 | 352.8324 | 390.1325 | 346.8347 | 407.5554 | |
| Profiles | |||||
|---|---|---|---|---|---|
| -profile | = 50 | 350.5315 | 401.0361 | 342.4973 | 433.3668 |
| = 100 | 338.9949 | 398.8109 | 335.5588 | 433.8537 | |
| = 500 | 333.2777 | 395.5772 | 331.5408 | 434.1682 | |
| = 1000 | 332.7525 | 395.0126 | 330.9463 | 434.1723 | |
| -profile | = 50 | 367.6339 | 403.9401 | 358.4562 | 436.5301 |
| = 100 | 350.0884 | 400.3097 | 345.5374 | 434.9102 | |
| = 500 | 340.1044 | 394.5435 | 338.5318 | 431.6631 | |
| = 1000 | 339.1756 | 393.5870 | 337.8357 | 431.0726 | |
| -profile | = 50 | 350.8708 | 398.4375 | 339.8652 | 420.952 |
| = 100 | 338.0843 | 396.1992 | 332.5311 | 421.3494 | |
| = 500 | 331.6981 | 393.3625 | 328.9072 | 420.6853 | |
| = 1000 | 331.1157 | 392.9302 | 328.5520 | 420.5504 | |
| -profile | = 50 | 360.7792 | 401.5390 | 352.3864 | 425.8502 |
| = 100 | 347.2884 | 398.8054 | 340.2270 | 425.4899 | |
| = 500 | 337.3306 | 395.3611 | 333.1242 | 424.8383 | |
| = 1000 | 336.3705 | 394.8309 | 332.4403 | 424.7290 | |
| Sigmoidal-profile | = 50 | 376.4948 | 394.1399 | 366.8533 | 403.9861 |
| = 100 | 359.9199 | 390.0668 | 351.1715 | 402.9769 | |
| = 500 | 348.5575 | 383.5699 | 342.9259 | 399.2144 | |
| = 1000 | 347.5143 | 382.5242 | 342.1573 | 398.5467 | |
| Ring and Stringer Number | TD | TI | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| -Profile | -Profile | -Profile | -Profile | Sigmoidal-Profile | -Profile | -Profile | -Profile | -Profile | Sigmoidal-Profile | |
| Unstiffened | 411.2273 | 408.5345 | 405.5307 | 408.2149 | 392.371 | 421.7055 | 419.1132 | 415.1666 | 418.5061 | 400.4704 |
| 459.2519 | 454.296 | 463.9345 | 460.9213 | 439.7066 | 472.9684 | 468.3331 | 476.1383 | 474.1699 | 450.2883 | |
| 432.5377 | 430.5091 | 424.9031 | 429.7281 | 409.3133 | 443.834 | 442.0279 | 435.547 | 440.66 | 418.4353 | |
| 508.4548 | 504.2132 | 515.1755 | 513.4648 | 480.9117 | 515.2078 | 512.2288 | 519.7585 | 519.4056 | 487.7804 | |
| 468.2045 | 463.572 | 477.4953 | 471.558 | 451.0799 | 482.7139 | 478.9919 | 490.3426 | 487.1171 | 462.3776 | |
| 441.8178 | 439.6434 | 433.3342 | 438.8732 | 416.2962 | 453.5255 | 451.6761 | 444.2205 | 450.2502 | 425.8656 | |
| 555.4144 | 553.2414 | 569.8029 | 568.5566 | 520.3784 | 550.762 | 548.6321 | 557.7685 | 557.7418 | 519.8421 | |
| 480.1307 | 475.8978 | 491.597 | 484.6137 | 464.2851 | 494.8228 | 491.5553 | 505.6045 | 500.4459 | 476.2802 | |
| 456.9784 | 454.8882 | 446.7671 | 453.9572 | 427.7454 | 468.3527 | 466.4062 | 457.7995 | 465.3265 | 437.6988 | |
| 595.4563 | 586.3257 | 605.6545 | 604.3793 | 563.6043 | 606.5443 | 606.4783 | 618.9873 | 617.3305 | 571.0981 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nejati, M.; Dimitri, R.; Tornabene, F.; Hossein Yas, M. Thermal Buckling of Nanocomposite Stiffened Cylindrical Shells Reinforced by Functionally Graded Wavy Carbon Nanotubes with Temperature-Dependent Properties. Appl. Sci. 2017, 7, 1223. https://doi.org/10.3390/app7121223
Nejati M, Dimitri R, Tornabene F, Hossein Yas M. Thermal Buckling of Nanocomposite Stiffened Cylindrical Shells Reinforced by Functionally Graded Wavy Carbon Nanotubes with Temperature-Dependent Properties. Applied Sciences. 2017; 7(12):1223. https://doi.org/10.3390/app7121223
Chicago/Turabian StyleNejati, Mohammad, Rossana Dimitri, Francesco Tornabene, and Mohammad Hossein Yas. 2017. "Thermal Buckling of Nanocomposite Stiffened Cylindrical Shells Reinforced by Functionally Graded Wavy Carbon Nanotubes with Temperature-Dependent Properties" Applied Sciences 7, no. 12: 1223. https://doi.org/10.3390/app7121223
APA StyleNejati, M., Dimitri, R., Tornabene, F., & Hossein Yas, M. (2017). Thermal Buckling of Nanocomposite Stiffened Cylindrical Shells Reinforced by Functionally Graded Wavy Carbon Nanotubes with Temperature-Dependent Properties. Applied Sciences, 7(12), 1223. https://doi.org/10.3390/app7121223








