Performance Evaluation of a Novel Propulsion System for the Spherical Underwater Robot (SURIII)
Abstract
1. Introduction
2. Mechanical Design and Analysis
2.1. Inspiration for Design
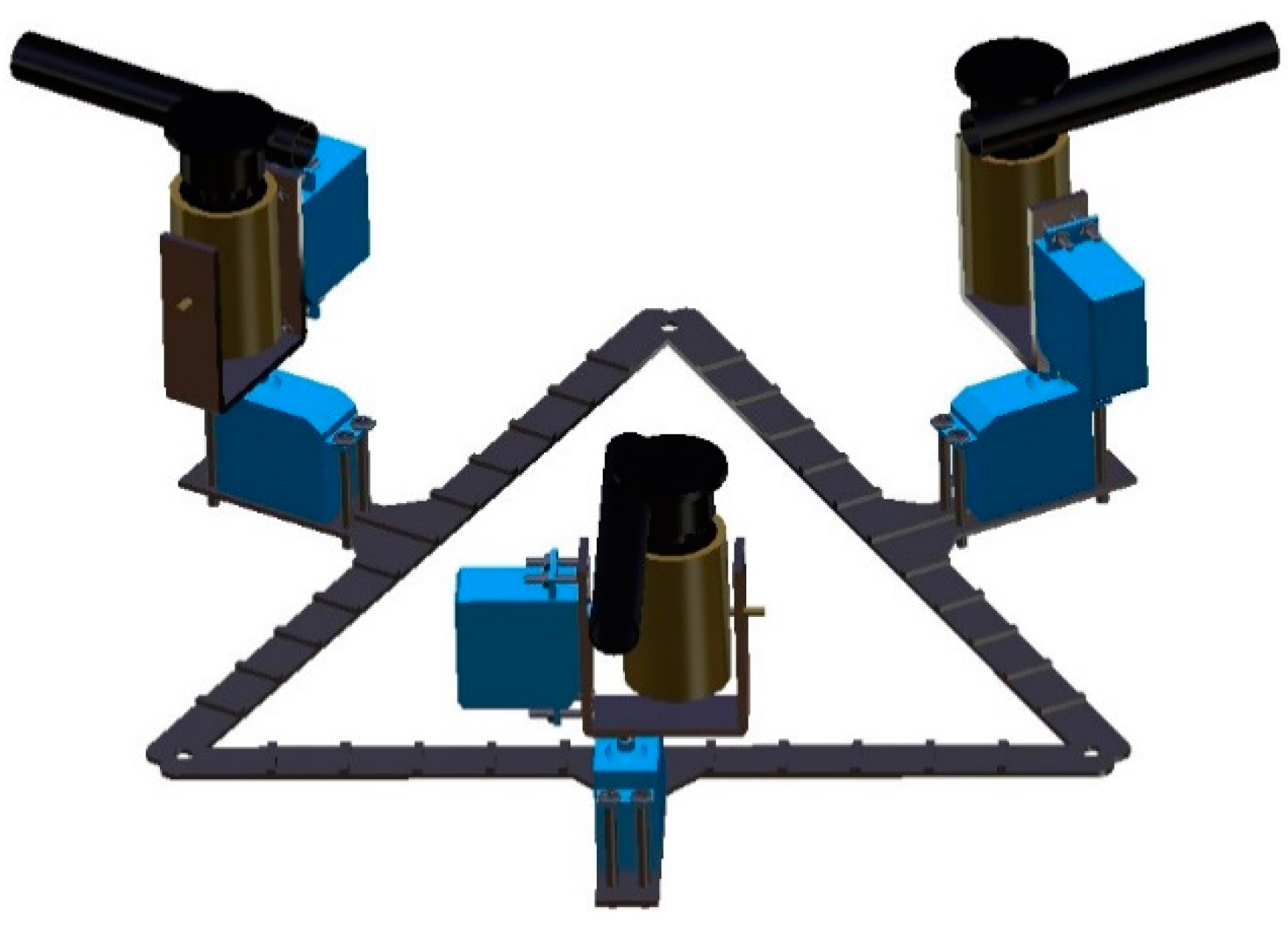
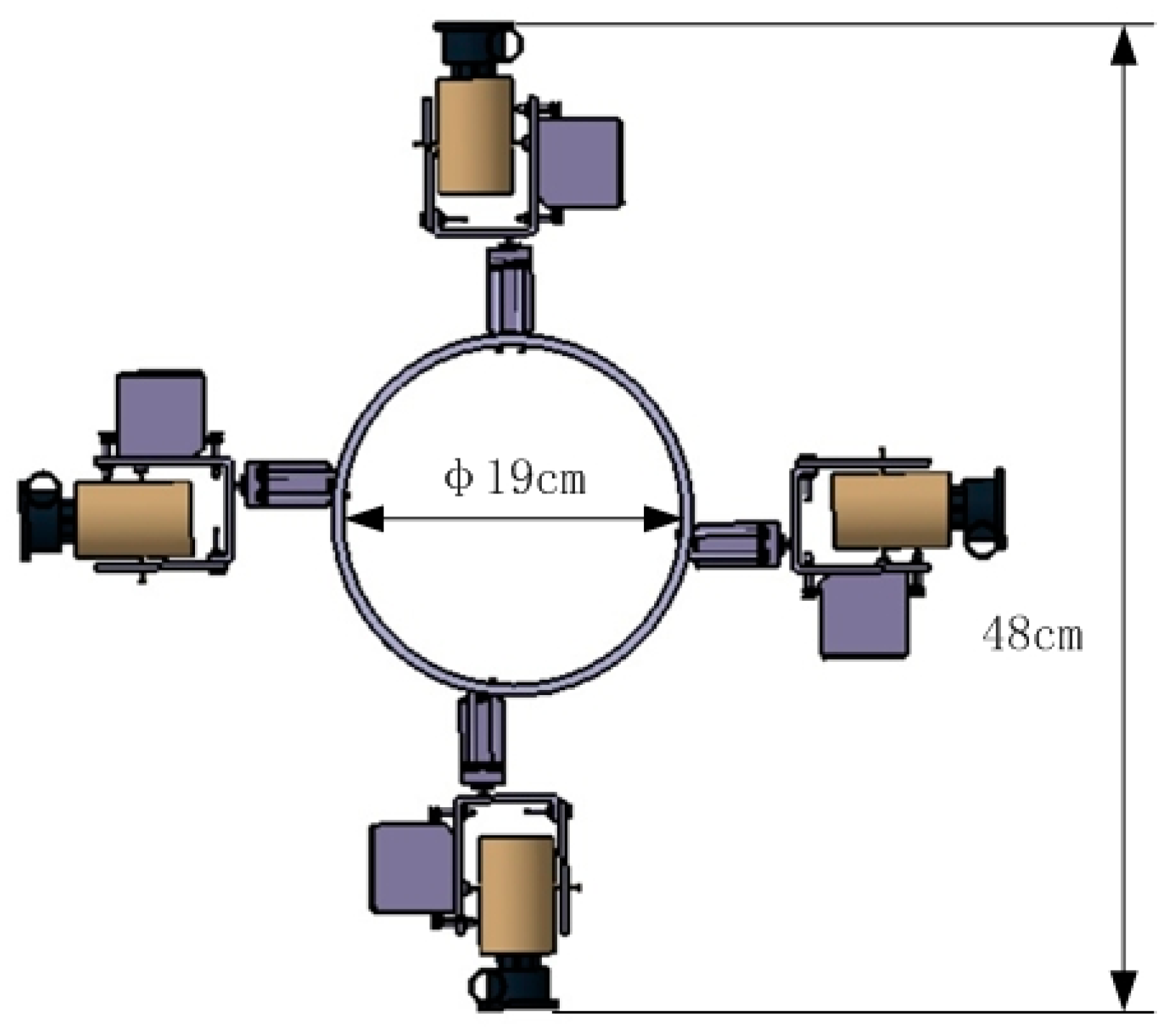
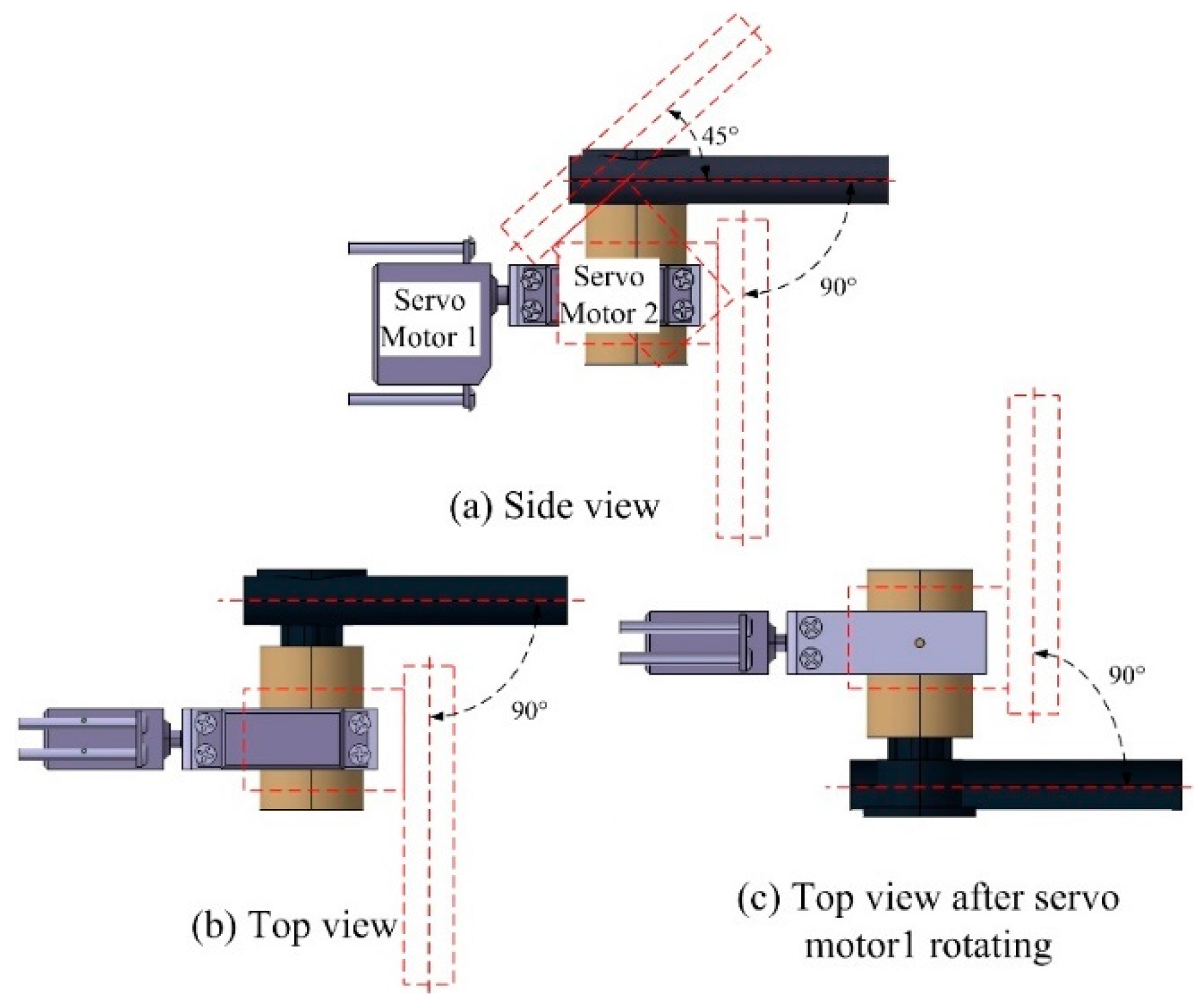
2.2. Mechanical Design and Analysis of Propulsion System
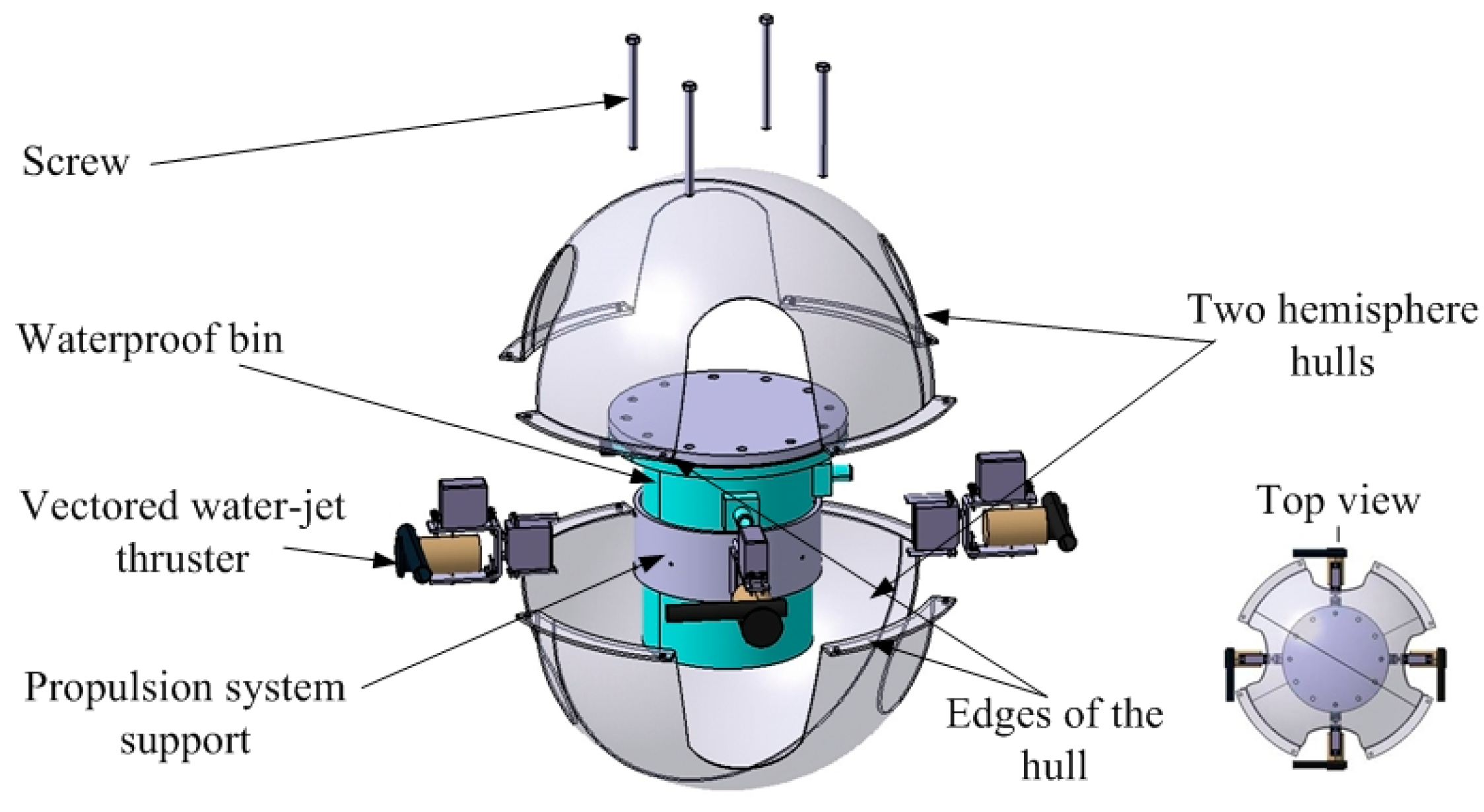
2.3. Structure Design of SURIII
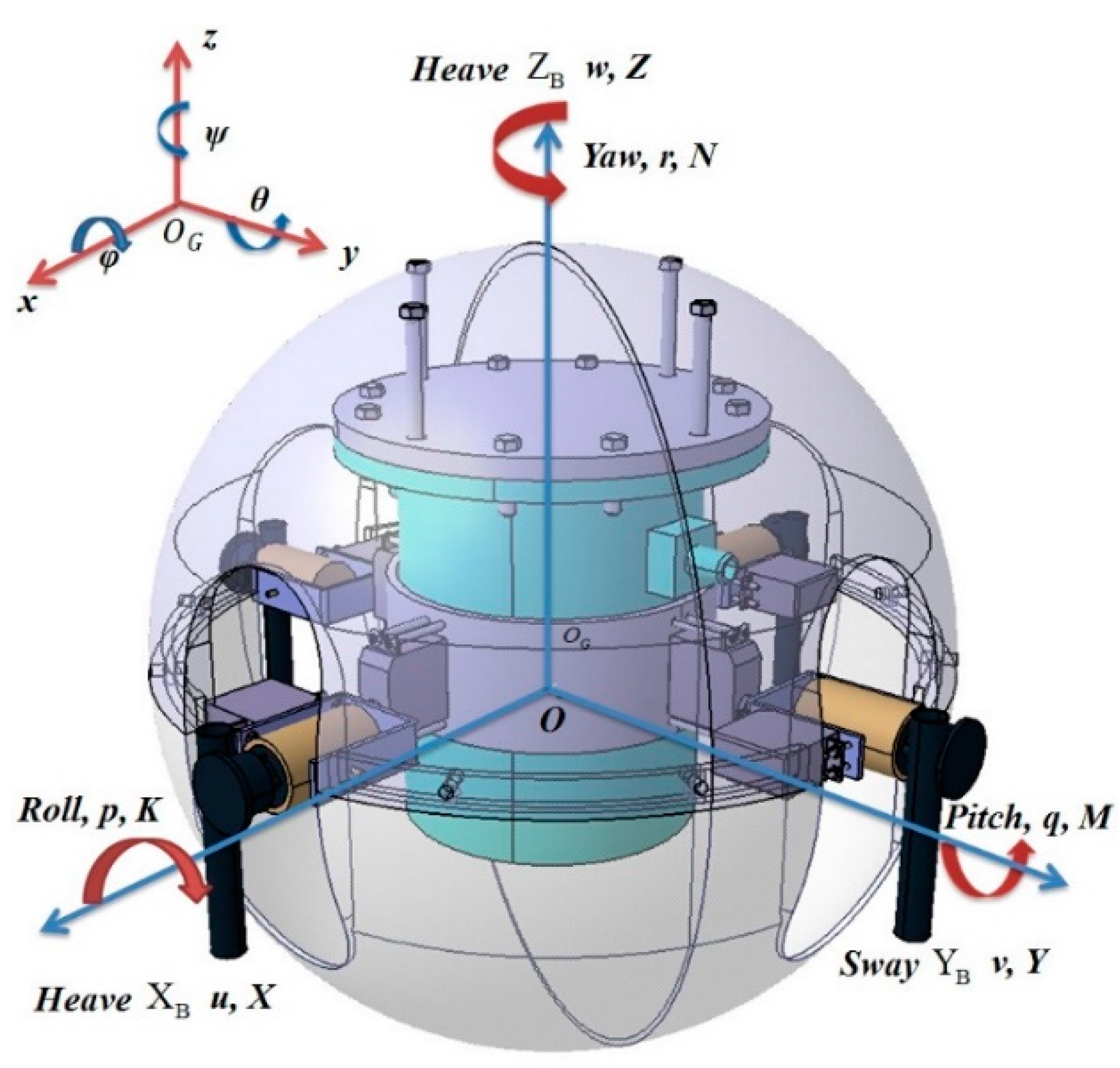
2.4. Motions of SURIII
3. Hydrodynamic Analysis
- SURIII is a spherical robot;
- The flow field is water;
- The temperature of flow field is 20 °C.
3.1. Dynamic Model of SURIII
3.2. Related Parameters
4. CFD Simulation
- Analysis of physical problems and pre-processor of the hydrodynamic model;
- Solver execution;
- Results of the post-processing.
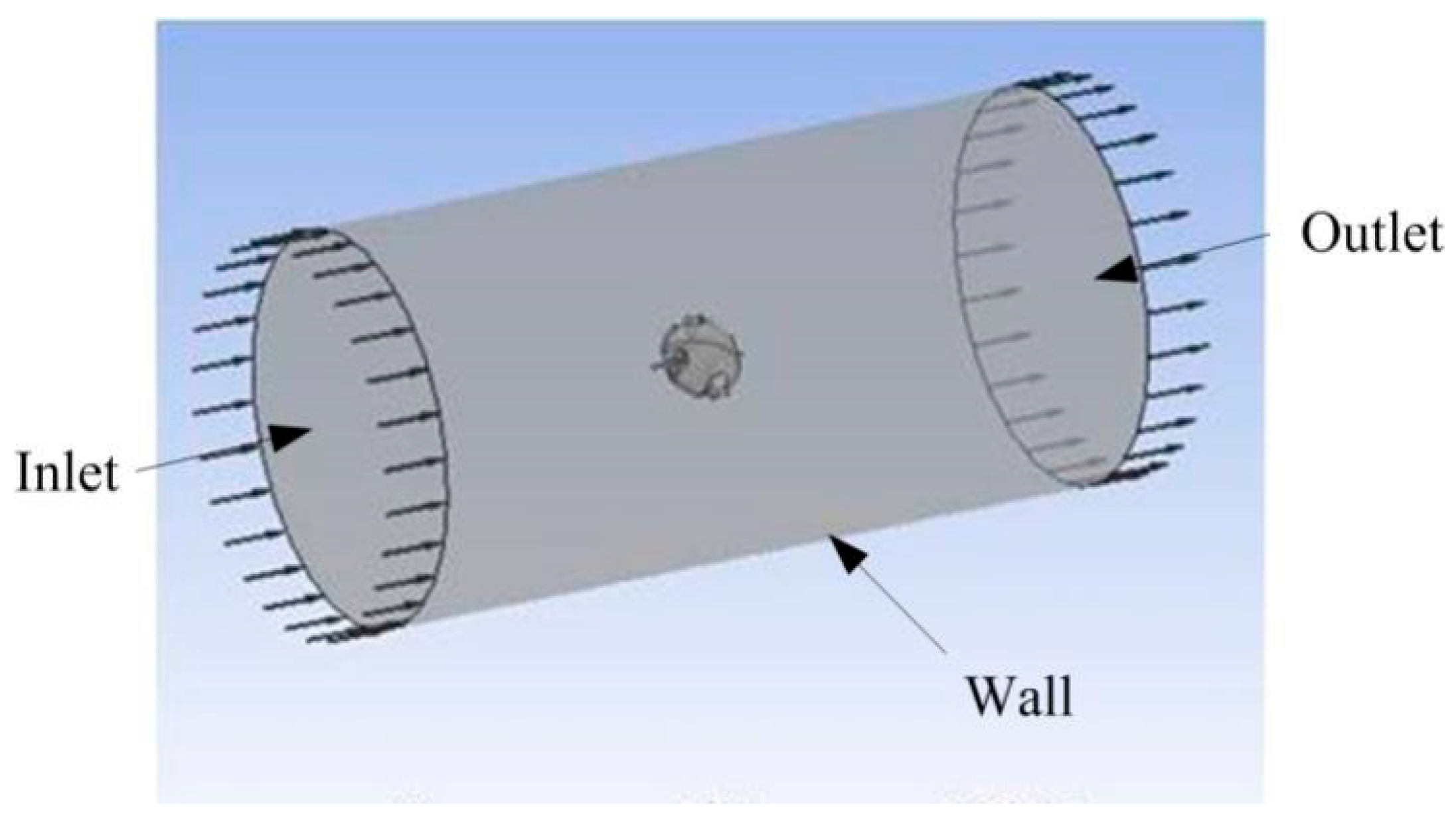
4.1. Pre-Processor of the CFD Simulation
- (1)
- The thruster has some complicated surfaces and their area are very small, so these surfaces are pre-processed as regular surfaces;
- (2)
- Some irregular solids have been changed to cylinder or cuboid shape;
- (3)
- Some parts such as screws and nuts have been omitted. And the simulation models are shown in Figure 12.
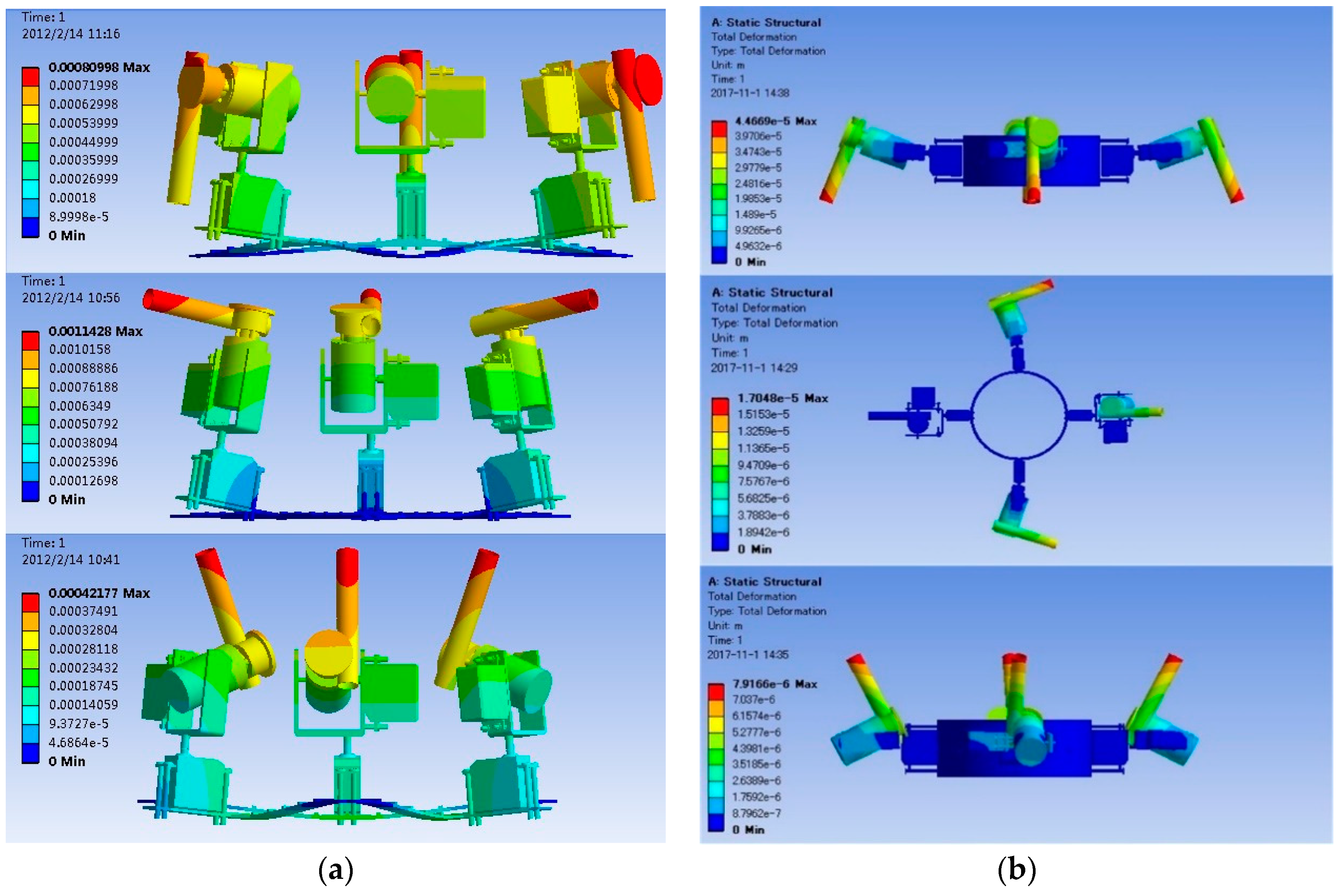
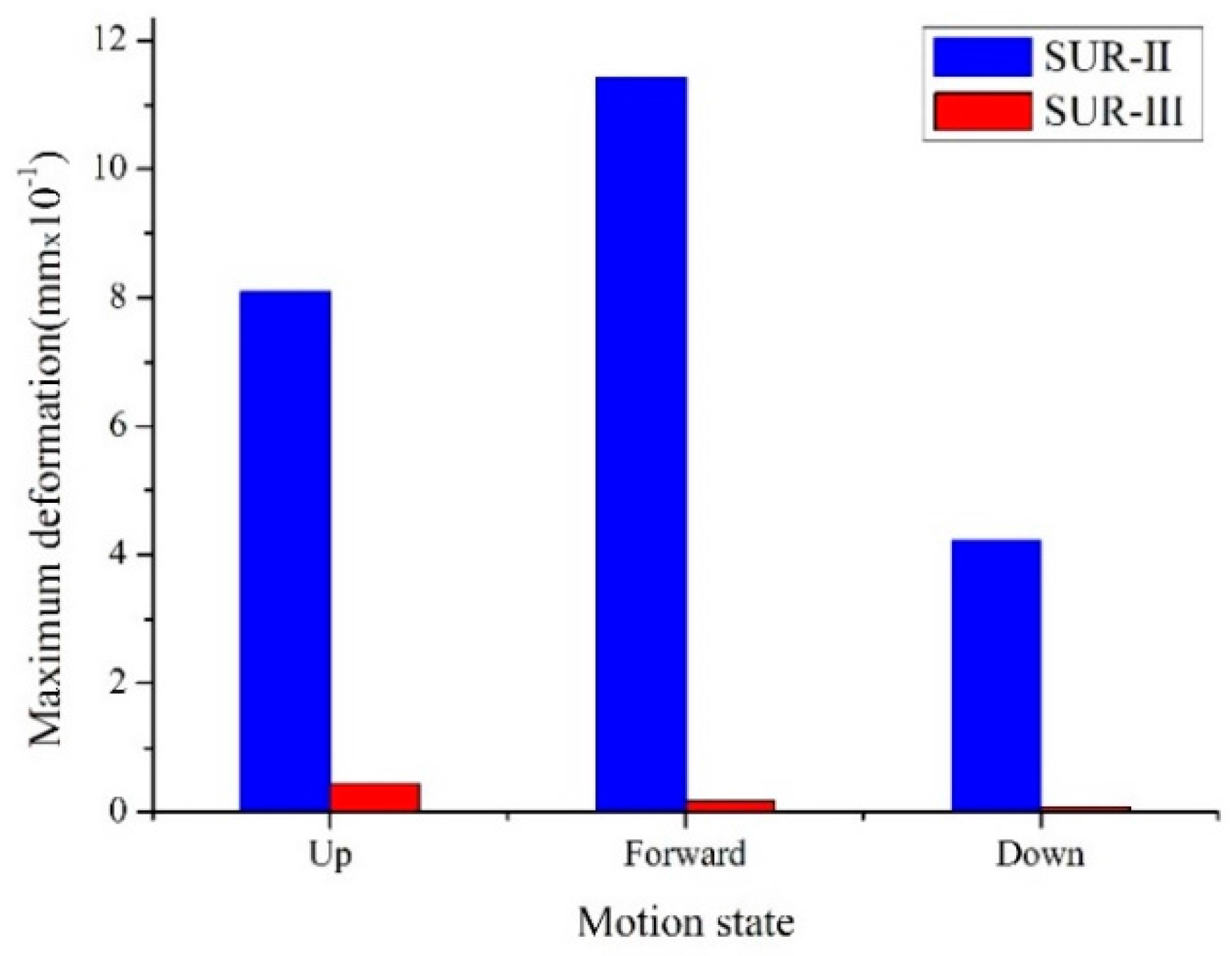
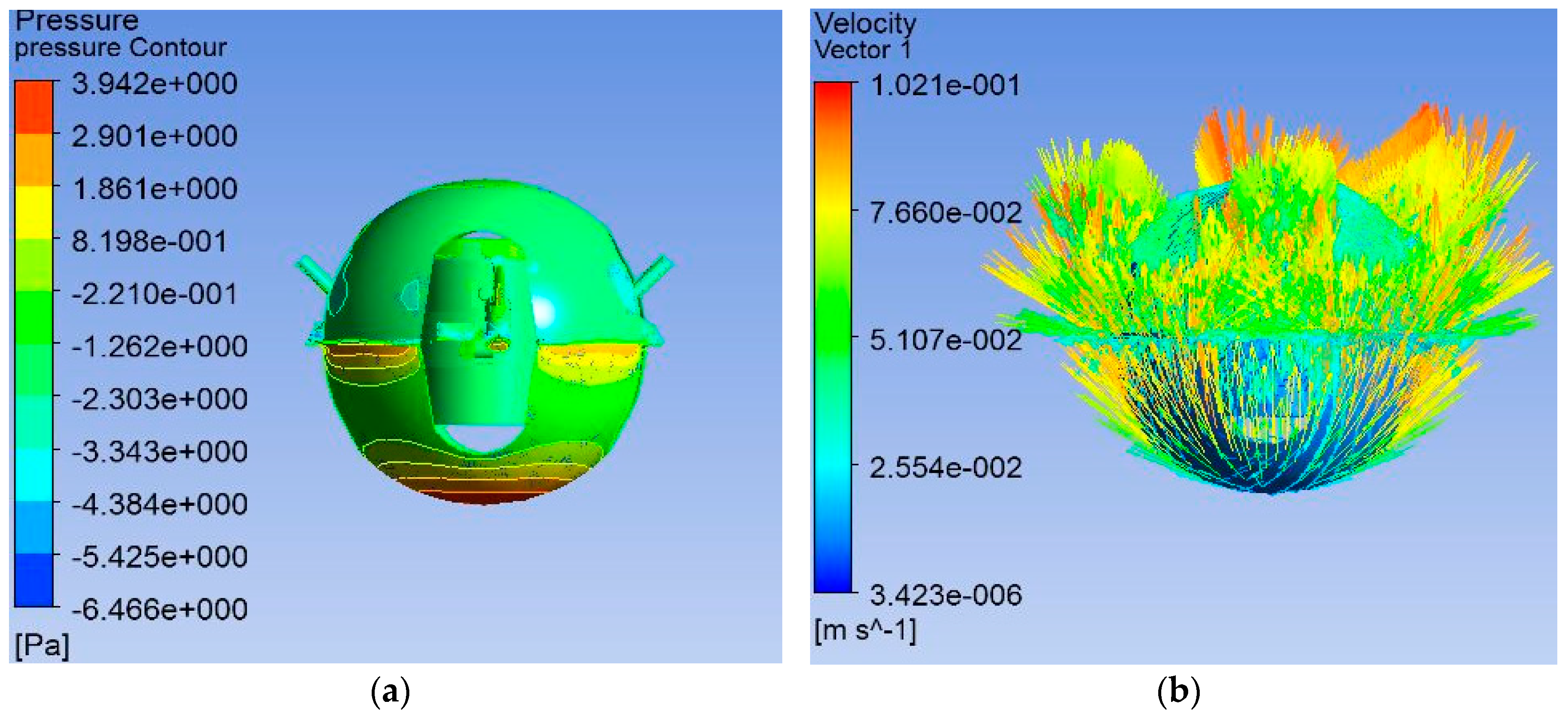
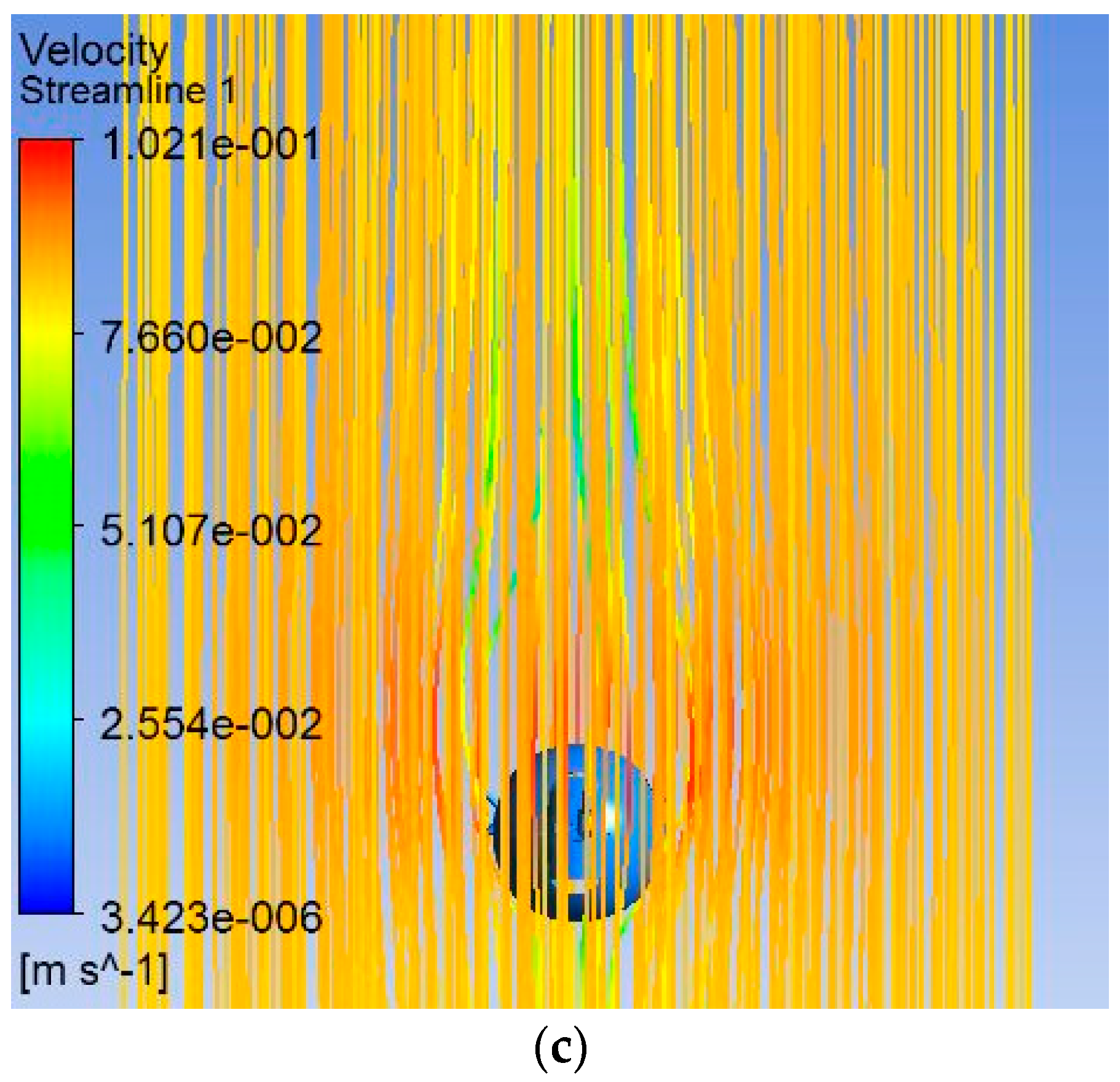
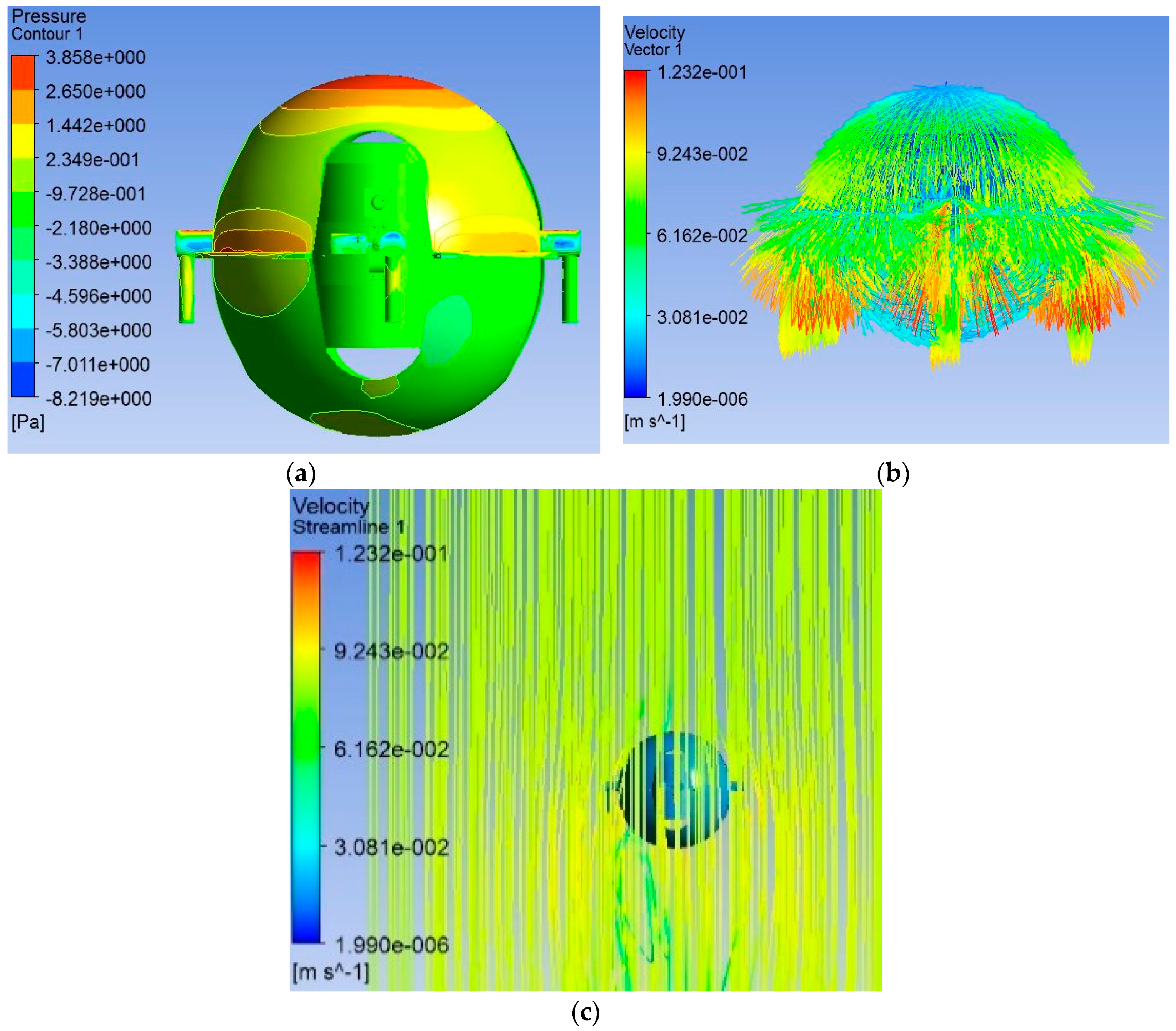
4.2. Results in the Post-Processing
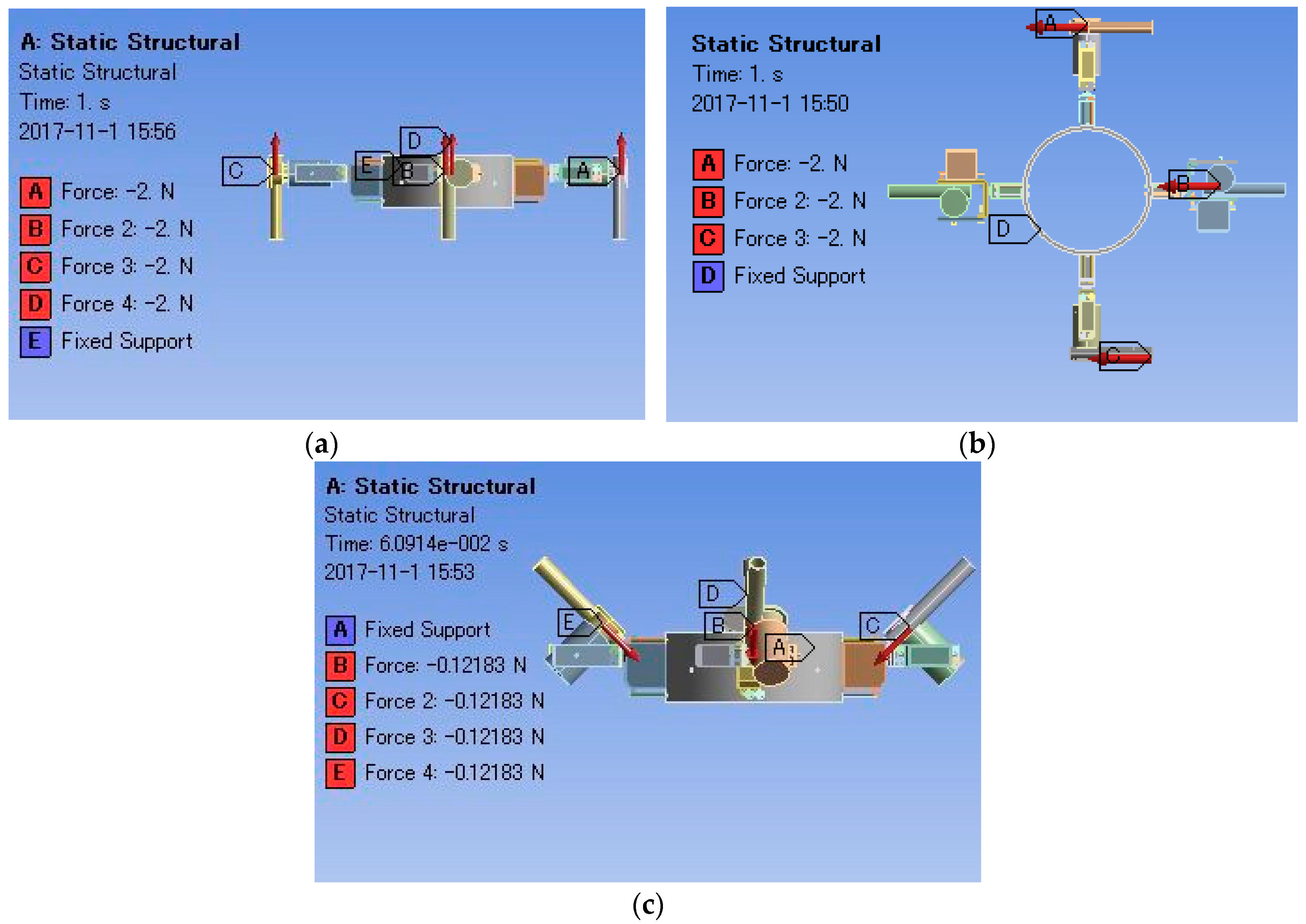
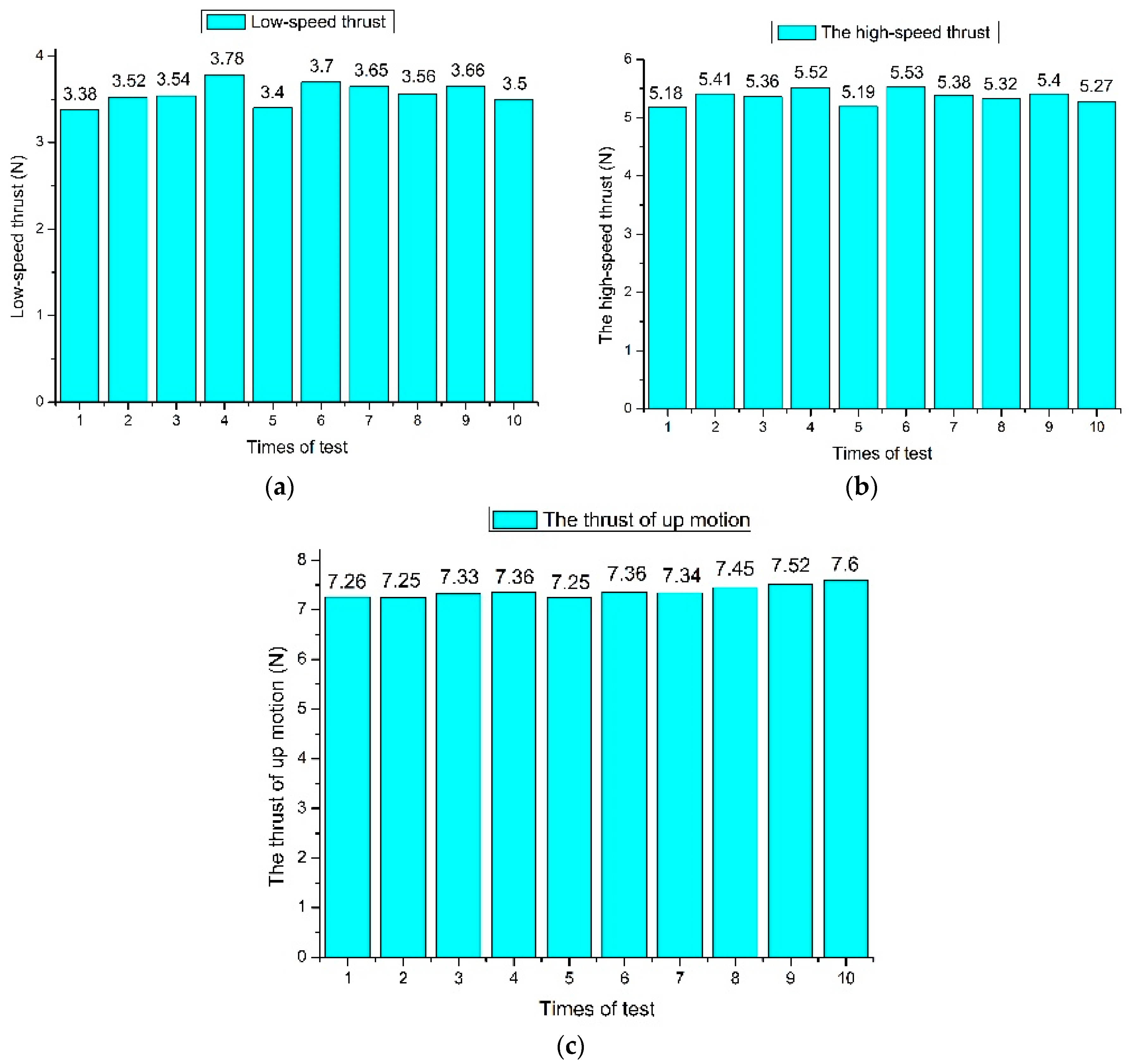
5. Experiments and Results
- Step 1:
- Choose #2 and #4 vectored water-jet thrusters to work (Figure 11c);
- Step 2:
- Adjust the direction of propulsive forces as the Y direction;
- Step 3:
- Set the load cell to obtain 200 values and provide the power supply at 7.2 V;
- Step 4:
- Stop for 30 s and repeat the step 3 and 4 for 10 times.
- Step 1:
- Choose #2, #3 and #4 vectored water-jet thrusters to work (Figure 11a);
- Step 2:
- Adjust the direction of propulsive forces as Y direction;
- Step 3:
- Set the load cell to obtain 200 values and provide the power supply at 7.2 V;
- Step 4:
- Stop for 30 s and repeat the step 3 and 4 for 10 times.
- Step 1:
- Choose #1, #2, #3 and #4 vectored water-jet thrusters to work (Figure 11e);
- Step 2:
- Adjust the direction of propulsive forces as Z direction;
- Step 3:
- Set the load cell to obtain 200 values and provide the power supply at 7.2 V;
- Step 4:
- Stop for 30 s and repeat the step 3 and 4 for 10 times.
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Galerne, E. Epaulard ROV used in NOAA polymetallic sulfide research. Sea Technol. 1983, 24, 40–42. [Google Scholar]
- Russell, B.W.; Veerle, A.I.H.; Timothy, P.L.B.; Bramley, J.M.; Douglas, P.C.; Brian, J.B.; Henry, A.R.; Kirsty, J.M.; Jeffrey, P.; Daniel, R.P.; et al. Autonomous Underwater Vehicles (AUVs): Their past, present and future contributions to the advancement of marine geoscience. Mar. Geol. 2014, 352, 451–468. [Google Scholar]
- Mazumdar, A.; Fittery, A.; Ubellacker, W.; Asada, H.H. A ball-shaped underwater robot for direct inspection of nuclear reactors and other water-filled infrastructure. In Proceedings of the Robotics and Automation (ICRA) 2013 IEEE International Conference, Karlsruhe, Germany, 6–10 May 2013; pp. 3415–3422. [Google Scholar]
- Bhattacharyya, S.; Asada, H.H. Single jet impinging verticial motion analysis of an underwater robot in the vicinity of a submerged surface. In Proceedings of the 2016 IEEE Oceans Conference, Shanghai, China, 10–13 April 2016; pp. 1–8. [Google Scholar]
- Kim, H.J.; Lee, J. Swimming Pattern Generator Based on Diving Beetles for Legged Underwater Robots. Int. J. Mater. Mech. Manuf. 2014, 2, 101–106. [Google Scholar]
- Lin, X.; Guo, S.; Tanaka, K.; Hata, S. Underwater experiments of a water-jet-based spherical underwater robot. In Proceedings of the 2011 IEEE International Conference on Mechatronics and Automation, Beijing, China, 7–10 August 2011; pp. 738–742. [Google Scholar]
- Lin, X.; Guo, S. Development of a spherical underwater robot equipped with multiple vectored water-jet-based thrusters. J. Intell. Robot. Syst. 2012, 67, 307–321. [Google Scholar] [CrossRef]
- Yue, C.; Guo, S.; Li, M.; Li, Y.; Hirata, H.; Ishihara, H. Mechatronic system and experiments of a spherical underwater robot: SUR-II. J. Intell. Robot. Syst. 2015, 80, 325. [Google Scholar] [CrossRef]
- Yue, C.; Guo, S.; Shi, L. Design and performance evaluation of a biomimetic microrobot for the father-son underwater intervention robotic system. Microsyst. Technol. 2016, 22, 831–840. [Google Scholar] [CrossRef]
- Li, Y.; Guo, S.; Yue, C. Preliminary Concept of a Novel Spherical Underwater Robot. Int. J. Mechatron. Autom. 2015, 5, 11–21. [Google Scholar] [CrossRef]
- Li, Y.; Guo, S.; Wang, Y. Design and Characteristics Evaluation of a Novel Spherical Underwater Robot. Robot. Auton. Syst. 2017, 94, 61–74. [Google Scholar] [CrossRef]
- Li, Y.; Guo, S. Communication between Spherical Underwater Robots Based on the Acoustic Communication Methods. In Proceedings of the 2016 IEEE International Conference on Mechatronics and Automation, Harbin, China, 7–10 August 2016; pp. 403–408. [Google Scholar]
- Kim, H.J.; Song, S.H. A turtle-like swimming robot using a smart soft composite (SSC) structure. Smart Mater. Struct. 2012, 22, 14007. [Google Scholar] [CrossRef]
- Yue, C.; Guo, S.; Li, Y.; Li, M. Bio- Inspired robot launching system for a mother-son underwater manipulation task. In Proceedings of the 2014 IEEE International Conference on Mechatronics and Automation, Tianjin, China, 3–6 August 2014; pp. 174–179. [Google Scholar]
- Watson, S.A.; Crutchley, D.J.P.; Green, P.N. The design and technical challenges of a micro-autonomous underwater vehicle AUV. In Proceedings of the 2011 IEEE/ICMA International Conference on Mechatronics and Automation, Beijing, China, 7–10 August 2011; pp. 567–572. [Google Scholar]
- Waston, S.A.; Green, P.N. Propulsion System for Micro-Autonomous Underwater Vehicles (μAUVs). In Proceedings of the 2010 IEEE Conference on Robotics, Automation and Mechatronics, Singapore, 28–30 June 2010; pp. 435–440. [Google Scholar]
- Fittery, A.; Mazumdar, A.; Lozano, M.; Asada, H.H. Omni-Egg: A smooth, spheroidal, appendage free underwater robot capable of 5 DOF motions. In Proceedings of the IEEE Oceans, Hampton Roads, VA, USA, 14–19 October 2012; pp. 1–5. [Google Scholar]
- Guo, S.; Du, J.; Ye, X.; Gao, H.; Gu, Y. Realtime adjusting control algorithm for the spherical underwater robot. Inf. Int. Interdiscip. J. 2010, 13, 2021–2029. [Google Scholar]
- Guo, S.; Du, J.; Ye, X.; Yan, R.; Gao, H. The computational design of a water-jet propulsion spherical underwater vehicle. In Proceedings of the 2011 IEEE International Conference on Mechatronics and Automation, Beijing, China, 7–10 August 2011; pp. 2375–2379. [Google Scholar]
- Gemmell, B.J.; Costello, J.H.; Colin, S.P.; Stewart, C.J.; Dabiri, J.O.; Tfti, D.; Priya, S. Passive energy recapture in jellyfish contributes to propulsive advantage over other metazoans. Proc. Natl. Acad. Sci. USA 2013, 110, 17904–17909. [Google Scholar] [CrossRef] [PubMed]
- Yue, C.; Guo, S.; Shi, L. Hydrodynamic Analysis of the Spherical Underwater Robot SUR-II. Int. J. Adv. Robot. Syst. 2013, 10, 1–12. [Google Scholar] [CrossRef]
- Jiang, X.; Feng, S.; Wang, L. Unmanned Underwater Robot; Liaoning Science and Technology Publishing House: Shengyang, China, 2000. [Google Scholar]
- Fossen, T.I. Guidance and Control of Ocean Vehicles; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1994. [Google Scholar]
- Lin, X.; Guo, S.; Tanaka, K.; Hata, S. Development and Evaluation of a Vectored Water-jet-based Spherical Underwater Vehicle. Information 2010, 13, 1985–1998. [Google Scholar]
- Houghton, E.L.; Carpenter, P.W. Aerodynamics for Engineering Students, 5th ed.; Butterworth-Heinemann: Oxford, UK, 2013; pp. 8–15. [Google Scholar]
- Ceylan, K.; Altunbas, A.; Kelbaliyez, G. A new model for estimation of drag force in the flow of Newtonian fluids around rigid or deformable particles. Powder Technol. 2011, 119, 250–256. [Google Scholar] [CrossRef]
- Kundu, P.K.; Ira, M.C.; David, R.D. Fluid Mechanics, 5th ed.; Academic Press: Cambridge, MA, USA, 2012; pp. 4251–4472. [Google Scholar]







| DoF | Surge | Sway | Heave | Roll | Pitch | Yaw |
|---|---|---|---|---|---|---|
| Utilization ratio | 100% | 31% | 96% | 33% | 7% | 100% |
| Re | Re < 104 | 104 < Re < 3 × 105 | 3 × 105 < Re < 106 |
|---|---|---|---|
| Cd | 24/Re + 6.48 × Re−0.573 + 0.36 | 0.4 | 0.4 |
| Cd | 30/Re + 0.46 | 0.46 | 0.46 |
| Cd | 24/Re + (1 + 0.0654 Re2/3)2/3 | 0.4 | 0.40 |
| Cd | (0.325 + (0.124 + 24/Re1/2)) | - | - |
| Cd | (0.63 + 4.8 × Re−0.5)2 | 0.4 | - |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, S.; Guo, S. Performance Evaluation of a Novel Propulsion System for the Spherical Underwater Robot (SURIII). Appl. Sci. 2017, 7, 1196. https://doi.org/10.3390/app7111196
Gu S, Guo S. Performance Evaluation of a Novel Propulsion System for the Spherical Underwater Robot (SURIII). Applied Sciences. 2017; 7(11):1196. https://doi.org/10.3390/app7111196
Chicago/Turabian StyleGu, Shuoxin, and Shuxiang Guo. 2017. "Performance Evaluation of a Novel Propulsion System for the Spherical Underwater Robot (SURIII)" Applied Sciences 7, no. 11: 1196. https://doi.org/10.3390/app7111196
APA StyleGu, S., & Guo, S. (2017). Performance Evaluation of a Novel Propulsion System for the Spherical Underwater Robot (SURIII). Applied Sciences, 7(11), 1196. https://doi.org/10.3390/app7111196






