Thickness Dependence of Switching Behavior in Ferroelectric BiFeO3 Thin Films: A Phase-Field Simulation
Abstract
1. Introduction
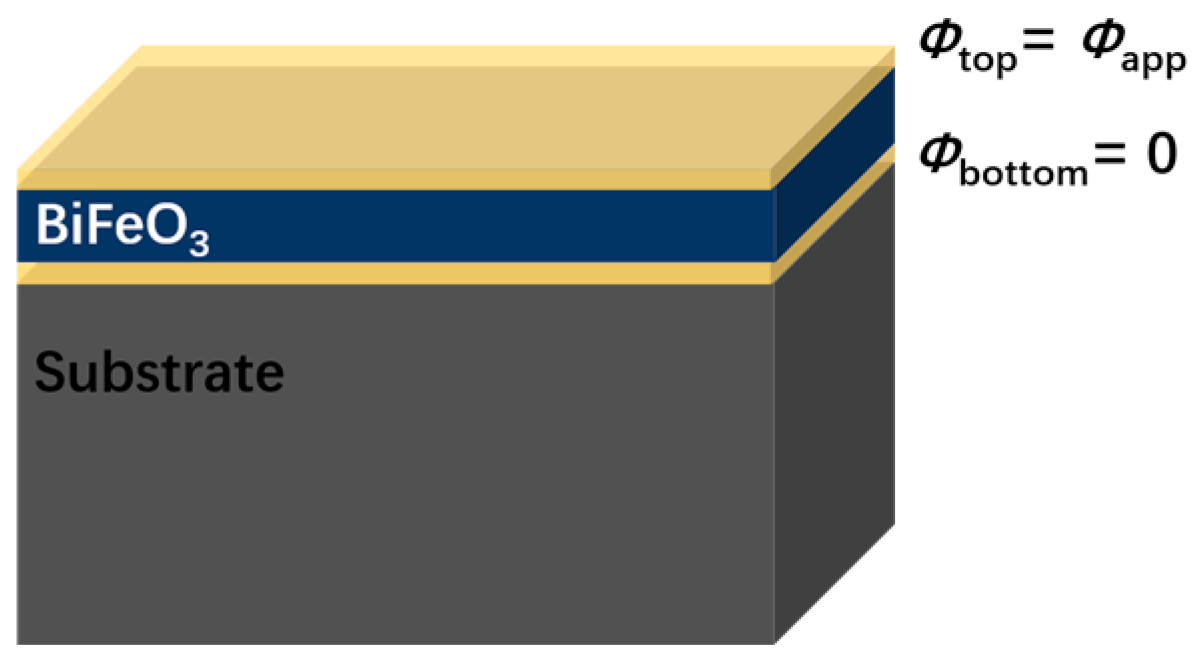
2. The Phase-Field Model
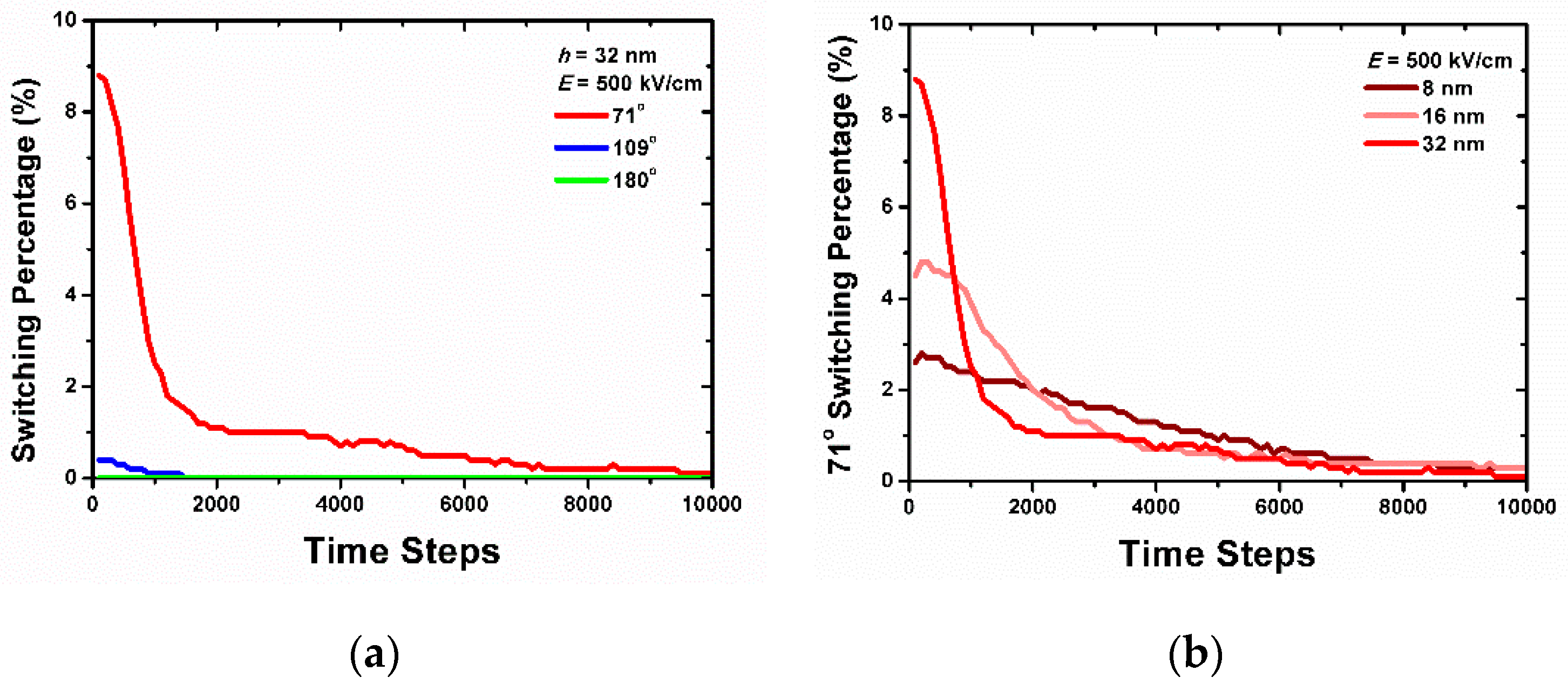
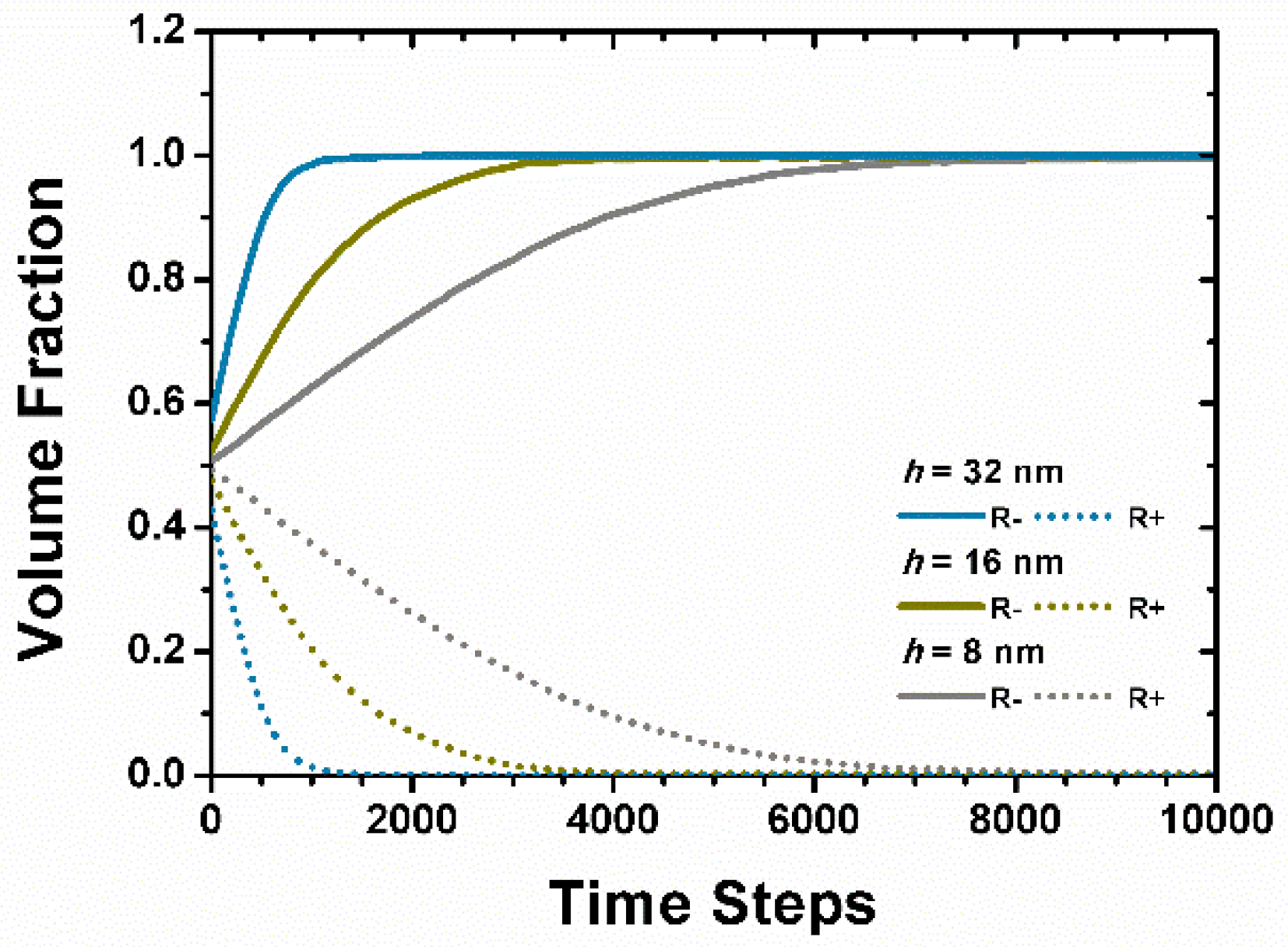
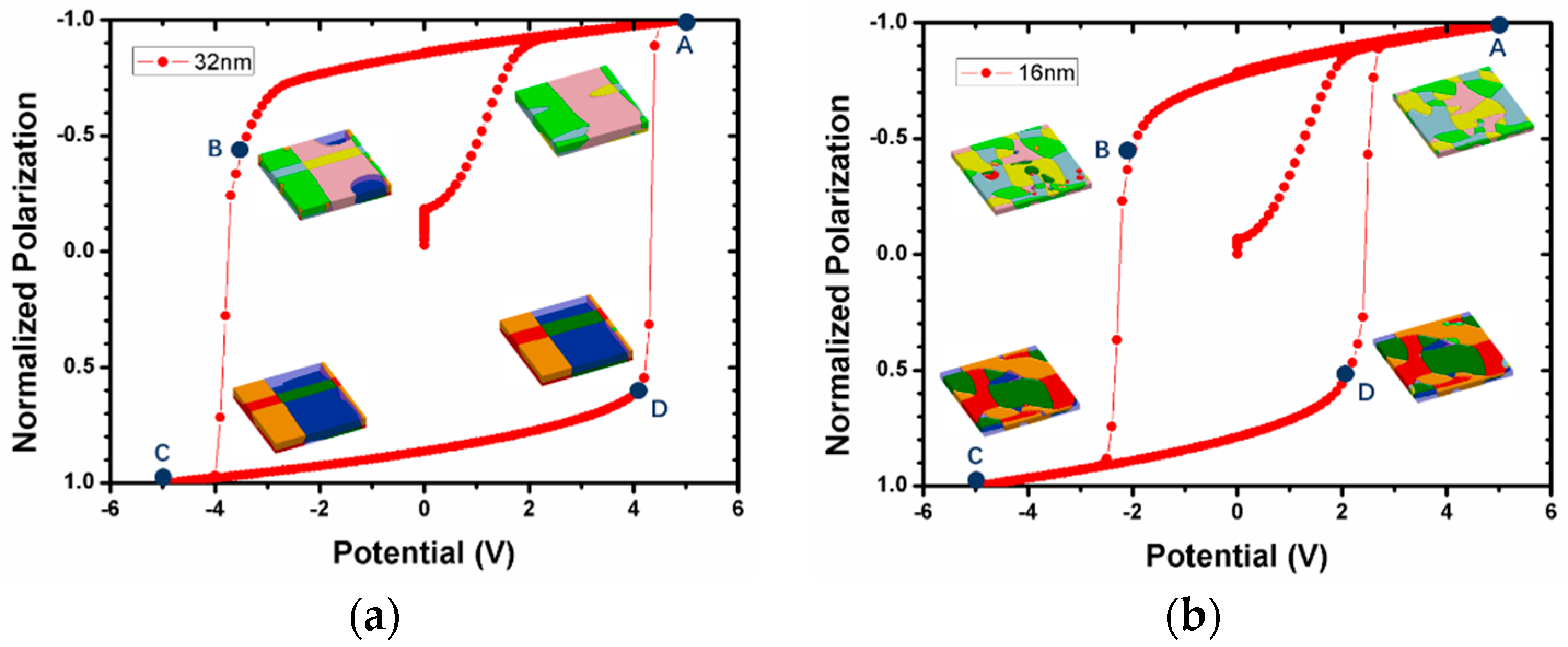
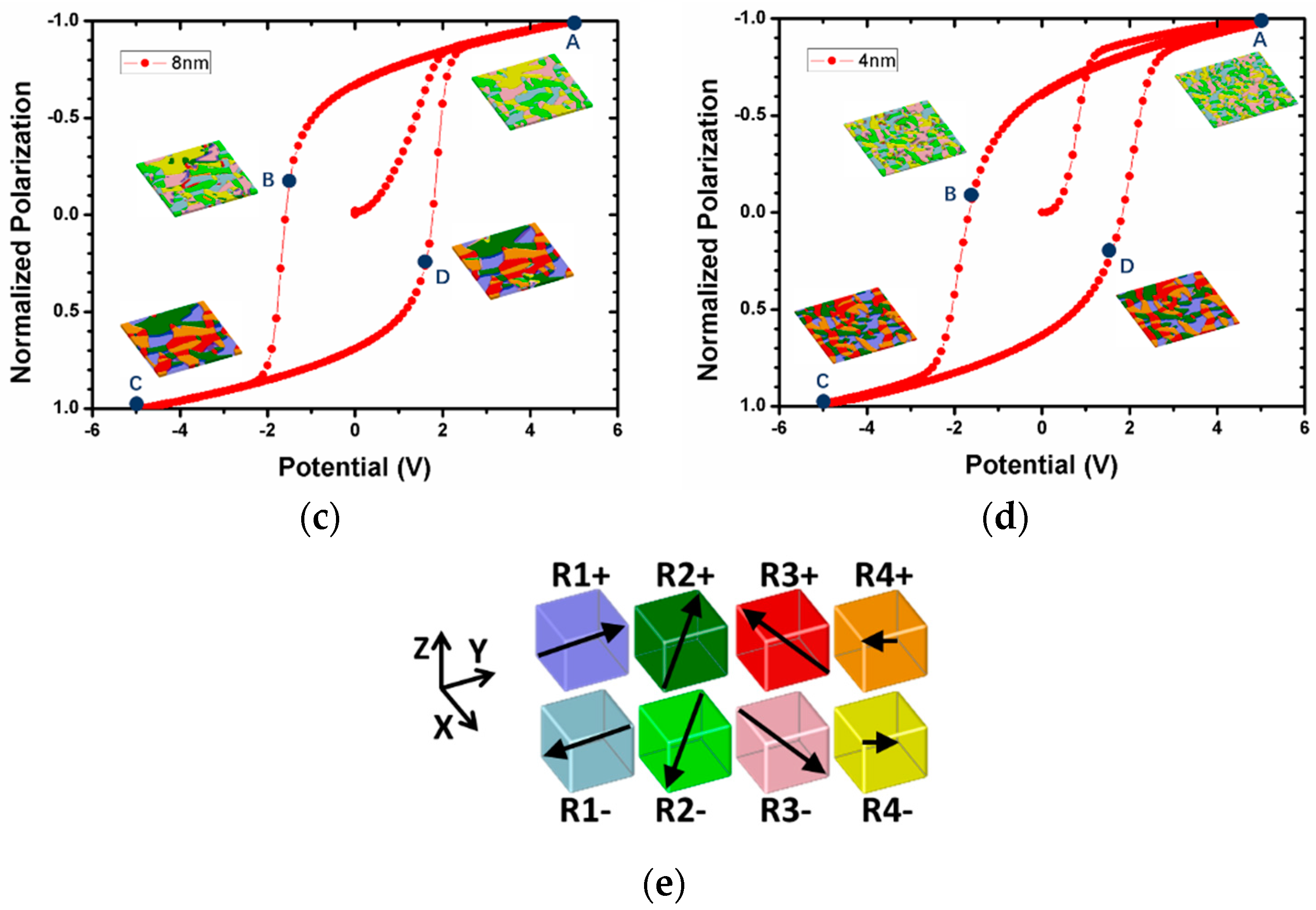
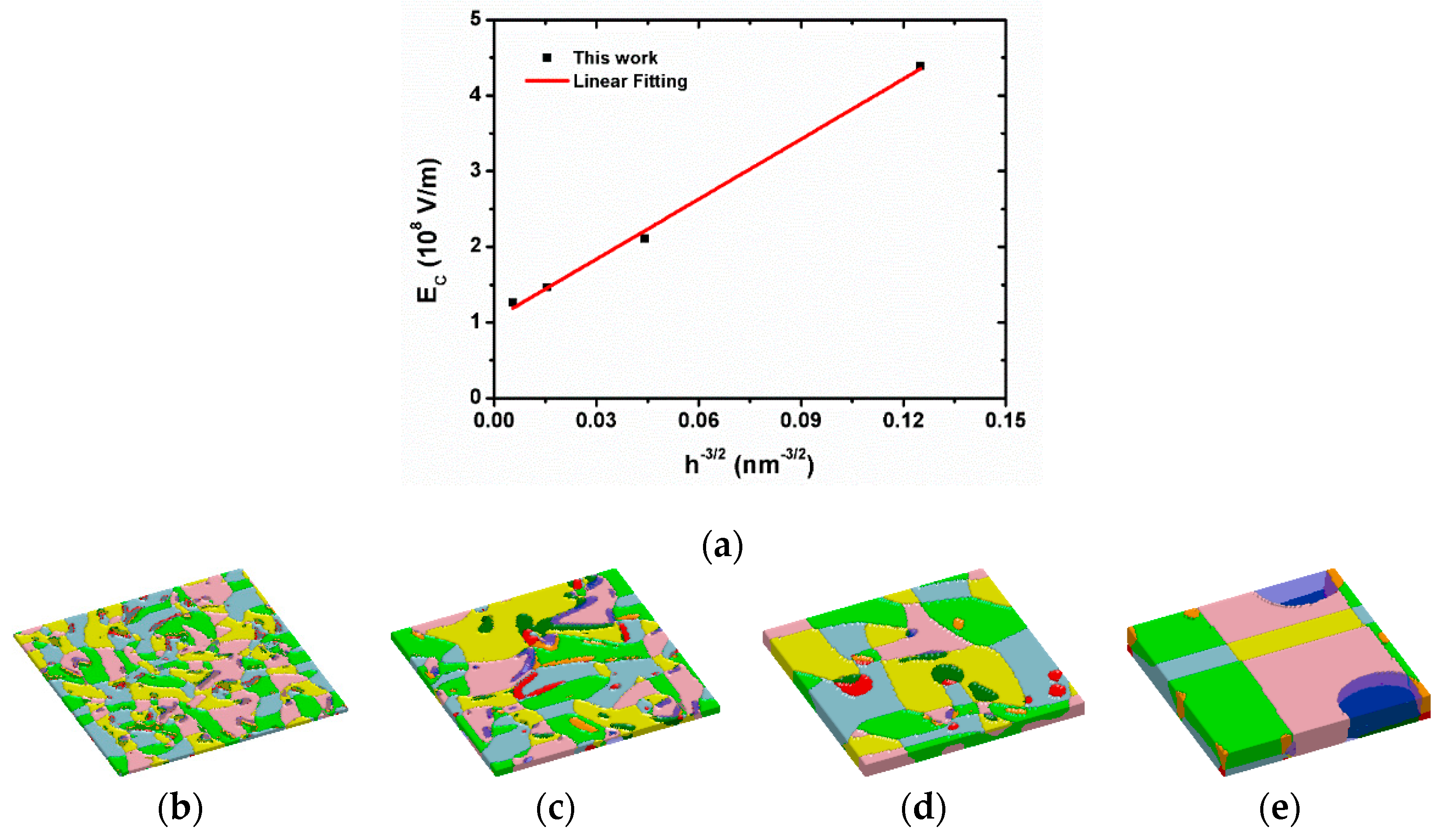
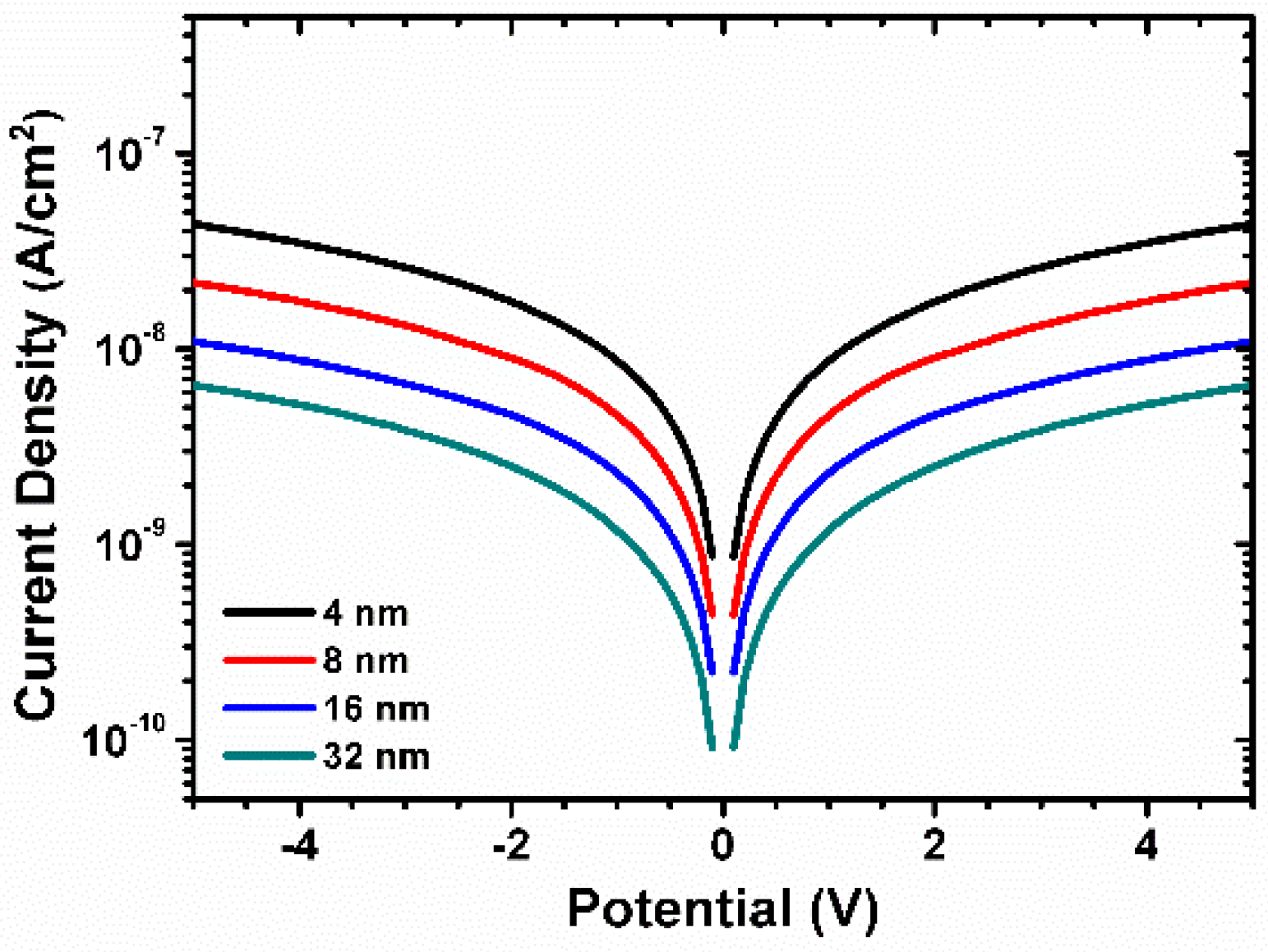
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, F.; Zhang, S.; Yang, T.; Xu, Z.; Zhang, N.; Liu, G.; Wang, J.; Wang, J.; Cheng, Z.; Ye, Z.-G. The origin of ultrahigh piezoelectricity in relaxor-ferroelectric solid solution crystals. Nat. Commun. 2016, 7, 13807. [Google Scholar] [CrossRef] [PubMed]
- Reed, E.J. Piezoelectricity: Now in two dimensions. Nat. Nanotechnol. 2015, 10, 106–107. [Google Scholar] [CrossRef] [PubMed]
- Tagantsev, A.K.; Yudin, P.V. Flexoelectricity in Solids: From Theory to Applications; World Scientific: Singapore, 2016. [Google Scholar]
- Gu, Y.; Li, M.; Morozovska, A.N.; Wang, Y.; Eliseev, E.A.; Gopalan, V.; Chen, L.-Q. Flexoelectricity and ferroelectric domain wall structures: Phase-field modeling and dft calculations. Phys. Rev. B 2014, 89, 174111. [Google Scholar] [CrossRef]
- Jiang, L.; Zhou, Y.; Zhang, Y.; Yang, Q.; Gu, Y.; Chen, L.-Q. Polarization switching of the incommensurate phases induced by flexoelectric coupling in ferroelectric thin films. Acta Mater. 2015, 90, 344–354. [Google Scholar] [CrossRef]
- Scott, J. Contribution to pyroelectricity from domain walls and substrate strain. Ferroelectrics 2014, 472, 19–28. [Google Scholar] [CrossRef]
- Hu, J.M.; Chen, L.Q.; Nan, C.W. Multiferroic heterostructures integrating ferroelectric and magnetic materials. Adv. Mater. 2016, 28, 15–39. [Google Scholar] [CrossRef] [PubMed]
- Jahani, S.; Jacob, Z. All-dielectric metamaterials. Nat. Nanotechnol. 2016, 11, 23–36. [Google Scholar] [CrossRef] [PubMed]
- Cao, G.; Huang, H.; Liang, D.; Ma, X. A phenomenological potential and ferroelectric properties of BaTiO3–CaTiO3 solid solution. Ceram. Int. 2017, 43, 6671–6676. [Google Scholar] [CrossRef]
- Li, J.; Nagaraj, B.; Liang, H.; Cao, W.; Lee, C.H.; Ramesh, R. Ultrafast polarization switching in thin-film ferroelectrics. Appl. Phys. Lett. 2004, 84, 1174–1176. [Google Scholar] [CrossRef]
- Hwang, S.; Lynch, C.; McMeeking, R. Ferroelectric/ferroelastic interactions and a polarization switching model. Acta Metall. Mater. 1995, 43, 2073–2084. [Google Scholar] [CrossRef]
- Chen, W.; Lynch, C. A micro-electro-mechanical model for polarization switching of ferroelectric materials. Acta Mater. 1998, 46, 5303–5311. [Google Scholar] [CrossRef]
- Wang, J.; Shi, S.-Q.; Chen, L.-Q.; Li, Y.; Zhang, T.-Y. Phase-field simulations of ferroelectric/ferroelastic polarization switching. Acta Mater. 2004, 52, 749–764. [Google Scholar] [CrossRef]
- Cao, G.; Cao, Y.; Huang, H.; Chen, L.-Q.; Ma, X. Analysis of multi-domain ferroelectric switching in BiFeO3 thin film using phase-field method. Comput. Mater. Sci. 2016, 115, 208–213. [Google Scholar] [CrossRef]
- Scott, J.F. Searching for new ferroelectrics and multiferroics: A user’s point of view. NPJ Comput. Mater. 2015, 1, 15006. [Google Scholar] [CrossRef][Green Version]
- Catalan, G.; Scott, J.F. Physics and applications of bismuth ferrite. Adv. Mater. 2009, 21, 2463–2485. [Google Scholar] [CrossRef]
- Béa, H.; Gajek, M.; Bibes, M.; Barthélémy, A. Spintronics with multiferroics. J. Phys. Condens. Matter 2008, 20, 434221. [Google Scholar] [CrossRef]
- Gajek, M.; Bibes, M.; Fusil, S.; Bouzehouane, K.; Fontcuberta, J.; Barthélémy, A.; Fert, A. Tunnel junctions with multiferroic barriers. Nat. Mater. 2007, 6, 296–302. [Google Scholar] [CrossRef] [PubMed]
- Baek, S.; Jang, H.; Folkman, C.; Li, Y.; Winchester, B.; Zhang, J.; He, Q.; Chu, Y.; Nelson, C.; Rzchowski, M. Ferroelastic switching for nanoscale non-volatile magnetoelectric devices. Nat. Mater. 2010, 9, 309–314. [Google Scholar] [CrossRef] [PubMed]
- Michel, C.; Moreau, J.-M.; Achenbach, G.D.; Gerson, R.; James, W.J. The atomic structure of BiFeO3. Solid State Commun. 1969, 7, 701–704. [Google Scholar] [CrossRef]
- Kubel, F.; Schmid, H. Structure of a ferroelectric and ferroelastic monodomain crystal of the perovskite BiFeO3. Acta Crystallogr. Sect. B 1990, 46, 698–702. [Google Scholar] [CrossRef]
- Zavaliche, F.; Yang, S.; Zhao, T.; Chu, Y.; Cruz, M.; Eom, C.; Ramesh, R. Multiferroic BiFeO3 films: Domain structure and polarization dynamics. Phase Transit. 2006, 79, 991–1017. [Google Scholar] [CrossRef]
- Wu, J.; Fan, Z.; Xiao, D.; Zhu, J.; Wang, J. Multiferroic bismuth ferrite-based materials for multifunctional applications: Ceramic bulks, thin films and nanostructures. Prog. Mater. Sci. 2016, 84, 335–402. [Google Scholar] [CrossRef]
- Singh, S.K.; Ishiwara, H. Reduced leakage current in BiFeO3 thin films on Si substrates formed by a chemical solution method. Jpn. J. Appl. Phys. 2005, 44, L734. [Google Scholar] [CrossRef]
- Singh, S.K.; Ueno, R.; Funakubo, H.; Uchida, H.; Koda, S.; Ishiwara, H. Dependence of ferroelectric properties on thickness of BiFeO3 thin films fabricated by chemical solution deposition. Jpn. J. Appl. Phys. 2005, 44, 8525. [Google Scholar] [CrossRef]
- Singh, S.; Ishiwara, H.; Maruyama, K. Enhanced polarization and reduced leakage current in BiFeO3 thin films fabricated by chemical solution deposition. J. Appl. Phys. 2006, 100, 064102. [Google Scholar] [CrossRef]
- Rajput, S.; Katoch, R.; Sahoo, K.; Sharma, G.; Singh, S.; Gupta, R.; Garg, A. Enhanced electrical insulation and ferroelectricity in La and Ni co-doped BiFeO3 thin films. J. Alloys Compd. 2015, 621, 339–344. [Google Scholar] [CrossRef]
- Lee, C.-C.; Wu, J.-M. Effect of film thickness on interface and electric properties of BiFeO3 thin films. Appl. Surf. Sci. 2007, 253, 7069–7073. [Google Scholar] [CrossRef]
- Tang, X.; Dai, J.; Zhu, X.; Lin, J.; Chang, Q.; Wu, D.; Song, W.; Sun, Y. Thickness-dependent dielectric, ferroelectric, and magnetodielectric properties of BiFeO3 thin films derived by chemical solution deposition. J. Am. Ceram. Soc. 2012, 95, 538–544. [Google Scholar] [CrossRef]
- Musleh Alrub, A.; Ong, L.-H. Thickness dependence of switching time and coercive field in ferroelectric thin films. J. Appl. Phys. 2011, 109, 084109. [Google Scholar] [CrossRef]
- Maksymovych, P.; Huijben, M.; Pan, M.; Jesse, S.; Balke, N.; Chu, Y.-H.; Chang, H.J.; Borisevich, A.Y.; Baddorf, A.P.; Rijnders, G. Ultrathin limit and dead-layer effects in local polarization switching of BiFeO3. Phys. Rev. B 2012, 85, 014119. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Choudhury, S.; Chen, L.; Chu, Y.; Zavaliche, F.; Cruz, M.; Ramesh, R.; Jia, Q. Computer simulation of ferroelectric domain structures in epitaxial BiFeO3 thin films. J. Appl. Phys. 2008, 103, 094111. [Google Scholar] [CrossRef]
- Chen, L.Q. Phase-field method of phase transitions/domain structures in ferroelectric thin films: A review. J. Am. Ceram. Soc. 2008, 91, 1835–1844. [Google Scholar] [CrossRef]
- Li, Y.; Hu, S.; Liu, Z.; Chen, L. Effect of electrical boundary conditions on ferroelectric domain structures in thin films. Appl. Phys. Lett. 2002, 81, 427–429. [Google Scholar] [CrossRef]
- Nagaraj, B.; Aggarwal, S.; Ramesh, R. Influence of contact electrodes on leakage characteristics in ferroelectric thin films. J. Appl. Phys. 2001, 90, 375–382. [Google Scholar] [CrossRef]
- Izyumskaya, N.; Alivov, Y.-I.; Cho, S.-J.; Morkoç, H.; Lee, H.; Kang, Y.-S. Processing, structure, properties, and applications of PZT thin films. Crit. Rev. Solid State Mater. Sci. 2007, 32, 111–202. [Google Scholar] [CrossRef]
- Tomczyk, M.; Stroppa, D.G.; Reaney, I.M.; Vilarinho, P.M. Growth of BiFeO3 thin films by chemical solution deposition: The role of electrodes. Phys. Chem. Chem. Phys. 2017, 19, 14337–14344. [Google Scholar] [CrossRef] [PubMed]
- Gotō, K. Thickness dependence of the domain width in thin crystals of BaFe12O19 and SrFe12O19. Jpn. J. Appl. Phys. 1966, 5, 117. [Google Scholar] [CrossRef]
- Huang, C.; Chen, L.; Wang, J.; He, Q.; Yang, S.; Chu, Y.; Ramesh, R. Phenomenological analysis of domain width in rhombohedral BiFeO3 films. Phys. Rev. B 2009, 80, 140101. [Google Scholar] [CrossRef]
- Kay, H.; Dunn, J. Thickness dependence of the nucleation field of triglycine sulphate. Philos. Mag. 1962, 7, 2027–2034. [Google Scholar] [CrossRef]
- Jo, J.; Kim, Y.; Noh, T.; Yoon, J.-G.; Song, T. Coercive fields in ultrathin BaTiO3 capacitors. Appl. Phys. Lett. 2006, 89, 232909. [Google Scholar] [CrossRef]
- Merz, W.J. Domain formation and domain wall motions in ferroelectric BaTiO3 single crystals. Phys. Rev. 1954, 95, 690. [Google Scholar] [CrossRef]
- Cao, Y.; Shen, J.; Randall, C.; Chen, L. Phase-field modeling of switchable diode-like current-voltage characteristics in ferroelectric BaTiO3. Appl. Phys. Lett. 2014, 104, 182905. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, G.; Huang, H.; Ma, X. Thickness Dependence of Switching Behavior in Ferroelectric BiFeO3 Thin Films: A Phase-Field Simulation. Appl. Sci. 2017, 7, 1162. https://doi.org/10.3390/app7111162
Cao G, Huang H, Ma X. Thickness Dependence of Switching Behavior in Ferroelectric BiFeO3 Thin Films: A Phase-Field Simulation. Applied Sciences. 2017; 7(11):1162. https://doi.org/10.3390/app7111162
Chicago/Turabian StyleCao, Guoping, Houbing Huang, and Xingqiao Ma. 2017. "Thickness Dependence of Switching Behavior in Ferroelectric BiFeO3 Thin Films: A Phase-Field Simulation" Applied Sciences 7, no. 11: 1162. https://doi.org/10.3390/app7111162
APA StyleCao, G., Huang, H., & Ma, X. (2017). Thickness Dependence of Switching Behavior in Ferroelectric BiFeO3 Thin Films: A Phase-Field Simulation. Applied Sciences, 7(11), 1162. https://doi.org/10.3390/app7111162




