Stochastic Unit Commitment of Wind-Integrated Power System Considering Air-Conditioning Loads for Demand Response
Abstract
:1. Introduction
2. Demand Response Modeling for ACL
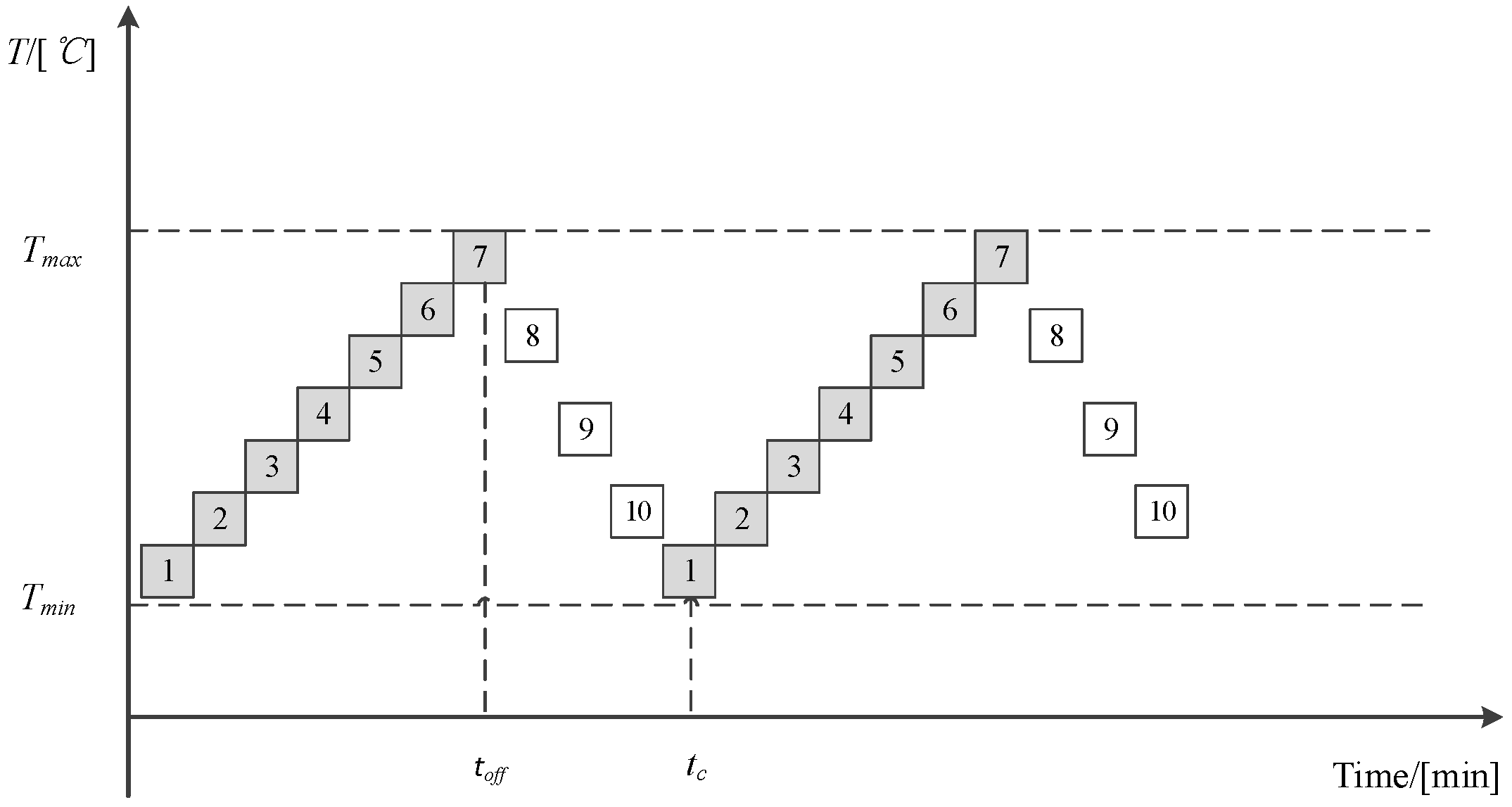
2.1. Thermal Parameter Model for the ACL
2.2. Cost Calculation for the DR of the ACL
2.3. Constraints for the DR of the ACL
3. Problem Formulation
3.1. Objective Function
3.2. Constraints
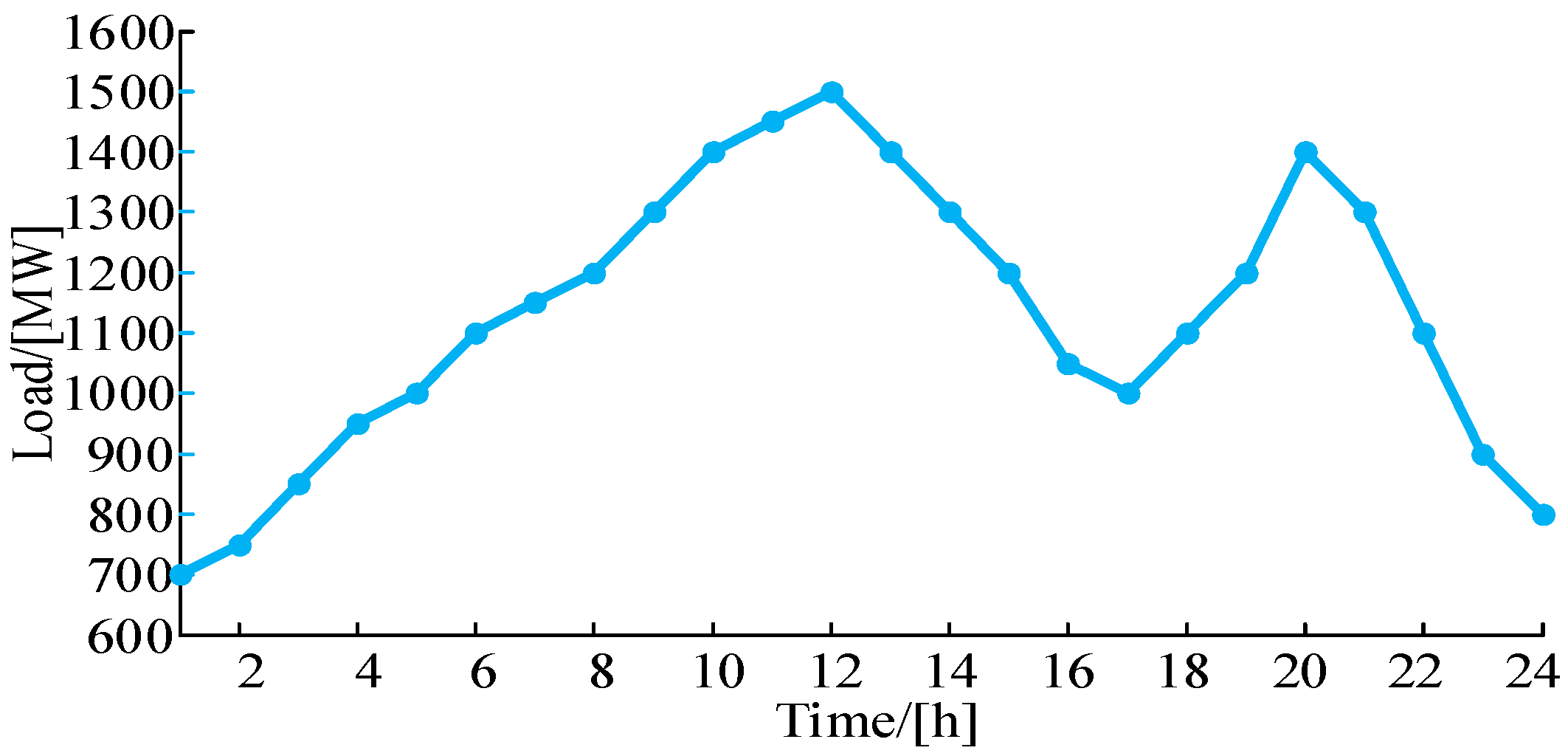
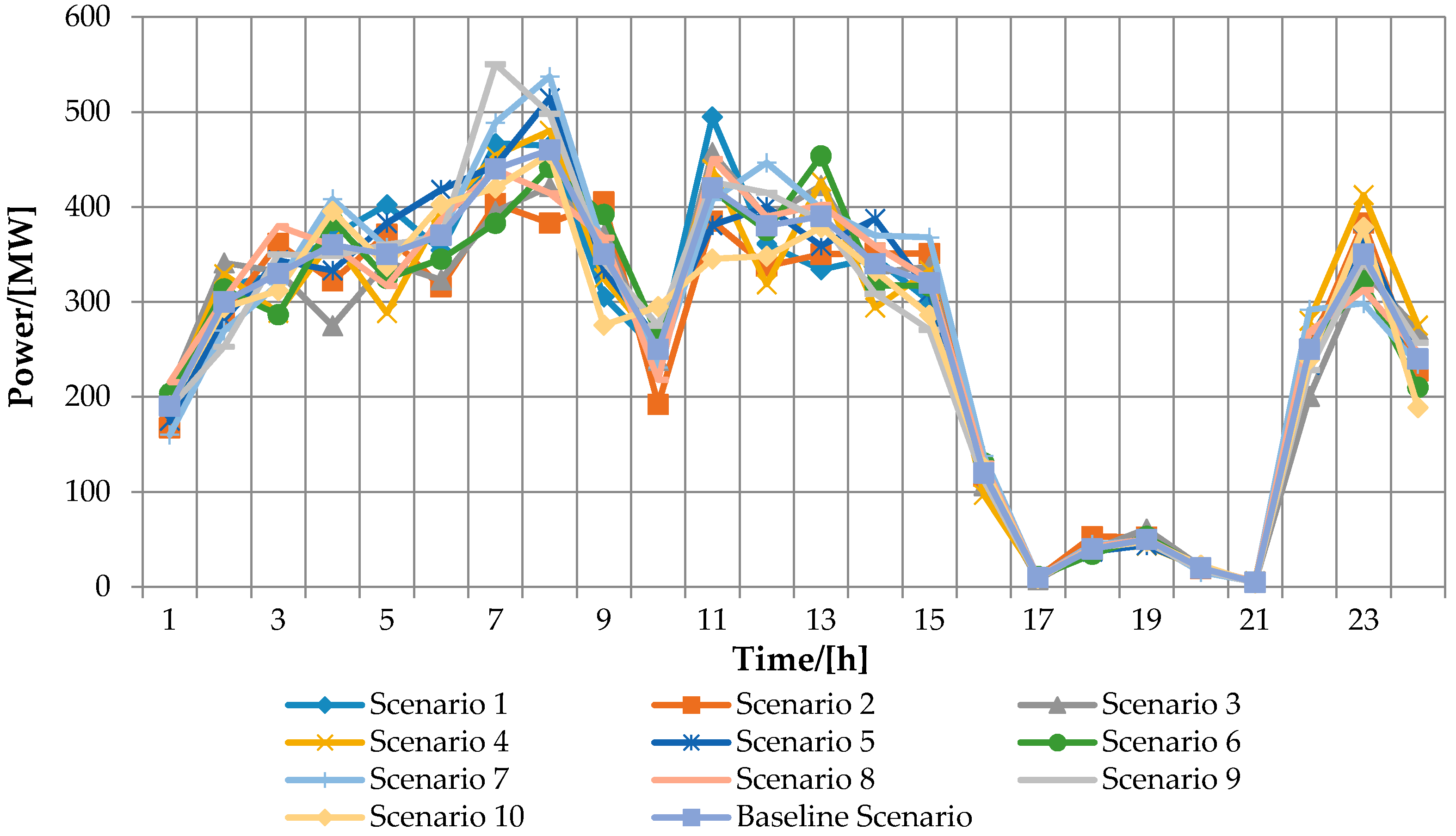
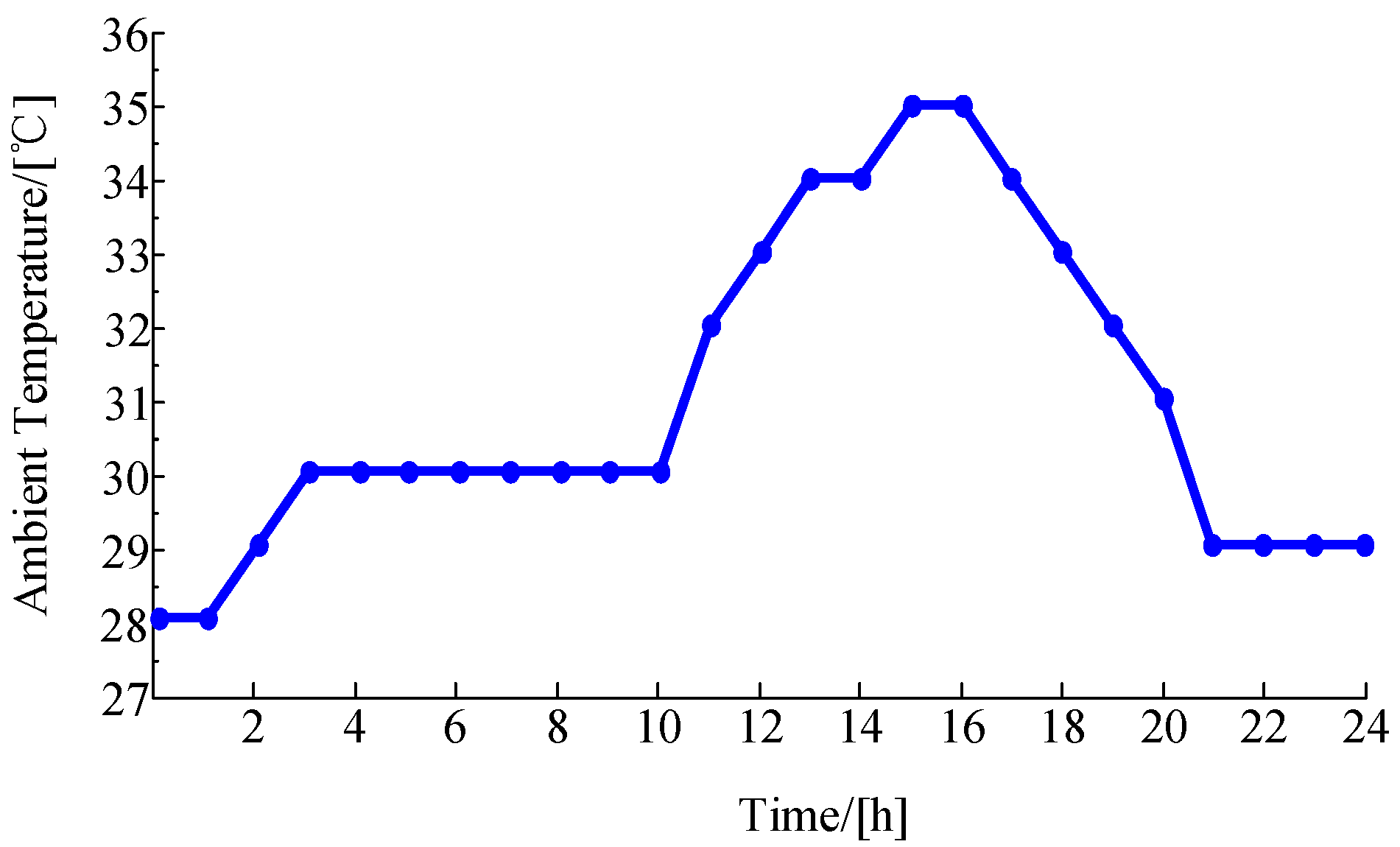
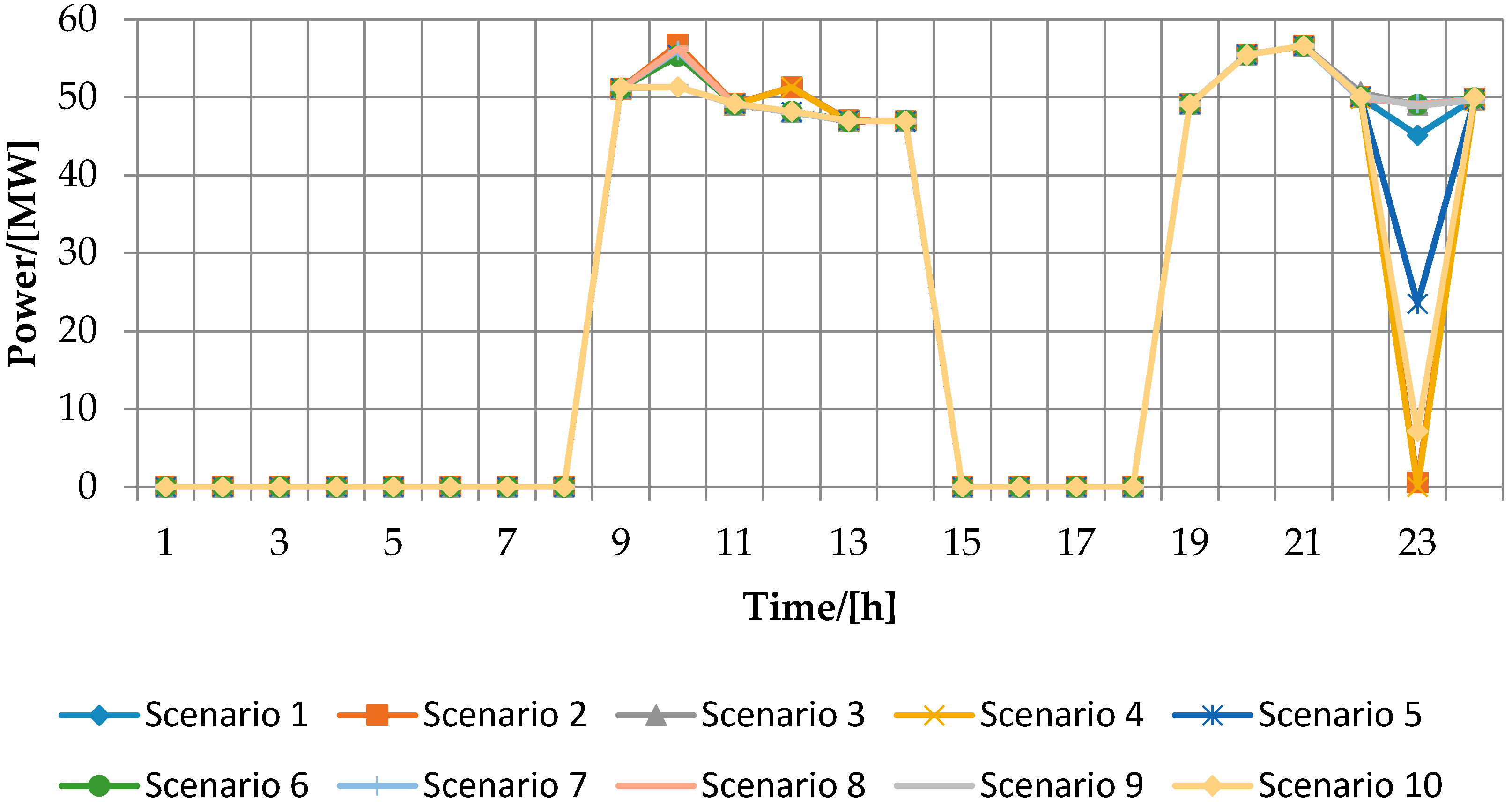
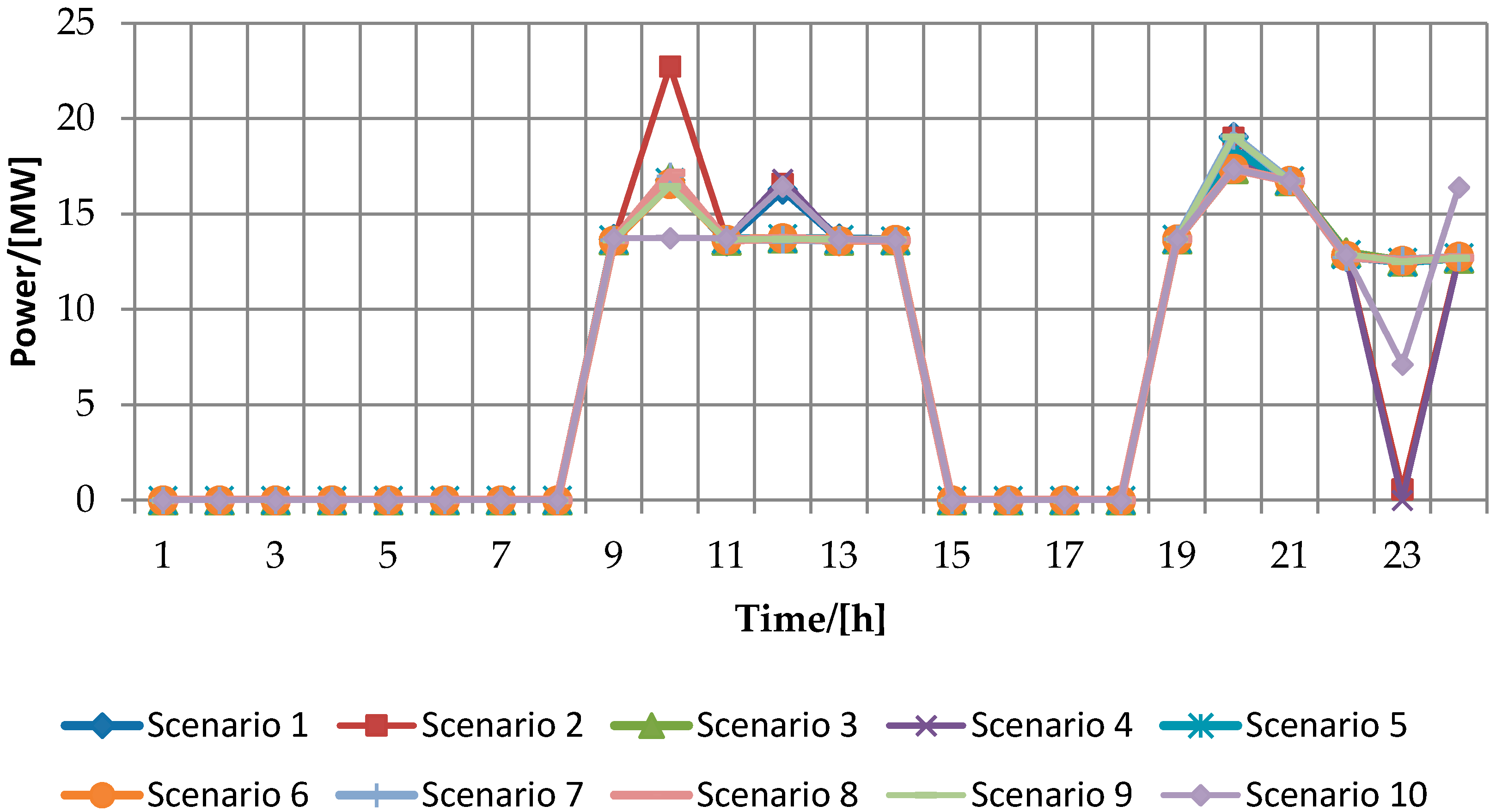
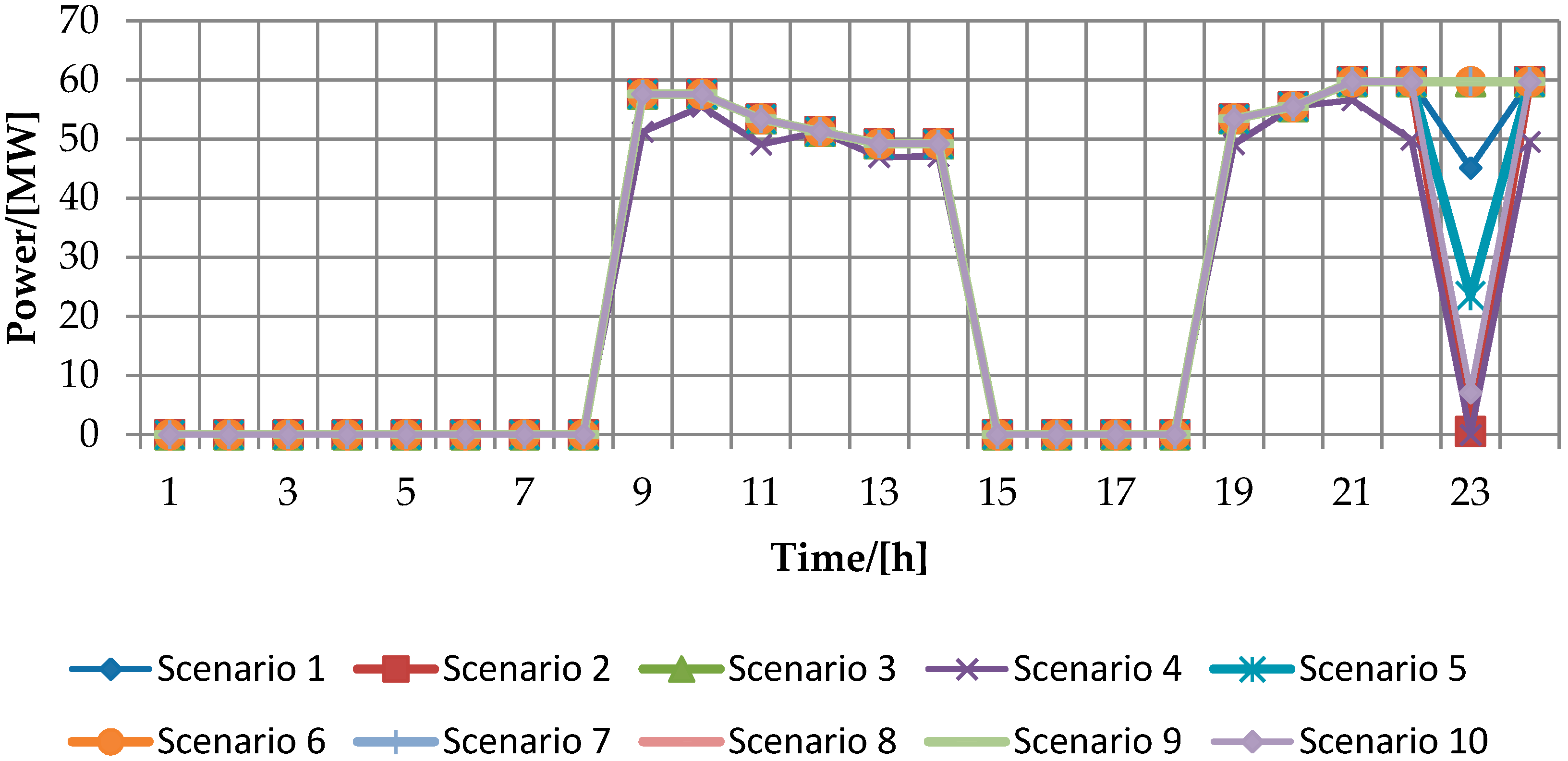
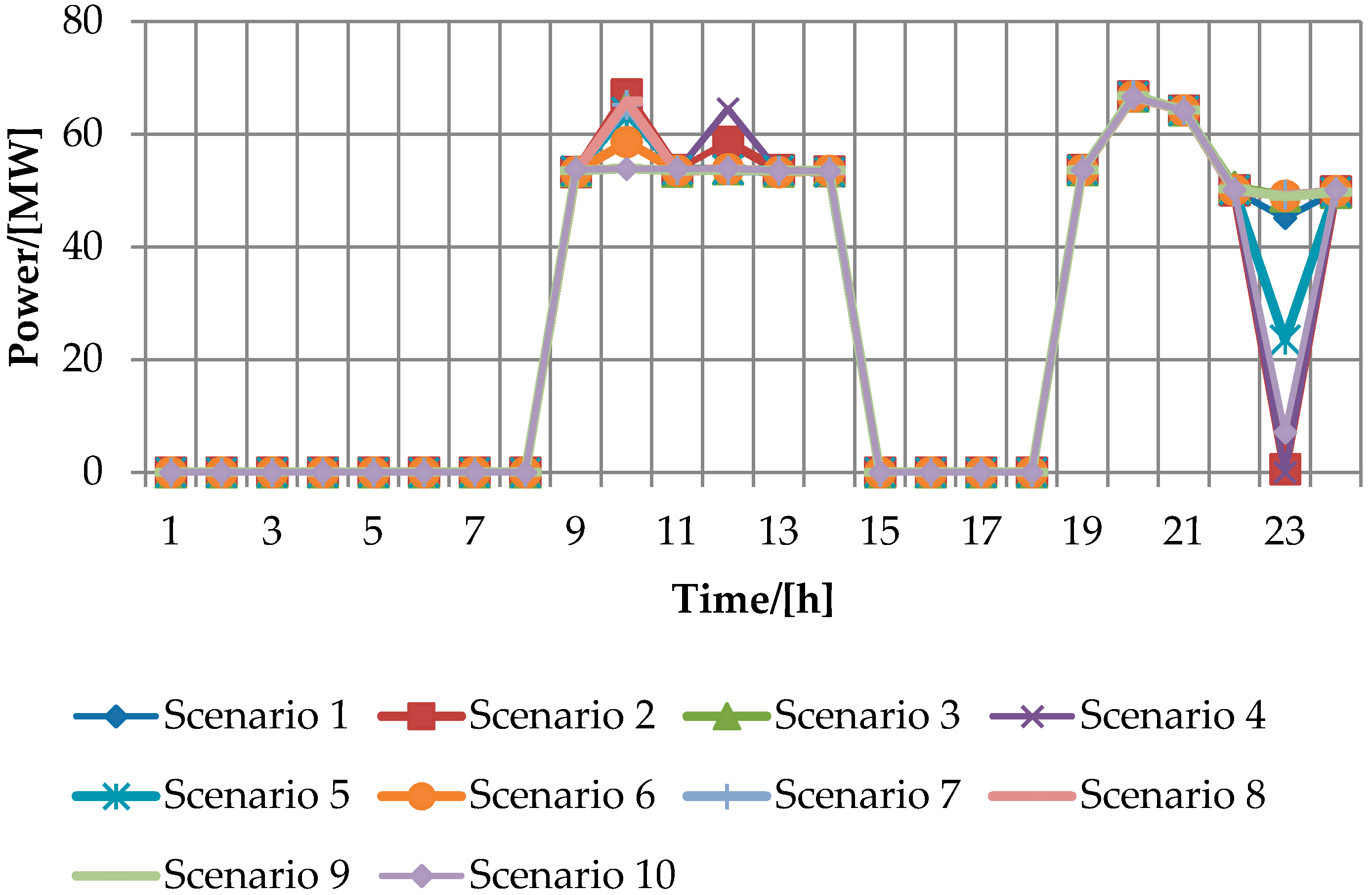
4. Case Study and Simulation Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- U.S. Department of Energy. 20% Wind Energy by 2030: Increasing Wind Energy’s Contribution to U.S. Electricity Supply. Available online: http://energy.gov/eere/wind/wind-program (accessed on 14 May 2016).
- Cheng, S.; Sun, W.B.; Liu, W.L. Multi-objective configuration optimization of a hybrid energy storage system. Appl. Sci. 2017, 7, 163. [Google Scholar] [CrossRef]
- Jiang, R.; Wang, J.; Guan, Y. Robust unit commitment with wind power and pumped storage hydro. IEEE Trans. Power Syst. 2012, 27, 800–810. [Google Scholar] [CrossRef]
- Ummels, B.C.; Gibescu, M.; Pelgrum, E.; Kling, W.L.; Brand, A.J. Impacts of wind power on thermal generation unit commitment and dispatch. IEEE Trans. Energy Convers. 2007, 22, 44–51. [Google Scholar] [CrossRef]
- Bouffard, F.; Galiana, F.D. Stochastic security for operations planning with significant wind power generation. IEEE Trans. Power Syst. 2008, 23, 306–316. [Google Scholar] [CrossRef]
- Babu, C.A.; Ashok, S. Peak load management in electrolytic process industries. IEEE Trans. Power Syst. 2008, 23, 399–405. [Google Scholar] [CrossRef]
- Linden, S.V.D. Bulk energy storage potential in the USA, current developments and future prospects. Energy 2006, 31, 3446–3457. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, J.; Dai, Y. Capacity allocation of a hybrid energy storage system for power system peak shaving at high wind power penetration level. Renew. Energy 2015, 75, 541–549. [Google Scholar] [CrossRef]
- Shao, S.; Pipattanasomporn, M.; Rahman, S. Demand response as a load shaping tool in an intelligent grid with electric vehicles. IEEE Trans. Smart Grid 2011, 2, 624–631. [Google Scholar] [CrossRef]
- Qela, B.; Mouftah, H.T. Peak load curtailment in a smart grid via fuzzy system approach. IEEE Trans. Smart Grid 2014, 5, 761–768. [Google Scholar] [CrossRef]
- Parvania, M.; Fotuhi-Firuzabad, M. Demand response scheduling by stochastic SCUC. IEEE Trans. Smart Grid 2010, 1, 89–98. [Google Scholar] [CrossRef]
- Vahedipour-Dahraie, M.; Najafi, H.; Anvari-Moghaddam, A.; Guerrero, J.M. Study of the effect of time-based rate demand response programs on stochastic day-ahead energy and reserve scheduling in islanded residential microgrids. Appl. Sci. 2017, 7, 378. [Google Scholar] [CrossRef]
- Assessment of Demand Response and Advanced Metering Staff Report (Docket AD06-2-000). Available online: https://www.smartgrid.gov/document/assessment_demand_response_advanced_metering_staff_report_docket_ad06_2_000 (accessed on 4 September 2015).
- Huang, K.Y.; Huang, Y.C. Integrating direct load control with interruptible load management to provide instantaneous reserves for ancillary services. IEEE Trans. Power Syst. 2004, 19, 1626–1634. [Google Scholar] [CrossRef]
- Lu, N. An evaluation of the HVAC load potential for providing load balancing service. IEEE Trans. Smart Grid 2012, 3, 1263–1270. [Google Scholar] [CrossRef]
- Lu, N.; Zhang, Y. Design considerations of a centralized load controller using thermostatically controlled appliances for continuous regulation reserves. IEEE Trans. Smart Grid 2013, 4, 914–921. [Google Scholar] [CrossRef]
- Hassan, N.U.; Khalid, Y.I.; Yuen, C.; Tushar, W. Customer engagement plans for peak load reduction in residential smart grids. IEEE Trans. Smart Grid 2015, 6, 3029–3041. [Google Scholar] [CrossRef]
- Tso, G.K.F.; Yau, K.K.W. A study of domestic energy usage patterns in Hong Kong. Energy 2003, 28, 1671–1682. [Google Scholar] [CrossRef]
- Li, C.; Shang, J.; Zhu, S.; Du, L.; Wu, C.; Wang, Q. An analysis of energy consumption caused by air temperature-affected accumulative effect of the air conditioning load. Autom. Electr. Power Syst. 2010, 34, 30–33. [Google Scholar]
- Horowitz, S.; Mauch, B.; Sowell, F. Forecasting residential air conditioning loads. Appl. Energy 2014, 132, 47–55. [Google Scholar] [CrossRef]
- Molina-Garcia, A.; Kessler, M.; Fuentes, J.A.; Gomez-Lazaro, E. Probabilistic characterization of thermostatically controlled loads to model the impact of demand response programs. IEEE Trans. Power Syst. 2011, 26, 241–251. [Google Scholar] [CrossRef]
- Bashash, S.; Fathy, H.K. Modeling and control insights into demand-side energy management through setpoint control of thermostatic loads. Am. Control Conf. 2011, 47, 4546–4553. [Google Scholar]
- Malhame, R.; Chong, C.Y. Electric load model synthesis by diffusion approximation of a high-order hybrid-state stochastic system. IEEE Trans. Autom. Control 1985, 30, 854–860. [Google Scholar] [CrossRef]
- Schlueter, R.A.; Park, G.L.; Reddoch, T.W.; Barnes, P.R.; Lawler, J.S. A modified unit commitment and generation control for utilities with large wind generation penetrations. IEEE Power Eng. Rev. 1985, 85, 1630–1636. [Google Scholar]
- Zhao, C.; Wang, J.; Watson, J.P.; Guan, Y. Multi-stage robust unit commitment considering wind and demand response uncertainties. IEEE Trans. Power Syst. 2013, 28, 2708–2717. [Google Scholar] [CrossRef]
- Sioshansi, R. Evaluating the impacts of real-time pricing on the cost and value of wind generation. IEEE Trans. Power Syst. 2010, 25, 741–748. [Google Scholar] [CrossRef]
- Molina, A.; Gabaldon, A.; Fuentes, J.A.; Alvarez, C. Implementation and assessment of physically based electrical load models: Application to direct load control residential programmes. IEE Proc. Gener. Transm. Distrib. 2003, 150, 61–66. [Google Scholar] [CrossRef]
- Bruning, S.F. A new way to calculate cooling loads. ASHRAE J. 2004, 46, 20–24. [Google Scholar]
- Wichakool, W.; Remscrim, Z.; Orji, U.A.; Leeb, S.B. Smart metering of variable power loads. IEEE Trans. Smart Grid 2015, 6, 189–198. [Google Scholar] [CrossRef]
- Fahrioglu, M.; Alvarado, F.L. Designing incentive compatible contracts for effective demand management. IEEE Trans. Power Syst. 2000, 15, 1255–1260. [Google Scholar] [CrossRef]
- Lu, N.; Chassin, D.P.; Widergren, S.E. Modeling uncertainties in aggregated thermostatically controlled loads using a state queueing model. IEEE Trans. Power Syst. 2005, 20, 725–733. [Google Scholar] [CrossRef]
- Carrión, M.; Arroyo, J.M. A computationally efficient mixed-integer linear formulation for the thermal unit commitment problem. IEEE Trans. Power Syst. 2006, 21, 1371–1378. [Google Scholar] [CrossRef]
- Arroyo, J.M.; Conejo, A.J. Optimal response of a thermal unit to an electricity spot market. IEEE Trans. Power Syst. 2000, 15, 1098–1104. [Google Scholar] [CrossRef]
- ILOG CPLEX Homepage 2009. Available online: http://www.ilog.com (accessed on 16 June 2016).
- Abdollahi, A.; Moghaddam, M.P.; Rashidinejad, M.; Sheikh-El-Eslami, M.K. Investigation of economic and environmental-driven demand response measures incorporating UC. IEEE Trans. Smart Grid 2012, 3, 12–25. [Google Scholar] [CrossRef]
- Yan, Y.; Wen, F.; Yang, S.; Macgill, I. Generation scheduling with fluctuating wind power. Autom. Electr. Power Syst. 2010, 34, 79–88. [Google Scholar]
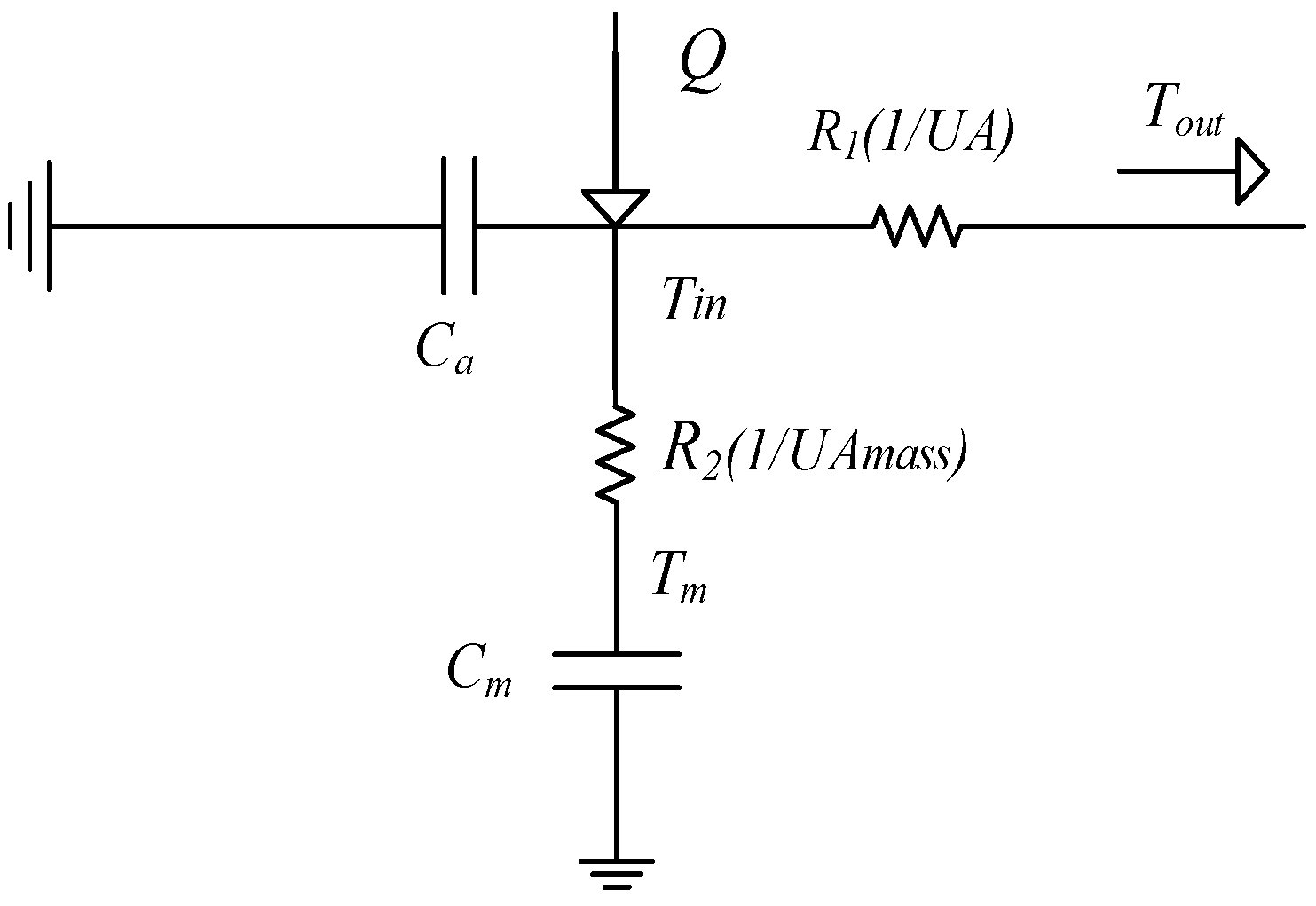
| Variable | Value | Variable | Value |
|---|---|---|---|
| Tmin/°C | 22 | e−Δt/RC | 0.96 |
| Tmax/°C | 27 | /kW | 2.5 |
| η | 2.5 | A | 0.18 |
| ACL Type | K1/$/((MW)2h) | K2/$/(MWh) |
|---|---|---|
| 1 | 0.3 | 4 |
| 2 | 0.2 | 5 |
| Mode Type | Unit Commitment (24 h) | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mode 1 | Units | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Mode 2 | Units | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Cost/($) | Mode 1 | Mode 2 |
|---|---|---|
| Power generation cost | 419,422.71 | 401,847.44 |
| Cost of start-up | 2920 | 2638 |
| Cost of ACL reduction | 0 | 6348.7 |
| Total cost of objective function | 422,342.71 | 410,834.14 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, X.; Zhou, M.; Li, G.; Lee, K.Y. Stochastic Unit Commitment of Wind-Integrated Power System Considering Air-Conditioning Loads for Demand Response. Appl. Sci. 2017, 7, 1154. https://doi.org/10.3390/app7111154
Han X, Zhou M, Li G, Lee KY. Stochastic Unit Commitment of Wind-Integrated Power System Considering Air-Conditioning Loads for Demand Response. Applied Sciences. 2017; 7(11):1154. https://doi.org/10.3390/app7111154
Chicago/Turabian StyleHan, Xiao, Ming Zhou, Gengyin Li, and Kwang Y. Lee. 2017. "Stochastic Unit Commitment of Wind-Integrated Power System Considering Air-Conditioning Loads for Demand Response" Applied Sciences 7, no. 11: 1154. https://doi.org/10.3390/app7111154
APA StyleHan, X., Zhou, M., Li, G., & Lee, K. Y. (2017). Stochastic Unit Commitment of Wind-Integrated Power System Considering Air-Conditioning Loads for Demand Response. Applied Sciences, 7(11), 1154. https://doi.org/10.3390/app7111154





