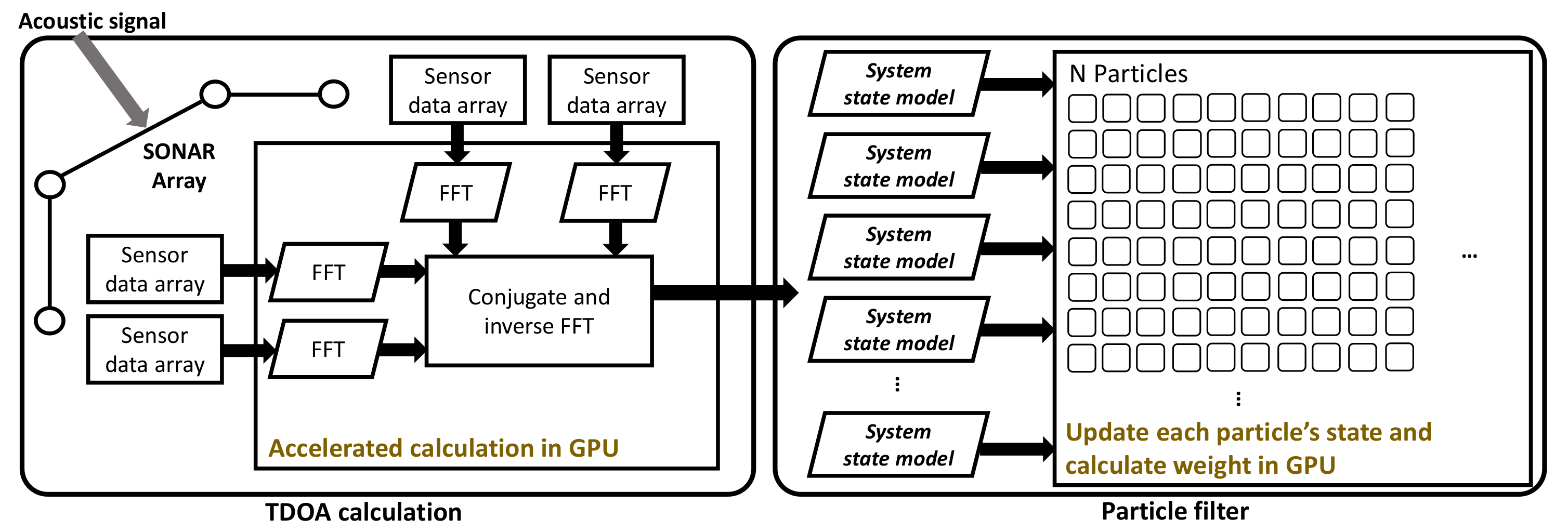
The proposed overall architecture of this paper is as follows. This paper focuses on accelerating the position estimation of a sound source based on a PF using an acoustic signal sensor array in a GPU. The TDOA measurement is required for the sound source localization based on the proposed GPU, and the location of the current target can be determined using three TDOA measurements in the three-dimensional space. In order to obtain three TDOA measurements, four acoustic sensors are required including one reference acoustic sensor. In this study, we used GCC-PHAT to obtain TDOA measurements. To obtain TDOA measurements at high speed, the GCC-PHAT process of the acoustic signal input by multiple sensors is performed in parallel using GPU.
The proposed method uses a PF to estimate the current state of a target using TDOA measurements, and we accelerate it. The PF process used in the study is as follows. Using the computed TDOA measurements and the state equations of the system, we predict the current state from the previous state of the system and obtain the observed value from the state of the updated system. Then, the weight of each particle is obtained by comparing with the actual measurement. In this process, we propose accelerating the state update and weight calculation process of the particle mentioned above by parallel operation of each particle in the kernel using GPU. Also, PF operation is customized using multiple system state equations based on GPU for tracking sudden movements of moving targets which also can be used for tracking multiple target. The proposed architecture is shown in
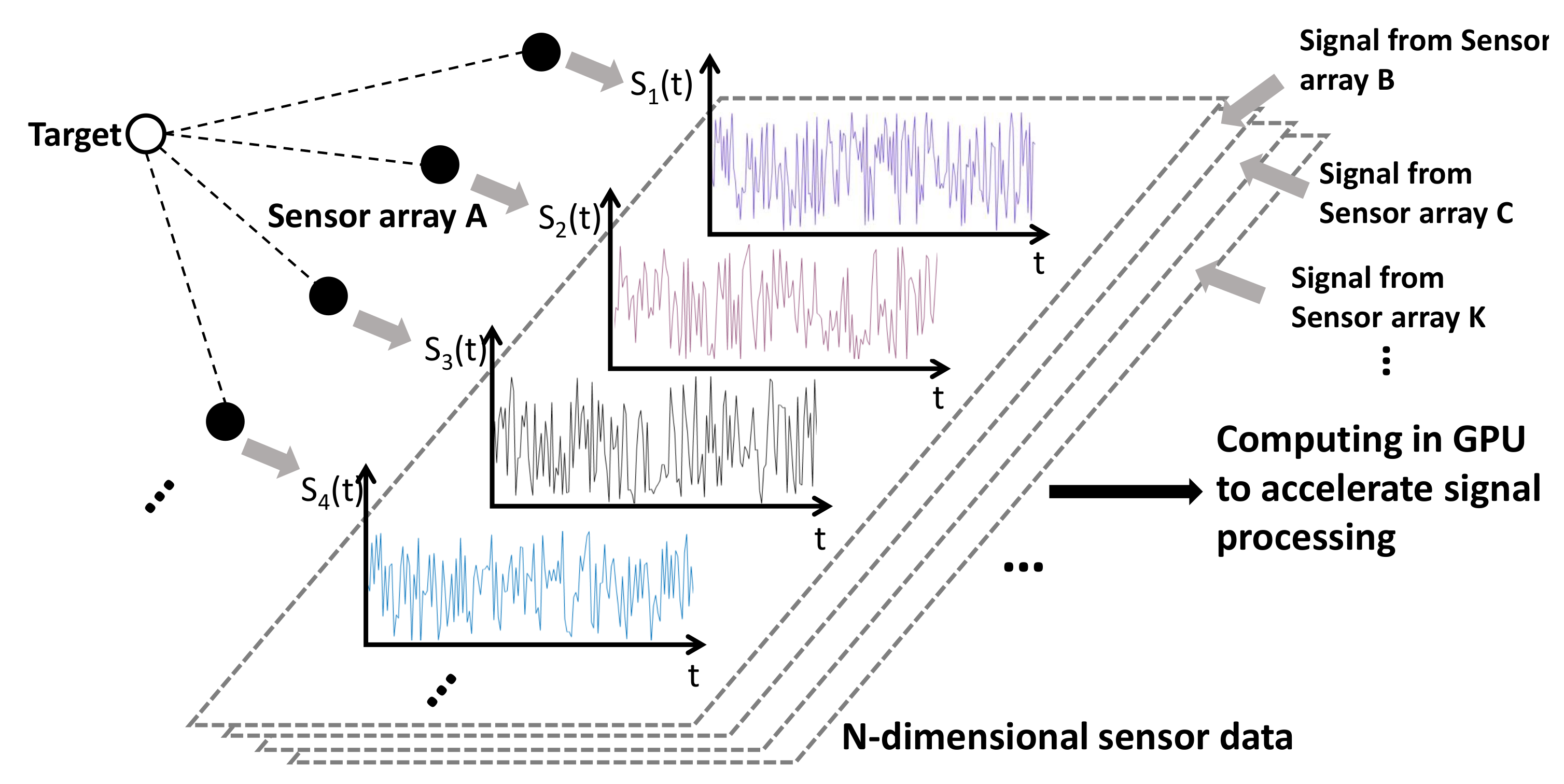
Figure 1. Moreover, this proposed architecture can be used in IoT applications as shown in
Figure 2, that is consisted with many sensors. Due to the amount of signal data from many sensors, it is reasonable using GPU in terms of high performance computing to accelerate signal processing for detecting target more accurately by increasing the number of sensors.
3.1. Particle Filter (PF) with Time Difference of Arrival (TDOA) Measurement
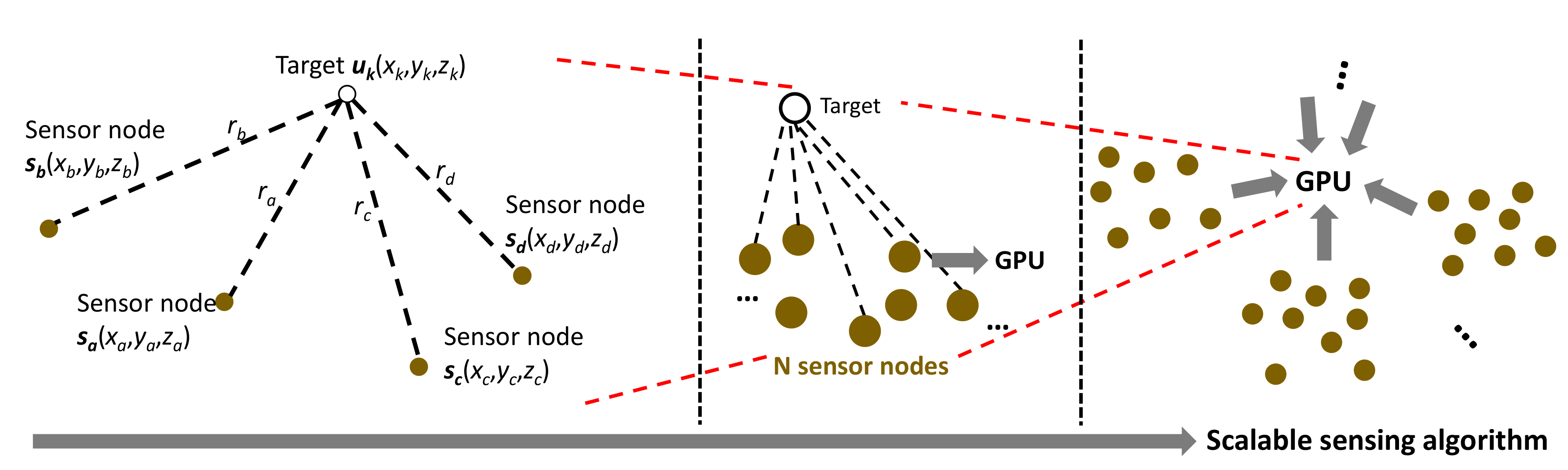
To estimate the movement of the acoustic signal source, we use the TDOA measurement obtained from the acoustic sensors. Four acoustic sensors including one reference sensor are used to estimate the position of the target in a three-dimensional space. The proposed PF is based target position estimation using TDOA measurements obtained in this structure. The PF is a method of probabilistically estimating the state of a target using N particles, also called the Monte Carlo method. Unlike the extended KF and unscented KF, the PF has strength in non-Gaussian and non-linear systems. The proposed algorithm is scalable to the number of sensors, and it is applicable even if the number of sensors is increased as shown in
Figure 3. The proposed architecture uses four sensors which is minimum number of sensors required to detect a target in three-dimensional space or can use more than minimum number of sensors. The PF processing can operated on the GPU using each sensor node set, and the proposed architecture can detect multiple targets in parallel using acoustic signal.
First, the state of the system used at PF processing is defined as follows. The state of the moving target is defined as a uniform speed motion. In this case, the system state equation for estimating the current state
in a previous state
is expressed by Equation (
1), where
denotes a position vector of the three-dimensional space at time k. A denotes a state transition equation matrix, and
denotes process noise. The observation model, which represents the relationship between the state of the system and the measured value, is defined by Equation (
2), where
denotes measured value and
denotes measurement noise.
In this study, we propose accelerating the position estimation of the target using TDOA measurements, and the measured value
is a TDOA measurement obtained from the signal input to each acoustic sensor. In Equation (
2), the relation between the system state and the TDOA measurements is represented by
h, and it can be obtained from the following procedure. The distance between the target and the sensor is defined by
in Equation (
3). Also the reference sensor for obtaining the TDOA measurement is defined as
, where
is the position vector of the target and
is the position vector of the
ath sensor. As shown in second line of Equation (
3) ,
is displacement value between distance to
and
from target, which can be represented with the velocity of source wave ‘c’ multiplied by the TDOA value between sensor
and
.
Figure 3’s left one shows the reference sensor and the other sensor. TDOA measurements used for the PF are obtained between reference sensor
and the other sensor. Equation (
4) is used to obtain the TDOA measurement value by using the distance from each reference sensor
and sensor
to the target. The velocity c is the speed of the sound wave in the water, which is 1500 m/s.
Therefore, the target location estimation by applying three TDOA measurement values is described with the following equation; Equation (
5) defines a relation
between the system state and the TDOA measurement. The state from three or more TDOA measurement values are represented in Equation (
6) by a matrix
H, where index ‘a’ represents reference sensor and index ‘X’ represents relative sensors.
The operation of the PF for estimating the position of the moving target using the relation between the system and the measurement is shown in Algorithm 1. The overall algorithm of the PF using the TDOA measurement is as follows. First, the state of the system for each particle is updated. Then, each particle predicts the observed value using the relational expression between the system state and the measurement values from each updated state. Additionally, the weight of each particle is calculated according to the probability distribution of the actual observed TDOA measurement value and the predicted measurement value. After that, the effective sample size (ESS) is calculated, then it is compared with threshold
[
23,
24]. The
is defined as a predefined threshold for resampling. In our implementation, the threshold
is defined as 0.8 times of number of particles. Therefore, if the ESS is below a predetermined number of samples, which is denoted as threshold
, the weight of each particle is resampled. The resampling process removes low weighted particles and selects particles with high weight to reduce errors due to probability distributions. The PF estimates the position of the moving target more accurately using the resampling process.
| Algorithm 1 PF |
- 1:
- 2:
- 3:
- 4:
for - 5:
- 6:
- 7:
- 8:
- 9:
- 10:
- 11:
if - 12:
- 13:
end if - 14:
- 15:
end for
|
3.3. Accelerated Algorithm Based on GPU
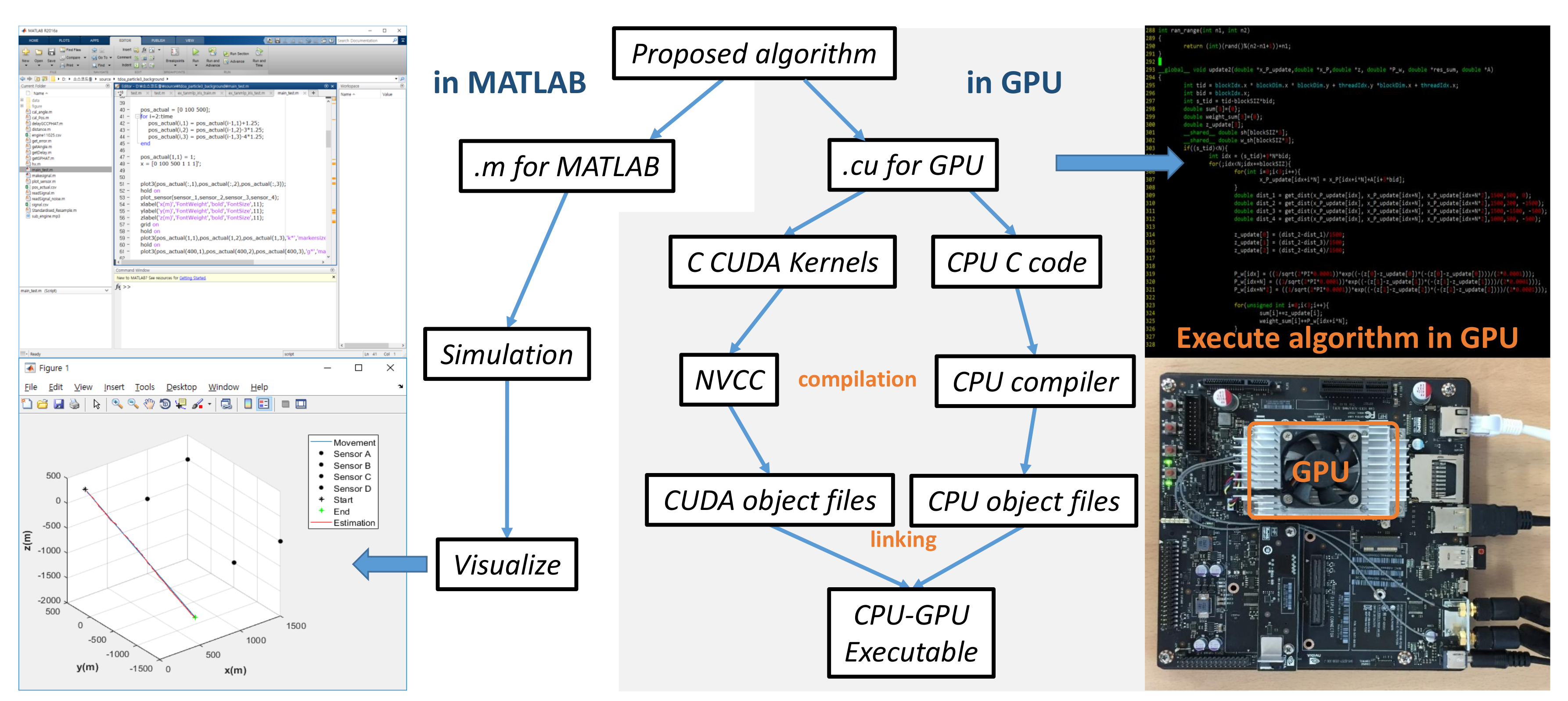
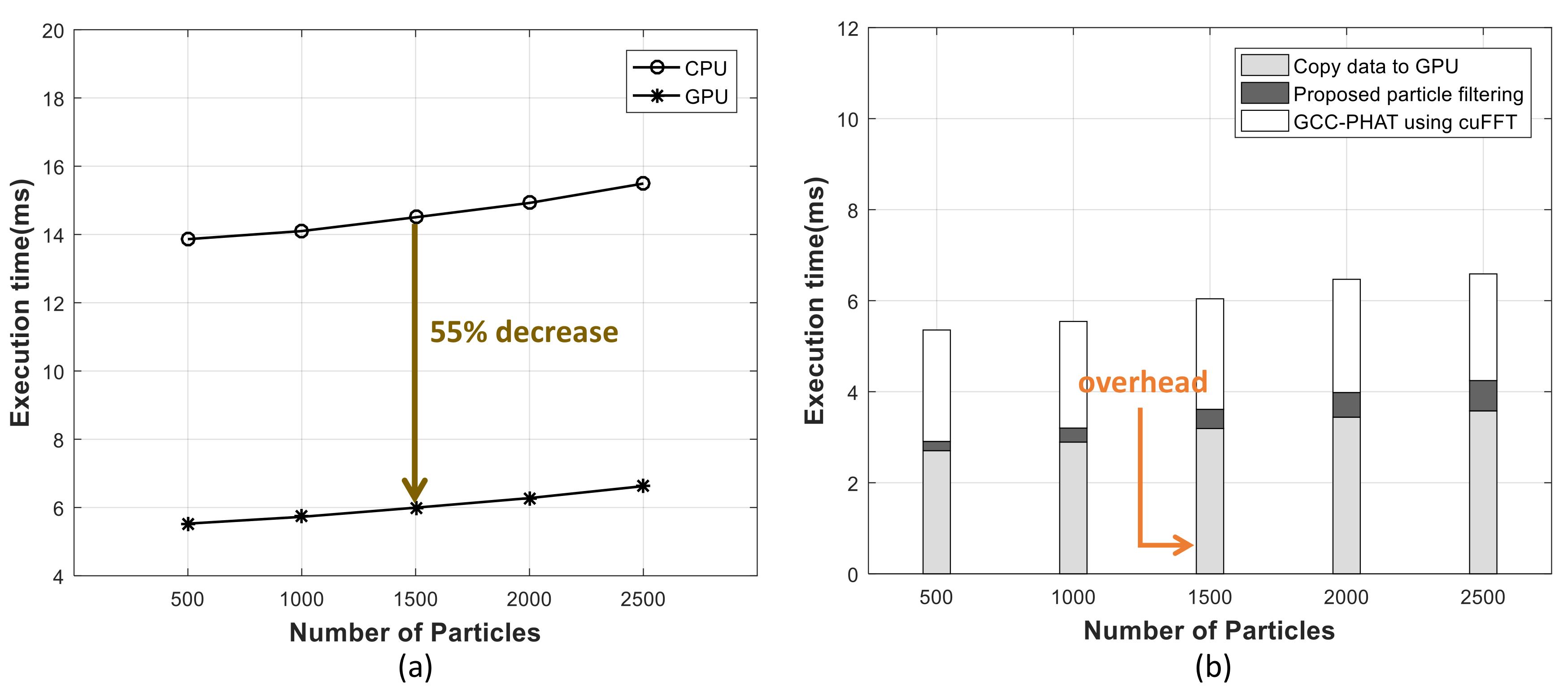
Our approach accelerates the proposed position estimation of a moving target using GPU. The GPU is an architecture that has strength in parallel computing, and is used for high-speed computation of a large amount of data. The proposed GPU-based moving target position estimation can be divided into the operation of obtaining the TDOA measurement value from the sensor, the operation of PF processing, and the tracking of the moving target using multiple system state equations.
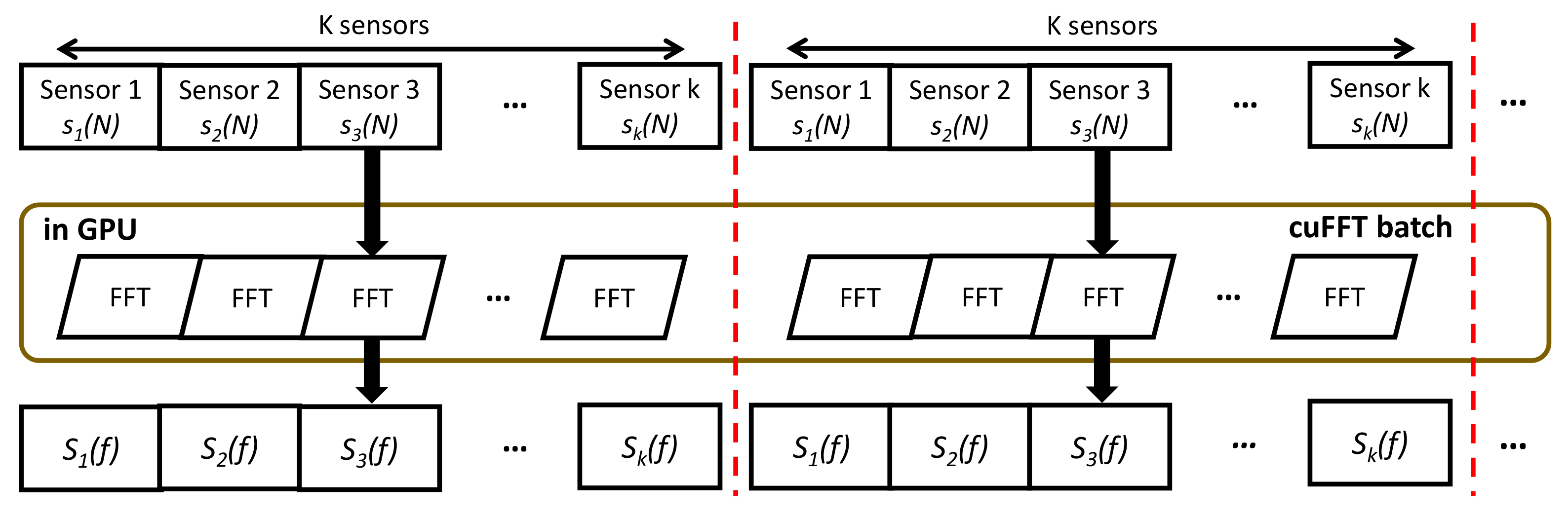
The calculation of the TDOA measurements in the frequency domain uses GCC-PHAT. Therefore, we use the cuFFT library supported by CUDA for accelerating the computation of TDOA measurements using Fast fourier transform. To accelerate Fourier transform on the data using the same coefficients, the Fourier transform operations for multiple sensors are processed in parallel as shown in
Figure 4 by using the batch function of cuFFT. At this time, when the number of sensors is K and the amount of data obtained from each sensor is N, the amount of data copied to the GPU device is K*N. Because the position estimation of the moving target using TDOA measurement is more accurate with the use of many sensors, the proposed accelerated TDOA measurement calculation has an advantage as the data amount increases. As mentioned before, since the proposed algorithm is scalable for number of sensors, the proposed parallel Fast fourier transform is also scalable in the number of sensors.
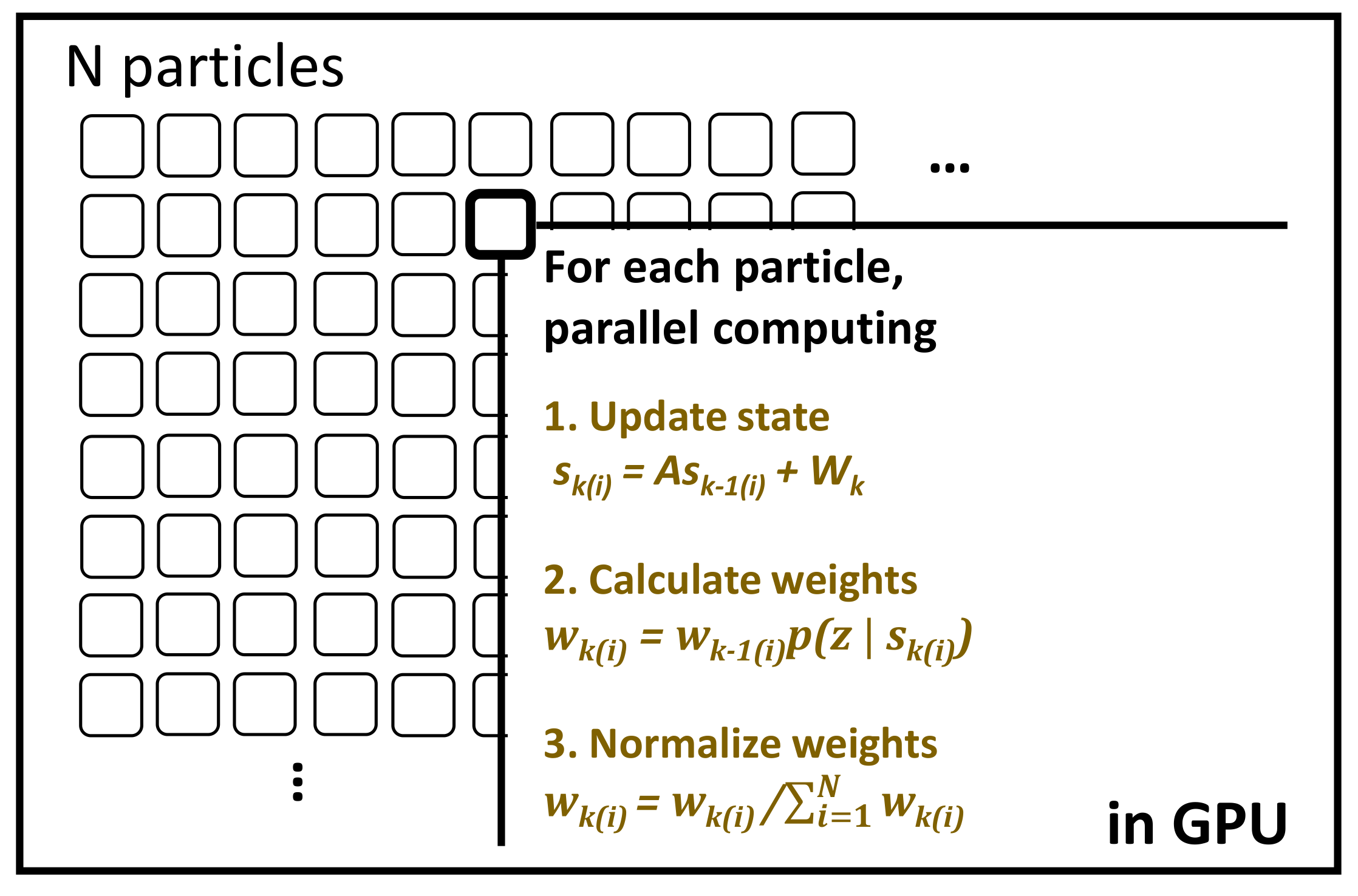
Also, we propose the parallel computing of the PF using GPU as shown in
Figure 5. Because the PF processing depends on the number of particles, the entire process can be accelerated by paralleling and accelerating the operation of each particle in GPU. In particular, the process of estimating the position of moving targets required the acceleration in performing the weight calculation process of each particle in parallel through the process of updating the state of each particle and calculating the measured value from the state.
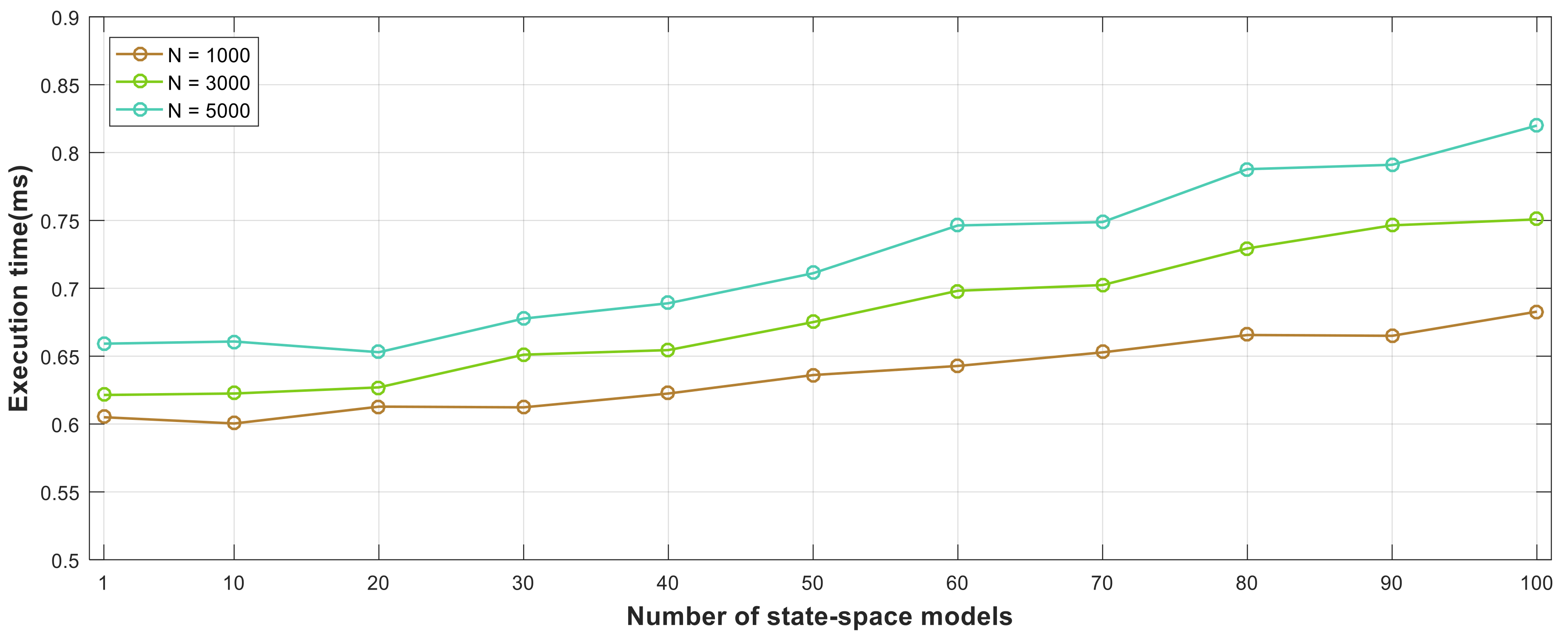
3.4. Target Tracking Using Multiple State-Space Models
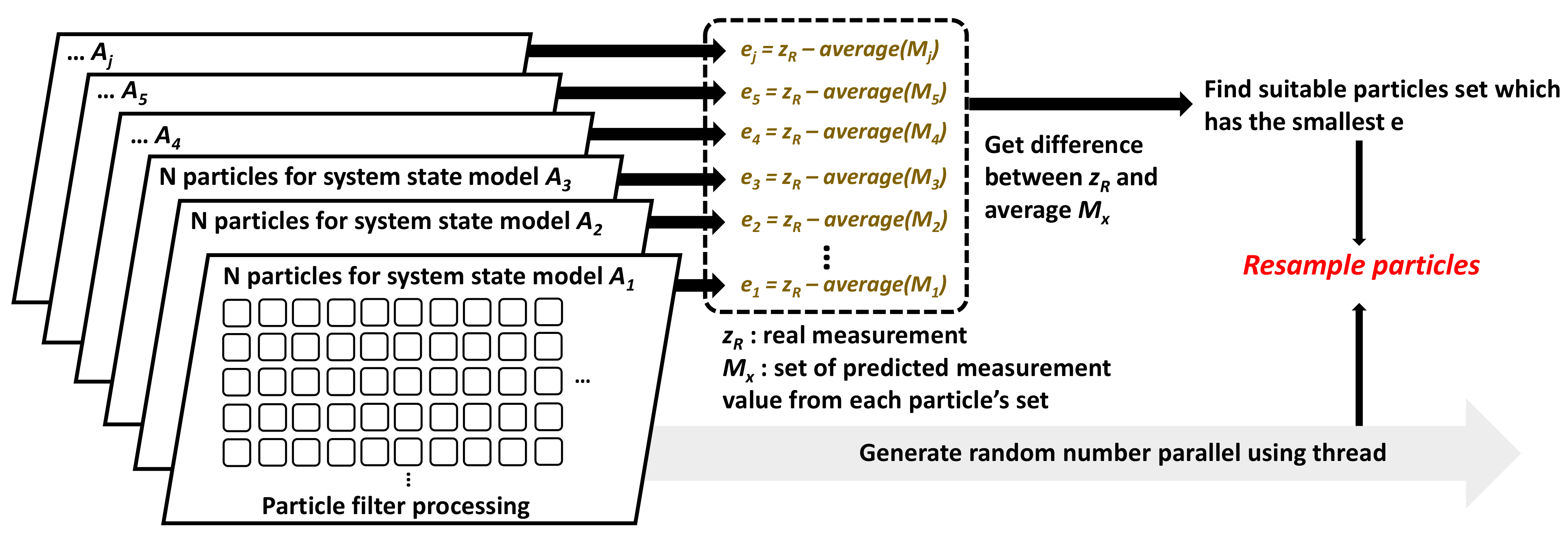
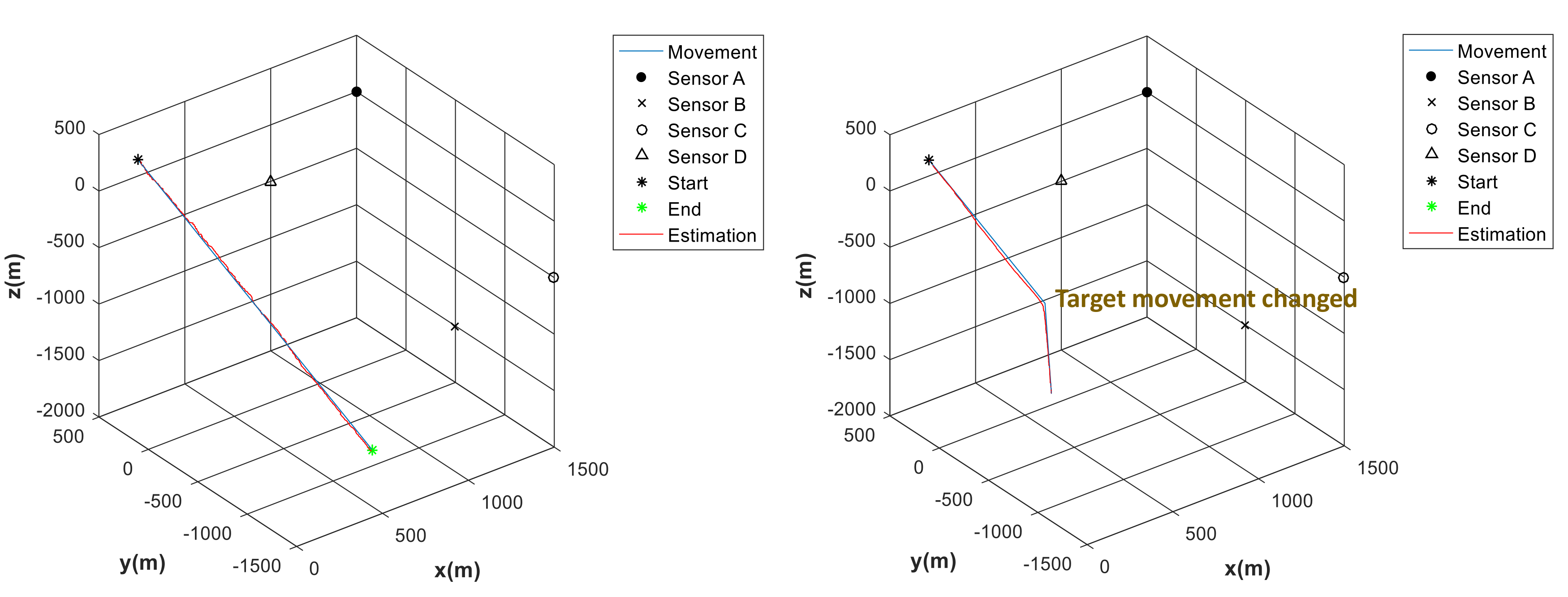
The KF and PF, which can be used for tracking the position of a target have system state equations based on Markov chains. In other words, if the target moves differently from the predefined system state equation, the estimation result in inaccurate. Therefore, in this paper, we define several other system state equations that are expected and go through them like the current system state equations. This proposed structure also can be used for multiple target tracking using multiple system models. From each multiple state update model, we obtain a measured value. Then the measured values are compared with actual measured values, and particles that have measured values with the smallest differences are selected for the remaining PF process. Using proposed method, tracking of sudden movements of a target can be easily enabled using multiple system state equations based on GPU.
The operation of the GPU-based PF using the proposed system state equations is shown in
Figure 6. The process of updating the state of each particle by multiple system state equations is performed in parallel using the kernel function in the GPU. For all particles obtained from the multiple state-space model, the state update process, weight calculation, and normalized process are performed in parallel. To obtain the particles of the state-space model suitable for the current system state, the predicted measured values are compared with actual measured values by finding the smallest difference. Then the particles with the smallest differences are selected and resampled. In our implementation, we use systematic resampling algorithm [
25,
26] in which the random number generation is required in resampling process. There is a study [
27] to accelerate resampling in GPU-based PF. In our study, for reducing the additional overhead running random number calculation during the resampling process, we utilized thread-based running method, which is provided by host CPU, in the process of copying data to the GPU.
Algorithm 3 describes the PF processing using multiple state-space models in GPU. The transition matrix is used to formulate multiple state-space models. The PF processing for the selected state-space model is performed in the individual block unit of GPU. This block runs the threads on which the corresponding particles are allocated. Through the synchronization between threads, the average measurement result can be estimated from the updated state, so that we could determine the appropriate state-space model, then continue to perform the remained PF processing incrementally.
| Algorithm 3 PF using multiple state-space models in GPU |
- 1:
- 2:
- 3:
- 4:
for - 5:
- 6:
- 7:
- 8:
- 9:
- 10:
if - 11:
- 12:
- 13:
- 14:
- 15:
if - 16:
- 17:
end if - 18:
- 19:
end if - 20:
end for
|