Control Strategies for Enhancing Frequency Stability by DFIGs in a Power System with High Percentage of Wind Power Penetration
Abstract
1. Introduction
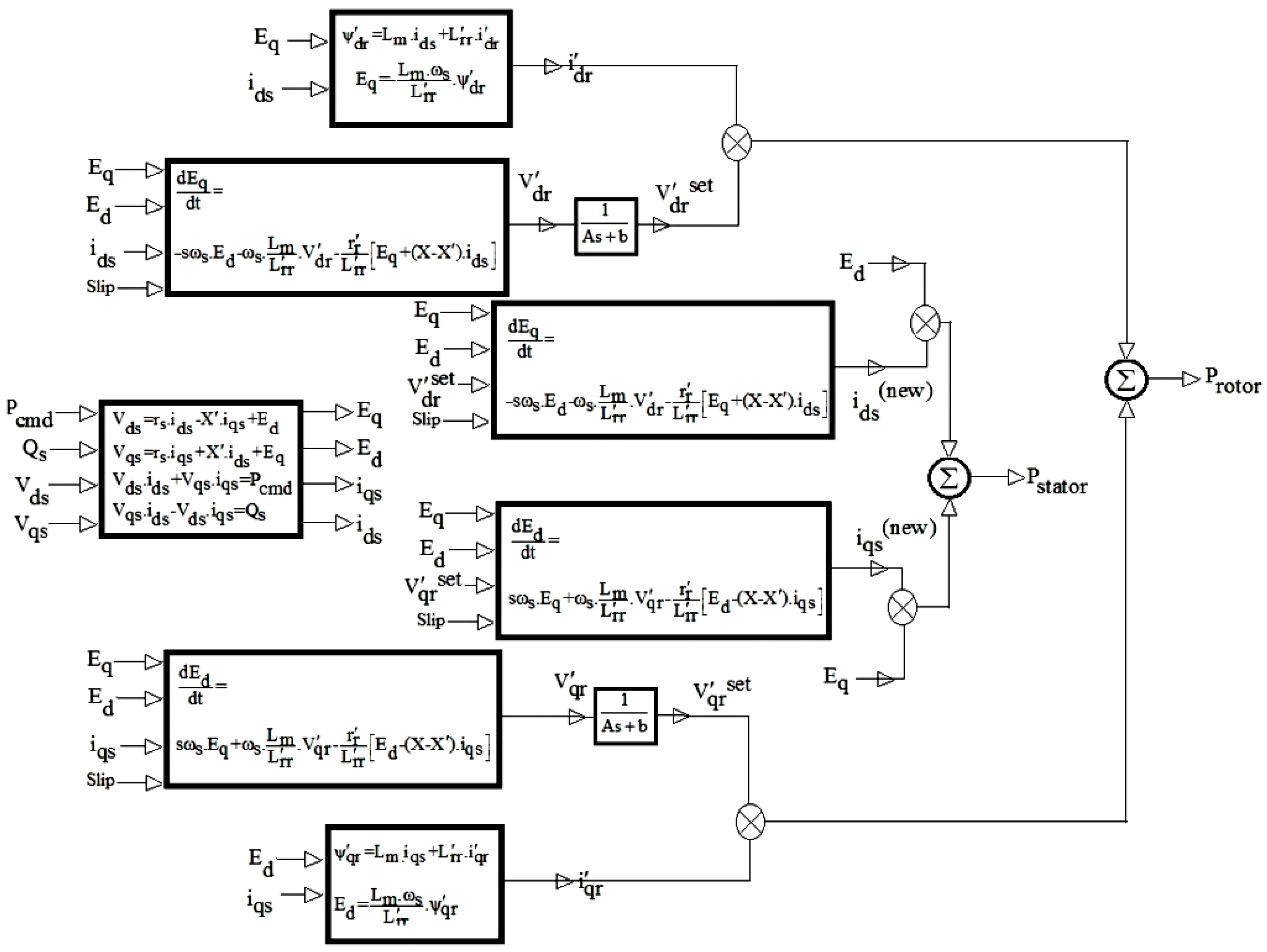
2. Transient Model of a Doubly Fed Induction Generator (DFIG)
2.1. Electrical Part
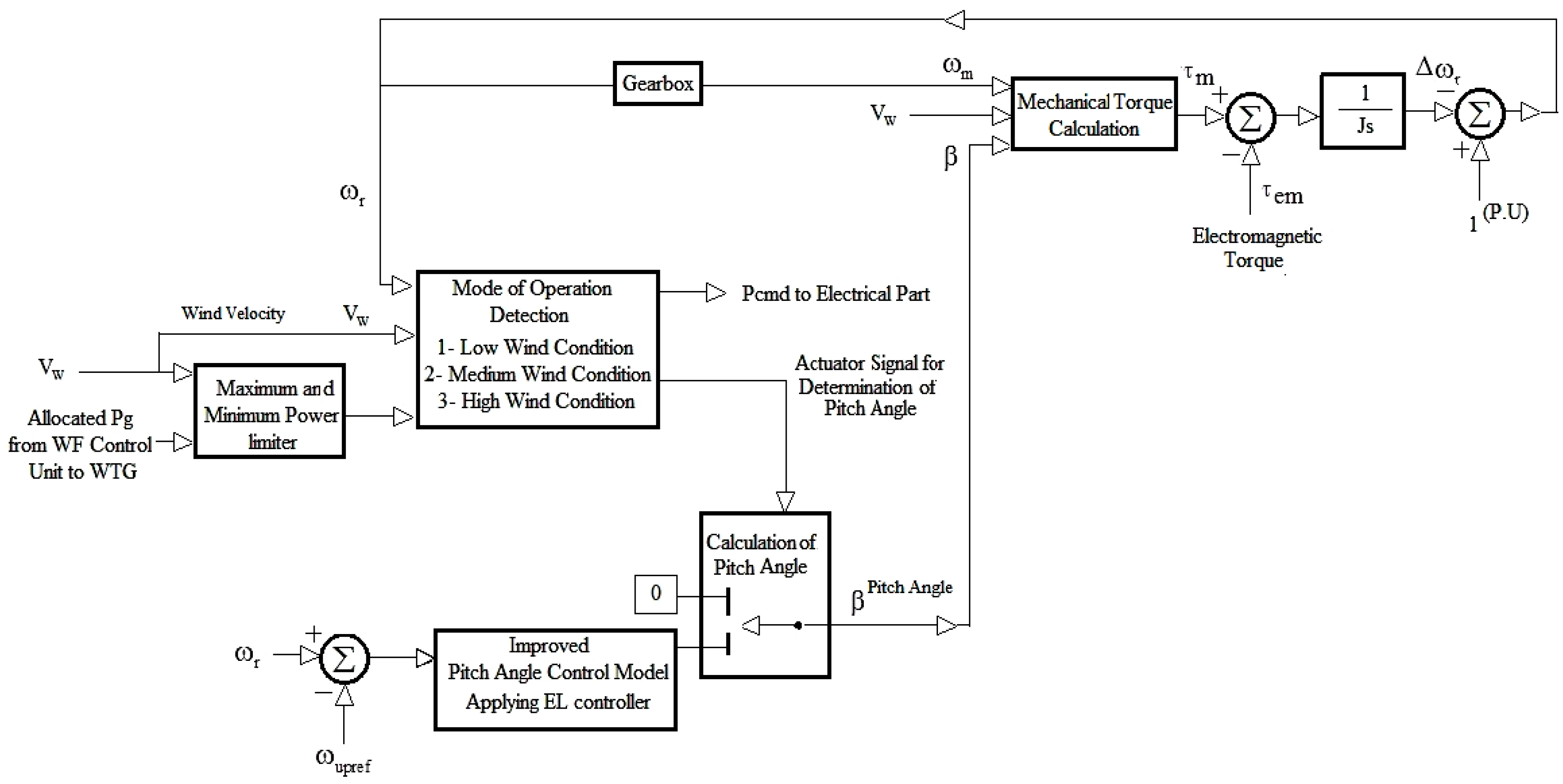
2.2. Mechanical Part
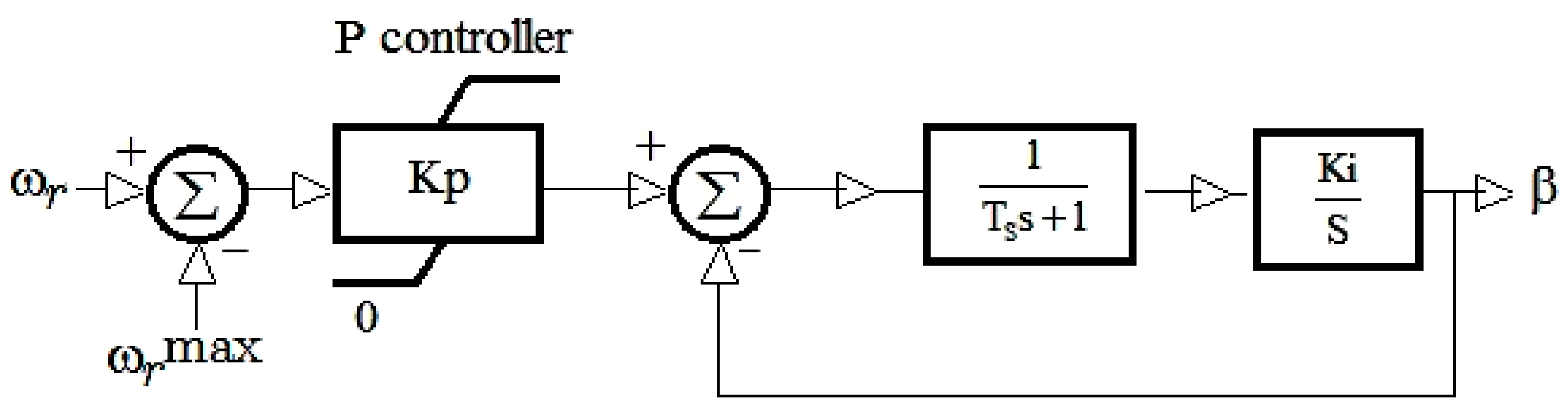
3. Control Strategy
3.1. Active Power Control of a DFIG
3.2. Fuzzy Logic Controller
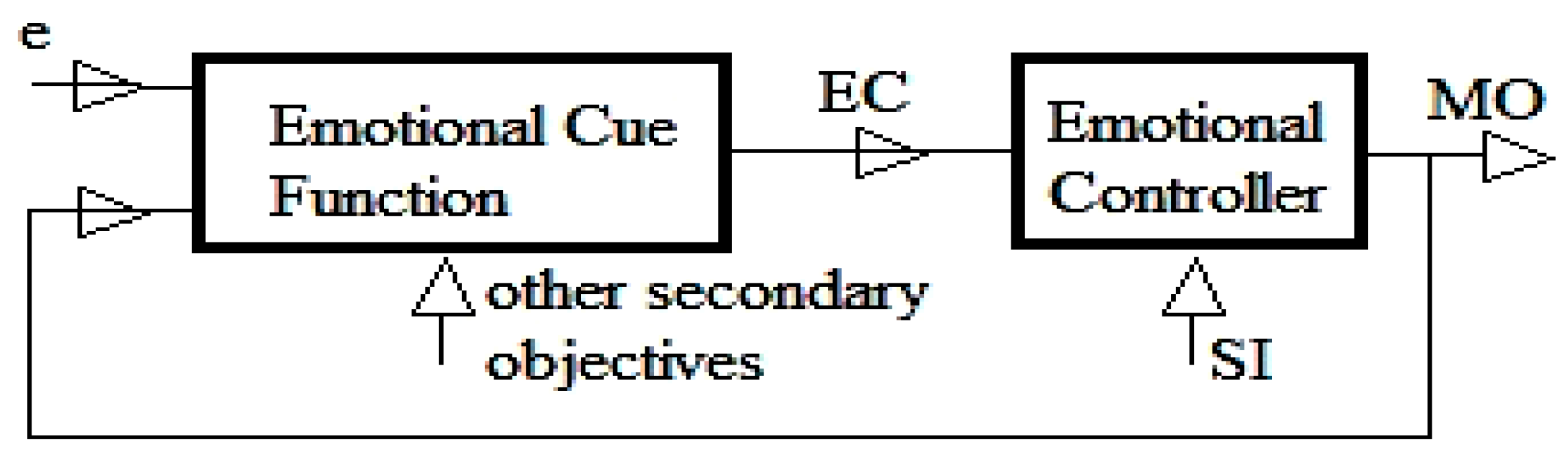
3.3. Emotional Learning Based Intelligent Controller
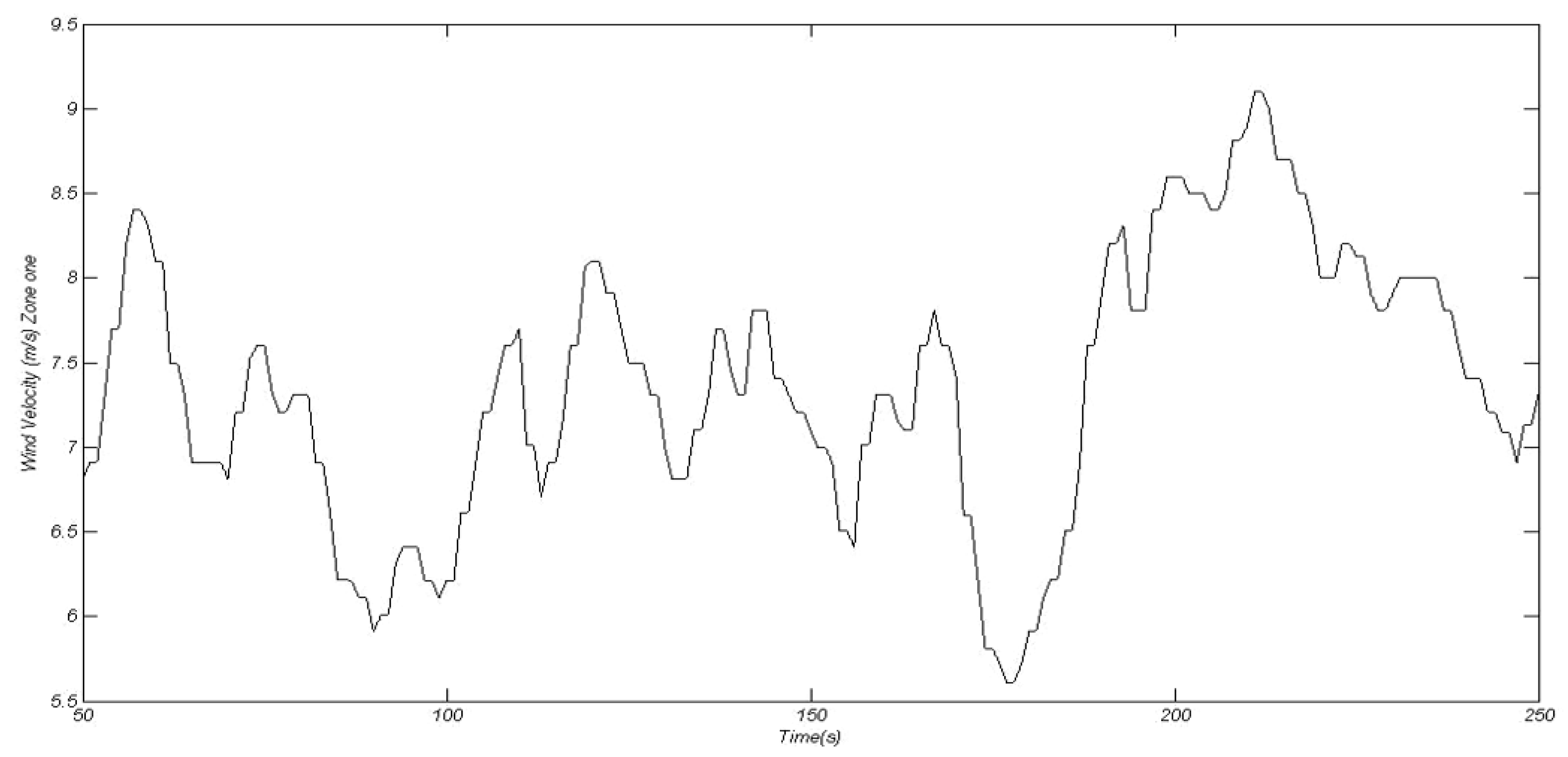
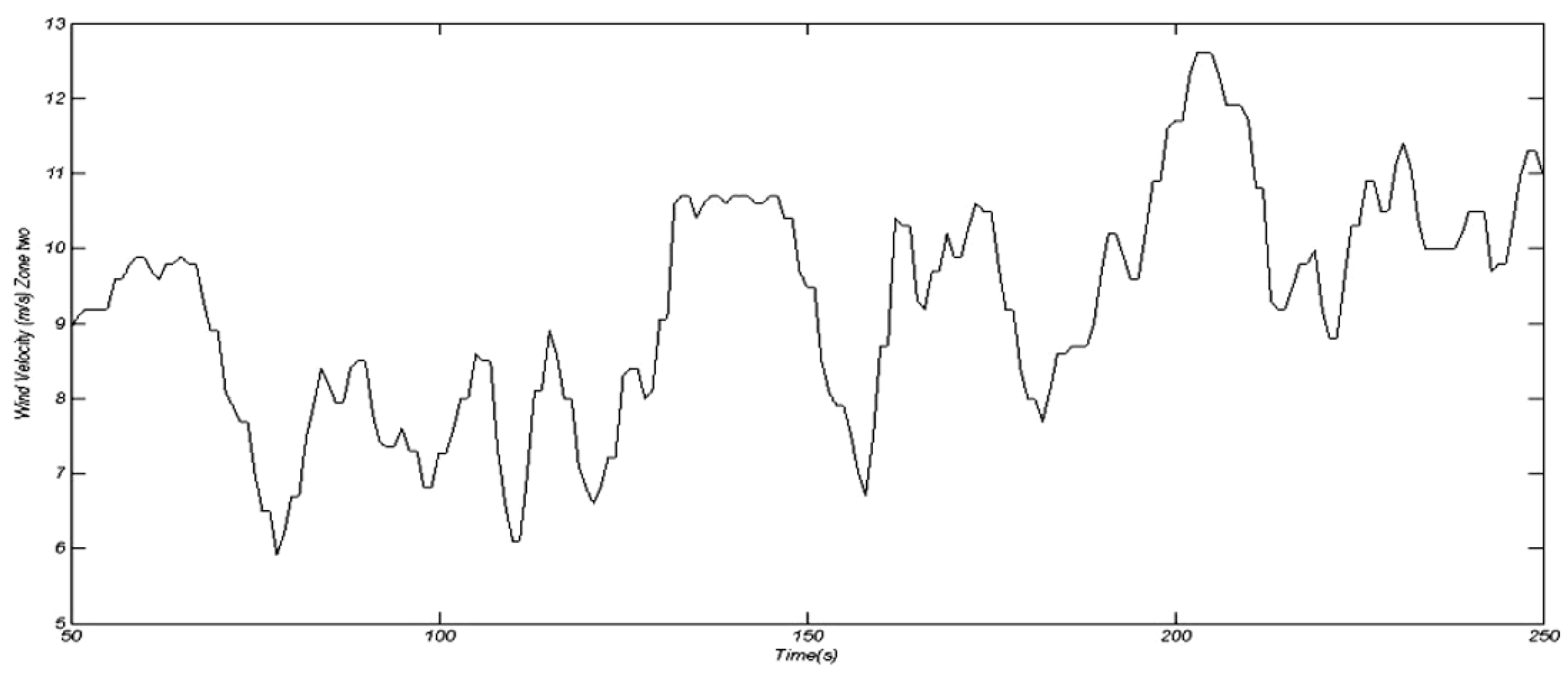
4. Geographical Dispersion of Wind Velocities in Wind Farm (WF)
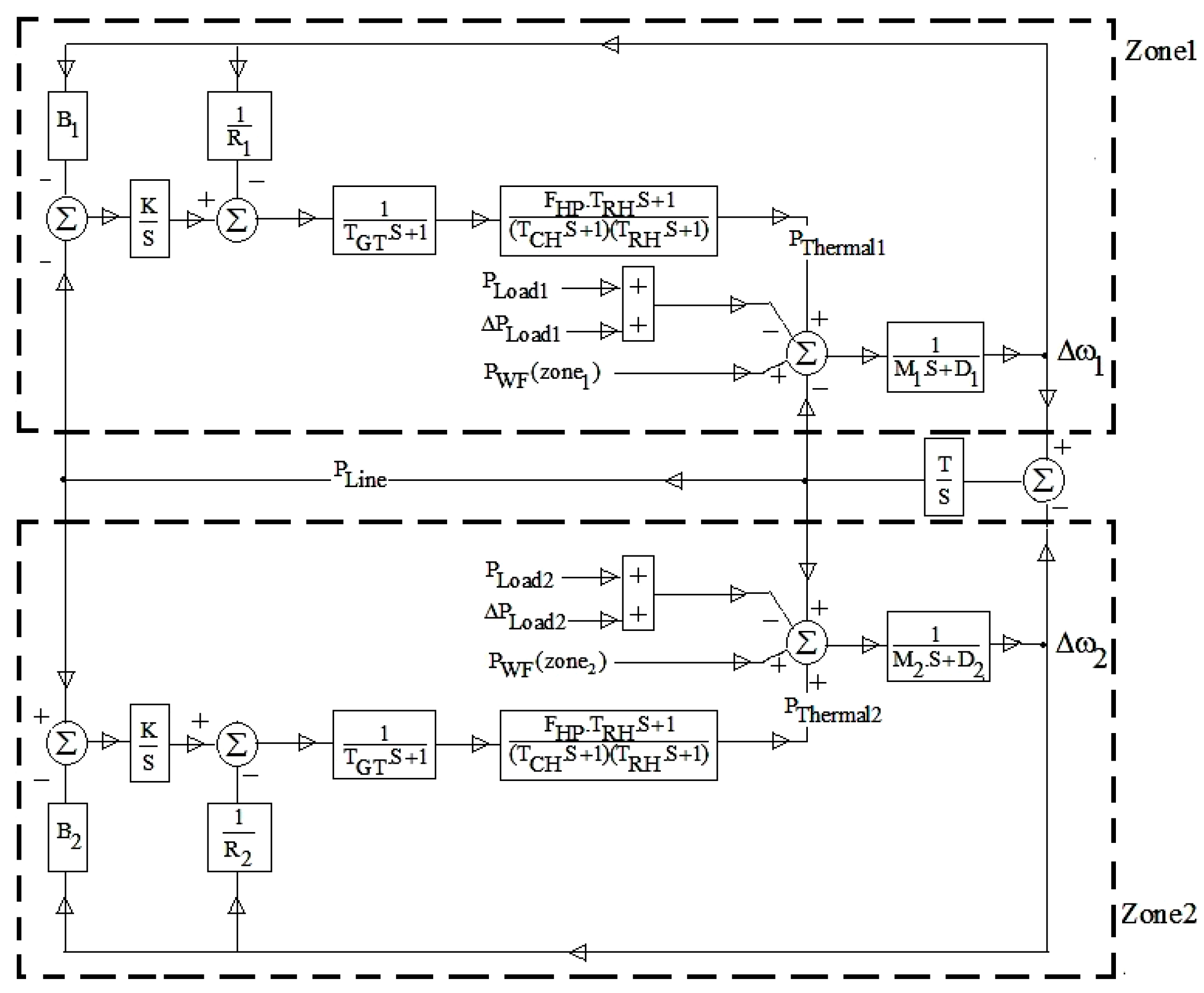
5. Contribution of Wind Power in Frequency Control
- Using a lookup table to allocate weighting factors to individual WTGs in two simulated WFs.
- Using FLC to allocate weighting factors to individual WTGs in two simulated WFs.
- Applying EL controller to set the best value of proportional controller in pitch angle controller and FLC to allocate weighting factors to individual WTGs in each of the two simulated WFs.
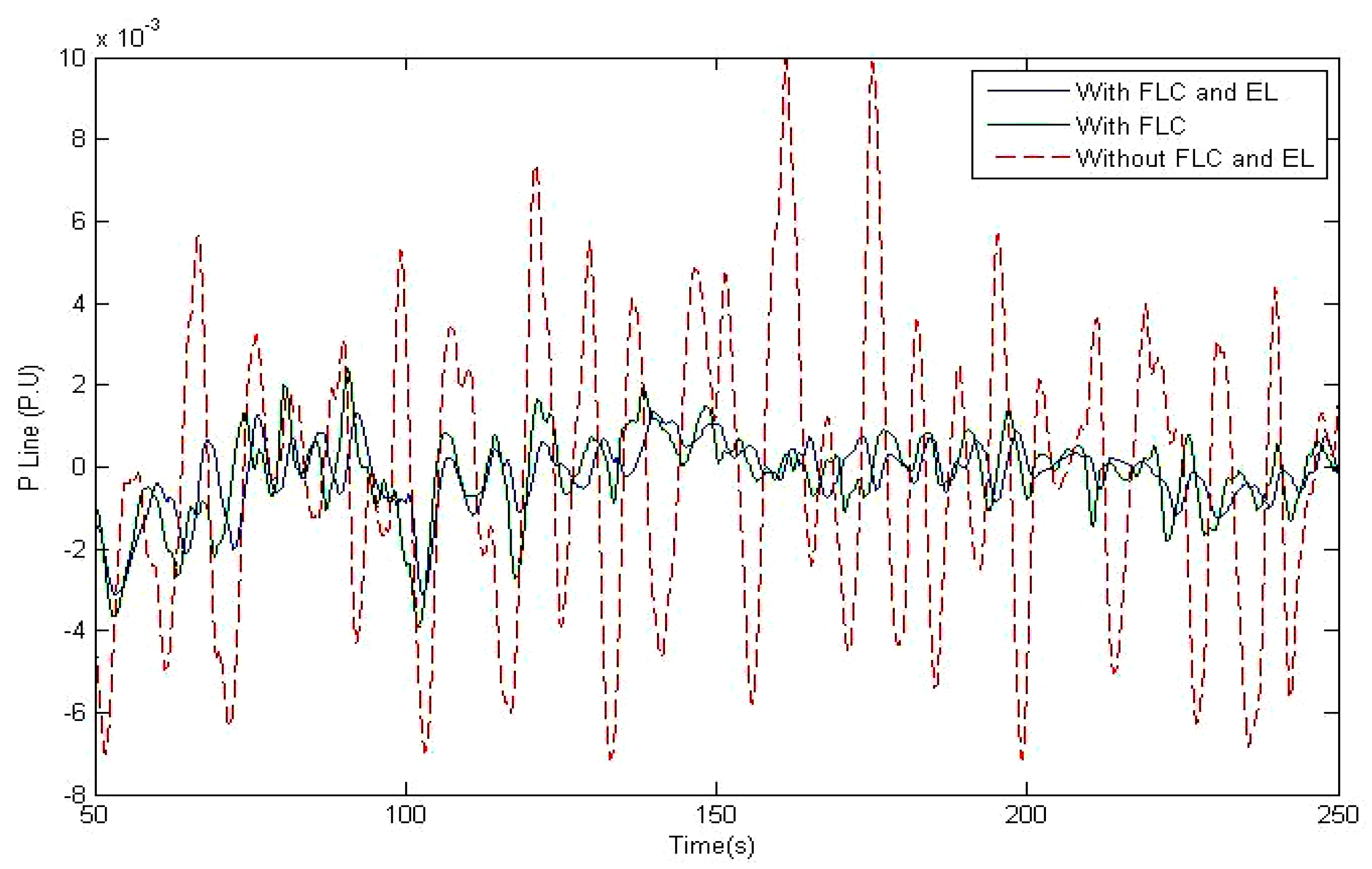
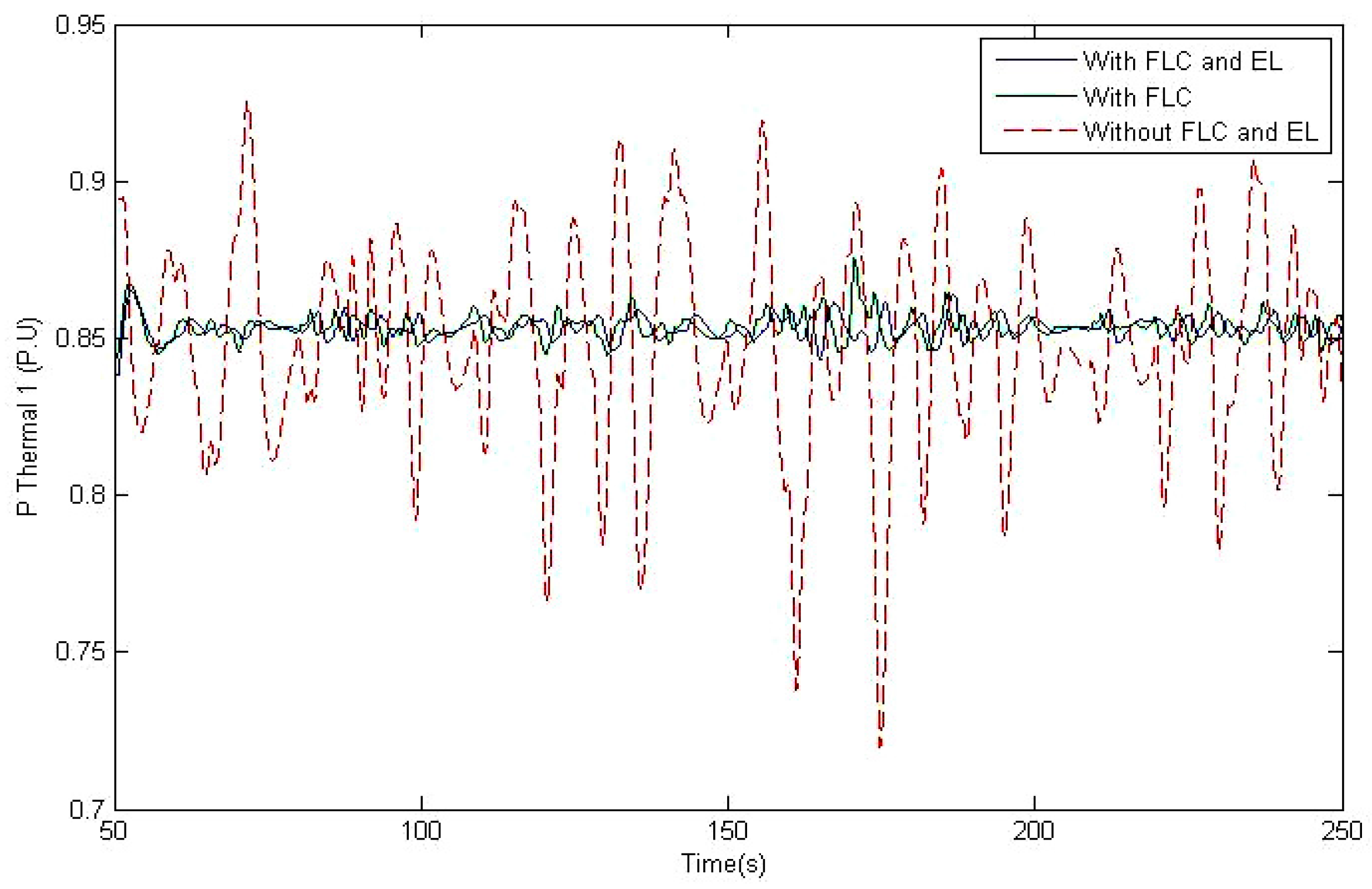
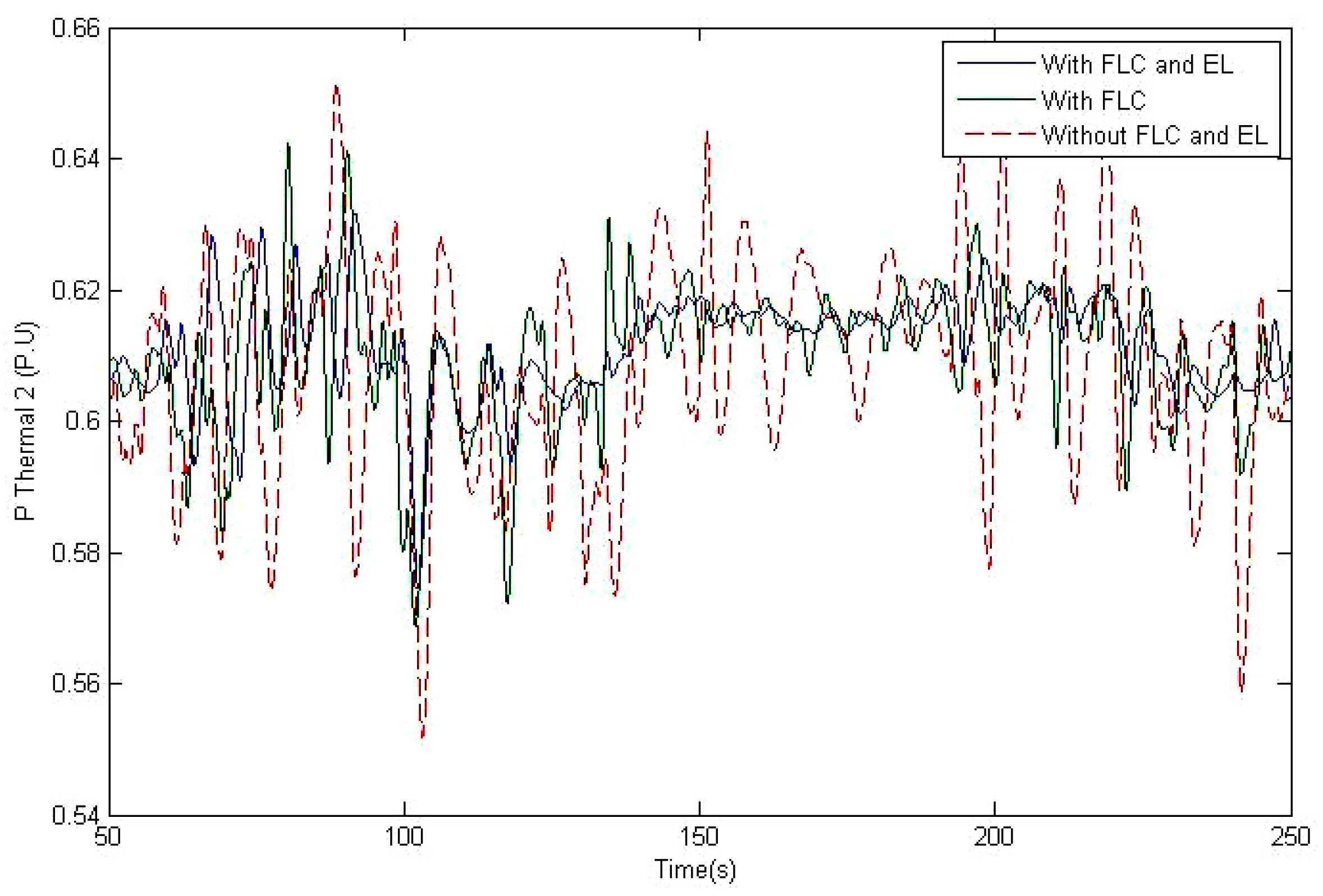
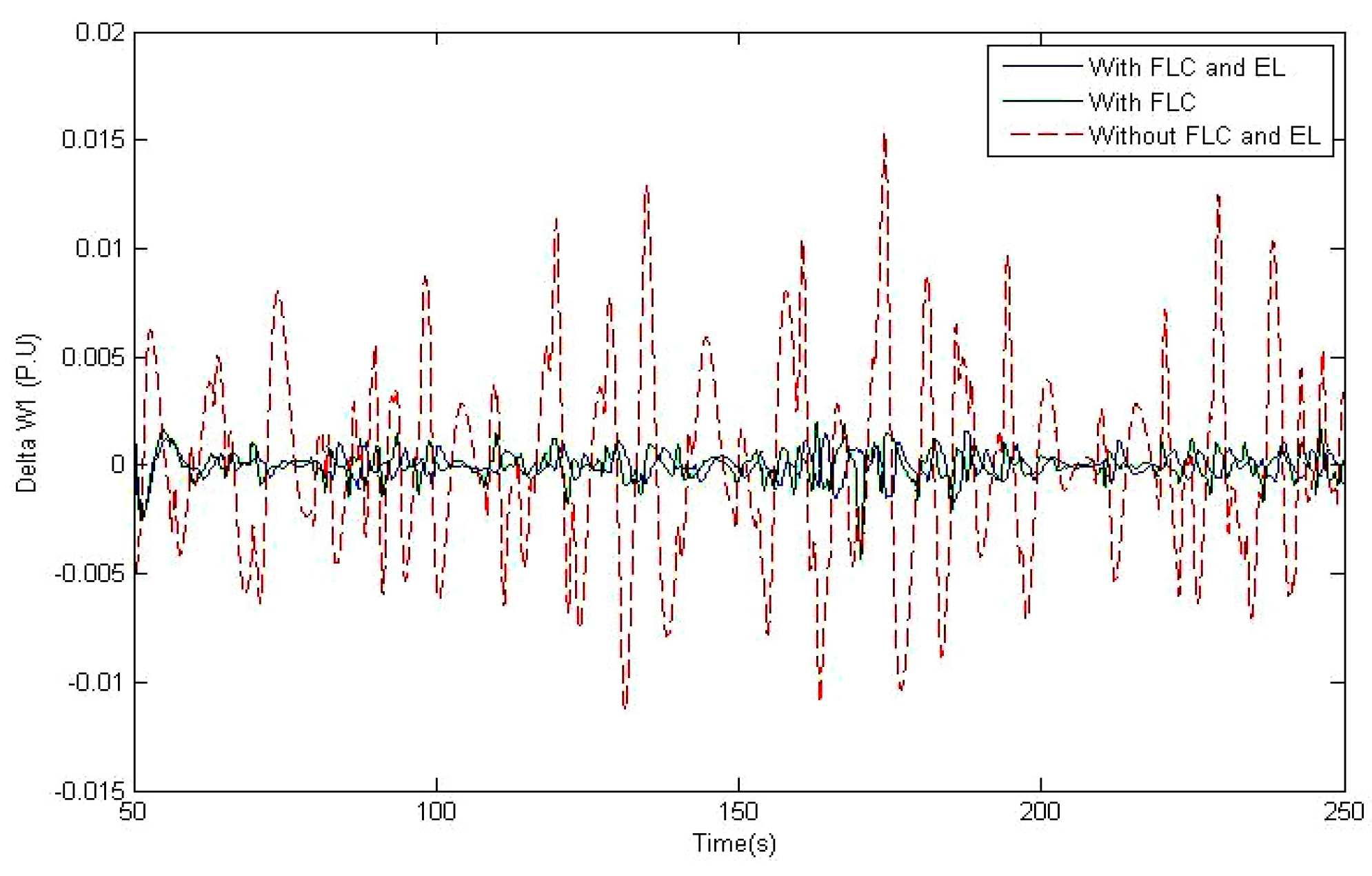
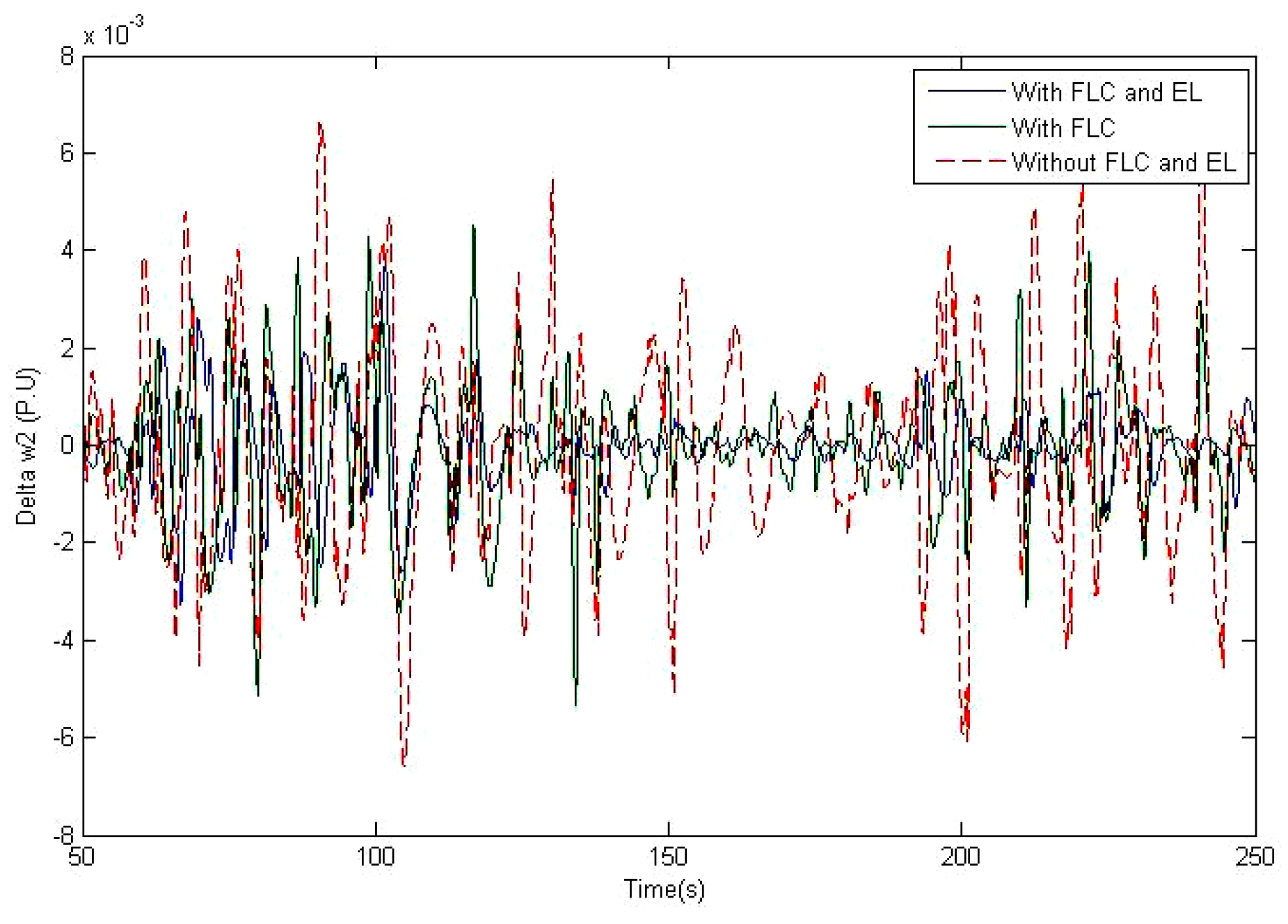
6. Simulation Results and Discussions
7. Conclusions
Author Contributions
Conflicts of Interest
References
- Kanna, O.; Hanba, S.; Asato, S.; Yamashita, K. A Method of Stabilization of a Wind Generator Power Using Back Stepping Algorithm. IEEJ Trans. Power Energy 1997, 117, 1513–1519. [Google Scholar] [CrossRef]
- Lei, Y.; Mullane, A.; Lightbody, G.; Yacamini, R. Modeling of the wind turbine with a doubly fed induction generator for grid integration studies. IEEE Trans. Energy Convers. 2006, 21, 257–264. [Google Scholar] [CrossRef]
- Steban, M.D.; Diez, J.J.; Lopez, J.S.; Negro, V. Why offshore wind energy? Renew. Energy 2011, 36, 444–450. [Google Scholar] [CrossRef]
- Chang-Chien, L.R.; Lin, W.T.; Yin, Y.C. Enhancing Frequency Response Control by DFIGs in the High Wind Penetrated Power Systems. IEEE Trans. Power Syst. 2011, 26, 710–718. [Google Scholar] [CrossRef]
- Ackermann, T.; Abbad, J.R.; Dudurych, I.M.; Erlich, I.; Holttinen, H.; Kristofferson, J.R.; Sorensen, P.E. European Balancing Act. IEEE Power Energy Mag. 2007, 5, 90–103. [Google Scholar] [CrossRef]
- Chang-Chien, L.R.; Hung, C.M.; Yin, Y.C. Dynamic Reserve Allocation for System Contingency by DFIG Wind Farms. IEEE Trans. Power Syst. 2008, 23, 729–736. [Google Scholar] [CrossRef]
- Chang-Chien, L.R.; Yin, Y.-C. Strategies for Operating Wind Power in a Similar Manner of Conventional Power Plant. IEEE Trans. Energy Convers. 2009, 24, 926–934. [Google Scholar] [CrossRef]
- Wood, A.J.; Wollenberg, B.F. Control of Generation. In Power Generation, Operation and Control, 2nd ed.; John Wiley and Sons: New York, NY, USA, 2013; pp. 345–360. ISBN 978-0-471-79055-6. [Google Scholar]
- Kundur, P. Control of Active Power and Reactive Power. In Power System Stability and Control; Balu, N.J., Lauby, M.G., Eds.; McGrawHill: New York, NY, USA, 1994; pp. 581–627. ISBN 978-0070359581. [Google Scholar]
- Rodriguez, J.M.; Fernandez, J.L.; Beato, D.; Iturbe, R.; Usaola, J.; Ledesma, P.; Wilhelmi, J.R. Incidence on Power System Dynamics of High Penetration of Fixed Speed and Doubly Fed Wind Energy Systems: Study of the Spanish Case. IEEE Trans. Power Syst. 2002, 4, 1089–1095. [Google Scholar] [CrossRef]
- Rueda, J.L.; Erlich, I. Impacts of large scale integration of wind power on power system small signal stability. In Proceedings of the First International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, Weihai, China, 6–9 July 2011; pp. 673–681. [Google Scholar]
- Slootweg, J.G.; Polinder, H.; Kling, W.L. Representing wind turbine electrical generating systems in fundamental frequency simulations. IEEE Trans. Energy Convers. 2003, 18, 516–524. [Google Scholar] [CrossRef]
- Slootweg, J.G.; Kling, W.L. The impact of large scale wind power generation on power system oscillations. Electr. Power Syst. Res. 2003, 67, 9–20. [Google Scholar] [CrossRef]
- Neris, A.; Vovos, N.; Giannakopaulos, G. A variable speed wind energy conversion scheme for connection to weak ac systems. IEEE Trans. Energy Convers. 1999, 14, 122–127. [Google Scholar] [CrossRef]
- Akhmatov, A. Analysis of Dynamic Behavior of Electric Power Systems with Large Amount of Wind Power. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 2003. [Google Scholar]
- ESB National Grid, Grid Code. Available online: http://www.eirgrid.com (accessed on 20 June 2017).
- Xue, Y.; Tai, N. Review of contribution to frequency control through variable speed wind turbine. Renew. Energy 2011, 36, 1671–1677. [Google Scholar] [CrossRef]
- Teninge, A.; Jecu, C.; Roye, D.; Bacha, S.; Duval, J.; Belhomme, R. Contribution to frequency control through wind turbine inertial energy storage. IET Renew. Power Gener. 2009, 3, 358–370. [Google Scholar] [CrossRef]
- Zhao, H.; Wu, Q.; Hu, S.; Xu, H.; Nygaard Rasmussen, C. Review of energy storage system for wind power integration support. Appl. Energy 2015, 137, 545–553. [Google Scholar] [CrossRef]
- De Almeida, R.G.; Pecas Lopes, J.A. Participation of doubly fed induction wind generators in system frequency regulation. IEEE Trans. Power Syst. 2007, 22, 944–950. [Google Scholar] [CrossRef]
- De Almeida, R.G.; Pecas Lopes, J.A.; Barreiros, J.A.L. Improving Power System Dynamic Behavior Through Doubly Fed Induction Machines Controlled by Static Converter Using Fuzzy Control. IEEE Trans. Power Syst. 2004, 19, 1942–1950. [Google Scholar] [CrossRef]
- Krause, P.C.; Wasynczuk, O. Symmetrical Induction Machines. In Analysis of Electric Machinery and Drive Systems, 2nd ed.; Akay, M., Anderson, J.B., Eds.; John Wiley and Sons: New York, NY, USA, 2002; pp. 141–181. ISBN 0-471-14326-X. [Google Scholar]
- Luo, C.; Banakar, H.; Baike, S.; Ooi, B. Strategies to smooth wind power fluctuations of wind turbine generator. IEEE Trans. Energy Convers. 2007, 22, 341–349. [Google Scholar] [CrossRef]
- Lee, C.C. Fuzzy logic in control systems: Fuzzy logic controller. IEEE Trans. Syst. 1990, 20, 404–418. [Google Scholar] [CrossRef]
- Moren, J.; Balkenius, C. A Computational Model of Emotional Learning in the Amygdala. In From Animals to Animats 6: Proceedings of the 6th International Conference on the Simulation of Adaptive Behavior, Cambridge; MIT Press: Cambridge, MA, USA, 2000; pp. 115–124. [Google Scholar]
- Fatourechi, M.; Lucas, C.; Khaki Sedigh, A. Reduction of Maximum Overshoot by means of Emotional Learning. In Proceedings of the 6th Annual CSI Computer Conference, Isfahan, Iran, 20–22 February 2001; pp. 460–467. [Google Scholar]
- Huang, G.; Zhen, Z.; Wang, D. Brain Emotional Learning Based Intelligent Controller for Nonlinear System. In Proceedings of the Second International Symposium on Intelligent Information Technology Application, Shanghai, China, 20–22 December 2008; pp. 660–663. [Google Scholar]
- Coelingh, J.P. Geographical Dispersion of Wind Power Output in Ireland; IWEA Irish Wind Energy Association: Kildare, Ireland, 1999; pp. 4–9. [Google Scholar]
- Wind Profile Calculator Considering Roughness Classes and Lengths. Available online: http://wind-data.ch (accessed on 1 July 2017).
- Wen, Z.W.; Ding, L.; He, S. Analysis on Effect of Parameters of Different Wind Generator on Power Grid Transient Stability. Energy Power Eng. 2013, 5, 363–367. [Google Scholar] [CrossRef]
- Wind Group Association. Wind Velocity Database of Binalood Wind Farm; Sun-Air Research Institute of Ferdwosi University: Mashhad, Iran, 2016. [Google Scholar]
- Tripathy, S.C.; Kalantar, M.; Balasubramanian, R. Dynamics and Stability of Wind and Diesel Turbine Generators with Superconducting Magnetic Energy Storage Unit on an Isolated Power System. IEEE Trans. Energy Convers. 1991, 6, 579–585. [Google Scholar] [CrossRef]
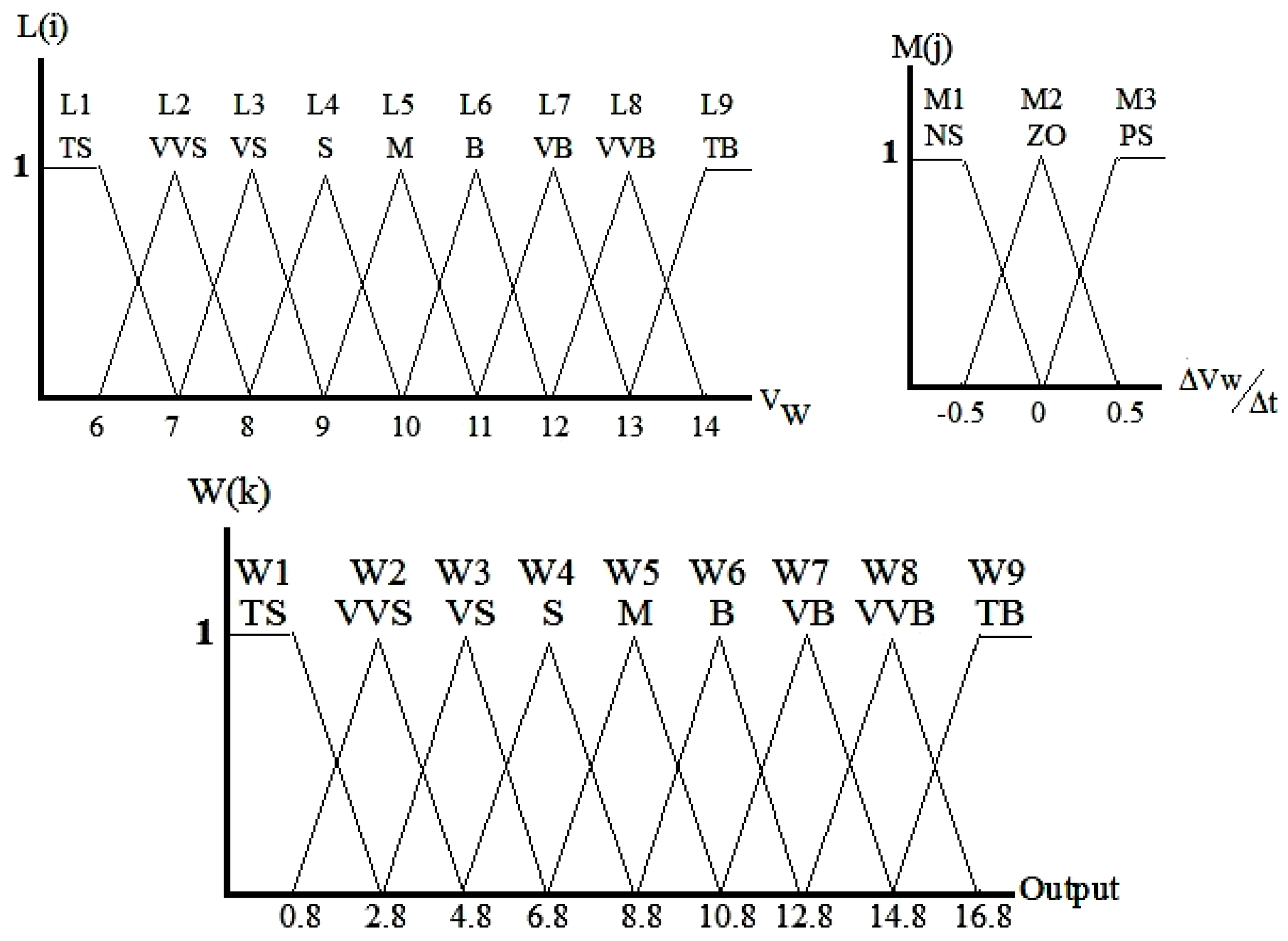
| Fuzzy Reasoning | ||||
|---|---|---|---|---|
| NS | ZO | PS | ||
| TS | TS | TS | VVS | |
| VVS | TS | VVS | VS | |
| VS | VVS | VS | S | |
| S | VS | S | M | |
| M | S | M | B | |
| B | M | B | VB | |
| VB | B | VB | VVB | |
| VVB | VB | VVB | TB | |
| TB | VVB | TB | TB | |
| Roughness Length Z | Land Cover Types |
|---|---|
| 0.0002 m | Water surfaces: seas and Lakes |
| 0.0024 m | Open terrain with smooth surface, e.g., concrete, airport runways, mown grass etc. |
| 0.03 m | Open agricultural land without fences and hedges; maybe some far apart buildings and very gentle hills |
| 0.055 m | Agricultural land with a few buildings and 8 m high hedges seperated by more than 1 km |
| 0.1 m | Agricultural land with a few buildings and 8 m high hedges seperated by approx. 500 m |
| 0.2 m | Agricultural land with many trees, bushes and plants, or 8 m high hedges seperated by approx. 250 m |
| 0.4 m | Towns, villages, agricultural land with many or high hedges, forests and uneven terrain |
| 0.6 m | Large towns with high buildings |
| 1.6 m | Large cities with high buildings and skyscrapers |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| FHP | 0.3 | M1, M2 | 5 |
| TRH | 7 s | D1, D2 | 1 |
| TCH | 0.3 s | k | 0.3 |
| TGT | 0.2 | R1 | 0.05 |
| T | 0.5 | B1 | 20.6 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Prated | 2 MW | Xm | 3.5 P.U |
| Lss | 3.6 P.U | rs | 0.0043 P.U |
| L’rr | 3.78 P.U | r’r | 0.012 P.U |
| Cf | 0.7 P.U | R | 50 m |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kazemi Golkhandan, R.; Aghaebrahimi, M.R.; Farshad, M. Control Strategies for Enhancing Frequency Stability by DFIGs in a Power System with High Percentage of Wind Power Penetration. Appl. Sci. 2017, 7, 1140. https://doi.org/10.3390/app7111140
Kazemi Golkhandan R, Aghaebrahimi MR, Farshad M. Control Strategies for Enhancing Frequency Stability by DFIGs in a Power System with High Percentage of Wind Power Penetration. Applied Sciences. 2017; 7(11):1140. https://doi.org/10.3390/app7111140
Chicago/Turabian StyleKazemi Golkhandan, Reza, Mohammad R. Aghaebrahimi, and Mohsen Farshad. 2017. "Control Strategies for Enhancing Frequency Stability by DFIGs in a Power System with High Percentage of Wind Power Penetration" Applied Sciences 7, no. 11: 1140. https://doi.org/10.3390/app7111140
APA StyleKazemi Golkhandan, R., Aghaebrahimi, M. R., & Farshad, M. (2017). Control Strategies for Enhancing Frequency Stability by DFIGs in a Power System with High Percentage of Wind Power Penetration. Applied Sciences, 7(11), 1140. https://doi.org/10.3390/app7111140




