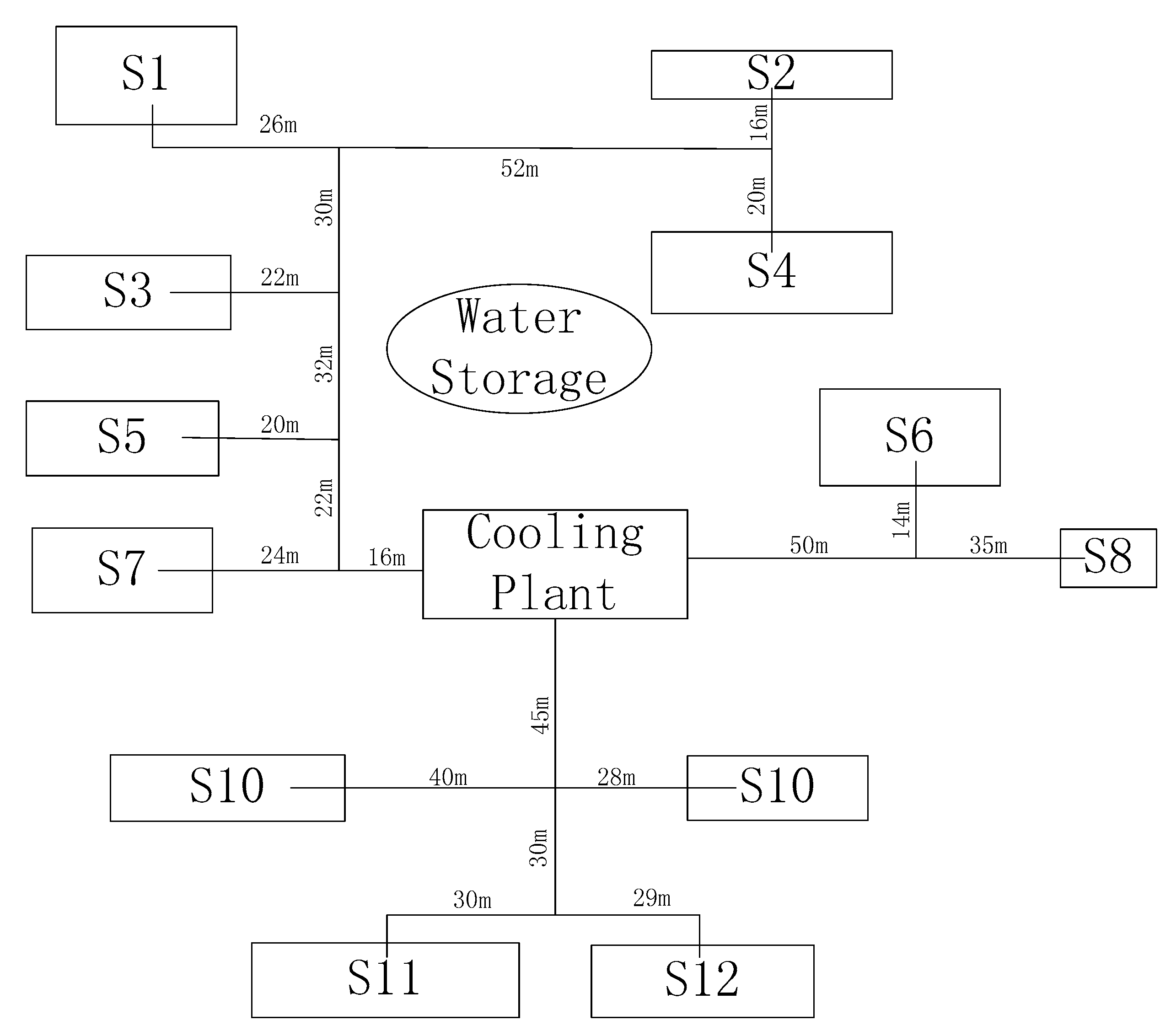1. Introduction
District cooling systems (DCSs), which generate cold water in a central plant that is distributed to end uses to fulfill its cooling demands, have become a widely used solution for large-area buildings in many countries [
1,
2]. Generally, there are two types of DCSs that differ according to the type of water that is produced at the central plant; the two types are as follows: (1) a centralized chilled water system; and, (2) a centralized cooling water system. In the first type, the central chiller is designed to have large cooling capacity to promote a high coefficient of performance (COP); additionally, the removal of terminal chillers makes it possible to more efficiently utilize the building space [
3]. It also provides an ideal platform for interrelated thermal technologies implementing tri-generation [
2] or thermal storage [
4]. The second system, also referred to as the water-loop heat pump system, produces cooling water via a cooling tower or natural sources, such as seawater and transports it to end-use chillers [
5]. This system is designed to utilize the distributed chillers to achieve variable cooling loads in end uses. Another advantage of this system is that it can incorporate vast varieties of cooling sources and recover the rejected heat inside of a building [
6,
7,
8]. Because systems with variable cooling loads are the focus of this study, the second system with centralized cooling water was selected for further research.
However, it should be noted that DCSs do possess limitations. For instance, the water transportation system consumes a large amount of energy, as an America-based study showed that the pumping system in a typical DCS consumed 30% of the total energy of the system [
9]. The reason for this can be explained by the design and control strategy of conventional central circulation pump (CCCP) systems. The central circulating pumps are designed for the most remote consumer; thus, the flow rate and pump head are quite excessive for the other consumers. Therefore, the remaining consumers must employ valves to control water flow, which responds slow and causes additional losses in local pressure. The use of throttling valves alters the resistance characteristics of the network, resulting in the low efficiency of pump operation. In addition, the precision of water flow control is reduced when the end-use cooling demand varies according to each consumer, which leads to an imbalance in cold supply. Under the assumption that a large flow of water would offset the cold supply imbalance, most of the pumps currently in use generate large flows, which again increases transport energy consumption [
10].
However, these problems can be solved by employing distributed variable-frequency pumps (DVFPs). When the cooling load varies, the chiller adjusts the heat that is released to condensing water side and the DVFP adjusts the pump speed to control the cooling water flow, maintain the supply, and return water temperature difference () at a preset value. Each DVFP is designed to provide the pressure drop in corresponding end-use building and main pipes. Thus, the main circulating pumps, which are also referred to as primary pumps (PPs), are removed and the transportation energy is reduced. By replacing the valves with pumps, the pump head is reduced and the resistance characteristics of the main pipes become relatively stable, thereby increasing pump efficiency. Additionally, variable-frequency pumps are able to rapidly and precisely adjust water flow, while maintaining a level of high-efficiency operation, preventing extra flow, and satisfying the specific cooling demand of each end-user.
Variable frequency pumps (VFPs) have been studied for many years and are implemented in a wide variety of applications in fields related to air-conditioning, district heating, and municipal water distribution. Some studies have focused on control strategies for VFPs. Ma and Wang optimized pump speed and sequence control in a complex air-conditioning system to save energy [
11]. Wang and Burnett developed a control strategy that implements an adaptive and derivative strategy to optimize the speed of pumps by resetting the pressure set point [
12]. Marchi studied the components in pumping systems to provide insight into the assessment of VFPS efficiency and energy consumption [
13]. Pan studied the performance of several check valves that were connected to DVFPs and the influence of these valves on energy consumption [
14]. Some studies also focused on the performance of DVFPs in actual projects and calculated the energy-saving and cost-saving potential; this includes the hydraulic performance of a district heating project in Kuerle, China [
15], the minimum of capital cost and energy consumption in a district heating projects in Dalian, China [
16], and a project involving a municipal water distribution system [
17]. Gamberi et al. simulated a multi-zone heating system and developed the Newton-Raphson method to solve various hydraulic problems [
18]. Sheng analyzed the factors affecting energy saving rate in the DVFPs system [
19]. Although these studies yielded significant contributions to the field, most current studies are focused on chilled water pumps and fail to adequately investigate cooling water pumps, the influence of cooling water temperature on the entire system, and, more significantly, the chiller performance. Furthermore, there is a lack of studies on timely effective system performance in response to cooling loads that fluctuate in real time.
Alternatively, thermal storage systems including water storage, ice storage, and eutectic salt storage systems have also been widely used in DCSs. Under the conditions of time-of-use tariff of electricity, thermal storage systems produce and store hot/cold water overnight at relatively cheaper electricity costs and release the stored contents at the peak price time. As a result, the system has been proven as cost-saving and peak shaving, which is beneficial for electric power plants [
20,
21]. Furthermore, the nominal cooling capacity can be reduced. As an example, many studies focusing on cold storage have aimed to optimize the control and performance. Kawashima et al. presented an optimal control strategy based on artificial neural networks to predict cooling loads [
22]. Chan et al. conducted simulations to evaluate the performance of a combined DCS and ice storage system, and studied the influence of tariff structures on the combined system [
23]. Hasnain reviewed the research on thermal storage and compared three cold storage media and rated ice storage [
24]. In contrast to the numerous studies on other types of storage systems, there is a lack of studies and applications on cooling water storage. Water temperature from cooling towers is low, due to the low environmental wet bulb temperature at night, plus the valley electrical price it is cost-efficient to use cooling towers to generate cooling water and store it overnight. Furthermore, cooling water with lower temperature supplied during daytime hours would increase the COP of the chiller, thereby further decreasing the electricity consumption. Additionally, with the assistance of water tanks, there is no need to keep pumps and cooling towers in constant operation; this provides a greater flexibility for the controlling system.
Therefore, by exploiting the advantages of each of the related components, a novel DVFP system with water storage (DVFP and WS) designed for implementation in a DCS with variable end-user-required cooling loads has been developed and is proposed in this paper. In this new system, chillers and variable-frequency pumps are installed at each end-use building and independently controlled while sharing a single cooling water loop. Cooling water is generated at a central cooling tower and is stored in a water tank that is located near the cooling tower. Then, the cold water in the water tank is transported to the end users. In this study, only the cooling water loop is discussed because the chilled water loop is distributed at each end use and operates independently. This paper first presents a schematic of the new system and introduces the principles of its design. Subsequently, a DCS with CCCPs in Beijing, China was selected for a case study. The system performance and energy consumption of CCCP and DVFP and WS systems are accordingly compared based on the results of the DCS case study. This procedure includes a field test of the current CCCP system to obtain operating data, a cooling load simulation by implementing DeST software (Designer’s Simulation Toolkit) under various weather conditions, modeling of the water networks and equipment, and a calculation of the operating parameters. The simulated building load and energy consumptions of the current system are found to be in agreement with the field test results, and, as compared to the current system, the DVFP and water storage (WS) system has been proven to have energy-saving potential.
2. Design Schematic and Principles
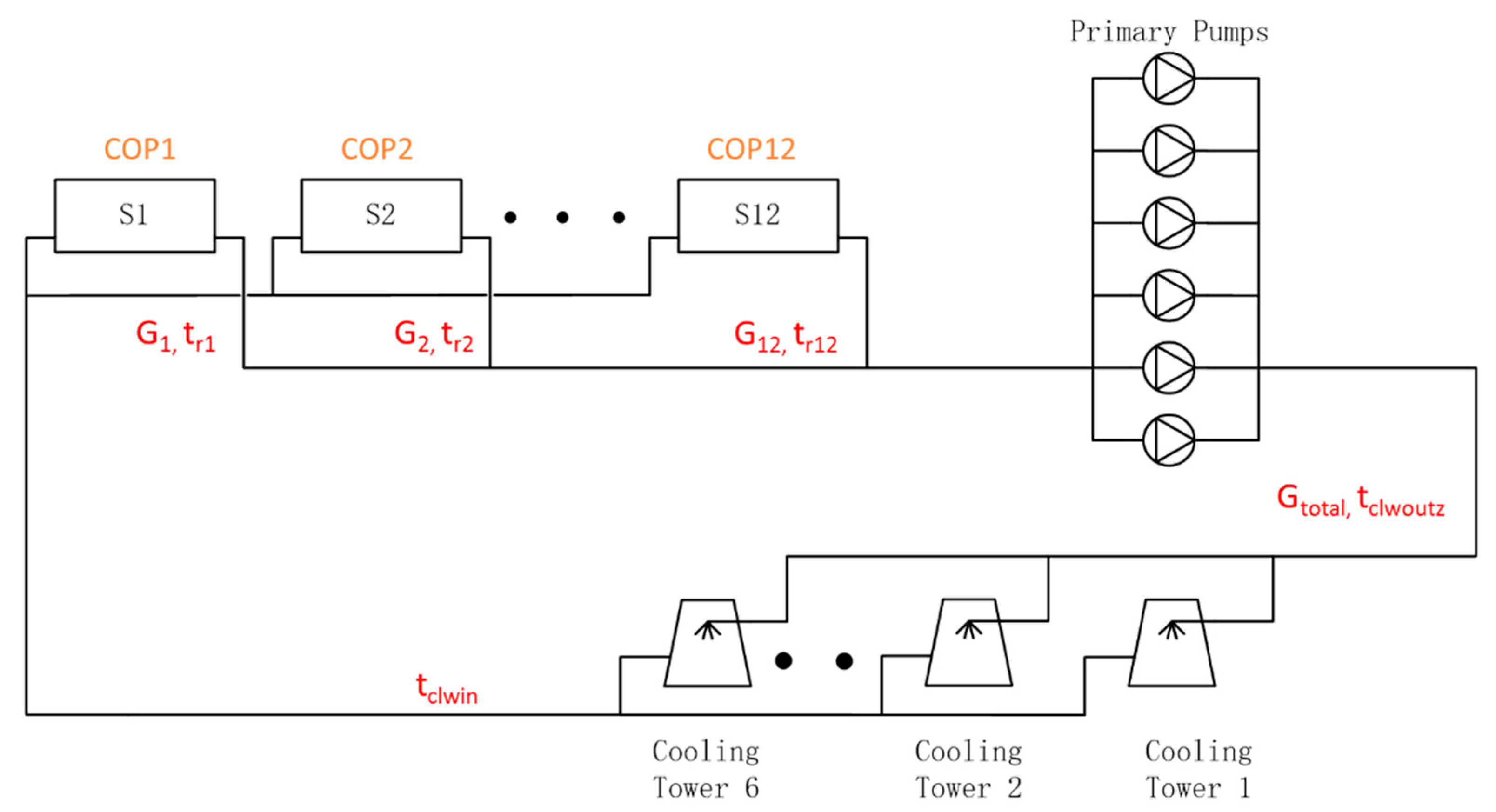
A descriptive schematic diagram of the current CCCP system is shown in
Figure 1. S1–S12 illustrate the terminal end users with chillers; the primary pumps are responsible for circulating the whole cooling water loop, whereas cooling towers are designed to coordinate with them. The power of primary pumps
in units W is given as:
where
is the pump head (unit: mH
2O),
is the total flow rate (unit: m
3/h), and
is the efficiency of the pump. The pump head, which is the total pressure drop of the entire water loop, is simply described as
where
is cooling tower pressure loss.
is the pressure loss in most unfavorable end use.
is the loss in main pipes. All of the units are in mH
2O. The losses in auxiliary equipment, such as check valves are also considered in corresponding components. For a CCCP system, because quantity control is only implemented on the primary pumps and cooling tower, the power of cooling towers is the product of the number of operating towers and nominal power. For water pumps, the relationship between the pump head and water flow rate can be written as a polynomial below:
where
,
, and
are obtained through pump operation curve-fitting data. Additionally, the relationship between pressure loss and flow rate in water loops can be written as
where
is the static pressure loss and
is calculated from the resistance characteristics of the pipes and auxiliary equipment. The pumps operate at the intersection of the pump curve (3) and loops curve (4).
End-use water flow is controlled by throttling valves fixed at each branch. During operation, the pumps operate at a constant speed and valve operation is variable; this alters the parameter in Equation (4), as well as the loops resistance curve, thereby changing the operating point of the pumps and decreasing pump efficiency as a result. Furthermore, water flow cannot be controlled by valves as precisely as is required by the end user; thus, imbalance of the cold supply between the nearest building and building frequently occurs. The actual water flow distributed at each end use is not related to the cooling load; thus, the and the subsequent COP of the chiller is affected. A common way to offset this imbalance is to increase the circulating water flow, which would also increase energy consumption.
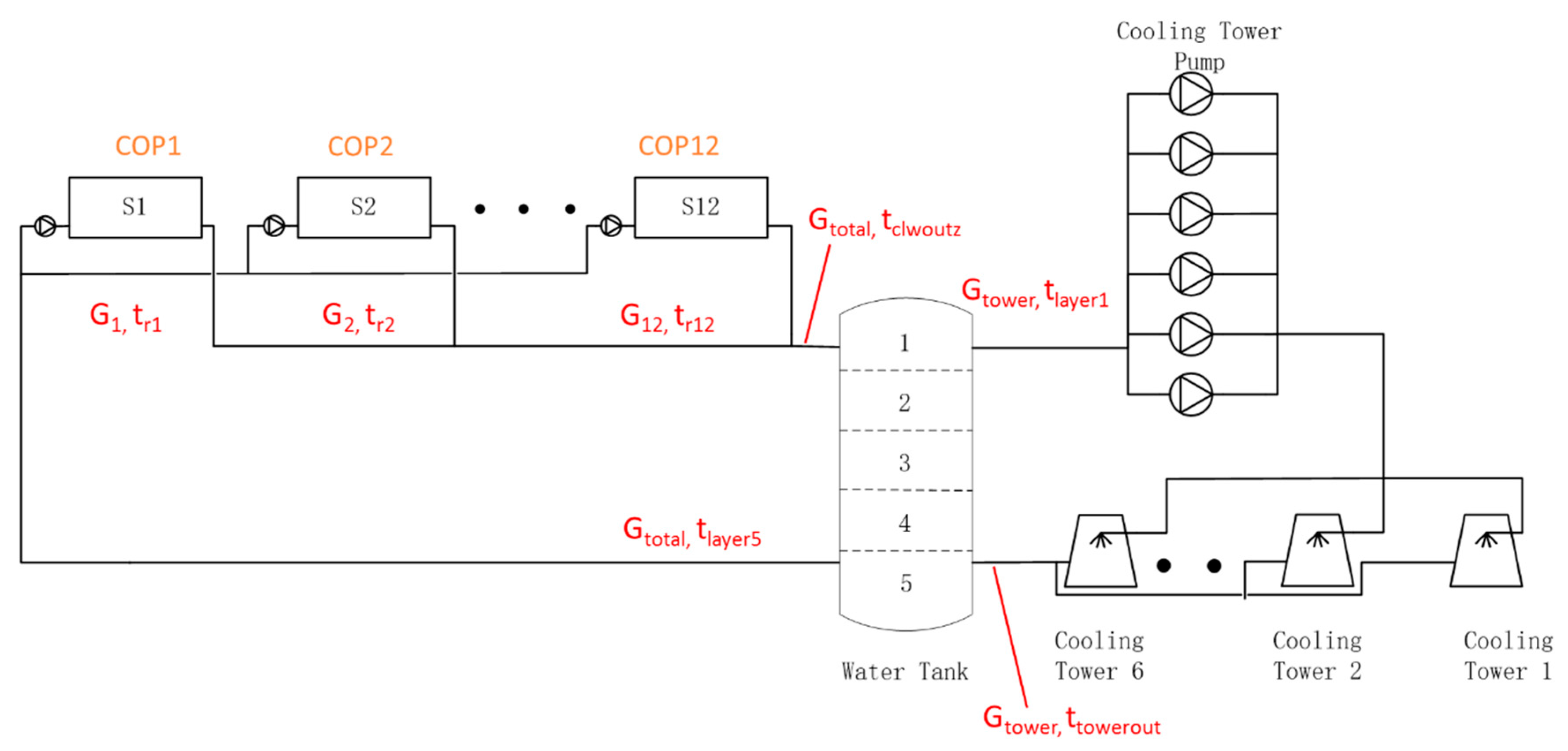
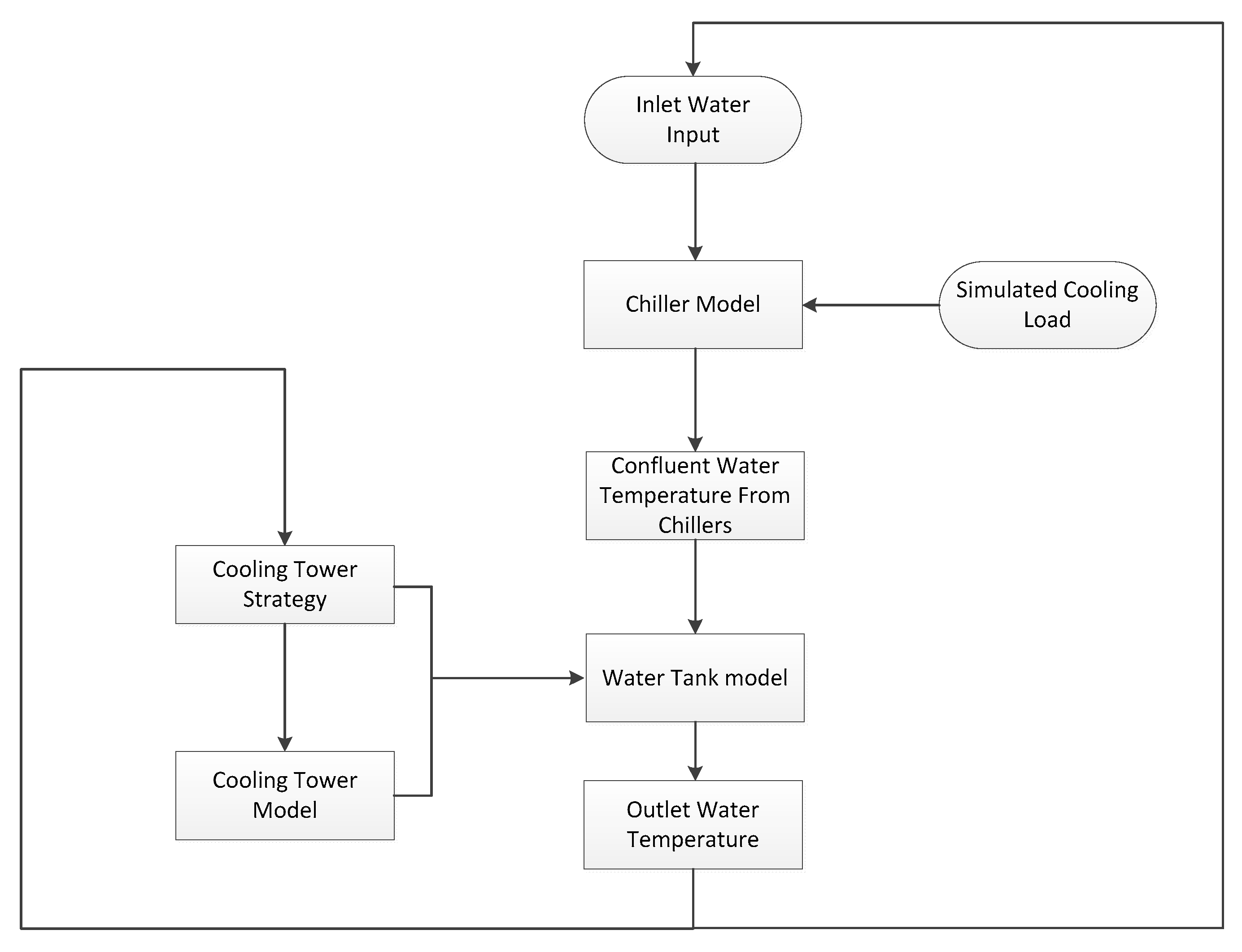
However, the DVFP and WS system shown in
Figure 2 has made many improvements. The water tank has partitioned the cooling water into two different sides: the source side and transportation side. On the transportation side, DVFPs fixed at each terminal are designed to initiate the pressure drop in the end-use water loop and corresponding main pipes. It is capable of varying the pump speed to control water flow. The flow rate of the
i-th pump
in pump curve (3) is
where
n is the operating frequency, which can be altered and
is the nominal flow rate of the pump, which is designed according to the maximum cooling load.
is the sum of
.
The resistance curve at the end use remains stable as the speed of the pumps changes, assuring pump efficiency. Note that the PPs are removed for this observation, the total power of DVFPs can be calculated as
where
is the pump head of the
i-th pump. Thus, the transportation energy-saving potential is feasible because the following occurs:
Water flow is controlled as required so there is no extra water flow.
The pump operating point remains stable to ensure pump efficiency.
The removal of valves prevents extra pressure loss.
The PPs are removed, and not all of the water flow needs to overcome main pipe resistance.
On the source side, the cooling towers and cooling tower pumps are quantity controlled to change the flow rate as required. In this case, the cooling tower pumps only provide the pressure loss on the source side; this drop is quite small. Additionally, the storage tank affords increased pump flexibility and cooling tower control flexibility. As based on the time-of-use electricity tariff, the cooling source would generate an increased amount of cold water and store it in the water tank during the time of minimum electricity cost, and subsequently reduce the usage during the peak cost time. In order to make full use of the water tank, it is stratified into several horizontal layers [
25]. Small holes exist throughout the partition to allow water to freely flow between layers. This study takes a five-layer water tank as an example. The relatively hot water returning from each chiller condenser flows into the top layer, where it is extracted and pumped into the cooling tower. The outlet water from the cooling tower flows into the bottom layer and is then pumped to the transportation side. Middle layers 2–4 are storage and transition layers between the relatively hot upper layer and cold bottom layer. This design minimizes the intermixing of the water, which is partitioned according to temperature level, to ensure that the water transported into the end use is always the coldest. It is considered as energy-saving because colder water decreases the condensing temperature and increases the COP of the chiller.
Although the energy-saving potential of current related systems has been briefly discussed, the new system proposed in this paper includes additional components, such as cooling tower pumps; thus, the total energy consumption and actual benefits of this system need to be studied in detail; and, these results are discussed below.
3. Project Case Study and Cooling Load Profile
A district cooling project employing CCCPs located in Northeast Beijing, China is selected as a case study. Field tests were performed to obtain basic information and system operating data, including energy consumption, water flow rate, and temperature. Based on these data, several models were developed to simulate cooling loads and system operation; the results have been compared to the test data.
The entire project is a commercial district comprising twelve independent sub-buildings noted as S1–S12, neighboring the central cooling plant. The location of the sub-buildings, in addition to a topological diagram of the cooling water networks, is shown in
Figure 3. The total floor area is 78,000 m
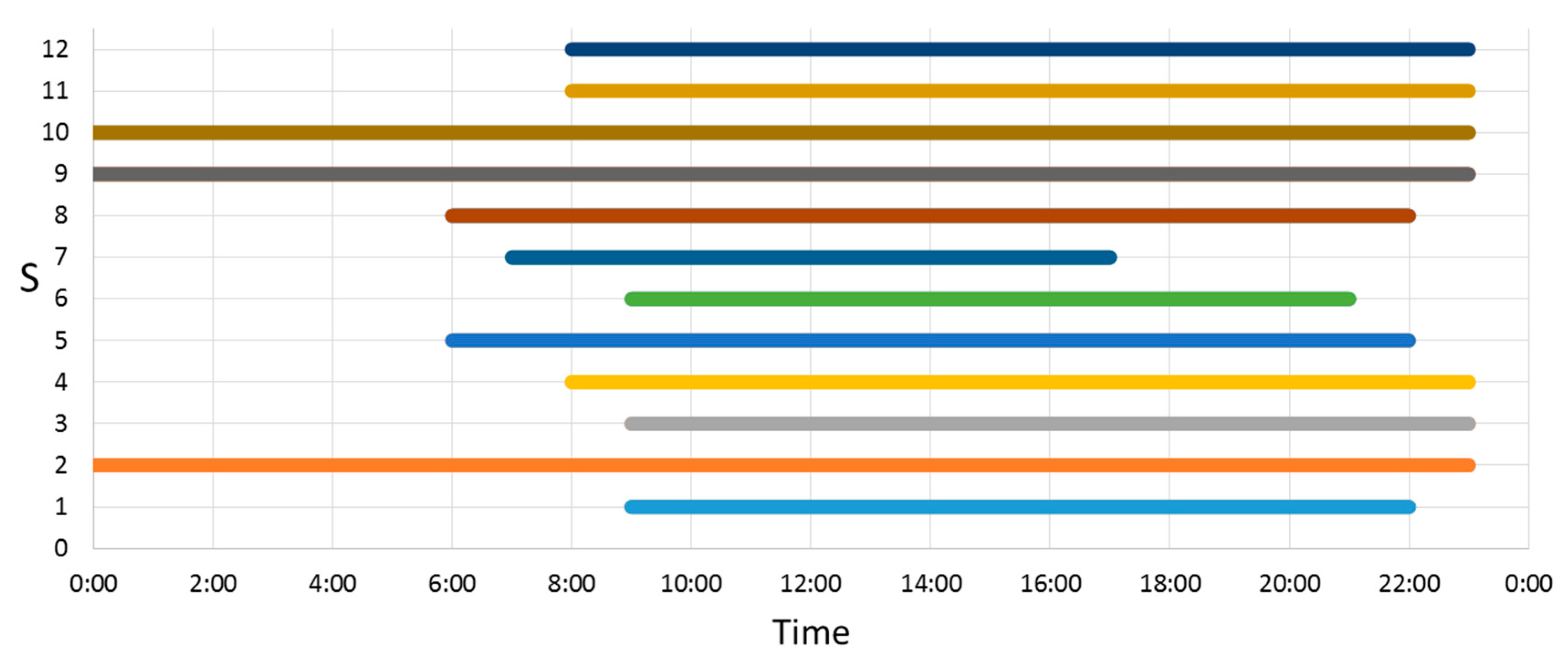
2. Most of these buildings are commercial buildings, including a cinema, restaurants, and retail stores. The time of operation of each of these buildings, which is shown in
Figure 4, is dependent on their function. For example, buildings S2, S9, and S10 operate 24 h a day, whereas the other buildings only operate during daytime hours; furthermore, the opening time of each building is different. These characteristics significantly influence the load profile. Additionally, there are chillers fixed at each end-use building to generate chilled water; on-site investigation revealed that these chillers are of the same model (nominal cooling capacity = 700 kW and COP = 3.5).
The tool used in this study to simulate cooling loads is a commercial software package named DeST, which has been proven to be useful in performing building load simulations [
26]. Besides, there are many other simulation tools on the market and each tool has its own advantages. Many studies have focused on the use of efficient tool to perform effective energy profile simulation of buildings [
27,
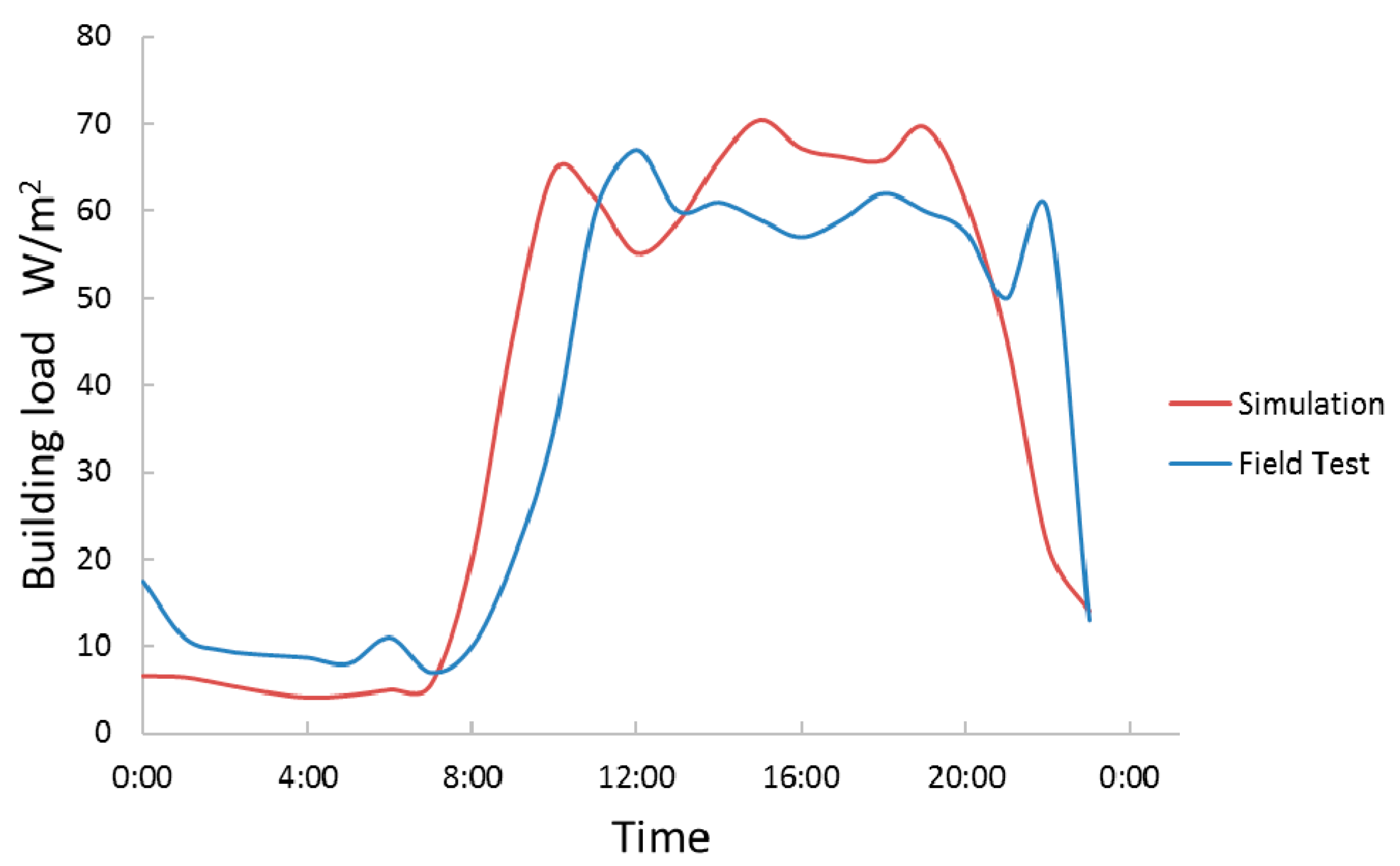
28]. The meteorological parameters are embedded in the software and 15 July is the full-load day (i.e., design day) in this study. All of the model settings, including building structure, materials, equipment, and lighting power density, are based on architectural drawings and the investigation of actual operation. This enabled simulation of the hourly cooling load of each sub-building on the design day. The hourly superposition of all of the building loads and a comparison with field test results are shown in
Figure 5. The accumulated cooling load on the full-load day derived by simulation is 69,900 kWh, while the field test result is 68,100 kWh. It can be concluded that the simulation results are in agreement with the field test results. Thus, the modeling and simulation process are confirmed to be reasonable and can be implemented to calculate cooling loads under various conditions. The basic information for each of the sub-buildings is presented in
Table 1, which also includes the peak cooling load and estimated cooling water flow, calculated at the ΔT = 4.5 °C and COP = 3.5; these results are presented in the next chapter. The maximum cooling load for all buildings is 5500 kW, 70.5 W/m
2.
4. Methods
The new system presented in this paper comprises two critical components: the DVFP component and the WS component. Two systems, the CCCP and the DVFP and WS, are evaluated, and their system performance is compared. Water distribution network models and equipment models are developed for each system to obtain hydraulic performance data, as well as thermal performance, respectively. The simulation flow of each system is designed via MATLAB software and links the aforementioned models. Based on the cooling load results that are calculated in
Section 3, the operating parameters of the system, such as temperature and water flow rate, can be calculated hourly. Subsequently, the electricity consumption and operation cost can be easily acquired for comparison. This chapter provides the details of the system-specific simulation methods, models, and process; the results are presented in the next chapter.
4.1. CCCP System
In the current operating system, a branched network is used for cooling water distribution. In this occasion, there is a unidirectional flow from the cooling plant to the end use. The topological diagram with marked pipe length, as is shown in
Figure 3, is developed for water distribution network models via HACNET software (a hydraulic simulation software developed by Tsinghua University). It should be noted that the marked pipe length includes the main pipe length and the branched pipe length inside the building. This software is proven useful in calculating the hydraulic performance of a given water network system [
29]. Pipe resistance, as well as the pressure loss in end uses, is derived from field test results. Generally, during the full-load hour (i.e., 15:00), the total cooling water flow rate required for all of the condensers is approximately 1200 m
3/h; at this time, the flow rate is found to be dependent on the water temperature difference (
) and COP. Under this condition, the frictional pressure losses in the main pipes, end-use loops, and cooling tower are 10, 10, and 5 m, respectively. The losses in the first two components include the losses in pipes and valves and other equipment. Consequently, six primary pumps (nominal parameters: 200 m
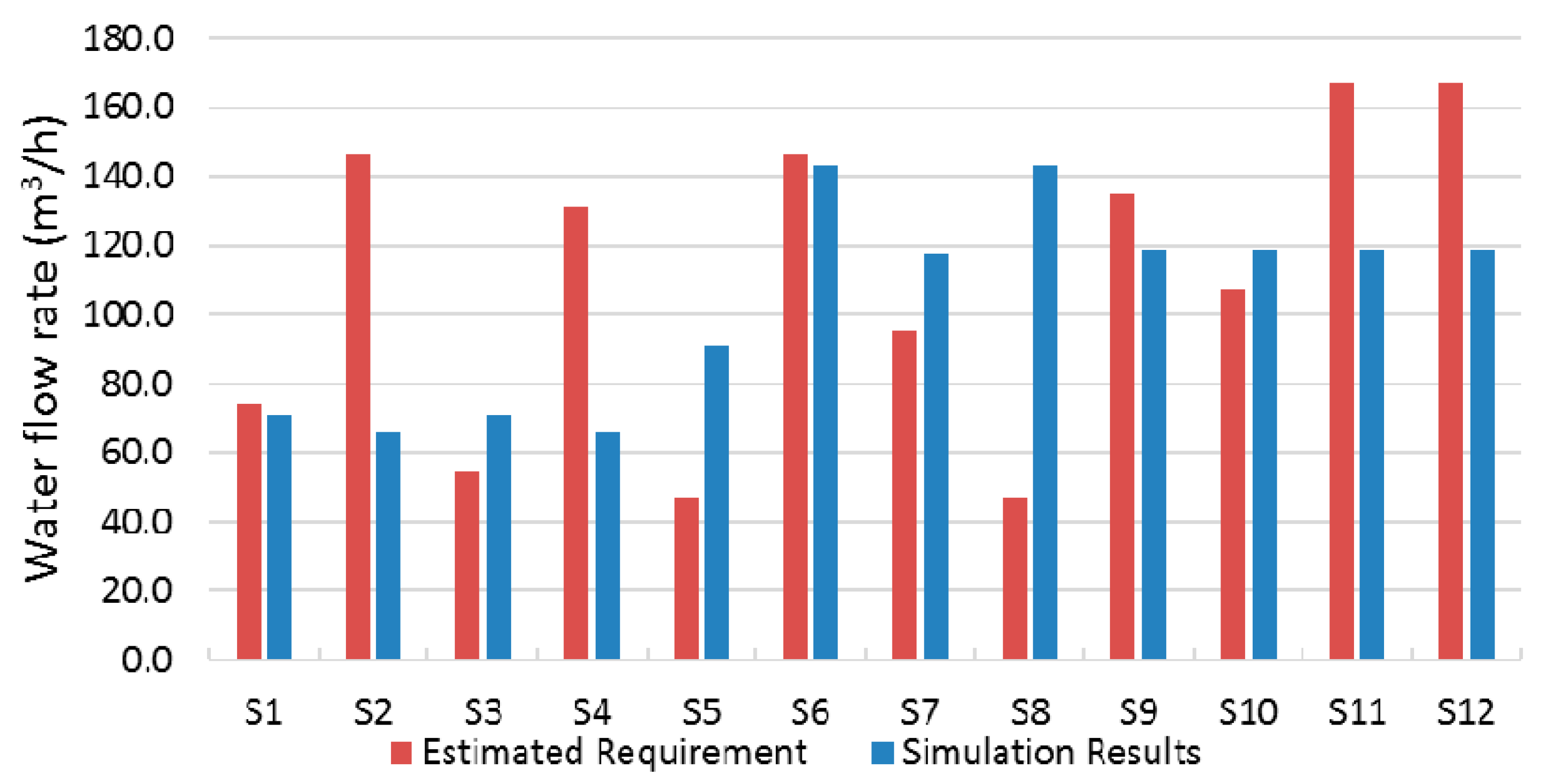
3/h, 25 m pump head) must be running to satisfy cooling water requirements. The characteristics of these pipes and equipment, including the pump curve, are input into the model and water flow distribution for each end use can be calculated hourly. The distributed water flow during the full-load hour (15:00), as compared to the estimated requirement according to the cooling load given in
Table 1, is illustrated in
Figure 6 as an example.
In most sub-buildings, the simulated flow rate (
Figure 6) is significantly different from the estimated requirement because of the differences in pipe length and the succeeding resistance. The nearest end use receives the largest water flow, while the most unfavorable end-use receives the least flow. In sub-building S8, the water flow difference between requirement and simulation results can be as much as 96 m
3/h, while in building S1 and S6 the difference is only 3 m
3/h. This leads to an imbalance in cold supplies and
values. Regarding the pumps, the operating point and efficiency was calculated via HACNET software, as based on water flow and pressure loss results.
A schematic diagram of the CCCP system has been presented in
Figure 1. It should be noted that, although the cooling load is only simulated once per hour, the minimum calculation time interval is set as one minute in consideration of the precision requirement of the control system and water tank simulation. For any minute in the day, the cooling load for each end use is calculated via ways talked above in
Section 3, and noted as
; then, heat rejection in the
i-th condenser
is
Based on the water flow rate for each end-use
that was calculated via HACNET software, the cooling water temperature difference in the
i-th condenser
can be determined as follows:
where
c is the heat capacity of the water. Because of the piping insulation and minimal temperature difference between the cooling water and environment, the thermal loss during transportation is neglected in this study. However, this hypothesis is applied to each system and does not significantly affect the results of comparison between systems. The outlet water from each condenser flows into the main pipe, and the confluent water temperature before this water enters the cooling tower (
) is given as
is the chiller inlet water temperature, which is considered as the same for each end use under the hypothesis that heat loss is neglected. The subsequent water flow through the cooling tower and the outlet water temperature of the cooling tower is defined as
where
is the efficiency of the cooling tower, which is set as 70% in this study.
is the wet-bulb temperature outdoors, as derived from the meteorology database. In the CCCP system, because there is no water storage, the outlet water from cooling tower flows directly to the end uses, and
is the cooling water inlet temperature
for the next time interval. Subsequently, a closed-loop successive simulation is designed. The COP and chiller model implemented in this simulation is a function of the chilled water temperature set point of the supply
, average cooling water temperature in the condenser
, and the cooling load ratio of the chiller
. This function is curve-fitted by using the actual operation curve of the chiller that was determined via the field test.
, which is the ratio of the operating chiller COP to its nominal COP (
), is expressed as follows:
Then the operating COP is given as
In this study, is preset as 7 °C, and thus remains constant.
When considering the above Equations (7)–(12), , which is calculated once per minute, affects the COP in the succeeding time interval. All of the operating parameters can be continuously calculated via this process.
As previously mentioned, the only control strategy is the quantity control for the pumps and cooling tower. Because no water storage system is included, all of the equipment must be operated overnight. During the daytime hours, the condenser inlet water temperature is regulated for minimal deviation from the 27 °C target temperature; this is the nominal parameter that is necessary to ensure high efficiency of the chiller.
4.2. Integrated Distributed Variable-Frequency Pump and Water Storage Systems
As previously mentioned, in the proposed system, the water storage tank has partitioned the water loop such that there are two sides: the transportation side and the source side, as is shown in
Figure 2.
On the transportation side, the variable-frequency pumps are fixed at each end use to control water flow. As has been described, these pumps initiate the pressure loss in the end-use and corresponding main pipes, which is significantly reduced to 15 mH
2O as the equations presented in
Section 4.1. The nominal flow rate
of these pumps is determined as based on the information presented in
Table 1. During the simulation, the water temperature difference
is maintained at 4.5 °C, which is the nominal parameter for the chiller. Then, the required frequency of the
i-th end-use pump
is
However, the variable frequency range of the pump is 25–50 Hz. Thus, if the calculated frequency exceeds this interval, the pump can only operate under the conditions of maximum or minimum frequency. The pump efficiency can be calculated because the operating point is determined as the intersection of the pump curve and loop curve. Then, the flow rate for each end use is determined. The chiller model is the same as that presented in Equations (11) and (12) in
Section 4.1.
On the source side, six cooling tower pumps with the same nominal water flow (200 m3/h) are fixed, but each of their pump heads are re-adjusted to 5 m because they only need to account for the pressure loss on the source side. Control of the cooling towers and pumps is interdependent, and their models can be described via Equation (10). The source-side water loop is relatively simple; this means that it possesses relatively few valves to maintain stable resistance characteristics and relatively high pump efficiency. In accordance with the electricity tariff, operation of the pumps and cooling towers is increased at night and is reduced during the peak cost period.
As mentioned in
Section 3, the water tank is stratified into five layers to preserve the distinction between water temperature levels. The volume of each layer is 400 m
3, which is defined as
. The total cooling water flow rate is
, which is calculated via processes occurring on the transportation side; alternatively, the cooling tower flow rate
is determined as based on the number of operating towers and pumps. The relative amounts of these two water flows determine the real-time vertical flow direction inside the water tank. Specifically, if
is larger than
, then an increased amount of water is pumped into the cooling tower and the water inside the tanks flows upwards. Conversely, if
is smaller than
, then the water flows downwards. Thus, the water tank models have two operating modes: the larger
mode and larger
mode. For each step in the simulation process, the program must compare the flow rate and decide which mode to run. The former mode is presented here as an example. Another point to be stated is that, in this study, water within one layer is assumed to be well mixed within one calculation step.
In the first layer, the water temperature is determined as follows:
The unit of and is m3/h. is the current temperature, and is the temperature for the succeeding time interval following mixture; at this point, becomes the inlet temperature of the cooling tower. The cooling tower model is identical to that expressed via Equation (10); the outlet temperature is noted as .
For the second to fourth layers, the temperature for the succeeding time interval can be determined as
After flowing through a transition layer, the water flows into the fifth layer with outlet water from the cooling tower. Thus, the temperature in the fifth layer following mixture is given as
Then, the water is pumped to the transportation side as the inlet water of chillers in the succeeding time step; this completes the one-step calculations. For an initial chiller inlet temperature and a given cooling load, the operating parameters can be gradually calculated. The simulation flow chart is shown in
Figure 7.
5. Results
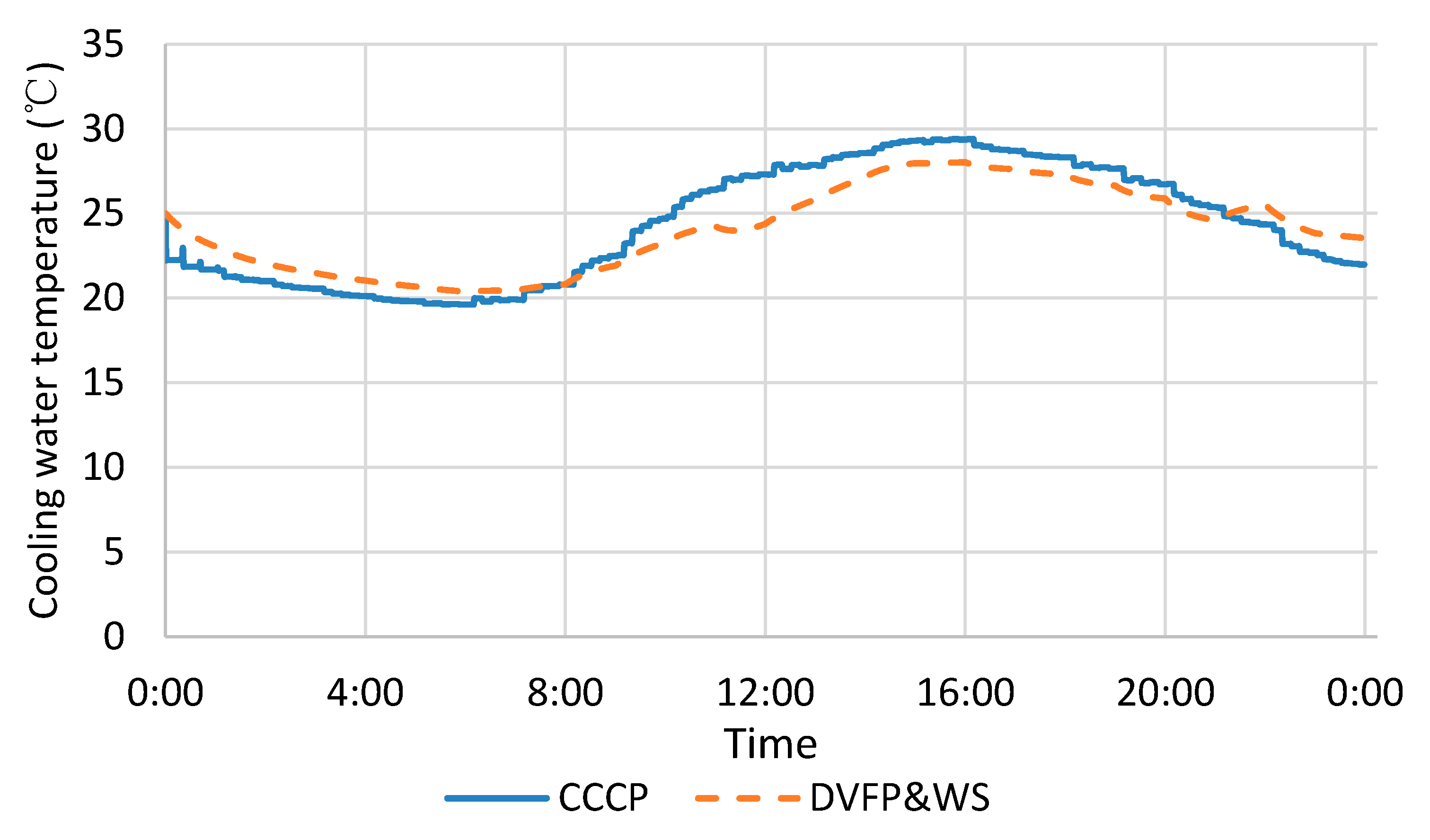
An appropriate inlet water temperature for chillers on a full-load day is illustrated in
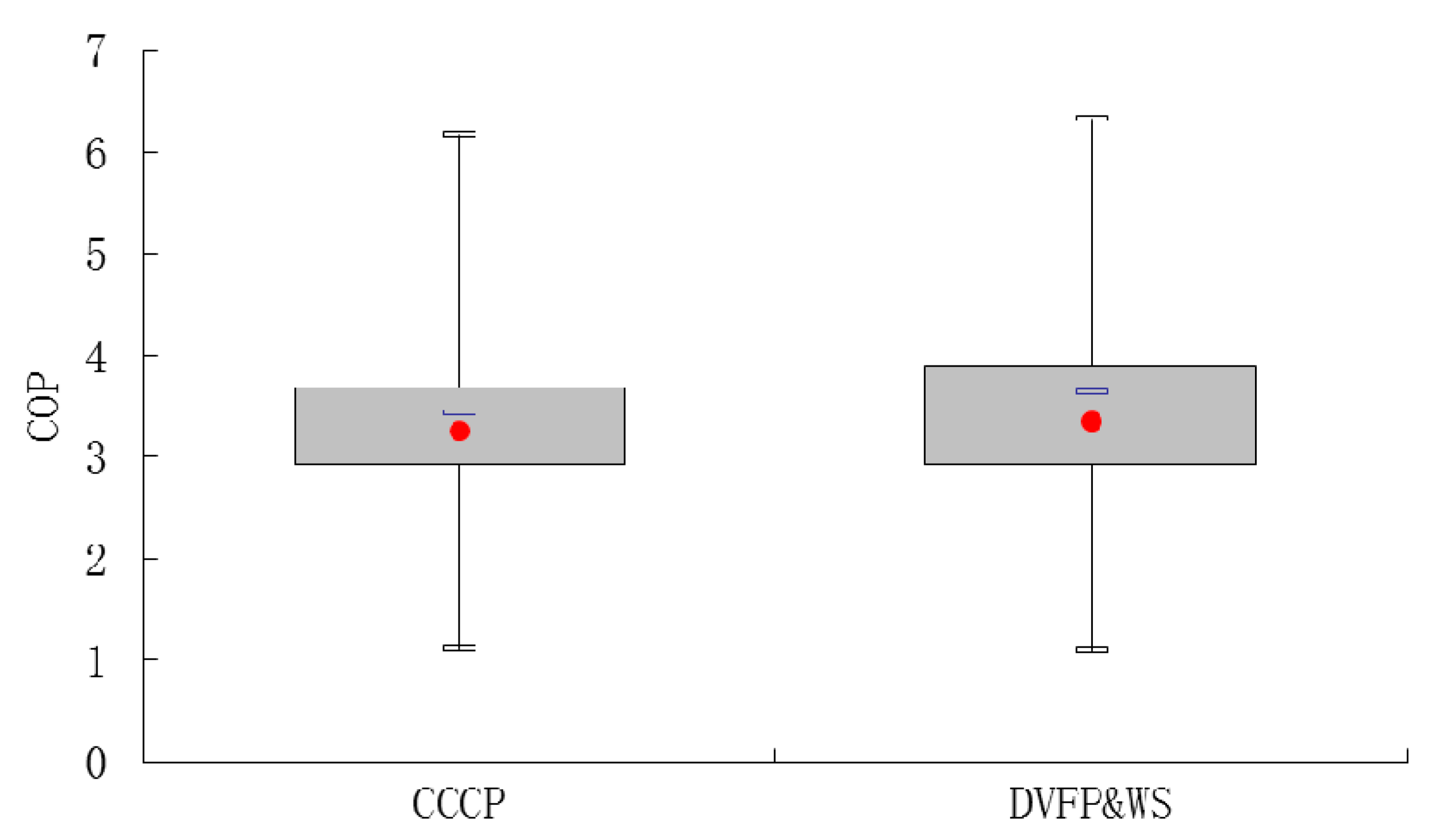
Figure 8. As expected, the water temperature in the CCCP system fluctuates more frequently than that in the DVFP and WS system because there is no water storage. However, with the implementation of water tanks, the DVFP and WS system stores cold water at night when the inlet temperature is lower and releases it during daytime hours. It is found that this low inlet temperature improves the average chiller COP
Figure 9. Another advantage of the proposed system is the implementation of the DVFP, which distributes water flow as required, and regulates the temperature difference
to ensure high chiller efficiency.
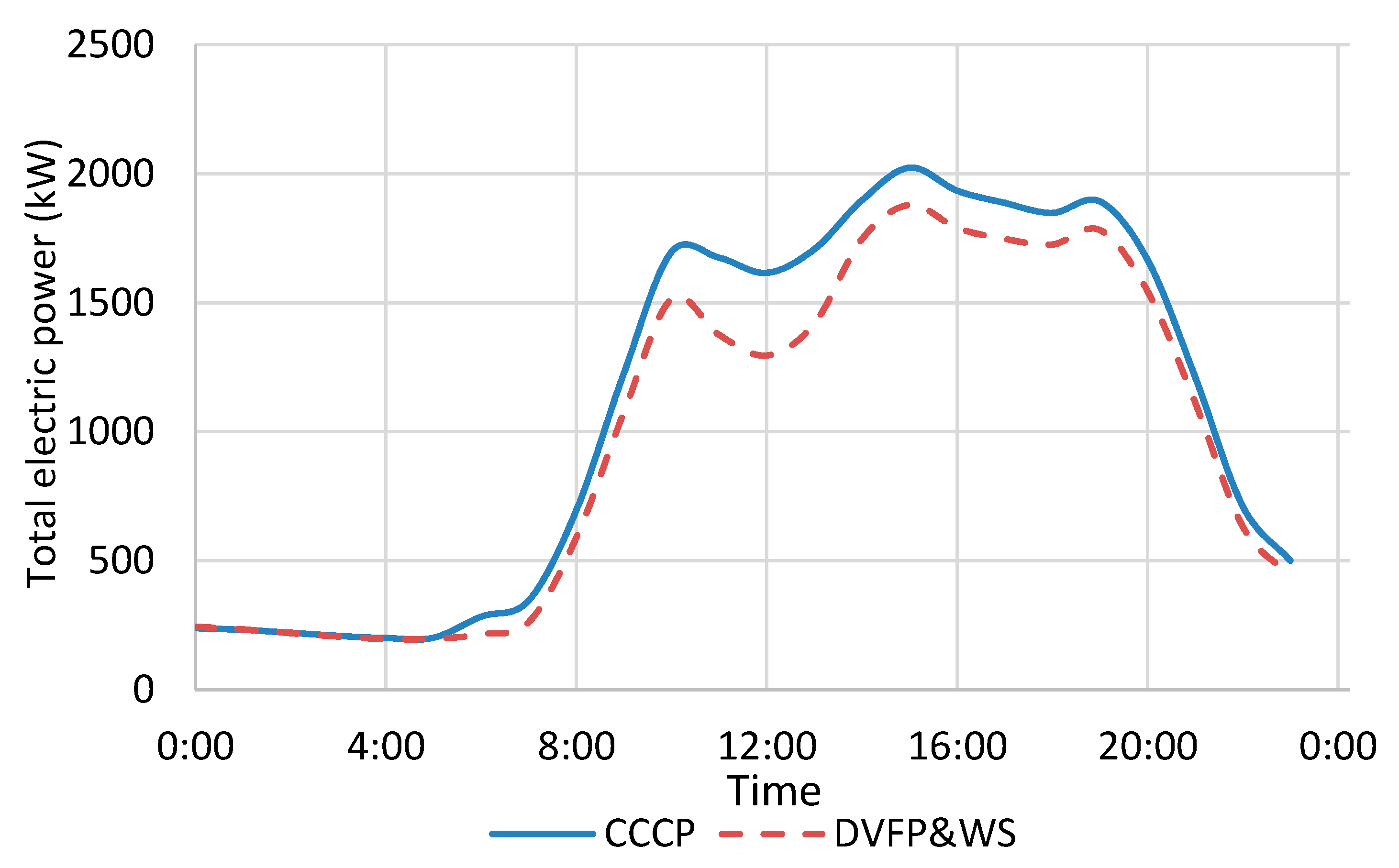
The effective total electric power of all equipment, including the chillers, pumps, and cooling towers, is shown in
Figure 10. It can be observed that, although the new system consumes more power at night, the benefits afforded by this system during the daytime hours are more significant, particularly during the peak hour at approximately 12:00, when the cooling tower and pump usage is reduced and the water tanks release cold. However, as it is limited by the size of the water tanks and capacity of water storage, the low temperature of the cold water stored in the tanks can only be sustained for a few hours. During the second peak hour of the day, which occurs at approximately 18:00, the comparative advantage of the proposed system is insignificant. A summary of electricity consumption on a full-load day is provided in
Table 2, which also provides details of the field test results for comparison.
The labels CTF and CTP in
Table 2 are abbreviations for the cooling tower fans and corresponding cooling tower pumps, respectively. It is observed that the simulated energy consumption in the CCCP system is lower than that measured via field testing, particularly for the pumps and cooling towers. This can be explained by the control strategy and the actual performance of the equipment. During operation, the pump control precision was observed to occasionally decrease to an undesirable level; moreover, the equipment was aging in some way that decreased efficiency, specifically affecting pump efficiency and cooling tower efficiency. However, regarding the total energy consumption, as compared to the CCCP system, the DVFP and WS system consumes 2696 kWh less electricity, equating to an approximately 10.3% in energy saved. As for transportation system (including all of the pumps), the DVFP and WS system consumes 1739 kWh less electricity than CCCP system, accounting for 57.4% of the energy in transportation system. Furthermore, as compared to the field test results, the total energy saved on a full-load day is 3674 kWh, equating to nearly 14%. Although CTPs are added to the DVFP and WS system, the sum of DVFP and CTP remains as less than PP for reasons, such as fluctuation in frequency and water loop pressure optimization. Despite this, the transportation system only consumes less than 15% of the total energy, thereby limiting the energy-saving potential.
Based on the simulation results of energy consumption, the daily electricity cost is calculated as according to the current tariff in Beijing. Calculations reveal the daily cost for the CCCP system to be 30,855 RMB, whereas the cost is 27,585 RMB for the DVFP and WS system. The daily cost saving equates to 10.6%.
In addition to the full-load-day study, energy consumption on a partial-load day is investigated to present a comprehensive view of system performance. The date is 30 May, and the simulated cooling load as simulated via DeST software is 56,000 kWh, which is 80% of the maximum cooling load. The simulation described above is performed, and energy consumption and cost are calculated.
Table 3 provides a comparison of the two days. It is found that the energy-saving potential is 13%, which is similar to that observed on a full-load day.
6. Conclusions
In this paper, the operating performance and energy efficiency of a novel DVFP and WS system that is applied to the cooling water operations in a DCS was analyzed. The basic principles and a schematic diagram of the proposed system have been presented, along with an analysis of the energy-saving potential. A DCS located in Beijing, China was selected for a case study; this included an on-site investigation of the system. Using this DCS as a reference, a series of simulations were conducted and effective operating data for two different systems exposed to various weather conditions were calculated. Through comparison with field test results and a simulated CCCP system, the proposed system demonstrates a 10% saving for both energy and cost part for the whole system.
The throttling valves present in the CCCP system were replaced with variable-frequency pumps to ensure appropriate water flow regulation; additionally, in contrast to the CCCP system, water pressure loss via valves was prevented. This resulted in increased pump efficiency, the prevention of excessive water flow, and a reduction of transportation energy consumption. In addition, the water storage tanks enabled the resourceful exploitation of the electric tariff and pump control flexibility. The cold water was stored at night and was released during the period when the cost of electricity was highest. Via the proposed system, not only were the operating costs of pumps and cooling towers reduced, but also the chiller COP was increased because of the low cooling water inlet temperature of the condenser.
It can be concluded that the size of the transportation system and the cooling load profile play an important role in the applicability of this new system. In a large district energy system with long pipes and various end uses, the transportation system consumes a majority of the energy; under these conditions, the advantages of the proposed system are more notable. As the concept of distributed variable-frequency pumps is currently being applied in large city-scale district heating systems, it would not be exceedingly difficult to begin implementing the proposed cooling system on an equivalent scale. Moreover, the DVFP and WS system is also applicable in systems with changing end-use cooling loads, as it can promptly initiate the changes that are necessary to maintain its level of efficiency by quickly adjusting flow as required. Thus, from what has been presented in this paper, it can be ascertained that there is significant potential of the DVFP and WS system application in many cases to save energy and reduce operating costs. However, some defects still exist in this study, in that all of the research works are based on a field test of the current system and simulation of the proposed system. There is a lack of the applications of DVFP and WS system in real operating projects and the real performance of this new system, which would be our future focus.