Study on the Hydrodynamic Performance of Typical Underwater Bionic Foils with Spanwise Flexibility
Abstract
:1. Introduction
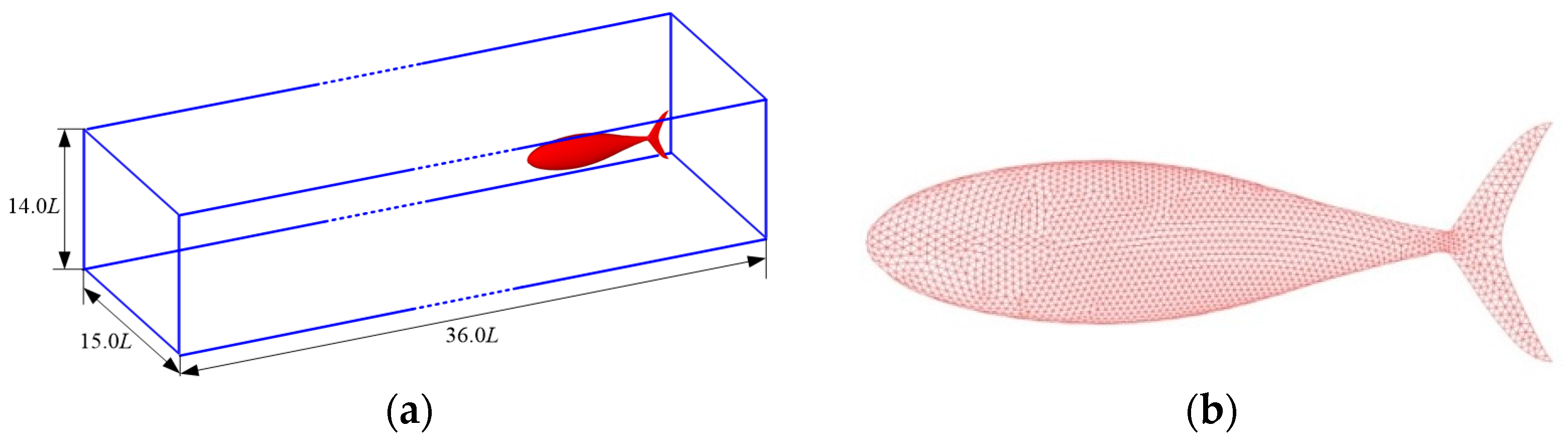
2. Materials and Methods
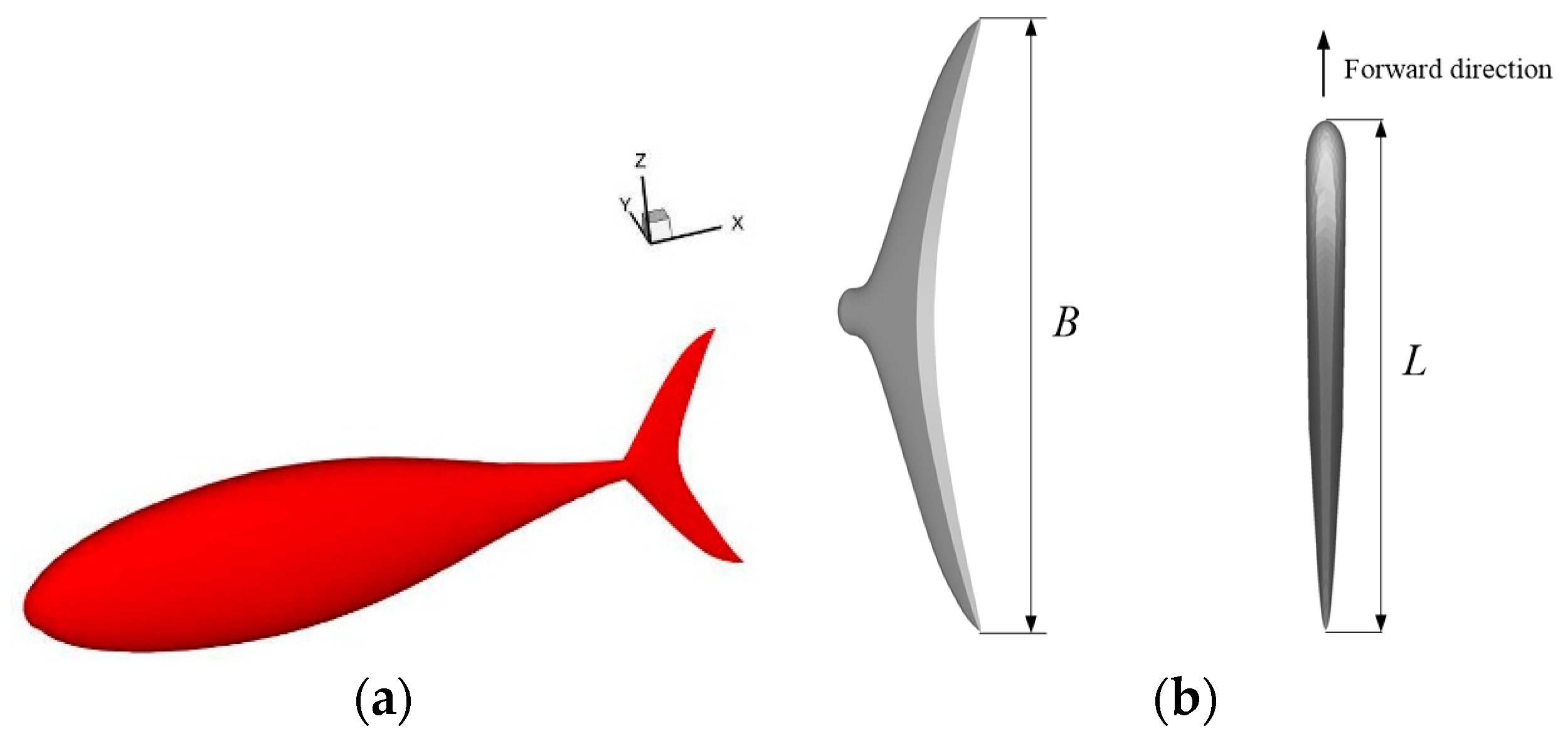
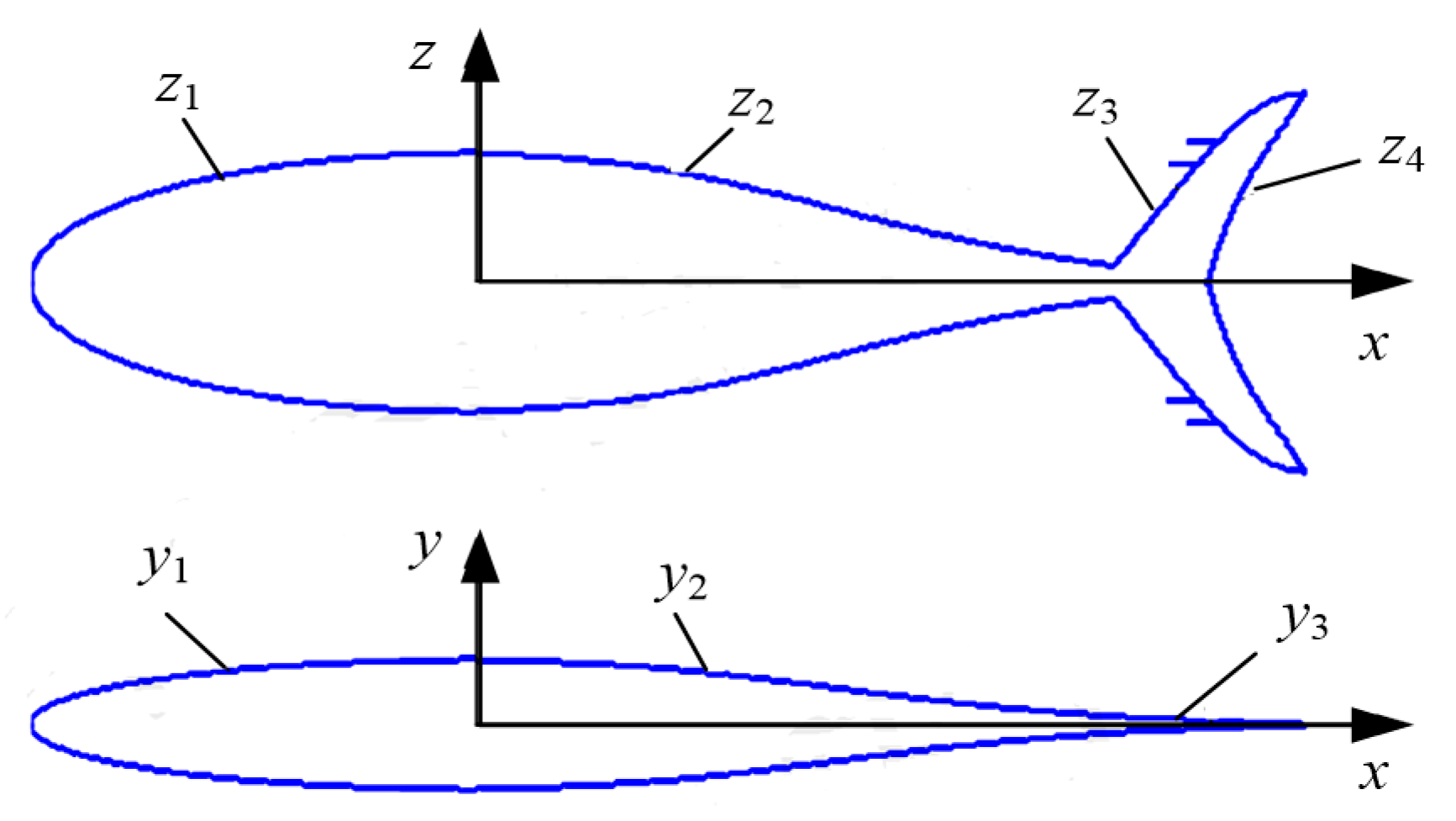
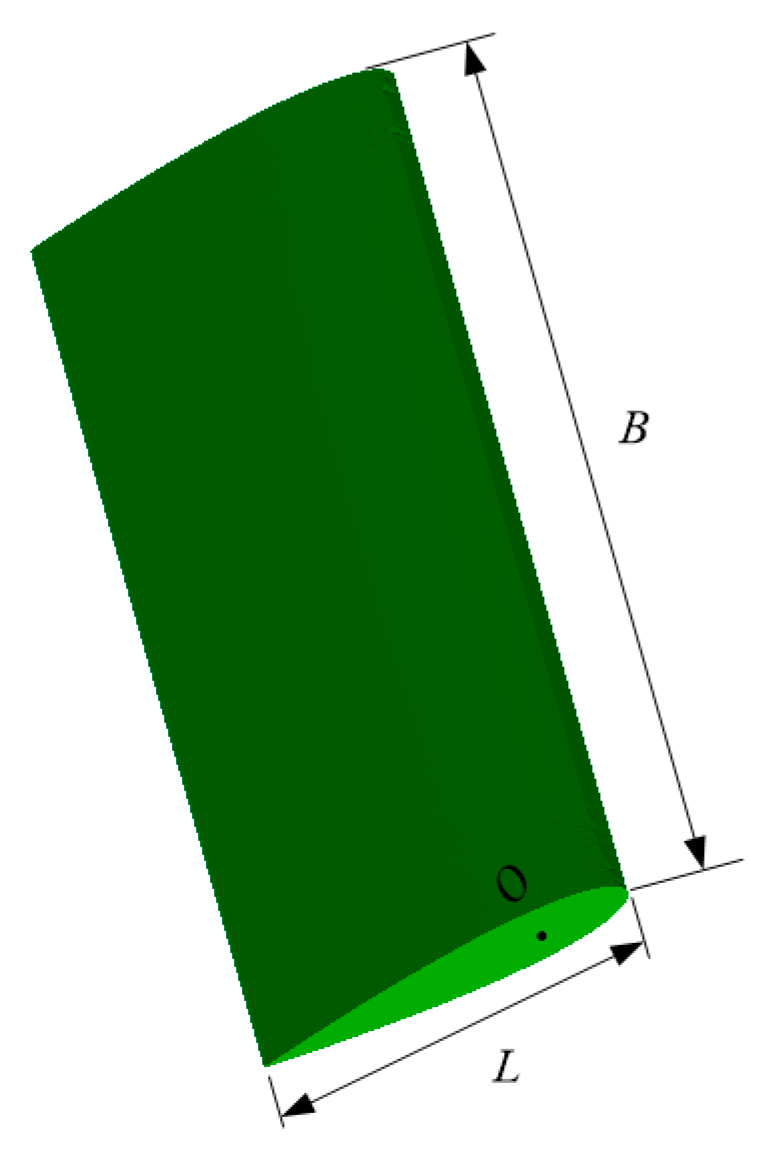
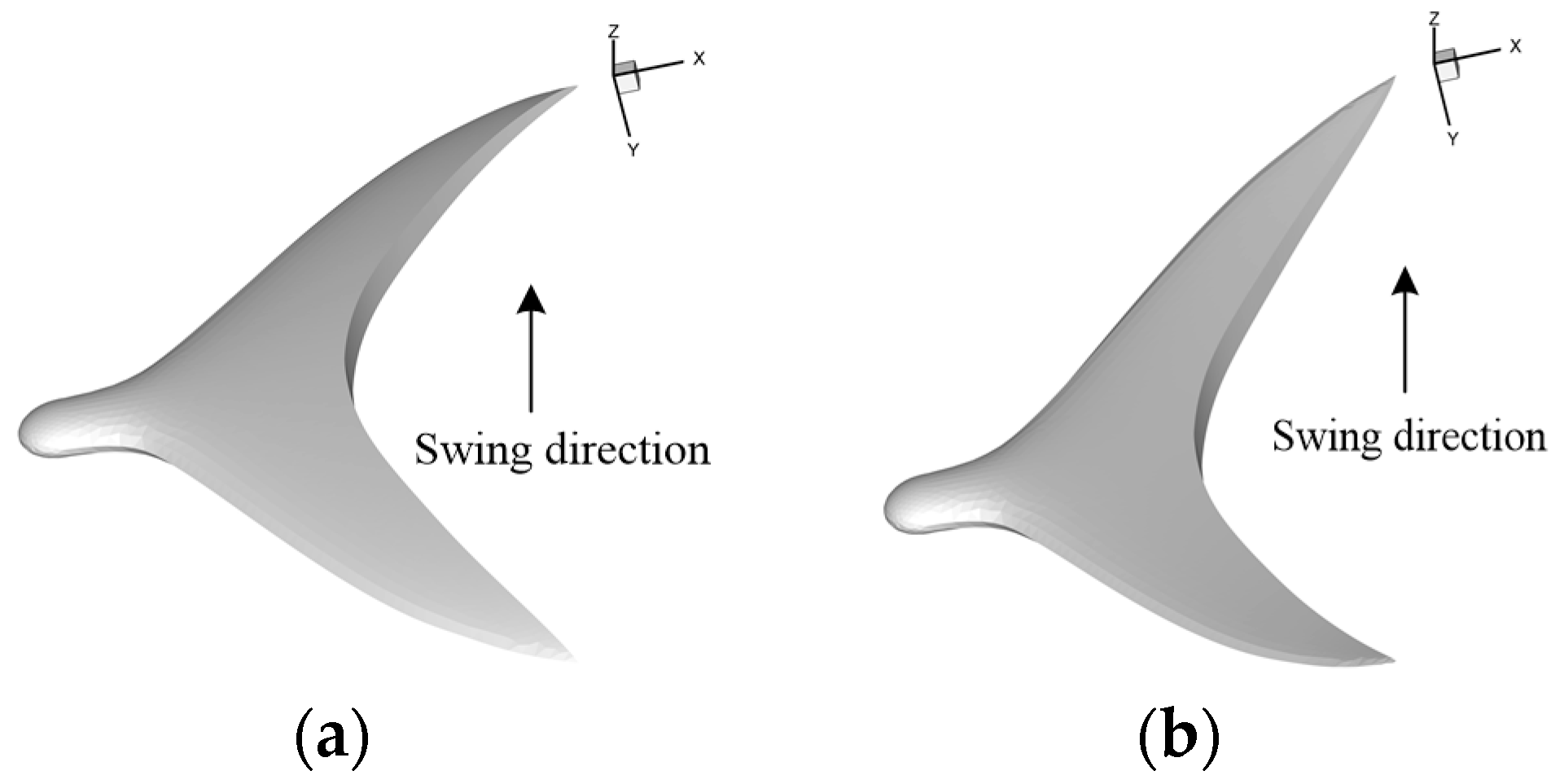
2.1. Geometric Model
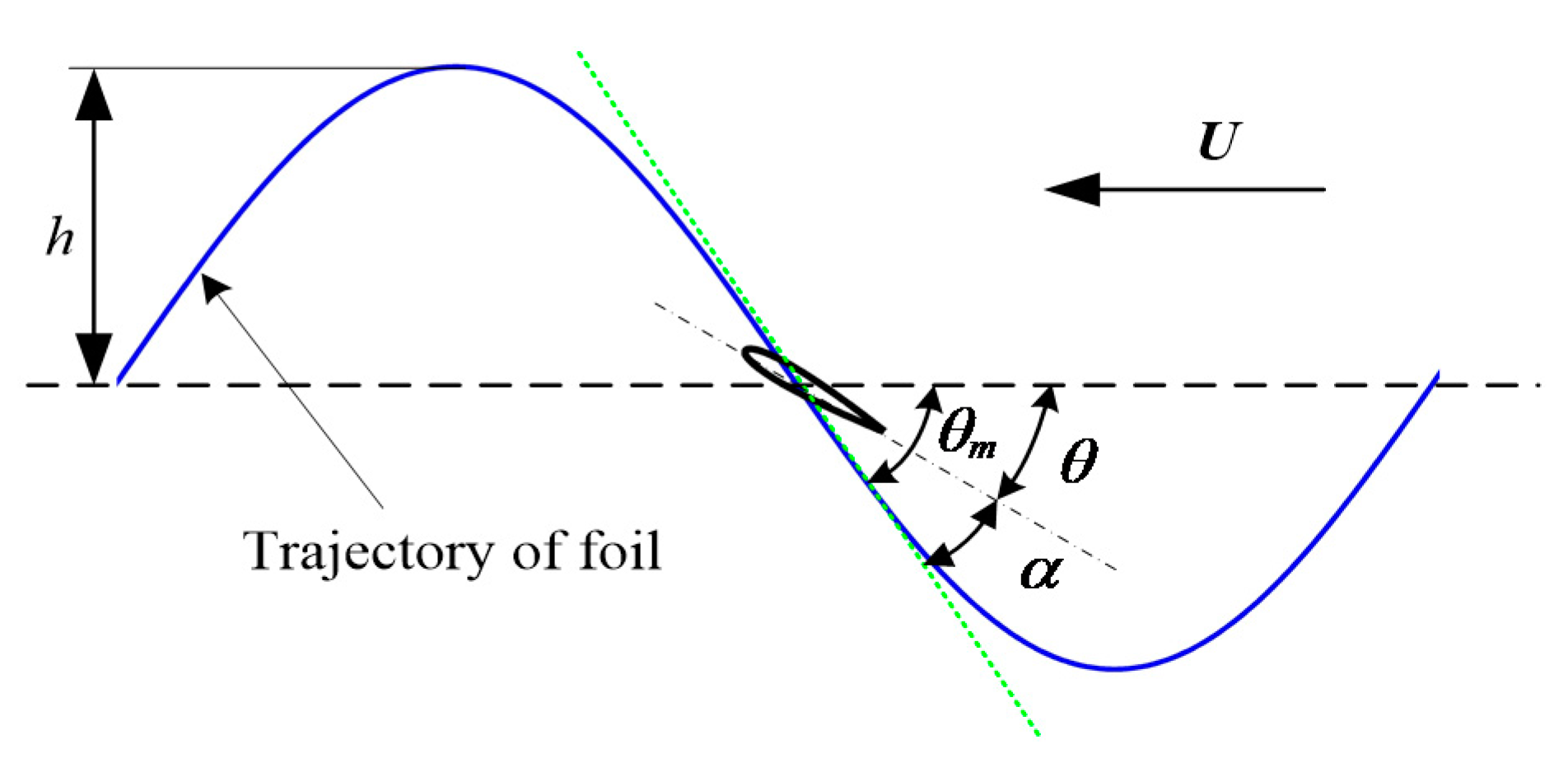
2.2. Motion Model
2.3. Flexibility Model
2.4. Numerical Solution
3. Results and Discussion
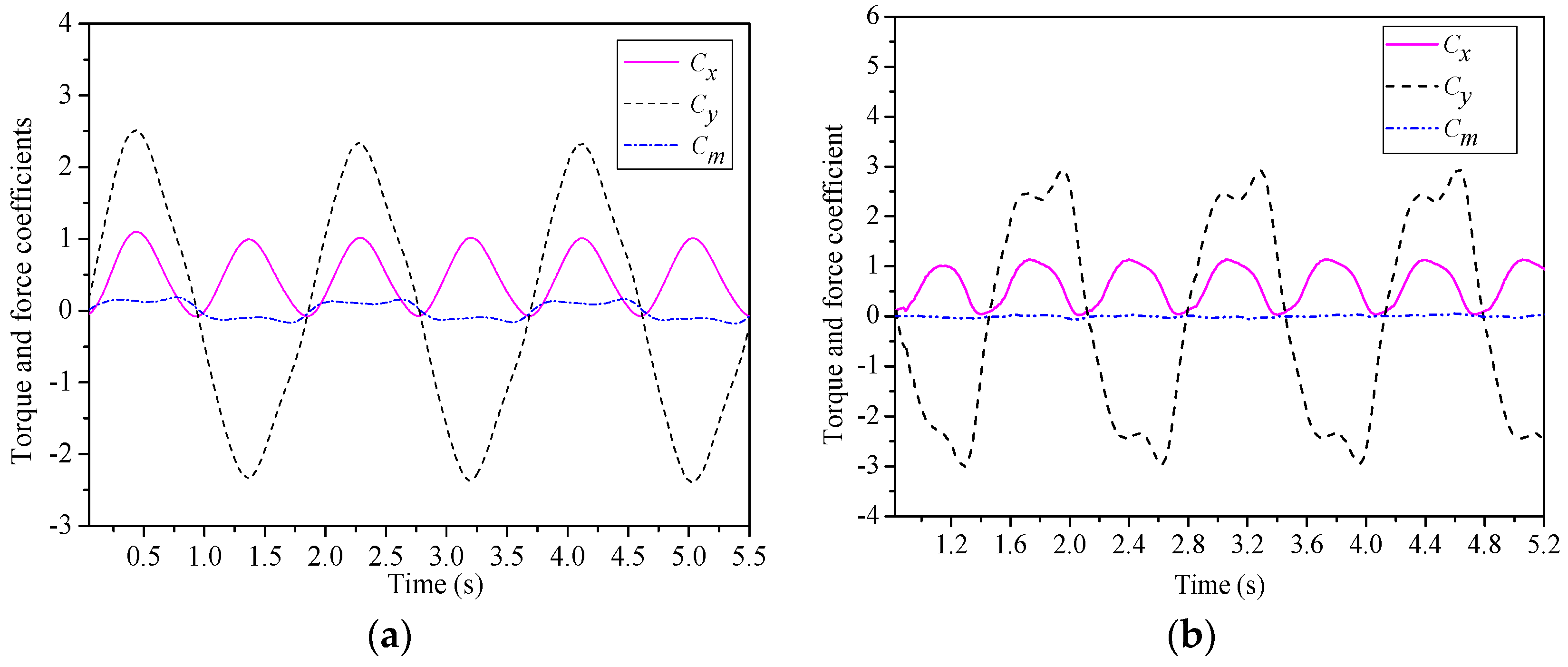
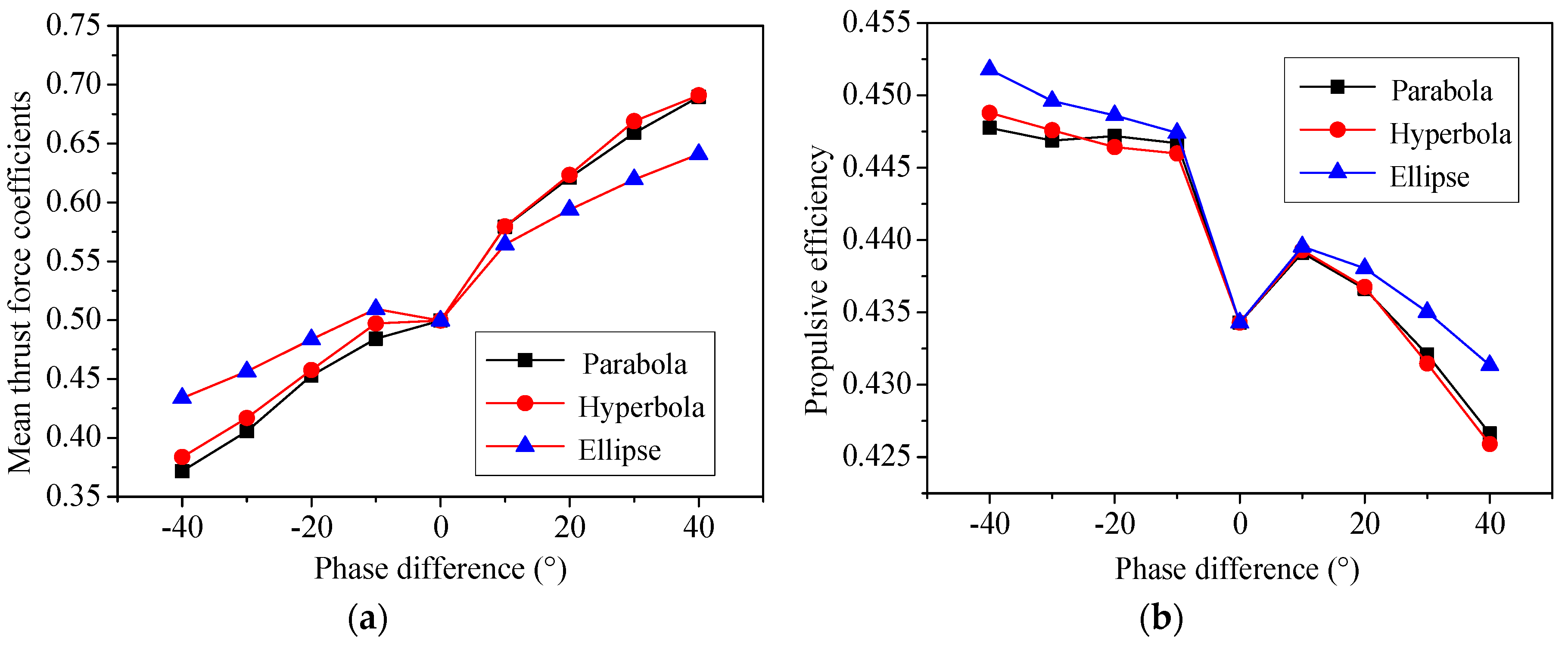
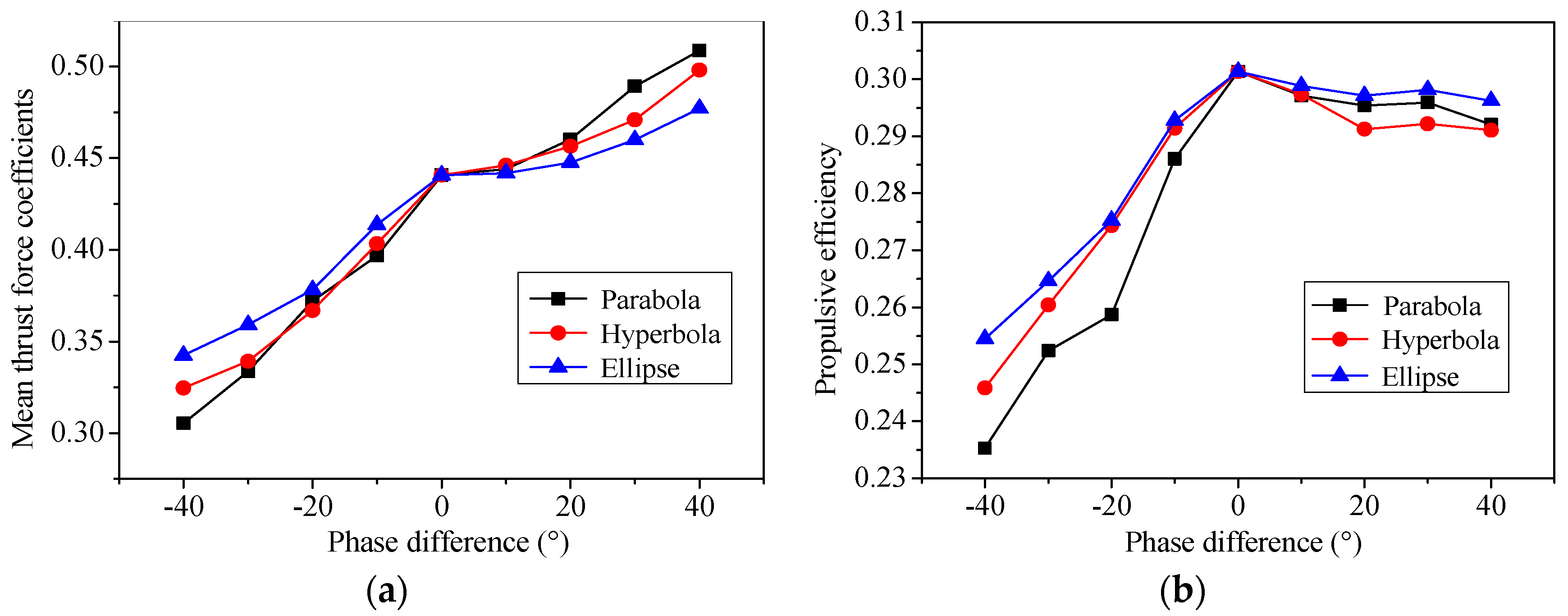
3.1. Rigid Foil
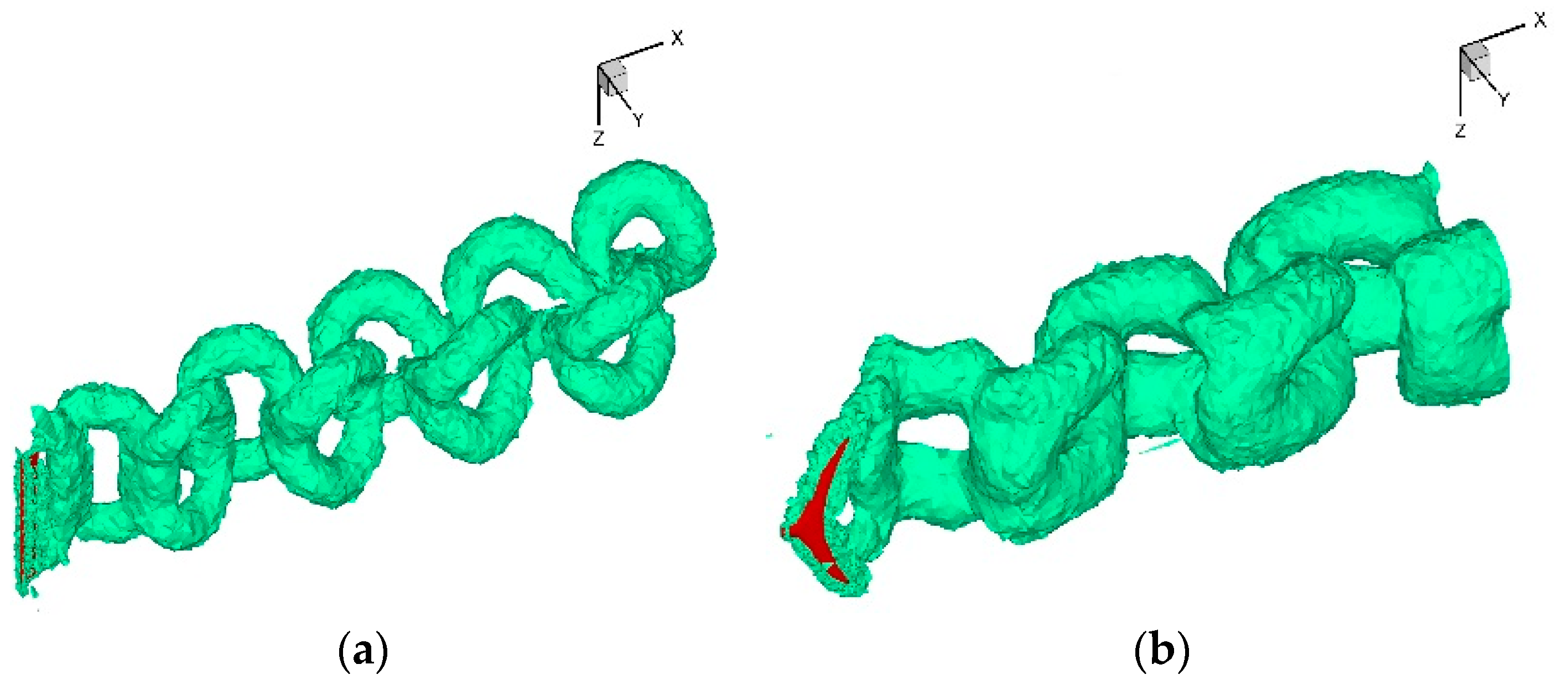
3.2. Flexible Foil
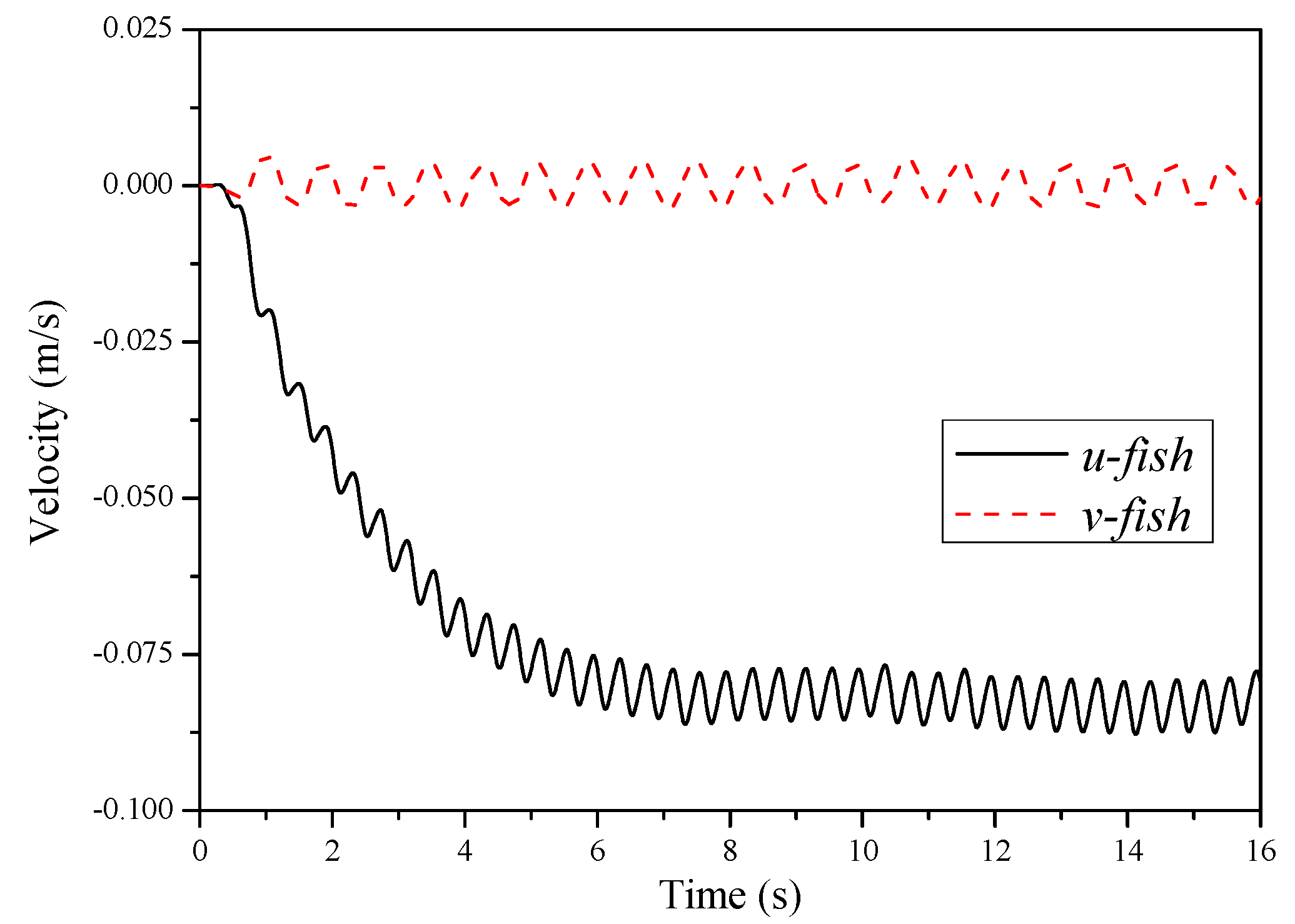
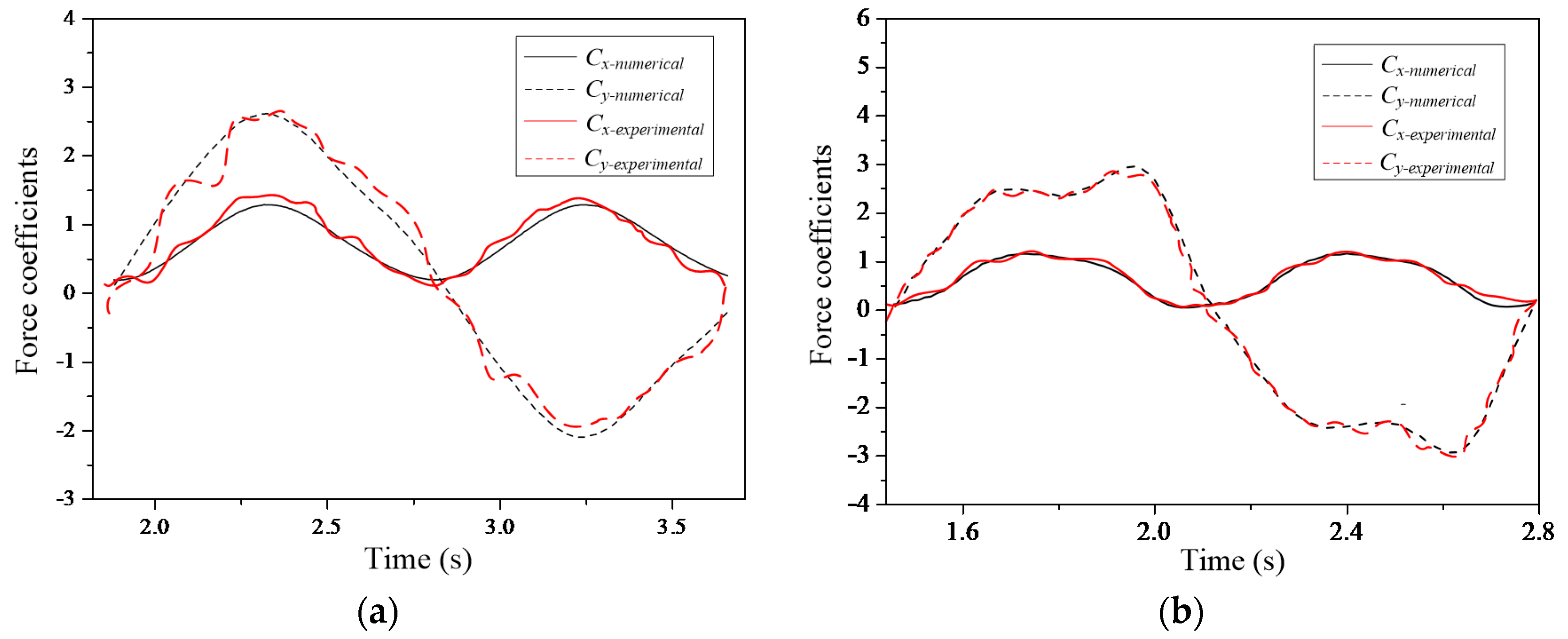
4. Experiments and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wu, T.Y. Fish Swimming and Bird/Insect Flight. Annu. Rev. Fluid Mech. 2011, 43, 25–58. [Google Scholar] [CrossRef]
- Wen, L.; Wang, T.M.; Wu, G.H.; Liang, J.H. Hydrodynamic investigation of a self-propelled robotic fish based on a force-feedback control method. Bioinspir. Biomim. 2012, 7, 36012. [Google Scholar] [CrossRef] [PubMed]
- Yan, Q.; Wang, L.; Liu, B.; Yang, J.; Zhang, S. A novel implementation of a flexible robotic fin actuated by shape memory alloy. J. Bionic Eng. 2012, 9, 156–165. [Google Scholar] [CrossRef]
- Zhou, C.; Low, K.H. Design and locomotion control of a biomimetic underwater vehicle with fin propulsion. IEEE/ASME Trans. Mechatron. 2012, 17, 25–35. [Google Scholar] [CrossRef]
- Szymik, B.G.; Satterlie, R.A. Changes in wingstroke kinematics associated with a change in swimming speed in a pteropod mollusk, Clionelimacina. J. Exp. Biol. 2011, 214, 3935–3947. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.Z.; Zhang, X.; He, G.W. Numerical simulation of a three-dimensional fish-like body swimming with finlets. Commun. Comput. Phys. 2012, 11, 1323–1333. [Google Scholar] [CrossRef]
- Zhu, X.; He, G.; Zhang, X. Flow-mediated interactions between two self-propelled flapping filaments in tandem configuration. Phys. Rev. Lett. 2014, 113, 238105. [Google Scholar] [CrossRef] [PubMed]
- Deng, H.B.; Xu, Y.Q.; Chen, D.D.; Dai, H.; Wu, J.; Tian, F.B. On numerical modeling of animal swimming and flight. Comput. Mech. 2013, 52, 1221–1242. [Google Scholar] [CrossRef]
- Wu, J.; Shu, C. Simulation of three-dimensional flows over moving objects by an improved immersed boundary—Lattice Boltzmann method. Int. J. Numer. Methods Fluids 2012, 68, 977–1004. [Google Scholar] [CrossRef]
- Li, G.J.; Zhu, L.D.; Lu, X.Y. Numerical studies on locomotion perfromance of fish-like tail fins. J. Hydrodyn. 2012, 24, 488–495. [Google Scholar] [CrossRef]
- Zhu, L.; He, G.; Wang, S.; Miller, L.; Zhang, X.; You, Q.; Fang, S. An immersed boundary method based on the lattice Boltzmann approach in three dimensions, with application. Comput. Math. Appl. 2011, 61, 3506–3518. [Google Scholar] [CrossRef]
- Tian, F.B.; Luo, H.X.; Zhu, L.D.; Liao, J.C.; Lu, X.Y. An efficient immersed boundary-lattice Boltzmann method for the hydrodynamic interaction of elastic filaments. J. Comput. Phys. 2011, 230, 7266–7283. [Google Scholar] [CrossRef] [PubMed]
- Unger, R.; Haupt, M.C.; Horst, P.; Radespiel, R. Fluid–structure analysis of a flexible flapping airfoil at low Reynolds number flow. J. Fluids Struct. 2012, 28, 72–88. [Google Scholar] [CrossRef]
- Tian, F.B.; Lu, X.Y.; Luo, H.X. Propulsive performance of a body with a traveling-wave surface. Phys. Rev. E 2012, 86, 16304. [Google Scholar] [CrossRef] [PubMed]
- Borazjani, I.; Sotiropoulos, F. On the role of form and kinematics on the hydrodynamics of self-propelled body/caudal fin swimming. J. Exp. Biol. 2010, 213, 89–107. [Google Scholar] [CrossRef] [PubMed]
- Borazjani, I.; Sotiropoulos, F. Numerical investigation of the hydrodynamics of carangiform swimming in the transitional and inertial flow regimes. J. Exp. Biol. 2008, 211, 1541–1558. [Google Scholar] [CrossRef] [PubMed]
- Wolfgang, M.J.; Anderson, J.M.; Grosenbaugh, M.A.; Yue, D.K.P.; Triantafyllou, M.S. Near-body flow dynamics in swimming fish. J. Exp. Biol. 1999, 202, 2303–2327. [Google Scholar] [PubMed]
- Zhu, Q.; Wolfgang, M.J.; Yue, D.K.P. Three-Dimensional flow structures and vorticity control in fish-like swimming. J. Fluid Mech. 2002, 468, 1–28. [Google Scholar] [CrossRef]
- Izraelevitz, J.S.; Triantafyllou, M.S. Adding in-line motion and model-based optimization offers exceptional force control authority in flapping foils. J. Fluid Mech. 2014, 742, 5–34. [Google Scholar] [CrossRef]
- Hu, J.; Xiao, Q. Three-dimensional effects on the translational locomotion of a passive heaving wing. J. Fluids Struct. 2014, 46, 77–88. [Google Scholar] [CrossRef]
- Han, R.; Zhang, J.; Cao, L.; Lu, X. Propulsive performance of a passively flapping plate in a uniform flow. J. Hydrodyn. 2015, 27, 496–501. [Google Scholar] [CrossRef]
- Tang, C.; Lu, X. Self-propulsion of a three-dimensional flapping flexible plate. J. Hydrodyn. 2016, 28, 1–9. [Google Scholar] [CrossRef]
- Kim, D.; Gharib, M. Characteristics of vortex formation and thrust performance in drag-based paddling propulsion. J. Exp. Biol. 2011, 214, 2283–2291. [Google Scholar] [CrossRef] [PubMed]
- Shao, X.M.; Pan, D.Y. Hydrodynamics of a flapping foil in the wake of a D-section cylinder. J. Hydrodyn. 2011, 23, 422–430. [Google Scholar] [CrossRef]
- Cubero, S.N. Design concepts for a hybrid dwimming and walking vehicle. Procedia Eng. 2012, 41, 1211–1220. [Google Scholar] [CrossRef]
- Mantia, L.M.; Dabnichki, P. Effect of the wing shape on the thrust of flapping wing. Appl. Math. Model. 2011, 35, 4979–4990. [Google Scholar] [CrossRef]
- Mantia, L.M.; Dabnichki, P. Influence of the wake model on the thrust of oscillating foil. Eng. Anal. Bound. Elem. 2011, 35, 404–414. [Google Scholar] [CrossRef]
- Mantia, L.M.; Dabnichki, P. Added mass effect on flapping foil. Eng. Anal. Bound. Elem. 2012, 36, 579–590. [Google Scholar] [CrossRef]
- Heathcote, S.; Wang, Z.; Gursul, I. Effect of spanwise flexibility on flapping wing propulsion. J. Fluids Struct. 2008, 24, 183–199. [Google Scholar] [CrossRef]
- Zhu, Q.; Shoele, K. Propulsion performance of a skeleton-strengthened fin. J. Exp. Biol. 2008, 211, 2087–2100. [Google Scholar] [CrossRef] [PubMed]
- Zhou, K.; Liu, J.K.; Chen, W.S. Numerical study on hydrodynamic performance of bionic caudal fin. Appl. Sci. 2016, 6, 15. [Google Scholar] [CrossRef]
- Bhalla, A.P.S.; Griffith, B.E.; Patankar, N.A. A forced damped oscillation framework for undulatory swimming provides new insights into how propulsion arises in active and passive swimming. PLoS Comput. Biol. 2013, 9, e1003097. [Google Scholar] [CrossRef] [PubMed]
- Bhalla, A.P.S.; Bale, R.; Griffith, B.E.; Patankar, N.A. A unified mathematical framework and an adaptive numerical method for fluid–structure interaction with rigid, deforming and elastic bodies. J. Comput. Phys. 2013, 250, 446–476. [Google Scholar] [CrossRef]
- Neveln, I.D.; Bale, R.; Bhalla, A.P.S.; Curet, O.M.; Patankar, N.A.; Maclver, M.A. Undulating fins produce off-axis thrust and flow structures. J. Exp. Biol. 2014, 217, 201–213. [Google Scholar] [CrossRef] [PubMed]





© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, K.; Liu, J.; Chen, W. Study on the Hydrodynamic Performance of Typical Underwater Bionic Foils with Spanwise Flexibility. Appl. Sci. 2017, 7, 1120. https://doi.org/10.3390/app7111120
Zhou K, Liu J, Chen W. Study on the Hydrodynamic Performance of Typical Underwater Bionic Foils with Spanwise Flexibility. Applied Sciences. 2017; 7(11):1120. https://doi.org/10.3390/app7111120
Chicago/Turabian StyleZhou, Kai, Junkao Liu, and Weishan Chen. 2017. "Study on the Hydrodynamic Performance of Typical Underwater Bionic Foils with Spanwise Flexibility" Applied Sciences 7, no. 11: 1120. https://doi.org/10.3390/app7111120
APA StyleZhou, K., Liu, J., & Chen, W. (2017). Study on the Hydrodynamic Performance of Typical Underwater Bionic Foils with Spanwise Flexibility. Applied Sciences, 7(11), 1120. https://doi.org/10.3390/app7111120





